Конус метрический: ГОСТ 25557-2016 от 01.01.2018 Конусы инструментальные. Основные размеры

alexxlab | 05.07.2023 | 0 | Разное

Содержание

Конус Морзе — РИНКОМ

Главная

Статьи

Конус Морзе Конус Морзе

13 декабря 2021

Гирин Кирилл

Конус Морзе – это вспомогательное приспособление, используемое для фиксации промышленного инструмента. Устройство обеспечивает быструю смену оснастки без потери точности выполнения операций. Прототип изделия был изготовлен в 1864 году, с тех пор оно успешно применяется в промышленности.

В материале:

Актуальные стандарты
Разновидности хвостовиков
- Хвостовики с лапкой
- Хвостовики с резьбой
- Хвостовики с фиксацией трением
- Условные обозначения хвостовиков
Метрические конусы Морзе
Укороченные конусы Морзе
Альтернативные решения
- Конусы 7:24
- Конусы HSK
- CAPTO
Переходники

Актуальные стандарты

Размеры конусов Морзе зависят от их исполнения. В продаже представлены изделия 8 типоразмеров – от КМ0 до КМ7. Характеристики каждого типоразмера прописаны в отраслевых нормативах. Там же отображается специфика совместимого оборудования.

Рис. 1 Конус Морзе с патроном и без него

Отечественные и зарубежные стандарты, регламентирующие изготовление конусов Морзе:

ISO 296;
DIN 228;
ГОСТ 25557-2016.

Конусы Морзе по ГОСТ представлены не всеми типоразмерами. В российском стандарте отсутствуют изделия, относящиеся к категории КМ7. Они заменены конусами №80, несовместимыми с аналогами зарубежного производства.

Разновидности хвостовиков

В продаже представлены токарные конусы Морзе с хвостовиками нескольких типов. Элементы различаются спецификой исполнения и особенностями фиксации.

Хвостовики с лапкой

Хвостовики с лапкой фиксируются путем заклинивания. Лапка попадает в соответствующий паз шпинделя, обеспечивая надежное крепление компонента.

Она исключает проворачивание изделия, существенно упрощает его извлечение при необходимости.

Рис. 2 Конус Морзе с патроном и хвостовиком с лапкой

Хвостовики с резьбой

Хвостовики с резьбой вкручиваются в шпиндель, надежно фиксируются в посадочном проеме. Размер и тип резьбы определяются конструктивным исполнением.

Рис. 3 Конус Морзе с патроном и резьбовым хвостовиком

Хвостовики с фиксацией трением

Тип хвостовиков, не содержащих лапок и резьбы. Удержание изделия осуществляется за счет сил трения, возникающих при плотном контакте элементов конуса и шпинделя.

Рис. 4 Конус Морзе с патроном, фиксирующийся за счет трения

Условные обозначения хвостовиков

На хвостовиках конусов Морзе могут присутствовать условные обозначения, определяющие специфику их конструкции.

Обозначения хвостовиков внутреннего типа:

BI –с пазом;
AI –с отверстием по оси;
BIK –с пазом и проемом для ОЖ;
AIK – с отверстием и проемом для ОЖ.

Обозначение хвостовиков наружного типа:

BE – с лапкой;
АЕ – с отверстием;
BEK –с лапкой и проемом для ОЖ;
АЕК – с резьбой и проемом для ОЖ.

Маркировка конуса Морзе для станков также указывается в сопроводительной документации.

Метрические конусы Морзе

Метрические конусы созданы для расширения модельного ряда существующих изделий. Угол конуса Морзе в данном исполнении составляет 1°25’56″. Продукция обозначается номером или буквами «КМ» с привязкой к размеру наибольшего диаметра.

Таблица №1. Размеры конусов Морзе метрического типа

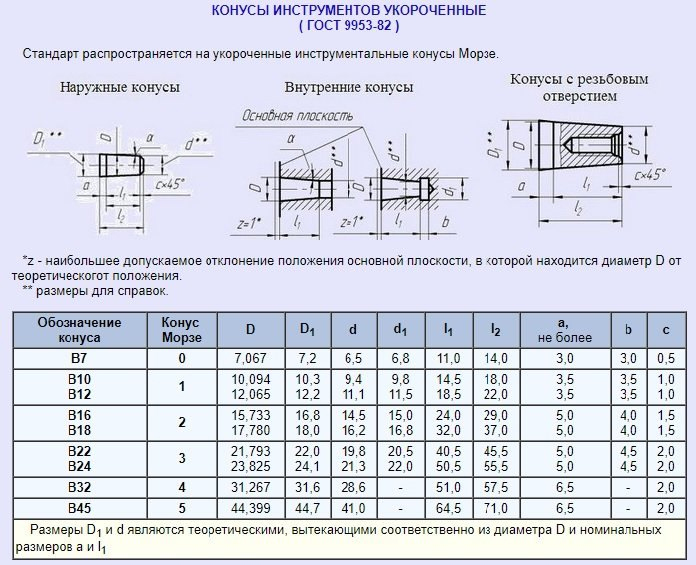
Укороченные конусы Морзе

Для решения ряда производственных задач длина классического конуса является чрезмерной. В данном случае целесообразно использование укороченных изделий. Длина таких конусов в 2 раза меньше оригинальной. Они оперативно фиксируются в шпинделе, позволяют качественно выполнять работы в ограниченном пространстве.

Укороченные модели пропорциональны конусам КМ, имеют соответствующие обозначения:

В7 – КМ0 длиной 14 мм;
В10 – КМ1 длиной 18 мм;
В12 – КМ1 длиной 22 мм;
В16 – КМ2 длиной 24 мм;
В18 – КМ 2 длиной 32 мм;
В22 – КМ3 длиной 45 мм;
В24 – КМ3 длиной 55 мм;
В32 – КМ4 длиной 57 мм.

Наиболее крупные конусы – В45. Они являются укороченной версией КМ5, имеют длину 71 мм.

Рис. 5 Конус 7:24

Альтернативные решения

В качестве замены конусов Морзе созданы аналогичные продукты. Они обладают рядом уникальных качеств, полностью или частично заменяют классические решения.

Конусы 7:24

Конусы 7:24 созданы для станков с возможность автоматизированной смены инструмента. Изделия лишены недостатков типовых конусов, связанных с заклиниванием, большими размерами и недостаточным контактом осевого упора.

Рис. 6 Конус 7:24

Продукция предназначена для предприятий с высокой степенью оснащенности, изготавливается в разных странах. Производители используют различные нормативы при производстве инструментальных конусов.

ISO 7388. Международный стандарт, применяемый многими предприятиями ЕС.
ГОСТ 25857-2014. Отечественный норматив, аналог стандарта ISO. Основные отличия кроются в параметрах используемых материалов.
DV и SK. Нормы, применяемые в Германии.
ANSI B15.18. Нормативные документы, используемые американскими производителями.
JIS B6339. Японская вариация инструментальных конусов. Размерность изделий определяется в дюймовой системе исчисления.

NFE 62540. Стандарт, используемый французскими производителями.
IS 2340. Индийский стандарт.

При обозначении типоразмеров изделий используются цифры от 10 до 80. Шаг градации равен 5.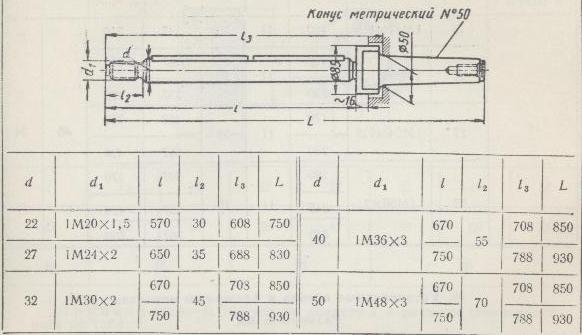 Ниже представлена таблица размеров инструментальных конусов, где D – максимальный диаметр конусного проема, L – его глубина, а DF – диаметр фланца.

Таблица №2. Размеры инструментальных конусов

Конусы HSK

Конусы типа HSK ориентированы на фрезерные станки. Продукция изготавливается в соответствии с ГОСТ Р 12164 и DIN 69893. Изделия обозначаются буквами от А до F, в наименовании прописывается диаметр фланца (минимальное значение – 25 мм, максимальное – 160 мм).

Преимущества решений серии HSK:

максимально быстрая замена металлорежущего инструмента;

умеренный вес;
возможность работы с резцами токарного типа;
прекрасная повторяемость;
высокие показатели жесткости.

Для работы с квадратными резцами требуются переходные элементы. Резцы некоторых производителей сразу имеют хвостовик HSK.

Рис.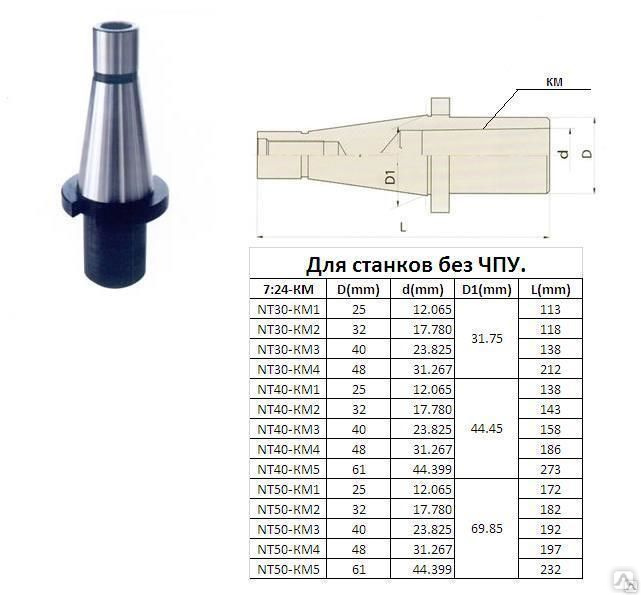 7 Продукция серии HSK

CAPTO

Конусы CAPTO позиционируются как премиальный аналог изделий серии HSK. Продукция выпускается согласно ISO 26623, имеет треугольное сечение. Угол поверхности посадки аналогичен классическим конусам. Изделие надежно фиксируется в рабочем проеме, обеспечивает хорошую повторяемость в различных осях.

Продукция линейки CAPTO оптимальна для черновой и получерновой обработки. Она обеспечивает высокую жесткость соединения, что может привести к преждевременному износу шпинделя при значительной нагрузке.

В модельном ряде производителя присутствует 6 конусов. Изделия имеют маркировку от С3 до С10 , диаметр рабочего фланца составляет от 32 до 100 мм.

Переходники

При работе с конусами используются переходные оправки и переходные втулки на конус Морзе. Они упрощают проведении работ, исключая покупку дополнительной оснастки и инструмента.

Рис. 8 Переходная втулка с КМ2 на КМ3

Специалисты рекомендуют приобретать сертифицированные конусы и переходные элементы.

Это обеспечит качественное выполнение работ, снизит вероятность поломок, сократит производственные издержки и расходы на дополнительную обработку заготовок.

Больше полезной информации

Полезные обзоры и статьи

Все статьи

4 апреля 2023

Фрезерование концевыми фрезами

30 июня 2022

Коническая резьба

11 января 2021

Классификация калибров для контроля деталей: особенности измерительного инструмента и ГОСТы

17 апреля 2019

Виды концевых фрез

Все статьи

Подписывайтесь на нас

Присылаем скидки на инструмент и только полезную информацию!

Не нашли нужной позиции в каталоге?

Мы готовы изготовить и поставить уникальные виды инструмента специально под ваш заказ!

Заказать

Каталог

Корзина Сравнить

Вход

Мы используем файлы cookie. Они помогают улучшить ваше взаимодействие с сайтом.

Принимаю

Конус морзе | это… Что такое Конус морзе?

ТолкованиеПеревод

Конус морзе

Конус инструментальный — конический хвостовик инструмента (сверло, зенкер, фреза, развёртка) и коническое отверстие соответствующего размера (гнездо) в шпинделе или задней бабке станка. Предназначено для быстрой смены инструмента с высокой точностью центрирования и надёжностью. Существуют различные конусы.

Содержание

1 Инструментальные метрические конусы и конусы Морзе
- 1.1 Конус Морзе
2 Конус 1:50
3 Конус 1:30
4 Конус 1:20
5 Конус 1:10
6 Конус 1:7
7 Конус 1:3
8 Конус 1:1,866
9 Конус 1:0,866
10 Конус 1:0,652
11 Конус 1:24
12 Конус 1:16
13 Конус 7:64
14 Конус 1:4
15 Конус 7:24
16 См. также
17 Примечания

Инструментальные метрические конусы и конусы Морзе

Инструментальные метрические конусы и конусы Морзе в настоящее время объединены в один стандарт (ГОСТ 25557-82 — Конусы инструментальные. Основные размеры.), это сложилось исторически из-за широкого распространения конуса Морзе и вследствие расширения диапазона размеров инструментальных конусов. Конструктивных различий между ними нет, основное различие в конусности; в конусе Морзе используется переменная конусность от 1:19,002 до 1:20,047, в метрических инструментальных конусах используется постоянная конусность 1:20

Конус Морзе

Один из самых широко применяемых креплений инструмента, подразделяется на восемь размеров, от 0 до 7^[1]^[2]^[3] и девять размеров укороченных конусов Морзе (B7, B10, B12, B16, B18, B22, B24, B32, B45)^[4]. Конус Морзе был предложен Стивеном А. Морзе (Stephen A. Morse) (также изобретатель спирального сверла) приблизительно в 1864.

Схема инструментального конуса (наружные конусы с лапкой, наружные конусы без лапки, внутренние конусы(гнёзда)).

Таблица 1

Размеры наружного и внутреннего конуса (по ГОСТ 25557-82), мм
	Обозначение конуса	Конусность	D	D₁	d	d₁	d₂	d_{3 max}	d_{4 max}	d₅	l_{1 max}	l_{2 max}	l_{3 max}	l_{4 max}	l_{5 min}	l₆
Метрический	4	1:20	4	4,1	2,9	–	–	–	2,5	3	23	25	–	–	25	21
Метрический	6	1:20	6	6,2	4,4	–	–	–	4	4,6	32	35	–	–	34	29
Морзе	0	1:19,212	9,045	9,2	6,4	–	6,1	6	6	6,7	50	53	56,3	59,5	52	49
	1	1:20,047	12,065	12,2	9,4	M6	9	8,7	9	9,7	53,5	57	62	65,5	56	52
	2	1:20,020	17,780	18	14,6	M10	14	13,5	14	14,9	64	69	75	80	67	62
	3	1:19,922	23,825	24,1	19,8	M12	19,1	18,5	19	20,2	80,1	86	94	99	84	78
	4	1:19,254	31,267	31,6	25,9	M16	25,2	25,2	24	26,5	102,5	109	117,5	124	107	98
	5	1:19,002	44,399	44,7	37,6	M20	36,5	35,7	35,7	38,2	129,5	136	149,5	156	135	125
	6	1:19,180	63,348	63,8	53,9	M24	52,4	51	51	54,6	182	190	210	218	188	177
Метрический	80	1:20	80	80,4	70,2	M30	69	67	67	71,5	196	204	220	228	202	186
	100	1:20	100	100,5	88,4	M36	87	85	85	90	232	242	260	270	240	220
	120	1:20	120	120,6	106,6	M36	105	102	102	108,5	268	280	300	312	276	254
	160	1:20	160	160,8	143	M48	141	138	138	145,5	340	356	380	396	350	321
	200	1:20	200	201	179,4	M48	177	174	174	182,5	412	432	460	480	424	388

Продолжение табл. 1

Размеры наружного и внутреннего конуса (по ГОСТ 25557-82), мм
	Обозначение конуса	a	b	e	c	R_max	r	t_max	i (min)	g	h
Метрический	4	2	–	–	–	–	–	2	–	2,2	8
Метрический	6	3	–	–	–	–	–	3	–	3,2	12
Морзе	0	3	3,9	10,5	6,5	4	1	4	–	3,9	15
	1	3,5	5,2	13,5	8,5	5	1,2	5	16	5,5	19
	2	5	6,3	16	10,5	6	1,6	5	24	6,3	22
	3	5	7,9	20	13	7	2	7	28	7,9	27
	4	6,5	11,9	24	16	8	2,5	9	32	11,9	32
	5	6,5	15,9	29	19	10	3	10	40	15,9	38
	6	8	19	40	27	13	4	16	50	19	47
Метрический	80	8	26	48	24	24	5	24	65	26	52
	100	10	32	58	28	30	5	30	80	32	60
	120	12	38	68	32	36	6	36	80	38	70
	160	16	50	88	40	48	8	48	100	50	90
	200	20	62	108	48	60	10	60	100	62	110

Стандарты:

ГОСТ 25557-82– Конусы инструментальные. Основные размеры.
ГОСТ 9953-82 — Конусы инструментов укороченные. Основные размеры.

Конус 1:50

Конусность 1 : 50 имеют установочные штифты, применяемые при необходимости дополнительного скрепления двух деталей зафиксированных резьбовым соединением, чтобы они не могли перемещаться одна относительно другой. Установочные штифты вставляются в отверстия, просверленные и развернутые одновременно в обеих деталях, после их сборки. Конусность 1:50 соответствует углу уклона 0°34′

Конус 1:30

Конус 1:20

Метрические конусы инструментов. Отверстия в шпинделях станков.

Конус 1:10

Конус 1:7

Конус 1:3

Конус 1:1,866

Конус 1:0,866

Конус 1:0,652

Конус 1:24

Конус 1:16

Конус 7:64

Конус 1:4

Конус 7:24

См. также

Конусное соединение

Примечания

↑ Техническая энциклопедия под ред. Мартенс Л. К. т.20 М.: Советская энциклопедия 1933 г.
↑ ГОСТ 25557-82 использует 7 размеров конусов, от 0 до 6.
↑ По таблице размеров конусов Морзе предоставленной на сайте MORSE CUTTING TOOLS предоставлено 9 размеров конусов.
↑ По ГОСТ 9953-82 — Конусы инструментов укороченные. Основные размеры.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

Конус аренатус
Контртеррористическая операция на Северном Кавказе

Полезное

домашнее задание и упражнения – Метрика конуса

Задавать вопрос

спросил 1 год, 3 месяца назад

Изменено 1 год, 3 месяца назад

Просмотрено 377 раз

$\begingroup$

Я пытаюсь решить следующую задачу (Eric Poisson’s The Mechanics of Black Hole Physics , Chapter 1, Problem 1):

Поверхность двумерного конуса вложена в трехмерное плоское пространство. Угол раскрытия конуса равен $2 \alpha$. Точки конуса, находящиеся на одинаковом расстоянии $r$ от вершины, образуют окружность, а $\phi$ — это угол, проходящий вдоль окружности.
Запишите метрику конуса через координаты $r$ и $\phi$. 92(\phi)$ всегда положительно;
Для постоянного радиуса у нас есть обычное уравнение периметра для окружности.
Причины, по которым это неверно:
Угол $2 \alpha$ не указан в метрике;
Я не уверен, но не должна ли эта метрика быть сингулярной при $r = 0$ из-за координатной сингулярности?
Я был бы рад, если бы был дан не ответ, а предположение, что может быть правильным или неправильным.
домашние задания и упражнения
общая теория относительности
дифференциальная геометрия
метрика-тензор
$\endgroup$
$\begingroup$
Ваша первая причина не согласиться с метрикой, которую вы предполагаете, довольно веская. 2$ (другими словами, вы не можете нанести на карту вершину конуса с помощью дифференцируемой карты). 92,$$ где $\mathrm{d}R = 0$, поскольку $R$ — константа.

Наконец, позвольте мне указать на другую проблему с вашей метрикой: при константе $r$ она не сводится к метрике окружности. На самом деле, я никогда не видел, чтобы кто-нибудь «угадывал» метрику многообразия. Обычно мы получаем его, вычисляя индуцированную метрику, когда эти методы доступны. В теории относительности мы часто либо постулируем метрику, либо решаем уравнения поля Эйнштейна.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Замечания о конусных метрических пространствах и теоремах о неподвижной точке стягивающих отображений | Теория фиксированной точки и алгоритмы для науки и техники

Замечания о конусных метрических пространствах и теоремах о неподвижной точке сжимающих отображений

Скачать PDF

Исследовательская статья
Открытый доступ
Опубликовано: 06 июня 2010 г.

Мохамед А Хамси ^1,2

Теория фиксированной точки и приложения том 2010 , Номер статьи: 315398 (2010) Процитировать эту статью

4899 доступов
58 цитирований
Сведения о показателях

Abstract

Мы обсуждаем недавно введенное понятие конусных метрических пространств. Мы также обсуждаем результаты существования неподвижных точек сжимающих отображений, определенных на таких метрических пространствах. В частности, мы показываем, что большинство новых результатов являются просто копиями классических.

1. Введение

Конусные метрические пространства были введены в [1]. Аналогичное понятие рассматривал также Жепецки в [2]. Тщательно определив сходимость и полноту в конических метрических пространствах, авторы доказали некоторые теоремы о неподвижных точках сжимающих отображений. Недавно в [3–8] появилось больше результатов о неподвижных точках в конусных метрических пространствах. Топологические вопросы в конусо-метрических пространствах изучались в [6], где было доказано, что всякое конусо-метрическое пространство является топологическим пространством с первой счетностью. Следовательно, непрерывность эквивалентна секвенциальной непрерывности, а компактность эквивалентна секвенциальной компактности. Следует упомянуть пионерскую работу Кильо [9]. ], который ввел понятие обобщенных метрических пространств. Его подход оказался очень успешным и использовался многими (см. ссылки в [10]). Мы считаем, что конические метрические пространства являются частным случаем обобщенных метрических пространств. В этой работе мы вводим структуру метрического типа в конусных метрических пространствах и показываем, что классические доказательства почти идентичны в этих метрических пространствах. Этот подход предполагает, что любое распространение известного результата о фиксированной точке на конические метрические пространства является излишним. Более того, базовое банахово пространство и связанное с ним подмножество конусов не являются необходимыми.

Для получения дополнительной информации о метрической теории с фиксированной точкой читатель может обратиться к книге [11].

2. Основные определения и результаты

Сначала давайте начнем с некоторых основных определений.

Определение 2.1.

Позвольте быть реальным банаховым пространством с нормой и подмножеством . Тогда называется конусом тогда и только тогда, когда

(1) замкнуто, непусто и , где – нулевой вектор в ;

(2)если , и , то ;

(3)если и , то .

Учитывая конус в банаховом пространстве, мы определяем частичный порядок относительно

(2.1)

Мы также пишем всякий раз и , а будем обозначать (где Int() обозначает внутреннюю часть ). Конус называется нормальным, если существует такое число , что для всех имеем

(2.2)

Наименьшее положительное число, удовлетворяющее этому неравенству, называется нормальной константой . Конус называется правильным, если всякая ограниченная сверху возрастающая последовательность сходится. Эквивалентно, конус называется правильным, если всякая ограниченная снизу убывающая последовательность сходится. Правильные конусы нормальные, и существуют нормальные конусы, которые не являются правильными.

Банахово пространство и конус будут опущены.

Определение 2.2.

Конусное метрическое пространство – это упорядоченная пара , где – любое множество и – отображение, удовлетворяющее

(1), то есть , для всех , и тогда и только тогда, когда ;

(2) для всех ;

(3), для всех .

Конвергенция определяется следующим образом.

Определение 2.3.

Позвольте быть метрическим пространством конуса, позвольте быть последовательностью в и . Если для любого с существует такое, что для всех , то называется сходящимся. Будем говорить сходится и писать .

Легко показать, что предел сходящейся последовательности уникален. Последовательности Коши и полнота определяются определением

2.4.

Позвольте быть метрическим пространством конуса, быть последовательностью в . Если для любого с существует такое, что для всех , то называется последовательностью Коши. Если каждая последовательность Коши сходится в , то называется полным конусным метрическим пространством.

Основные свойства сходящихся последовательностей и последовательностей Коши можно найти в [1]. Фактически свойства и их доказательства идентичны классическим метрическим. Поскольку эта работа касается свойства неподвижной точки отображений, нам понадобится следующее свойство.

Определение 2.5.

Позвольте быть метрическим пространством конуса. Отображение называется липшицевым, если существует такое, что

(2.3)

для всех . Наименьшая постоянная, которая удовлетворяет приведенному выше неравенству, называется константой Липшица , обозначаемой . В частности, это сокращение, если .

Как мы упоминали ранее, конусные метрические пространства имеют структуру метрического типа. Действительно, мы имеем следующий результат.

Теорема 2.6.

Позвольте быть метрическим конусом над банаховым пространством с конусом, который является нормальным с нормальной постоянной . Отображение, определяемое удовлетворяет следующим свойствам:

(1) тогда и только тогда, когда ;

(2), для любого ;

(3), для любых точек , .

Доказательство.

Доказательства (1) и (2) просты и оставлены читателю. Для доказательства (3) пусть – любые точки в . Используя неравенство треугольника, которому удовлетворяет , получаем

(2. 4)

Поскольку нормально с константой, получаем

(2.5)

откуда следует

(2.6)

Это завершает доказательство теоремы.

Обратите внимание, что свойство (3) обескураживает, поскольку оно не дает классического неравенства треугольника, которому удовлетворяет расстояние. Но есть много примеров, когда неравенство треугольника не выполняется (см., например, [12]).

Приведенный выше результат предлагает следующее определение.

Определение 2.7.

Пусть будет множество. Позвольте быть функцией, которая удовлетворяет

(1) тогда и только тогда, когда ;

(2), для любого ;

(3), для любых точек , , для некоторой константы .

Пара называется пространством метрического типа.

Аналогично мы определяем сходимость и полноту в пространствах метрического типа.

Определение 2.8.

Позвольте быть пространством метрического типа.

(1)Последовательность сходится тогда и только тогда, когда .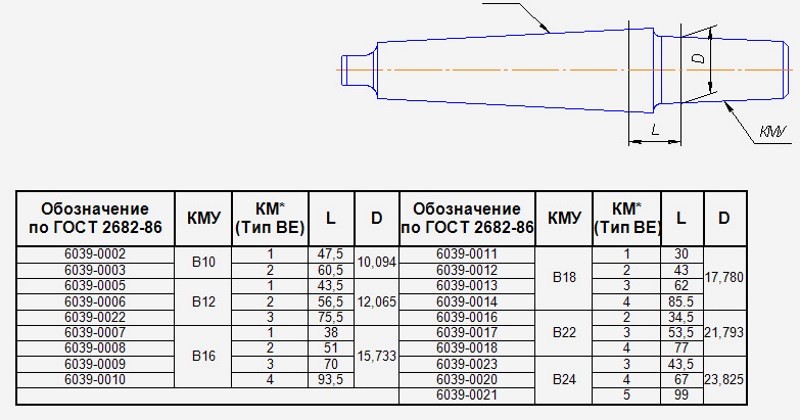

(2)Последовательность Коши тогда и только тогда, когда .

является полным тогда и только тогда, когда любая последовательность Коши в сходится.

3. Некоторые результаты с фиксированной точкой

Пусть будет карта. называется липшицевым, если существует константа такая, что

(3.1)

для любого . Наименьшую константу обозначим .

Теорема 3.1.

Позвольте быть полным пространством метрического типа. Пусть такое отображение является липшицевым для всех и что . Тогда имеет единственную неподвижную точку. Более того, для любого орбита сходится к .

Доказательство.

Пусть . Для любого имеем

(3.2)

Отсюда

(3.3)

Так как сходится, то . Это вынуждает быть последовательностью Коши. Так как полная, то сходится к некоторой точке . Сначала покажем, что это неподвижная точка . Так как

(3.4)

получаем

(3.5)

Если положить , то получим , или . Далее покажем, что имеет не более одной неподвижной точки.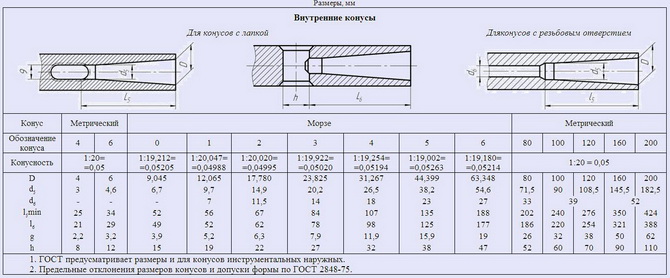 Действительно, пусть и две неподвижные точки . Тогда у нас есть

(3.6)

для любого . Так как , мы получаем , или . Поэтому имеем для любого , что завершает доказательство теоремы.

Условие необходимо, так как условию (3) удовлетворяет . На самом деле более естественным условием должно быть

() для любых точек , для некоторой константы .

Пример такого удовлетворения приведен ниже.

Пример 3.2.

Пусть – множество измеримых по Лебегу функций на таких, что

(3.7)

Определить с помощью

(3.8)

Тогда удовлетворяет следующим свойствам:

тогда и только тогда, когда ;

, для любого ;

, для любых точек.

В следующем результате мы рассматриваем случай пространств метрического типа, когда удовлетворяет . Напомним, что подмножество называется ограниченным, если .

Теорема 3.3.

Позвольте быть полным пространством метрического типа, где удовлетворяет вместо (3). Позвольте быть отображение такое, что является липшицевым для любых и .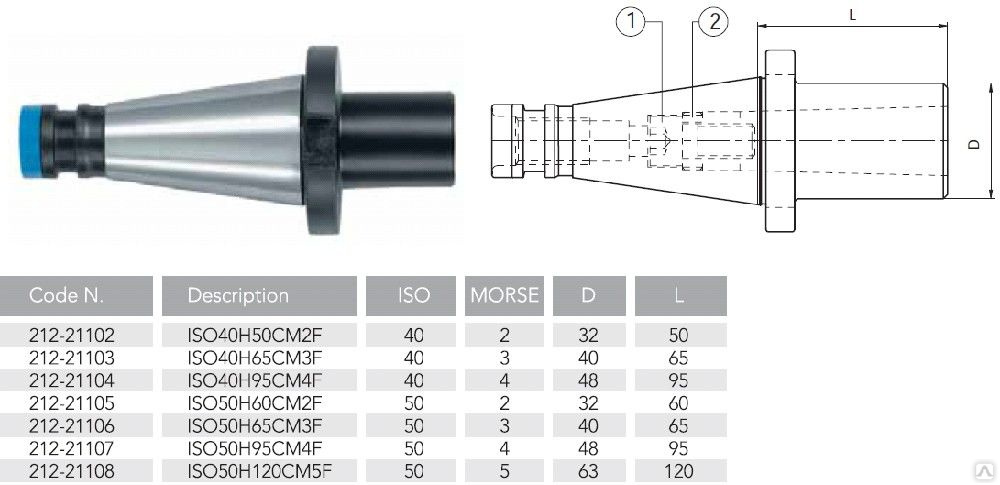 Тогда имеет единственную неподвижную точку тогда и только тогда, когда существует ограниченная орбита. Более того, если имеет неподвижную точку , то для любого , орбита сходится к .

Доказательство.

Ясно, что если имеет неподвижную точку, то его орбита ограничена. Обратно пусть такое, что ограничено, т. е. существует такое, что для любого . Пусть имеем

(3.9)

Так как , то последовательность Коши. Следовательно, сходится к некоторой точке, так как является полным. Оставшаяся часть доказательства проводится так же, как и в предыдущей теореме.

Связь между приведенными выше результатами и основными теоремами работы [1] дается в следующем следствии.

Следствие 3.4.

Позвольте быть метрическим конусом над банаховым пространством с конусом, который является нормальным с нормальной постоянной . Считать определяемым . Позвольте быть сокращением с константой . Тогда

(3.10)

для любого и . Следовательно, для любого . Поэтому сходится, что означает, что имеет единственную неподвижную точку , и любая орбита сходится к .

Из определения в приведенном выше Следствии мы легко видим, что -конвергенция и -конвергенция идентичны.

Замечание 3.5.

В [1] авторы привели пример отображения, которое является сокращением для, но не для евклидова расстояния. Из приведенного выше следствия мы видим, что . Так как не может быть меньше 1, то не может быть сокращения для . Поэтому приведенные выше теоремы были сформулированы в терминах .

Используя описанные выше идеи, можно доказать результаты о неподвижных точках для отображений, стягивающих орбиты, и получить результаты, подобные теореме, например, в [1].

Ссылки

Huang L-G, Zhang X: Конусные метрические пространства и теоремы о неподвижных точках сжимающих отображений. Журнал математического анализа и приложений 2007, 332 (2): 1468–1476. 10.1016/j.jmaa.2005.03.087
Статья MathSciNet МАТЕМАТИКА Google Scholar
“>
Жепецки Б: О теоремах о неподвижных точках типа Майя. Публикации Математического института 1980, 28(42): 179–186.
MathSciNet МАТЕМАТИКА Google Scholar
Abbas M, Jungck G: Общие результаты о неподвижных точках для некоммутирующих отображений без непрерывности в конусных метрических пространствах. Журнал математического анализа и приложений 2008, 341 (1): 416–420. 10.1016/j.jmaa.2007.09.070
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Илич Д., Ракочевич В.: Общие неподвижные точки для карт на конусном метрическом пространстве. Журнал математического анализа и приложений 2008, 341 (2): 876–882. 10.1016/j.jmaa.2007.10.065
Статья MathSciNet МАТЕМАТИКА Google Scholar
“>
Резапур С., Хамлбарани Р.: Некоторые примечания к статье: «Конусные метрические пространства и теоремы о неподвижных точках сжимающих отображений». Журнал математического анализа и приложений 2008, 345 (2): 719–724. 10.1016/j.jmaa.2008.04.049
Статья MathSciNet МАТЕМАТИКА Google Scholar
Туркоглу Д., Абулоха М.: Конусные метрические пространства и теоремы о неподвижных точках в диаметрально сжимающих отображениях. Acta Mathematica Sinica 2010, 26 (3):489–496.
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Туркоглу Д., Абулоха М., Абдельжавад Т.: ККМ-отображения в конусных метрических пространствах и некоторые теоремы о неподвижных точках. Нелинейный анализ: теория, методы и приложения 2010, 72 (1):348–353. 10.1016/j. na.2009.06.058
Статья MathSciNet МАТЕМАТИКА Google Scholar
Vetro P: Общие неподвижные точки в конусных метрических пространствах. Rendiconti del Circolo Matematico в Палермо. Серия II 2007, 56 (3):464–468. 10.1007/BF03032097
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Quillio A: Применение свойства Хелли к частично упорядоченным множествам. Журнал комбинаторной теории. Серия А 1983, 35 (2): 185–198. 10.1016/0097-3165(83)-7
Артикул MathSciNet МАТЕМАТИКА Google Scholar
Jawhari E, Misane D, Pouzet M: Ретракты: графы и упорядоченные множества с метрической точки зрения. В Комбинаторика и упорядоченные множества (Арката, Калифорния, 1985), Contemporary Mathematics . Том 57 . Американское математическое общество, Провиденс, Род-Айленд, США; 1986: 175–226.
Глава Google Scholar
Хамси М.А., Кирк В.А.: Введение в метрические пространства и теорию неподвижной точки, чистую и прикладную математику . Wiley-Interscience, Нью-Йорк, США; 2001:х+302.
Книга МАТЕМАТИКА Google Scholar
Хамси М.А., Козловский В.М., Райх С.: Теория неподвижных точек в модулярных функциональных пространствах. Нелинейный анализ: теория, методы и приложения 1990, 14 (11):935–953. 10.1016/0362-546X(90)
-S
Артикул MathSciNet МАТЕМАТИКА Google Scholar

Download references

Author information

Authors and Affiliations

Department of Mathematical Science, The University of Texas at El Paso, El Paso, TX, 79968, USA
MohamedA Khamsi
Department of Математика и статистика, Университет нефти и полезных ископаемых имени короля Фахда, PO.