Конусность на чертеже обозначение: Знак конусности
alexxlab | 09.05.2023 | 0 | Разное
Обозначение уклона и конусности
Уклоны
Уклон, величина, характеризующая наклон одной прямой линии к другой. Выражают дробью или в %.
– угол направлен в сторону уклона |
Рисунок 6.1
6.2 Конусность
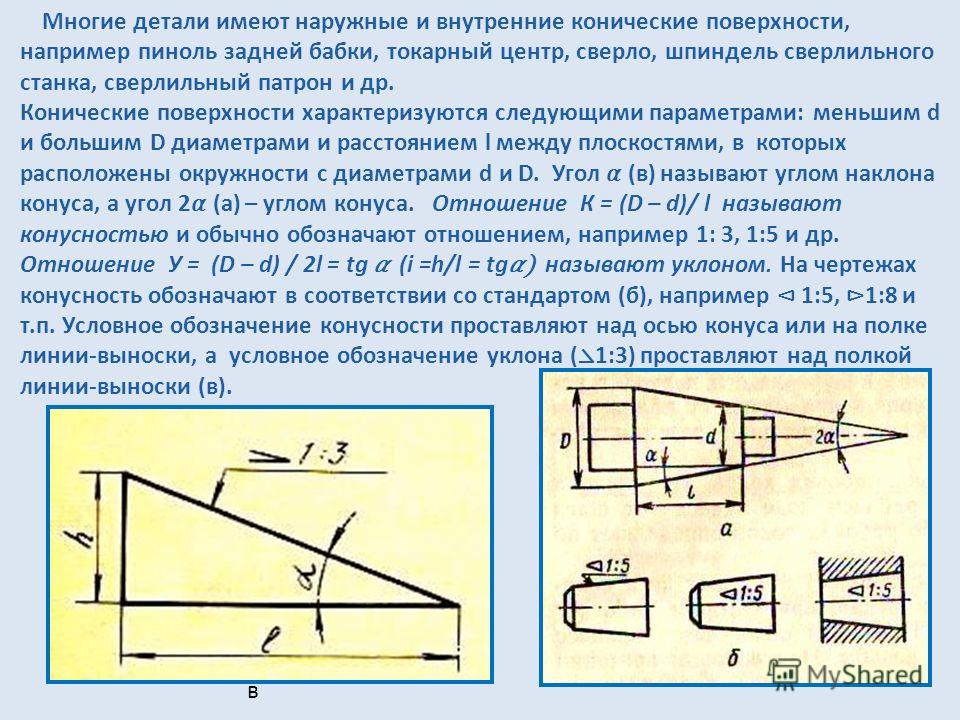
Конусность ( С ) – это отношение диаметра основания конуса к его высоте. Для усеченного конуса
Рисунок 6.2
Вопросы для самоконтроля.
Что такое уклон?
Что такое конусность?
Сопряжение линий и лекальные кривые
Сопряжения применяются во многих деталях машин для плавного перехода линий.
Для
построения сопряжений необходимо уметь
строить касательную в данной точке
окружности (рисунок 7.
Рисунок 7.1
в г
Рисунок 7.1
Изложенное позволяет легко уяснить последовательность решений задач на сопряжения, приведенных ни рисунке 7.2. ∂, е, ж, и, к.
∂ е ж
и к
Рисунок 7.2
Лекальные
кривые обводят при помощи лекал. Наиболее
часто применяют в технике следующее:
Наиболее
часто применяют в технике следующее:
7.1 Эллипс. Эллипсом называется замкнутая кривая, для которой сумма расстояний от любой точки до двух точек – фокусов эллипса – есть величина постоянная. Для построения эллипса проводят две концентрические окружности, диаметры которых равны осям эллипса (рисунок 7.3). Эти окружности делят на несколько равных частей (12-16). Через точки деления на большей окружности проводят вертикальные линии, через соответствующие точки деления на малой окружности – горизонтальные линии. Пересечение этих линий даст точки эллипса I, II, III
Рисунок 7.3
7.2Парабола. Параболой называется кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки, называемой фокусом параболы.
Даны
вершина параболы О, одна из точек параболы
D и направление оси ОС (рисунок 7.4). На
отрезках ОС и СD строят прямоугольник,
стороны этого прямоугольника ОВ и ВD
делят на произвольное одинаковое число
равных частей и нумеруют точки деления
согласно рис. Вершину О соединяют с
точками деления стороны ВD, а из точек
деления отрезка ОВ проводят прямые,
параллельные оси. Пересечение прямых,
проходящих через точки с одинаковыми
номерами, определяет ряд точек параболы
(другие способы построения параболы
см. в рекомендуемой литературе).
Вершину О соединяют с
точками деления стороны ВD, а из точек
деления отрезка ОВ проводят прямые,
параллельные оси. Пересечение прямых,
проходящих через точки с одинаковыми
номерами, определяет ряд точек параболы
(другие способы построения параболы
см. в рекомендуемой литературе).
7.3 Циклоида. Траектория точки А, принадлежащей окружности, перекатываемой без скольжения по прямой, называется циклоидой (рисунок 7.5). Для ее построения от исходного положения точки А на направляющей прямой отк5ладывают отрезок АА 1, равный длине данной окружности – 2πR. Окружность и отрезок АА1 делят на одинаковое число равных частей.
Восставляя
перпендикуляры из точек деления прямой
АА1 до пересечения с прямой, проходящей
через центр данной окружности параллельно
АА1,
намечают ряд последовательных положений
центра перекатываемой окружности О1,
О2,
О3,…,
О8. Описывая из этих центров окружности
радиуса R, отмечают точки пересечения
с ними прямых, проходящих параллельно
АА1 через
точки деления окружности 1, 2, 3, 4 и т.д.
Описывая из этих центров окружности
радиуса R, отмечают точки пересечения
с ними прямых, проходящих параллельно
АА1 через
точки деления окружности 1, 2, 3, 4 и т.д.
Рисунок 7.5
В
пересечении горизонтальной прямой,
проходящей через точку 1, с окружностью,
описанной из центра О
Синусоида. Для построения синусоиды делят окружность заданного радиуса на равные части (6, 8, 12, и т.д.) и на продолжении осевой линии от условного начала – точки А – проводят отрезок прямой АВ, равный 2πR. Затем прямую делят на такое же число равных частей, как и окружность (6, 8, 12 и т. Д.). Из точек окружности 1,2, 3, …, 12 проводят прямые линии параллельно выбранной прямой до пересечения с соответствующими перпендикулярами, восстановленными или опущенными из точек деления прямой.
 Полученные точки
пересечения (1/,
2 / ,
3/,
…, 12/)
и будут точками синусоиды с периодом
колебания, равным 2πR.
Полученные точки
пересечения (1/,
2 / ,
3/,
…, 12/)
и будут точками синусоиды с периодом
колебания, равным 2πR.
π
Рисунок 7.6
7.5 Эвольвента (развертка круга). Эвольвентой называется траектория, описываемая каждой точкой прямой линии, перекатываемой по окружности без скольжения.
В машиностроении по эвольвенте очерчивают профиль головок зубьев зубчатых колес.
Для
построения эвольвенты окружность
предварительно делят на произвольное
число n равных частей; в точках деления
проводят касательные к окружности,
направленные в одну сторону. На
касательной, проведенной через последнюю
точку деления, откладывают отрезок,
равный длине окружности 2πR,
и делят его на то же число n равных частей.
Откладывая на первой касательной одно
деление, равное
,
на второй – два, на третьей – три и т.д.,
получают ряд точек I, II, III,IV
и т.
Вопросы для самоконтроля.
На каких двух положениях геометрии основано построение сопряжений?
Перечислите элементы сопряжений.
Как построить эллипс?
Практическая работа по Инженерной графике на тему Конусность
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ БУРЯТИЯ
Государственное бюджетное профессиональное образовательное учреждение
«Авиационный техникум»
ОП.01. Инженерная графика
программы подготовки специалистов среднего звена (ППССЗ)
по специальности
15.02.08 Технология машиностроения (базовой подготовки)
Практическая работа №2:
Тема «Построение и обозначение конусности»
Улан-Удэ, 2019 г.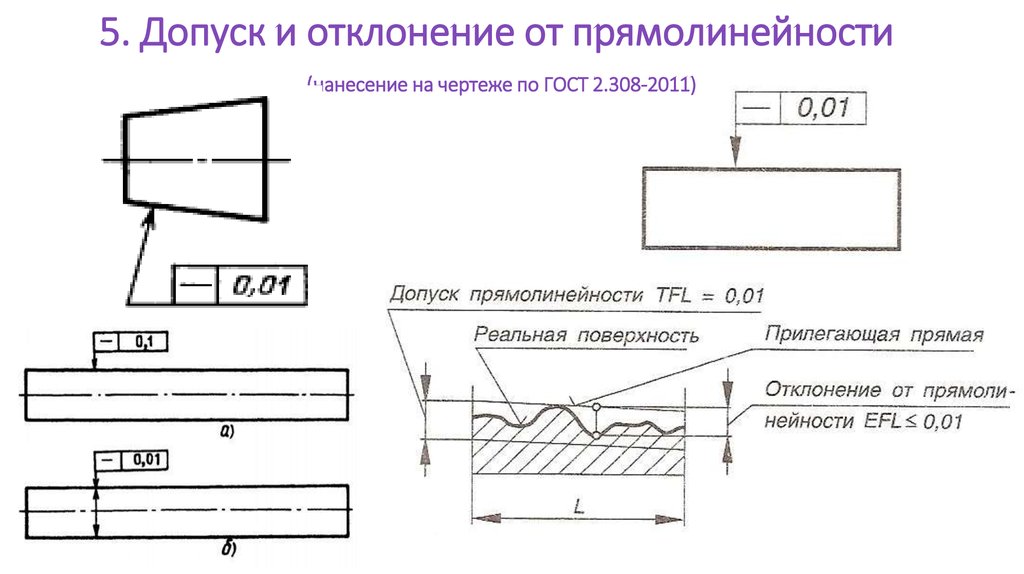
Тема «Построение и обозначение конусности»
Практическая работа №2:
Учебная цель: Научиться построению и определению конусности.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
выполнять чертежи технических деталей в ручной графике;
читать чертежи;
оформлять конструкторскую документацию в соответствии с технической документацией;
знать:
законы, методы, приемы проекционного черчения;
правила выполнения и чтения конструкторской и технологической документации;
правила оформления чертежей, геометрические построения и правила вычерчивания технических деталей;
требования стандартов Единой системы конструкторской документации (далее – ЕСКД) и Единой системы технологической документации (далее – ЕСТД) к оформлению и составлению чертежей и схем
Задачи практической работы:
На формате А4 выполнить основную надпись ГОСТ2. 104-2006.
104-2006.
Выполнить задание по варианту.
Расставить размеры по ГОСТ 2.307-68
Ответить на вопросы.
Сделать вывод от проделанной работы.
Рисунок 1 Образец готовой работы
Обеспеченность занятия:
Учебно-методическая литература:
Боголюбов С.К. Индивидуальные задания по курсу черчения: Учебное пособие для средних специальных заведений. 3-е изд., стереотипное. Перепечатка со второго издания 1994г.-М.: ООО ИД «Альянс», 2007.-368с.
В.П.Куликов, А.В.Кузин: учебник. Инженерная графика -3-е изд., испр.-М.: ФОРУМ, 2009.-368с.
Технические средства обучения:
Экран.
Практическое оборудование и инструменты:
Стол ученический;
Стул ученический;
Бумага для черчения ф.А4;
Карандаш чернографитный твердость М;
Карандаш чернографитный твердость Т;
Ластик;
Циркуль;
Точилка для карандашей механическая;
Линейка металлическая 30см.
Рабочая папка формата А4.
Практическая работа №2 в электронном или бумажном варианте.
Краткие теоретические и учебно-методические материалы по теме практической работы.
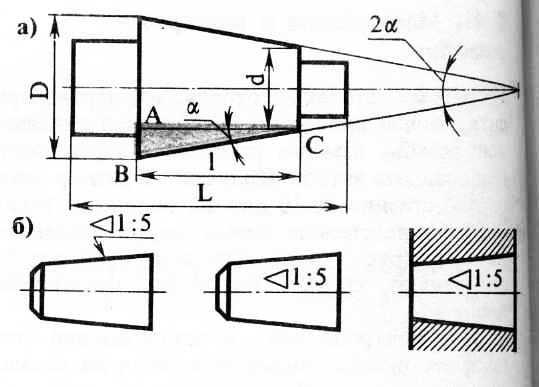
Конусностью – называется отношение диаметра основания конуса к его высоте. Рисунок 2 (б)
Обозначается конусность буквой с.
Рисунок 2 Виды конусности и ее обозначение
Если конус усеченный с диаметром основания D и d и высотой L, то конусность определяют по формуле:
c=
Если известны конусность с, диаметр одного из оснований конуса d и высота конуса L, можно определить второй диаметр конуса:
D=cL+d
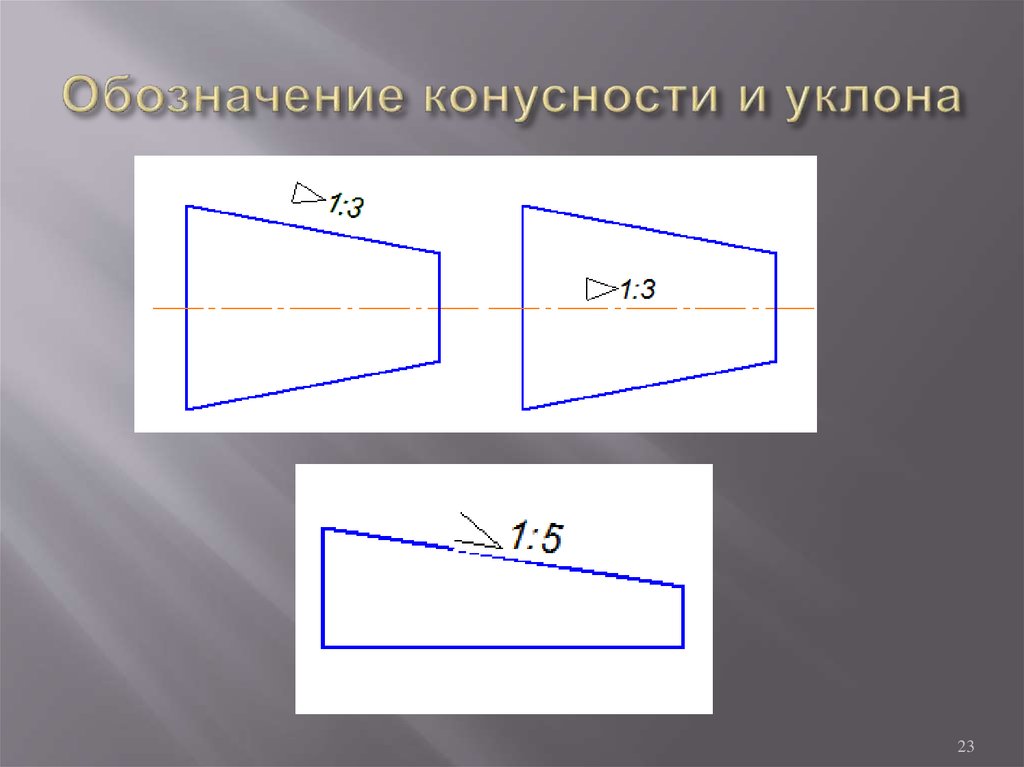
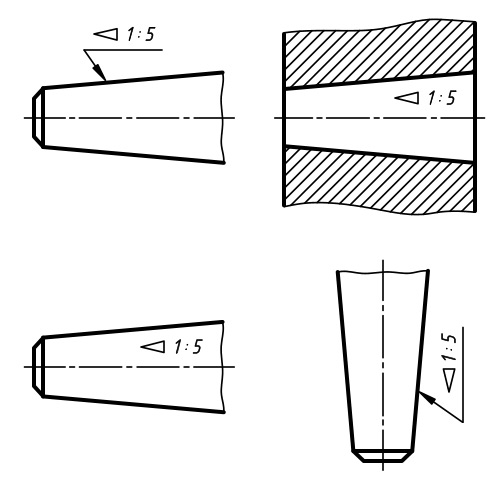
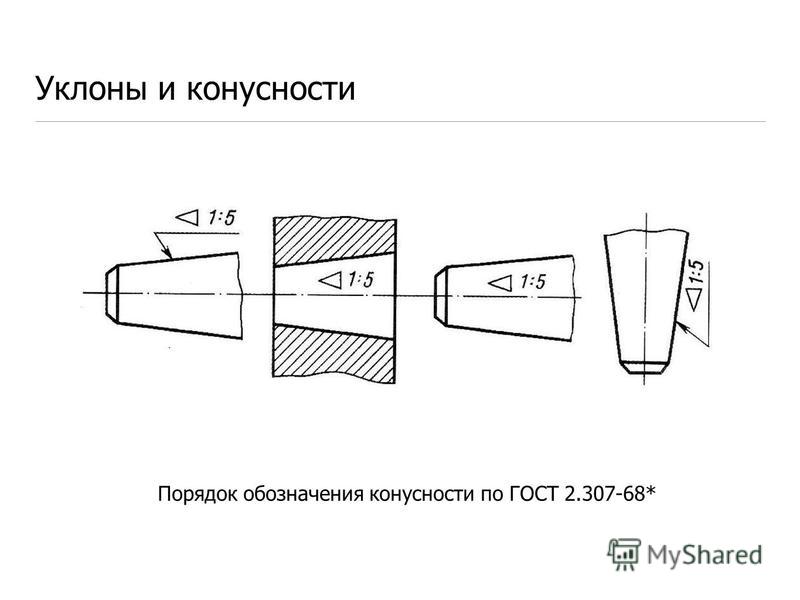
Перед размерным числом, характеризующим конусность, наносят знак “∆ ”, острый угол которого должен быть направлен в сторону вершины конуса
Знак конуса и конусность в виде соотношения следует наносить над осевой линией или на полке линии-выноски.
Рисунок 3 Обозначение конусности ГОСТ 2.307-68
По заданным размерам и величине конусности выполнены выполнить изображение детали. Обозначить конусность. Подсчитать размер отмеченный звездочкой: d* для пробки, l* для заглушки, D* для втулки.
Инструкция по выполнению практической работы
На формате А4 вычертить основную надпись ГОСТ2.104-2006.
Выполнить расчет конусности в зависимости от данных варианта.
Выполнить чертеж по полученным размерам.
Расставить размеры по ГОСТ 2.307-68
Заполнить основные надписи шрифтом ГОСТ 2.304-81 «шрифты чертежные» тип А.
Ответить на вопросы.
Сделать вывод от проделанной работы.
Вопросы для закрепления теоретического материала
к практической работе:
Что такое конусность?
По какой формуле находится конусность?
Какой буквой обозначается конусность?
Каким знаком обозначается конусность?
Как размещают знак конусности?
В какую сторону должен быть направлен острый угол знака про обозначении конусности?
Критерии оценки
Если чертеж выполнен верно и аккуратно – отлично
Если выполнен верно, есть незначительные помарки и замечания преподавателя – хорошо
Если менее пяти не верных размера – удовлетворительно.
Если чертеж содержит более пяти грубых ошибок – неудовлетворительно.
9
Справочное руководство по символам GD&Tот Sigmetrix
При определении геометрических размеров и допусков (GD&T) уникальный набор символов GD&T используется для определения взаимосвязей между элементами детали и эталонными измерениями. Дизайнеры и инженеры используют этот международный язык в своих чертежах для точного описания элементов деталей на основе размера, формы, ориентации и расположения.
Вы ищете обучение GD&T? Мы обучаем GD&T, поэтому каждый член команды:
- Понимает, что означает GD&T
- Понимает, как работает GD&T
- Понимает влияние GD&T на функционирование продукта, производство, контроль и сборку
- Понимает влияние GD&T на протяжении всего жизненного цикла продукта 3 чтобы ваш персонал по проектированию, производству, контролю, сборке, качеству и обслуживанию, а также ваши поставщики понимали GD&T, как это необходимо для достижения успеха и производства продукции самого высокого качества с наименьшими возможными затратами.
ПОСМОТРЕТЬ ВСЕ ДОСТУПНЫЕ КУРСЫ GD&T
Чтобы загрузить бесплатную копию Справочного руководства по символам GD&T, нажмите здесь.
| GD&T Symbol | Control Type | Name | Summary Description | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Form | Straightness | Controls the straightness of a feature in relation to собственная совершенная форма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Форма | Плоховая. | контролирует плоскостность поверхности по отношению к своей собственной идеальной форме | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Форма | Circulars форма независимыми поперечными сечениями | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Форма | Цилиндричность | Подобно круглости, но применяется одновременно ко всей поверхности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Профиль | Профиль поверхности | Управляет размером и формой элемента. Кроме того, он управляет положением и ориентацией при использовании опорной системы отсчета. Кроме того, он управляет положением и ориентацией при использовании опорной системы отсчета. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Профиль | Профиль линии | Аналогично профилю поверхности, применяется к поперечным сечениям элемента | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | PERPENDITITY | Ориентация | PERPENDILETY | Ориентация | PERPENDILETY | . перпендикулярно первичной системе отсчета своей системы отсчета|||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | Angularity | Ориентация управления элементом под определенным углом по отношению к первичному батору контроля | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ориентация | 7 | 5. 10032 10032 | 9 | . номинально параллелен первичной системе отсчета своей системы отсчета отсчета | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Местоположение | Положение | Управляет положением и ориентацией элемента относительно его системы отсчета от начала до конца | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Location | Concentricity | Controls concentricity of a surface of revolution to a central datum | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Location | Symmetry | Controls the symmetry of two surfaces about a central datum | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выступ | Круговой выбег | Управляет округлостью и соосностью каждого кругового сегмента поверхности независимо относительно коаксиальной базы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Биение | Общее биение | Контролирует округлость, прямолинейность, соосность и конусность цилиндрической поверхности относительно коаксиальной исходной точки вещь из прошлого! Уникальное современное решение Sigmetrix ускоряет процесс проектирования, экономя драгоценное время и сокращая производственные затраты, такие как брак и заказы на изменение, экономя тысячи долларов каждый год.
|
Программное обеспечение Sigmetrix для обучения, оптимизации и анализа допусков.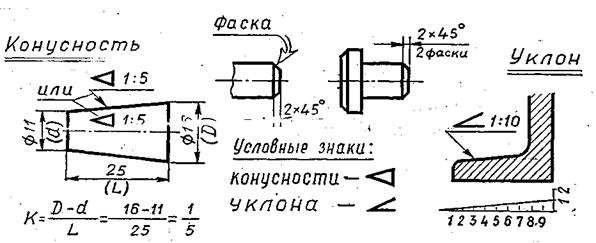 Для получения дополнительной информации о программном обеспечении GD&T Advisor или любых наших решениях и услугах для анализа допусков свяжитесь с нами по адресу [email protected] или через наш веб-сайт здесь.
Для получения дополнительной информации о программном обеспечении GD&T Advisor или любых наших решениях и услугах для анализа допусков свяжитесь с нами по адресу [email protected] или через наш веб-сайт здесь.
GD&T Символы и термины | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 Полученные точки
пересечения (1/,
2 / ,
3/,
…, 12/)
и будут точками синусоиды с периодом
колебания, равным 2πR.
Полученные точки
пересечения (1/,
2 / ,
3/,
…, 12/)
и будут точками синусоиды с периодом
колебания, равным 2πR. Каждое из наших профессионально разработанных программ использует всемирно признанные символы GD&T на протяжении всего процесса моделирования и составления отчетов.
Каждое из наших профессионально разработанных программ использует всемирно признанные символы GD&T на протяжении всего процесса моделирования и составления отчетов.
 От базовой плоскости или базовой
ось.
От базовой плоскости или базовой
ось.



 Базовое измерение всегда связано с элементом управления функцией.
кадра или опорной цели. (теоретически точный размер в ISO)
Базовое измерение всегда связано с элементом управления функцией.
кадра или опорной цели. (теоретически точный размер в ISO)
 Этот символ всегда отображается с вертикальным
нога влево.
Этот символ всегда отображается с вертикальным
нога влево. Этот символ
предшествует значению глубины без пробела между ними.
Этот символ
предшествует значению глубины без пробела между ними.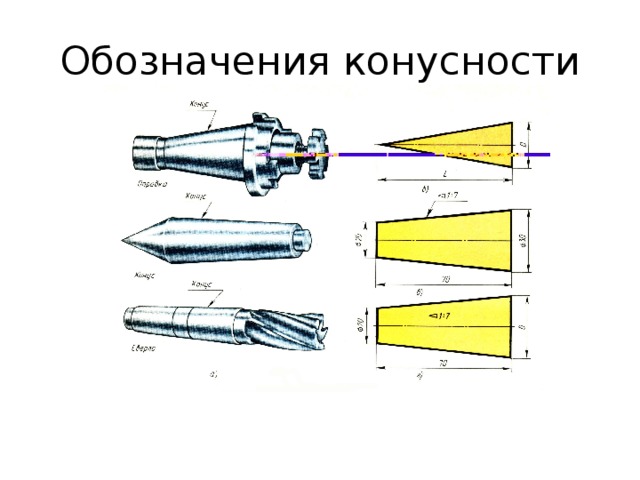 Символ
размещается над размером.
Символ
размещается над размером. Кроме того, позиционный допуск может использоваться для контроля
расположение сферического элемента относительно других элементов детали.
символ сферического диаметра предшествует размеру элемента
и значение позиционного допуска, чтобы указать сферическую зону допуска.
Кроме того, позиционный допуск может использоваться для контроля
расположение сферического элемента относительно других элементов детали.
символ сферического диаметра предшествует размеру элемента
и значение позиционного допуска, чтобы указать сферическую зону допуска.
 Применяя статистические допуски, допуски
отдельных компонентов могут быть увеличены или зазоры между сопрягаемыми
части могут быть уменьшены. Повышенная переносимость или улучшенная посадка могут уменьшить
производственных затрат или улучшения характеристик продукта, но должны быть
используется там, где будет использоваться соответствующий статистический контроль процесса.
Следовательно, следует уделить внимание указанию требуемых Cp и
/или Cpk или другие показатели производительности процесса.
Применяя статистические допуски, допуски
отдельных компонентов могут быть увеличены или зазоры между сопрягаемыми
части могут быть уменьшены. Повышенная переносимость или улучшенная посадка могут уменьшить
производственных затрат или улучшения характеристик продукта, но должны быть
используется там, где будет использоваться соответствующий статистический контроль процесса.
Следовательно, следует уделить внимание указанию требуемых Cp и
/или Cpk или другие показатели производительности процесса.