Косозубое зубчатое колесо: Косозубое зубчатое колесо – Большая Энциклопедия Нефти и Газа, статья, страница 1

alexxlab | 30.07.1986 | 0 | Разное

Зубчатое колесо цилиндрическое, коническое, прямозубое, косозубое

Зубчатое колесо (шестерня) цилиндрическое, коническое, прямозубое, косозубое и другие виды.

 

 

Зубчатое колесо или шестерня представляет собой деталь, которая в зависимости от применения может быть с разным количеством зубьев, выполненных в различных формах, располагающихся на цилиндрической или конической поверхности, и которая входит в зацепление с зубьями другого зубчатого колеса.

 

Зубчатое колесо (шестерня)

Цилиндрические зубчатые колеса (шестерни)

Конические зубчатые колеса (шестерни)

 

Зубчатое колесо (шестерня):

Зубчатое колесо или шестерня представляет собой деталь, которая в зависимости от применения может быть с разным количеством зубьев, выполненных в различных формах, располагающихся на цилиндрической или конической поверхности, и которая входит в зацепление с зубьями другого зубчатого колеса.

Зубчатые колеса или шестерни, за счет сцепления зубьев, выполняют следующие задачи: передача вращательного движения от одной детали к другой с изменением крутящего момента, увеличением или уменьшением скорости, а также преобразование вращательного движения в поступательное с помощью зубчатой рейки.

Зубчатые передачи широко применяются как в машиностроении, так и в приборостроении.

Зубчатые колеса подразделяются на виды в зависимости от применения и бывают цилиндрическими и коническими.

 

Цилиндрические зубчатые колеса (шестерни):

Цилиндрические зубчатые колеса используются в передачах, где оси валов располагаются параллельно относительно друг друга. При этом они могут располагаться как горизонтально, так и вертикально.

В зависимости от формы продольной линии зуба зубчатые колеса бывают: прямозубые, косозубые и шевронные.

 

Рис. 1. Цилиндрические зубчатые колеса: прямозубые, косозубые и шевронные

 

Прямозубое колесо. Этот вид шестерен ввиду своей простой конструкции является наиболее внедряемым в различных системах. В таком виде зубья шестерен располагаются в плоскости, которая перпендикулярна оси вращения. В отличии от косозубых и шевронных колес у данного вида предельный крутящий момент ниже.

Косозубое колесо. Зубья для данного вида колес выполняются под определенным углом к оси вращения шестерен, а по форме образуют часть винтовой линии. По сравнению с прямозубым колесом при работе зубьев данного вида зацепление зубьев происходит плавнее, а за счет увеличенной площади контакта предельный крутящий момент выше. Но для работы колес с косым зубом приходится применять упорные подшипники, так как возникает механическая сила, направленная вдоль оси. В основном косозубые колёса используются там, где нужны передачи большого крутящего момента на высоких скоростях.

Шевронное колесо. Этот вид имеет зубья, которые выполнены в форме буквы V на плоскости вращения колеса. Главной особенностью шевронных колес является то, что силы на осях обеих половин компенсируются, вследствие чего отпадает необходимость в использовании упорных подшипников. Различают шевронное и многошевронное цилиндрическое зубчатое колесо, состоящее соответственно из двух и более полушевронов, а также шевронное цилиндрическое зубчатое колесо со сплошным венцом и разделенными полушевронами.

В отдельные виды выделяются: цилиндрическое колесо с круговыми зубьями, цилиндрическое колесо со смещением (без смещения), циклоидальное, эвольвентное и цевочное цилиндрическое колеса.

Колесо с круговыми зубьями. Передачу с такими колесами называют передачей Новикова. При такой передаче контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс. Зубья данного вида колеса выполнены в виде полукруга, радиус которого подбирается под нужные требования. Колеса с круговыми зубьями в сравнении с косозубыми обладают более высокой нагрузочной способностью зацепления, высокой плавностью и бесшумностью работы, но при тех же условиях работы у них снижен КПД и ресурс работы, что не позволяет их применять широко.

Колесо со смещением либо без смещения. Это зубчатое колесо, зубья которого образованы при номинальном положении исходной производящей рейки, характеризуемом отсутствием касания (касанием) делительных поверхностей исходной производящей рейки и обрабатываемого зубчатого колеса.

Циклоидальное колесо. В данном виде профили зубьев шестерни выполнены по циклоидальной кривой. Однако при таком способе зацепления шестерен имеется большой недобор чувствительности из-за изменения расстояния между осями. Циклоидальное колесо  применяется в основном в приборостроении. Колесо сложно в изготовлении, поскольку при его создании требуется использование очень многих специальных зуборезных инструментов.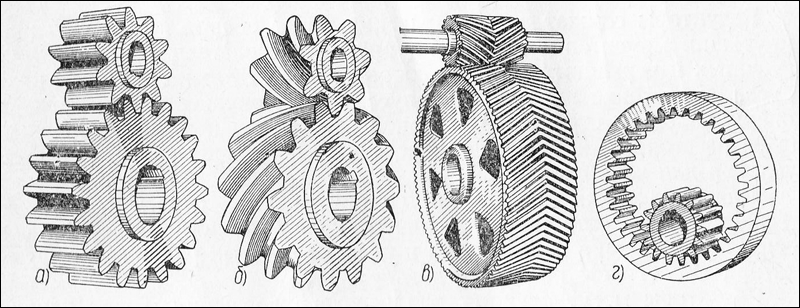

Цевочное колесо. В данном случае зубья одного из колес имеют вид пальцев в форме цилиндра. Такой вид шестерен образовался на базе циклоидального колеса и получил более широкое применение как в машиностроении, так и в приборостроении.

 

Конические зубчатые колеса (шестерни):

Конические зубчатые колеса используются в передачах, где оси валов пересекаются либо перекрещиваются. Данный тип колес так же широко применяется в машиностроении. Конические зубчатые колеса позволяют решать многие конструкторские задачи, часто встречающиеся в разработке сложных механизмов.

Рис. 2. Конические зубчатые колеса

Различают множество видов конических зубчатых колес.

Колесо с прямыми зубьями. Данная деталь имеет зубья прямой формы, теоретические линии которых проходят через конусную вершину. Данный вид является наиболее простым по технологии изготовления. Прямозубые конические колёса используют при низких окружных скоростях. Передача с такими колесами обеспечивает передаточное отношение до 3.

Колесо с тангенциальными зубьями. Такое колесо имеет прямые зубья, теоретические линии которых расположены касательно к окружности. У данного вида колеса угол спирали различен для различных точек линии зуба. Угол спирали в средней точке зубчатого венца выступает в качестве величины, которая характеризует наклон зубьев.

Колесо с криволинейными зубьями. Такой вид колес имеет ряд преимуществ, среди которых выделяются: мягкий вход, наименьший шум при работе, наибольшая нагрузка и большие окружные скорости. Данный вид передачи встречается среди видов, перечисленных ниже.

Колесо с круговыми зубьями. В данном виде шестерни зубья нарезаны в виде дуги по окружности с определенным углом наклона, который называют углом спирали. Такие шестерни мягко входят в зацепление, вследствие чего издают минимум шума.

Они отличаются большей прочностью и допустимостью больших отклонений при установке.

Колесо с нулевым углом наклона зубьев. Такое изделие представляет собой колесо с круговыми зубьями, угол наклона зубьев которого в одной из точек делительной средней линии зуба равняется нулю. Колеса с нулевым наклоном зубьев еще называют «Зерол». Данный вид колес в своей работе дает минимальные осевые нагрузки и широко применяется в передачах с большими скоростями, в том числе в авиастроении, поскольку скорость у них может достигать более 70 метров в секунду. Колеса с нулевым наклоном зубьев могут заменять передачи, в которых были установлены прямозубые шестерни.

Колесо с эвольвентной линией зубьев. В данном типе шестерни при развертке конической основы зубья будут иметь тип эвольвенты основной окружности. Передача зубьев дает непрерывный крутящий переход, который исключает возможность проскальзывания.

Колесо с прямыми зубьями кругового профиля. Данный вид колес имеет профиль зубьев приблизительно круглой формы, у которых поверхность боковин выполнена огибанием рабочей части инструмента, и совершает движение в плоскости по кругу оси инструмента, а также производит поступательное движение мимо зубьев данного типа колеса. Колеса с прямыми зубьями кругового профиля также называют колесом Ривасайкл.

Колесо с круговыми зубьями, образованными сферой. Данное колесо имеет форму зуба, образованную при помощи зацепления на станке поверхностью сферической формы. Колесо также отличается повышенной бесшумностью, плавностью хода и более высокой окружной скоростью.

Плоское колесо. У данного вида колес угол делительного конуса является 90 градусов.

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

 

 

Коэффициент востребованности 1 746

Косозубое зубчатое колесо

Авторы патента:

КОВАЛЕВ НИКОЛАЙ АЛЕКСАНДРОВИЧ

F16H55/16 – относящиеся только к зубьям

 

ИСАНИЕ

Союз Советских

Социалистических

Республик

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ (6l ) Дополнительное к авт. свид-ву № 688751 (22) Заявлено 14.09.77 (2!) 2521736/25-28 с присоединением заявки №вЂ” (23) Приоритет— (51) M Кл з

F 16 Н 55/16

Гееударственнмй нюмнтет

СССР (53) УДК 621 833. .!2(088.8 )

Опубликовано 07.06.82. Бюллетень № 21

Дата опубликования описания 17.06.82

Ilo делам нзабретеннй н нткрмтий (72) Автор изобретения

Н. А. Ковалев (7E ) заявитель ” ЕиЫюа»т ц » (54) КОСОЗУБОЕ ЗУБЧАТОЕ КОЛ ECO

Изобретение относится к машиностроению, а именно к зубчатым передачам.

По основному авт. св. № 688751 известно косозубое зубчатое колесо, концы зубьев которого выполнены консольными (1).

Однако подобное выполнение консольной части зуба, форма которой в поперечном сечении полностью соответствует форме поперечного сечения основной части зуба, в ряде конкретных применений не позволяет существенно уменьшить динамические наг- 1о рузки на зубья при входе их в зацепление.

Цель изобретения — снижение динамических нагрузок на зубья при входе их в зацепление.

Эта цель достигается тем, что в косозубом зубчатом колесе, концы зубьев которого выполнены консольными, последний имеет на консольной части зуба срез, поверхность которого проходит через крайние точки активного участка рабочего профиля зуба в его торцевом сечении и точку перехода 2р нерабочего профиля в поверхность впадины.

На фиг. 1 изображен зубчатый обод косо.зубого (шевронного) колеса, разрез; на фиг. 2 — вид А на фиг. 1.

Косозубое (шевронное) зубчатое колесо

1 содержит зубья 2 с консольной частью 3.

На консольной части 3 зуба 2 имеется срез 4, поверхность которого проходит через крайние точки а и в активного участка рабочего профиля в его торцевом сечении и точку с перехода нерабочего профиля в поверхность впадины.

При работе косозубого колеса 1 началь-. ный контакт возникает в точке в у ведущего колеса и в точке а — у ведомого. При этом упругая податливость зуба 2 увеличена за счет изгиба и кручения заостренной консоли. По мере поворота колес точка контакта зубьев постепенно перемещается от крайних точек консоли к ее основанию и переходит с консольной части 3 зуба 2 на более жесткую среднюю часть. В результате этого нарастание нагрузки на зуб 2 при его входе в зацепление происходит постепенно.

Использование предлагаемой конструкции зубчатого колеса позволяет снизить динамические нагрузки, вибрации и уровень шумов в процессе работы зубчатой передачи.

934095

Формула изобретения

Составитель В. Антипов

Редактор В.Лазаренко Техред А. Бойкас Корректор М. Коста

Заказ 389О/26 Тираж 990 Подписное

ВНИИПИ Государственного комитета СССР по делам изобретений и открытий

113035, Москва, Ж вЂ” 35, Раушская наб., д. 4/5

Филиал ППП «Патент», г. Ужгород, ул. Проектная, 4

Косозубое зубчатое колесо по авт. св. № 688751, отличающееся тем, что, с целью уменьшения динамических нагрузок на зубья при входе их в зацепление, консольный конец зуба имеет срез, поверхность которого проходит через крайние точки активного участка рабочего профиля зуба в его торцевом сечении и точку перехода нерабочего профиля в поверхность впадины.

Источники информации, принятые во внимание при экспертизе

1. Авторское свидетельство СССР № 688751, кл. F 16 Н 55/16, 1979.

  

 

Похожие патенты:

Косозубое зубчатое колесо // 929929

Косозубое зубчатое колесо // 688751

Армированное зубчатое колесо // 644992

Армированное зубчатое колесо // 577341

Армированное зубчатое колесо // 523221

Соединение зубчатых секций, имеющих т-образное основание, с телом вращения // 254960

Патент 210572 // 210572

Зубчатое колесо // 44747

Эластичные зубья сцепления // 42767

Зубчатое колесо со съемными зубьями // 42766

Зубчатое колесо // 2112173

Изобретение относится к машиностроению, в частности к зубчатым передачам

Зубчатая передача // 2183774

Изобретение относится к области машиностроения

Зубчатый венец с упругими кассетами // 2433322

Изобретение относится к машиностроению и может быть использовано в приводах крупногабаритных механизмов

Зубчатое колесо с демпфирующим элементом // 2448293

Изобретение относится к элементам зубчатых передач, прежде всего для электрических ручных машин

Зубчатое колесо // 2010145

Изобретение относится к области машиностроения и может быть использовано в зубчатых передачах

Зубчатое колесо // 2029188

Изобретение относится к машиностроению и может быть применено в различных устройствах, например в цепных передачах

Зубчатое колесо // 1070361

Зубчатое колесо // 1620749

Изобретение относится к машиностроению

Винтовая зубчатая передача // 1703900

Изобретение относится к машиностроению и может быть использовано в кинематических нереверсивных винтовых передачах

Зубчатое колесо // 2494297

Изобретение относится к машиностроению, в частности – к зубчатым передачам, и может быть использовано в зубчатых колесах, работающих в режиме ударных нагрузок. Зубчатое колесо содержит тело (1) и зубчатый венец с зубьями (2). В зубьях по оси (4) их симметрии со стороны вершин (5) в сторону оснований, на всю ширину зубьев, выполнены прорези (6), заполненные упругим материалом, например, резиной. Изобретение направлено на повышение прочности зубьев зубчатых колес при их работе в режиме ударных нагрузок. 1 ил.

Построение эвольвентного цилиндрического прямозубого и косозубого зубчатого колеса для Solidworks Статьи и уроки по работе с 3d моделями

Главная \ Новости \ Статьи и уроки по работе с 3d моделями \ Основы работы в GearTrax: Построение эвольвентного цилиндрического прямозубого и косозубого зубчатого колеса для SolidWorks « Назад Основы работы в GearTrax: Построение эвольвентного цилиндрического прямозубого и косозубого зубчатого колеса для SolidWorks  В сегодняшнем уроке мы рассмотрим основы работы в программе GearTrax – приложение компании Camnetics Inc. , USA для создания различных трансмиссионных деталей (зубчатых колес, звездочек, червяков, шкивов и т.д.) Данный урок будет разбит на части для удобства восприятия и освоения программы. В сегодняшней части урока, мы познакомимся, как создавать эвольвентные цилиндрические прямозубые и косозубые зубчатые колеса для САПР Solidworks в приложении Geartrax. Принцип работы программы прост:  создаваемый объект, параметры которого определены в программе, формируется в CAD-системе (в нашем случае SolidWorks). Контуры зубьев описываются сплайном или совокупностью окружностей, имитирующих эвольвентный профиль. Полученная кинематическая пара визуализируется в окне программы с имитацией движения (визуализация доступна только цилиндрических колес). В данной программе можно создавать цилиндрические прямозубые и косозубые зубчатые колеса, конические зубчатые колеса с прямыми и круговыми зубьями, элементы архимедова червячного колеса, шкивы клиновых и поликлиновых передач, а также передач с зубчатыми ремнями, звездочки цепных передач, элементы шлицевых соединений с эвольвентными зубьями. GearTrax интуитивно понятен как для новичка, так и для профессионала в области проектирования зубчатых колес. Благодаря окну визуализации, которое показывает созданную кинематическую пару, можно увидеть картину зацепления и если что-то не устраивает с легкостью отредактировать и вновь увидеть полученный результат. Благодаря GearTrax время создания зубчатых колес и других трансмиссионных деталей минимизируется. То, на что раньше могли уйти часы и дни сейчас с легкость получается за секунды! Приступим к освоению программы. После открытия программы перед нами появляется следующее окно: Сегодня мы будем работать во вкладке Spur/Helical (эвольвентные цилиндрические прямозубые и косозубые зубчатые колеса). Пройдемся немного по основному окну программы. В разделе Pitch Data мы выбираем на основе каких данных будем проектировать зубчатое колесо:  Diametral pitches (диаметральный шаг), Module pitches (модульный ряд), Non-standard pitches (нестандартное зубчатое колесо). В соответствии с выбранным параметром мы будем выбирать для построения зубчатого колеса либо диаметральный шаг или модуль. В подразделе Standards мы можем выбрать угол профиля эвольвентного зацепления (изначально стоит 20). В разделе Number of Teeth мы задаем количество зубьев шестерни (pinion) и зубчатого колеса (gear). В разделе Gear Type мы выбираем тип зубчатого колеса: Spur (цилиндрическое прямозубое зубчатое колесо), Helical R.H. (цилиндрическое косозубое (правое) зубчатое колесо), Helical L.H. (цилиндрическое косозубое (левое) зубчатое колесо). Если выбрать Helical R.H. или Helical L.H., то становится активен подраздел Helix angle (угол наклона зубьев). В разделе Internal Gear мы выбираем тип зацепления: внутреннее или наружное. Изначально стоит наружное зацепление, т.е. галочка напротив Internal gear set убрана. Если же поставить галочку напротив Internal gear set, то активируется внутренне зацепление. Так же становится доступен подраздел O.D.: в нем задается диаметр заготовки колеса с внутренним зацеплением. В разделе Tooth Pattern мы выбираем какое из колеc зацепления («gear» – «колесо» или «pinion» – «шестерня») мы будем реализовывать в Solidworks. По умолчанию установлено «Gear active». В разделе Gear Data приведены рассчитанные программой параметры зубчатого колеса (Pitch diameter – делительный диаметр, Major diameter – диаметр выступов, Minor diameter – диаметр впадин и т.д.). Такие параметры как Add mod. coef. (коэффициент смещения) и Face width (ширина зубчатого венца) мы можем изменить, нажав на зеленый квадрат в верхнем правом углу поля ввода. В появившемся окне мы можем менять параметры как для «gear», так и для «pinion». Если требуется построить нестандартное зубчатое колесо, например, с углом профиля 300, то в разделе Pitch Data надо выбрать Non-standard pitches. Тогда в разделе Gear Type все параметры становятся изменяемыми. Для того чтоб их изменить надо нажать на напротив поля ввода нужного параметра на зелёный квадрат в верхнем правом углу. И так, когда мы разобрались с навигацией по программе, теперь построим прямозубое цилиндрическое зубчатое колесо с модулем m=4, количеством зубьев z=66 и шириной зубчатого венца b=40 мм. В разделе Pitch Data в первом выпадающем списке выбираем Module pitches (модульный ряд). Во втором выпадающем списке выбираем 4.0 Module. Далее в разделе Number of Teeth указываем количество зубьев Gear (зубчатое колесо) равное 66. В разделе Gear Data напротив подраздела Face width около поля ввода нажимаем на зеленый квадрат в верхнем правом углу и в появившемся окне напротив параметра Face Wight, Gear вводим 40 и нажимаем ОК. Теперь нам остается только нажать на клавишу Create и зубчатое колесо построится в SolidWorks! Примечание: Для правильной работы модуля необходимо в параметрах “Язык и региональные стандарты” во вкладке “Форматы” поставить “Английский” язык. В этом случае SolidWorks запустится в английской конфигурации. В ином случае программа будет выдавать сообщение о невыбранном языке и не сделает массив компонентов на экране появится следующее окно: Нажмите ОК и построение колеса продолжится, однако будет построен только один зуб. Для построения оставшихся 65 зубьев воспользуйтесь командой массив. К небольшим недостаткам программы также можно отнести ограниченный ряд модулей, предлагаемых программой. Нет возможности построить мелкомодульные колеса. Статья подготовлена коллективом Metal Working Group. Перепечатка, копирование, воспроизведение или иное использование материалов, статей и уроков, размещённых на сайте, разрешается при условии ссылки на www.metalworkinggroup.ru. Поделиться:   Комментариев пока нет Пожалуйста, авторизуйтесь, чтобы оставить комментарий. Авторизация Введите Ваш логин или e-mail: Пароль : запомнить Регистрация Забыли пароль?

Модуль зубьев зубчатого колеса: расчет, стандартные, определение

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Зубчатое колесо

Содержание

Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.

Скачать ГОСТ 9563-60

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.

Для расчета этого параметра применяют следующие формулы:

m=t/π,

где t — шаг.

Параметры зубчатых колес

Модуль зубчатого колеса можно рассчитать и следующим образом:

m=h/2,25,

где h — высота зубца.

И, наконец,

m=De/(z+2),

где De — диаметр окружности выступов,а z — число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки.

Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Исходные данные и замеры

На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.

Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.

Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.

Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.

Результаты расчетов

Для более крупных потребуются измерения и вычисления.

Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:

m=De/(z+2)

Последовательность действий следующая:

• измерить диаметр штангенциркулем;
• сосчитать зубцы;
• разделить диаметр на z+2;
• округлить результат до ближайшего целого числа.

Зубец колеса и его параметры

Данный метод подходит как для прямозубых колес, так и для косозубых.

Расчет параметров колеса и шестерни косозубой передачи

Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.

Косозубое цилиндрическое зубчатое колесо – определение термина

Термин и определение

цилиндрическое зубчатое колесо с винтовыми зубьями, теоретические линии которых эквидистантны и на развертке соосной цилиндрической поверхности являются параллельными прямыми.

Еще термины по предмету «Детали машин»

Абсолютный эксцентриситет

расстояние между осью вала и осью радиального подшипника при данных рабочих условиях.

Боковая контактирующая поверхность

боковая поверхность зуба шкива, соприкасающаяся с зубом ремня.

Пространство между зубьями

расстояние между двумя последовательными зубьями шкива.

Похожие

• Цилиндрическое зубчатое колесо
• Цевочное цилиндрическое зубчатое колесо
• Циклоидальное цилиндрическое зубчатое колесо
• Шевронное цилиндрическое зубчатое колесо
• Эвольвентное цилиндрическое зубчатое колесо
• Угол осевого перекрытия зубчатого колеса косозубой цилиндрической передачи
• Косозубая цилиндрическая передача
• Высота зуба цилиндрического зубчатого колеса
• Нормальный модуль цилиндрического зубчатого колеса
• Цилиндрическое зубчатое колесо с криволинейными зубьями
• Цилиндрическое зубчатое колесо с круговыми зубьями
• Ширина венца цилиндрического зубчатого колеса
• Эквивалентное прямозубое цилиндрическое зубчатое колесо
• Зубчатое колесо
• Высота до хорды зуба цилиндрического зубчатого колеса
• Граничная высота зуба цилиндрического зубчатого колеса
• Делительный (начальный) цилиндр цилиндрического зубчатого колеса
• Цилиндрическая зубчатая передача
• Ведомое зубчатое колесо
• Ведущее зубчатое колесо

Смотреть больше терминов

Научные статьи на тему «Косозубое цилиндрическое зубчатое колесо»

В работе рассматривается теория определения угла в плане при нарезании косозубых зубчатых колес червячными фрезами как общего случая нарезания цилиндрических зубчатых колес. Установлено изменение этого угла в зависимости от конструктивных параметров нарезаемого колеса и расположения зуба фрезы относительно линии зацепления.

Научный журнал

Creative Commons

В работе определены зависимости, выраженные векторными функциями, описывающие боковые эвольвентные поверхности прямозубых и косозубых зубьев цилиндрических зубчатых колес.

Научный журнал

Creative Commons

Повышай знания с онлайн-тренажером от Автор24!

• 📝 Напиши термин
• ✍️ Выбери определение из предложенных или загрузи свое
• 🤝 Тренажер от Автор24 поможет тебе выучить термины, с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

Элементы зубчатого колеса – Теория механизмов машин (Физика)

Лекция 14.

Цилиндрические зубчатые передачи.

Передача непрерывного прошения от одного вала к другому с заданным переда­точным отношением чаще всего осуществляется с помощью зубчатых механизмов. Зубчатые механизмы получили очень широкое применение как в машиностроении, так и в приборостроении благодаря большой надежности и точности в воспроиз­ведения заданного закона движения. Если оси вращения валов параллельны, то применяется цилиндрическая зубчатая передача, аксоидами колес которой являют­ся цилиндры. Такая передача относится к категории плоских механизмов. В лекциях 14-16 излагаются основы синтеза цилиндрической зубчатой передачи по заданному передаточному отношению. Эти основы называются геометрическим расчетом зубчатой передачи.

Элементы зубчатого колеса.

Цилиндрические   зубчатые передачи, как отмечалось ранее, могут быть внешнего и внутреннего зацеплений. Следует также указать реечное зацепление, разграничительное между внешним и внутренним зацеплениями. Простая зубчатая передача имеет два подвижных звена, которыми являются зубчатые колеса. Рассмотрим элементы зубчатого колеса (рис. 14.l).

Поверхность (1), отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность (2), ограничивающая зубья со стороны, противоположной телу зубчато­го колеса, – поверхность вершин зубьев. Пространство между двумя соседними зубьями (3) – впадина. Поверхность, ограничи­вающая зуб со стороны впадины (4), называется боковой поверхностью зуба.

Боковая поверхность состоит из главной (5) и переход­ной (6) поверхностей. Главная поверхность – это та часть бо­ковой поверхности зуба, которая, взаимодействуя с главной по­верхностью другого зуба, обеспечивает заданное передаточное от­ношение. Переходная поверхность соединяет главную поверхность с поверхностью впадин.

Главной поверхностью чаще всего является эвольвентная по­верхность. так как среди цилиндрических передач особое рас­пространение получили эвольвентные цилиндрические передачи. Объясняется это тем, что они имеют весьма значительные преиму­щества перед другими передачами. Так, эвольвентные передачи допускают, в определенных пределах, изменение межосевого расстояния, сохраняя при этом по­стоянство передаточного отноше­ния, чего другие передачи не до­пускают, и обладают хорошими эксплуатационными качествами. Изготовление эвольвентных колес и инструмента для их нарезания является наиболее простым, что имеет очень важное практическое значение.

Рассмотрим образование эвольвентных поверхностей, которые будут являться главными поверх­ностями прямого и косого зубьев. На рис. 14.2, а в перспективе по­казана главная поверхность прямого зуба, которую можно пред­ставить как совокупность совершенно одинаковых эвольвент (Э, Э’), расположенных в плоскостях, перпендикулярных оси колеса. Эти эвольвенты являются траекториями точек образующей прямой КК’, принадлежащей плоскости N, которая перекатывается по основ­ному цилиндру 1 без скольжения. Начальные точки всех эвольвент распола-гаются на образующей K_bK_b^’ основного ци-линдра. Пересе­чение главной поверхности прямого зуба с любым соосным ци­линдром 2 происходит по образующей этого цилиндра (например, прямая КК’). Эта прямая параллельна оси колеса и называется линией прямого зуба. Главная поверхность прямого зуба является эвольвентной линейчатой цилиндрической поверхностью.

Главная поверхность косого зуба (рис. 14.2, б) также может быть представлена как совокупность одинаковых эвольвент (Э, Э’), расположенных в плоскостях, перпендикулярных оси колеса; од­нако в этом случае образующая прямая КК’ расположена на плоскости N под некоторым углом к оси колеса. Благодаря этому при перекатывании плоскости N по основному цилиндру 1 без скольжения начальные точки эвольвент располагаются по винтовой линии K_bK_b^’ на основном цилиндре. В пересечении с любым соос­ным цилиндром 2 главная поверхность косого зуба образует вин­товую линию КК*, называемую линией косого зуба. Главная по­верхность косого зуба является эвольвентной линейчатой винтовой поверхностью.

Таким образом, основное сходство главных поверхностей пря­мого и косого зубьев состоит в том, что в любом торцовом сече­нии, т. е. в сечении плоскостью, перпендикулярной оси колеса, они имеют эвольвенту.

На рис. 14.3, а изображено зубчатое колесо с внешними зубья­ми. Наибольший радиус r_a имеет окружность вершин. На рис. 14,3. б изображено зубчатое колесо с внутренними зубьями. В этом случае тело колеса имеет форму кольца, внутрь полости которого зубья обращены своими вершинами. Поэтому радиус r_a окружности вер­шин внутренних зубьев меньше радиуса r_f окружности впадин, ко­торый является, таким образом, наибольшим. На рис. 14.3 изобра­жены также эвольвентный профиль зуба, основная окружность, на базе которой он построен (радиус r_b), а также делительная окружность радиуса г и окружность произвольного радиуса r_y.

На рис. 14.З буквой  обозначен KON, равный углу профиля зуба в точке K, находящейся на делительной окружности прямозубого колеса. Этот угол стандартизован и ра­вен 20°. Таким образом, делительная окружность прямозубого ко­леса является той окружностью, которая пересекает профиль зуба в точке, для которой угол профиля равен стандартному углу =20°.

Если длину окружностей – делительной, основной и произволь­ного радиуса – поделить на число зубьев z, то получим расстояния между профилями двух соседних зубьев, называемые шагом, т. е. получим шаг по делительной окружности р, шаг по основной ок­ружности p_b и шаг по окружности произвольного радиуса p_y. Дуги р, p_b и p_y соответствуют одному и тому же угловому шагу = p/r = p_b/r_b = p_y/r_y.  Отсюда следует, что шаги пропорциональны радиусам соответствующих окружностей. Угловой шаг мож­но выразить и так: = 360°/z.

Важным элементом колеса является шаг по делительной окруж­ности. Выразим длину делительной окружности через шаг р и число зубьев колеса z: 2r = pz. Отсюда диаметр делительной окружности d = (p/)*z = mz. Отношение  p/ обозначают буквой m и называют модулем зубьев колеса (единица модуля – мм). Мо­дуль стандартизован, причем стандарт предусматривает целый ряд значений модуля. Через модуль выражают радиус делительной окружности и все линейные размеры как колеса, так и передачи:

                                                       r = m*z/2 ;                                              (14.1)

                                                       p = *m.                                                (14.2)

         Радиус основной окружности находится из KON (рис. 14.3, а):

                                                                                 (14. 3)

         Радиус произвольной окружности колеса выражается следующим образом:

                                                                              (14.4)

Так как шаги пропорциональны радиусам, то шаг по основной окружности:

а шаг по окружности произвольного радиуса:

                                                                              (14.5)

Основными параметрами колес являются модуль m и число зубьев z. Размеры делительных окружностей характеризуют раз­меры колес и передачи. Поскольку модуль определяется из прочностного расчета, а число зубьев назначает конструктор, то для уменьшения габаритов зубчатой передачи надо уменьшать числа зубьев ее колес [см. уравнение (14.1]

Для колес с внутренними зубьями радиусы основной и дели­тельной окружностей и шаги по этим окружностям определяют но тем же формулам, что и для колеса с внешними зубьями.

Шаг зубьев колеса по любой окружности можно представить как сумму толщины зуба s_y и ширины впадины e_y, т. е.

Колеса одного и того же модуля, имеющие одно и то же число зубьев, могут отличаться друг от друга толщиной зуба по дели­тельной окружности.

Различают:

1) колеса с равноделенным шагом, у которых по делительной окружности толщина зуба равна ширине впадины и, следовательно, половине шага

s = e = m/2;

2) колеса, у которых s > е, т. е. s > m/2;

3) колеса, у которых s < е, т. е. s < m/2.

На рис. 14.3, в изображены центральные углы 2 и 2_у, соответствующие дуговым толщинам зуба s и s_у, а также эвольвентные углы inv и inv_y. Из рисунка следует:

_b =  + inv = _y + inv_y

отсюда

_y =  + inv – inv_y

          Выражая угловые толщины через линейные _y = s_y/(2r_y) и = s/(2r) и подставляя из значения в уравнение, ранее составленное для _y, получим формулу для определения толщины внешнего зуба:

                                      s_y = r_y (s/r + 2inv – 2 inv_y)                                 (14. 6)

          Аналогично составляется формула для определения толщины s_y внутреннего зуба:

                                      s_y = r_y (s/r – 2inv + 2 inv_y)

Если безгранично увели­чивать число зубьев колеса, а следовательно, и радиусы всех окружностей, то в пре­деле при z =  все окруж­ности преобразуются в па­раллельные прямые, а эвольвентный профиль зуба ста­нет прямолинейным, что имеет очень важное практическое значение. При z =  получим зубчатую рейку (рис. 14.4). В любом месте прямолинейной части зуба рейки профильный угол будет одним и тем же, равным .

Прямая UU, по которой толщина зуба рейки в точности равна ширине впадины, т. е. равна половине шага, называется делитель­ной прямой. Шаг зубьев рейки, измеренный по любой прямой, па­раллельной делительной, имеет одинаковое значение p =m. Шаг рейки, замеренный по нормали n–n к ее профилю, равен mcos, т. е.  равен шагу р_b по основной окружности колеса, модуль которого такой же, как и модуль рейки.

Основные положения станочного зацепления.

Реечное станочное зацепление.

Способы изготовления зубчатых колес. В настоящее время зубчатые колеса изготавливают способами ко­пирования и огибания.

По первому способу изготовляют зубчатые колеса в основном только с равноделенным шагом. При этом большинство их вы­полняется с заведомой погрешностью. Второй способ – способ огибания такими существенными недостатками не обладает: этим спо­собом можно изготовить самые разнообразные зубчатые колеса и притом теоретически точно. Поэтому способ огибания нашел распространение и представляет особый интерес.

При способе огибания заготовке, из которой изготовляют зуб­чатое колесо, и режущему инструменту, имеющему зубчатую форму (червячная фреза, гребенка, долбяк), сообщают на станке такие движения относительно друг друга, которые воспроизводят процесс зацепления. Это зацепление называют станочным.

Помимо движений, воспроизводящих процесс зацепления ин­струменту сообщается еще технологическое движение резания. При этом режущие кромки инструмента описывают по­верхность, называемую производящей. Укажем, что производящая поверхность и изготавливаемая боковая поверхность зуба являются взаимоогибаемыми, откуда сам способ и получил свое наименование.

При расчете геометрических параметров элементов высшей кинематической пары учитывают технологиче­ские возможности изготовления деталей на формообразующих станках (металлорежущих, прокатных станах, прессах и т. д.). Геометрия соответствующего формообразующего инструмента тес­ным образом связана с производящими поверхностями. Для инструментов, осуществляющих процесс формообразова­ния путем срезания стружки, такой производящей поверхностью является воображаемая поверхность, содержащая режущие кромки инструмента или образуемая при их главном движении, необходи­мом для резания. Если режущие кромки – прямые, а главное дви­жение – прямолинейное, то производящей поверхностью является плоскость. Если режущие кромки криволинейные, а главное дви­жение – прямолинейное, то производящей поверхностью является цилиндрическая поверхность (например, эвольвентная поверхность для долбяков).

Зацепление проектируемой поверхности зубьев с производящей поверхностью по аналогии с зацеплением нарезаемого колеса с производящей поверхностью режущего инструмента называют станочным зацеплением. Этот термин был предложен В. А. Гавриленко, крупным ученым, обобщившим и развившим основные положения теории зацепления эвольвентных передач. Сущность станочного зацепления заключается в том, что про­изводящая поверхность (поверхность режущих кромок инструмен­та) и проектируемая поверхность зуба («нарезаемого » колеса) имеют такое же относительное движение, какое имели бы зубчатые колеса при зацеплении друг с другом при взаимодействии аксоидных поверхностей.

При нарезании цилиндрических зубчатых колес оси произво­дящего колеса (т. е. воображаемого зубчатого колеса, у которого боковые поверхности являются производящими поверхностями) и проектируемого («нарезаемого » ) колеса параллельны между собой и аксоидами являются цилиндры. Если производящее колесо имеет конечное число зубьев, то режущими инструментами являются долбяк (рис. 14.5 е), абразивный хон (рис, 14.5 ж), которыми можно обрабатывать боковые поверхности зубьев колес с различными числами зубьев (рис, 14.5, з). При бесконечно большом ра­диусе аксоида производящего колеса инструмент должен иметь бесконечно большое число зубьев, т. е. превратиться в рейку. В этом случае инструментом   обычно   являются   червячная   фреза (рис. 14.5, б) или абразивный червячный круг (рис. 14.5, г), у ко­торых реечный производящий контур (рис. 14.5, д) расположен на винтовой поверхности. Частным случаем является инструмент, называемый зуборезной гребенкой (рис. 14.5, а) или пара тарельчатых шлифовальных кругов (рис. 14.5, в). Главным движением резания у долбяка, гребенки и абразивного хона является поступательное движение, а у червячной фрезы и

шлифоваль­ных кругов – вращательное движение.

В процессе движения огибания (обкатки) основной шаг инстру­мента по профильной нормали соответствует основному шагу про­ектируемого («нарезаемого » ) колеса. Процесс перехода от формо­образования одного зуба к другому в процессе обкатки осуще­ствляется автоматически при непрерывном относительном движении (рис. 14.5, д. з).

Если производящую поверхность рассечь плоскостью, перпен­дикулярной оси нарезаемого колеса, то в сечении получим ис­ходный производящий контур (ИПК). Станочное зацепление есть зацепление ИПК с профилем зуба нарезаемого колеса.

Рассмотрим реечное станочное зацепление, т. е. такое, когда ИПК имеет очертания зубчатой рейки. Эвольвентные кромки это­го ИПК прямолинейны. Режущий инструмент (чер­вячная фреза или гребенка), образующий своим главным движени­ем эвольвентный реечный ИПК, обладает очень ценным свойством: его можно изготовить, сравнительно дешево и точно. Геометрия зубьев нарезаемого колеса определяется параметрами ИПК реечного инструмента и его расположением по отношению к колесу.

Исходный производящий контур эвольвентного реечного инстру­мента. Форма я размеры ИПК стандартизованы. Эвольвентные части профиля зубьев ИПК (рис. 14.6, а) прямолинейны и на­клонены к оси зуба под углом . Переходы от прямолинейной части зуба к основанию впадины и к вершине осуществлены по дуге радиусом _t. Точки сопряжения отмечены на ИПК буквами А, С, D, Е. Прямолинейная часть CD является эвольвентной, а скругления АС и DE – неэвольвентной частью контура. Прямая, разделяющая зуб по высоте на две равные части, называется делительной. На ИПК отмечаются еще четыре линии, параллельные делительной прямой и проходящие по основаниям впадин зубьев, по их вер­шинам и через точки сопряжения С и О. Расстояния между этими прямыми выражают размеры зуба исходного производящего кон­тура по высоте и измеряются соответственно величинами h_a = h_a^*m и C = c^*m, где h_a^* – коэффициент высоты зуба, с^* – коэффициент радиального зазора. Согласно стандарту: h_a^* = 1,0 ; с^* = 0,25. Прямые, проходящие через точки С и D, называются пря­мыми граничных точек.

Размерами вдоль делительной прямой являются шаг, толщина зуба н ширина впадины. Шаг р исходного производящего контура, измеренный по любой прямой, параллельной делительной, есть ве­личина постоянная, равная m, где m – стандартный модуль. Тол­щина зуба ИПК по делительной прямом равна ширине впадины s₀ = e₀ = m/2, а вместе они составляют шаг. Угол профиля зуба стандартизован:  = 20°. Радиус скругления (дуги DE)

                                                                                     (14.7)

Таким образом. ИПК реечного инструмента характеризуется четырьмя стандартными параметрами: m, , h_a^*, c^*.

Реечное станочное зацепление и коэффициент смещения. Рееч­ное станочное зацепление, как и всякое зацепление, имеет началь­ные линии. Ими являются станочно-начальная прямая рейки и станочно-начальная окружность колеса, которые катятся друг по другу без скольжения. Можно показать, что в реечном станочном зацеплении радиус r_w0 станочно-начальной окружности равен радиусу делительной окружности r.

Угол реечного станочного зацепления _w0 равен профильному углу а исходного производящего контура (как углы с взаимно перпендикулярными сторонами). Отметим также, что угол профиля зуба колеса в точке, находящейся на делительной окружности, равен профильному углу  исходного производящего контура.

На станке инструмент можно расположить по-разному относи­тельно нарезаемого колеса. Поэтому в станочном зацеплении де­лительная прямая ИПК может располагаться различным образом по отношению к делительной окружности колеса: I) она может касаться делительной окружности – нулевая установка инструмен­та; 2) быть отодвинутой от нее — положительная установка; 3) пе­ресекать ее—отрицательная установка.

Расстояние между делительной прямой и делительной окруж­ностью называется смещением инструмента. Его выражают в виде произведения модуля m на коэффициент смещения х и ему присваивают знак. При нулевой установке смещение mх > 0, х > 0. При положительной установке mх > 0, х> 0. При отрицательной установке смещением является стрелка сегмента, которую делитель­ная прямая отсекает от делительной окружности; в этом случае mx < 0, x < 0.

На рис. 14.6, а изображено реечное станочное зацепление при нарезании зубчатого колеса с положительным смещением и указаны все элементы производящего исходного контура, нарезаемого коле­са и станочного зацепления.

Линия реечного станочного зацепления начинается в точке N и через полюс P₀ уходит в бесконечность. Длина ее активной части ограничена точками В₁^’ и B^’’, находящимися на пересечении линии станочного зацепления с прямой QQ граничных точек и окруж­ностью вершин (рис. 14.6, а)

         Профиль зуба колеса имеет эвольвентную и неэвольвентную части. Переход эвольвснтного профиля в неэпольвентиый находится на окружности граничных точек колеса, радиус которой r_l = OB₁^‘.

Расстояние между окружностью вершин зубьев колеса и прямой впадин ИПК представляет собой станочный зазор С₀. Величина его складывается из двух частей: с^*m, ym, где у — коэффи­циент уравнительного смещения.

Размеры изготовляемого зубчатого колеса с внешними зубьями. Диаметр вершин прямозубого колеса (рис. 14.6, а):

                                                                     (14.8)

     Высота зуба из того же рисунка:

                                                                                  (14.9)

Если x = 0 (смещения инструмента нет) и у = 0, то d_a = m(z + 2h_a^*),        h = m(2h_a^* + с^*), и при стандартных значениях h_a^* = 1,0 и с^* = 0,25 получим      d_a = m(z+2) и h = 2,25m.

Стачочно-начальная прямая перекатывается по станочно-начальной окружности (она же делительная) без скольжения. По­этому толщина зуба s по делительной окружности нарезаемого колеса равна ширине ММ впадины по станочно-начальной прямой ИПК (рис. 14.6, б).

Отрезок ММ складывается из ширины впадины ИПК по де­лительной прямой e₀ = m/2 и двух катетов, каждый из которых равен xm tg, поэтому:                                   

                                           s = m/2 + 2 xm tg                                        (14.10)

Если инструмент установлен относительно колеса без смещения (xm = 0), то s = m/2; значит, толщина зуба s по делительной ок­ружности колеса равна ширине впадины е, так как s + е =m. В этом случае получается колесо с равноделенным шагом s = e, Если xm > 0, то s > m/2 и, следовательно, s > e. Если xm  < 0, то s < m/2, и поэтому s < e.

При нарезании косозубых колес применяется тот же инструмент 1, что для прямозубых, но устанавливается он наклонно под углом  по отношению к торцовой плоскости t – t колеса (заготовки) (рис. 14.6, в). На этом рисунке показана развертка 2 делительного цилиндра косозубого колеса, в результате чего винтовые линии косого зуба преобразо­вались в прямые линии. В торцовой плоскости t – t косозубого колеса вследствие наклона инструмента шаг увеличивается и становится равным p/cos, а следова­тельно, и модуль в торцовой плоскости будет нестандарт­ным, равным m/cos. По­этому при расчете линейных размеров косозубого колеса по формулам, в которые входит стандартный модуль, вместо m следует подставлять m/cos, например делительный диаметр косозубого колеса d = zm/ cos.

Обратим внимание на размеры h_a^*m, c^*m, xm, y*m, перпенди­кулярные делительной прямой (рис. 14.6, а), которые принято назы­вать размерами по высоте. На рис. 14.6 в эти размеры расположены перпендикулярно плоскости рисунка. Поэтому при повороте инстру­мента на угол  размеры по высоте не изменяются. А отсюда следует, что когда в уравнениях встречаются произведения h_am, cm, xm, ym, то их при расчете косозубой передачи можно под­ставлять в эти уравнения без всякого пересчета сомножителей. Так, например, формула диаметра вершин косозубого колеса может быть записана следующим образом: d_a = d + 2(h_a^*m + xm – y*m).

Угол профиля исходного производящего контура при нарезании косозубого колеса увеличивается по сравнению со стандартной величиной  = 20°, поскольку размеры по высоте не изменяются, а шаг в торцовом сечении увеличивается. Расчетный угол профиля _t исходного производящего контура при нарезании косозубых ко­лес определяют по формуле:

На рис. 14.7 сравниваются профили зубьев трех колес, имею­щих одинаковые числа зубьев, нарезанные одним и тем же ин­струментом, но с различными смещениями: x₁ < x₂ < x₃. Колеса имеют одинаковые радиусы делительных и основных окружностей; следовательно, профили зубьев всех трех колес очерчены по одной и той же эвольвенте. Но толщины зубьев s₁, (дуга ab), s₂ (дуга ас), s₃ (дуга af) и радиусы окружностей вершин r_a1, r_a2, r_a3, у колес будут разные. По мере увеличения х толщина зуба у основания увеличивается, а у вершины уменьшается, т. е. коэффициент сме­щения существенно влияет на форму зуба. Следовательно, назначая при проектировании тот или иной коэффициент смещения, можно влиять на форму зубьев колёс и на качество зубчатой передачи, наделяя её желательными свойствами.

Контрольные вопросы к лекции N14

1. Что называют зубчатым колесом?

Информация в лекции “Воля как волевое действие” поможет Вам.

2. Расскажите об основных элементах зубчатого колеса.

3. Запишите формулы окружного и углового шагов эвольвентного зубчатого колеса.

4. Какие методы изготовления зубчатых колёс Вы знаете?

5. В чём заключается сущность изготовления эвольвентных колёс методом огибания?

6. Дайте определение станочного зацепления.

7. Выведите формулы для определения основных размеров зубчатого колеса () используя схему станочного зацепления.

Винтовые шестерни | KHK Производитель зубчатых колес

• org/ListItem”> ТОП
>
• Винтовые шестерни

Косозубые шестерни – бесшумная работа

Косозубые шестерни – это один из типов цилиндрических шестерен с наклонной дорожкой зубьев. По сравнению с прямозубыми зубчатыми колесами они имеют большее передаточное число, бесшумность, меньшую вибрацию и способность передавать большую силу. Пара косозубых шестерен имеет одинаковый угол наклона винтовой линии, но направление винтовой линии противоположно.

Когда опорная часть зубчатого колеса находится в нормальной плоскости, путем наклона зубофрезерного инструмента можно использовать зубофрезерный станок и зубофрезерный инструмент для изготовления косозубых шестерен. Из-за искривления зубьев их изготовление имеет недостаток, заключающийся в более сложном производстве.

Косозубые зубчатые колеса производства KHK можно разделить на две группы по опорному сечению зубчатых колес, находящемуся в плоскости вращения (поперечный модуль) и нормальной плоскости (нормальный модуль). Если базовое сечение находится в плоскости вращения, межосевое расстояние идентично цилиндрическим зубчатым колесам, если они имеют одинаковый модуль и количество зубьев. Это позволяет легко заменять цилиндрические шестерни. Однако в этом случае требуются специальные фрезы и шлифовальные камни, что приводит к удорожанию производства. С другой стороны, если опорное сечение находится в нормальной плоскости, можно использовать зубофрезерные инструменты и шлифовальные камни. Однако тот же модуль и число зубьев в прямозубых шестернях уже не соответствуют межосевому расстоянию косозубых шестерен, и замена становится очень сложной. Кроме того, межосевое расстояние обычно не является целым числом.

В то время как прямозубые зубчатые колеса не создают осевой силы тяги, косозубые шестерни создают осевую силу тяги из-за скручивания в следе зубьев. Поэтому желательно использовать упорные подшипники для поглощения этой силы. Однако объединение правосторонних и левосторонних косозубых шестерен в двойные косозубые шестерни устранит осевую силу.

Косозубые шестерни часто используются в автомобильных трансмиссиях, заменяя прямозубые шестерни.

Пожалуйста, укажите здесь номер детали для цены и чертежа шестерни

ВНИМАНИЕ: Использование чертежей САПР
Профиль зуба, показанный на чертеже САПР, отличается от фактического профиля зубчатого колеса.
Также обратите внимание, что детали любой фаски, скругления или прорези на чертеже САПР могут отличаться от реальных значений или формы на реальном изделии.

Техническая информация о косозубых зубчатых колесах

С помощью этих технических данных вы можете просмотреть исчерпывающую информацию о косозубых зубчатых колесах KHK, включая их характеристики, а также советы и предупреждения при их выборе и использовании.

KHG

Шлифованные косозубые шестерни

Модуль: 1 – 3
Материал: SCM440
Закалка: Термическая очистка, индукционная закалка зубьев шестерни
Покрытие зубьев: Шлифованные зубья
Сплав: JIS N6

900 износостойкость и бесшумность, а также допускает вторичные операции. Может использоваться на том же межосевом расстоянии, что и прямозубая шестерня.

Щелкните здесь, чтобы выбрать косозубые шестерни. Щелкните здесь, чтобы выбрать серию E для KHG

SH

Стальные косозубые шестерни

Модуль : 2 – 3
Материал : S45C
Закалка : Нет
Покрытие зуба : Обрезной (без шлифовки)
Сорт : JIS N8

Обладает большей прочностью и бесшумностью, чем цилиндрические шестерни из нержавеющей стали.

Нажмите здесь, чтобы выбрать косозубые шестерни

Формы зубьев косозубых шестерен

Эта статья воспроизводится с разрешения.
Masao Kubota, Haguruma Nyumon, Tokyo: Ohmsha, Ltd., 1963.

Формирование винтовых зубчатых колес

Если сделать несколько надрезов на цилиндрическом зубчатом колесе перпендикулярно его оси и расположить путем небольшого вращения каждой отрезанной детали, как в лестнице, как показано на рисунке 3. 1, то зацепление становится более гладким благодаря контактам, происходящим в фазах. В целом коэффициент контакта увеличивается, так что даже когда обычное цилиндрическое зубчатое колесо имеет небольшое количество зубьев и коэффициент контакта меньше 1, такое расположение (называемое ступенчатым зубчатым колесом) обеспечивает передачу.

Рисунок 3.1 Ступенчатая передача

В ступенчатой ​​передаче, если деление сделать бесконечно узким и линия зубьев равномерно закручена относительно направления вала, другими словами, геликоидами с валом в центре, она становится косозубой шестерню, как показано на рисунке 3.2.

Рис. 3.2 Косозубая шестерня

Косозубая шестерня способна плавно передавать вращение с меньшей вибрацией и шумом и поэтому подходит для высокоскоростного вращения. Однако, поскольку сила, перпендикулярная поверхности зуба (нормальная нагрузка), содержит составляющую в направлении оси шестерни, она создает осевое усилие, требующее упорного подшипника. Для уравновешивания сил тяги в зубчатом колесе существуют зубчатые колеса, которые сочетают в себе косозубые зубчатые колеса с противоположным углом закручивания, называемые двойным косозубым зубчатым колесом или зубчатым колесом типа «елочка» (аналогичным по форме костям селедки), как показано на рисунках 3.3 и 3.4. Напротив, обычные косозубые шестерни иногда называют одинарными косозубыми шестернями. Косозубые шестерни часто используются в больших зубчатых передачах морского применения.

Однако, если есть какая-либо ошибка в фазировании правого и левого зубчатых рядов или если косозубые шестерни не входят в зацепление должным образом, зубчатая передача создает переменное усилие в осевом направлении, вызывая вибрацию. Также при наличии погрешностей направления в относительных линиях зубьев между ведущими и ведомыми колесами при косозубых передачах можно внести исправления регулировкой положения подшипников, а при шевронных передачах это невозможно. По этим причинам компания Maag Gear Company и другие компании рекомендуют использовать закаленные и отшлифованные косозубые шестерни для больших зубчатых колес на кораблях.

Рисунок 3.3 Шестерня типа «елочка»

Рисунок 3.4 Типы шестерен типа «елочка»

Вместо косозубых шестерен иногда используются дугообразные зубья, как показано на Рисунке 3.5.

Рисунок 3.5 Зубчатое колесо с дугой окружности

Эффективность косозубых зубчатых колес

Косозубые зубчатые колеса представляют собой зубчатые колеса с параллельными валами, и их зацепление почти полностью контактирует с контактом качения, поэтому их общий коэффициент полезного действия высок, в пределах 90-99,5%.

Радиальный модуль и обычный модуль

Для эвольвентных косозубых зубчатых колес используются обычные (перпендикулярные к зубьям) модульные системы и другие, использующие радиальные (перпендикулярные к валу) модульные системы, которые имеют базовые плоскости зубьев различной формы.

В качестве стандартных косозубых передач KHK предлагает две линейки радиальных модульных систем серии KHG и обычных модульных систем серии SH, и мы перечислим конкретные различия между ними ниже.

Во-первых, винтовые зубчатые колеса обычной модульной системы имеют то преимущество, что в них можно использовать такие же режущие инструменты, как фрезы и шлифовальные камни, что и прямозубые зубчатые колеса. Другими словами, по сравнению с новым производством радиально-модульных косозубых передач, которые обсуждались позже, их можно сделать более экономичными. С другой стороны, из-за угла наклона винтовой линии, по сравнению с теми же модулем и числом зубьев, диаметр делительной окружности становится большим, и заменить прямозубые цилиндрические колеса с тем же модулем и числом зубьев на косозубые колеса без изменения невозможно. межосевое расстояние, что является недостатком обычной модульной системы.

Также трудно поддерживать расстояние между центрами легко управляемых целых чисел. Преимущества и достоинства радиальной модульной системы противоположны обычной модульной системе. Первое преимущество, на которое можно указать, заключается в том, что фактическое значение шага становится малым по сравнению с нормальным шагом даже при изменении угла наклона винтовой линии, что позволяет заменить их прямозубыми шестернями того же модуля и числа зубьев при сохранении того же центральное расстояние. Что касается недостатка, то, поскольку фактический радиальный шаг изменяется с каждым углом наклона спирали, становится необходимым приобретать фрезы и шлифовальные круги для каждого угла спирали, что потенциально приводит к увеличению производственных затрат.

Ссылки по теме :
Типы зубчатых колес – Подробное описание типов зубчатых колес
Эквивалентные таблицы каждого стандарта, касающиеся сырья и классов точности зубчатых колес Как они работают

Косозубые шестерни — это компоненты силовой передачи, которые в основном используются для уменьшения скорости и увеличения крутящего момента между вращающимися валами. По сути, их можно разделить на две группы: те, которые передают мощность между параллельными валами, и те, которые передают мощность между непараллельными валами, обычно называемые шестернями с поперечной осью. Хотя косозубая шестерня в разрезе имеет ту же форму эвольвентного зуба, что и прямозубая шестерня, она срезана под углом к ​​вращению заготовки шестерни. Этот угол известен как угол спирали. Здесь описаны косозубые шестерни, а также обсуждение их работы и общих применений.

Основы работы с винтовой передачей

Цилиндрическое зубчатое колесо технически представляет собой косозубое колесо с углом наклона спирали 0°. Для винтовых зубчатых колес углы наклона винтовой линии обычно составляют от 15 до 30 °. Стандартная форма зуба шестерни идентифицируется как эвольвентная шпора 20°. Когда-то эвольвентные цилиндрические зубчатые колеса 14-1/2° были обычным явлением, но это уже не так. Эти последние обозначения степени относятся к углу давления зуба, линии контакта, которой следуют два зуба, когда они входят в зацепление и выходят из него. Только для эвольвентных зубчатых колес угол зацепления остается неизменным на всем протяжении зацепления отдельных зубьев. Гениальность эвольвентной формы зуба заключается в том, что она обеспечивает теоретически постоянное соотношение скоростей, даже если межцентровые расстояния не установлены идеально. Эту потребность в постоянном передаточном отношении иногда называют фундаментальным законом зубчатой ​​передачи.

Лучший способ понять, что такое косозубая шестерня, — это представить множество одинаковых прямозубых шестерен, вырезанных из бумаги и склеенных вместе таким образом, чтобы каждый последующий слой немного продвигался вперед по сравнению с предыдущим. Чтобы такая система работала, сопряженная шестерня должна располагаться слоями в противоположном направлении. Таким образом, сопрягающиеся косозубые шестерни на параллельных валах обязательно бывают правовинтовыми и левовинтовыми.

Рукоятка приводит к осевым нагрузкам, которые не создаются сопряженными прямозубыми шестернями. Конструкции, использующие косозубые шестерни, должны справляться с осевой нагрузкой за счет использования шариковых или роликовых подшипников, способных выдерживать осевую нагрузку.

Шестерни типа «елочка»

предлагают метод устранения тяги на основе зубчатых передач. Половина лица разрезается одной рукой, а другая половина разрезается противоположной рукой, эффективно уравновешивая усилие, создаваемое шестерней. В зависимости от метода производства, используемого для изготовления таких двойных косозубых шестерен, может потребоваться центральная желобка для зазора инструмента или зубья могут быть расположены в шахматном порядке.

Исключением для хиральности являются шестерни с поперечной осью, у которых валы расположены перпендикулярно. В этих случаях две шестерни будут одной рукой. Валы косозубых передач могут пересекаться под любым углом.

Преимущества

Снова рассматривая бумажную модель, легко увидеть, что каждый слой цилиндрического зубчатого колеса сопрягается со своим спичкой незадолго до того, как следующий слой вступает в контакт, отличие от цилиндрических зубчатых колес, где контакт происходит в один и тот же момент по всей поверхности зуба. Поскольку ширина каждого зуба больше, в любой момент времени контактирует больше зубов. Таким образом, косозубые шестерни передают нагрузки более плавно, чем прямозубые. Это приводит к большей грузоподъемности, более тихой работе и более высокой скорости.

Из-за осевых нагрузок и повышенного трения скольжения между зубьями косозубые шестерни работают с меньшим КПД, чем прямозубые.

Приложения

Звук, издаваемый автомобилем с механической коробкой передач при движении задним ходом, довольно хорошо демонстрирует бесшумность косозубых передач. Этот отчетливый вой связан с использованием цилиндрических шестерен для заднего хода (поэтому они могут быть «сдвинуты» — все остальные шестерни находятся в постоянном зацеплении). Косозубые шестерни используются для передних скоростей и заметно тише. В некоторых полноприводных раздаточных коробках используются цилиндрические шестерни для низкого диапазона, когда скорость низкая и шум не вызывает возражений.

Промышленные редукторы

доступны как с цилиндрическими, так и с косозубыми передачами. Дебаты о том, что использовать, сосредоточены на деталях приложения. Там, где шум вызывает беспокойство, целесообразно использовать косозубые передачи, особенно если зубчатая передача будет работать на средних и высоких скоростях. Там, где пространство ограничено или важен вес, цилиндрические зубчатые передачи могут быть лучшим решением, поскольку требования к упорным подшипникам сведены к минимуму. Цилиндрические зубчатые колеса, как правило, менее затратны в производстве, чем косозубые, хотя разница незначительна. Затраты добавляются при проектировании более прочных опор/подшипников вала, необходимых для косозубых передач.

Это обсуждение предполагает наличие параллельных валов. Для поперечных валов выбор больше не между цилиндрическими и косозубыми зубчатыми колесами, а между косозубыми, коническими и червячными зубчатыми колесами. Косозубые передачи предлагают менее дорогое решение для передачи движения между скрещенными валами, но их способность передавать большие нагрузки меньше по сравнению с их возможностями на параллельных валах. Одним из распространенных применений косозубых зубчатых колес со скрещенными осями является зубчатая пара, используемая для привода распределителя автомобильного двигателя / вала масляного насоса.

Конические шестерни обеспечивают значительно большую производительность, чем косозубые шестерни, хотя и при более высоких затратах. Червячные передачи имеют серьезные передаточные числа, но требуют регулирования температуры смазки из-за огромного трения скольжения, которое они производят.

Говоря о конических зубчатых колесах, косозубые формы зубьев часто используются для производства так называемых спирально-конических зубчатых колес. Информацию об этих компонентах можно найти в нашей сопутствующей статье о конических зубчатых колесах.

Шестерни типа «елочка»

иногда могут быть заменены прямозубыми прямозубыми шестернями, но более сложное производство делает их более дорогостоящими. Шестерни типа «елочка» почти всегда используются в очень больших трансмиссиях, таких как корабельные главные редукторы.

Как правило, шестерни изготавливаются из чугуна марки AGMA 20, при этом доступны более высокие марки для повышения прочности при повышенных затратах. Сталь часто используется в качестве материала шестерни, зацепляющейся с чугунной шестерней, чтобы обеспечить лучший баланс износа компонентов. Термическая обработка может привести к деформации зубчатых колес, поэтому ее обычно используют только для зубчатых колес из легированных сталей. Шлифование после термической обработки может улучшить профиль зубьев. Бронза также используется для изготовления шестерен. Различные пластмассы также используются для изготовления шестерен, иногда в качестве шестерни, которая сопрягается с чугунной или стальной шестерней.

Резюме

В этой статье представлено краткое описание косозубых зубчатых колес, их основных принципов работы, преимуществ перед другими типами зубчатых колес и типичных областей применения. Для получения дополнительной информации о сопутствующих продуктах обратитесь к другим нашим руководствам или посетите платформу поиска поставщиков Thomas, чтобы найти потенциальные источники поставок или просмотреть подробную информацию о конкретных продуктах. Дополнительную информацию о зубчатых колесах можно найти на веб-странице Американской ассоциации производителей зубчатых колес.

Другие товары для шестерен

• Типы звездочек — руководство по покупке Томаса
• Все о прямозубых зубчатых колесах: что это такое и как они работают
• О сцеплениях — краткое руководство
• Понимание передач
• Все о конических зубчатых колесах — что это такое и как они работают
• Все о червячных передачах — что это такое и как они работают
• Все о реечных передачах — что это такое и как они работают
• Материалы для шестерен, классификация и применение
• Определения терминологии передач
• Top Gears Производители и поставщики

Другие товары от Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Машины, инструменты и расходные материалы

Надежный косозубый редуктор NORD DRIVESYSTEMS для приводов по всему миру

Приводные системы NORD

• Товары
  • задняя часть
  • Товары
  • • Панель управления myNORD
    • Поиск продукта
    • Идентификация устройства
    • Конфигуратор продукта
  • Редукторы НОВЫЙ
  • МАКСДРАЙВ® НОВЫЙ
  • Моторы НОВЫЙ
  • Приводная электроника НОВЫЙ
  • Классы эффективности двигателя
• Решения
• Документация
  • задняя часть
  • Документация
  • • Панель управления myNORD
    • Поиск продукта
    • Идентификация устройства
    • Конфигуратор продукта
  • Руководства
  • Каталоги
  • Флаеры и брошюры
  • Запасные части
  • Программного обеспечения
  • Чертежи
  • Сертификаты
  • Формы
• Карьера
  • задняя часть
  • Карьера
  • • Панель управления myNORD
    • Поиск продукта
    • Идентификация устройства
    • Конфигуратор продукта
  • комбинированные_исследования
  • Бакалаврская и магистерская диссертация
  • Доступные позиции
  • Преимущества
  • Контакт
• Компания
  • задняя часть
  • Компания
  • • Панель управления myNORD
    • Поиск продукта
    • Идентификация устройства
    • Конфигуратор продукта
  • Архив новостей
  • Выставки
  • О нас
  • Где купить
  • Партнер с НОРД
  • обслуживание
  • Новостная рассылка
• мойНОРД
• Поиск

  Энергоэффективная работа в сочетании с высоким крутящим моментом 230 000 фунт-дюйм. Приводы допускают промывку и имеют гибкие конструкции входов и решения для монтажа редуктора.

  Цилиндрический мотор-редуктор UNICASE™

  Гибкое и надежное решение

  • Производительность: 0,12 кВт – 160 кВт
    
  • Диапазон крутящего момента: 10 Нм – 26 000 Нм
    
  Подробная информация о продукте Конфигуратор продукта

  Цилиндрический цилиндрический редуктор NORDBLOC.1®

  Инновационный исполнитель

  • Производительность: 0,12 кВт – 37 кВт
    
  • Диапазон крутящего момента: 30 Нм – 3 300 Нм
    
  Подробная информация о продукте Конфигуратор продукта

  Стандартный цилиндрический редуктор

  Проверенная классика

  • Производительность: 0,12 кВт – 7,5 кВт
    
  • Диапазон крутящего момента: 50 Нм – 700 Нм
    
  Подробная информация о продукте

  Двигатели с цилиндрическим рядным редуктором для широкого спектра применений

  Двигатели с цилиндрическим рядным редуктором от NORD имеют высокую удельную мощность и большое количество специальных опций. Редукторы выпускаются трех серий и многих типоразмеров для широкого спектра применений.

  Цилиндрические линейные редукторы NORD впечатляют выдающимися характеристиками:

  • Мощный
    Наши косозубые редукторы обеспечивают максимальный крутящий момент 230 000 фунт-дюйм (как промышленные мотор-редукторы до 2 200 000 фунт-дюйм).
  • Эффективность
    Исключительная эффективность редуктора повышает производительность приложения.
  • Hygienic
    Цилиндрические редукторы NORD благодаря гладкой поверхности корпуса можно промывать.
  • Надежный
    При необходимости мы можем обработать цилиндрические мотор-редукторы NORDBLOC.1 антикоррозионной защитой nsd tupH, которая работает даже в самых суровых условиях.

  Всегда правильное решение: наши линейные цилиндрические мотор-редукторы
  Нет двух одинаковых приложений. По этой причине NORD предлагает три различных решения для приводов с косозубыми редукторами. Все встроенные продукты доступны в версиях с опорами, фланцами или на опорах/фланец.

  Многоцелевое решение
  Стандартные цилиндрические рядные мотор-редукторы имеют широкий спектр применения и обеспечивают проверенное качество. Этот тип мотор-редуктора доступен от NORD в шести типоразмерах, в двух- или трехступенчатой ​​версии с диапазоном крутящего момента от 440 до 6160 фунт-дюйм. Мы производим шестерни для косозубых редукторов из высокоизносостойкой цементируемой стали.

  Компактный и мощный
  Наши линейные цилиндрические мотор-редукторы UNICASE имеют компактную конструкцию и жесткий на кручение чугунный корпус. Они оснащены эффективными двигателями для максимально экономичной работы даже при максимальном крутящем моменте в 230 000 фунт-дюйм.

  Узнайте больше о наших мощных цилиндрических мотор-редукторах UNICASE!
  Узнать больше

  Простота обслуживания: цилиндрические мотор-редукторы с возможностью промывки

  В серии NORDBLOC. 1 мы уделили большое внимание гладкой, легко чистящейся поверхности. Эта характеристика особенно важна для пользователей в гигиенически критичных отраслях, таких как пищевая или фармацевтическая промышленность.

  Цилиндрический цилиндрический редуктор NORDBLOC.1 поставляется с литым под давлением алюминиевым корпусом (серия SK771.1) или чугунным корпусом (серия SK772.1 и выше).

  Алюминиевый корпус серии NORDBLOC.1 обеспечивает естественную защиту от коррозии. При необходимости NORD также может обеспечить дополнительную защиту с помощью инновационной обработки поверхности nsd tupH. В отличие от обычной краски, она не отслаивается, что является большим преимуществом в суровых условиях. Цилиндрические линейные мотор-редукторы NORDBLOC.1 оптимизируют производство на предприятии по производству шоколада Zotter в Австрии.
  Подробнее.

  Заказные косозубые шестерни

  Запрос котировок и загрузка файлов

  Посмотреть детали
  и спецификации

  Посмотреть спецификации
  для тысяч
  нестандартных передач
  и скачать
  их модели

  Щелкните, чтобы просмотреть детали и характеристики
  

  Пользовательские 3D модели
  

  Создать пользовательский
  3D-моделей всего за
  файлов любого формата

  Нажмите, чтобы
  Создание 3D-моделей

  Запрос
  A
  Цитата

  Узнайте цены и
  варианты сроков изготовления
  на основе ваших спецификаций
  фотографии, образцы или
  модели

  Нажмите, чтобы
  Запросить цену

  АВАРИЙНАЯ СЛУЖБА
  

  Кризис – 48 часов

  Срочный – 72 часа

  Критический – 1 неделя

  Быстрый – 2 недели

  Стандартный – 3 недели

  
  

  Щелкните для
  Аварийная служба
  

  Параметры времени производства: Щелкните здесь для получения дополнительной информации.	Кризис	Срочный	Критический	Быстрый	Стандарт
  	48 часов	72 часа	1 неделя	2 недели	3 недели

  
  

  Параметры времени производства: Щелкните здесь для получения дополнительной информации.
  Кризис	48 часов
  Срочный	72 часа
  Критический	1 неделя
  Быстрый	2 недели
  Стандарт	3 недели

  
  

  Нестандартные косозубые шестерни

  
  

  Нажмите здесь, чтобы построить модели косозубых шестерен в САПР.

  ВИНТОВЫЕ ЗУБЧАТЫЕ ШЕСТЕРНИ при использовании на параллельных валах аналогичны прямозубые шестерни. Если скорость превышает 1000 футов в минуту, косозубые шестерни обеспечивают более прочную и плавную ходовую часть зубчатой ​​передачи.

  Этот тип зубчатой ​​передачи имеет угол наклона винтовой линии 45°. Материалы доступны закаленная сталь, сталь, нержавеющая сталь, алюминий, бронза, нейлон и неметаллические (фенольные).

  Торцевая тяга создается косозубыми зубчатыми колесами, но это можно преодолеть с помощью упорных шайб или других подходящих типов упорных подшипников.

  При использовании на валах под прямым углом эти шестерни обычно известны как «спиральные шестерни». В этом приложении у них только точечный контакт между зубами и поэтому не подходят для передачи каких-либо заметное количество лошадиных сил.

  RUSH GEARS также продает устройства для измерения зубьев шестерен под названием GEAR ИЗМЕРЕНИЯ! Gear Gages уменьшают количество ошибок, экономят время и деньги, когда поиск и заказ передач. Эти шаблоны презентаций доступны в девять наборов для определения всех стандартных размеров шага: диаметральный шаг «DP», Круговой шаг «CP», внешние эвольвентные шлицы, метрический модуль «MOD», Короткий зуб, мелкие смолы, грубые смолы и необычные смолы. Ссылаться в раздел ИЗМЕРИТЕЛЬНЫЕ МЕХАНИЗМЫ для каталожных номеров при заказе.

  Цилиндрические редукторы | Р серия

  Они отличаются идеальным соотношением производительности и занимаемой площади, в том числе и для вашей области применения: двадцать типоразмеров цилиндрических редукторов с плавно регулируемыми значениями крутящего момента и передаточного числа. Высокая эффективность включена.

  Цилиндрические редукторы серии R: высокий КПД и широкий диапазон передаточных чисел

  На рисунке показаны мотор-редукторы с цилиндрическими редукторами. На рисунке показаны мотор-редукторы с цилиндрическими редукторами.

  Цилиндрические редукторы — это «скрытая классика» в нашем ассортименте редукторов: 6 одноступенчатых и 15 двух- и трехступенчатых типоразмеров рамы охватывают диапазон крутящего момента от 50 до 18 000 Нм. Эта серия редукторов значительно опережает и по передаточным отношениям: от i = 1,30 до i = 289,74, а в двойных редукторах даже i = 27 001. Номинальный крутящий момент и передаточное отношение редуктора с такой тонкой ступенчатостью трудно найти на рынке. .

  Потребность в высокой выходной скорости или малом весе, конечно, также удовлетворяется редуктором R. Всегда с высоким уровнем эффективности наши 9Цилиндрические редукторы 0590 обеспечивают оптимальное соотношение между выходным крутящим моментом и монтажным пространством. Это означает, что цилиндрический редуктор почти всегда подходит для вашего применения.

  Только половина решения без двигателя? Затем воспользуйтесь нашей модульной концепцией и объедините редукторы серии R с асинхронным двигателем с цилиндрическим мотор-редуктором R..DR.. или с серводвигателем с цилиндрическим мотор-редуктором R..CMP с сервоприводом по вашему выбору. Или просто выберите отдельный двигатель переменного тока или серводвигатель, соответствующий вашим требованиям.

  Варианты цилиндрических редукторов серии RX/R/RM

  • Одноступенчатая или многоступенчатая
  • На лапах или на фланце
  • На лапах и на фланце
  • На фланце с удлиненным корпусом подшипника

  Вернуться к началу

  Настройка вашего индивидуального продукта

  • Подробная информация о вашем индивидуальном продукте

  Настроить продукт сейчас

  Наверх

  Ваши льготы

  • Комплексное предложение

    , потому что 6 одноступенчатых и 15 двух- и трехступенчатых типоразмеров рамы предлагают точно ступенчатый номинальный крутящий момент и передаточные числа.

  • Простая комбинация

    , потому что вы можете легко комбинировать свой цилиндрический редуктор с двигателем переменного тока или серводвигателем по вашему выбору из нашей модульной системы двигателей.

  Наверх

  Серия

  RX (одноступенчатая)

  Функции

  • Высокоэффективные косозубые редукторы шести типоразмеров
  • Высокая выходная скорость, крутящий момент до 830 Н·м
  • Передаточное число редуктора до i = 8,65
  • Поставляется в исполнении на лапах или с фланцем

  Технические данные

  Размеры 57 / 67 / 77 / 87 / 97 / 107

  Закрыть таблицу

  Передаточное отношение редуктора	я	1,30 – 8,65
  Макс. выходной крутящий момент	Н·м	69 – 830
  Диапазон мощности двигателя (Монтаж через адаптер двигателя AM)	кВт	0,12 – 45

  Мы приготовили для вас стол здесь.

  Области применения

  • Роликовые конвейеры
  • Ленточные конвейеры
  • Цепные конвейеры

  Наверх

  Серия R (две и три ступени)

  Функции

  • 15 типоразмеров
  • Оптимальное соотношение производительности и занимаемой площади
  • Наконец-то ступенчатые размеры и передаточные числа
  • Также доступны с уменьшенным люфтом

  Технические данные

  Размеры 07 / 17 / 27 / 37 / 47 / 57 / 67 / 77 / 87 / 97 / 107 / 127 / 137 / 147

  Закрыть таблицу

  Передаточное отношение редуктора	я	3,21 – 289,74
  Двойное передаточное отношение редуктора	и	90 – 27 001
  Макс. выходной крутящий момент R07 – R167 R127	Н·м	50 – 18 000* 6 000
  Диапазон мощности двигателя (Монтаж через адаптер двигателя AM)	кВт	0,12 – 90
  *Также с уменьшенным люфтом

  Мы приготовили для вас стол здесь.

  Области применения

  • Поворотные столы
  • Насосы и вентиляторы
  • Установки очистки сточных вод
  • Роликовые конвейеры
  • Ленточные конвейеры
  • Цепные конвейеры
  • Угловой транспортер
  4

  Наверх

  Серия RM (две и три ступени)

  Функции

  • Цилиндрические редукторы с удлиненной ступицей выходного подшипника
  • Специально разработаны для мешалок
  • Десять типоразмеров рамы
    • Предлагаются редукторы с передаточным числом до i = 289,74
    • Допускают высокие радиальные и осевые нагрузки, а также изгибающие моменты

      4

    Технические данные

    Размеры 57 / 67 / 77 / 87 / 97 / 107 / 127 / 137 / 147 / 167

    Закрыть таблицу

    Передаточное отношение редуктора	я	4,29 – 289,74
    Двойное передаточное отношение редуктора	и	134 – 27 001
    Макс. выходной крутящий момент	Н·м	450 – 18 000
    Диапазон мощности двигателя (Монтаж через адаптер двигателя AM)	кВт	0,12 – 160

    Мы приготовили для вас стол здесь.

    Области применения

    • Мешалки
    • Блендеры
    • Миксеры
    • Мешалки

    Наверх

    Наверх

    Охлаждение и смазка высокоскоростных косозубых передач

    Косозубые шестерни используются для снижения скорости центробежных компрессоров и турбин, чтобы соответствовать номинальным скоростям двигателя и генератора. Надлежащая смазка и охлаждение имеют решающее значение для успешной работы этих передач. Когда шестерни входят в зацепление, поверхности зубьев катятся и скользят друг относительно друга (рис. 1 и 2).

    
    Рис. 1. Терминология косозубых зубчатых колес

    
    Рис. 2. Направление скольжения

    Это зацепление создает огромные контактные и касательные напряжения. Масло используется для смазывания сопряженных зубьев шестерни и предотвращения задиров, износа и точечной коррозии поверхностей зубьев шестерни из-за контакта металла с металлом.

    Вязкость масла увеличивается с давлением; поэтому масло может разъединить зубья сопрягаемой шестерни, несмотря на огромную нагрузку. Масло также используется для охлаждения зубьев шестерен и предотвращения перегрева зубьев и перегрева масла.

    В этой статье представлены различные вопросы, связанные с надлежащими требованиями к смазке и охлаждению высокоскоростных косозубых передач. Высокоскоростные косозубые зубчатые колеса определяются как те зубчатые колеса, которые работают со скоростями делительной линии более 120 м/с.

    Повреждение поверхности зубчатого колеса

    Сопрягаемые поверхности зубьев шестерни не идеально гладкие. Поверхности полны мелких неровностей, таких как следы механической обработки. Это называется шероховатостью поверхности.

    Если масляная пленка достаточно толстая, неровности от сопряженных зубьев шестерни не соприкасаются друг с другом. Согласно теории упругогидродинамической смазки (ЭГС), смазка попадает в один из трех режимов. В режимах 1 и 2 имеется некоторый контакт между зубьями сопрягаемой шестерни.

    Большинство высокоскоростных передач относятся к режиму 3, при котором образуется полная масляная пленка EHL, а неровности на поверхностях зубьев не соприкасаются друг с другом.

    Повреждения зубьев шестерен включают задиры, износ и поверхностную усталость (микропиттинг и макропиттинг). ANSI/AGMA 1010-E95 (1995) содержит описания и изображения этих типов повреждений.

    Задиры

    Задиры – это повреждение поверхности зуба в результате сваривания и надрыва поверхности зуба боковой стороной сопряженного зуба. Он характеризуется радиальными линиями царапин (рис. 3). Задиры возникают, когда толщина масляной пленки меньше общей шероховатости шестерни и шестерни, и возникает контакт металла с металлом.

    
    Рис. 3. Задиры (любезно предоставлено ANSI/AGMA 1010-E95)
    Легкая (слева), тяжелая (справа)

    Согласно AGMA 925-A03 (2003 г.), «основной механизм задира вызван интенсивным теплом трения, генерируемым сочетанием высокой скорости скольжения и высокого контактного напряжения».

    Задиры обычно не начинаются на делительной линии, потому что скорость скольжения равна нулю. Таким образом, задиры обычно начинаются либо в верхней, либо в нижней половине или корне зубов. Температура контакта равна температуре вспышки плюс температура зуба перед входом в сетку. АГМА 925-A03 (2003) указывает:

    «Температура вспышки — это рассчитанное повышение температуры поверхности зуба шестерни в заданной точке вдоль линии действия в результате комбинированного воздействия геометрии зуба шестерни, нагрузки, трения, скорости и свойств материала во время работы».

    Несколько источников могут вызвать более высокие температуры зубьев при высокой скорости линии шага. Согласно AGMA 925-A03 (2003 г.), «при скоростях линии подачи выше 80 м/с потери при взбалтывании, выбросе масла между зацепляющимися зубьями и потери на парусность становятся важными источниками тепла, которые необходимо учитывать».

    Другим фактором является то, насколько эффективно масляный спрей охлаждает зубы. При распылении на зубчатое зацепление масло должно покрывать поверхности зубьев в течение небольшого промежутка времени, прежде чем оно будет отброшено. При высоких скоростях линии шага зубья могут двигаться настолько быстро по отношению к скорости масла, что не все зубья покрываются маслом.

    Одежда

    Износ определяется как удаление или смещение металла с поверхностей зубьев шестерни. Повреждения из-за задиров или точечной коррозии обычно не считаются износом. Износ уменьшает толщину зуба и может изменить контур зуба.

    Износ может быть результатом механического, химического или электрического воздействия. Для правильно спроектированных зубчатых колес, работающих в режиме смазки 3, степень износа должна быть настолько незначительной, чтобы первоначальные следы механической обработки все еще были видны через год или более службы.

    Этот низкий уровень износа также предполагает, что подаваемое масло хорошо фильтруется и что отсутствует абразивный износ из-за взвешенных в масле твердых частиц.

    Микропиттинг

    Микропиттинг представляет собой инцидент с высокой контактной усталостью при качении, который возникает в области контактной полосы Герца. Это функция комбинированных скоростей качения и скольжения, нагрузки, температуры, удельной толщины пленки и самого смазочного материала. АГМА 925-A03 (2003) говорится: ямки обычно имеют глубину от 10 до 20 мкм, длину от 25 до 100 мкм и ширину от 10 до 20 мкм.

    Из-за размера ямок микропиттинг может быть трудно увидеть. Если микропиттинг продвинется достаточно далеко, микроямки сливаются, и поверхность приобретает матовый вид (рис. 4).

    
    Рис. 4. Микропиттинг
    (любезно предоставлено ANSI/AGMA 1010-E95)

    Микропиттинг может привести к снижению точности зубьев шестерен, что увеличивает нагрузку на зубья шестерен, вибрацию и шум. Микропиттинг может привести к макропиттингу и поломке зубьев шестерни.

    Существует базовое непонимание механизма микропиттинга. Одна теория утверждает, что микропиттинг начинается, когда неровности на поверхности зубьев шестерни несут значительную часть нагрузки. Затем эти неровности деформируются, что создает локальные остаточные растягивающие напряжения.

    Тогда циклическая нагрузка становится достаточно высокой, чтобы вызвать локальные усталостные трещины, которые принимают форму небольших ямок. Таким образом, шероховатость поверхности является важным фактором риска образования микропиттинга. Согласно АГМА 925-A03 (2003), в некоторых случаях микропиттинг был устранен, когда поверхности зубьев шестерни были обработаны до зеркального блеска.

    Микропиттинг может возникнуть в любом месте на поверхности зуба шестерни. Однако, по словам исследователей Кардиса и Вебстера, это обычно начинается в областях, связанных с высокой скоростью скольжения, то есть в нижней или верхней части профиля зуба, а не на делительной линии, где скорость скольжения равна нулю.

    Смазочные материалы также играют ключевую роль в риске микропиттинга. Исследования, проведенные Кардисом и Вебстером, показали, что микропиттинг чаще возникает в редукторах, в которых используются масла с противозадирными присадками.

    Кроме того, стойкость к микропиттингу имеет тенденцию к снижению при более высоких температурах зубьев шестерни, но сообщалось, что другие добавки фактически улучшают стойкость к микропиттингу при более высоких температурах.

    Макропиттинг

    Макропиттинг также является явлением поверхностной усталости. Эти ямки обычно имеют диаметр порядка 0,5–1,0 мм и достаточно велики, чтобы их можно было увидеть невооруженным глазом (рис. 5).

    
    Рис. 4. Микропиттинг
    (любезно предоставлено ANSI/AGMA 1010-E95)

    Макропыщины обычно возникают, если имеются высокие неровности и происходит контакт металла с металлом между сцепляющимися зубами. Однако в высокоскоростных передачах поверхность обычно очень гладкая, а масляная пленка достаточно толстая, чтобы предотвратить контакт металла с металлом.

    В этих случаях причиной макроямок обычно является включение или небольшая пустота в материале, которые обеспечивают точку зарождения трещины, а подповерхностные касательные напряжения распространяют трещину.

    Тепловые проблемы

    Еще одно назначение смазочных масел — охлаждение поверхностей зубьев шестерен. Испытания Мартинальи показали, что зубья высокоскоростных косозубых колес могут деформироваться из-за неравномерного распределения температуры по ширине зацепления. Во многих случаях рабочие стороны шестерни и шестерни должны быть изменены, чтобы учесть это искажение.

    При очень высоких скоростях тангажа также могут возникнуть проблемы с перегревом воздушно-масляной смеси, попавшей в зацепление зубчатого колеса. Лак и нагар также могут образовываться на поверхностях зубьев шестерен. Эти отложения закрывают люфт и вызывают локальные перегрузки и выход из строя зубьев шестерни.

    Механизмы распыления зубчатых колес

    Масло обычно впрыскивается в зубчатое зацепление из распылителя. Распылитель проходит по ширине шестерен и оснащен небольшими форсунками, которые используются для создания небольших масляных струй, распыляющих масло в сетку. Основываясь на опросе нескольких производителей зубчатых передач, не существует единого мнения о том, следует ли распылять масло внутрь зацепления, наружу зацепления или и в то, и в другое.

    Это зависит от опыта производителя редуктора. Важно, чтобы зубья шестерни были смочены маслом для надлежащей смазки и чтобы достаточное количество масла попало в пространство зубьев для достаточного охлаждения.

    Некоторые производители редукторов используют специальные перегородки для уменьшения потерь воздуха внутри редукторов. Воздух внутри редуктора ускоряется из-за высокой скорости вращения шестерен.

    Энергия, необходимая для ускорения воздуха, является потерей. За счет установки пластин близко к сторонам шестерен количество ускоряемого воздуха ограничивается, и эти потери уменьшаются. Эти пластины также можно использовать в качестве щитов, чтобы предотвратить попадание масла, выдавливаемого из подшипников, на шестерни, вызывая ускорение, что может привести к дополнительным потерям.

    Наконец, другие производители редукторов используют в редукторе фальш-дно. Обычно это перфорированная пластина, которая устанавливается между шестернями и днищем коробки передач. Он используется для облегчения слива масла, предотвращая подъем масла в нижней части коробки передач и повторное ускорение.

    Специальные исполнения

    Greiner и Langenbeck провели испытания с раздельной подачей смазки и охлаждающего масла, чтобы проследить влияние такой схемы на температуру шестерни (нагрузочную способность по истиранию) и на эффективность.

    Один набор форсунок использовался для распыления смазки в зацеплении или вне зацепления, а другой набор форсунок использовался для распыления полотен зубчатых колес для охлаждения. Были проведены измерения температуры, потерь мощности и износа для множества конфигураций форсунок, потоков масла и разделения потоков.

    По результатам испытаний разделение подачи смазочного и охлаждающего масла привело к снижению расхода масла на 60% (по сравнению с первоначально рекомендованным расходом масла), снижению температуры зубьев шестерни и небольшому повышению эффективности.

    Одна компания запатентовала редуктор, работающий в вакууме и практически исключающий потери на ветер. Сообщается, что это изобретение позволило снизить потери мощности коробки передач на 50 процентов по сравнению с обычными коробками передач.

    Одним задокументированным случаем было сравнение двух редукторов мощностью 90 МВт: одного с обычным зацеплением, а другого с вакуумным редуктором. Расчетные потери в обычном редукторе при полной нагрузке составили 1407 кВт, а потери в вакуумном редукторе – 628 кВт. Это разница 779кВт, или около одного процента от номинальной мощности.

    Некоторые компании также производят высокоскоростные косозубые колеса со специальными осевыми канавками (рис. 6).

    
    Рис. 6. Осевые канавки для высокоскоростной передачи

    Эти канавки обеспечивают выход смеси горячего воздуха и масла перед перегревом и позволяют подавать свежее, холодное масло в зацепление зубчатого колеса в промежуточной точке зацепления. Как правило, эти канавки добавляются на кулачковую шестерню, а иногда и на кулачковую шестерню и шестерню. Хотя на рис. 6 показана только одна канавка, в других конструкциях их может быть больше.

    Различные высокоскоростные редукторы также оснащены специальным устройством распыления высокого давления/высокой скорости, которое устанавливается близко к зацеплению зубчатого колеса (рис. 7).

    
    Рис. 7. Система распыления шестерен высокого давления

    Как указано выше, для надлежащего охлаждения важно, чтобы масло покрывало поверхности зубьев в течение небольшого промежутка времени, прежде чем оно будет отброшено. При высоких скоростях линии шага может потребоваться масло с более высокой скоростью, чтобы обеспечить достаточное количество охлаждающего масла в пространствах зубьев, прежде чем оно застрянет в следующем зубе и вылетит из зубчатого зацепления. Как правило, для охлаждения требуется больше масла, чем для смазки.

    Таким образом, хотя на поверхности зубьев шестерни может быть достаточно масла для смазки, его может не хватить для охлаждения.

    Конечным пользователям доступно множество хороших источников, которые могут помочь в оценке конструкций высокоскоростных винтовых зубчатых колес. Хотя проблемы со смазкой и охлаждением возникают редко, решить их бывает непросто. При оценке высокоскоростных косозубых передач важно понимать опыт производителя. Смазка и охлаждение являются сложными вопросами, и необходимо учитывать ряд параметров.

    Примечание редактора:
    Воспроизведено с разрешения Лаборатории турбомашин (http://turbolab.tamu.edu). Из Труды тридцать третьего симпозиума по турбомашинам , Лаборатория турбомашин, Техасский университет A&M, Колледж-Стейшн, Техас, с.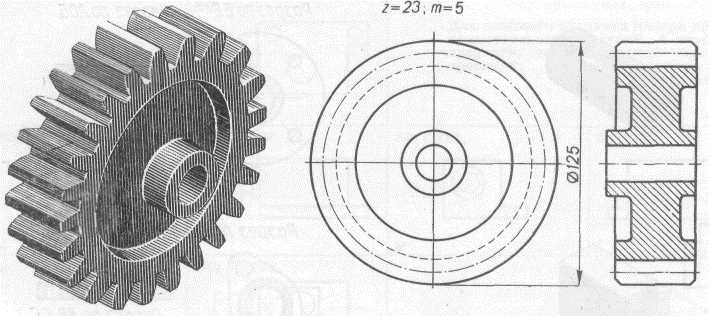 41-48, Copyright 2004.

    Каталожные номера

    1. АГМА 925-А03. «Влияние смазки на повреждение поверхности зубчатого колеса». Первое издание, AGMA, Александрия, Вирджиния, 2003 г.

    2. АНСИ/АГМА 1010-Е95. «Внешний вид зубчатых колес – терминология износа и выхода из строя». Первое издание, AGMA, Александрия, Вирджиния, 1995 г.

       .

    3. Кардис А. и Вебстер М. «Оценка микропиттинга трансмиссионного масла». Gear Technology , сентябрь/октябрь 2000 г., с. 30-35.

    4. Дадли, Д. Справочник по практическому проектированию зубчатых колес. Нью-Йорк, McGraw-Hill Book Company, 1984.

    5. Грейнер, Дж. и Лангенбек, К. «Разделение смазки и охлаждения в зубчатых передачах с маслоструйной смазкой». Бумага AGMA номер 91 FTM 13, 1991.

    6. Мартиналья, Л. «Тепловое поведение высокоскоростных зубчатых колес и коррекция зубьев для таких зубчатых колес». Международный симпозиум ASME/AGMA по зубчатым передачам и трансмиссиям, Сан-Франциско, Калифорния, 1972 г.