Кулисные механизмы: Кулисный механизм – Машиноведение
alexxlab | 19.03.2023 | 0 | Разное
Кулисные механизмы
Кулисные механизмы предназначены для преобразования вращательного движения входного звена во вращательное движение выходного звена. Обычно в приборах (РЗГ) применяются в качестве промежуточных преобразователей между рычажной передачей и зубчатой передачей.
КМ с параллельными осями sin типа | |||||
b- расстояние между опорами, R- Длина рычага. 1-Кулиса 2- рычаг. | Функция преобразования: Схемные параметры: | ||||
КМ с параллельными осями sin типа модифицированный | |||||
Функция преобразования: Схемные параметры: | |||||
КМ с параллельными осями tg типа | |||||
Функция преобразования: Схемные параметры: | |||||
| КМ с параллельными осями tg типа модифицированный | |||||
Функция преобразования: Схемные параметры: | |||||
Кулисные ПМ с пересекающимися осями Это
– пространственные ПМ. КМ с пересекающимися осями sin типа | |||||
Функция преобразования: Схемные параметры: | |||||
КМ с пересекающимися осями tg типа | |||||
Функция преобразования: Схемные параметры: | |||||
Поводковые механизмы Оси
Поводковых механизмов могут пересекаться
под углом 90º или отличным от него. Поводковый Механизм sin типа | |||||
Функция преобразования: Схемные параметры: Если =1 , то =0, означает ли это линейность ФП ??? | |||||
Поводковый Механизм tg типа | |||||
Функция преобразования: Схемные параметры: | |||||
Конструирование
Рычажных ПМ.
(Для к/п)
Появление момента от дисбаланса звена ПМ связано с тем, что центр масс звена находится не на оси вращения и, таким образом, даже в неподвижном состоянии в механизме возникают моменты и силы, обусловленные наличием гравитации, которые стремятся повернуть звенья, создают силовое воздействие на взаимосвязанные звенья.
Эту проблему надо обязательно учитывать при проектировании звеньев, выборе их конфигурации, материалов и пространственного расположения в приборе и машине.
Форма звеньев в механизмах техн. систем очень разнообразна: есть и симметричные детали асимметричные, у которых ц.т. не лежит на оси вращения.
На
Рис. приведена конструкция рычага
кулисного механизма тангенсного типа
с параллельными осями.
Большая часть изгибов и прочих, кажущихся, “излишеств” формы обусловлена конструкцией всего прибора в сборе (детали не должны задевать друг за друга, при этом быть компактными и легкими). Однако конструкция звена также играет решающую роль с точки зрения получение момента дисбаланса.
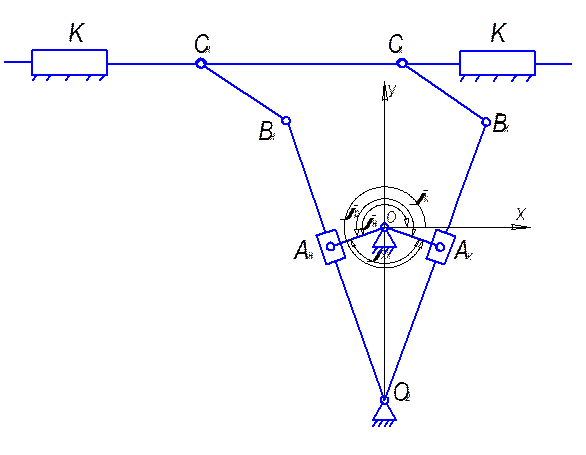
20. Кулисный механизм схема ,характеристики, достоинства ,недостатки, передаточное отношение механизма.
Наиболее часто применяют для преобразования
вращательного движения кривошипа 1 в
качательное движение кулисы 3. Камень
кулисы 2 перемещается вдоль нее по
направляющим. Кулисные механизмы могут
быть использованы также для преобразования
равномерного вращательного движения
в неравномерное вращательное движение
при а<r. Кулисы с камнем применяют также
в тангесных(а), синусных(б) и др механизмах
для замены высших кинематических пар
низшими. 2+2arcosβ)/[r(acosβ+r)]
Дифференц по времени выражение для ω3
=>получаем угловое ускорение кулисы
ε3=d2α/dt2 => ε3=ω12[ra(r2-a2)sinβ]/(a2+r2+2arcosβ)2
2+2arcosβ)/[r(acosβ+r)]
Дифференц по времени выражение для ω3
=>получаем угловое ускорение кулисы
ε3=d2α/dt2 => ε3=ω12[ra(r2-a2)sinβ]/(a2+r2+2arcosβ)2
Наиболее характерным является применение кулисных механизмов в устройствах для получения прерывистого движения, например в производственных автоматах, работающих по определенному циклу, в киноаппаратуре. В таких устройствах используют мальтийский крест. Лопасти 2 креста, имеющие пазы, представляют собой кулисы.
Достоинства: простота конструкции, изготовления, регулировки и эксплуатации. надежность в работе, малые габариты.
Недостатки: ограниченность угловых и линейных перемещений, зазоры в шарнирах, передаточное отношение непостоянно.
21. Кривошипно-ползунный механизм схема, характеристики, достоинства ,недостатки, передаточное отношение механизма.
 2
α/ℓ)
2
α/ℓ)Достоинства: простота конструкции, изготовления, регулировки и эксплуатации. надежность в работе, малые габариты.
Недостатки: ограниченность угловых и линейных перемещений, зазоры в шарнирах, передаточное отношение непостоянно.
ЧЕТЫРЕХЗУБЧАТЫЙ МЕХАНИЗМ
Четырехзвенный механизм с четырьмя вращающимися шарнирами обычно называют четырехзвенным механизмом
Применение четырехзвенных механизмов в машинах многочисленно. Некоторые типичные области применения включают:
a) Корреляцию угловых поворотов звеньев, соединенных с фиксированным звеном (общеизвестное как корреляция углов кривошипа или функция поколение ). В таких приложениях мы хотели бы иметь определенное функциональное соотношение, такое как q 14 = f(q 12 ), которое будет реализовано четырехзвенниковым механизмом.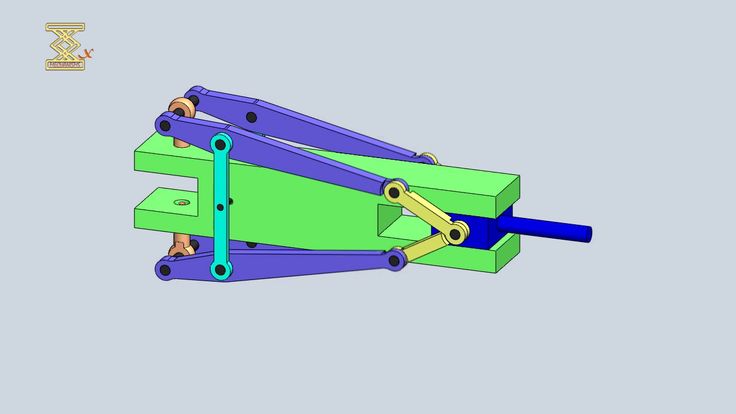 Простым примером будет преобразование линейной шкалы в логарифмическую в пределах определенного диапазона.
Простым примером будет преобразование линейной шкалы в логарифмическую в пределах определенного диапазона.
b) Ссылка, не имеющая связи с фиксированной связью, называется муфта звено. Точка на этом канале (известная как ответвитель точка ) будет описывать путь на фиксированном канале, который называется ответвитель-точка-кривая . При правильном выборе размеров звеньев могут быть найдены полезные кривые, такие как прямая линия или дуга окружности. Эту кривую точек соединителя можно использовать в качестве выходных данных четырехзвенного механизма (например, прерывистого привода пленки, показанного ниже
). c) Положения соединительного звена могут использоваться как выходные данные четырехзвенникового механизма. Как показано на рисунке ниже, четырехзвенный механизм, используемый для самосвала, требует, чтобы центр тяжести самосвала перемещался по наклонной прямой во время его наклона (почему?).
Вышеупомянутые приложения могут быть решены методами синтеза, которые выходят за рамки темы. В этой главе мы обсудим некоторые основные характеристики четырехтактника.
Самосвал
4.1.1. Теорема Грасгофа
Характеристики движения четырехзвенного механизма будут зависеть от соотношения размеров длины звеньев. Ссылки, подключенные к фиксированной ссылке, могут иметь два разных типа движения:
i) Звено может иметь полный оборот вокруг фиксированной оси (мы называем этот тип звена кривошип )
- Звено может колебаться (раскачиваться) между двумя ограничивающими углами (мы называем этот тип звена коромыслом ).
В четырехзвенниковом механизме возможны следующие три различных типа движения:
i) Оба звена, соединенные с фиксированным звеном, могут иметь полное вращение. Этот тип четырехзвенников называется “двойной кривошип ” или “ тяга “.
Этот тип четырехзвенников называется “двойной кривошип ” или “ тяга “.
ii) Оба звена, соединенные с фиксированным звеном, могут только колебаться. Этот тип четырехрычажной рукоятки называется «двойной рокер ».
iii) Одно из звеньев, соединенных с фиксированным звеном, колеблется, а другое совершает полный оборот. Этот тип четырехрычажной рукоятки называется кривошип-коромысло .
Тип движения зависит от длины звеньев. Теорема Грасгофа (или Правило Грасгофа ) дает следующие критерии для этих различных условий: l = длина самого длинного звена
s= длина кратчайшего звена
p,q = длина двух промежуточных звеньев
Справедливы следующие утверждения (приведены без доказательства.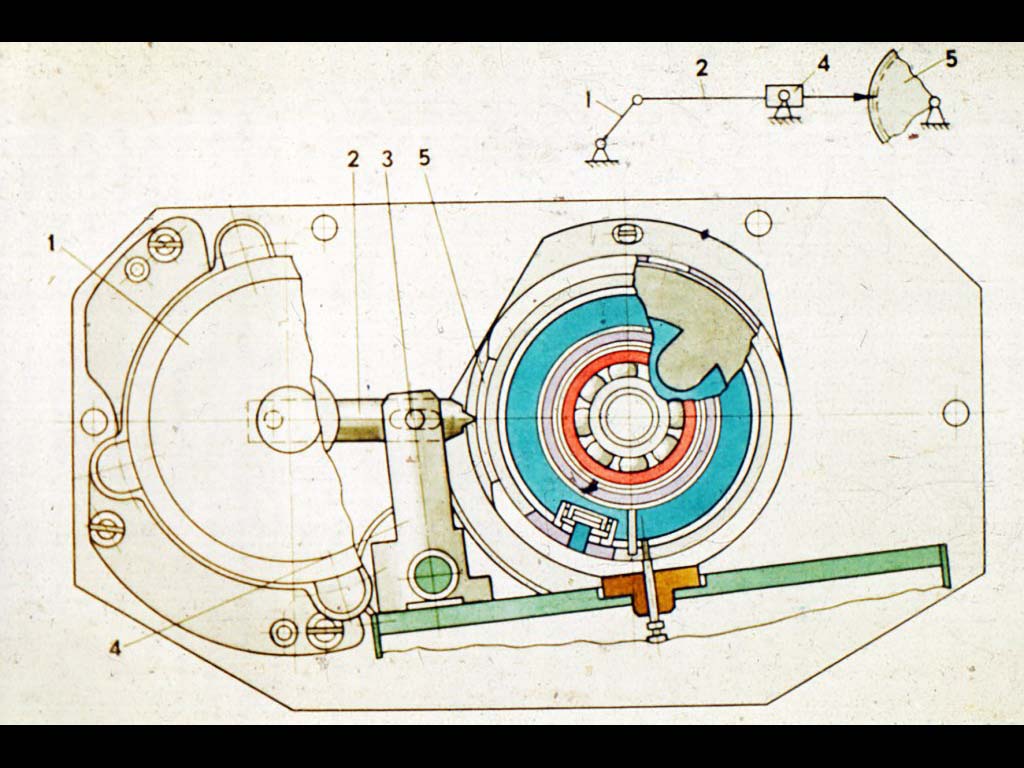 Можно доказать эти утверждения, используя уравнение вход-выход для четырех стержней. Доказательство теоремы см. в Приложении AIII).
Можно доказать эти утверждения, используя уравнение вход-выход для четырех стержней. Доказательство теоремы см. в Приложении AIII).
:
1. Если l + s < p + q (если сумма длин самого короткого и самого длинного звеньев меньше суммы двух промежуточных звеньев)
Тогда:
a, b) Возможны два различных кривошипно-кулисных механизма. В каждом случае самым коротким звеном является кривошип, фиксированным звеном является одно из соседних звеньев.
Два разных кривошипно-коромысловых механизма
c) Один двойной кривошип (перетаскивание) возможен, когда самым коротким звеном является рама.
d) Возможен один двухкулисный механизм, когда звено, противоположное самому короткому звену, является рамой.
- If l + s > p + q (если сумма длин самого длинного и самого короткого звена больше суммы длин двух промежуточных звеньев).

Возможны только двухкулисные механизмы (четыре различных механизма, в зависимости от неподвижного звена).
- Если l + s = p + q , будут получены четыре возможных механизма в (1). Однако эти механизмы будут страдать от состояния, известного как точка изменения. Осевые линии всех звеньев коллинеарны в этом положении. Следящий механизм может изменить направление вращения. Это неопределенная позиция.
4. i) A параллелограмм 9Связь 0005 является частным случаем (3), когда противоположные ссылки равны. Все четырехвозможные механизмы являются двухкривошипными, страдающими условием развязки (рис. 7.5а). Можно управлять механизмами в точке переключения с помощью конфигурации, как показано
ii) Дельтовидная связь является еще одним частным случаем (3), в котором два равных звена соединены с двумя равными более длинными звеньями, как показано на рис.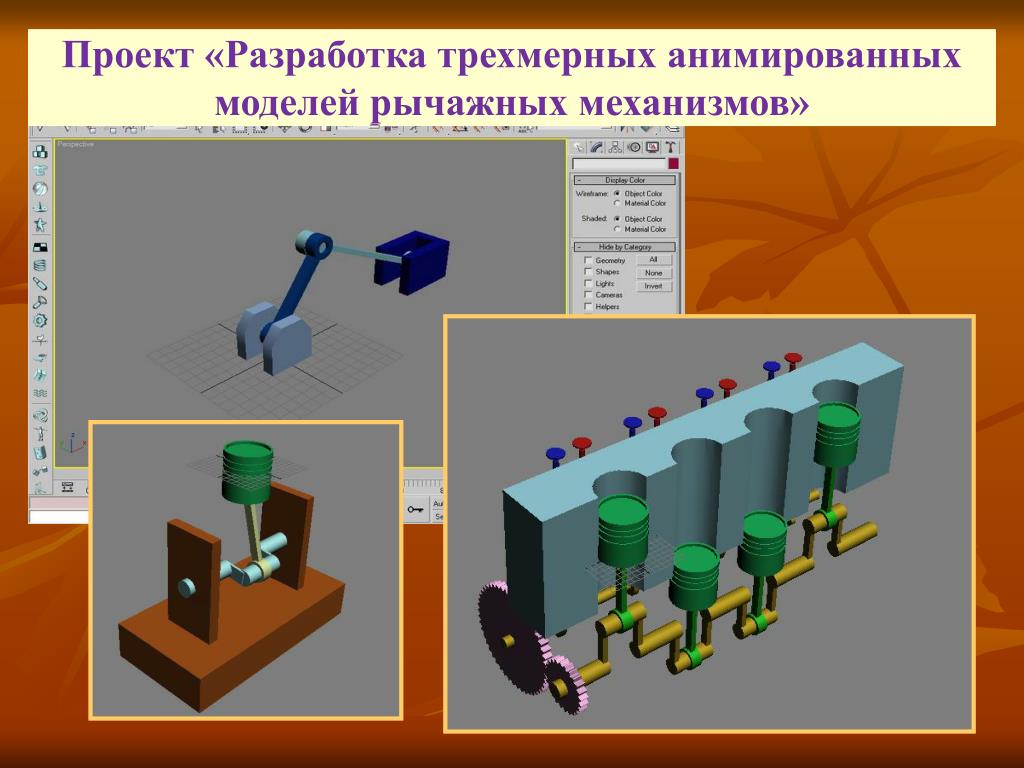 7.6. С длинным звеном в качестве рамы возможен кривошипно-кулисный механизм. Рама в качестве короткого звена может давать двухкривошипный механизм, в котором короткое звено может вращаться дважды, а длинное звено в качестве толкателя будет вращаться один раз (этот механизм также известен как 9-кривошипный механизм).0004 Механизм Galloway , запатентованный в 1844 г.) (рис. 7.6.).
7.6. С длинным звеном в качестве рамы возможен кривошипно-кулисный механизм. Рама в качестве короткого звена может давать двухкривошипный механизм, в котором короткое звено может вращаться дважды, а длинное звено в качестве толкателя будет вращаться один раз (этот механизм также известен как 9-кривошипный механизм).0004 Механизм Galloway , запатентованный в 1844 г.) (рис. 7.6.).
Обратите внимание, что если мы умножим или разделим все длины звеньев на константу, соотношение длин звеньев, следовательно, тип четырехзвенного соединения или угловые повороты звеньев не изменятся. Следовательно, именно соотношение длин звеньев, а не длин звеньев в целом, определяет тип четырехтактника. Если нас интересует вращение только звеньев, то механизмы с одинаковым соотношением длин звеньев будут иметь одинаковые характеристики движения, независимо от того, насколько большим или маленьким будет механизм (это масштабирование похоже на умножение уравнения контура на некоторую константу).
Из этих типов четырехзвенных механизмов кривошипно-кулисный механизм имеет особое значение в конструкции машин, поскольку непрерывное вращение может быть преобразовано в колебание посредством этого типа четырехзвенного механизма (это утверждение не обязательно означает, что другие четыре -барные пропорции не используются). Теперь мы обсудим четырехзвенный механизм с кривошипно-коромысловым механизмом и важную проблему, связанную с ним.
4.1.2. Положения мертвой точки кривошипно-коромысловых механизмов
В кривошипно-кулисных механизмах коромысло колеблется между двумя ограничивающими углами (как правило, кривошип является входом, а коромысло – выходом). Положения механизма, когда коромысло находится в крайнем положении, называются мертвыми точками положениями четырехзвенного механизма. Мы также можем определить положение мертвой точки, учитывая скорость коромысла при этих предельных углах. Поскольку коромысло движется в одном направлении до того, как оно достигает предельного угла, и так как оно движется в противоположном направлении после прохождения этого предельного положения, скорость коромысла в предельном положении должна быть равна нулю. Следовательно, мы можем определить положение мертвой точки как положение, в котором коромысло имеет мгновенную нулевую скорость. Рассмотрим кривошипно-коромысловый механизм в произвольном положении (рис. 7.8). Предположим, что кривошип вращается со скоростью w 12 , угловая скорость коромысла (см. анализ скорости четырехзвенного механизма):
Поскольку коромысло движется в одном направлении до того, как оно достигает предельного угла, и так как оно движется в противоположном направлении после прохождения этого предельного положения, скорость коромысла в предельном положении должна быть равна нулю. Следовательно, мы можем определить положение мертвой точки как положение, в котором коромысло имеет мгновенную нулевую скорость. Рассмотрим кривошипно-коромысловый механизм в произвольном положении (рис. 7.8). Предположим, что кривошип вращается со скоростью w 12 , угловая скорость коромысла (см. анализ скорости четырехзвенного механизма):
Из этого уравнения мы можем утверждать, что угловая скорость коромысла будет равна нулю, когда sin(q 12 -q 13 )=0 или когда q 12 -q 13 =0 или p. В этих положениях углы сцепки и кривошипа равны или отличаются на p (сцепка и кривошип коллинеарны – вдоль одной линии в выдвинутом или сложенном положении). Отсюда мы получаем два предельных положения коромысла, как показано ниже.
Отсюда мы получаем два предельных положения коромысла, как показано ниже.
Выдвинутое положение мертвой точки — это когда кривошип и соединительные звенья выдвинуты (q 12 = q 13 ), а сложенное положение мертвой точки — это когда кривошип и соединительное звено сложены друг над другом (q 13 =q 12 +p). Угол колебания коромысла между мертвыми точками и измеренный от выдвинутой мертвой точки до сложенной мертвой точки, называется углом поворота , г. Есть соответствующее вращение кривошипа, ф. Иногда вместо соответствующего угла поворота коленчатого вала используется соотношение времени между прямыми и обратными колебаниями (ходами). Если мы предположим, что кривошип вращается с постоянной скоростью, мы определим соотношение времени как:
Ход коромысла вперед – это когда коромысло перемещается из выдвинутого в сложенное положение мертвой точки в направлении против часовой стрелки (в машинном оборудовании ход вперед – это направление движения, во время которого коромысло выполняет работу. Это определение не обязательно должно соответствовать кинематическому определению приведено выше).
Это определение не обязательно должно соответствовать кинематическому определению приведено выше).
В случае четырехзвенных механизмов с кривошипно-коромысловыми пропорциями, если мы возьмем зеркальное отображение механизма по отношению к неподвижному звену, мы получим еще один четырехзвенный механизм с кривошипно-коромысловыми пропорциями и тем же углом поворота y. Однако, когда кривошип вращается из положения выдвинутой мертвой точки в сложенное положение против часовой стрелки, коромысло будет вращаться по часовой стрелке, а вращение кривошипа равно 360 0 – f.
Причина, по которой предельное положение называется положением мертвой точки, заключается в том, что, когда механизм находится в этом положении и если к коромыслу приложена сила, механизм не будет двигаться, например, механизм заблокирован по отношению к входному движению или усилию от коромысла. Иногда эта характеристика может быть очень полезной.
4.1.3. Угол передачи
При рассмотрении кинематических характеристик механизма очень важно понимать, как механизм будет работать в нагруженных условиях на практике. Под производительностью механизма мы понимаем эффективную передачу движения (и силы) от входного звена к выходному звену. Это также означает, что для постоянного входного крутящего момента в хорошо работающем механизме мы должны получить максимально возможный выходной крутящий момент, а силы подшипника должны быть минимальными. Конечно, крутящий момент и сила не являются величинами, которые были в кинематике, и какую бы кинематическую величину мы ни использовали для определения характеристик механизма, эта величина будет лишь приблизительно соответствовать статической силовой характеристике механизма. Динамические характеристики, являющиеся функцией массы и момента инерции твердых тел, могут в несколько раз превышать статические силы, а поведение механизма под действием динамических сил не может быть предсказано кинематикой. Тем не менее, какое-то эмпирическое правило поведения механизма под нагрузкой лучше, чем его отсутствие. Alt определил угол передачи как:
Под производительностью механизма мы понимаем эффективную передачу движения (и силы) от входного звена к выходному звену. Это также означает, что для постоянного входного крутящего момента в хорошо работающем механизме мы должны получить максимально возможный выходной крутящий момент, а силы подшипника должны быть минимальными. Конечно, крутящий момент и сила не являются величинами, которые были в кинематике, и какую бы кинематическую величину мы ни использовали для определения характеристик механизма, эта величина будет лишь приблизительно соответствовать статической силовой характеристике механизма. Динамические характеристики, являющиеся функцией массы и момента инерции твердых тел, могут в несколько раз превышать статические силы, а поведение механизма под действием динамических сил не может быть предсказано кинематикой. Тем не менее, какое-то эмпирическое правило поведения механизма под нагрузкой лучше, чем его отсутствие. Alt определил угол передачи как:
или угол передачи может быть определен как:
Ниже показаны углы передачи для четырехзвенного механизма и кривошипно-кривошипного механизма. Это простой параметр, в котором не учитываются ни силы, ни скорости. Однако о работоспособности механизма можно судить на этапе кинематического проектирования.
Это простой параметр, в котором не учитываются ни силы, ни скорости. Однако о работоспособности механизма можно судить на этапе кинематического проектирования.
Ясно, что оптимальное значение угла передачи равно 90 0 . Так как угол будет постоянно изменяться в течение цикла движения механизма, будет положение, при котором угол передачи будет больше всего отклоняться от 90 0 . На практике установлено, что если максимальное отклонение угла передачи от 90 0 превышает 40 0 или 50 0 (в зависимости от типа применения) механизм заблокируется. В некоторых случаях это максимальное отклонение должно находиться в пределах 20 0 (например, поршневые насосы), а в некоторых других случаях допускается максимальное отклонение до 70 0 (например, шасси самолета). Необходимо рассмотреть практическое применение механизма, чтобы ограничить это отклонение (в случае сомнений постарайтесь, чтобы это отклонение не превышало 40 0 или 50 0 ).
Можно выразить угол передачи через угол поворота кривошипа и длины звеньев как (записав теорему косинусов для AB 0 , используя треугольники A 0 AB 0 и ABB 0 и приравняв длину AB 0 ).
(1)
или
(2)
Минимум и максимум угла передачи можно определить, взяв производную уравнения (2) по q 12 и приравнивается к нулю:
(3)
Минимальное и максимальное значения угла передачи будут, когда sin(q 12 )=0 или когда q 12 =0 или p (когда кривошип и неподвижное звено коллинеарны в выдвинутом или сложенном положениях). Минимальное и максимальное значение угла передачи для четырехзвенникового механизма будет определяться как:
(4)
Критический угол передачи равен mmin или mmax, в зависимости от того, что больше всего отличается от 90 0 . Иногда для углов передачи больше 90 0 вместо m (180 0 -m) используется значение угла передачи. В таком случае имеется два минимальных значения угла передачи ( m мин1 =m мин , м мин2 =180 0 -м макс ) Наиболее критический угол передачи является минимальным из m мин1 и m мин2 . Обратите внимание, что отклонение угла передачи от 90 0 в двух крайних положениях будет равным, если:
Иногда для углов передачи больше 90 0 вместо m (180 0 -m) используется значение угла передачи. В таком случае имеется два минимальных значения угла передачи ( m мин1 =m мин , м мин2 =180 0 -м макс ) Наиболее критический угол передачи является минимальным из m мин1 и m мин2 . Обратите внимание, что отклонение угла передачи от 90 0 в двух крайних положениях будет равным, если:
(5)
Такие четырехзвенные механизмы известны как центральные четырехзвенные . В центрических четырехзвенных механизмах кратность времени равна единице (обороты кривошипа между мертвыми точками 180 0 ), и они будут иметь лучшие характеристики передачи усилия по сравнению с другими пропорциями кривошипа-коромысла.
Пример 4. 1.
1.
Определить угол поворота, соответствующий поворот кривошипа и максимальное отклонение угла передачи от 90 0 для четырехзвенного механизма, длина звеньев которого: a 2 = 4, a 3 = 8, a 4 =6, а 1 =7.
Поскольку сумма длин наибольшего и наименьшего звеньев (4+8=12) меньше длин двух промежуточных звеньев (6+7=13), то механизм кривошипно-кулисный, а звено 2 кривошипно-шатунное. . В мертвых точках, поскольку кривошип и соединительные звенья коллинеарны, четырехзвенный механизм имеет треугольную форму.
Применение теоремы косинусов для расширенной мертвой точки:
Или b=20,85 0
и
Или y 1 = 45,38 0
Для мертвой точки со сгибом:
или
f=217,96 0
Или
y=99,85 0
Максимальный и минимальный угол передачи:
M мин = 18,57 0 (D 1 = 71,43 0 ) и M MAX = 102,64 0 (D 2 = 12,64 0 ).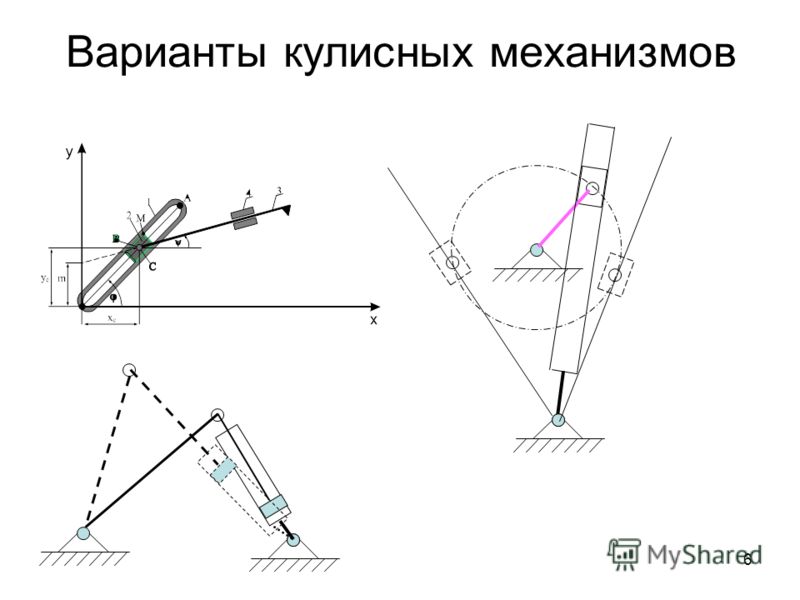 поскольку m min больше всего отклоняется от 90 0 , m min является критическим углом передачи.
поскольку m min больше всего отклоняется от 90 0 , m min является критическим углом передачи.
Классическая проблема угла передачи
Проектирование тяговых механизмов с оптимальным углом передачи
©es
Конструкция сферического кривошипно-коромыслового механизма с оптимальной передачей | Дж. Мануф. науч. англ.
Пропустить пункт назначения навигации
Научно-исследовательские работы
Джемиль Багчи
Информация об авторе и статье
Дж. Инж. Инд . May 1973, 95(2): 577-583
https://doi.org/10.1115/1.3438193
Опубликовано в Интернете: 1 мая 1973 г.
История статьи
Получено:
25 апреля 1972 г.
Онлайн:
15 июля 2010 г.
- Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Делиться
- Фейсбук
- Твиттер
- MailTo
Иконка Цитировать Цитировать
Разрешения
- Поиск по сайту
Ссылка
Bagci, C. (1 мая 1973 г.). «Проектирование сферического кривошипно-коромыслового механизма с оптимальной передачей». КАК Я. Дж. Инж. Инд . май 1973 г.; 95(2): 577–583. https://doi.org/10.1115/1.3438193
(1 мая 1973 г.). «Проектирование сферического кривошипно-коромыслового механизма с оптимальной передачей». КАК Я. Дж. Инж. Инд . май 1973 г.; 95(2): 577–583. https://doi.org/10.1115/1.3438193
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
- Процит
- Медларс
Расширенный поиск
Пространственные и сферические механизмы не должны быть рассчитаны на оптимальные характеристики передачи, как плоские механизмы. Коэффициенты пропускания и углы передачи в пространственном и сферическом механизмах определяются углами перекоса между осями пар на звеньях. Сферический кривошипно-коромысловый механизм оптимизирован для удовлетворения заданного соотношения времени опережения и возврата и для оптимальной передачи крутящего момента к крутящему моменту.


 Оси
перпендикулярны и лежат в одной
плоскости. В этой же плоскости в начальном
положении находится и центр контактирующего
элемента – СФЕРЫ. Второй контактирующий
элемент плоскость расположена в нач.
положении // плоскости осей механизма.
Оси
перпендикулярны и лежат в одной
плоскости. В этой же плоскости в начальном
положении находится и центр контактирующего
элемента – СФЕРЫ. Второй контактирующий
элемент плоскость расположена в нач.
положении // плоскости осей механизма.