Максимальная кинетическая энергия: Максимальная кинетическая энергия груза: формула
alexxlab | 05.04.2021 | 0 | Разное
Максимальная кинетическая энергия груза: формула
Кинетическая энергия
Определение 1
Кинетическая энергия – внутренняя энергия движущегося тела, обусловленная его инертностью (массой) и скоростью. Она равна энергии, которую нужно затратить, чтобы снизить скорость этого тела до нуля.
Например, движущийся автомобиль невозможно остановить мгновенно. Для остановки необходимо затратить энергию трения тормозных колодок о тормозные диски колес и шин об асфальт.
Замечание 1
Кинетическая и потенциальная энергия измеряются в джоулях ($1 Дж = Н \cdot м$).
В некоторых физических системах происходят циклические преобразования потенциальной (запасенной) энергии в кинетическую и обратно. Такие системы называются маятниками. Например, для груза, подвешенного на нити, потенциальная энергия максимальна, когда он отклонен на максимальный угол от вертикали. Мгновенная скорость груза в этот момент равна нулю и, следовательно, нулю равна и кинетическая энергия.
Проще всего изучать переход кинетической и потенциальной энергий друг в друга на примере пружинного маятника, где действует, если пренебречь силой трения, лишь сила упругости. Когда пружину сжимают, энергия запасается. Когда отпускают – потенциальная энергия, сохраненная в кристаллической решетке материала, высвобождается и превращается в кинетическую, разгоняя груз. Когда скорость груза достигает максимума, он продолжает движение по инерции, растягивая пружину в противоположном направлении, вновь запасая энергию и снижая скорость. Характеристики такого колебательного движения зависят только от материала пружины, толщины проволоки, из которой она намотана, диаметра и количества витков. Все эти факторы описываются единым параметром – коэффициентом упругости.
Максимальная кинетическая энергия груза
Для простого пружинного маятника полную энергию груза в любой момент времени можно выразить как
$E = E_p + E_k = \frac{m \cdot v^2}{2} + \frac{k \cdot x^2}{2}$, где:
- $E_p$ – потенциальная энергия,
- $E_k$ – кинетическая энергия,
- $m$ – масса,
- $v$ – моментальная скорость,
- $k$ – коэффициент упругости,
- $x$ – приращение длины пружины в данный момент.
 2}{2} \implies x_{max} = \sqrt{\frac{2 \cdot 0,25}{2000}} \approx 0,016 м$.
2}{2} \implies x_{max} = \sqrt{\frac{2 \cdot 0,25}{2000}} \approx 0,016 м$.Ответ: $\approx 1,6 мм$.
Урок 22. фотоэффект – Физика – 11 класс
Физика, 11 класс
Урок 22. Фотоэффект
Перечень вопросов, рассматриваемых на уроке:
- предмет и задачи квантовой физики;
- гипотеза М. Планка о квантах;
- опыты А.Г. Столетова;
- определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
- уравнение Эйнштейна для фотоэффекта;
- законы фотоэффекта.
Глоссарий по теме:
Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Фотоэффект – это вырывание электронов из вещества под действием света.
Квант – (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.

Ток насыщения – некоторое предельное значение силы фототока.
Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г.
 С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.
С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
Коэффициент пропорциональности получил название постоянной Планка, и она равна:
h = 6,63 ∙ 10-34 Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.
Схема установки для изучения законов фотоэффекта
Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
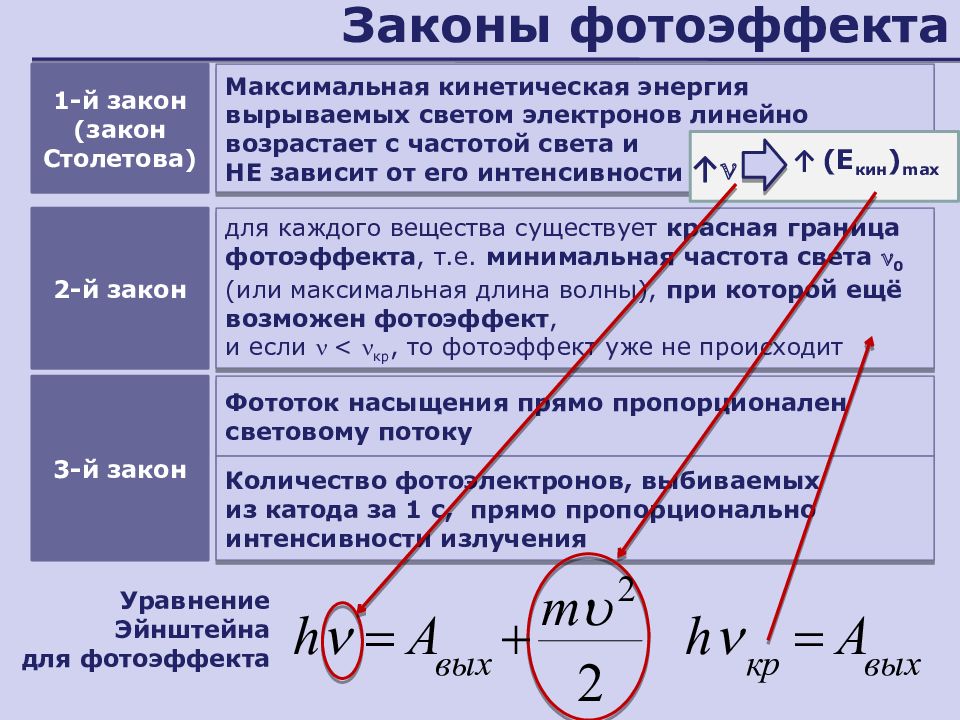
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
hνmin = Aв
где Ав – работа выхода электронов;
h – постоянная Планка;
νmin – частота излучения, соответствующая красной границе фотоэффекта;
с – скорость света;
λкр – длина волны, соответствующая красной границе.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
Работа выхода
– это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Задерживающее напряжение
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
где – максимальная кинетическая энергия электронов;
Е – заряд электрона;
– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Работа выхода
Запирающее напряжение
Решение:
Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.
Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:
Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

Ответ:
Работа выхода
Запирающее напряжение
не изменится
увеличится
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
Решение.
Запишем уравнение для фотоэффекта через длину волны:
Условие связи красной границы фотоэффекта и работы выхода:
Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
Подставляя численные значения, получаем: λ ≈ 215 нм.
Ответ: λ ≈ 215 нм.
Максимальная кинетическая энергия электронов, вырываемых с поверхности цезия
Условие задачи:
Максимальная кинетическая энергия электронов, вырываемых с поверхности цезия под действием фотонов с энергией 3,2 эВ, равна 1,3 эВ.
 На сколько увеличится кинетическая энергия электронов при увеличении частоты падающего света в 2 раза?
На сколько увеличится кинетическая энергия электронов при увеличении частоты падающего света в 2 раза?Задача №11.2.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(E_1=3,2\) эВ, \(E_{к1}=1,3\) эВ, \(\nu_2=2{\nu_1}\), \(\Delta E_{к}-?\)
Решение задачи:
Согласно формуле Планка, энергия фотона \(E\) пропорциональна частоте колебаний \(\nu\) и определяется следующим образом:
\[E = h\nu\]
Из этой формулы видно, что при увеличении частоты падающего света в 2 раза его энергия также возрастает в 2 раза, то есть верно записать:
\[{E_2} = 2{E_1}\;\;\;\;(1)\]
Согласно уравнению Эйнштейна для фотоэффекта энергия поглощенного кванта \(E\) идет на совершение работы выхода \(A_{вых}\) и на сообщение кинетической энергии вылетевшему электрону \(E_к\). Поэтому:
\[E = {A_{вых}} + {E_к}\;\;\;\;(2)\]
Запишем формулу (2) для двух случаев, описанных в условии задачи:
\[\left\{ \begin{gathered}
{E_1} = {A_{вых}} + {E_{к1}} \hfill \\
{E_2} = {A_{вых}} + {E_{к2}} \hfill \\
\end{gathered} \right.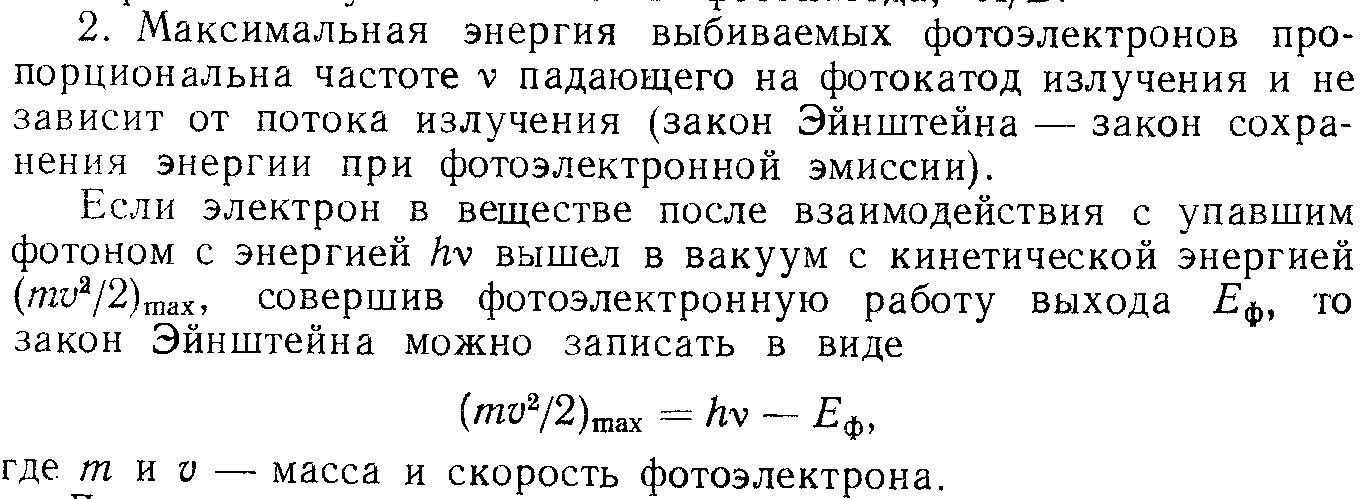 { – 19}}\;Дж\]
{ – 19}}\;Дж\]Ответ: 5,12·10
-19 Дж.Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Репетитор-онлайн — подготовка к ЦТ
Пример 7. Длина волны света, падающего на металлическую пластинку, уменьшилась от 500 до 420 нм. Определить работу выхода электрона, если известно, что максимальная кинетическая энергия фотоэлектронов увеличилась при этом в 2,50 раза.
Решение. При изменении режимов обучения работа выхода электронов из вещества не изменяется:
A вых = const.
Запишем уравнение Эйнштейна дважды:
- для света с длиной волны λ1 —
E γ1 = A вых + T e 1,
где E γ1 — энергия фотона, E γ1 = hc/λ1; h — постоянная Планка, h = 6,63 ⋅ 10−34 Дж ⋅ с; c — скорость света в вакууме, c = 3,00 ⋅ 108 м/с; T e 1 — максимальная кинетическая энергия фотоэлектронов в первом случае;
- света с длиной волны λ2 —
E γ2 = A вых + T e 2,
где E γ2 — энергия фотона, E γ2 = hc/λ2; T e 2 — максимальная кинетическая энергия фотоэлектронов во втором случае.

Из уравнения Эйнштейна выразим максимальную кинетическую энергию фотоэлектронов:
- для света с длиной волны λ1 —
T e 1 = E γ1 − A вых;
- света с длиной волны λ2 —
T e 2 = E γ2 − A вых.
По условию задачи
T e 2 = 2,5T e 1,
или с учетом явного вида выражений для T e 1 и T e 2:
E γ2 − A вых = 2,5(E γ1 − A вых).
Выразим отсюда работу выхода электронов из вещества:
Aвых=2,5Eγ1−Eγ21,5=2,5hcλ1−hcλ21,5=hc(2,5λ2−λ1)1,5λ1λ2.

Вычислим:
Aвых=6,63⋅10−34⋅3,00⋅108(2,5⋅420⋅10−9−500⋅10−9)1,5⋅420⋅500⋅10−18=
=3,47⋅10−19 Дж.
Выполним перевод полученного значения работы выхода из джоулей в электронвольты:
Aвых≈3,47⋅10−191,6⋅10−19=2,17 эВ.
Работа выхода электронов из поверхности данного вещества составляет 2,17 эВ.
Фотоэффект: кинетическая энергия электронов
В этой статье мы вычислим как работу выхода, так и кинетическую энергию электронов, определим их скорость и импульс.
Задача 1. Максимальная кинетическая энергия электронов, вылетающих из рубидия при его освещении ультрафиолетовыми лучами с длиной волны м‚ Дж. Определить работу выхода электронов из рубидия и красную границу фотоэффекта.
Определим работу выхода:
В электронвольтах это
Красная граница фотоэффекта:
Ответ: Дж, или 2,14 эВ, нм.
Задача 2. Серебряную пластинку освещают светом с частотой Гц. Гц. Найти максимальную кинетическую энергию фотоэлектронов.
Гц. Найти максимальную кинетическую энергию фотоэлектронов.Работа выхода электронов из серебра равна .
Тогда
Ответ: Дж, или 4 эВ.
Задача 3. Вольфрамовую пластину освещают светом с длиной волны . Найти максимальный импульс вылетающих из пластины электронов.
Тогда скорость электронов равна
А импульс тогда равен (работа выхода для вольфрама )
Ответ: кг м/с.
Задача 4. Пластину освещают монохроматическим излучением с длиной волны . Известно, что наибольшее значение импульса, передаваемого пластине одним фотоэлектроном, равно кгм/с. Определить работу выхода электрона из вещества пластины.Импульс равен , поэтому
Ответ: Дж, или 3,6 эВ.
Задача 5. Какой скоростью обладают электроны, вырванные с поверхности натрия, при облучении его светом, частота которого Гц? Определить наибольшую длину волны излучения, вызывающего фотоэффект.

Наибольшая длина волны – это красная граница фотоэффекта. Работа выхода для натрия равна . Поэтому
Теперь определим скорость электронов:
Тогда скорость электронов равна
Ответ: нм, м/с.
Задача 6. Максимальная скорость фотоэлектронов, вырванных с поверхности меди при фотоэффекте м /с. Определить частоту света, вызывающего фотоэффект.Работа выхода для меди равна .
Ответ: Гц.
Задача 7. На металлическую пластину, красная граница фотоэффекта для которой мкм, падает фотон с длиной волны мкм. Во сколько раз скорость фотона больше скорости фотоэлектрона?
Скорость фотоэлектрона равна
Скорость фотона – скорость света. Найдем отношение скоростей:
Ответ: в 642 раза.
Максимальная кинетическая энергия груза на пружине
/
/
Максимальная кинетическая энергия груза на пружине
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:
Запуск колебательного движения тела осуществляется с помощью кнопки Старт . Остановить процесс в любой момент времени позволяет кнопка Стоп .
Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени. Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия.
Задание 7. Верхний конец пружины идеального пружинного маятника неподвижно закреплён, как показано на рисунке. Масса груза маятника равна m, жёсткость пружины равна k.
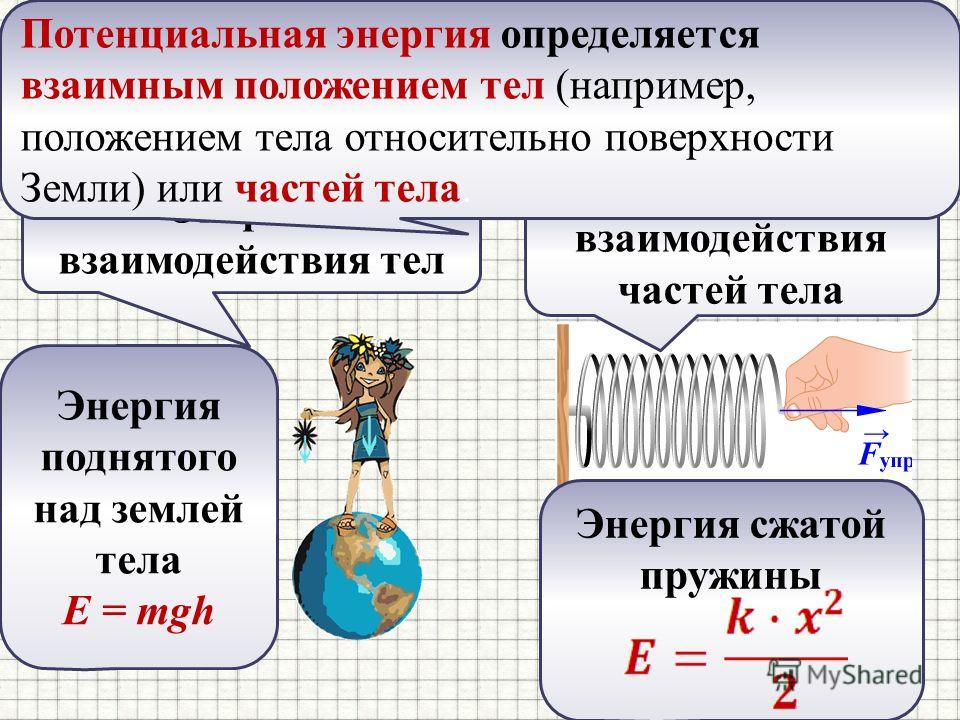 Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.
Груз оттянули вниз на расстояние x от положения равновесия и отпустили с начальной скоростью, равной нулю. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих колебания маятника.Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
1) амплитуда колебаний скорости
2) циклическая частота колебаний
3) максимальная кинетическая энергия груза
4) период колебаний
А) Имеем пружинный маятник массой m и жесткостью пружины k, тогда период свободных колебаний этого маятника определяется по формуле , а частота как . Циклическая частота , следовательно, для буквы А имеем ответ под номером 2.
Б) Для пружинного маятника известны формулы кинетической энергии и потенциальной энергии . Учитывая, что начальная скорость тела равна 0, то вся потенциальная энергия переходит в кинетическую, то есть .
 Ответ под номером 3.
Ответ под номером 3.Пружинный маятник, состоящий из груза и лёгкой пружины, совершает колебания. В момент, когда груз находится в крайнем положении, его немного подталкивают вдоль оси пружины в направлении от положения
равновесия. Как в результате этого изменяются максимальная кинетическая энергия груза маятника и частота его колебаний?
Для каждой величины определите соответствующий характер изменения:
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Максимальная кинетическая энергия груза маятника Частота колебаний маятника Груз подтолкнули от положения равновесия, откуда следует, что амплитуда колебаний груза увеличится. При этом увеличится также и максимальная потенциальная энергия пружины.
 По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.
По закону сохранения энергии, это приведет к увеличению максимальной кинетической энергии груза маятника.Период и частота пружинного маятника зависят только от массы груза и жесткости пружины. Таким образом, при увеличении амплитуды колебаний груза, частота колебаний маятника не изменится.
Законы фотоэлектрического эффекта, фототок насыщения, работа выхода, уравнение Эйнштейна для фнешнего фотоэффекта. Тесты онлайн, подготовка к ЦТ, курсы по физике в Минске
Тестирование онлайн
Фотоэффект. Основные понятия
Фотон, фотоэффект
Фотоэлектрический эффект
Фотоэффектом называется явление взаимодействия электромагнитного излучения с веществом, в результате которого энергия излучения передается электронам вещества. Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами.
 Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.Уравнение Эйнштейна для фотоэффекта
На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии электрона:
Законы внешнего фотоэффекта
Столетовым Александром Григорьевичем (1839 – 1896) экспериментально были установлены законы внешнего фотоэффекта.
Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
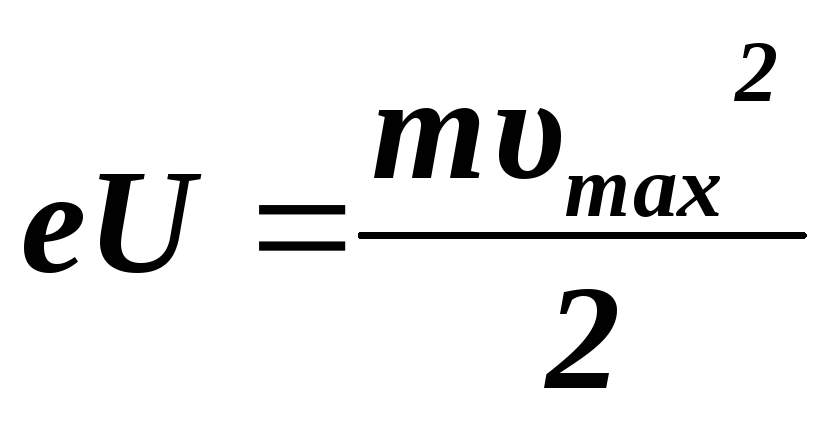
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля. Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового излучения.
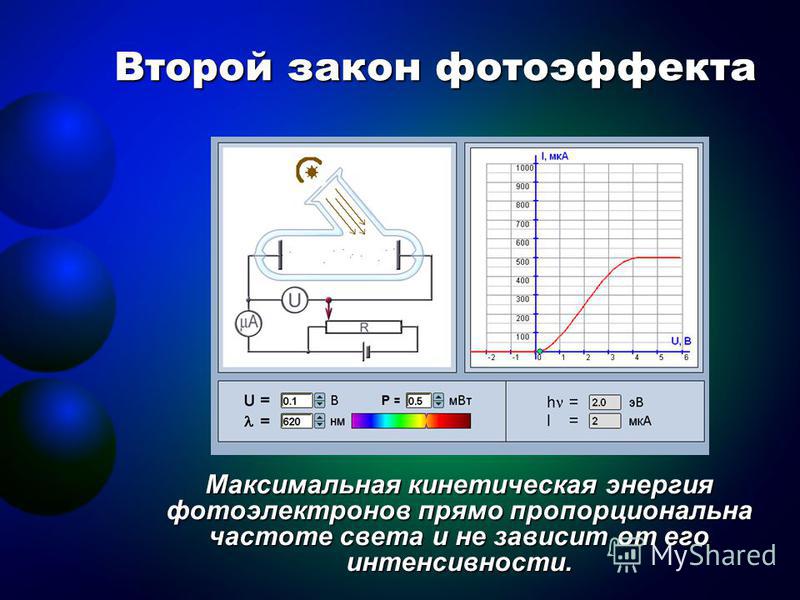 Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.Фотоэлектрический эффект | Физика
Цели обучения
К концу этого раздела вы сможете:
- Опишите типичный эксперимент с фотоэлектрическим эффектом.
- Определите максимальную кинетическую энергию фотоэлектронов, испускаемых фотонами одной энергии или длины волны, если задана максимальная кинетическая энергия фотоэлектронов для другой энергии или длины волны фотонов.
Когда свет падает на материалы, он может выбрасывать из них электроны.Это называется фотоэлектрическим эффектом , что означает, что свет (фото , фото ) производит электричество. Одно из распространенных применений фотоэлектрического эффекта – это экспонометры, например, те, которые регулируют автоматическую диафрагму на различных типах камер. Аналогичным образом, другое применение – солнечные элементы, которые вы, вероятно, использовали в своем калькуляторе или видели на крыше или на дорожных знаках.
 Они используют фотоэлектрический эффект для преобразования света в электричество для работы различных устройств.
Они используют фотоэлектрический эффект для преобразования света в электричество для работы различных устройств.Рисунок 1.Фотоэлектрический эффект можно наблюдать, позволяя свету падать на металлическую пластину в этой откачанной трубке. Электроны, испускаемые светом, собираются на коллекторном проводе и измеряются как ток. Затем можно отрегулировать замедляющее напряжение между коллекторным проводом и пластиной, чтобы определить энергию выброшенных электронов. Например, если он достаточно отрицательный, никакие электроны не достигнут провода. (кредит: П. П. Урон)
Этот эффект известен уже более века и может быть изучен с помощью устройства, подобного показанному на рисунке 1.На этом рисунке показана вакуумная трубка с металлической пластиной и коллекторным проводом, которые соединены источником переменного напряжения, причем коллектор более отрицательный, чем пластина. Когда свет (или другое электромагнитное излучение) попадает на пластину в откачанной трубке, она может выбрасывать электроны.
 Если энергия электронов в электрон-вольтах (эВ) превышает разность потенциалов между пластиной и проводом в вольтах, некоторое количество электронов будет собираться на проводе. Поскольку энергия электронов в эВ составляет эВ, , где q – заряд электрона, а В, – разность потенциалов, энергию электронов можно измерить, регулируя тормозящее напряжение между проводом и пластиной.Напряжение, при котором электроны не достигают провода, равно энергии в эВ. Например, если –3,00 В едва останавливает электроны, их энергия составляет 3,00 эВ. Количество выброшенных электронов можно определить, измерив ток между проводом и пластиной. Чем больше света, тем больше электронов; небольшая схема позволяет использовать это устройство в качестве экспонометра.
Если энергия электронов в электрон-вольтах (эВ) превышает разность потенциалов между пластиной и проводом в вольтах, некоторое количество электронов будет собираться на проводе. Поскольку энергия электронов в эВ составляет эВ, , где q – заряд электрона, а В, – разность потенциалов, энергию электронов можно измерить, регулируя тормозящее напряжение между проводом и пластиной.Напряжение, при котором электроны не достигают провода, равно энергии в эВ. Например, если –3,00 В едва останавливает электроны, их энергия составляет 3,00 эВ. Количество выброшенных электронов можно определить, измерив ток между проводом и пластиной. Чем больше света, тем больше электронов; небольшая схема позволяет использовать это устройство в качестве экспонометра.Что действительно важно в фотоэлектрическом эффекте, так это то, что Альберт Эйнштейн вывел из него. Эйнштейн понял, что существует несколько характеристик фотоэлектрического эффекта, которые можно объяснить, только если ЭМ-излучение само квантовать : очевидно, непрерывный поток энергии в ЭМ-волне на самом деле состоит из квантов энергии, называемых фотонами.
 В своем объяснении фотоэлектрического эффекта Эйнштейн определил квантованную единицу или квант электромагнитной энергии, которую мы теперь называем фотоном , с энергией, пропорциональной частоте электромагнитного излучения. В форме уравнения энергия фотона равна E = hf , где E – энергия фотона с частотой f и h – постоянная Планка. Эта революционная идея похожа на квантование Планком энергетических состояний в генераторах черного тела, но это совсем другое.Это квантование самого электромагнитного излучения. ЭМ-волны состоят из фотонов и не являются непрерывными гладкими волнами, как описано в предыдущих главах, посвященных оптике. Их энергия поглощается и испускается кусками, а не непрерывно. Это в точности согласуется с квантованием уровней энергии в генераторах черного тела Планком, поскольку эти генераторы увеличивают и уменьшают свою энергию с шагом hf за счет поглощения и испускания фотонов с E = hf .
В своем объяснении фотоэлектрического эффекта Эйнштейн определил квантованную единицу или квант электромагнитной энергии, которую мы теперь называем фотоном , с энергией, пропорциональной частоте электромагнитного излучения. В форме уравнения энергия фотона равна E = hf , где E – энергия фотона с частотой f и h – постоянная Планка. Эта революционная идея похожа на квантование Планком энергетических состояний в генераторах черного тела, но это совсем другое.Это квантование самого электромагнитного излучения. ЭМ-волны состоят из фотонов и не являются непрерывными гладкими волнами, как описано в предыдущих главах, посвященных оптике. Их энергия поглощается и испускается кусками, а не непрерывно. Это в точности согласуется с квантованием уровней энергии в генераторах черного тела Планком, поскольку эти генераторы увеличивают и уменьшают свою энергию с шагом hf за счет поглощения и испускания фотонов с E = hf . Мы не наблюдаем это своими глазами, потому что в обычных источниках света так много фотонов, что отдельные фотоны остаются незамеченными.(См. Рис. 2.) Следующий раздел текста (Энергии фотонов и электромагнитный спектр) посвящен обсуждению фотонов и некоторых их характеристик и значений. А пока мы будем использовать концепцию фотона для объяснения фотоэлектрического эффекта, как это делал Эйнштейн.
Мы не наблюдаем это своими глазами, потому что в обычных источниках света так много фотонов, что отдельные фотоны остаются незамеченными.(См. Рис. 2.) Следующий раздел текста (Энергии фотонов и электромагнитный спектр) посвящен обсуждению фотонов и некоторых их характеристик и значений. А пока мы будем использовать концепцию фотона для объяснения фотоэлектрического эффекта, как это делал Эйнштейн.Рис. 2. Электромагнитная волна с частотой f состоит из фотонов или отдельных квантов электромагнитного излучения. Энергия каждого фотона составляет E = hf , где h – постоянная Планка, а f – частота электромагнитного излучения.Более высокая интенсивность означает больше фотонов на единицу площади. Фонарь излучает большое количество фотонов с множеством разных частот, следовательно, другие имеют энергию E ′ = hf ′ и так далее.
Фотоэлектрический эффект имеет свойства, описанные ниже. Все эти свойства согласуются с идеей о том, что отдельные фотоны электромагнитного излучения поглощаются отдельными электронами в материале, при этом электрон получает энергию фотона.
 Некоторые из этих свойств несовместимы с представлением о том, что электромагнитное излучение представляет собой простую волну.Для простоты рассмотрим, что происходит с монохроматическим электромагнитным излучением, в котором все фотоны имеют одинаковую энергию hf .
Некоторые из этих свойств несовместимы с представлением о том, что электромагнитное излучение представляет собой простую волну.Для простоты рассмотрим, что происходит с монохроматическим электромагнитным излучением, в котором все фотоны имеют одинаковую энергию hf .- Если мы изменим частоту электромагнитного излучения, падающего на материал, мы обнаружим следующее: для данного материала существует пороговая частота f 0 для электромагнитного излучения, ниже которой электроны не выбрасываются, независимо от интенсивность. Отдельные фотоны взаимодействуют с отдельными электронами. Таким образом, если энергия фотона слишком мала, чтобы оторвать электрон, электроны выбрасываться не будут.Если бы электромагнитное излучение было простой волной, достаточную энергию можно было бы получить, увеличивая интенсивность.
- Как только электромагнитное излучение попадает на материал, электроны выбрасываются без задержки . Как только отдельный фотон достаточно высокой частоты поглощается отдельным электроном, электрон выбрасывается. Если бы электромагнитное излучение было простой волной, потребовалось бы несколько минут для того, чтобы на металлическую поверхность поступила энергия, достаточная для выброса электрона.
- Число электронов, выбрасываемых в единицу времени, пропорционально интенсивности электромагнитного излучения и никаким другим характеристикам.ЭМ-излучение высокой интенсивности состоит из большого количества фотонов на единицу площади, причем все фотоны имеют одинаковую характеристическую энергию hf .
- Если мы изменим интенсивность электромагнитного излучения и измерим энергию выброшенных электронов, мы найдем следующее: Максимальная кинетическая энергия выброшенных электронов не зависит от интенсивности электромагнитного излучения . Поскольку в материале так много электронов, крайне маловероятно, что два фотона будут взаимодействовать с одним и тем же электроном одновременно, тем самым увеличивая передаваемую им энергию.Вместо этого (как отмечено в пункте 3 выше), повышенная интенсивность приводит к выбрасыванию большего количества электронов той же энергии. Если бы электромагнитное излучение было простой волной, более высокая интенсивность могла бы дать больше энергии, и электроны с более высокой энергией были бы выброшены.
- Кинетическая энергия выброшенного электрона равна энергии фотона за вычетом энергии связи электрона в конкретном материале. Отдельный фотон может отдать всю свою энергию электрону. Энергия фотона частично используется для отрыва электрона от материала.Остальное идет на кинетическую энергию выброшенного электрона. В форме уравнения это дается следующим образом: KE e = hf – BE, где KE e – максимальная кинетическая энергия выброшенного электрона, hf – энергия фотона, а BE – максимальная кинетическая энергия выброшенного электрона. энергия связи электрона с конкретным материалом. (BE иногда называют работой выхода материала.) Это уравнение, введенное Эйнштейном в 1905 году, объясняет свойства фотоэлектрического эффекта количественно.Отдельный фотон электромагнитного излучения (по-другому не приходит) взаимодействует с отдельным электроном, выделяя достаточно энергии, BE, чтобы оторвать его, а остальная часть переходит в кинетическую энергию. Энергия связи BE = hf 0 , где f 0 – пороговая частота для конкретного материала. На рисунке 3 показан график максимального значения KE e в зависимости от частоты падающего электромагнитного излучения, падающего на конкретный материал.
Рисунок 3.Фотоэлектрический эффект. График кинетической энергии выброшенного электрона, KE e , в зависимости от частоты электромагнитного излучения, падающего на определенный материал. Существует пороговая частота, ниже которой электроны не выбрасываются, потому что отдельный фотон, взаимодействующий с отдельным электроном, имеет недостаточную энергию, чтобы оторвать его. Выше пороговой энергии KE e линейно увеличивается с f , что соответствует KE e = hf – BE.Наклон этой линии составляет h – данные могут быть использованы для экспериментального определения постоянной Планка. Эйнштейн дал первое успешное объяснение таким данным, предложив идею фотонов – квантов электромагнитного излучения.
Идея Эйнштейна о квантовании электромагнитного излучения сыграла решающую роль в зарождении квантовой механики. Это гораздо более общая концепция, чем может предполагать ее объяснение фотоэлектрического эффекта. Все ЭМ-излучение также можно моделировать в виде фотонов, и характеристики ЭМ-излучения полностью соответствуют этому факту.(Как мы увидим в следующем разделе, многие аспекты электромагнитного излучения, такие как опасность ультрафиолетового (УФ) излучения, можно объяснить только свойствами фотонов.) Более известный своей современной теорией относительности Эйнштейн заложил важное семя для квантовая механика в 1905 году, в том же году он опубликовал свою первую статью по специальной теории относительности. Его объяснение фотоэлектрического эффекта легло в основу Нобелевской премии, присужденной ему в 1921 году. Хотя в этой награде были отмечены и другие его вклады в теоретическую физику, специальная и общая теория относительности не были полностью признаны, несмотря на то, что были частично подтверждены экспериментом. к 1921 г.Хотя этот великий человек почитается как герой, он так и не получил Нобелевской премии за свою самую известную работу – относительность.
Пример 1. Расчет энергии фотона и фотоэлектрического эффекта: фиолетовый свет
1. Какова энергия в джоулях и электрон-вольтах у фотона фиолетового света с длиной волны 420 нм?
2. Какова максимальная кинетическая энергия электронов, выбрасываемых из кальция фиолетовым светом с длиной волны 420 нм, при условии, что энергия связи (или работа выхода) электронов для металлического кальция равна 2.71 эВ?
Стратегия
Чтобы решить часть 1, обратите внимание, что энергия фотона определяется как E = hf . Для Части 2, как только энергия фотона вычислена, это прямое применение KE e = hf – BE для определения максимальной кинетической энергии выброшенного электрона, поскольку BE дано.
Решение для Части 1
Энергия фотона определяется как E = hf .
Поскольку нам дается длина волны, а не частота, мы решаем знакомую зависимость c = fλ для частоты, получая [латекс] f = \ frac {c} {\ lambda} \\ [/ latex ].{-19} \ text {J}} = 2,96 \ text {eV} \\ [/ latex]
Решение для Части 2
Теперь определение кинетической энергии выброшенного электрона представляет собой простое приложение уравнения KE e = hf – BE. Подстановка энергии фотона и энергии связи дает KE e = hf – BE = 2,96 эВ – 2,71 эВ = 0,246 эВ.
Обсуждение
Энергия этого 420-нм фотона фиолетового света составляет крошечную долю джоуля, и поэтому неудивительно, что нам было бы трудно ощутить непосредственно один фотон – люди больше настроены на энергии порядка джоулей. .Но глядя на энергию в электрон-вольтах, мы видим, что у этого фотона достаточно энергии, чтобы воздействовать на атомы и молекулы. Молекула ДНК может быть разрушена с помощью энергии около 1 эВ, а типичные атомные и молекулярные энергии имеют порядок эВ, так что УФ-фотон в этом примере может иметь биологические эффекты. Выброшенный электрон (так называемый фотоэлектрон ) имеет довольно низкую энергию, и он не улетит далеко, кроме как в вакууме. Электрон будет остановлен тормозящим потенциалом, равным нулю.26 эВ. Фактически, если бы длина волны фотона была больше, а его энергия меньше 2,71 эВ, то формула дала бы отрицательную кинетическую энергию, что невозможно. Это просто означает, что фотоны с длиной волны 420 нм с их энергией 2,96 эВ ненамного превышают порог частоты. Вы можете сами убедиться, что пороговая длина волны составляет 459 нм (синий свет). Это означает, что если в люксметре используется металлический кальций, он будет нечувствителен к длинам волн более длинных, чем у синего света. Такой люксметр, например, будет совершенно нечувствителен к красному свету.
Исследования PhET: фотоэлектрический эффект
Посмотрите, как свет сбивает электроны с металлической мишени, и воссоздайте эксперимент, положивший начало квантовой механике.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Фотоэлектрический эффект – это процесс, при котором электромагнитное излучение выбрасывает электроны из материала.
- Эйнштейн предложил фотоны как кванты электромагнитного излучения с энергией E = hf , где f – частота излучения.
- Все электромагнитное излучение состоит из фотонов. Как объяснил Эйнштейн, все характеристики фотоэлектрического эффекта обусловлены взаимодействием отдельных фотонов с отдельными электронами.
- Максимальная кинетическая энергия KE e выброшенных электронов (фотоэлектронов) определяется как KE e = hf – BE, где hf – энергия фотона, а BE – энергия связи (или работа функция) электрона к конкретному материалу.
Концептуальные вопросы
- Является ли видимый свет единственным типом электромагнитного излучения, которое может вызвать фотоэлектрический эффект?
- Какие аспекты фотоэлектрического эффекта нельзя объяснить без фотонов? Что можно объяснить без фотонов? Последнее несовместимо с существованием фотонов?
- Является ли фотоэлектрический эффект прямым следствием волнового характера электромагнитного излучения или характера частиц электромагнитного излучения? Кратко объясните.
- Изоляторы (неметаллы) имеют более высокий БЭ, чем металлы, и фотонам труднее выбрасывать электроны из изоляторов. Обсудите, как это связано со свободными зарядами в металлах, которые делают их хорошими проводниками.
- Если вы поднимете и встряхнете кусок металла, в котором есть электроны, которые могут двигаться как ток, электроны не выпадут. Но если нагреть металл, электроны могут испариться. Объясните оба эти факта, поскольку они относятся к количеству и распределению энергии, связанной с встряхиванием объекта по сравнению с его нагреванием.
Задачи и упражнения
- Какое электромагнитное излучение с самой длинной длиной волны может выбрасывать фотоэлектрон из серебра, учитывая, что энергия связи составляет 4,73 эВ? Это в видимом диапазоне?
- Найдите фотон с самой длинной волной, который может выбросить электрон из калия, учитывая, что энергия связи составляет 2,24 эВ. Это видимое электромагнитное излучение?
- Какова энергия связи электронов в магнии в эВ, если длина самой длинной волны фотона, способного испускать электроны, составляет 337 нм?
- Вычислите энергию связи электронов в алюминии в эВ, если длина волны самого длинноволнового фотона, способного их выбросить, составляет 304 нм.
- Какова максимальная кинетическая энергия в эВ электронов, выброшенных из металлического натрия электромагнитным излучением с длиной волны 450 нм, при условии, что энергия связи составляет 2,28 эВ?
- УФ-излучение с длиной волны 120 нм падает на металлическое золото, с которым электроны связаны силой 4,82 эВ. Какова максимальная кинетическая энергия выброшенных фотоэлектронов?
- Фиолетовый свет с длиной волны 400 нм излучает электроны с максимальной кинетической энергией 0,860 эВ из металлического натрия. Какова энергия связи электронов с металлическим натрием?
- УФ-излучение с длиной волны 300 нм падает на металлический уран, выбрасывая 0.Электроны с энергией 500 эВ. Какова энергия связи электронов с металлическим ураном?
- (a) Какова длина волны электромагнитного излучения, которое выбрасывает электроны с энергией 2,00 эВ из металлического кальция, учитывая, что энергия связи составляет 2,71 эВ? (б) Что это за тип электромагнитного излучения?
- Найдите длину волны фотонов, которые выбрасывают электроны с энергией 0,100 эВ из калия, учитывая, что энергия связи равна 2,24 эВ. Эти фотоны видны?
- Какова максимальная скорость электронов, выбрасываемых из материала фотонами с длиной волны 80 нм, если они связаны с материалом 4.73 эВ?
- Фотоэлектроны из материала с энергией связи 2,71 эВ испускаются фотонами с длиной волны 420 нм. После выброса, сколько времени требуется этим электронам, чтобы пройти 2,50 см к устройству обнаружения?
- Лазер с выходной мощностью 2,00 мВт на длине волны 400 нм проецируется на металлический кальций. (а) Сколько электронов выбрасывается в секунду? (б) Какая мощность уносится электронами при энергии связи 2,71 эВ?
- (a) Рассчитайте количество фотоэлектронов, выбрасываемых за секунду из 1.Металлический натрий площадью 00 мм 2 под воздействием электромагнитного излучения с длиной волны 500 нм и интенсивностью 1,30 кВт / м 2 (интенсивность солнечного света над атмосферой Земли). (б) Учитывая, что энергия связи составляет 2,28 эВ, какая мощность уносится электронами? (c) Электроны уносят меньше энергии, чем приносят фотоны. Куда девается другая сила? Как его восстановить?
- Неоправданные результаты. Красный свет с длиной волны 700 нм проецируется на металлический магний, с которым связаны электроны 3.68 эВ. (a) Используйте KE e = hf – BE для расчета кинетической энергии выброшенных электронов. б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
- Неоправданные результаты. (a) Какова энергия связи электронов с материалом, из которого электроны с энергией 4,00 эВ выбрасываются электромагнитным излучением с длиной волны 400 нм? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
фотоэлектрический эффект: явление, при котором некоторые материалы выбрасывают электроны, когда на них попадает свет.
фотон: квант или частица электромагнитного излучения
энергия фотона: количество энергии фотона; E = hf
энергия связи: также называется работой выхода; количество энергии, необходимое для выброса электрона из материала
Избранные решения проблем и упражнения
1.263 нм
3. 3.69 эВ
5. 0,483 эВ
7. 2,25 эВ
9. (а) 264 нм; (б) Ультрафиолет
11. 1,95 × 10 6 м / с
13. (а) 4.02 × 10 15 с; (б) 0,256 мВт
15. (a) −1.90 эВ; (б) отрицательная кинетическая энергия; (c) Электроны будут выбиты.
Фотоэлектрический эффект – Гипертекст по физике
Обсуждение
дилемма
При определенных обстоятельствах свет можно использовать для выталкивания электронов, освобождая их от поверхности твердого тела.Этот процесс называется фотоэлектрическим эффектом (или фотоэлектрической эмиссией или фотоэмиссией ), материал, который может проявлять это явление, называется фотоэмиссионным , а выброшенные электроны называются фотоэлектронами ; но нет ничего, что отличало бы их от других электронов. Все электроны идентичны друг другу по массе, заряду, спину и магнитному моменту.
Фотоэлектрический эффект был впервые обнаружен в 1887 году Генрихом Герцем во время экспериментов с генератором искрового разрядника (самое раннее устройство, которое можно было назвать радио).В этих экспериментах искры, возникающие между двумя небольшими металлическими сферами в передатчике, вызывают искры, которые прыгают между двумя разными металлическими сферами в приемнике. По сравнению с более поздними радиоустройствами, с генератором искрового разрядника было заведомо трудно работать. Воздушный зазор часто должен быть меньше миллиметра, чтобы приемник надежно воспроизводил искру передатчика. Герц обнаружил, что он может увеличить чувствительность своего устройства с искровым разрядником, освещая его видимым или ультрафиолетовым светом.Более поздние исследования J.J. Томсон показал, что эта повышенная чувствительность была результатом воздействия света на электроны – частицы, которую он обнаружил в 1897 году.
Хотя это интересно, вряд ли это удивительно. Все формы электромагнитного излучения переносят энергию, и довольно легко представить, что эта энергия используется для выталкивания крошечных частиц с отрицательным зарядом с поверхности металла, где они изначально не так сильно ограничены. Однако эпоха современной физики – это одно из совершенно неожиданных и необъяснимых открытий.Последующие исследования фотоэлектрического эффекта дали результаты, не укладывающиеся в классическую теорию электромагнитного излучения. Когда он взаимодействовал с электронами, свет просто не вел себя так, как предполагалось. Теоретически для устранения этой разрыва требовалось нечто большее, чем просто заплатка. Это означало перестроить большую часть физики с нуля.
Именно Филипп Ленард, помощник Герца, провел самые ранние и окончательные исследования фотоэлектрического эффекта. Ленард использовал металлические поверхности, которые сначала очищались, а затем выдерживались под вакуумом, так что эффект можно было изучить только на металле и не подвергался никаким поверхностным загрязнениям или окислению.Металлический образец помещался в вакуумированную стеклянную трубку со второй металлической пластиной, установленной на противоположном конце. Затем трубку устанавливали или ограничивали таким образом, чтобы свет падал только на первую металлическую пластину, сделанную из исследуемого фотоэмиссионного материала. Такая трубка называется фотоэлементом (формально) или электрическим глазом (неофициально). Ленард подключил свой фотоэлемент к цепи с регулируемым источником питания, вольтметром и микроамперметром, как показано на схеме ниже.Затем он осветил фотоэмиссионную поверхность светом разной частоты и интенсивности.
Выбивая электроны из фотоэмиссионной пластины, она получит небольшой положительный заряд. Поскольку вторая пластина была соединена с первой проводкой схемы, она тоже стала бы положительной, что затем привлекло бы фотоэлектроны, свободно плавающие в вакууме, где они приземлились бы и вернулись обратно к пластине, с которой они начали. Имейте в виду, что этот эксперимент не создает электроны из света, он просто использует энергию света, чтобы толкать электроны, которые уже находятся в цепи.Фотоэлектрический ток, создаваемый этим средством, был довольно мал, но его можно было измерить с помощью микроамперметра (чувствительного гальванометра с максимальным отклонением всего в несколько микроампер). Он также служит мерой скорости, с которой фотоэлектроны покидают поверхность фотоэмиссионного материала.
Обратите внимание на то, как источник питания подключен к цепи – его отрицательный конец подключен к пластине, которая не подсвечивается. Это создает разность потенциалов, которая пытается подтолкнуть фотоэлектроны обратно к фотоэмиссионной поверхности.Когда источник питания установлен на низкое напряжение, он захватывает наименее энергичные электроны, уменьшая ток через микроамперметр. Повышение напряжения заставляет все больше энергичных электронов возвращаться, пока, наконец, ни один из них не сможет покинуть металлическую поверхность, и микроамперметр не покажет ноль. Потенциал, при котором это происходит, называется тормозным потенциалом . Это мера максимальной кинетической энергии электронов, испускаемых в результате фотоэлектрического эффекта.
Ленард обнаружил, что интенсивность падающего света не влияет на максимальную кинетическую энергию фотоэлектронов.Те, что испускались в результате воздействия очень яркого света, имели такую же энергию, как и те, которые испускались в результате воздействия очень тусклого света с той же частотой . Однако в соответствии с законом сохранения энергии из яркого источника было выброшено больше электронов, чем из тусклого.
Более поздние эксперименты, проведенные другими, в первую очередь американским физиком Робертом Милликеном в 1914 году, показали, что свет с частотами ниже определенного значения отсечки, называемого пороговой частотой , не будет выбрасывать фотоэлектроны с поверхности металла, независимо от того, насколько ярким был источник.Эти результаты были совершенно неожиданными. Учитывая, что можно перемещать электроны с помощью света и учитывая, что энергия в луче света связана с его интенсивностью, классическая физика предсказывала бы, что более интенсивный луч света будет излучать электроны с большей энергией, чем менее интенсивный луч нет неважно какая частота . Однако это было не так.
Зеленый свет действительно испускает фотоэлектроны (даже если он очень тусклый). Синий свет излучает фотоэлектроны с большей энергией, чем зеленый свет (даже если он очень тусклый). На самом деле, возможно, эти результаты не так уж типичны. Большинство элементов имеют пороговые частоты, которые являются ультрафиолетовыми, и только некоторые из них опускаются достаточно низко, чтобы быть зелеными или желтыми, как в примере, показанном выше. Все материалы с самыми низкими пороговыми частотами являются полупроводниками. Некоторые имеют пороговые частоты в инфракрасной области спектра.
Классическая модель света описывает его как поперечную электромагнитную волну.В конце XIX века в этом не было сомнений. Волновая природа света была подтверждена, когда ее успешно применили для объяснения таких оптических явлений, как дифракция, интерференция, поляризация, отражение и преломление. Если мы можем представить свет как волны в электромагнитном океане и добиться в этом успеха, то для нас не составит большого труда представить электроны на металлической поверхности как нечто вроде привязанных буев, плавающих в электромагнитной гавани. Вместе с ними приходят волны (свет), которые тянут и тянут буи (электроны).Слабые волны не действуют, но сильные могут просто выдернуть буй из причала и бросить его по течению. Волновая модель света предсказывала бы отношение энергии-амплитуды, а не отношение энергии-частоты, описанное выше. Фотоэлектрические эксперименты описывают электромагнитный океан, в котором чудовищные волны не опрокинут каноэ, а крошечные волны подбросят вас в воздух.
Если этого было недостаточно, фотоэлектроны, кажется, выскакивают из поверхности слишком быстро. Когда интенсивность света очень низкая, скорость, с которой энергия доставляется к поверхности, совершенно вялая.Любому электрону требуется некоторое время, чтобы захватить достаточно этой диффузной энергии, чтобы освободиться. Должно, но это не так. В тот момент, когда свет соответствующей частоты любой интенсивности падает на фотоэмиссионную поверхность, по крайней мере, один электрон всегда вылетает немедленно ( t <10 −9 с). Продолжая аналогию с океаном, представьте себе гавань, полную маленьких лодок (электронов). Море спокойное, за исключением крошечной ряби на поверхности (низкая интенсивность, коротковолновый свет).Большинство лодок в гавани не подвержены воздействию этих волн, но одну из них вырывают из гавани и отправляют вверх, как реактивный самолет. Что-то здесь не так. Никакие механические волны не ведут себя так, а вот свет.
новая идея
Двумя факторами, влияющими на максимальную кинетическую энергию фотоэлектронов, являются частота падающего излучения и материал на поверхности. Как показано на графике ниже, энергия электронов увеличивается с частотой простым линейным образом выше порогового значения.Все три кривые имеют одинаковый наклон (равный постоянной Планка ), что показывает, что отношение энергии к частоте является постоянным для всех материалов. Фотоэмиссия ниже пороговой частоты не происходит. Каждая кривая имеет различную точку пересечения на оси энергии, которая показывает, что пороговая частота является функцией материала.
Увеличить Гением, который понял, что здесь происходит, был никто иной, как самый известный в мире физик Альберт Эйнштейн.В 1905 году Эйнштейн понял, что свет ведет себя так, как если бы он состоял из крошечных частиц (первоначально называвшихся квантами , а позже названных фотонами ), и что энергия каждой частицы была пропорциональна частоте электромагнитного излучения, которое было часть. Вспомните из предыдущего раздела этой книги, что Макс Планк изобрел понятие квантованного электромагнитного излучения как способ решения технической проблемы с идеализированными источниками электромагнитного излучения, называемыми черными телами.Напомним также, что Планк не верил, что излучение на самом деле разбивается на маленькие части, как показал его математический анализ. Он думал, что все это было всего лишь изобретением, которое дало ему правильные ответы. Гений Эйнштейна заключался в признании того, что изобретение Планка на самом деле было разумным описанием реальности. То, что мы воспринимаем как непрерывную волну электромагнитного излучения, на самом деле является потоком дискретных частиц.
Es scheint mir nun in der Tat, daß die Beobachtungen über die «schwarze Strahlung», Photolumineszenz, die Erzeugung von Kathodenstrahlen durch ultraviolettes Licht und andere die Erzeugung bez.Verwandlung des Lichtes betreffende Erscheinungsgruppen besser verstandlich erscheinen unter der Annahme, daß die Energie des Lichtes diskontinuierlich im Raume verteilt sei. Nach der hier ins Auge zu fassenden Annahme ist bei Ausbreitung eines von einem Punkte ausgehenden Lichtstrahles die Energie nicht kontinuierlich auf größer und größer werdencle Räume verteilt, sondvern oh esquten bestehten Diesel Endgenne aus teilen und nur als Ganze Absorbert und erzeugt werden können.
Альберт Эйнштейн, 1905
На самом деле, мне кажется, что наблюдения “излучения черного тела”, фотолюминесценции, образования катодных лучей ультрафиолетовым светом и других явлений, связанных с излучением или преобразованием света, можно лучше понять, если предположить, что энергия свет распространяется в пространстве прерывисто. Согласно рассмотренному здесь допущению, когда световой луч, исходящий из точки, распространяется, энергия не распределяется непрерывно по постоянно увеличивающемуся объему, а состоит из конечного числа квантов энергии, локализованных в пространстве, которые движутся, не разделяясь. и которые могут поглощаться или выделяться только целиком.
Альберт Эйнштейн, 1905
уравнения
Эйнштейн и Милликен описали фотоэлектрический эффект с помощью формулы (в современных обозначениях), которая связывает максимальную кинетическую энергию ( K max ) фотоэлектронов с частотой поглощенных фотонов ( f ) и пороговой частотой ( f 0 ) фотоэмиссионной поверхности.
K макс. = h ( f – f 0 )
или, если хотите, энергии поглощенных фотонов ( E ) и работы выхода (φ) поверхности
K макс = E – φ
, где первый член – это энергия поглощенных фотонов ( E ) с частотой ( f ) или длиной волны (λ)
, а второй член – работа выхода (φ) поверхности с пороговой частотой ( f 0 ) или пороговой длиной волны (λ 0 )
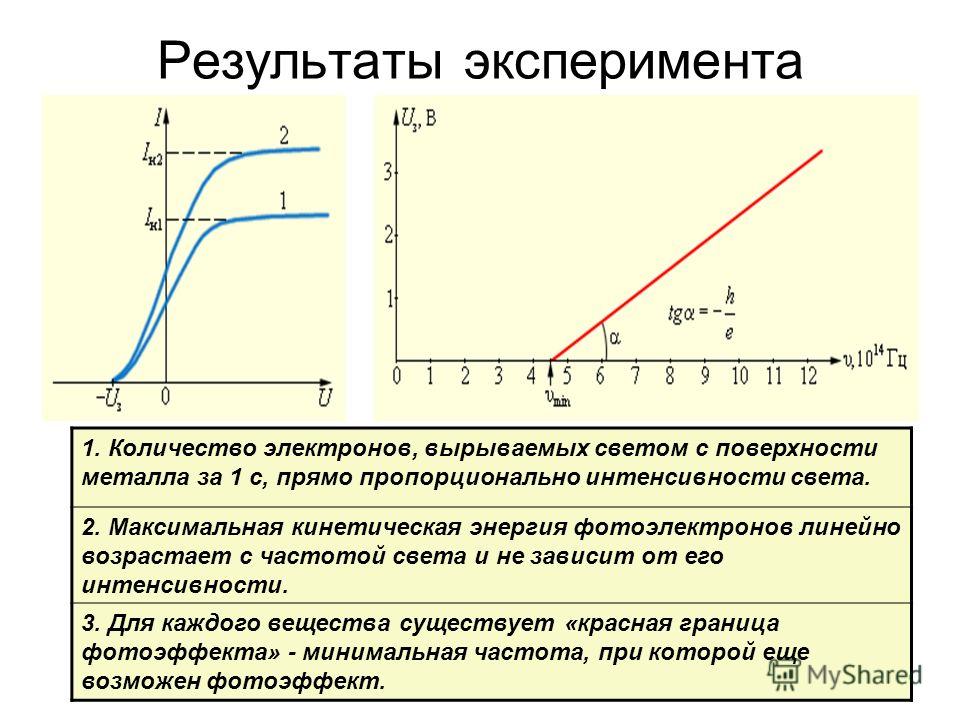
Максимальная кинетическая энергия ( K max ) фотоэлектронов (с зарядом e ) может быть определена из тормозящего потенциала ( V 0 ).
Таким образом…
K макс = эВ 0
Если заряд ( e ) выражен в кулонах, энергия будет рассчитываться в джоулях. Когда заряд ( e ) задан в элементарных зарядах, энергия будет рассчитана в электрон-вольт . В результате получается множество констант. Используйте тот, который больше всего подходит для вашей проблемы.
Постоянная Планка с вариациями единиц СИ приемлемо
единиц, отличных от системы СИh 6.63 × 10 −34 Дж с 4,14 × 10 −15 эВ с HC 1,99 × 10 −25 Дж м 1240 эВ нм Наконец, скорость ( n / t ), с которой фотоэлектроны (с зарядом e ) испускаются с фотоэмиссионной поверхности, может быть определена по фотоэлектрическому току ( I ).
Таким образом…
технология
- “электрический глаз”, экспонометр, звуковая дорожка фильма
- фотопроводимость: увеличение электропроводности неметаллического твердого тела при воздействии электромагнитного излучения.Увеличение проводимости связано с добавлением свободных электронов, высвобождаемых при столкновении с фотонами. Скорость, с которой генерируются свободные электроны, и время, в течение которого они остаются свободными, определяет величину увеличения.
- фотогальваника: выброшенный электрон проходит через излучающий материал, чтобы войти в твердый электрод, контактирующий с фотоэмиттером (вместо путешествия через вакуум к аноду), что приводит к прямому преобразованию лучистой энергии в электрическую
- фотостатическое копирование
Объяснитель урока: кинетическая энергия фотоэлектронов
В этом объяснителе мы узнаем, как рассчитать максимально возможную кинетическую энергию электронов, выбрасываемых с поверхности. металла за счет фотоэффекта.
Фотоэлектрический эффект – это процесс выхода электронов с поверхности металла после поглощения электромагнитного излучения. Экспериментальная установка, использованная для наблюдения фотоэлектрического эффекта, показана на диаграмме ниже.
Две отдельные металлические пластины присоединены к цепи, к которой последовательно подключен амперметр. Металлические пластины заключены в вакуумная камера, чтобы воздух не влиял на эксперимент. Свет направлен на одну из металлических пластин.Если падающий свет имеет достаточно большую энергию, электроны выбрасываются с поверхности металла. Эти выброшенные электроны известны как «Фотоэлектроны». Амперметр определяет ток, когда фотоэлектроны достигают соседней пластины.
Напомним, что свет можно моделировать как частицу. Частицы света известны как фотоны. Каждый фотон имеет дискретное количество энергия, описываемая формулой 𝐸 = ℎ𝑓, где представляет постоянную Планка, а 𝑓 представляет частоту фотона.
Каждый падающий фотон передает энергию одному электрону на поверхности металла. Электрон уйдет с поверхности если у фотона достаточно большой энергии. Поскольку энергия фотона определяется частотой, не имеет значения, какая амплитуда световой волны – фотоэлектрический эффект индуцируется, пока свет имеет достаточно высокую частоту. Отношения между энергией и частотой, а также независимость этих значений от амплитуды, показаны в таблице ниже.
Теперь, когда мы установили основы фотоэлектрического эффекта, давайте подробнее рассмотрим передачу энергии между фотоны и электроны.
Напомним, что в атомных ядрах электроны находятся на дискретных уровнях энергии. На каждом уровне электроны имеют разное количество энергии. которые удерживают их привязанными к атомной системе; это количество энергии называется «работой выхода». Мы можем рассматривать работа выхода, обозначаемая 𝑊, как барьер, удерживающий электрон на связи с материалом.Если количество энергии электрону передается величина, превышающая работу выхода, барьер преодолевается и электрон освобождается от своей связи.
Проводящие материалы, такие как металлы, имеют относительно низкую работу выхода. Таким образом, самые удаленные электроны на металлической поверхности могут в некоторой степени легко покинуть материал, если они наберут достаточно энергии. Это то, что происходит при фотоэффекте.
Если электрон получает энергию, превышающую работу выхода, оставшаяся энергия становится кинетической энергией электрон.Это можно наблюдать, поскольку фотоэлектроны часто покидают поверхность металла со значительными скоростями.
Мы можем определить максимальную кинетическую энергию фотоэлектрона, если знаем энергию, передаваемую фотоном и работа выхода для металлической поверхности. Количество кинетической энергии, которую имеет полученный фотоэлектрон, равно энергии что фотон передается ему за вычетом работы выхода, которую необходимо было преодолеть.
Давайте формально определим эту взаимосвязь.
Определение: максимальная кинетическая энергия фотоэлектрона при заданной частоте
Максимальная кинетическая энергия фотоэлектрона определяется выражением 𝐸 = ℎ𝑓 − 𝑊, макс. где ℎ – постоянная Планка, 𝑓 – частота падающего фотона, а 𝑊 – работа выхода металлической поверхности.
Мы попрактикуемся в использовании этого уравнения в следующем примере.
Пример 1: Расчет максимальной кинетической энергии фотоэлектронов
Полированная металлическая поверхность в вакууме освещается светом лазера, в результате чего электроны испускаются из поверхность металла.Свет имеет частоту 2,00 × 10 Гц. Работа выхода металл 1,40 эВ. Какая максимальная кинетическая энергия электроны могут иметь? Используйте значение 4,14 × 10 эВ⋅с для Постоянная Планка. Ответьте в электрон-вольтах.
Ответ
Начнем с того, что вспомним уравнение для максимальной кинетической энергии фотоэлектрона: 𝐸 = ℎ𝑓 − 𝑊.max
Нам даны значения для ℎ, 𝑓 и 𝑊; подставляя их, мы имеем 𝐸 = 4.14 × 10⋅2,00 × 10 − 1,40 = 6,88.maxeVsHzeVeV
Таким образом, мы обнаружили, что максимальная кинетическая энергия, которую могут иметь электроны, равна 6,88 эВ.
Часто бывает полезно построить график уравнения максимальной кинетической энергии фотоэлектрона. Сюжет фотоэлектронной кинетики энергия в зависимости от частоты падающего фотона показана ниже.
Напомним, что для выброса электрона падающий фотон должен иметь достаточно высокую частоту (и, следовательно, энергию), чтобы преодолеть рабочую функцию.По этой причине мы регистрируем нулевую энергию фотоэлектронов для низкочастотного света, как показано на рисунке горизонтальная часть графика. Это показывает, где падающий свет имеет слишком низкую энергию для удаления электронов, поэтому мы обнаруживаем нет фотоэлектронов и кинетической энергии.
Однако при достаточно высокой частоте фотонов работа выхода преодолевается. Напомним, что работа выхода материала – это постоянное значение, поэтому после его преодоления кинетическая энергия фотоэлектронов увеличивается с увеличением частоты падающего фотона. увеличивается.Таким образом, 𝐸max прямо пропорционально 𝑓, и соотношение линейный, как показано на наклонной, увеличивающейся части графика.
Мы можем определить некоторые свойства прибора, анализируя его график зависимости 𝐸max от 𝑓. В частности, нас интересует точка, в которой график отклоняется от горизонтальной оси, как выделено на рисунке ниже. Эта точка возникает при значении пороговой частоты, которое мы назовем 𝑓.
Это определяет поворотный момент в эксперименте, когда фотоны передают достаточно энергии, чтобы электроны были выброшены.Здесь «оставшаяся» кинетическая энергия фотоэлектронов равна нулю, поскольку энергия фотона едва хватает на преодоление работы выхода.
Мы можем использовать эту информацию для экспериментального определения работы выхода материала. Для начала переставим Формула максимальной кинетической энергии для решения относительно for: 𝑊 = ℎ𝑓 − 𝐸.max
Напомним, что 𝐸 = 0max на пороговой частоте,. Подставляя эти значения в, мы имеем 𝑊 = ℎ𝑓.
Таким образом, на пороговой частоте работа выхода равна энергии падающего фотона.Мы будем практиковать этот метод определения работы выхода в следующей паре примеров.
Пример 2: Определение рабочей функции с использованием графика зависимости энергии электрона от энергии фотона
Перестраиваемый лазер используется для освещения поверхности металла светом разных частот. Выше определенного Частота света, электроны испускаются с поверхности металла. На графике показана максимальная кинетическая энергия электронов, испускаемых против энергии фотонов.Какова работа выхода металла?
Ответ
Этот график иллюстрирует взаимосвязь между энергией падающего фотона и максимальной кинетической энергией фотоэлектрона. уходя с металлической поверхности. Напомним уравнение, связывающее эти значения, 𝐸 = ℎ𝑓 − 𝑊, макс. где ℎ𝑓 описывает энергию падающего фотона с учетом его частоты и планковского постоянная, ℎ. Мы хотим найти работу выхода для этой металлической поверхности, поэтому мы изменим это уравнение на решить для 𝑊: 𝑊 = ℎ𝑓 − 𝐸.max
Мы можем использовать значения координат из любой точки на графике, чтобы подставить их в это уравнение. Как правило, самый простой способ работа с “пороговой частотой” 𝑓 или горизонтальным отрезком графика, поскольку в этой точке 𝐸 = 0max. Таким образом, мы можем исключить член 𝐸max в уравнении, и мы остаемся с 𝑊 = ℎ𝑓.
Следовательно, энергия фотона в этой точке равна работе выхода материала.
График пересекает горизонтальную ось в точке 2.6 эВ, поэтому мы обнаружили, что работа выхода металла составляет 2,6 эВ.
Пример 3: Определение работы работы с использованием графика зависимости энергии электрона от энергии фотона
На графике показана максимальная кинетическая энергия фотоэлектронов, когда разные металлы освещаются разным светом. частоты.
- Какой металл имеет наименьшую работу выхода?
- Какой металл имеет самую высокую работу выхода?
Ответ
Часть 1
Напомним формулу для максимальной кинетической энергии фотоэлектрона, 𝐸 = ℎ𝑓 − 𝑊, макс. где 𝑊 – работа выхода, а ℎ𝑓 – значение энергии фотона, которое зависит от фотона. частота и постоянная Планка ℎ.
Этот график иллюстрирует свойства пяти различных элементов. Все пять линий на графике имеют одинаковый наклон и выделяются только их пересечениями по горизонтальной оси.
Мы можем узнать об элементах, где их графики пересекаются с горизонтальной осью, потому что это значение описывает, где падающие фотоны имеют достаточно энергии, чтобы преодолеть работу выхода. Таким образом, 𝐸 = 0max, но фотоэлектроны все еще создаются. Мы можем подставить это значение, чтобы определить связь между работой выхода. и энергия фотона: 0 = ℎ𝑓 − 𝑊, или же ℎ𝑓 = 𝑊.
Следовательно, энергия фотона в этой точке равна работе выхода материала.
Меньшая точка пересечения по горизонтальной оси означает, что для преодоления работы выхода требуется более низкое значение энергии фотона. Таким образом, мы можем сравнивать величины работы выхода материалов, сравнивая их пороговые значения энергии фотонов. Линия цезия имеет наименьшее горизонтальное пересечение.
Таким образом, мы обнаружили, что цезий имеет самую низкую работу выхода.
Часть 2
Снова проверив график, мы видим, что платина является элементом с наибольшей энергией фотонов на пороге. где 𝐸 = 0max.
Следовательно, платина имеет наивысшую работу выхода.
Мы изучили, как определить работу выхода материала по графику зависимости его кинетической энергии электронов от частота падающего фотона. Теперь предположим, что мы хотим знать, как это связано с длиной волны падающего света, а не с частотой. Для этого мы должны разработать взаимосвязь между частотой и длиной волны света, чтобы мы могли заменить 𝑓 из нашего уравнения и подставить 𝜆 в.
Мы можем связать частоту и длину волны, используя уравнение скорости волны для электромагнитной волны, 𝑐 = 𝜆𝑓, где 𝑐 – скорость света.Решая эту формулу для частоты, мы имеем 𝑓 = 𝑐𝜆.
Теперь вспомним уравнение кинетической энергии электрона, 𝑊 = ℎ𝑓 − 𝐸.max
Наконец, мы можем сделать замену для частоты: 𝑊 = ℎ𝑐𝜆 − 𝐸.max
Это уравнение позволяет связать работу выхода и максимальную кинетическую энергию фотоэлектрона с длиной волны падающего света.
Мы можем изменить эту формулу, чтобы определить максимальную кинетическую энергию фотоэлектрона при заданной длине волны падающего фотона как указано ниже.
Определение: максимальная кинетическая энергия фотоэлектрона при заданной длине волны
Максимальная кинетическая энергия фотоэлектрона определяется выражением 𝐸 = ℎ𝑐𝜆 − 𝑊, макс. где ℎ – постоянная Планка, 𝑐 – скорость света, 𝜆 – длина волны падающего фотона, а 𝑊 – работа выхода металлической поверхности.
Обратите внимание, что в частотной форме уравнения в числителе появляется 𝑓, что позволяет использовать линейный соотношение между 𝑓 и 𝐸макс. Напротив, в форме длины волны уравнения, появляется в знаменателе, что означает, что график 𝐸max против 𝜆 не имеет линейного наклона.Общий вид графика кинетической энергии электронов в зависимости от длины волны фотона показано ниже.
Обратите внимание, что фотоэлектроны не испускаются, когда длина волны фотона превышает определенное значение. Это потому, что по мере того, как мы увеличиваем длину волны падающего света, мы одновременно уменьшаем его частоту (и, следовательно, энергию). Давай попрактикуемся используя это соотношение в паре примеров.
Пример 4: Определение рабочей функции с использованием графика зависимости энергии электрона от длины волны фотона
Перестраиваемый лазер используется для освещения поверхности металла светом с разными длинами волн.Когда длина волны света короче определенного значения, электроны испускаются с поверхности металла. График показывает максимальная кинетическая энергия испускаемых электронов относительно длины волны фотонов.
- Какова максимальная длина волны света, при которой электроны будут испускаться с поверхности металла?
- Какова работа выхода металла? Используйте значение 4,14 × 10 эВ⋅с для постоянная Планка.Дайте ответ в электрон-вольтах до двух знаков после запятой.
Ответ
Часть 1
Для начала вспомним формулу максимальной кинетической энергии фотоэлектрона в зависимости от длины волны падающего фотона: 𝐸 = ℎ𝑐𝜆 − 𝑊.max
Существует обратная зависимость между энергией фотона и длиной волны. Таким образом, выше определенной пороговой длины волны, фотоны не обладают достаточной энергией, чтобы преодолеть барьер работы выхода и вызвать фотоэлектрический эффект.
Эта точка видна на графике, где 𝐸 = 0max. Длина волны в этой точке представляет максимальная длина волны света, при которой электроны будут выбрасываться с поверхности. Эта точка находится на горизонтальная ось при 𝜆 = 300 нм.
Таким образом, максимальная длина волны падающего света, которая вызывает испускание электронов с поверхности металла, равна 300 нм.
Часть 2
Напомним, что формула для работы выхода с учетом длины волны падающего фотона имеет следующий вид: 𝑊 = ℎ𝑐𝜆 − 𝐸.max
Чтобы найти работу выхода металла, мы можем подставить значение горизонтального пересечения графика в это уравнение. Мы должны преобразовать нанометры в метры, поэтому это пороговое значение длины волны равно 300 = 300 × 10 нм. На этой длине волны падающего света кинетическая энергия электрона равна нулю, поэтому мы исключим max. Далее подставляем в значения постоянной Планка и скорости света, и мы можем вычислить работу выхода: 𝑊 = 4.14 × 10⋅3,0 × 10300 × 10 = 4,14.eVsmeVms
Таким образом, мы нашли, что работа выхода металла составляет 4,14 эВ.
Пример 5: Расчет свойств экспериментального устройства для фотоэлектрического эффекта
На схеме показана электрическая схема. Схема содержит анод и катод в вакуумной камере. Анод и катод подключены к амперметру и батарее последовательно. Катод сделан из никеля.
- Для освещения никелевого катода используется свет с разными длинами волн.Когда длина волны света равна короче 248 нм, амперметр показывает показание 12,8 мА. Что это работа выхода никеля? Используйте значение 4,14 × 10 эВ⋅с для постоянная Планка. Ответьте с точностью до двух знаков после запятой.
- Первоначально лазер, используемый для освещения катода, имел выходную мощность 64 мВт. Если бы это было увеличено до 128 мВт, какой бы ток в схема быть? Ответьте с точностью до одного десятичного знака.
Ответ
Часть 1
Давайте начнем с напоминания формулы для работы выхода для данной длины волны падающего фотона, 𝑊 = ℎ𝑐𝜆 − 𝐸.max
Мы знаем, что когда падающий свет имеет достаточно большую энергию, электроны будут испускаться с поверхности меди, вызывая амперметр для определения тока.
Здесь мы знаем, что амперметр определяет ток только тогда, когда длина волны падающего света меньше, чем 248 мА.На этой пороговой длине волны значение, которое мы назовем 𝜆, падающие фотоны имеют достаточно энергии, чтобы преодолеть работу функциональный барьер. Таким образом, для фотоэлектронов не останется кинетической энергии, то есть 𝐸 = 0max, поэтому формула принимает вид 𝑊 = ℎ𝑐𝜆.
Чтобы вычислить работу выхода, подставим значения постоянной Планка, скорости света и пороговая длина волны: 𝑊 = 4,14 × 10⋅3,0 × 10248 × 10 = 5,01.eVsmeVms
Таким образом, мы нашли, что работа выхода никеля равна 5.01 эВ.
Часть 2
Мощность лазера дает количество энергии в секунду. Фотоны переносят энергию лазерного луча, поэтому, если включить лазер, вдвое больше энергии в секунду он излучает вдвое больше фотонов в секунду. Напомним тот случай фотон взаимодействует с одним электроном на поверхности металла. Таким образом, при вдвое большем количестве фотонов, падающих на поверхность, будет быть вдвое больше электронов, получающих энергию и покидающих поверхность.
Следовательно, если мощность лазера удваивается, то удваивается и ток. Поскольку амперметр первоначально обнаружил ток 12,8 мА, теперь он будет определять удвоенное значение.
Таким образом, ток в цепи будет 25,6 мА.
В заключение резюмируем некоторые важные концепции.
Ключевые моменты
- Фотоэлектрический эффект – это явление удаления электронов с металлической поверхности путем попадания на нее света. Фотоэлектрон – это электрон, испускаемый с поверхности после получения энергии от падающего фотона.
- Работа выхода материала – это минимальное количество энергии, необходимое для удаления электрона с его поверхности, и его значение можно найти из графика зависимости кинетической энергии электрона от энергии фотона.
- Энергия света пропорциональна его частоте и обратно пропорциональна длине волны.
- Мы можем связать работу выхода,, и максимальную энергию электрона, ,max, заданной частоты, используя формулу 𝐸 = ℎ𝑓 − 𝑊max, где ℎ – постоянная Планка.
- e может связать работу выхода и максимальную энергию электрона 𝐸max, заданной длине волны по формуле 𝐸 = ℎ𝑐𝜆 − 𝑊max, где ℎ – постоянная Планка, а 𝑐 – скорость света.
Фотоэлектрический эффект – Университетская физика, том 3
Цели обучения
К концу этого раздела вы сможете:
- Опишите физические характеристики фотоэффекта
- Объясните, почему фотоэлектрический эффект не может быть объяснен классической физикой
- Опишите, как идея Эйнштейна о частице излучения объясняет фотоэлектрический эффект
Когда металлическая поверхность подвергается воздействию монохроматической электромагнитной волны достаточно короткой длины (или, что эквивалентно, выше пороговой частоты), падающее излучение поглощается, и открытая поверхность испускает электроны.Это явление известно как фотоэлектрический эффект. Электроны, которые испускаются в этом процессе, называются фотоэлектронами.
Схема экспериментальной установки для исследования фотоэффекта (рисунок). Материал мишени служит анодом, который становится эмиттером фотоэлектронов при освещении монохроматическим излучением. Мы называем этот электрод фотоэлектродом. Фотоэлектроны собираются на катоде, который имеет более низкий потенциал по сравнению с анодом.Разность потенциалов между электродами можно увеличивать или уменьшать, а также менять полярность. Электроды заключены в вакуумированную стеклянную трубку, чтобы фотоэлектроны не теряли свою кинетическую энергию при столкновениях с молекулами воздуха в пространстве между электродами.
Когда материал мишени не подвергается воздействию излучения, в этой цепи не регистрируется ток, потому что цепь разорвана (обратите внимание, есть зазор между электродами). Но когда материал мишени подключается к отрицательному выводу батареи и подвергается воздействию излучения, в этой цепи регистрируется ток; этот ток называется фототоком.Предположим, что теперь мы меняем местами разность потенциалов между электродами, так что целевой материал теперь соединяется с положительной клеммой батареи, а затем мы медленно увеличиваем напряжение. Фототок постепенно затухает и в конечном итоге полностью перестает течь при некотором значении этого обратного напряжения. Разность потенциалов, при которой фототок перестает течь, называется тормозным потенциалом.
Характеристики фотоэффекта
Фотоэлектрический эффект имеет три важные характеристики, которые не могут быть объяснены классической физикой: (1) отсутствие времени запаздывания, (2) независимость кинетической энергии фотоэлектронов от интенсивности падающего излучения и (3) наличие частоты среза.Давайте рассмотрим каждую из этих характеристик.
Отсутствие запаздывания
Когда излучение попадает на материал мишени в электроде, электроны испускаются почти мгновенно, даже при очень низкой интенсивности падающего излучения. Это отсутствие запаздывания противоречит нашему пониманию, основанному на классической физике. Классическая физика предсказывает, что для низкоэнергетического излучения потребуется значительное время, прежде чем облученные электроны смогут набрать достаточно энергии, чтобы покинуть поверхность электрода; однако такого накопления энергии не наблюдается.
Интенсивность падающего излучения и кинетическая энергия фотоэлектронов
Типичные экспериментальные кривые показаны на (Рисунок), где фототок нанесен в зависимости от приложенной разности потенциалов между электродами. Для положительной разности потенциалов ток неуклонно растет, пока не достигнет плато. Дальнейшее увеличение потенциала за пределами этой точки вообще не приводит к увеличению фототока. Чем выше интенсивность излучения, тем выше фототок.Для отрицательной разности потенциалов по мере увеличения абсолютного значения разности потенциалов значение фототока уменьшается и становится равным нулю при остановочном потенциале. При любой интенсивности падающего излучения, независимо от того, является ли интенсивность высокой или низкой, значение тормозящего потенциала всегда остается на одном уровне.
Чтобы понять, почему этот результат необычен с точки зрения классической физики, мы сначала должны проанализировать энергию фотоэлектронов. Фотоэлектрон, покидающий поверхность, имеет кинетическую энергию К .Он получил эту энергию от падающей электромагнитной волны. В пространстве между электродами фотоэлектрон движется в электрическом потенциале, и его энергия изменяется на величину, где – разность потенциалов, и поскольку нет сил, кроме электрической силы, применяя теорему работы-энергии, мы получаем баланс энергии для фотоэлектрон, где – изменение кинетической энергии фотоэлектрона. При приложении тормозящего потенциала фотоэлектрон теряет свою первоначальную кинетическую энергию и останавливается.Таким образом, его энергетический баланс становится таким, что при наличии тормозящего потенциала наибольшая кинетическая энергия, которую может иметь фотоэлектрон, – это его начальная кинетическая энергия, которую он имеет на поверхности фотоэлектрода. Следовательно, наибольшую кинетическую энергию фотоэлектронов можно непосредственно измерить путем измерения тормозного потенциала:
Здесь мы видим, где классическая теория расходится с экспериментальными результатами. В классической теории фотоэлектрон непрерывно поглощает электромагнитную энергию; это означает, что, когда падающее излучение имеет высокую интенсивность, ожидается, что кинетическая энергия на (Рисунок) будет высокой.Точно так же, когда излучение имеет низкую интенсивность, ожидается, что кинетическая энергия будет низкой. Но эксперимент показывает, что максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности света.
Измеренный фототок в зависимости от приложенной разности потенциалов показывает, что для любой интенсивности падающего излучения, будь то интенсивность высокой (верхняя кривая) или низкой (нижняя кривая), значение тормозящего потенциала всегда одинаково.
Наличие частоты среза
Для любой металлической поверхности существует минимальная частота падающего излучения, ниже которой фототок не возникает.Значение этой частоты отсечки для фотоэлектрического эффекта является физическим свойством металла: разные материалы имеют разные значения частоты отсечки. Экспериментальные данные показывают типичный линейный тренд (см. (Рисунок)). Кинетическая энергия фотоэлектронов на поверхности линейно растет с увеличением частоты падающего излучения. Измерения для всех металлических поверхностей дают линейные графики с одним уклоном. Ни одно из этих наблюдаемых явлений не соответствует классическому пониманию природы.Согласно классическому описанию кинетическая энергия фотоэлектронов вообще не должна зависеть от частоты падающего излучения и не должно быть частоты отсечки. Вместо этого в классической картине электроны получают энергию от падающей электромагнитной волны непрерывным образом, и количество получаемой ими энергии зависит только от интенсивности падающего света и ничего больше. Итак, в классическом понимании, пока светит свет, ожидается, что фотоэлектрический эффект будет продолжаться.
Кинетическая энергия фотоэлектронов на поверхности в зависимости от частоты падающего излучения. Фотоэлектрический эффект может возникать только выше пороговой частоты. Измерения для всех металлических поверхностей дают линейные графики с одним наклоном. Каждая металлическая поверхность имеет свою частоту среза.Рабочая функция
Фотоэлектрический эффект объяснил в 1905 г. А. Эйнштейн. Эйнштейн рассуждал, что если гипотеза Планка о квантах энергии верна для описания обмена энергией между электромагнитным излучением и стенками полости, она также должна работать для описания поглощения энергии электромагнитного излучения поверхностью фотоэлектрода.Он предположил, что электромагнитная волна переносит свою энергию дискретными пакетами. Постулат Эйнштейна выходит за рамки гипотезы Планка, поскольку утверждает, что сам свет состоит из квантов энергии. Другими словами, он утверждает, что электромагнитные волны квантуются.
Согласно подходу Эйнштейна, пучок монохроматического света с частотой f состоит из фотонов. Фотон – это частица света. Каждый фотон движется со скоростью света и несет квант энергии. Энергия фотона зависит только от его частоты f .Явно энергия фотона равна
где – постоянная Планка. При фотоэлектрическом эффекте фотоны достигают поверхности металла, и каждый фотон отдает всех своей энергии только одному электрону на поверхности металла. Эта передача энергии от фотона к электрону происходит по типу «все или ничего», и не существует дробных передач, при которых фотон потерял бы только часть своей энергии и выжил бы. Суть квантового явления состоит в том, что либо фотон передает всю свою энергию и перестает существовать, либо передачи нет вообще.Это контрастирует с классической картиной, где разрешена дробная передача энергии. При таком квантовом понимании баланс энергии для электрона на поверхности, которая получает энергию от фотона, равен
.где – кинетическая энергия (рисунок), которую электрон имеет в тот самый момент, когда он отрывается от поверхности. В этом уравнении баланса энергии – энергия, необходимая для отрыва фотоэлектрона от поверхности. Эта энергия называется работой выхода металла.Каждый металл имеет свою характерную работу выхода, как показано на (Рисунок). Чтобы получить кинетическую энергию фотоэлектронов на поверхности, мы просто инвертируем уравнение баланса энергии и используем (рисунок) для выражения энергии поглощенного фотона. Это дает нам выражение для кинетической энергии фотоэлектронов, которая явно зависит от частоты падающего излучения:
Это уравнение имеет простую математическую форму, но его физика глубокая. Теперь мы можем более подробно остановиться на физическом значении (рисунок).
Типичные значения рабочей функции для некоторых распространенных металлов Металл (эВ) Na 2,46 Al 4,08 Пб 4,14 Zn 4,31 Fe 4,50 Cu 4,70 Ag 4.73 Pt 6,35 В интерпретации Эйнштейна взаимодействия происходят между отдельными электронами и отдельными фотонами. Отсутствие запаздывания означает, что эти индивидуальные взаимодействия происходят мгновенно. Это время взаимодействия нельзя увеличить за счет уменьшения интенсивности света. Интенсивность света соответствует количеству фотонов, приходящих на поверхность металла в единицу времени. Даже при очень низкой интенсивности света фотоэлектрический эффект все еще возникает, потому что взаимодействие происходит между одним электроном и одним фотоном.Пока существует хотя бы один фотон с достаточной энергией, чтобы передать его связанному электрону, фотоэлектрон будет появляться на поверхности фотоэлектрода.
Наличие частоты отсечки для фотоэлектрического эффекта следует из (Рисунок), поскольку кинетическая энергия фотоэлектрона может принимать только положительные значения. Это означает, что должна быть некоторая пороговая частота, для которой кинетическая энергия равна нулю. Таким образом, мы получаем явную формулу для частоты среза:
Частота отсечки зависит только от работы выхода металла и прямо пропорциональна ей.Когда работа выхода велика (когда электроны быстро связаны с поверхностью металла), энергия порогового фотона должна быть большой, чтобы образовался фотоэлектрон, и тогда соответствующая пороговая частота велика. Фотоны с частотами, превышающими пороговую, всегда производят фотоэлектроны, потому что у них есть фотоны с частотами меньше, чем у них недостаточно энергии для производства фотоэлектронов. Следовательно, когда падающее излучение имеет частоту ниже частоты отсечки, фотоэлектрический эффект не наблюдается.Поскольку частота f и длина волны электромагнитных волн связаны фундаментальным соотношением (где – скорость света в вакууме), частота отсечки имеет соответствующую длину волны отсечки
.В этом уравнении наши наблюдения можно переформулировать следующим образом эквивалентным образом: когда падающее излучение имеет длину волны, превышающую длину волны отсечки, фотоэлектрический эффект не возникает.
Фотоэлектрический эффект для серебра Излучение с длиной волны 300 нм падает на поверхность серебра.Будут ли наблюдаться фотоэлектроны?
Стратегия Фотоэлектроны могут быть выброшены с поверхности металла только тогда, когда падающее излучение имеет более короткую длину волны, чем длина волны отсечки. Работа выхода серебра равна ((Рисунок)). Для оценки используем (рисунок).
Решение Пороговая длина волны для наблюдения фотоэлектрического эффекта в серебре
.Падающее излучение имеет длину волны 300 нм, которая больше длины волны отсечки; следовательно, фотоэлектроны не наблюдаются.
Значение Если бы фотоэлектрод был сделан из натрия, а не из серебра, длина волны отсечки была бы 504 нм, и наблюдались бы фотоэлектроны.
(рисунок) в модели Эйнштейна говорит нам, что максимальная кинетическая энергия фотоэлектронов является линейной функцией частоты падающего излучения, что показано на (рисунок). Для любого металла наклон этого графика равен постоянной Планка. Пересечение с осью – дает нам значение работы выхода, характерное для металла.С другой стороны, его можно непосредственно измерить в эксперименте, измерив значение тормозящего потенциала (см. (Рисунок)), при котором фототок останавливается. Эти прямые измерения позволяют нам экспериментально определить значение постоянной Планка, а также работу выхода материалов.
МодельЭйнштейна также дает прямое объяснение значений фототока, показанных на (Рисунок). Например, удвоение интенсивности излучения приводит к удвоению количества фотонов, падающих на поверхность в единицу времени.Чем больше количество фотонов, тем больше количество фотоэлектронов, что приводит к большему фототоку в цепи. Так интенсивность излучения влияет на фототок. Фототок должен достичь плато при некотором значении разности потенциалов, потому что в единицу времени количество фотоэлектронов равно количеству падающих фотонов, а количество падающих фотонов вообще не зависит от приложенной разности потенциалов, а только от интенсивность падающего излучения.Тормозной потенциал не изменяется с интенсивностью излучения, поскольку кинетическая энергия фотоэлектронов (см. (Рисунок)) не зависит от интенсивности излучения.
Энергия фотонов и кинетическая энергия фотоэлектронов Фиолетовый свет с длиной волны 430 нм падает на кальциевый фотоэлектрод с работой выхода 2,71 эВ.
Найдите энергию падающих фотонов и максимальную кинетическую энергию выброшенных электронов.
Стратегия Энергия падающего фотона – это то, что мы используем. Чтобы получить максимальную энергию выброшенных электронов, мы используем (рисунок).
Решение
Значение В этой экспериментальной установке фотоэлектроны перестают течь при останавливающем потенциале 0,17 В.
Проверьте свое понимание Желтый свет с длиной волны 589 нм падает на поверхность, работа выхода которой составляет 1,20 эВ. Каков останавливающий потенциал? Какая длина волны отсечки?
В; 1040 нм
Калькулятор фотоэлектрического эффекта
Калькулятор фотоэлектрического эффекта даст вам представление о принципах фотоэлектрического эффекта, которые были объяснены Эйнштейном в 1905 году.Это был значительный шаг в развитии квантовой физики, которую мы знаем сегодня. Продолжайте читать, если хотите узнать, что такое фотоэлектрический эффект и как его описать с помощью определения фотоэлектрического эффекта. Вы увидите, что это квантовое явление находит применение в нашей повседневной жизни, среди прочего, в фотоэлектрических датчиках, которые обнаруживают и определяют интенсивность падающего света (с помощью уравнения фотоэлектрического эффекта вы можете проверить, будут ли они вообще работать при солнечном свете).
Что такое фотоэлектрический эффект?
Все в природе состоит из атомов, состоящих из ядра, и электронов, вращающихся вокруг ядра. Воспользуйтесь нашим калькулятором модели Бора, чтобы узнать больше о структуре атома. Фотоэлектрический эффект – это квантовое явление, при котором электроны испускаются с поверхности материала под действием падающего света. Такая фотоэмиссия может происходить для любого материала, но наиболее заметна она у металлов.
Но почему вообще существует фотоэффект? Лучи света состоят из элементарных частиц – фотонов, обладающих определенной энергией.С другой стороны, каждый электрон связан с ядром с определенной энергией связи (вы можете быстро оценить эту энергию для водорода). Теперь, если фотон сталкивается с электроном и энергия фотона превышает энергию связи электрона, он может вырваться из ядра с некоторой кинетической энергией, вызывая фотоэлектрический эффект.
Определение фотоэлектрического эффекта
Эйнштейн предложил объяснение фотоэлектрического эффекта, используя концепцию, согласно которой свет состоит из крошечных пакетов энергии, известных как фотоны.В нашем калькуляторе фотоэлектрического эффекта используется следующее определение фотоэлектрического эффекта:
KE = h * (f - f0)где
-
KE– максимальная кинетическая энергия выброшенного электрона, -
f– частота падающего фотона, -
f0– пороговая частота (соответствующая энергии связи) определенного материала, -
ч– постоянная Планкач = 6,626 * 10 ^ (- 34) Дж * с.
Из фотоэлектрического уравнения видно, что условие
f> f0необходимо для возникновения фотоэлектрического эффекта (поскольку кинетическая энергия положительна). Величинаϕ = h * f0называется работой выхода (выражается в единицах энергии) и соответствует пороговой частоте.В нашем калькуляторе фотоэлектрического эффекта энергия падающего фотона и работа выхода выражаются как частоты. Вы можете перейти в расширенный режим, если хотите использовать длину волны или просто энергию.Проверьте наш калькулятор энергии фотонов, чтобы узнать, какова связь между частотой, длиной волны и энергией фонона.
Фотоэлектрический датчик
Описание фотоэлектрического эффекта кажется очень теоретическим, но находит много практических применений. Фотоэлементы, например, используются для обнаружения света (в фотоэлектрических датчиках) или для сбора результирующего тока электронов (в солнечных элементах). Другие приложения включают:
- технология обработки изображений (цифровые камеры),
- фотоумножитель (усиливает ток детектируемого фотона),
- химический анализ материала.
Расчет кинетической энергии – Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса – изображению, ссылке, тексту и т. д. – относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Физика (потенциальная энергия и кинетическая энергия) –
Потенциальная энергия – это возможная энергия, которую объект имеет в зависимости от его положения.
Формула
Потенциальная энергия (PE) = масса * сила тяжести * высота
Как мы можем использовать эту формулу, чтобы лучше понимать движения? Давайте посмотрим на спортсменов, прыгающих с боксов и обратно…
Если мы смотрим на двух спортсменов, стоящих на одном прямоугольнике роста, мы сразу узнаем, что переменные Рост (высота прямоугольника) и Гравитация уравнения будут одинаковыми, но если вес (Масса) двух спортсменов разный, тогда должен сразу знать, что у более тяжелого будет больше ПЭ.
Аналогичный пример можно использовать для демонстрации различий в PE между двумя спортсменами одинаковой массы на разной высоте бокса. Опять же, поскольку сила тяжести такая же, как и вес (масса), мы можем сразу определить, что у спортсмена на более высоком квадрате будет большая потенциальная энергия.
Тот же спортсмен в более высоком боксе будет иметь более высокий PE (больший рост) Тот же спортсмен в меньшем боксе будет иметь более низкий PE (меньший рост).Кинетическая энергия (KE) – это количество энергии, которое объект получает от движения.2
PE = Масса * Плотность * Высота
Если мы посмотрим на PE, единственное, что мы действительно можем изменить, чтобы повлиять на PE, – это высота, на которой находится объект или спортсмен. Масса (вес спортсмена) не может быть изменена, как и сила тяжести. Однако мы всегда можем поместить спортсмена на более высокий или меньший ящик, из которого он спрыгнет.
Теперь, глядя на KE, какая часть формулы PE будет влиять на скоростной аспект формулы KE? ВЫСОТА .
Чем выше расположен объект, тем дальше он должен упасть и тем с большей скоростью будет объект при контакте.Другими словами, чем выше PE, тем больше у объекта потенциал для достижения более высокого KE. Ключевое слово – потенциал. Просто потому, что PE действительно высокий, не означает, что последующее действие приведет к чрезвычайно высокому KE, но это только в том случае, если один из аспектов уравнения KE уменьшается (обычно высота).
Например, если у вас есть спортсмен, перепрыгивающий из 6-футового бокса в 4-футовый бокс, атлет уменьшит свою потенциальную энергию, уменьшив рост на 2 фута, но у вас будет это снижение PE только за счет последующего развития KE. (падение с 6 до 4 футов).Даже несмотря на то, что потенциальная энергия с 6 до 4 футов снижена, у спортсмена все равно будет потенциальная энергия.
Приземление на ящик снизит KE при ударе за счет сохранения некоторой части PE (у спортсмена все еще есть PE, пока он находится на боксе) В верхней части прыжка PE спортсмена будет самым высоким, а KE будет самым низкимПотенциальная энергия спортсмена на высоте 6 футов:
Масса (200 фунтов) * Высота (6 футов) * Гравитация 9.8 м / с
Потенциальная энергия спортсмена на высоте 4 футов:
Масса (200 фунтов) * Высота (4 фута) * Плотность 9,8 м / с
Атлет должен был использовать кинетическую энергию, чтобы переместиться с 6 футов на 4 фута, что и позволило снизить PE.

