Максимальный прогиб балки металлической: Предельный прогиб

alexxlab | 17.02.2023 | 0 | Разное

Основные формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Содержание

• 1 Виды балок
  • 1.1 Деревянные
  • 1.2 Стальные
• 2 Прочность и жесткость балки
• 3 Расчет на жесткость
• 4 Расчет моментов инерции и сопротивления сечения
• 5 Определение максимальной нагрузки и прогиба
• 6 Особенности расчета на прогиб
• 7 Пример подсчета прогиба

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео: 

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет балок на прогиб

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.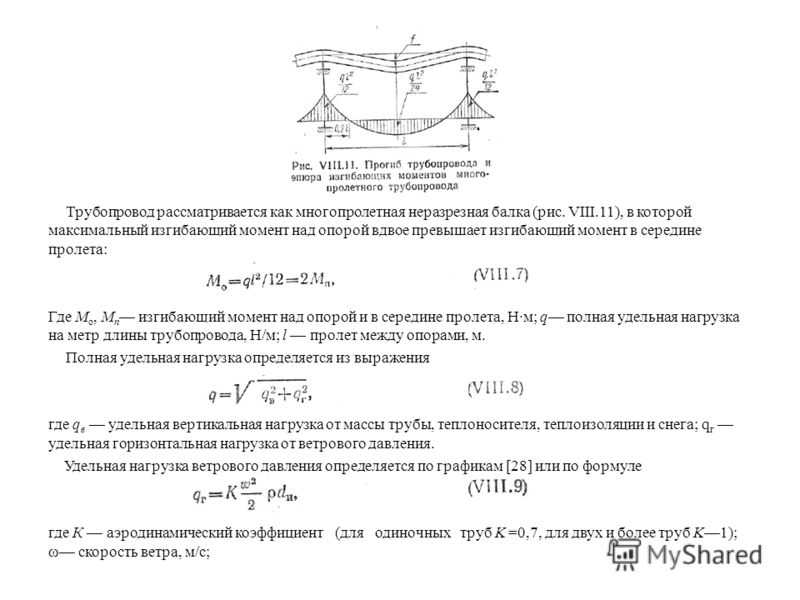

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

 

Поверочный расчёт металлических балок перекрытия третьего этажа после надстройки

Проведём тщательную проверку существующих балок перекрытия третьего этажа при планировании надстройки дополнительного этажа. В этом случае необходимо произвести усиление перекрытия путём установки дополнительных балок из двутавра № 20 между существующими балками. Средний шаг балок 0,50 м. Проектируемая конструкция перекрытия третьего этажа после надстройки дополнительного этажа приведена в таблице.

Равномерно распределённые нагрузки на перекрытие третьего этажа после надстройки этажа.

Наименование нагрузки	Нормативная нагрузка, КН/м²	γf	Расчётная нагрузка, кН/м²
Постоянные нагрузки 2 листа ГВЛ γ = 8,4 кН/м³, t = 25 мм.	0,21	1,2	0,25
Половая рейка t = 40 мм.	0,24	1,1	0,26
Минплита γ = 75 кН/м³, t = 200 мм.	0,15	1,2	0,18
Накат из досок t = 60 мм.	0,36	1,1	0,40
Подшивка из листов ГВЛ, 2 слоя t = 25 мм.	0,21	1,2	0,25
Двутавр № 20, шаг 0,50 м.	0,38	1,05	0,40
Перегородки кирпичные	1	1,2	1,2
Временные нагрузки На перекрытие (служебные помещения)	2,0	1,2	2,40
Итого:	4,55		5,34

Балки перекрытия из двутавра № 20.

Шаг балок 0,5 м. Пролёт балки l = 4,22 м.

Расчётный пролёт lр = l · 1,03 = 4,22 · 1,03 = 4,35 м.

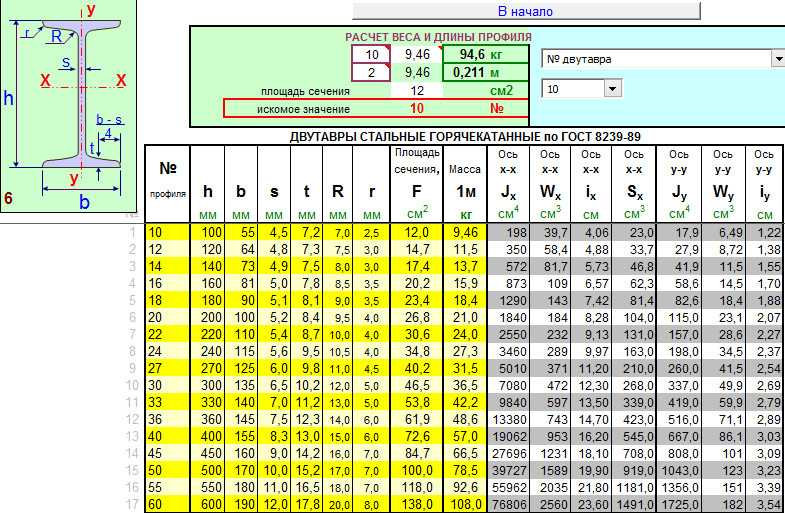
Геометрические характеристики двутавра № 20 (по ГОСТ 8239 – 89):

• момент сопротивления Wx = 180 cм³;

• момент инерции Ix = 1840 см³;

• статический момент Sx = 104 см³;

• толщина стенки t = 5,2 мм = 0,52 см.

Для существующих металлических балок марка стали по объективным причинам не определена, поэтому в запас принимаем расчётное сопротивление стали Ry = 170 МПа. Коэффициент условий работы γс = 1. Модуль упругости стали Е = 2,06 · 10⁵ МПа.

Нагрузка на 1 пог. м балки при шаге 0,5 м:

нормативная qн = 4,55 · 0,5 = 2,28 кН/м;

расчётная qр = 5,34 · 0,5 = 2,67 кН/м.

Проверка несущей способности балки

Максимальный изгибающий момент в пролёте:

М = (qр · lр²) / 8 = (2,67 · 4,35²) / 8 = 6,3 кН/м.

Напряжение на изгиб:

σ = М / Wx = 6,3 · 10³ / 180 = 35 МПа < Ry = 170 МПа.

Прочность балки на изгиб обеспечена.

Запас прочности составляет:

((170 – 35) / 170) · 100 = 79%.

Максимальная поперечная сила на опоре:

Q = (qр · lр) / 2 = (2,67 · 4,35) / 2 = 5,8 кН.

Касательное напряжение:

τ = (Q · Sx) / (Ix · t) = (5,8 · 104) / (1840 · 0,52) =

= 0,63 кН/см² < Rs = 9,86 кН/см²;

Rs = 0,58 · Ry = 0,58 · 170 = 98,6 МПа = 9,86 кН/см².

Прочность балки по поперечной силе обеспечена.

Расчёт общей устойчивости балки не требуется, так как верх балок закреплён с помощью поперечных стальных уголков, устанавливаемых с шагом 2,0 м.

Несущая способность балки обеспечена.

Проверка жёсткости балки

Максимальный прогиб балки в середине пролёта определяется по формуле:

fmax = ((5 / 384) · (qн · lр⁴) / (Е · Ix)) =

= (5 · 2,28 · 4,35⁴) / (384 · 2,06 · 10⁸ ·1840 · 10^-8) = 0,003 м = 0,3 см.

Предельное значение прогиба:

fu = (lр / 250) = 4,35 / 250 = 0,017 м = 1,7 см.

Условие fmax = 0,3 см < fu = 1,7 см соблюдается.

Запас составляет:

((1,7 – 0,3) / 1,7) · 100 = 82%.

Жёсткость балки перекрытия из двутавра № 20 обеспечена.

24- Легкий подход к прогибу стальных балок.

/ Стальные балки. / Автор Магед Камел

Содержание

1. Прогиб стальных балок часть 1.
   • Краткое содержание видео.
   • Каковы недостатки прогиба стальных балок?
   • Каковы параметры прогиба стальных балок?
   • Приспособление для КСГМГ на прогиб.

Краткое содержание видео.

видео включает в себя обсуждение критериев прогиба, недостатки чрезмерного прогиба стальных балок и решение 5.1, из которого прогиб стальных балок определяет конструкцию. У видео есть субтитры и субтитры на английском языке.

Вы можете щелкнуть любое изображение, чтобы увеличить его, затем нажать маленькую стрелку, чтобы просмотреть все остальные изображения в виде слайд-шоу.

Это содержание лекции каковы параметры прогиба?

Каковы недостатки прогиба стальных балок?

Это цитата из книги проф. Маккормака, глава 10. прогиб обычно ограничивается Прогиб должен контролироваться максимальным значением, так как он может повредить другие материалы и не создавать пластических трещин.

Прогиб может привести к повреждению других материалов, прикрепленных к рассматриваемой балке или поддерживаемых ею. Во-вторых, внешний вид конструкций часто повреждается из-за чрезмерных прогибов, которые придают плохой вид.

Пункт третий, потеря доверия из-за появления прогиба для здания.

И последнее. Может потребоваться, чтобы несколько разных балок, несущих одинаковые нагрузки, прогибались на одинаковую величину, чтобы с точки зрения внешнего вида была одинаковая величина прогиба.

Каковы параметры прогиба стальных балок?

Отклонения временной нагрузки составляют примерно L/360 длины пролета. Но читатель должен заметить, что ограничение прогиба стальных балок попадает в область эксплуатационной пригодности. Следовательно, прогибы определяются для рабочих нагрузок, поэтому мы не можем использовать предельные нагрузки, например, комбинацию нагрузок 1,2D+1,60L для оценки прогиба.

 Какие инструменты позволяют определить отклонение? Мы используем метод площади моментов , и мы преобразуем площадь моментов в нагрузки, из которых мы оцениваем поперечные силы, что дает нам значение уклона.

В то время как из изгиба, вызванного моментными нагрузками, мы можем оценить значения прогиба, а также использовать метод сопряженной балки , который превращает концевую консольную часть в неподвижную опору и преобразует шарнирный конец в шарнирные опоры.

Третий метод виртуальная работа .

94/384*EI для свободно опертой балки при равномерной нагрузке.

Положение КСГМГ на прогиб.

IBC, который является международным строительным кодексом, в котором значения отклонения балки подразделяются на три категории, цитата из книги профессора Фредрика Роланда по проектированию стали для гражданского PE.

Первый пункт относится к элементам крыши Временная нагрузка L и снеговая нагрузка S или ветровая нагрузка W, или ветровая нагрузка W, третья категория — статическая нагрузка плюс временная нагрузка D+L, для каждой категории элементы крыши, если опорная штукатурка потолки значение прогиба
допускается для динамической нагрузки L=L/360, а для снеговой нагрузки s или ветровой нагрузки W прогиб =L/360, для D+L прогиб равен L/360.

 В то время как для элементов крыши, если они поддерживают негипсовые перекрытия, значения прогиба увеличиваются и становятся для динамической нагрузки L=L/240, а для снеговой нагрузки s или ветровой нагрузки W=L/240, для D+L прогиб составляет л/180.

Для элементов перекрытий у нас нет снеговых нагрузок Допустимый прогиб, допустимый при динамических нагрузках L = пролёт/360, а для нагрузок D+L прогиб будет рассматриваться как (пролёт/240). 92/8), L как длина пролета в дюймах, w в тысячах фунтов на дюйм и E как 29000ksi, мы можем получить значение c1.

На следующем рисунке показано, как мы получаем значение c1 для прогиба свободно опертой балки при равномерной нагрузке.

Это pdf-файл, использованный в иллюстрации к этому сообщению.

Как внешний ресурс для отклонения. Глава 8 – Гибка элементов
Это ссылка на следующий пост, решенная задача 5-1-часть 1-2.

Формула прогиба балок с диаграммами для всех условий .

15. 05.2021 19.07.2020 от Вики

когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что это отклонение балок . Максимальный прогиб балок происходит там, где уклон равен нулю.

Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.

Общие и стандартные уравнения для прогиба балок приведены ниже:

 

 

Где,
M = изгибающий момент,
E = модуль Юнга,
I = момент инерции.

Продукт E.I известен как жесткость на изгиб .

Существует множество типов балок, и для этих разных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.

1. Свободно опертая балка с центральной точечной нагрузкой:

Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки в точке C.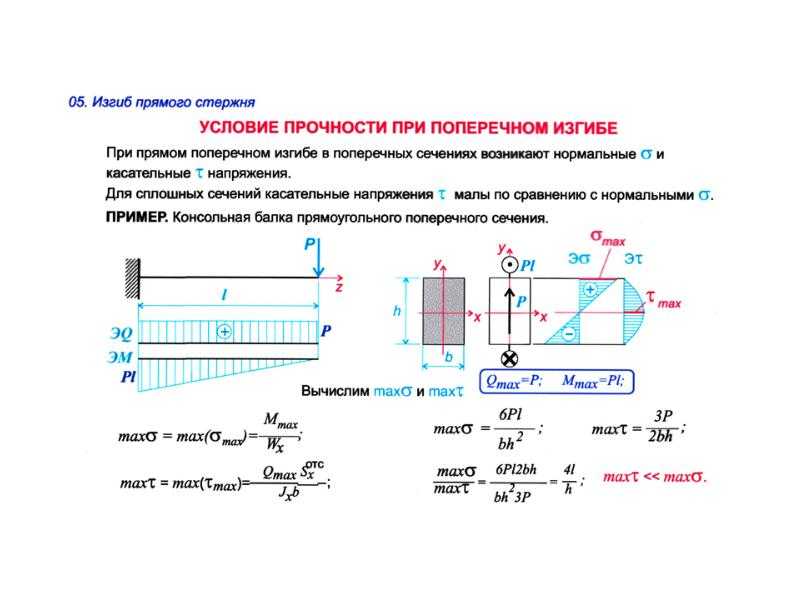 Прогиб при точка C будет:

2. Свободно опертая балка с внецентренной точечной нагрузкой:

Свободно опертая балка AB длиной l несет нагрузку l 90 в центральной точке.0043 C как показано на рис. Отклонение балки определяется следующим образом:

Так как b > a , то максимальное отклонение происходит в CB , а его расстояние от B определяется как:

и определяется как максимальное отклонение :

3. Свободно опертая балка с равномерно распределенной нагрузкой :

Свободно опертая балка AB с равномерно распределенной нагрузкой w /единица длины показана на рисунке ,

Максимальное отклонение происходит в средней точке C и определяется как:

4 Постепенно меняющаяся нагрузка:

Свободно опертая балка из AB длиной l , несущая постепенно изменяющуюся нагрузку от нуля на B до веса на единицу длины на A , показана на рисунке ниже,

Максимальное отклонение луча возникает, когда x = 0,519 L , и его значение определяется как:

5. Contilever Beam с точечной нагрузкой на свободном конце:

A Cantilever. балка АВ длиной l , несущая на свободном конце точечную нагрузку, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:

The maximum deflection occurs at the free end (when x = 0 ) and its value is given by

6. Cantilever Beam With a Uniformly Distributed Load :

A cantilever балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, показана на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением

Максимальное отклонение происходит на свободном конце (когда x = 0), и его значение определяется

, когда консоль частично загружается, как показано на рис. расстояние от фиксированного конца) определяется как:

и максимальное отклонение происходит на B чьи значения даны

7. Консольный луч с постепенно изменяющейся нагрузкой:

Кантилеверная луча AB длины L . Сталопроницаемая нагрузка от Zero B L Степенью нагрузки с Zero B 4 на единицу длины A показан на рис. Прогиб в любом сечении X на расстоянии x от B определяется как

Максимальный прогиб происходит на свободном конце (при x = 0) и его значение определяется как

8. Неподвижная балка, несущая центральную точечную нагрузку:

Неподвижная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , и его значение определяется формулой

9.