Масса объем плотность формула – Масса через плотность и объем | Формулы и расчеты онлайн
alexxlab | 07.09.2020 | 0 | Разное
ФИЗИКА: Задачи на плотность, массу и объем
Задачи на плотность, массу и объем с решением
Формулы, используемые в задачах по физике на плотность, массу и объем.
Название величины | Обозначение | Единицы измерения | Формула |
Масса | m | кг | m = p * V |
Объем | V | м3 | V = m / p |
Плотность | p | кг/м3 | p = m / V |
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см3?

Задача № 2. Определите объем кирпича, если его масса 5 кг?

Задача № 3. Определите массу стальной детали объёмом 120 см3
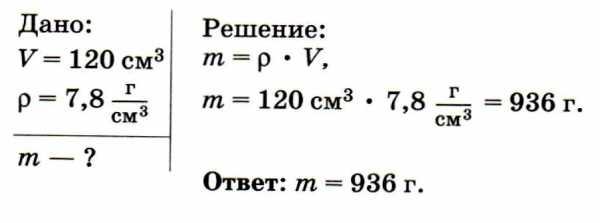
Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5. Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см3.
Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ:
РЕШЕНИЕ: Объем кубика VK = а3 = 216 см3. Объем стенок VС можно вычислить, зная массу кубика mК и плотность меди р: VС = mК / р = 91 см3. Следовательно, объем полости VП = VK — VC = 125 см3. Поскольку 125 см3 = (5 см)3, полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.
Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.
Задачи на плотность, массу и объем с решением. Таблица плотности веществ.
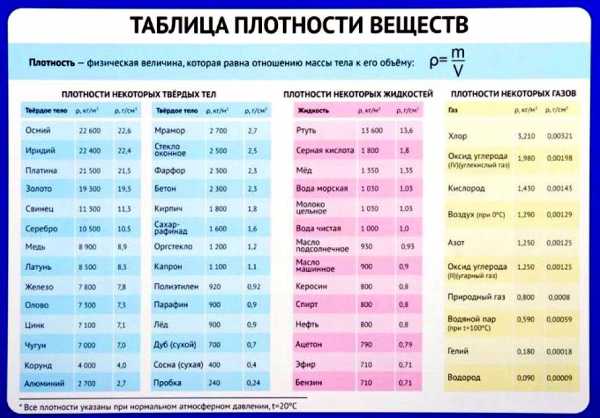
Справочный материал «Задачи на плотность, массу и объем»

Конспект урока «Задачи на плотность, массу и объем с решением».
Следующая тема: «Задачи на силу тяжести и вес тела».
Как найти массу, зная плотность
Вам понадобится
- калькулятор или компьютер, линейка, рулетка, мерная емкость
Инструкция
Чтобы найти массу , зная плотность, разделите объем тела или вещества на его плотность. То есть воспользуйтесь формулой: m = V / ρ, где:V – объем,ρ – плотность,
V – объем.Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения (СИ). Для этого, переведите объем в кубометры (м³), а плотность – в килограммы на кубометр (кг/м³). В этом случае значение массы получится в килограммах. Если плотность и объем заданы в одной системе единиц, то предварительный перевод в СИ производить необязательно. Масса тела или вещества в таком случае будет измеряться в той единице измерения массы, которая указана в числителе единицы измерения плотности (единицы измерения объема при расчете сократятся).
Так, например, если объем задан в литрах, а плотность в граммах на литр, то расчетная масса получится в граммах.
Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.
Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть:Vпр.пар. = a*b*c, где:Vпр.пар. – объем прямоугольного параллелепипеда, а
a, b, c – значения его длины, ширины и высоты (толщины), соответственно.
Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
www.kakprosto.ru
Формула плотности вещества в физике
Определение и формула плотности вещества
ОпределениеПлотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы (dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой . И так:
Виды плотности вещества
Применяя выражение (1) для определения плотности, говорят о плотности тела в точке.
Плотность тела зависит от материала тела и его термодинамического состояния.
В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова ( ), то определяют следующей формулой:
где m – масса тела, V – объем тела.
Если тело является неоднородным, то иногда пользуются понятием средней плотности , которая рассчитывается как:
где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности. Объемную плотность рассчитывают так же как (3). Объем определяют, включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.).
При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу:
где – молярная масса газа, – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль.
Единицы измерения плотности вещества
В соответствии с определением, можно записать, что единицами измерения плотности в системе СИ служит: []=кг/м3
в СГС: []=г/(см)3
При этом: 1 кг/м3 = (10)-3 г/(см)3 .
Примеры решения задач
ПримерЗадание. Какова плотность воды, если объем, который занимает одна молекула H2O, примерно равен м3? Считайте, что молекулы в воде плотно упакованы.
Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:
где m0 – масса молекулы воды. Найдем m0, используя известное соотношение:
www.webmath.ru
Как найти массу, зная плотность и объем
Вам понадобится
- – компьютер или калькулятор;
- – рулетка;
- – мерная емкость;
- – линейка.
Инструкция
Как известно, предметы, имеющие один и тот же объем, но сделанные из разных материалов, будут иметь разную массу (дерево и металл, стекло и пластмасса). Массы тел, изготовленных из одного и того же вещества (без пустот), прямо пропорциональны объему рассматриваемых предметов. Иначе говоря, постоянной величиной является отношение массы предмета к его объему. Эта величина носит название «плотность вещества . В дальнейшем обозначим ее буквой d.Исходя из определения, d=m/V, где
m – масса предмета (кг),
V — его объем (м3).
Как видно из формулы, плотность вещества – это масса единицы его объема.
Узнать плотность вещества, из которого изготовлен предмет, можно из таблицы плотностей в приложении к учебнику физики или на сайте http://www.kristallikov.net/page15.html, где приведены плотности практически всех существующих веществ.
Объем предмета можно рассчитать по формуле: V=S*h, гдеV – объем (м3),
S – площадь основания предмета (м2),
H – высота предмета (м).
Если нет возможности с точностью произвести измерение геометрических размеров тела, воспользуйтесь законом Архимеда. Для этого возьмите сосуд, имеющий шкалу (или деления) для измерения объема жидкости, опустите предмет в воду (в сам сосуд, снабженный делениями). Объем, на который увеличится содержимое сосуда, – и есть объем погруженного в него тела.
Если известны плотность d и объем V предмета, всегда можно найти его массу, пользуясь формулой: m=V*d. Перед расчетом массы приведите все единицы измерения в одну систему, например, в интернациональную систему измерения СИ.
Вывод из приведенных формул следующий: чтобы получить искомое значение массы, зная плотность и объем, надо умножить значение объема тела на значение плотности вещества, из которого оно сделано.
www.kakprosto.ru
Масса сплошной детали | Математика для ювелиров
9.05.2013 // Владимир ТруновЭто странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
Отсюда масса:
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8. Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
tvlad.ru
Как найти массу?
Многие из нас в школьное время задавались вопросом: «Как найти массу тела»? Сейчас мы попытаемся ответить на этот вопрос.
Нахождение массы через его объем
Допустим, в вашем распоряжении есть бочка на двести литров. Вы намерены целиком заполнить ее дизельным топливом, используемом вами для отопления своей небольшой котельной. Как найти массу этой бочки, наполненной соляркой? Давайте попробуем решить эту простейшую на первый взгляд задачу вместе с вами.
Решить задачу, как найти массу вещества через его объем, довольно легко. Для этого следует применить формулу удельной плотности вещества
p = m/v,
где p является удельной плотностью вещества;
m – его массой;
v – занимаемым объемом.
В качестве меры массы будут использоваться граммы, килограммы и тонны. Меры объёмов: сантиметры кубические, дециметры и метры. Удельная плотность будет вычисляться в кг/дм³, кг/м³, г/см³, т/м³.
Таким образом, в соответствии с условиями задачи в нашем распоряжении есть бочка объемом двести литров. Это значит, что ее объем равняется 2 м³.
Но вы хотите узнать, как найти массу. Из вышеназванной формулы она выводится так:
m = p*v
Сначала нам требуется найти значение р – удельной плотности дизельного топлива. Найти данное значение можно, используя справочник.
В книге мы находим, что р = 860,0 кг/м³.
Затем полученные значения мы подставляем в формулу:
m = 860*2 = 1720,0 (кг)
Таким образом, ответ на вопрос, как найти массу, был найден. Одна тонна и семьсот двадцать килограммов – это вес двухсот литров летнего дизтоплива. Затем вы можете точно так же сделать приблизительный расчет общего веса бочки и мощности стеллажа под бочку с соляром.
Нахождение массы через плотность и объем
Очень часто в практических заданиях по физике можно встретить такие величины, как масса, плотность и объем. Для того чтобы решить задачу, как найти массу тела, вам требуется знать его объем и плотность.
Предметы, которые вам будут нужны:
1) Рулетка.
2) Калькулятор (компьютер).
3) Емкость для измерения.
4) Линейка.
Известно, что у предметов с равным объемом, но изготовленных из различных материалов, будет разная масса (например, металл и дерево). Массы тел, которые изготовлены из определенного материала (без пустот), прямо пропорциональны объему рассматриваемых предметов. В противном случае, константа – это отношение массы к объему предметы. Этот показатель называется «плотностью вещества». Мы будем его обозначать буквой d.
Теперь требуется решить задачу, как найти массу в соответствии с формулой d = m/V, где
m является массой предмета (в килограммах),
V является его объемом (в метрах кубических).
Таким образом, плотность вещества является массой единицы его объема.
Если вам необходимо найти плотность материала, из которого создан предмет, то следует воспользоваться таблицей плотностей, которую можно найти в стандартном учебнике по физике.
Объем предмета вычисляется по формуле V = h * S, где
V – объем (м³),
H – высота предмета (м),
S – площадь основания предмета (м²).
В том случае, если вы не можете четко измерить геометрические параметры тела, то вам следует прибегнуть к помощи законов Архимеда. Для этого вам понадобится сосуд, у которого есть шкала, служащая для измерений объема жидкостей и опустить предмет в воду, то есть в сосуд, на котором есть деления. Тот объем, на который будет увеличено содержимое сосуда, является объемом тела, которое погружено в него.
Зная объем V и плотность d предмета, вы можете легко найти его массу по формуле m = d * V. Перед тем, как вычислить массу, требуется привести все измерительные единицы в единую систему, например, в систему СИ, являющуюся интернациональной измерительной системой.
В соответствии с вышеназванными формулами можно сделать следующий вывод: для нахождения требуемой величины массы с известным объемом и известной плотностью требуется умножить значение плотности материала, из которого изготовлено тело, на объем тела.
fb.ru
Формула расчета массы через плотность тела — Студопедия.Нет
Масса тела может быть рассчитана как:
где – плотность вещества тела, где интегрирование проводится по объему тела. Если тело однородное ( ), то масса может быть рассчитана как:
Масса в специальной теории относительности
В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:
где E – полная энергия свободного тела, p- импульс тела, c – скорость света.
Релятивистская масса частицы определяется формулой:
где m0 – масс покоя частицы, v – скорость движения частицы.
Основной единицей измерения массы в системе СИ является: [m]=кг.
В СГС: [m]=гр.
Тела, изготовленные из разных веществ, при одинаковых объемах имеют разные массы. Например, железо объемом 1 м3 имеет массу 7800 кг, а свинец того же объема — 13000 кг.
Физическую величину, показывающую, чему равна масса вещества в единице объема (т. е., например, в одном кубическом метре или в одном кубическом сантиметре), называют плотностью вещества.
Чтобы выяснить, как найти плотность данного вещества, рассмотрим следующий пример. Известно, что льдина объемом 2 м3 имеет массу 1800 кг. Тогда 1 м3 льда будет иметь массу, в 2 раза меньшую. Разделив 1800 кг на 2 м3, получим 900 кг/м3. Это и есть плотность льда.
Итак, чтобы определить плотность вещества, надо массу тела разделить на его объем: Обозначим величины, входящие в это выражение, буквами:
m — масса тела, V — объем тела, ρ — плотность тела (ρ—греческая буква «ро»).
Тогда формулу для вычисления плотности можно записать в следующем виде: Единицей плотности в СИ является килограмм на кубический метр (1 кг/м3). На практике плотность вещества выражают также в граммах на кубический сантиметр (г/см3). Для установления связи между этими единицами учтем, что
1 г = 0,001 кг, 1 см3 = 0,000001 м3.
Поэтому Плотность одного и того же вещества в твердом, жидком и газообразном состоянии различна. Например, плотность воды равна 1000 кг/м3, льда — 900 кг/м3, а водяного пара (при 00 С и нормальном атмосферном давлении) – 0,59 кг/м3.
Таблица 3
Плотности некоторых твердых тел
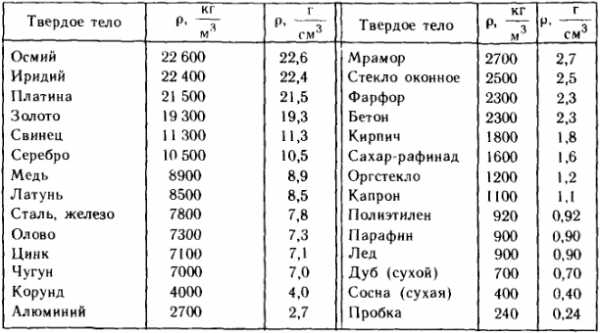
Таблица 4
Плотности некоторых жидкостей
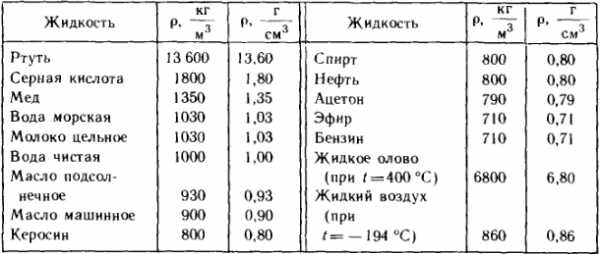
Таблица 5
Плотности некоторых газов
Мы знаем, что скорость тела относительно Земли изменяется тогда, когда на него действуют другие тела. Проиллюстрируем это новыми примерами.
Толкая вагонетку (рис. 25), ее приводят в движение. В этом случае скорость вагонетки изменяется под действием руки человека.
Опустим на воду пробку, на которой лежит железная скрепка. Магнит, притягивая скрепку, приводит ее и пробку в движение (рис. 26). В этом случае магнит — то тело, которое изменяет скорость скрепки и пробки.
При действии руки на шар (рис. 27, а) витки пружины начинают двигаться, и пружина сжимается. Отпустив ее, мы увидим, как пружина, распрямляясь, приводит в движение шар (рис. 27, б). Сначала действующим телом здесь была рука человека. Затем действующим телом стала пружина. 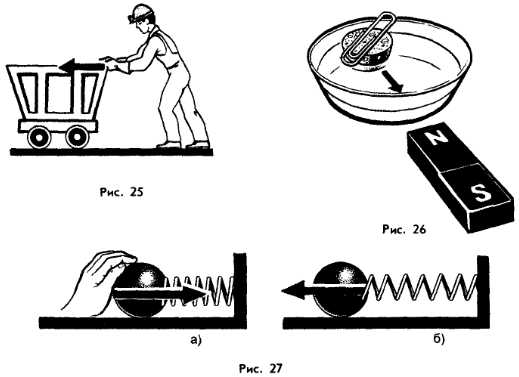
Во всех приведенных примерах причиной изменения скорости тела было действие, оказываемое на него другими телами.
Мерой этого действия является векторная физическая величина, называемая силой.
Как и другие векторные величины, сила характеризуется не только числовым значением, но и своим направлением. Стрелки, изображенные на рисунках 25—27, как раз и указывают это направление.
Силу обычно обозначают буквой F, однако есть и другие обозначения, о которых вы узнаете позже.
Если сила к телу не приложена (F = 0), то это означает, что никакого действия на него не оказывается, и потому скорость такого тела относительно Земли не изменяется. Если же, наоборот, сила F ≠ 0, то тело испытывает некоторое воздействие, и его скорость изменяется. При этом, чем больше сила F, тем значительнее изменяется скорость тела относительно Земли.
Единицей силы в СИ является ньютон (1 Н). 1 Н — это сила, которая за 1 с изменяет скорость тела массой 1 кг на 1 м/с. Эта единица названа в честь великого английского ученого И. Ньютона (1642—1727).
На практике применяются также килоньютоны и миллиньютоны:
1 кН = 1000 Н, 1 мН = 0,001 Н.
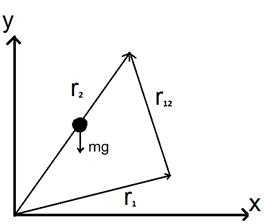
Принцип суперпозиции (наложения) сил заключается в том, что действие нескольких сил можно заменить действием одной -равнодействующей. Например, одновременное механическое действие на данное тело двух других тел, приложенных к одной точке, всегда может быть заменено действием одного тела так, что сила F, описывающая результирующее воздействие, определяется векторной суммой сил F1 и F2, действующих со стороны каждого тела.
Если, силы, действующие на данное тело не изменяются в присутствии третьего, то в этом случае составляющие сил определяются независимо от присутствия какого-либо тела, а их суммарное воздействие равно сумме воздействий каждого тела системы на данное.
studopedia.net

