Модуль нормальный зубчатого колеса: Таблица стандартных модулей зубчатых колес
alexxlab | 07.05.2023 | 0 | Разное
Таблица стандартных модулей зубчатых колес
- Точение
- Фрезерование
- ЧПУ
- Таблицы
- Таблицы
- Таблица модулей зубчатых колес
ГОСТ 9563 – 60
| 1-й ряд | 2-й ряд | 1-й ряд | 2-й ряд |
|---|---|---|---|
0. 05 05 |
0.055 | 2.5 | 2.75 |
| 0.06 | 0.07 | 3 | 3.5 |
| 0.08 | 0.09 | 4 | 4.5 |
| 0.1 | 0.11 | 5 | 5.5 |
| 0.12 | 0.14 | 6 | 7 |
| 0.15 | 0.18 | 8 | 9 |
| 0.2 | 0.22 | 10 | 11 |
| 0.25 | 0.28 | 12 | 14 |
| 0.3 | 0.35 | 16 | 18 |
| 0.4 | 0.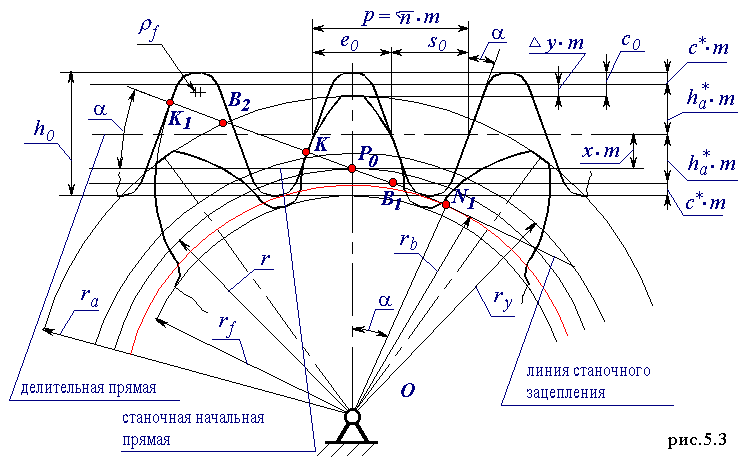 45 45 |
20 | 22 |
| 0.5 | 0.55 | 25 | 28 |
| 0.6 | 0.7 | 32 | 36 |
| 0.8 | 0.9 | 40 | 45 |
| 1 | 1.125 | 50 | 55 |
| 1.25 | 1.375 | 60 | 70 |
| 1.5 | 1.75 | 80 | 90 |
| 2 | 2.25 | 100 | |
| Modules of gears | |||
|
Модули, данной таблицы, выбираемые
из ячеек первого ряда, следует использовать в приоритетном порядке.  |
|||
Написать письмо
Lektsia_Zubchatye_peredachi_i_kolesa
Модуль «Нормирование точности зубчатых передач и колес»
Введение
В данном материале рассмотрим особенности нормирования зубчатых передач и колес, элементы расчета и конструирования. Данный материал связан с теорией мо-
дуля «Разъемные соединения. Нормирование точности шпоночных и шлицевых со-
единений».
Зубчатые механизмы являются наиболее распространенным в машиностроении и приборостроении видом механических передач. Такие передачи применяют для пере-
дачи вращательного движения с одного вала на другой или для преобразования вра-
щательного движения в поступательное и изменение скорости вращения валов.
Зубчатые передачи можно классифицировать по различным признакам.
По характеру расположения валов:
–с параллельными осями;
–с пересекающимися осями;
–с скрещивающимися осями.
По форме профилей зубьев:
–эвольвентные;
–циклоидальные;
–круговые и другие.
Передачи с внешним и внутренним зацеплением.
В зависимости от назначения передачи зубья могут быть прямыми, косыми, шев-
ронными, криволинейными (рисунок 1). Общий вид зубчатой передачи представлен на рисунке 2. В настоящее время эвольвентные передачи получили наибольшее рас-
пространение.
Рисунок 1 – Виды зубчатых передач
Рисунок 2 – Общий вид зубчатой передачи
1.1 Основные понятия в теории зубчатых передач
Рассматриваемые основные понятия зубчатой передачи даны в соответст-
вии с ГОСТ 6530 и представлены глоссарии электронного курса в категории
«Зубчатые передачи».
1.2 Элементы зубчатого колеса
Наиболее часто в различных машинах применяют зубчатые колёса средне-
го диаметра (примерно от 80 до 200 мм). Такие колёса изготавливают дисковы-
ми (рисунок 3а). Колёса большего диаметра делают со спицами (рисунок 3б), а
небольшого – сплошным, т. е. без диска и без спиц (рисунок 3в).
е. без диска и без спиц (рисунок 3в).
а) б) в)
а – дисковое зубчатое колесо; б – зубчатое колесо со спицами; в – сплошное зубчатое колесо
Рисунок 3 – Виды зубчатых колес Основными элементами зубчатого колеса (рисунок 4) являются зубья, ка-
ждый зуб состоит из головки зуба и ножки.
Рисунок 4 – Условные изображения элементов зубчатого колеса Зубья находятся на ободе колеса и вместе с ободом составляют зубчатый
венец, более тонкая часть колеса – диск соединяет ступицу с ободом, внутри ступицы делают отверстие для вала с пазом для шпонки. Шлицевое соедине-
ние представлено на рисунке 4 показаны условные изображения элементов зуб-
чатого колеса.
Основным геометрическим параметром, определяющим все элементы пе-
редачи, является модуль m, который выбирается в зависимости от передаваемой нагрузки из нормального ряда модулей по ГОСТ 9563.
Зубчатые колеса с модулем от 0,05 мм до 1 мм принято называть мелкомо-
дульными; от 1 до 10 мм – среднемодульными и свыше 10 мм − крупномодуль-
ными.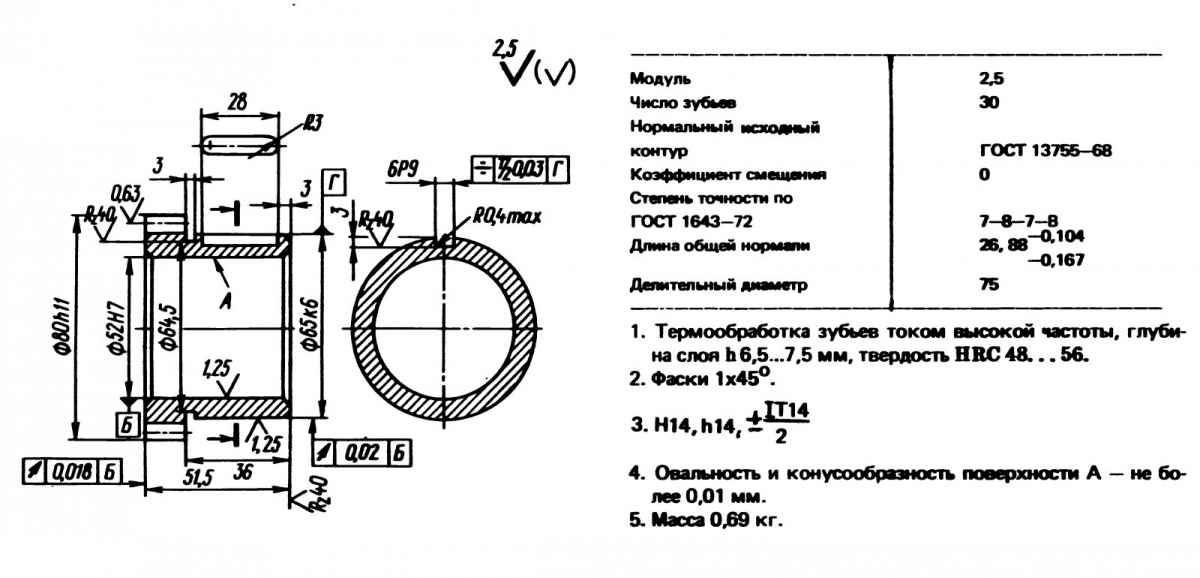
Мелкомодульные передачи (m 1) используются при малых нагрузках (в
приборостроении, при ручном приводе). Чем больше передаваемая нагрузка,
тем больше должен быть модуль и ширина зубчатого венца В. Рекомендуется принимать В = (3…15) m.
Число зубьев колес принято обозначать буквой Z а в передаче для ведуще-
го (шестерни) и ведомого колес – Z1 и Z2 соответственно.
В зубчатой передаче число оборотов зависит от числа зубьев колеса.
Передаточное число i = n1 = z2 , где n1 и n2 число оборотов в минуту ве- n2 z1
дущего и ведомого колеса.
Межосевое расстояние (делительное) в передаче a = m(Z1+Z2)/2.
К основным параметрам зубчатого колеса 1относятся:
da – окружность вершин – это самая большая окружность, ограничиваю-
щая вершины головок зубьев колес: её условно изображают сплошной основ-
ной линией.
d – делительная окружность (диаметр делительной окружности), деля-
щая каждый зуб на две неравные части: меньшую – головку зуба и большую – ножку зуба: её условно изображают штрихпунктирной тонкой линией.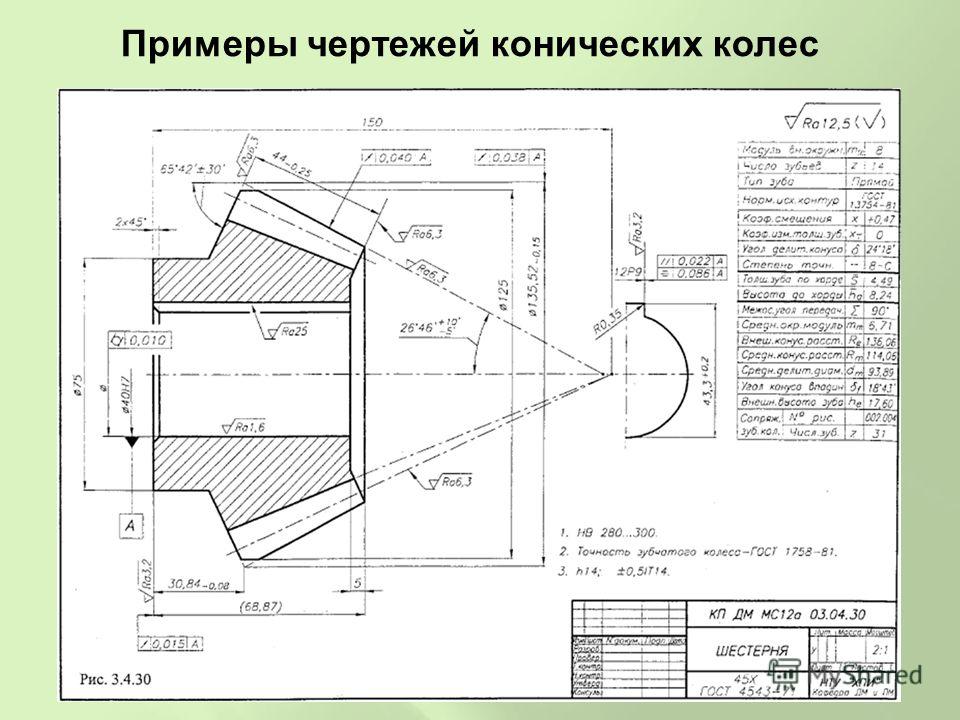
df – окружность впадин, – окружность впадин, проходящая по очертаниям впадин между зубьями: её условно изображают сплошной тонкой линией.
dоб – окружность обода, обозначающая внутреннее очертание обода. dст – окружность ступицы, обозначающая внешнее очертание ступицы. dВ – диаметр окружности отверстия для вала.
h – высота зуба.
ha – высота головки зуба. hf – высота ножки зуба.
Pn – нормальный шаг зубьев – кратчайшее расстояние по делительной или начальной поверхности зубчатого колеса между эквидистантными од-
ноименными теоретическими линиями соседних зубьев.
S – толщина зуба по делительной окружности S = pt /2 = π m/2 на высоте головки зуба ha; толщина зуба по постоянной хорде Sc=1,387 m, измеренная на высоте hc=0,7476 m от вершины зуба. Этот показатель не зависит от числа зубьев колеса, а зависит только от модуля;
Z – число зубьев.
1 Основные формулы расчета каждого из показателей приведены в методическом указании к выполнению задания, выложенному в электронном курсе в модуле 6 «Нормирование точности зубчатых передач и колес»
m – нормальный модуль зубьев – это линейная величина в π раз мень-
шая нормального шага зубьев.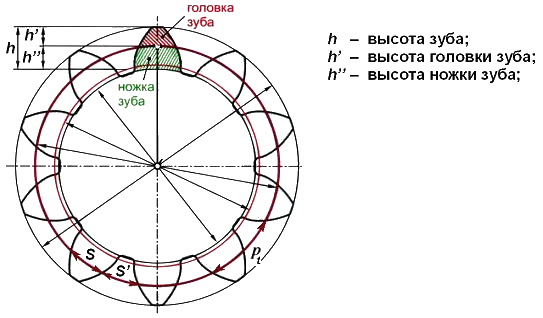 Модуль – это число, которое показывает сколько миллиметров диаметра делительной окружности приходится на один зуб зубчатого колеса.
Модуль – это число, которое показывает сколько миллиметров диаметра делительной окружности приходится на один зуб зубчатого колеса.
bпаза – ширина шпоночного паза. tj – глубина шпоночного паза.
Длина общей нормали это расстояние между двумя параллельными плоскостями, касательными к двум разноименным, активным боковым поверх-
ностям зубьев колеса. Номинальное значение длины общей нормали определя-
ется по формуле:
W=pt (Zw−1) +S,
где Zw= 0,111 z + 0,5 или Zw= z/9+1 – число охватываемых при измерении зубьев, которое необходимо округлять до ближайшего целого числа (см.таблицу 1). Для колес с углом зацепления формула принимает вид:
W=m [1,476 (2Zw – 1) +0,014 Z].
Длина общей нормали прямо пропорциональна модулю, поэтому в табли-
цах справочников указывается значение длины общей нормали для m=1 (см.
таблицу 1). При изменении модуля табличное значение необходимо умножить на величину модуля.
Средняя длина общей нормали определяется по результатам измерения всех длин у колеса от зуба к зубу, как среднее арифметическое значение:
| z |
|
|
|
| Wi |
| W1 W2 . | . |
Wm | 1 |
| ||
z |
| |||
|
| z | ||
Ввиду погрешностей обработки, у одного зубчатого колеса длина общей нормали изменяется от зуба к зубу.
Для размещения смазки и исключения заклинивания требуется увеличи-
вать или уменьшать толщину зуба. Теоретическое зацепление считается двух-
профильным, когда контакт идет по обеим сторонам зуба.
Реальная передача имеет однопрофильное зацепление, т.е. по рабочим профилям контакт, а по нерабочим зазор.
Таблица 1– Геометрические параметры зубчатого колеса при m = 1, α= 20 °С
Число | Количе- | Длина | Диаметр |
|
| Количе- | Длина | Диаметр |
зубьев | ство охва- | общей | основной |
| Число | ство охва- | общей | основной |
Z | тываемых | норма- | окружно- |
| зубьевZ | тываемых | норма- | окруж- |
коле- | зубьев | ли | сти |
| колеса | зубьев | ли | ности |
са | Zw | W, мм | db, мм |
|
| Zw | W, мм | db, мм |
12 |
| 4,596 | 11,276 |
| 51 |
| 16951 | 47,924 |
|
|
|
|
|
|
|
|
|
15 |
| 4,938 | 14,095 |
| 52 | 6 | 16,965 | 48,864 |
|
|
|
|
|
|
|
| |
16 | 2 | 4,652 | 15,035 |
| 53 | 16,978 | 49,804 | |
|
| |||||||
|
|
|
|
|
|
|
|
|
17 |
| 4,666 | 15,975 |
| 54 |
| 16,992 | 50,743 |
|
|
|
|
|
|
|
|
|
18 |
| 4,680 | 16,914 |
| 55 |
| 19,959 | 51,683 |
|
|
|
|
|
|
|
|
|
20 |
| 7,660 | 18,794 |
| 56 |
| 19,973 | 52,623 |
|
|
|
|
|
|
|
|
|
22 |
| 7,688 | 20,673 |
| 57 |
| 19,987 | 53,562 |
23 |
| 7,702 | 21,613 |
| 58 | 7 | 20,001 | 54,502 |
|
|
|
|
|
|
|
|
|
24 | 3 | 7,716 | 22,557 |
| 59 |
| 20,015 | 55,442 |
|
|
|
|
|
|
|
|
|
25 |
| 7,730 | 23,492 |
| 60 |
| 20,029 | 56,382 |
|
|
|
|
|
|
|
|
|
26 |
| 7,744 | 24,432 |
| 62 |
| 20,057 | 58,261 |
|
|
|
|
|
|
|
|
|
27 |
| 7,758 | 25372 |
| 65 |
| 23,051 | 61,08 |
|
|
|
|
|
|
|
|
|
28 |
| 10,725 | 26,311 |
| 66 |
| 23,065 | 62,02 |
|
|
|
|
|
| 8 |
|
|
29 |
| 10,739 | 27,251 |
| 68 | 23,093 | 63,899 | |
|
|
|
|
|
|
|
|
|
30 |
| 10,753 | 28,191 |
| 70 |
| 23,121 | 66,778 |
31 |
| 10,767 | 29,13 |
| 72 |
| 23,149 | 67,578 |
| 4 |
|
|
|
|
|
|
|
32 | 10,781 | 30,07 |
| 75 |
| 26,051 | 70,477 | |
|
|
|
|
|
|
|
|
|
33 |
| 10,795 | 31,001 |
| 76 |
| 26,157 | 71,416 |
|
|
|
|
|
| 9 |
|
|
34 |
| 10,809 | 31,95 |
| 78 | 26,185 | 73,296 | |
|
|
|
|
|
|
|
|
|
35 |
| 10,872 | 32,889 |
| 79 |
| 26,199 | 74,236 |
|
|
|
|
|
|
|
|
|
36 |
| 10,836 | 33,829 |
| 80 |
| 26,213 | 75,175 |
|
|
|
|
|
|
|
|
|
37 |
| 13,803 | 34,769 |
| 82 |
| 29,194 | 77,055 |
|
|
|
|
|
| 10 |
|
|
38 |
| 13,817 | 35,708 |
| 85 | 29,236 | 79,874 | |
|
|
|
|
|
|
|
|
|
39 |
| 13,831 | 36,648 |
| 90 |
| 29,306 | 84,572 |
|
|
|
|
|
|
|
|
|
40 |
| 13,845 | 37,588 |
| 92 |
| 32,286 | 86,452 |
| 5 |
|
|
|
|
|
|
|
41 | 13,859 | 38,527 |
| 94 |
| 32,314 | 88,331 | |
|
|
|
|
|
| 11 |
|
|
42 |
| 13,873 | 39. |
| 95 | 32,328 | 89,271 | |
|
|
|
|
|
|
|
|
|
43 |
| 13,887 | 40,407 |
| 98 |
| 32,369 | 92,09 |
|
|
|
|
|
|
|
|
|
44 |
| 13,900 | 41,346 |
| 100 |
| 32,398 | 93,97 |
|
|
|
|
|
|
|
|
|
45 |
| 13,914 | 42,286 |
| 100 | 12 | 35,350 | 93,97 |
|
|
|
|
|
|
|
| |
46 |
| 16,881 | 43,226 |
| 105 | 35,420 | 98,668 | |
|
|
| ||||||
|
|
|
|
|
|
|
|
|
47 |
| 16,895 | 44,166 |
| 108 |
| 38,414 | 101,468 |
| 6 |
|
|
|
|
|
|
|
48 | 16,909 | 45,105 |
| 110 | 13 | 38,442 | 103,336 | |
|
|
|
|
|
|
|
| |
49 |
| 16,923 | 46,045 |
| 122 | 38,47 | 105,246 | |
|
|
| ||||||
|
|
|
|
|
|
|
|
|
50 |
| 16,937 | 46,985 |
| 115 |
| 38,512 | 108,066 |
|
|
|
|
|
|
|
|
|
Величина бокового зазора зависит от условий эксплуатации: температуры,
смазки, нагрузки, условий загрязнения и других требований (см. пункты «Сте-
пункты «Сте-
пени точности и виды сопряжения» и «Выбор степени точности зубчатой пере-
дачи»).
У зубчатого колеса различают окружной шаг по делительной окружности: pt=360/Z= m,
и шаг зацепления или основной шаг (шаг по основной окружности): pb=pt cos = m cos .
Рисунок 5 – Схема измерения шаговых параметров зубчатого колеса:
a – окружного шага; б – шага зацепления
Контроль окружного шага может быть выполнен накладным шагомером или универсальным зубоизмерительным прибором. Базирующие наконечники опираются на наружный (или внутренний) диаметр (рисунок 5, а). Широко ис-
пользуется метод измерения от «первого шага», принятого за номинальное зна-
чение с определением отклонений от него. Измерив по всей окружности Z раз,
можно построить график и определить накопленную погрешность окружного шага.
Шаг зацепления (основной шаг) контролируется в плоскости, касательной к основному цилиндру (рисунок 5, б). Настройка прибора производиться на
ноль по блоку кольцевых мер длины, равному номинальному значению шага зацепления. Метод измерения относительный, так как прибор показывает по-
Метод измерения относительный, так как прибор показывает по-
грешность шага зацепления:
рb = рbr – рb ном.
2 Допуски цилиндрических зубчатых передач
Точность изготовления зубчатых передач и червячных колес задается сте-
пенью по нормам кинематической точности, плавности работы и контакта зубь-
ев в передаче, а требования к боковому зазору – видом сопряжений и видом до-
пуска бокового зазора. К нормам точности относятся допуски и отклонения, ог-
раничивающие отдельные виды погрешностей.
1 Кинематическая погрешность передачи – разность между действи-
тельным и номинальным (расчетным) углами поворота ведомого зубчатого ко-
леса передачи. Выражается в линейных величинах длиной дуги его делитель-
ной окружности (Рисунок 6).
,
где | – число зубьев ведущего зубчатого колеса; | – число зубьев ведомого зубчатого ко- | |
леса; | – действительный угол поворота ведущего зубчатого колеса; | – действительный | |
угол поворота ведомого зубчатого колеса; – номинальный угол поворота ведомого зубчатого колеса
Рисунок 6
1.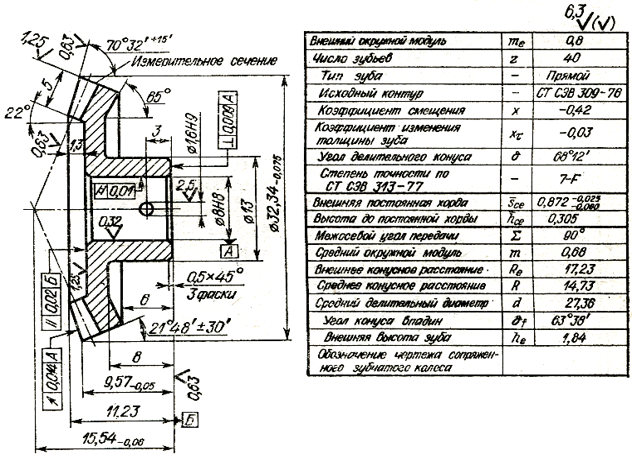 1 Наибольшая кинематическая погрешность передачи – наибольшая алгебраическая разность значений кинематической погрешности передачи за полный цикл изменения относительного положения зубчатых колес (т.е. в пре-
1 Наибольшая кинематическая погрешность передачи – наибольшая алгебраическая разность значений кинематической погрешности передачи за полный цикл изменения относительного положения зубчатых колес (т.е. в пре-
делах числа оборотов большего зубчатого колеса, равного частному от деления числа зубьев меньшего зубчатого колеса на общий наибольший делитель чисел зубьев обоих зубчатых колес передачи) (Рисунок 7).
– угол поворота большего колеса; – общий наибольший делитель чисел зубьев и соответственно шестерни и колеса; I – наибольшая кинематическая погрешность передачи ; II – полный цикл изменения относительного положения зубчатых колес
Рисунок 7
1.2 Допуск на кинематическую погрешность передачи
2 Кинематическая погрешность зубчатого колеса – разность между действительным и номинальным (расчетным) углами поворота зубчатого коле-
са на его рабочей оси, ведомого измерительным зубчатым колесом при номи-
нальном взаимном положении осей вращения этих колес. Выражается в линей-
Выражается в линей-
ных величинах длиной дуги делительной окружности.
Примечания: 1 Под рабочей осью зубчатого колеса понимается ось, вокруг которой оно вращается в передаче.
2 Под измерительным зубчатым колесом понимается зубчатое колесо повышенной точности, применяемое в качестве измерительного элемента для однопрофильного и двух-
профильного методов контроля зубчатых колес.
2.1 Наибольшая кинематическая погрешность зубчатого колеса – наи-
большая алгебраическая разность значений кинематической погрешности зуб-
чатого колеса в пределах его полного оборота (Рисунок 8).
Калькулятор нормального модуля косозубого зубчатого колеса
✖Поперечный модуль косозубого зубчатого колеса — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения.ⓘ Поперечный модуль косозубого зубчатого колеса [м] of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CalibreCentimeterChainCubit (греческий)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerUSFermiFinger (Cloth)Finger (Cloth) Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan (Cloth) Солнечный радиусTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | ||
✖Угол винтовой передачи — это угол между любой косозубой шестерней и осевой линией справа, круглым цилиндром или конусом. | CircleCycleDegreeGonGradianMilMilliradianMinuteMinutes of ArcPointQuadrantQuartercircleRadianRevolutionRight AngleSecondSemicircleSextantSignTurn | +10% -10% |
✖Нормальный модуль косозубого зубчатого колеса определяется как единица размера, указывающая, насколько большим или малым является косозубое зубчатое колесо.ⓘ Нормальный модуль косозубого зубчатого колеса [m n ] | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Нормальный модуль винтового зубчатого колеса
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Поперечный модуль косозубого зубчатого колеса: 3,4 миллиметра –> 0,0034 метра (проверьте преобразование здесь)
Угол наклона косозубого зубчатого колеса: 25 Градус –> 0,4363323129985 Радиан (Проверьте преобразование здесь)
ШАГ 2: Вычислите формулу
ШАГ 3: Преобразуйте результат в единицу измерения
0,00308144647592473 Метр (проверьте конвертацию 3,007 44463759 метр) здесь0067 < 14 Калькулятор соотношения зубов
Нормальный модуль винтовой шестерни с заданным межосевым расстоянием между двумя шестернями
Идти Нормальный модуль косозубой шестерни = Расстояние от центра до центра косозубой шестерни * (2 * cos (угол наклона косозубой шестерни)) / (количество зубьев на 1-й косозубой шестерне + количество зубьев 2-й косозубой шестерни) 92)
Угол подъема винтовой шестерни с учетом диаметра окружности приложения
Идти Угол наклона косозубой шестерни = acos(Количество зубьев косозубой шестерни/((Дополнение Диаметр окружности косозубой шестерни/Нормальный модуль косозубой шестерни)-2))
Нормальный модуль косозубого зубчатого колеса с учетом диаметра окружности приложения
Идти Нормальный модуль косозубого зубчатого колеса = Дополнение Диаметр окружности косозубого зубчатого колеса/((Число зубьев на косозубом зубчатом колесе/cos(Угол наклона косозубого зубчатого колеса))+2)
Количество зубьев на шестерне с учетом диаметра окружности приложения
Идти Количество зубьев на косозубой шестерне = ((дополнительный диаметр окружности косозубой шестерни/нормальный модуль косозубой шестерни)-2)*cos(угол наклона косозубой шестерни)
Приложение Диаметр окружности шестерни
Идти Дополнение Диаметр окружности косозубой шестерни = Нормальный модуль косозубой шестерни*((Число зубьев косозубой шестерни/cos(Угол винтовой шестерни))+2)
Нормальный модуль косозубого колеса с заданным диаметром делительной окружности
Идти
Нормальный модуль косозубой шестерни = диаметр делительной окружности косозубой шестерни * cos (угол наклона косозубой шестерни) / количество зубьев косозубой шестерни.
Виртуальное количество зубьев на винтовой передаче
Идти Виртуальное количество зубьев на косозубом колесе = 2*pi*Виртуальный радиус делительной окружности для косозубого зубчатого колеса/нормальный круговой шаг косозубого зубчатого колеса 9(3))*Виртуальное количество зубьев на косозубом колесе
Виртуальное количество зубьев на косозубом колесе задано Фактическое количество зубьев
Идти Виртуальное количество зубьев на косозубой шестерне = количество зубьев на косозубой шестерне/(cos(угол винтовой шестерни))^3
Обычный модуль винтовой передачи
Идти Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса)
Приложение о шестернях с учетом диаметра окружности приложения
Идти Дополнение по косозубому зубчатому колесу = (дополнение диаметр окружности косозубого зубчатого колеса-диаметр делительной окружности косозубого зубчатого колеса)/2
Приложение Диаметр окружности зубчатого колеса с учетом диаметра делительной окружности
Идти Дополнение Диаметр окружности косозубой шестерни = 2*Дополнение косозубой шестерни+Диаметр делительной окружности косозубой шестерни
Дедендум Диаметр окружности зубчатого колеса с учетом диаметра делительной окружности
Идти Диаметр делительной окружности косозубой шестерни = Диаметр делительной окружности косозубой шестерни-2 * Дедендум косозубой шестерни
Нормальный модуль формулы винтовой передачи
Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса)
m n = m*cos(ψ)
Дайте определение косозубым зубчатым колесам?
Косозубая шестерня имеет цилиндрическую делительную поверхность и зубья, которые следуют по спирали на делительном цилиндре.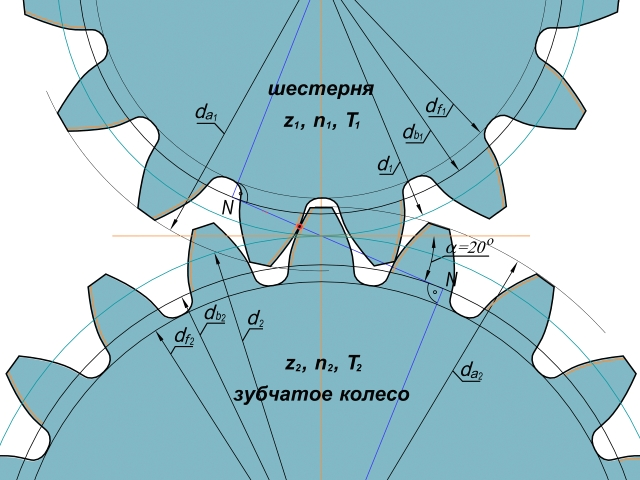 У наружных косозубых шестерен зубья выступают наружу, а у внутренних косозубых шестерен зубья выступают внутрь.
У наружных косозубых шестерен зубья выступают наружу, а у внутренних косозубых шестерен зубья выступают внутрь.
Как рассчитать нормальный модуль винтовой передачи?
Калькулятор нормального модуля косозубого зубчатого колеса использует Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса) для расчета нормального модуля косозубого зубчатого колеса, формула нормального модуля косозубого зубчатого колеса определяется как модуль опорная точка зуба ортогональна спирали резьбы. Нормальный модуль косозубого колеса обозначается м n символ.
Как рассчитать нормальный модуль винтовой передачи с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для нормального модуля косозубого зубчатого колеса, введите поперечный модуль косозубого зубчатого колеса (м) и угол наклона косозубого зубчатого колеса (ψ) и нажмите кнопку расчета. Вот как можно объяснить расчет нормального модуля винтовой передачи с заданными входными значениями -> 3,081446 = 0,0034*cos(0,4363323129985) .
Вот как можно объяснить расчет нормального модуля винтовой передачи с заданными входными значениями -> 3,081446 = 0,0034*cos(0,4363323129985) .
Часто задаваемые вопросы
Что такое обычный модуль винтовой передачи?
Формула нормального модуля косозубого зубчатого колеса определяется как модуль базы зуба, ортогональной спирали резьбы, и представляется как m n = m*cos(ψ) или Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого колеса Шестерня*cos(Угол винтовой шестерни) . Поперечный модуль косозубого зубчатого колеса — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения, а угол наклона косозубого зубчатого колеса — это угол между любым косозубым зубчатым колесом и осевой линией на его правом круговом цилиндре или конусе.
Как рассчитать нормальный модуль винтовой передачи?
Формула нормального модуля косозубого зубчатого колеса определяется как модуль базовой точки зуба, ортогональный спирали резьбы, который рассчитывается с использованием Нормальный модуль косозубого зубчатого колеса = Поперечный модуль косозубого зубчатого колеса*cos(Угол винтового зубчатого колеса) . Для расчета нормального модуля косозубой шестерни вам потребуется поперечный модуль косозубой шестерни (м) и угол подъема косозубой шестерни (ψ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для поперечного модуля винтовой шестерни и угла наклона винтовой шестерни и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Для расчета нормального модуля косозубой шестерни вам потребуется поперечный модуль косозубой шестерни (м) и угол подъема косозубой шестерни (ψ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для поперечного модуля винтовой шестерни и угла наклона винтовой шестерни и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета нормального модуля винтовой передачи?
В этой формуле Нормальный модуль косозубого зубчатого колеса использует поперечный модуль косозубого зубчатого колеса и угол подъема косозубого зубчатого колеса. Мы можем использовать 4 других способа (способов) для расчета того же самого, которые заключаются в следующем:
- Нормальный модуль косозубой шестерни = Дополнение Диаметр окружности косозубой шестерни/((Число зубьев на косозубой шестерне/cos(Угол спирали косозубой шестерни))+2)
- Нормальный модуль косозубой шестерни = диаметр делительной окружности косозубой шестерни*cos(угол винтовой шестерни)/количество зубьев косозубой шестерни 92)
Поделиться
Скопировано!
Определение толщины зубьев различных типов шестерен
Чтобы определить размер зубьев шестерни после учета допусков на люфт, сначала необходимо определить, какой должна быть номинальная толщина зубьев. Существует три метода определения этого значения: измерение толщины зуба по хорде, измерение размаха и измерение над штифтом или шариком. В этой статье мы обсудим измерения толщины хорды зуба.
Существует три метода определения этого значения: измерение толщины зуба по хорде, измерение размаха и измерение над штифтом или шариком. В этой статье мы обсудим измерения толщины хорды зуба.
В методе измерения толщины зуба по хорде используется штангенциркуль, который отсчитывается от диаметра вершины зубчатого колеса. Толщина измеряется на эталонной окружности, как показано на рис. 1.
Рис. 1: Метод определения толщины хорды зуба.Для прямозубых зубчатых колес формулы для расчета толщины хордового зуба подробно описаны в Таблице 1.
Для зубчатой рейки, независимо от того, являются ли они прямыми зубьями или косозубыми, формулы упрощены, поскольку профиль зуба зубчатого колеса трапецеидальный. Эти формулы подробно описаны в таблице 2.
Таблица 1: Уравнения для толщины хорды зуба цилиндрического зубчатого колеса. Таблица 2: Толщина хорды зуба рейки. Измерение косозубых зубчатых колес может выполняться либо в нормальной плоскости, либо в поперечной плоскости, в зависимости от того, как нарезаны зубчатые колеса. Формулы для измерений в нормальной плоскости подробно представлены в таблице 3, а формулы для измерений в поперечной плоскости — в таблице 4. толщина зубьев косозубых колес в поперечной системе.
Формулы для измерений в нормальной плоскости подробно представлены в таблице 3, а формулы для измерений в поперечной плоскости — в таблице 4. толщина зубьев косозубых колес в поперечной системе.
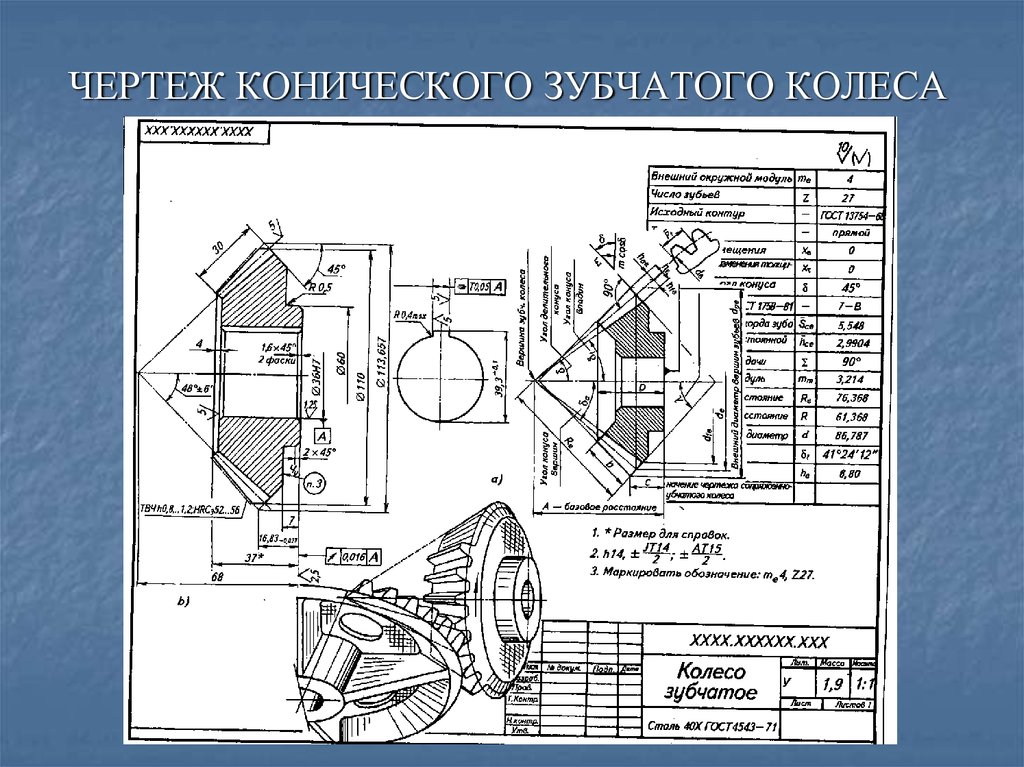
Измерение прямозубых конических зубчатых передач зависит от системы зубьев. Формулы для измерений в стандартной системе подробно описаны в Таблице 5, а формулы для измерений конических зубчатых колес, нарезанных с использованием системы Глисона, подробно описаны в Таблице 6.
Уравнения для толщины хорды прямозубых конических шестерен Глисона. Рисунок 2: Диаграмма для определения коэффициента толщины зуба k для прямолинейных конических шестерен ГлисонаЕсли прямая коническая шестерня нарезается фрезой Gleason для прямой конической обработки, угол зуба следует отрегулировать в соответствии с:
Этот угол используется в качестве ориентира при определении толщины зуба s при настройке зуборезного станка.
Для спирально-конических зубчатых колес, нарезанных по системе Глисона, формулы для расчета хордовой толщины зуба приведены в Таблице 7.


 467
467 ⓘ Угол наклона винтовой передачи. Gear [ψ]
ⓘ Угол наклона винтовой передачи. Gear [ψ]