Модуль силы упругости: Механическое напряжение. Модуль Юнга. Закон Гука — урок. Физика, 10 класс.

alexxlab | 07.04.2023 | 0 | Разное

Зависимость силы упругости от деформации. Закон Гука

Зависимость сил упругости от деформации была установлена экспериментально английским физиком Робертом Гуком в середине XVII в. Давайте и мы обратимся к опыту.

Подвесим к потолку легкий резиновый шнур длиной l0 (рис. 99, а). К нижнему концу шнура прикрепим груз небольшой массы m. Начнем постепенно отпускать груз, чтобы он медленно двигался вниз, а шнур все больше и больше растягивался. Когда мы перестанем удерживать груз, длина шнура станет равной l1, а груз будет висеть неподвижно в системе отсчета, связанной с Землей (рис. 99, б). Величина Δl1 = l1 – l0 будет удлинением шнура.

Определим силу, с которой тело массой m действует на шнур. Для этого воспользуемся известными нам законами Ньютона. Так как ускорение груза равно нулю, то согласно второму закону Ньютона сумма всех сил, действующих на груз, равна нулю. Иначе говоря, силы, действующие на груз, скомпенсировали (уравновесили) друг друга.

Выясним, какие это силы. Во-первых, как мы уже знаем, на груз действует сила тяжести, равная по модулю m · g и направленная вертикально вниз в отрицательном направлении оси X. Во-вторых, на груз действует сила упругости растянутого шнура. Именно эта сиаа компенсирует (уравновешивает) действие силы тяжести. Запишем второй закон Ньютона для груза с учетом того, что его ускорение равно нулю, а сила тяжести направлена в отрицательном направлении оси X:

0 = Fупр – m · g.

Следовательно, значение силы упругости Fупр = m · g, т. е. положительно. Поэтому сила упругости шнура, действующая на груз, направлена в положительном направлении оси X – вертикально вверх. При этом нижний конец деформированного шнура сместился в отрицательном направлении оси X – вниз. Таким образом, сила упругости шнура направлена в сторону, противоположную вызвавшему ее смещению. Иначе говоря, шнур стремится вернуться в исходное, нерастянутое состояние.

Снимем висящий груз. Если деформация шнура была упругой, то длина шнура станет первоначальной.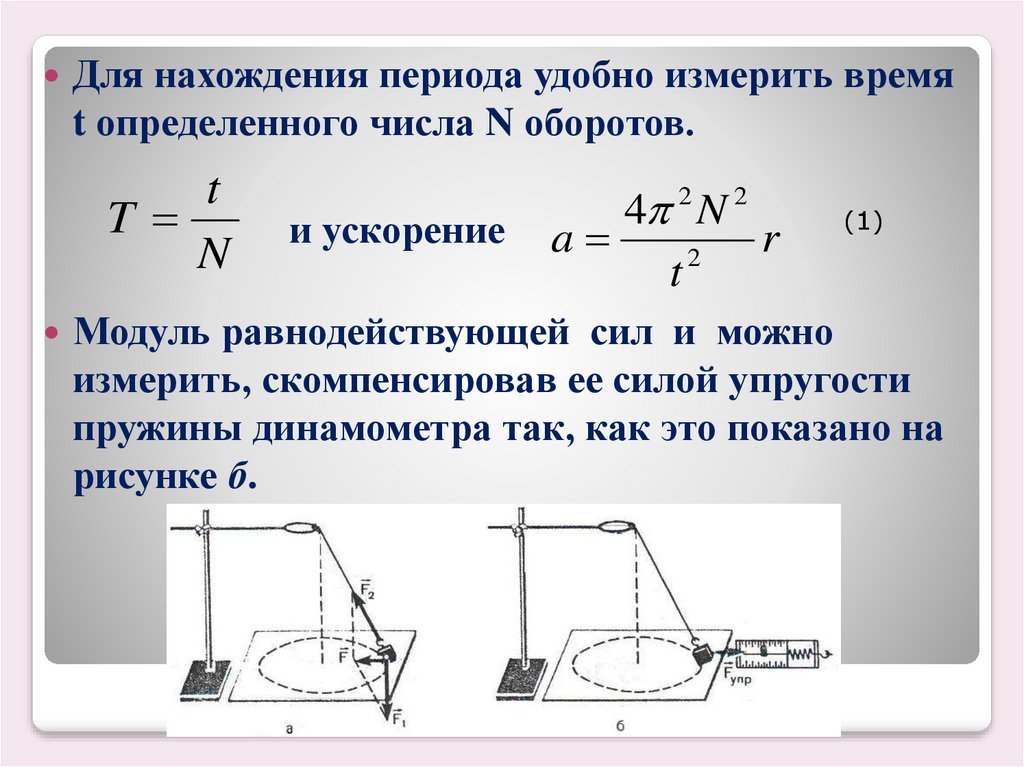

Аккуратно подвесим на шнур груз массой 2m. Измерим длину растянутого шнура l2. Если шнур деформировался упруго, то удлинение шнура Δl2 = l2 – l0 под действием силы 2m · g будет равно 2Δl1 (рис. 100). Продолжая увеличивать массы подвешиваемых грузов, можно прийти к следующему выводу: при упругих деформациях шнура увеличение в n раз массы подвешиваемого груза приводит к увеличению удлинения шнура также в n раз. Следовательно, удлинение шнура при упругих деформациях пропорционально модулю силы упругости.

При упругих деформациях отношение модуля силы упругости |Fупр| к удлинению шнура Δl является постоянным. Это отношение характеризует упругие свойства деформируемого тела и называется коэффициентом жесткости (жесткостью) этого тела.

Обычно коэффициент жесткости обозначают латинской буквой k. Так как перемещение Δl незакрепленного конца шнура направлено в сторону, противоположную силе Fупр этот факт часто записывают в виде:

Fупр = -k · Δl.

Гук опытным путем установил:
для любого тела при упругих деформациях эти деформации прямо пропорциональны вызывающим их силам.
F = k · Δl.

Это утверждение называют законом Гука.

Отметим, что в шнуре или нити силы упругости возникают лишь при попытке увеличить их длину (растянуть). В пружинах и стержнях силы упругости возникают не только при их растяжении, но и при сжатии.

При упругих деформациях сжатия и растяжения жесткость тела не изменяется. Поскольку при растяжении длина тела увеличивается, а при сжатии уменьшается, в первом случае удлинение тела считают положительным (Δl > 0), а во втором – отрицательным (Δl 0.

Эксперименты показывают, что для любого тела существует определенное критическое значение модуля деформирующих его сил Fкр, начиная с которого деформации тела перестают быть упругими. То есть после прекращения действия деформирующих сил, модули которых превышали Fкр, размеры (и форма) тела не возвращаются к исходным. В этом случае в теле остаются остаточные деформации. При действии на тело таких сил его жесткость перестает быть постоянной (возможно даже разрушение тела).

На рис. 102 показан примерный вид графика зависимости модуля деформирующих сил F от удлинения шнура Δl. Обратим внимание на то, что на этом графике выделяются две области. В пределах области I график имеет вид прямой линии, проходящей через начало координат. Эту область называют областью малых деформаций, или малых деформирующих сил. В этой области выполняется закон Гука. Область II область больших деформаций, или больших деформирующих сил, ограничена точкой (Δl

max, Fmax), в которой происходит разрыв шнура. В этой области зависимость силы упругости от величины деформаций не является линейной.

В области I деформации шнура являются упругими, в области II – пластическими.

Итоги

Закон Гука.
Для любого тела при упругих деформациях эти деформации прямо пропорциональны вызывающим их силам.
F = k · Δl,
где k – коэффициент жесткости (жесткость) тела.

Вопросы

  1. В каких случаях возникают силы упругости? Куда направлены эти силы при деформациях сжатия и растяжения? Зарисуйте примеры таких деформаций и укажите на рисунках направления действующих сил упругости.
  2. Как соотносятся силы упругости и силы, вызывающие деформации?
  3. Что такое жесткость тела? При каких деформациях жесткость тела не изменяется? Приведите примеры тел различной жесткости.

Упражнения

1. Определите жесткость пружины при упругих деформациях, используя рис. 101. Считайте длину недеформированной пружины l0 = 1 см.

2. Определите массу груза на пружине, прикрепленной к неподвижному штативу (рис. 103). Жесткость пружины k = 3 Н/см. Длина недеформированной пружины l0 = 5 см.

3. Каково соотношение между силами упругости, действующими на руку и стол со стороны сжатой пружины (см. рис. 96), если пружина в сжатом состоянии покоится относительно Земли? Рассмотрите два случая: а) пружина легкая; б) пружина тяжелая.

PhysBook:Электронный учебник физики — PhysBook

Содержание

  • 1 Учебники
  • 2 Механика
    • 2.1 Кинематика
    • 2.2 Динамика
    • 2.3 Законы сохранения
    • 2.4 Статика
    • 2.5 Механические колебания и волны
  • 3 Термодинамика и МКТ
    • 3. 1 МКТ
    • 3.2 Термодинамика
  • 4 Электродинамика
    • 4.1 Электростатика
    • 4.2 Электрический ток
    • 4.3 Магнетизм
    • 4.4 Электромагнитные колебания и волны
  • 5 Оптика. СТО
    • 5.1 Геометрическая оптика
    • 5.
      2 Волновая оптика
    • 5.3 Фотометрия
    • 5.4 Квантовая оптика
    • 5.5 Излучение и спектры
    • 5.6 СТО
  • 6 Атомная и ядерная
    • 6.1 Атомная физика. Квантовая теория
    • 6.2 Ядерная физика
  • 7 Общие темы
  • 8 Новые страницы

Здесь размещена информация по школьной физике:

  1. материалы из учебников, лекций, рефератов, журналов;
  2. разработки уроков, тем;
  3. flash-анимации, фотографии, рисунки различных физических процессов;
  4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике

Новые страницы

Запрос не дал результатов.

Измерение модуля упругости поверхностей мягких культур и трехмерных гидрогелей с помощью атомно-силовой микроскопии

  • Эванс, Н. Д. и Джентльмен, Э.

    Роль структуры материала и механических свойств во взаимодействиях клеток и матрикса. Дж. Матер. хим. B 2 , 2345–2356 (2014).

    Артикул КАС пабмед Google Scholar

  • Engler, A.J., Sen, S., Sweeney, H.L. & Discher, D.E. Эластичность матрикса определяет спецификацию стволовых клеток. Cell 126 , 677–689 (2006).

    Артикул КАС пабмед Google Scholar

  • Evans, N.D. et al. Жесткость субстрата влияет на ранние события дифференцировки в эмбриональных стволовых клетках. евро. Клетка. Матер. 18 , 1–14 (2009).

    Артикул КАС пабмед Google Scholar

  • Кришнан, Р. и др. Жесткость субстрата способствует разрушению эндотелиального монослоя за счет усиления физических сил. утра. Дж. Физиол. Клеточная физиол. 300 , C146–C154 (2011 г.).

    Артикул КАС пабмед Google Scholar

  • Маммото А., Маммото Т. и Ингбер Д. Э. Механочувствительные механизмы регуляции транскрипции. J. Cell Sci. 125 , 3061–3073 (2012).

    КАС пабмед ПабМед Центральный Google Scholar

  • Engler, A.J. et al. Myotubes оптимально дифференцируются на субстратах с тканеподобной жесткостью: патологические последствия для мягких или жестких микроокружений. Дж. Сотовый. биол. 166 , 877–887 (2004).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Уэллс, Р. Г. Роль жесткости матрикса в регулировании поведения клеток. Гепатология 47 , 1394–1400 (2008).

    Артикул КАС пабмед Google Scholar

  • “>

    Левенталь, К. Р. и др. Сшивание матрикса вызывает прогрессирование опухоли за счет усиления передачи сигналов интегрина. Cell 139 , 891–906 (2009).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Мартин Л.Дж. и Бойд Н.Ф. Маммографическая плотность. Потенциальные механизмы риска рака молочной железы, связанные с маммографической плотностью: гипотезы, основанные на эпидемиологических данных. Рак молочной железы Res. 10 , 201–215 (2008).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Wei, S.C. et al. Жесткость матрикса управляет эпителиально-мезенхимальным переходом и метастазированием опухоли через путь механотрансдукции TWIST1-G3BP2. Нац. Клеточная биол. 17 , 678 (2015).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • “>

    Баумгарт, Ф. Жесткость – неизвестный мир механики? Травмы 31 , 14–84 (2000).

    Артикул Google Scholar

  • Криг, М. и др. Механобиология на основе атомно-силовой микроскопии. Нац. Преподобный физ. 1 , 41–57 (2019).

    Артикул Google Scholar

  • Томпсон, Д. В. О росте и форме , изд. 1942 г. (издательство Кембриджского университета, 1917 г.).

  • Эмерман, Дж. Т. и Пителька, Д. Р. Поддержание и индукция морфологической дифференцировки диссоциированного эпителия молочной железы на плавающих коллагеновых мембранах. In Vitro 13 , 316–328 (1977).

    Артикул КАС пабмед Google Scholar

  • Pelham, R. J. & Wang, Y. Передвижение клеток и фокальные спайки регулируются гибкостью субстрата. Проц. Натл акад. науч. США 94 , 13661–13665 (1997).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Discher, D.E., Janmey, P. & Wang, Y.L. Тканевые клетки чувствуют и реагируют на жесткость своего субстрата. Наука 310 , 1139–1143 (2005).

    Артикул КАС пабмед Google Scholar

  • Foyt, D. A. et al. Гипоксия влияет на реакцию МСК человека на жесткость субстрата во время хондрогенной дифференцировки. Акта Биоматер. 15 , 73–83 (2019).

    Артикул Google Scholar

  • Чин М.Х.В., Норман М.Д.А., Джентльмен Э., Коппенс М.-О. & Day, RM. Интегрированное в гидрогель культуральное устройство для исследования активации Т-клеток с помощью физико-химических сигналов. Приложение ACS Матер. Интерфейсы 12 , 47355–47367 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Huebsch, N. et al. Использование опосредованных тракцией манипуляций с интерфейсом клетки/матрикса для управления судьбой стволовых клеток. Нац. Матер. 9 , 518–526 (2010).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Хетан, С. и др. Опосредованная деградацией клеточная тяга направляет судьбу стволовых клеток в ковалентно сшитых трехмерных гидрогелях. Нац. Матер. 12 , 458–465 (2013).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Blache, U., Stevens, M.M. & Gentleman, E. Использование секретируемого матрикса для создания тканей. Нац. Биомед. англ. 4 , 357–363 (2020).

    Артикул пабмед Google Scholar

  • Ferreira, S.A. et al. Двунаправленные взаимодействия клеток и перицеллюлярного матрикса определяют судьбу стволовых клеток. Нац. коммун. 9 , 4049 (2018).

    Артикул пабмед Google Scholar

  • Лебель, С., Маук, Р. Л. и Бердик, Дж. А. Локальное отложение зарождающегося белка и ремоделирование направляют механосенсорное восприятие и судьбу мезенхимальных стромальных клеток в трехмерных гидрогелях. Нац. Матер. 18 , 883–891 (2019).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Jowett, G.M. et al. ILC1 управляет ремоделированием кишечного эпителия и матрикса. Нац. Матер. 20 , 250–259 (2021).

    Артикул КАС пабмед Google Scholar

  • Barriga, E.H., Franze, K., Charras, G. & Mayor, R. Жесткость тканей координирует морфогенез, вызывая коллективную миграцию клеток in vivo. Природа 554 , 523–527 (2018).

    Артикул КАС пабмед Google Scholar

  • Gilbert, P. M. et al. Эластичность субстрата регулирует самообновление стволовых клеток скелетных мышц в культуре. Наука 329 , 1078–1081 (2010).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Макки, С. Т., Ласт, Дж. А., Рассел, П. и Мерфи, С. Дж. Измерение модуля Юнга в зависимости от вдавливания и растяжения для мягких биологических тканей. Ткань англ. Часть B Ред. 17 , 155–164 (2011).

    Артикул пабмед Google Scholar

  • “>

    Денисин А.К. и Прюитт Б.Л. Настройка диапазона жесткости полиакриламидного геля для применения в механобиологии. Приложение ACS Матер. Интерфейсы 8 , 21893–21902 (2016 г.).

    Артикул КАС пабмед Google Scholar

  • Прагер-Хуторский М. и др. Поляризация фибробластов представляет собой процесс, зависящий от жесткости матрикса, контролируемый механосенсорной фокальной адгезией. Нац. Клеточная биол. 13 , 1457–1465 (2011).

    Артикул КАС пабмед Google Scholar

  • Trappmann, B. et al. Связывание внеклеточного матрикса регулирует судьбу стволовых клеток. Нац. Матер. 11 , 642–649 (2012).

    Артикул КАС пабмед Google Scholar

  • Wen, J.H. et al. Взаимодействие жесткости матрикса и связывания белков при дифференцировке стволовых клеток. Нац. Матер. 13 , 979–987 (2014).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Ойен М.Л. Наноиндентирование биологических и биомиметических материалов. Экспл. Тех. 37 , 73–87 (2013).

    Артикул Google Scholar

  • Мегон, В., Рухпур, Н. и Готро, Дж. Э. Влияние поверхностной адгезии и неоднородности образца на многомасштабную механическую характеристику мягких биоматериалов. Науч. Респ. 8 , 6780 (2018).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Шульц, К.М. и Фурст, Э.М. Микрореология биоматериалов, гидрогелей. Мягкая материя 8 , 6198–6205 (2012).

    Артикул КАС Google Scholar

  • “>

    Циманн Ф., Радлер Дж. и Сакманн Э. Локальные измерения вязкоупругих модулей запутанных актиновых сетей с использованием микрореометра с колеблющимися магнитными шариками. Биофиз. J. 66 , 2210–2216 (1994).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Кампас, О. и др. Количественная оценка механических сил, генерируемых клетками, в живых эмбриональных тканях. Нац. Методы 11 , 183–189 (2014).

    Артикул КАС пабмед Google Scholar

  • Ван С. и Ларин К. В. Оптическая когерентная эластография для характеристики тканей: обзор. J. Биофотоника 8 , 279–302 (2015).

    Артикул пабмед Google Scholar

  • Scarcelli, G. & Yun, S.H. Конфокальная микроскопия Бриллюэна для трехмерной механической визуализации. Нац. Фотоника 2 , 39–43 (2007).

    Артикул пабмед ПабМед Центральный Google Scholar

  • Ши, Ю., Глейзер, К. Дж., Венкатеш, С. К., Бен-Абрахам, Э. И. и Эхман, Р. Л. Возможность использования 3D-МР-эластографии для определения жесткости поджелудочной железы у здоровых добровольцев. Дж. Магн. Резон. Imaging 41 , 369–375 (2015).

    Артикул пабмед Google Scholar

  • Анвари, А., Дхьяни, М., Стивен, А.Е. и Самир, А.Е. Надежность оценок модуля упругости ткани при фолликулярных новообразованиях щитовидной железы с помощью поперечно-волновой эластографии. утра. Дж. Рентгенол. 206 , 609–616 (2016).

    Артикул Google Scholar

  • Шульц, К. М., Кибурц, К. А. и Ансет, К. С. Измерение динамических взаимодействий клеток и материала и ремоделирования во время трехмерной миграции мезенхимальных стволовых клеток человека в гидрогелях. Проц. Натл акад. науч. США 112 , E3757 (2015).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Йофе, А. Д. Физика поверхностей. Контемп. физ. 29 , 411–414 (1988).

    Артикул Google Scholar

  • Стонтон, Дж. Р., Досс, Б. Л., Линдсей, С. и Рос, Р. Сопоставление конфокальной микроскопии и атомно-силового вдавливания показывает, что метастатические раковые клетки становятся жесткими во время инвазии в матрикс коллагена I. Науч. Респ. 6 , 19686 (2016).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Rheinlaender, J. et al. Жесткость клеток коры не зависит от механики субстрата. Нац. Матер. 19 , 1019–1025 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • “>

    Саймон К. Р. Механика . (Аддисон-Уэсли, 1971).

  • Loebel, C. et al. Метаболическая маркировка для исследования пространственно-временного накопления матрикса на границе хондроцитов и гидрогеля. Доп. Функц. Матер. 30 , 12 (2020).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Димитриадис, Э. К., Хоркей, Ф., Мареска, Дж., Качар, Б. и Чедвик, Р. С. Определение модулей упругости тонких слоев мягкого материала с использованием атомно-силового микроскопа. Биофиз. J. 82 , 2798–2810 (2002).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Селби А., Мальдонадо-Кодина К. и Дерби Б. Влияние толщины образца на наноиндентирование гидрогелей: измерение механических свойств мягких контактных линз. Дж. Мех. Поведение Биомед. Матер. 35 , 144–156 (2014).

    Артикул КАС пабмед Google Scholar

  • Юнг Ю. Г., Лоун Б. Р., Мартынюк М., Хуанг Х. и Ху Х. З. Оценка модуля упругости и твердости тонких пленок методом наноиндентирования. Дж. Матер. Рез. 19 , 3076–3080 (2004).

    Артикул КАС Google Scholar

  • Сирги Л., Понти Дж., Брогги Ф. и Росси Ф. Исследование эластичности и адгезии живых клеток с помощью атомно-силовой микроскопии. евро. Биофиз. J. 37 , 935–945 (2008).

    Артикул КАС пабмед Google Scholar

  • Buxboim, A., Rajagopal, K., Brown, A.E. & Discher, D.E. Насколько глубоко чувствуют клетки: методы для тонких гелей. J. Phys. Конденс. Иметь значение. 22 , 194116 (2010).

    Артикул пабмед Google Scholar

  • Tusan, C.G. et al. Коллективное поведение клеток при механочувствительном измерении толщины подложки. Биофиз. J. 114 , 2743–2755 (2018).

    Артикул КАС пабмед Google Scholar

  • Лин, Д. К. и Хоркей, Ф. Наномеханика полимерных гелей и биологических тканей: критический обзор аналитических подходов в режиме Герца и за его пределами. Soft Matter 4 , 669–682 (2008).

    Артикул КАС пабмед Google Scholar

  • Каррильо, Ф. и др. Наноиндентирование полидиметилсилоксановых эластомеров: влияние сшивки, работы адгезии и жидкой среды на модуль упругости. Дж. Матер. Рез. 20 , 2820–2830 (2005).

    Артикул КАС Google Scholar

  • “>

    Гарсия, П. Д., Герреро, С. Р. и Гарсия, Р. Нанореология живых клеток, измеренная с помощью кривых сила-расстояние на основе АСМ. Nanoscale 12 , 9133–9143 (2020).

    Артикул КАС пабмед Google Scholar

  • Ефремов Ю.М., Окадзима Т. и Раман А. Измерение вязкоупругости мягких биологических образцов с помощью атомно-силовой микроскопии. Soft Matter 16 , 64–81 (2020).

    Артикул КАС пабмед Google Scholar

  • Gautier, H. O. B. et al. в Методы клеточной биологии Vol. 125 211–235 (Академическое издательство, 2015).

  • Flory, PJ Принципы химии полимеров (Cornell University Press, 1953).

  • Offeddu, G.S., Axpe, E., Harley, B.A.C. & Oyen, M.L. Взаимосвязь между проницаемостью и диффузионной способностью в гидрогелях полиэтиленгликоля. AIP Adv 8 , 105006 (2018).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Ойен М.Л. Наноиндентирование гидратированных материалов и тканей. Курс. мнение Твердотельный материал. науч. 19 , 317–323 (2015).

    Артикул Google Scholar

  • Сэдер, Дж. Э., Чон, Дж. В. М. и Малвейни, П. Калибровка прямоугольных кантилеверов атомно-силового микроскопа. Rev. Sci. Инструм. 70 , 3967–3969 (1999).

    Артикул КАС Google Scholar

  • Кливленд Дж. П., Манн С., Бочек Д. и Хансма П. К. Неразрушающий метод определения жесткости кантилеверов для сканирующей силовой микроскопии. Rev.Sci. Инструм. 64 , 403–405 (1993).

    Артикул КАС Google Scholar

  • “>

    Тории А., Сасаки М., Хане К. и Окума С. Метод определения жесткости кантилеверов для атомно-силовой микроскопии. Изм. науч. Технол. 7 , 179–184 (1996).

    Артикул КАС Google Scholar

  • Гибсон, С. Т., Уотсон, Г. С. и Мира, С. Определение пружинных констант зондов для силовой микроскопии/спектроскопии. Нанотехнологии 7 , 259–262 (1996).

    Артикул Google Scholar

  • Гейтс, Р. С. и Рейтсма, М. Г. Точная калибровка константы пружины кантилевера атомно-силового микроскопа с использованием эталонного массива кантилеверов. Rev.Sci. Инструм. 78 , 086101 (2007).

    Артикул пабмед Google Scholar

  • Хаттер, Дж. Л. и Беххофер, Дж. Калибровка наконечников атомно-силового микроскопа. Rev. Sci. Инструм 64 , 1868–1873 (1993).

    Артикул КАС Google Scholar

  • Паласио, М.Л.Б. и Бхушан, Б. Методы калибровки нормальной и боковой силы для кантилеверов АСМ. Крит. Преподобный твердотельный материал. науч. 35 , 73–104 (2010).

    Артикул КАС Google Scholar

  • Schillers, H. et al. Стандартизированная процедура наномеханической атомно-силовой микроскопии (SNAP) для измерения мягких и биологических образцов. Науч. Респ. 7 , 5117 (2017).

    Артикул пабмед Google Scholar

  • Ойен М.Л. и Кук Р.Ф. Практическое руководство по анализу данных наноиндентирования. Дж. Мех. Поведение Биомед. Матер. 2 , 396–407 (2009).

    Артикул пабмед Google Scholar

  • “>

    Оливер, В. К. и Фарр, Г. М. Усовершенствованный метод определения твердости и модуля упругости с использованием экспериментов по вдавливанию с измерением нагрузки и смещения. Дж. Матер. Рез. 7 , 1564–1583 (1992).

    Артикул КАС Google Scholar

  • Кон, Дж. К. и Эбенштейн, Д. М. Устранение ошибок адгезии при наноиндентировании податливых полимеров и гидрогелей. Дж. Мех. Поведение Биомед. Матер. 20 , 316–326 (2013).

    Артикул КАС пабмед Google Scholar

  • Li, M., Liu, L., Xi, N. & Wang, Y. Наноразмерный мониторинг действия лекарств на клеточную мембрану с помощью атомно-силовой микроскопии. Акта Фармакол. Грех. 36 , 769–782 (2015).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • “>

    McCracken, K.W., Howell, J.C., Wells, J.M. & Spence, J.R. Создание кишечной ткани человека из плюрипотентных стволовых клеток in vitro. Нац. протокол 6 , 1920–1928 (2014).

    Артикул Google Scholar

  • Це, Дж. Р. и Энглер, А. Дж. Подготовка гидрогелевых подложек с регулируемыми механическими свойствами. Курс. протокол Биол стволовых клеток. 47 , 16.10.11–16.10.16 (2010).

    Google Scholar

  • Shu, X.Z., Liu, Y., Luo, Y., Roberts, M.C. & Prestwich, G.D. Дисульфидные сшитые гиалуроновые гидрогели. Биомакромолекулы 3 , 1304–1311 (2002).

    Артикул КАС пабмед Google Scholar

  • Ferreira, S.A. et al. Соседние клетки подавляют сигналы трехмерного гидрогелевого матрикса, вызывая покой МСК человека. Биоматериалы 176 , 13–23 (2018).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Клоксин А. М., Каско А. М., Салинас С. Н. и Ансет К. С. Фоторазлагаемые гидрогели для динамической настройки физических и химических свойств. Наука 324 , 59 (2009).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Lutolf, M. P. et al. Синтетические матричные гидрогели, чувствительные к металлопротеиназе, для проведения регенерации тканей: инженерные характеристики клеточной инвазии. Проц. Натл акад. науч. США 100 , 5413 (2003).

    Артикул КАС пабмед ПабМед Центральный Google Scholar

  • Burnham, N. A. et al. Сравнение методов калибровки кантилеверов атомно-силовой микроскопии. Нанотехнологии 14 , 1–6 (2003).

    Артикул КАС Google Scholar

  • Каин, Л. и др. Калибровка коллоидных зондов с помощью атомно-силовой микроскопии для микромеханической оценки. Дж. Мех. Поведение Биомед. Матер. 85 , 225–236 (2018).

    Артикул пабмед Google Scholar

  • Чигизола М., Пуричелли Л., Беллон Л. и Подеста А. Большие коллоидные зонды для атомно-силовой микроскопии: вопросы изготовления и калибровки. Дж. Мол. Признать. 34 , e2879 (2020).

    ПабМед Google Scholar

  • Батт Х. Дж. и Яшке М. Расчет теплового шума в атомно-силовой микроскопии. Нанотехнологии 6 , 1–7 (1995).

    Артикул Google Scholar

    • Модуль упругости полимеров и коэффициент Пуассона

    В таблицах ниже показаны значения модуля Юнга (модуля упругости) и коэффициента Пуассона при комнатной температуре для нескольких жестких полимеров, используемых в технике. Свойства материала выражаются в средних значениях или в диапазонах, которые могут существенно варьироваться в зависимости от обработки и качества материала или возможного присутствия минеральных наполнителей. Точные значения могут быть измерены с помощью неразрушающего контроля Sonelastic 9.0809 ® Испытания систем при комнатной температуре, а также при низких и умеренных температурах.

    Полимеры
    Материал Модуль упругости Коэффициент Пуассона
    ГПа 10 6 фунтов на кв. дюйм
    Полимеры
    Поливинилхлорид (ПВХ): 2,41-4,14 ​​ 0,35-0,60 0,38
    Эпоксидная смола: 2,41 0,35 –
    Фенопласт: 2,76-4,83 0,40-0,70 –
    Нейлон 6,6: 1,59–3,79 0,230-0,550 0,39
    Полибутилентерефталат (ПБТ): 1. 93-3.00 0,280-0,435 –
    Поликарбонат (ПК): 2,38 0,345 0,36
    Полиэстер (термоактивный): 2,06-4,41 0,30-0,64 –
    Полистирено (PS): 2,28-3,28 0,330-0,475 0,33
    Полиэфирэфиркетон (PEEK): 1,10 0,16 –
    Полиэтилен низкой плотности (LDPE): 1,08 0,157 –
    Полиэтилентерефталат (ПЭТ): 2,76-4,14 ​​ 0,40-0,60 –
    Полиметилметакрилат (ПММА): 2,24–3,24 0,325-0,470 –
    Полипропилен (ПП): 1,14–1,55 0,165-0,225 –
    Значения только для справки.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *