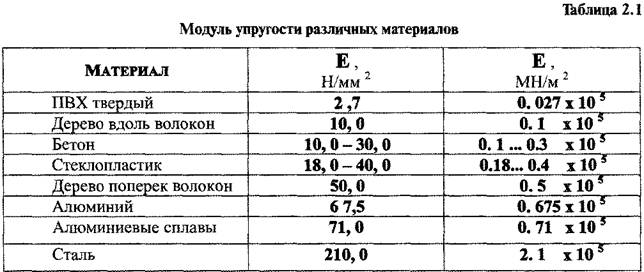
Модуль упругости чугуна: Модуль упругости (Модуль Юнга): понятие, формулы, как определить

alexxlab | 22.06.2023 | 0 | Разное

Упругие и неупругие свойства чугуна » Строительно-информационный портал

Значения упругих и неупругих свойств чугуна регламентируются иногда техническими условиями (например, на поршневые кольца), по в ГОСТах и стандартах обычно не оговариваются. Между тем эти свойства имеют большое значение, так как они в известной мере определяют не только величину напряжений и жесткость конструкции, но и чувствительность к надрезам, а также надежность, долговечность и конструкционную прочность отливок.

Характерной особенностью этих свойств, особенно упругих, является почти исключительная зависимость их от графитных включений. Действительно, как видно из рис. 169, уменьшение количества графита, особенно пластинчатого, повышает модуль нормальной упругости. Так же действует замена пластинчатого графита шаровидным или компактным. Поэтому наибольшим модулем при прочих равных условиях характеризуется белый, затем высокопрочный, ковкий и, наконец, серый чугуны:

Однако влияние это снижается с уменьшением количества графита (рис. 169, а). В сером чугуне модуль упругости в значительной мере зависит также от размеров графитных включений, причем влияние это по некоторым данным превышает даже влияние количества графита (рис. 169, б). В то же время распределение графита, в том числе и междендритное, не оказывает в этом отношении практического влияния. Так же мало влияние матрицы (некоторое увеличение модуля упругости при перлитизации структуры связано, по-видимому, с уменьшением количества графита):

Таким образом, модуль нормальной (и касательной) упругости можно, действительно, считать зависимым в основном от графитных выделений.

Эту зависимость до сих пор объясняли только тем, что полости, занятые графитом, действуют как пустоты, уменьшая живое сечение образца и образуя в нем надрезы (так называемые сужающее и надрезывающее действия графита). Полагали, что это является единственной причиной увеличения общего уровня напряжений и образования пиков напряжений, ведущих к увеличению деформаций, понижению модуля упругости и раннему образованию малых по величине пластических деформаций (рис. 170, б). Эта точка зрения, исключающая активную роль самого графита, основывалась на известных исследованиях А. Тума, из которых следовало, что надрезы в стали (рис. 170, а) оказывают на ее упругие свойства примерно такое же влияние, как графит в чугуне (рис. 170, б). Однако оказалось, что указанные особенности упругих свойств чугуна, в частности зависимость модуля упругости от напряжения, наличие упругого гистерезиса и различие в поведении при растягивающих, изгибающих и сжимающих нагрузках невозможно объяснить одной только теорией надрезов. Поэтому в дополнение к ней в последнее время привлекаются еще представления об активном сопротивлении деформации графита, с одной стороны, и об обратимых и остаточных деформациях занятых им полостей — с другой.

Недостаточность теории надрезов видна, например, из того, что деформация надрезанных стальных образцов при растяжении описывается кривой OPMP на рис. 171, а, так что при повторной нагрузке деформация, несмотря на надрезы, изменяется по прямой MP, как у идеально упругого тела с постоянным модулем упругости (МП || ОТ). Деформации же чугуна изменяются при повторной нагрузке по веретенообразной кривой М’Р, и только после многих циклов чугун приближается к идеально упругому телу. Такой характер гистерезисной кривой объясняется тем, что графит оказывает, хотя и небольшое, но определенное сопротивление деформациям (Егр = 500 – 1500 кГ/мм2). При этом благодаря трению деформации начинаются только после того, как напряжение превзойдет значение S (рис. 171, б). При уменьшении напряжения (начиная с точки С) деформация начинает по той же причине уменьшаться только после снижения напряжения на 2 S и при полном снятии напряжения (точка А) в чугуне остается деформация OA. При дальнейшем изменении знака напряжений деформация вновь будет сначала оставаться постоянной, а потом возрастать по кривой ВС, так что гистерезисная петля по идеализированной схеме (рис. 171, б) имеет форму ABCD. В действительности же благодаря наличию многих различно ориентированных пластинок графита углы гистерезисной петли срезаются и она приобретает форму М’Р, согласно рис. 171, а.

Особенностью чугуна, главным образом серого, является зависимость модуля упругости от напряжения. Методика определения этой функции заключается в применении этапов возрастающей нагрузки с поэтапной последовательной разгрузкой, как это показано на рис. 172. По мере увеличения нагрузки (рис. 172, а) площадь гистерезисной петли увеличивается, а модуль упругости, определяемый углом наклона касательной к нагрузочной ветви гистерезисной петли, постепенно уменьшается. Таким образом, модуль упругости оказывается прямолинейной функцией напряжения (рис. 172, б)

где E0 — значение модуля упругости, получающееся путем экстраполяции прямой на рис. 172, б до о = 0;

k — коэффициент, определяющийся углом наклона прямой.

Такое уменьшение модуля упругости объясняется тем, что кроме упругих деформаций матрицы образуются еще обратимые деформации полостей, занятых графитом, причем интенсивность образования этих деформаций возрастает с увеличением нагрузки. Точно так же остаточные деформации, образующиеся в чугуне, обязаны своим происхождением как пластическим деформациям матрицы, так и остаточным деформациям полостей графита. Эти деформации особенно резко проявляются на поверхности образцов, где они приводят к образованию трещин, как показано на рис. 173. Общие деформации чугуна (Ее). как показано Г. Гильбертом могут, быть представлены как сумма

где емобр — обратимые (упругие) деформации матрицы;

епобр — обратимые деформации полостей графита;

емост — остаточные (пластические) деформации матрицы;

епост — остаточные деформации полостей графита.

Модуль упругости E при любом напряжении о определяется обратимыми деформациями, т. е.

и так как епобр изменяются не по прямой линии, а резко возрастают с повышением напряжений, то E падает с увеличением напряжения. При нулевом же напряжении епобр = 0 и, следовательно, Е0 характеризует только упругие деформации матрицы, линейно возрастающие с увеличением напряжения:

Измеряя деформации чугуна не только в продольном, но и в поперечном направлении, можно определить отдельные составляющие общей деформации как при растяжении, так и при сжатии чугуна.

При циклическом нагружении и разгружении определяются общие и остаточные (емост+епост) деформации, а путем вычитания, следовательно, и обратимые деформации (емобр+епобр). Проведя касательную к кривой общей деформации в ее начальной точке определяют E0, а следовательно, и емобр = о/Е0, после чего легко найти епобр. Точно так же можно произвести разделение остаточных деформаций.

Из рис. 174 следует, что при малых напряжениях главную роль играют деформации матрицы, особенно упругие. При больших же напряжениях эту роль начинают играть деформации полостей графита, главным образом остаточные. При этом полости графита принимают участие в образовании деформаций только в том направлении, где происходит увеличение размеров (продольном при растяжении и поперечном при сжатии). В направлении же уменьшения размеров (поперечном при растяжении и продольном при сжатии) полости графита, сопротивляясь сжатию, не влияют на деформацию, которая определяется в этом случае только матрицей.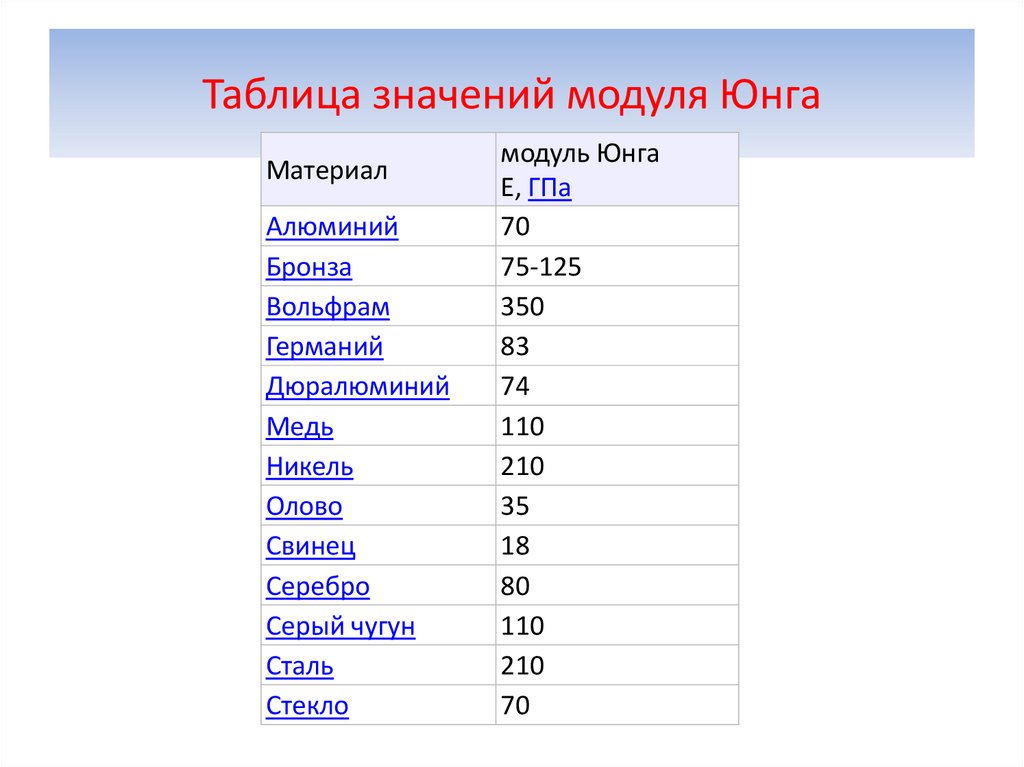 Поэтому модули упругости в продольном направлении при растяжении и в поперечном направлении при сжатии понижаются с увеличением напряжений, а в поперечном направлении при растяжении и в продольном при сжатии — остаются постоянными и от величины напряжений не зависят. В этих случаях они выражают в чистом виде только упругие свойства матрицы (E0). Из этого также следует, как видно из рис. 174, что коэффициент Пуассона в условиях растяжения понижается с увеличением напряжений. Экстраполируя его значение до o = 0, можно определить u = 0,26, характерное для строго упругого состояния и соответствующее деформации одной только матрицы. С увеличением же напряжения величина u прямолинейно понижается, так что аналогично (III.12) можно принять для случая растяжения (рис. 174)

В случае сжатия u = u0 = 0,26 остается постоянным в пределах обычно действующих напряжений (рис. 174), как в идеально упругом материале, в более же напряженной области u резко увеличивается и достигает значения 0,5 и больше, что свидетельствует об увеличении объема образца в условиях сжатия.

В противоположность серому чугуну, чугун с шаровидным графитом ведет себя в большом интервале напряжений аналогично стали, хотя имеются и некоторые различия: модуль упругости его немного ниже, на кривой растяжения отсутствует площадка текучести, а пределы упругости и текучести при сжатии несколько больше, чем при растяжении (рис. 175, а и б). В области же выше предела упругости полости, занятые графитом, и в этом случае несколько увеличиваются в объеме, хотя значительно меньше, чем в сером чугуне. Это увеличение объема, происходящее вследствие того, что продольные деформации больше поперечных, частично обратимо, частично необратимо. Однако указанные изменения мало влияют на коэффициент Пуассона, который начинает увеличиваться только с образованием пластических деформаций.

Таким образом, отступления от закона Гука, характерные для графитизированного чугуна, главным образом серого (оп этого чугуна = 0,5/0,7 кГ/мм2), являются следствием не только раннего образования пластических деформаций, но и возрастающих с напряжениями упругих деформаций полостей графита. Как видно из рис. 176, эти отступления возрастают с увеличением количества и размеров графитных выделений, а следовательно, с понижением марки чугуна. Однако с увеличением числа циклов (нагрузки и разгрузки)образование остаточных деформаций замедляется, и после 50—100 циклов чугун (даже серый) начинает вести себя как упругий материал (рис. 177). В обычных же условиях, характеризуя упругие свойства серого чугуна, следует различать модуль упругости при малых нагрузках (E0), определяемый углом касательной к начальной точке кривой и средний или эффективный модуль упругости (E), характеризующий величину упругих деформаций при данном напряжении.

Большое значение для чугуна как конструкционного материала имеют также его неупругие свойства, определяемые внутренним трением, вследствие чего циклические нагружения чугуна, в противоположность идеально упругому телу, совершаются с потерей энергии, превращающейся в теплоту, и, таким образом, колебания с той или иной скоростью гасятся (амортизируются). Величина потери энергии определяется площадью петли кривой «напряжение—деформация», так как они обусловливаются отставанием по фазе деформаций от напряжений, в частности образованием необратимых деформаций. Из сказанного ясно, что эти явления особенно резко проявляются в сером чугуне, где вследствие неоднородности структуры и наличия пластинчатого графита циклические колебания затухают быстрее, чем в других сплавах (рис. 178, а), вследствие образования микросдвигов и пластических деформаций. Это свойство амортизации (циклическая вязкость или демпфирующая способность) может определяться при любом виде нагружения и измеряется либо логарифмическим декрементом, представляющим натуральный логарифм отношения амплитуд двух последовательных колебаний при свободном затухании (bц), либо аналогичной величиной, вычисленной из резонансной кривой при сохраняющейся нагрузке (b’ц), либо отношением величины потери энергии ко всей упругой энергии цикла (ф):

ANx — разница между двумя частотами по обе стороны резонансной частоты соответственно одной и той же амплитуде Aх;

Pn и Pn+1 — энергии двух последовательных колебаний.

Циклическая вязкость характеризует не только ограничение амплитуд вынужденных и резонансных колебаний, но и опасность разрушения конструкции из-за резонанса колебаний, она в известной мере определяет чувствительность к надрезам в условиях знакопеременной нагрузки и конструкционную прочность отливок, а также некоторые физические свойства чугуна, например, термостойкость.

Согласно И.В. Кудрявцеву, сопоставление циклической вязкости стали и чугуна характеризуется данными рис. 178, б. Усматривается, что серый чугун имеет в этом отношении большое преимущество не только перед сталью, но и по сравнению с высокопрочным чугуном. При этом можно видеть, что циклическая вязкость в сером чугуне интенсивно растет уже при самых малых напряжениях, в высокопрочном чугуне этот интенсивный рост начинается позже (при о = 5 кГ/мм2), в стали же циклическая вязкость начинает быстро расти только при напряжениях около 10 кГ/мм2, а до этого остается практически без изменения на очень низком уровне. Поэтому циклическую вязкость разных сплавов сопоставляют часто при разных напряжениях, например, при 1/3о0,2. Однако и в этом случае преимущества серого чугуна резко выявляются:

Указанное превосходство серого чугуна проявляется также при сопоставлении значений логарифмического декремента:

Основной структурной фазой, повышающей величину циклической вязкости чугуна, является графит, который сам характеризуется большой демпфирующей способностью: чем больше его количество и крупнее его выделения, тем выше циклическая вязкость (рис. 179). При этом междендритный графит понижает ее так же, как и прочность, что в некоторой мере оправдывает имеющиеся в литературе утверждения о связи между прочностью и циклической вязкостью (рис. 178, в). Однако эта связь далеко не однозначна, так как в противоположность прочности циклическая вязкость в малой степени зависит от структуры матрицы, хотя некоторое повышение циклической вязкости с процессом ферритизации и наблюдается. Наибольшей циклической вязкостью характеризуется мартенситная структура. Поэтому отпуск после закалки понижает демпфирующую способность, а ферритизация матрицы несколько повышает ее, что видно из следующих данных:

Несколько лучшей является корреляция между циклической вязкостью и модулем упругости, так как оба эти свойства главным образом зависят от графита. Однако и в этом отношении имеются противоречия, в частности междендритный графит в сильной степени понижает циклическую вязкость, но не влияет на модуль упругости. В силу указанного связь циклической вязкости с модулем упругости и тем более с прочностью часто нарушается и характеризуется большими колебаниями:

Поэтому возможно подобрать чугун, который характеризовался бы одновременно как повышенными значениями прочности и модуля упругости, так и удовлетворительной циклической вязкостью.

С модулем упругости и с циклической вязкостью тесно связаны и акустические свойства, который также определяются внутренним трением. Например, скорость звука при продольных волнах выражается

где d — плотность в г/см3;

u — коэффициент Пуассона.

Пользуясь этим выражением, можно рассчитать скорость звука для разных металлов (табл. 12).

Модуль упругости стали и формулы его расчета

О чем речь? Модуль упругости стали требуется при проектировании стальных изделий и элементов конструкций. Он показывает стойкость материала к разнонаправленным нагрузкам. Это одна из важнейших характеристик металла.

Как определять? Показатель рассчитывается по определенной формуле и зависит от вида стали и добавок в нее. Помимо этого, для расчетов используются специальные нормативы и практические испытания материала. Требуются точные вычисления, так как в противном случае изделию грозит деформация, способная привести к его разрушению.

Вопросы, рассмотренные в материале:

• Формула модуля упругости стали
• Типы модулей упругости стали
• Особенности модуля упругости стали
• Определение модуля упругости стали
• Другие коэффициенты для оценки свойств стали

Формула модуля упругости стали

Инженерное проектирование является направлением в сфере строительства, призванным решить целый ряд задач.

Так, возведению любых объектов предшествует подготовка проекта. На данном этапе необходимо провести расчеты, чтобы подобрать оптимальное сечение профиля стальных конструкций и избежать разрушения готового здания.

Важным показателем, обеспечивающим прочность будущего объекта, считается модуль упругости стали. Его использование в расчетах позволяет защитить здание от преждевременных деформаций металлопроката. Сила упругости проявляется при деформации тела – она стремится восстановить его прежние размеры и форму и является следствием электромагнитного взаимодействия атомов и молекул.

Благодаря модулю упругости как физической величине (Е) описывают упругую сопротивляемость материала изделия приложенным нагрузкам. В случае с модулем упругости стали и других материалов нагрузки могут быть:

• продольные – растягивающие и сжимающие;
• поперечные, то есть изгибающие или на сдвиг;
• объемные или скручивающие.

Данный показатель принято измерять в паскалях, мегапаскалях (МПа) и кгс/см2. От его значения напрямую зависит сопротивляемость материала нагрузкам, прочность предмета и предел разрушения. Так, у стали модуль упругости равен до 220 ГПа, у алюминия он находится на уровне в 70 ГПа, у чугуна – 120 ГПа, железа – 190 ГПа.

Для его вычисления используют формулу: E= σ / ε, где σ – напряжение, соответствующее силе, поделенной на площадь ее воздействия; ε – упругая деформация, определяемая как отношение удлинения образца с начала деформации к сжатию при завершении воздействия.

Рекомендуем статьи

• Титан и его сплавы: свойства, применение
• Сплавы черных металлов: классификация и особенности производства
• Плавление латуни в различных условиях

Коэффициент E иначе обозначают как модуль Юнга в честь Томаса Юнга, английского физика XIX века. Модуль Юнга определяется свойствами материала, тогда как размеры и форма объекта не оказывают на него влияния. Показатель меняется в широких пределах в зависимости от конкретного материала. Допустим, у стали он равен ≈ 2·1011 Н/м2, а для резины он в пять раз меньше ≈ 2·106 Н/м2.

Напряжение измеряется в паскалях, а раз деформация считается безразмерной величиной, то Е принято указывать в паскалях.

Существует альтернативное определение, согласно которому модуль упругости представляет собой напряжение, которое достаточно, чтобы увеличить длину образца вдвое. Для подавляющего числа материалов эта формулировка является неточной. Дело в том, что данное значение значительно больше предела текучести материала или значения, когда удлинение делается нелинейным, но при этом оказывается более интуитивным.

Типы модулей упругости стали

Есть множество способов изменения напряжения и деформации, в том числе применение различных направлений действия силы. В связи с этим существует большое количество типов модулей упругости, среди которых основными считаются:

1. Модуль Юнга, обозначаемый символом E. Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.
2. Модуль сдвига или модуль жесткости. Обозначается символом G и описывает способность материала сопротивляться изменению формы при сохранении объема. Вычисляется как отношение напряжения сдвига к деформации сдвига. Последнюю определяют как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига входит в число составляющих вязкости.
3. Модуль объемной упругости или объемного сжатия. Для его обозначения используют символ K. Показатель позволяет определить способность объекта изменять объем под воздействием всестороннего нормального напряжения (объемного), которое является одинаковым по всем направлениям.

Допустим, такое напряжение может появляться под действием гидростатического давления. Данный модуль вычисляется как отношение величины объемного напряжения к величине относительного объемного сжатия. K отличается от E и G тем, что для невязкой жидкости он не равен нулю, а для несжимаемой жидкости – бесконечен.

Это далеко не весь перечень модулей упругости, также существуют коэффициент Пуассона, параметры Ламе.

Описанная методика определения показателя применяется при вычислении Е для:

• стальных изделий;
• медных предметов;
• прочих упругих образцов.

Особенности модуля упругости стали

Сталь является прочным материалом с высоким модулем упругости. Самые высокие показатели устойчивости к воздействиям имеют стальные сплавы с измененной кристаллической решеткой. Они отличаются значительным пределом текучести, определяемым опытным путем.

Особенности упругого поведения стальных изделий зависят от того, насколько сложны связи в кристаллической решетке. Решетка формируется в соответствии с типом материала – легирующей сталью. Благодаря наличию углерода решетка становится более твердой, но избыточное количество данного компонента негативно сказывается на пластичности и пружинистых свойствах сплава, влияет на значение модуля упругости стали. Не допустить подобного эффекта удается за счет внесения легирующих добавок, к которым относятся:

• кремний;
• никель;
• вольфрам;
• марганец.

Хотя указанные элементы повышают упругость, не всегда с их помощью можно обеспечить требуемый результат. Тогда прибегают к термообработке, поскольку под влиянием температуры свойства стали меняются: пропадают слабые участки, выравнивается показатель текучести отдельных фрагментов.

На данный момент существует свыше нескольких сотен марок стали, каждая из которых имеет свои свойства. Далее приведены популярные марки стали и соответствующий им модуль упругости E:

Низкоуглеродистая

В пределах 180

Ст3

В пределах 189

Ст10

В пределах 192

Ст45

В пределах 223

Ст40Х

В пределах 260

65Г

В пределах 275

Х12МФ

В пределах 320

9ХС

В пределах 302

ХВГ

В пределах 302

4Х5МФС

В пределах 315

3Х3М3Ф

В пределах 310

Р6М5

В пределах 320

Р9

В пределах 330

Р18

В пределах 340

Р12МФ5

В пределах 310

У7

В пределах 315

У8

В пределах 315

У9

В пределах 330

У10

В пределах 330

У11

В пределах 340

У12

В пределах 315

У13

В пределах 315

Модуль упругости не относится к постоянным величинам, так как зависит от места воздействия нагрузки. Правда, для некоторых материалов, например, стали 3 или 10 первого и второго рода, алюминия, меди, показатель сохраняется при растяжении и сжатии. Для разных марок стали модуль упругости отличается незначительно. По этой причине в процессе подготовки проекта E округляют, а подобные погрешности не учитывают.

Определение модуля упругости стали

Хотя твердые тела справляются с воздействием больших нагрузок, однако как только достигнуты определенные значения, они меняют форму и резко разрушаются. Чтобы определить момент, в который появятся трещины, разрыв, узнают модуль упругости стали посредством простых испытаний.

Госстандарты предлагают несколько возможных видов лабораторных исследований материала:

• нагружение в течение продолжительного периода времени;
• быстрые и длительные удары;
• воздействие на растягивание и сжатие;
• давление посредством гидравлики.

По модулю упругости стали удается понять, насколько жесткой и устойчивой будет оставаться конструкция, когда на нее будут воздействовать определенные нагрузки.

Чтобы узнать приблизительный показатель, прибегают к детальному изучению, выведению диаграммы напряжений. Для этого во время испытаний образец на специальных установках медленно растягивают до определенного предела. После этого результаты нормальных и относительных напряжений делят – итоговый показатель и является искомой величиной.

Модуль упругости ряда материалов содержится в нормативных документах. Так, определить его для конкретной марки стали можно, используя специальные таблицы, которые входят в состав нормативных документов в области строительства. Речь идет о строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ), указывающих искомые модули упругости стали.

Так, модуль упругости Юнга для белого и серого чугуна составляет 115–160 ГПа, а для ковкого находится на уровне 155. Модуль упругости углеродистой стали С245 может быть 200–210 ГПа. У легированной он немного выше: 210–220 ГПа. Для рядовых марок стали Ст. 3 и Ст.5 он равен 210 ГПа, а сталь Ст.45, 25Г2С и 30ХГС имеет показатель 200 ГПа.

Получается, у различных марок стали модуль упругости мало отличается, чего нельзя сказать о готовых изделиях. Рассмотрим в качестве примера аналогичный показатель для канатов:

• пряди и свивки проволоки, обладающие высокой прочностью – 200 ГПа;
• стальные тросы, имеющие металлический стержень – 150 ГПа;
• стальные канаты, в которых предусмотрен органический сердечник – 130 ГПа.

Модуль сдвига или жесткости (G) обычно имеет меньшие значения, которые указываются в тех же таблицах. Для прокатной стали этот модуль составляет 84 ГПа, для углеродистой и легированной 80-81 ГПа, а для типов стали Ст.3 и Ст.45 – 80 ГПа.

Значения параметра упругости отличаются, поскольку наблюдается одновременное действие сразу трех основных модулей – каждый из них вычисляют отдельным методом. При этом разница небольшая, а значит, можно считать, что достигается достаточно высокая точность определения упругости. Нет смысла концентрироваться только на вычислениях и формулах – разумнее принять за константу конкретную величину упругости.

Комплексный расчет вместо вычисления по отдельным модулям позволяет получить значение Е = 200 ГПа. Показатель будет отличаться в зависимости от присадок, использованных в стали, а также особенностей изделия, например, наличия элементов из других веществ. Однако разница окажется невелика. Модуль упругости стали зависит в первую очередь от доли углерода. Тогда как задействованный способ обработки, то есть горячий прокат либо холодная штамповка, мало воздействует на показатель.

Выбирая стальные изделия, важно опираться также на расчетное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Данный показатель регламентируется наравне с модулем упругости стали и других материалов таблицами ГОСТов и СНиПов. Он имеет аналогичную размерность, что и модуль упругости, но его значения на три порядка меньше.

Для показателя принимают во внимание расчетное и нормативное сопротивление. Первое необходимо для выполнения расчетов прочности конструкций. Например, для стали С255 при толщине проката 10–20 мм оно составляет 240 МПа, тогда как нормативное находится на уровне 245 МПа. Для проката 20–30 мм расчетное сопротивление равно 230 МПа.

Другие коэффициенты для оценки свойств стали

Благодаря модулю упругости удается заранее понять, как различные типы стали и другие материалы будут вести себя в определенной ситуации. Однако с его помощью нельзя определить, как изменится вещество в иных обстоятельствах. Чтобы расчеты были более эффективны, прибегают к следующим показателям:

1. Коэффициент жесткости – свидетельствует об уровне пластичности материала, исчисляется в килограмм-силах (кгс).
2. Относительное продольное удлинение – измеряется в процентах. Формула для его вычисления предполагает учет длины образца и ее абсолютное изменение.
3. Относительное поперечное удлинение – определяется по аналогии с предыдущим показателем с тем отличием, что для расчетов нужна не длина, а диаметр.
4. Коэффициент Пуассона – представляет собой соотношение продольного относительного удлинения к поперечному. Позволяет определить, каким образом изменится форма заготовки в зависимости от разных значений силы и мест ее приложения.
5. Модуль сдвига – свидетельствует о поведении упругих материалов, подвергаемых воздействию усилий по касательной. Показатель необходим, чтобы оценить воздействие ветра с перпендикулярным направлением и предельной величиной усилия.
6. Модуль объемной упругости – демонстрирует изменение объема тела в случае равномерного, но при этом разностороннего приложения усилий.

Определить возможности применения стали позволяет предел упругости, исчисляемый в паскалях. По нему можно понять напряжение, которое вызовет разрушение, необратимую деформацию изделия.

При подготовке проекта конструкций важно использовать минимум два разных модуля упругости стали. Опираясь на коэффициент жесткости, проектировщик получает возможность перейти к другим видам сопротивления внешнему воздействию: упругости при изгибе и объемной упругости.

Строительство любого объекта предполагает использование набора конструкторских расчетов и грамотный подбор материалов в соответствии с их прочностью. Обеспечить безопасность зданий можно лишь при наличии у проектировщиков наиболее полных представлений о процессах, протекающих внутри материалов.

Модуль упругости черных металлов и коэффициент Пуассона

В таблицах ниже приведены значения модуля Юнга (модуля упругости) и коэффициента Пуассона при комнатной температуре для некоторых черных металлов, используемых в технике. Свойства материала выражаются в средних значениях или в диапазонах, которые могут существенно варьироваться в зависимости от обработки и качества материала. Точные значения могут быть измерены с помощью неразрушающих испытаний систем Sonelastic ^® при комнатной температуре, а также при низких и высоких температурах.

Чугун

Материал	Модуль упругости		Коэффициент Пуассона
	ГПа	10 6 фунтов на кв. дюйм
Чугун
Серый чугун марки G1800:	66-97	9.6-14	0,26
Серый чугун марки G4000:	110-138	16-20	0,26
Ковкий чугун марки 60-40-18:	169	24,5	0,29
Чугун ковкий марки 80-55-06:	168	24,4	0,31
Чугун ковкий марки 120-90-02:	164	23,8	0,28
Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® .

Основное применение:
– Марка G1800: применяется там, где сопротивление не является критическим.
– Марка G4000: блоки и поршни двигателей.
– Марка 60-40-18: детали, работающие под давлением, такие как клапаны и насосы.
– Марка и классы 80-55-06 120-90-02: Зубчатые передачи и высокоомные детали.

Серый чугун обладает высоким демпфированием, что является желательным свойством для деталей и конструкций, подверженных вибрации, и высокой износостойкостью, несмотря на то, что он хрупкий. Кроме того, это один из самых дешевых металлических материалов. Чугуны с шаровидным графитом более пластичны и устойчивы, чем серые чугуны, и имеют свойства, аналогичные стали.

Контроль качества и оценка узловатости могут быть выполнены путем измерения демпфирования и вибрации материала. Демпфирование и модули упругости (модуль Юнга, модуль сдвига и коэффициент Пуассона) можно одновременно и точно охарактеризовать с помощью неразрушающего Sonelastic 9.0003® Испытания систем при комнатной температуре, а также при низких и высоких температурах.

Знание точных значений жизненно важно для оптимизации использования материала и для надежности моделирования с помощью конечных элементов. Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.

Нержавеющая сталь

Материал	Модуль упругости		Коэффициент Пуассона
	ГПа	10 6 фунтов на кв. дюйм
Нержавеющая сталь
Нержавеющий сплав 304:	193	28	0,30
Нержавеющий сплав 316 и 316L:	193	28	0,30
Нержавеющий сплав 440 A:	200	29	0,30
Нержавеющий сплав 17-7PH:	204	29,5	0,30
Значения только для справки.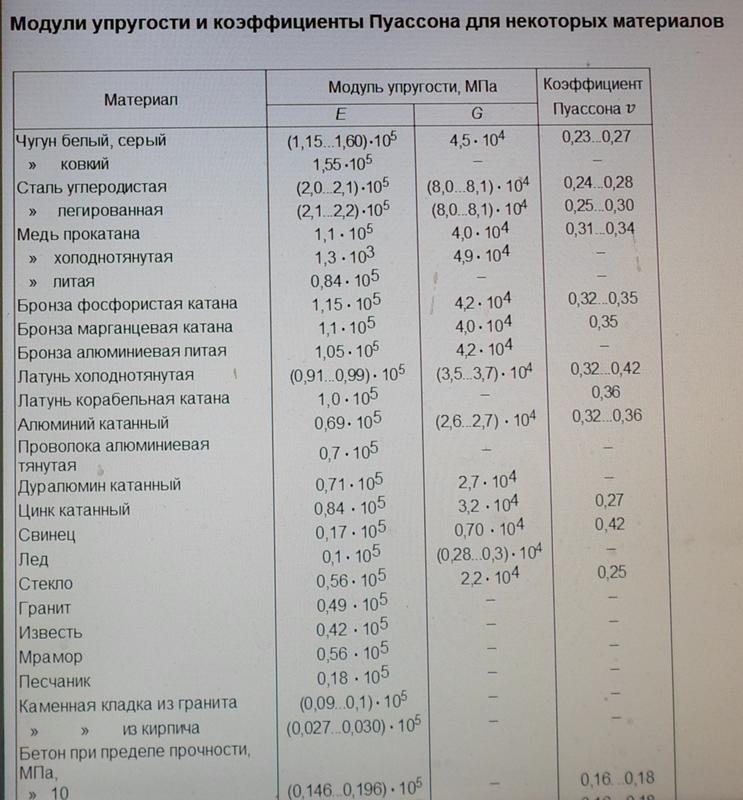 Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® .

Основное применение:
– Нержавеющая сталь 304: оборудование для пищевой промышленности.
– Нержавеющая сталь 316 и 316L: оборудование, требующее высоконадежных припоев.
– Нержавеющая сталь 440 А: столовые приборы, хирургические инструменты и подшипники.
– Нержавеющая сталь17-7PH: пружины из нержавеющей стали.

Процессы формования, применяемые к этим материалам, увеличивают модули упругости и демпфирование, что можно точно охарактеризовать с помощью неразрушающего тестирования систем Sonelastic ^® при комнатной температуре, а также при низких и высоких температурах и/или времени отверждения. Знание точных значений жизненно важно для оптимизации использования материала и для надежности моделирования с помощью конечных элементов. Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.

Обычные стали и низколегированные стали

Материал	Модуль упругости		Коэффициент Пуассона
	ГПа	10 6 фунтов на кв. дюйм
Нержавеющая сталь
Сталь А36	207	30	0,30
Нержавеющий сплав 316 и 316L:	207	30	0,30
Нержавеющий сплав 440 A:	207	30	0,30
Нержавеющий сплав 17-7PH:	207	30	0,30
Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ® .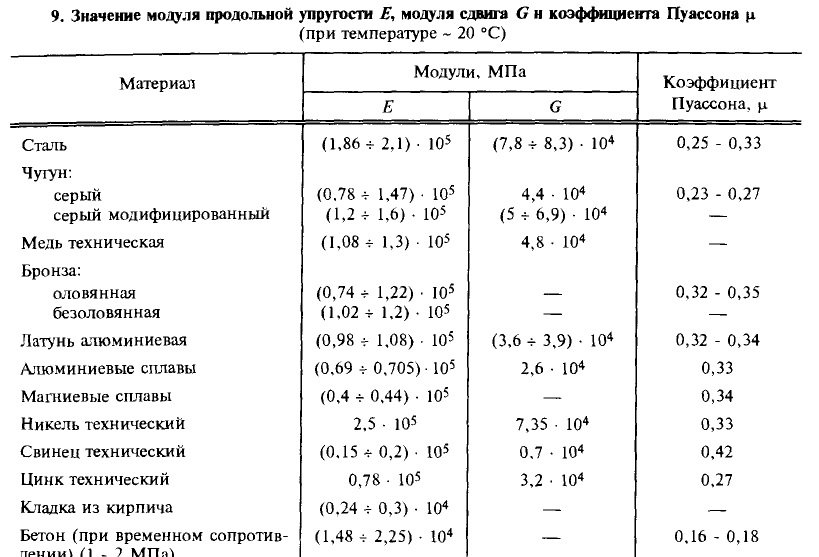

Процессы формовки, применяемые к этим материалам, увеличивают модули упругости и демпфирование, что можно точно охарактеризовать с помощью неразрушающих испытаний систем Sonelastic ^® при комнатной температуре, а также при низких и высоких температурах. Знание точных значений жизненно важно для оптимизации использования материала и для надежности анализа методом конечных элементов (FEA). Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.

Ссылки

ASM Handbooks, Vol. 1 и 2, Справочник по инженерным материалам, Vol. 1 и 4, Справочник по металлам: свойства и выбор: цветные сплавы и чистые металлы, Vol. 2, 9-е издание, и Advance Materials and Processes, Vol. 146, № 4, ASM International, Materials Park, OH.

Откройте для себя системы Sonelastic

^® Система Sonelastic® для образцов малого размера
Система Sonelastic® для образцов среднего размера
Система Sonelastic® для образцов среднего размера
Система Sonelastic® для средних образцов

Модуль Юнга железа

Типичные значения модуля Юнга чугунов при комнатной температуре приведены в следующей таблице.

класс

Значения модуля упругости для чугуна
Материал	Модуль упругости
	ГПа	10 6 фунтов на кв. дюйм
Ковкий чугун	170	25
Серый чугун
ASTM А 48 класс 20	66 – 97*	9,6 – 14*
ASTM А 48 класс 25	79 – 102	11,5 – 14,8
ASTM А 48 класс 30	90 – 113*	13,0 – 16,4 *
ASTM А 48 класс 40	110 – 138*	16 – 20 *
ASTM А 48 класс 50	130 – 157*	18,8 – 22,8*
Высокопрочный чугун**
60-40-18 класс	169	24,5
65-45-12	168	24,4
Оценка 80-55-06	168	24,4
120-90-02	164	23,8

Примечание*: Серый чугун не подчиняется критерию Гука.