Модуль упругости материала – Модуль упругости (Модуль Юнга): понятие, формулы, как определить
alexxlab | 17.04.2020 | 0 | Разное
Модуль упругости стали и других материалов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
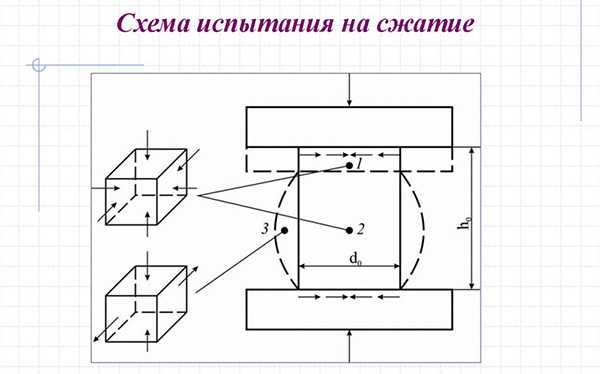
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
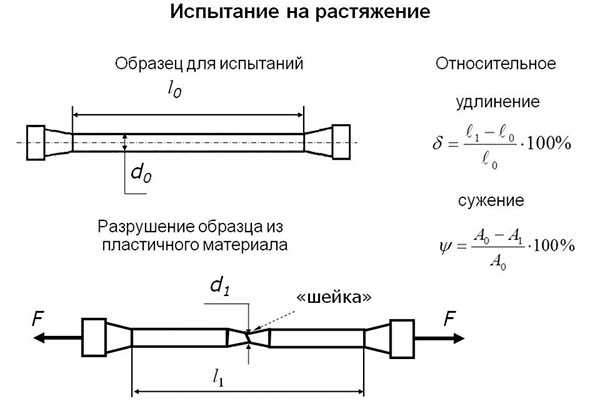
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
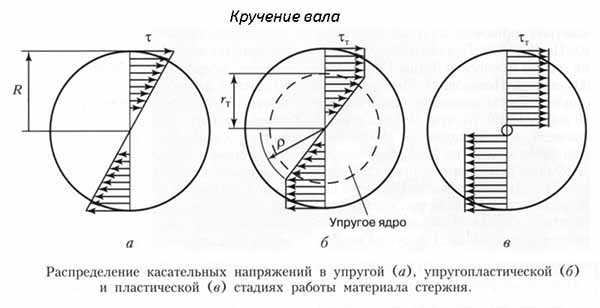
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
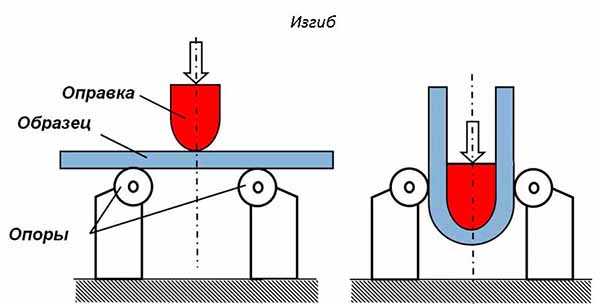
Понятие о модуле упругости
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:

Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Рейтинг автора
Автор статьи
Образование: Высшее, доктор технических наук, профессор.
Написано статей
metmastanki.ru
Модуль Юнга (упругости I рода)
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.
Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).
E=σ/ε=tgα
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Таблица 1
Материал | Модуль Юнга |
Сталь | 200 |
Чугун | 120 |
Серый чугун | 110 |
Алюминий | 70 |
Дюралюминий | 74 |
Титан | 120 |
Бронза | 100 |
Латунь | 95 |
Медь | 110 |
Олово | 35 |
Хром | 300 |
Никель | 210 |
Кремний | 110 |
Свинец | 18 |
Бетон | 20 |
Дерево | 10 |
Стекло | 70 |
Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:
σ=Eε
Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:
EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;
EI – жесткость поперечного сечения при изгибе,
где I – осевой момент инерции сечения балки.
Модуль упругости II рода (модуль сдвига) >
Примеры решения задач >
isopromat.ru
📌 Модули упругости – это… 🎓 Что такое Модули упругости?
величины, характеризующие упругие свойства материала. В случае малых деформаций, когда справедлив Гука закон, т. е. имеет место линейная зависимость между напряжениями и деформациями, М. у. представляют собой коэффициент пропорциональности в этих соотношениях. Одностороннему нормальному напряжению σ, возникающему при простом растяжении (сжатии), соответствует в направлении растяжения модуль продольной упругости Е (модуль Юнга). Он равен отношению нормального напряжения σ к относительному удлинению ε, вызванному этим напряжением в направлении его действия: Е = σ/ ε, и характеризует способность материала сопротивляться растяжению. Напряжённому состоянию чистого сдвига, при котором по двум взаимно перпендикулярным площадкам действуют только касательные напряжения τ, соответствует модуль сдвига G. Модуль сдвига равен отношению касательного напряжения τ к величине угла сдвига γ, определяющего искажение прямого угла между плоскостями, по которым действуют касательные напряжения, т. е. G = τ/γ. Модуль сдвига определяет способность материала сопротивляться изменению формы при сохранении его объёма. Всестороннему нормальному напряжению σ, одинаковому по всем направлениям (возникающему, например, при гидростатическом давлении), соответствует модуль объёмного сжатия K — объёмный модуль упругости. Он равен отношению величины нормального напряжения σ к величине относительного объёмного сжатия Δ, вызванного этим напряжением: K = σ/Δ. Объёмный модуль упругости характеризует способность материала сопротивляться изменению его объёма, не сопровождающемуся изменением формы. К постоянным величинам, характеризующим упругие свойства материала, относится также Пуассона коэффициент ν. Величина его равна отношению абсолютному значения относительного поперечного сжатия сечения ε’ (при одностороннем растяжении) к относительному продольному удлинению ε, т. е. ν = |ε’|/ε.В случае однородного изотропного тела М. у. одинаковы по всем направлениям. Четыре постоянные величины Е, G, K и ν связаны между собой двумя соотношениями:
Следовательно, только две из них являются независимыми величинами и упругие свойства изотропного тела определяются двумя упругими постоянными. В случае анизотропного материала постоянные Е, G и ν принимают различные значения в различных направлениях и величины их могут изменяться в широких пределах. Количество М. у. анизотропного материала зависит от структуры материала. Анизотропное тело, лишённое всякой симметрии в отношении упругих свойств, имеет 21 М. у. При наличии симметрии в материале число М. у. сокращается.
М. у. устанавливаются экспериментально-механическим испытанием образцов изучаемых материалов. М. у. не являются строго постоянными величинами для одного и того же материала, их значения меняются в зависимости от химического состава материала, от его предварительной обработки (термическая обработка, прокат, ковка и др.). Значения М. у. также зависят от температуры материала.
Лит.: Фридман Я. Б., Механические свойства металлов, 2 изд., М., 1952.
dic.academic.ru
Определение модуля упругости I рода
Лабораторная работа № 3
Цель работы – опытная проверка справедливости закона Гука при растяжении и определение модуля упругости I рода.
Основные сведения
Экспериментальные исследования на растяжение (сжатие) стандартных образцов показывают, что абсолютные удлинения, получающиеся в начальной стадии растяжения (сжатия), остаются прямопропорциональными растягивающей (сжимающей) силе и зависят от первоначальной длины образца l0 и площади поперечного сечения А:
Величина ЕА называется жесткостью стержня при растяжении и сжатии.
Коэффициент Е носит название модуля упругости I рода (используют также название «модуль Юнга» или «модуль продольной упругости«) и является основной физической постоянной, характеризующей упругие свойства (жесткость) материала при линейной деформации.
Чем больше значение Е, тем меньше при прочих равных условиях продольная деформация. Из формулы (3.1) следует, что модуль упругости
имеет размерность, что и напряжение, — в [Па] или кратных единицах — [кПа], [МПа], а для экспериментального определения его потребуется замерить величины: F, A, l, Δl.
Испытания проводятся на испытательной машине типа Р-5.
Испытывается образец квадратного сечения. Влияние возможной неточности изготовления образца на центральное приложение нагрузки устраняется за счет установки двух тензометров на противоположных продольных гранях образца.
В качестве тензодатчиков используются тензометры Аистова. Среднее удлинение, получаемое из показания двух тензодатчиков, принимают равным удлинению оси образца.
Диапазон нагрузок зависит от состояния и класса точности установки и предела пропорциональности материала образца. Минимальная загрузка зависит от жесткости самой установки (выборка лифтов, затяжка клиньев и т.п.) и определяется опытным путем. Максимальная загрузка рассчитывается по формуле
Зная диапазон нагрузок, определяют количество и величину ступеней нагружения ΔF.
Порядок выполнения и обработка результатов
Перед началом выполнения лабораторной работы необходимо ознакомиться с устройством машины Р-5 и рычажным тензометром Аистова.
Образец с закрепленными на нем тензодатчиками устанавливают в захватах машины и приводят в рабочее состояние.
Производят предварительное (минимальное) нагружение образца начальной нагрузкой и при этой нагрузке снимают показания приборов.
Далее нагрузку увеличивают плавно равными ступенями ΔF (5-6 ступеней) и производят соответственно снятие показаний с тензометров.
Доводить нагрузку до очередного значения нужно плавно, не «перескакивая» нужное значение. После осуществления загрузки последней ступени следует разгрузить образец до нагрузки, соответствующей минимальной.
При очередной ступени загрузки результаты опыта заносят в таблицу. Каждому приращению ΔF будет соответствовать приращение ΔП1i и ΔП2i, по которым подсчитывают среднее значение
ΔПср = (ΔП1i + ΔП2i)/2.
Истинное значение удлинения образца находим как
Δlсрi = ΔПсрiК,
где К = 10-3 мм – цена 1 деления тензометра Аистова.
По значениям нагрузки F и суммарному нарастанию удлинения оси образца строят график диаграммы растяжения образца в координатах F : Δl, по которому проверяют линейность зависимости (справедливость закона Гука).
Для среднего приращения нагрузки (ступени нагружения) определяют среднюю продольную абсолютную деформацию
где П – число ступеней нагружения.
Модуль продольной упругости
где l – база тензометра Аистова.
Полученное в опыте значение модуля упругости Еоп сравнивают с табличным ЕТ = 2·1011 Па и определяют погрешность опыта.
В заключение работы делают выводы.
Контрольные вопросы
- Как формулируется закон Гука для линейного напряженного состояния? Как ограничить верхнюю максимальную нагрузку?
- Каковы границы применения закона Гука?
- Что характеризует модуль упругости Е, от чего он зависит и какова его размерность?
- По какому геометрическому выражению с использованием диаграммы напряжений можно определить Е?
- Почему при определении деформаций растянутого образца используют два тензометра?
Определение коэффициента Пуассона >
Другие лабораторные работы >
isopromat.ru
| Формулы преобразования | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Упругие свойства гомогенных изотропных линейно-упругих материалов уникально определяются любыми двумя модулями упругости. Таким образом, имея два модуля, остальные можно вычислить по следующим формулам: | |||||||||
| (λ,G){\displaystyle (\lambda ,\,G)} | (E,G){\displaystyle (E,\,G)} | (K,λ){\displaystyle (K,\,\lambda )} | (K,G){\displaystyle (K,\,G)} | (λ,ν){\displaystyle (\lambda ,\,\nu )} | (G,ν){\displaystyle (G,\,\nu )} | (E,ν){\displaystyle (E,\,\nu )} | (K,ν){\displaystyle (K,\,\nu )} | (K,E){\displaystyle (K,\,E)} | |
| K={\displaystyle K=}модуль объемной упругости | λ+2G3{\displaystyle \lambda +{\frac {2G}{3}}} | EG3(3G−E){\displaystyle {\frac {EG}{3(3G-E)}}} | λ1+ν3ν{\displaystyle \lambda {\frac {1+\nu }{3\nu }}} | 2G(1+ν)3(1−2ν){\displaystyle {\frac {2G(1+\nu )}{3(1-2\nu )}}} | E3(1−2ν){\displaystyle {\frac {E}{3(1-2\nu )}}} | ||||
| E={\displaystyle E=}модуль продольной упругости Юнга | G3λ+2Gλ+G{\displaystyle G{\frac {3\lambda +2G}{\lambda +G}}} | 9KK−λ3K−λ{\displaystyle 9K{\frac {K-\lambda }{3K-\lambda }}} | 9KG3K+G{\displaystyle {\frac {9KG}{3K+G}}} | λ(1+ν)(1−2ν)ν{\displaystyle {\frac {\lambda (1+\nu )(1-2\nu )}{\nu }}} | 2G(1+ν){\displaystyle 2G(1+\nu )} | 3K(1−2ν){\displaystyle 3K(1-2\nu )} | |||
| λ={\displaystyle \lambda =}первый параметр Ламе | GE−2G3G−E{\displaystyle G{\frac {E-2G}{3G-E}}} | K−2G3{\displaystyle K-{\frac {2G}{3}}} | 2Gν1−2ν{\displaystyle {\frac {2G\nu }{1-2\nu }}} | Eν(1+ν)(1−2ν){\displaystyle {\frac {E\nu }{(1+\nu )(1-2\nu )}}} | 3Kν1+ν{\displaystyle {\frac {3K\nu }{1+\nu }}} | 3K(3K−E)9K−E{\displaystyle {\frac {3K(3K-E)}{9K-E}}} | |||
| G={\displaystyle G=}модуль сдвига или второй параметр Ламе | 3K−λ2{\displaystyle 3{\frac {K-\lambda }{2}}} | λ1−2ν2ν{\displaystyle \lambda {\frac {1-2\nu }{2\nu }}} | E2+2ν{\displaystyle {\frac {E}{2+2\nu }}} | 3K1−2ν2+2ν{\displaystyle 3K{\frac {1-2\nu }{2+2\nu }}} | 3KE9K−E{\displaystyle {\frac {3KE}{9K-E}}} | ||||
| ν={\displaystyle \nu =}коэф. пуассона | λ2(λ+G){\displaystyle {\frac {\lambda }{2(\lambda +G)}}} | E2G−1{\displaystyle {\frac {E}{2G}}-1} | λ3K−λ{\displaystyle {\frac {\lambda }{3K-\lambda }}} | 3K−2G2(3K+G){\displaystyle {\frac {3K-2G}{2(3K+G)}}} | 3K−E6K{\displaystyle {\frac {3K-E}{6K}}} | ||||
| M={\displaystyle M=} | λ+2G{\displaystyle \lambda +2G} | G4G−E3G−E{\displaystyle G{\frac {4G-E}{3G-E}}} | 3K−2λ{\displaystyle 3K-2\lambda } | K+4G3{\displaystyle K+{\frac {4G}{3}}} | λ1−νν{\displaystyle \lambda {\frac {1-\nu }{\nu }}} | G2−2ν1−2ν{\displaystyle G{\frac {2-2\nu }{1-2\nu }}} | E1−ν(1+ν)(1−2ν){\displaystyle E{\frac {1-\nu }{(1+\nu )(1-2\nu )}}} | 3K1−ν1+ν{\displaystyle 3K{\frac {1-\nu }{1+\nu }}} | 3K3K+E9K−E{\displaystyle 3K{\frac {3K+E}{9K-E}}} |
ru-wiki.org
Модуль – упругость – композиционный материал
Модуль – упругость – композиционный материал
Cтраница 1
Модуль упругости композиционных материалов может изменяться в требуемом направлении в зависимости от схемы армирования. Высокая надежность в работе конструкций из композиционных материалов связана с особенностями распространения в них трещин. В обычных сплавах трещина развивается быстро и скорость роста ее в период работы конструкции детали возрастает. В композиционных материалах трещина обычно возникает и развивается в матрице и встречает препятствия на границе матрица – упрочнителъ. Армирующий элемент тормозит ее распространение, задерживая на некоторое время ее рост. [2]
Вычислив модуль упругости композиционного материала по приведенным формулам, можно рассчитать жесткость при растяжении элемента конструкции любого поперечного сечения. [4]
Анализ модулей упругости композиционных материалов с волокнистыми, пластинчатыми дисперсными наполнителями, а также полиармированных материалов, в которых присутствуют наполнители обоих типов, будет производиться с использованием структурных параметров, рассмотренных в гл. Различие имеется в количественных значениях соответствующих фаз на структурных диаграммах и методах вычисления их эффективных модулей упругости. Рассмотрение начнем с модулей упругости материалов с пластинчатыми наполнителями, поскольку большинство древесно – полимерных композиционных материалов относятся к данному классу. [6]
Вследствие высокого удельного модуля упругости композиционного материала на основе алюминия и углеродных волокон перспективным является его использование в производстве коробок трансмиссии вертолетов, подвергающихся высоким вибрационным нагрузкам. [7]
Значения предела прочности при растяжении и модуля упругости композиционных материалов приблизительно в 3 раза выше, чем у лучших алюминиевых сплавов. Делением указанных значений на плотность материала получают истинную меру его эффективности массы – показатели удельной прочности и удельного модуля упругости. [8]
Данные табл. 1 свидетельствуют о повышении удельного модуля упругости композиционного материала вследствие упрочнения волокнами. Удельный модуль упругости борного волокна примерно в 6 раз выше, чем у любых стандартных конструкционных металлов, включая стали, алюминий, молибден, медь, магний, что является следствием более жесткой ковалентной связи по сравнению с металлической. Жесткость металлической связи, в свою очередь, более высокая, чем жесткость в органических смолах. В то время как материалы с металлической связью имеют удельный модуль упругости – 2500 км, наиболее типичный уровень этой характеристики для материалов на основе органической смолы составляет около 250 км. Из-за низкой жесткости смол композиционные материалы на их основе имеют низкий модуль упругости в направлении, перпендикулярном направлению укладки волокна, и малый модуль сдвига. Преимущество однонаправленного боралкшиниевого композиционного материала в отношении жесткости распространяется я на материал с волокнами, уложенными в различных направлениях, поскольку волокна, не ориентированные в направлении действия главных напряжений, вносят значительный вклад в величину модуля упругости материала в этом направлении. [9]
В основу построения расчетных зависимостей, определяющих усредненные модули упругости трехмерно-армированного композиционного материала принимается гипотеза о равенстве нормальных деформаций растяжения-сжатия всех точек, находящихся на грани куба. [10]
Пуассона v / и т не вносят существенного вклада ни в один из модулей упругости композиционного материала. [11]
Пуассона v / и vm не вносят существенного вклада ни в один из модулей упругости композиционного материала. [12]
Установлено также, что независимо от природы наполнителя и вида среды относительное уменьшение модуля упругости композиционных материалов на основе термореактивных смол имеет линейную зависимость от количества низкомолекулярного вещества, сорбированного композицией, при условии, что процесс сорбции определяется законом диффузии. [13]
Термопласты обладают нелинейными вязкоупругими свойствами. Поэтому модуль упругости композиционных материалов на основе термопластов зависит не только от времени, но и от уровня деформации. [15]
Страницы: 1 2
www.ngpedia.ru
Модули упругости материалов – Справочник химика 21
Из уравнения (5.33) видно, что ЪТ не зависит от среднего уровня нагрузок, тем не менее, недавние исследования показали, что константа термоупругости зависит от нагрузок это объясняется зависимостью модуля упругости материалов от температуры [78]. [c.169]Данные, приведенные в упомянутых таблицах, свидетельствуют о непосредственной связи собственных частот с размерами образца, а также с характеристиками упругости и плотностью материала. Поэтому широко применяют определение модуля упругости материалов по резонансным частотам стержня, изготовленного из исследуемого Материала. Чаще всего, возбуждая продольные резонансные колебания, определяют модуль упругости Е в соответствии с формулой [c.152]
Формулы для определения усилий и напряжений приведены для стыка рассматриваемых элементов. Чтобы найти усилия и напряжения в произвольном сечении элемента, следует использовать соответствующие выражения для данного элемента, суммируя алгебраически их значения от нагружения внутренним давлением и краевыми силами и моментами Мд, полученными для данной составной конструкции, причем для сферического сегмента в качестве Яд следует принимать разность (Яд — Я), учитывающую наличие распорной силы. Формулы приведены при условии, что модули упругости материалов сопрягаемых элементов конструкции одинаковы [c.270]
Е и Е1—модули упругости материалов цилиндра и поршня (А И —коэффициенты Пуассона для материалов цилиндра и поршня. [c.130]
Для ряда конструкций определяющим являются не столько абсолютные значения прочности и модуля упругости материалов, сколько их удельные значения — отношение прочности и модуля упругости к плотности материала — ар/р и /р. Удельная прочность стекловолокнитов намного превосходит удельную прочность, а удельный модуль упругости соизмерим с удельным модулем упругости металлических конструкционных материалов (табл. 1У.12). [c.151]Предел прочности и модуль упругости материалов [c.371]
Жесткость элемента выбирается такой, чтобы его деформация при ударе была пренебрежимо мала по сравнению с деформацией призмы, что достигается соблюдением соотношений при выборе его материала и толщины Н йкл, где Е и р — модули упругости материалов элемента и призмы и ккл — толщины накладки и клеевого слоя. [c.110]
Среди различных факторов, оказывающих влияние на термические напряжения в покрытиях, можно выделить первичные и вторичные. К первичным следует отнести различия в значениях к. т. р. и модулях упругости материалов покрытия и металла геометрические размеры образцов ползучесть материала покрытия и металлов предел текучести металлов , интервалы размягчения покрытия, когда теряются упругие свойства материала покрытия. Эти факторы оказывают непосредственное влияние на величину напряжений в покрытиях и могут быть учтены количественно с помощью теории. термоупругости, термопластичности и т. д. [c.24]
Зависимость величины прогиба от соотношения модулей упругости можно вычислить по формуле (I. 54) и при неизвестных абсолютных величинах модулей упругости. Для определения же напряжений необходимо знать абсолютные величины модулей упругости материалов. Однако анализ деформаций позволяет получить зависимость их от соотношения модулей упругости для прогибающейся полосы [c.30]
Здесь Еб, Е, и Е — модули упругости материалов болта и частей шатуна Рб, я — плош,ади сечений болта и соединяемых частей шатуна 6, /1 и /2 —длины болта и соединяемых деталей. [c.258]
Расчет цилиндров высокого давления и их втулок производят по формулам для толстостенных цилиндров, учитывая напряжения при посадке втулки и различие модулей упругости материалов цилиндра и втулки. Ввиду пульсирующей нагрузки, при выборе запаса прочности принимают во внимание усталостную характеристику. материала. [c.135]
На рис. 48 показана диаграмма усилий, построенная в предположении, что модуль упругости материалов деталей не изменяется. Это допущение может быть принято при условии, что температура деталей при проведении процессов не превышает 200° С. [c.83]
Давление уплотнения /о должно быть достаточным для того, чтобы материал прокладки заполнил бы неровности от обработки уплотняемых поверхностей. Величина /о или отвечающее ему е может быть найдена экспериментально. Уравнение (8.12) по заданным параметрам и модулям упругости материалов деталей конструкций и величине затяга Q позволяет на
www.chem21.info

