Модуль упругости стали: Модуль упругости стали: таблица, характеристики
alexxlab | 26.04.2023 | 0 | Разное
|
Основные таблицы и графики, необходимые для механических расчетов Таблица 1 – Поправочный коэффициент η к нормативным допускаемым напряжениям
Таблица 2 – Нормативное допускаемое напряжение σ*
Таблица 3 – Определение расчетного давления р
Таблица 4 – Модуль продольной упругости Е
Таблица 5 – Предел текучести материала
Таблица 6 – Шаг трубок при размещении их по вершинам равносторонних треугольников
Рисунок 1 – График для определения коэффициента Рисунок 2 – График для определения коэффициента k, зависящего от гибкости ребра Таблица 7 – Физические свойства черных металлов и сплавов Таблица 8 – Сортамент труб из теплостойкой стали 12ХМ Таблица 9 – Сортамент труб из углеродистой стали 10 и 20 Таблица 10 – Сортамент труб из высоколегированных сталей Таблица 11 – Линзы для компенсаторов из углеродистой стали* * Примечание Если МПа, то диаметр линзового компенсатора определяется по формуле где D – внутренний диаметр аппарата, мм – давление в межтрубном пространстве, МПа – допускаемое напряжение материала корпуса, МПа Таблица 12 – Коэффициенты при расчете линзового компенсатора
Таблица 13 – Величина удельного ветрового напора q
Рисунок 3 – График для определения коэффициента пульсации Рисунок 4 – График для определения коэффициента динамичности Рисунок 5 – График к расчету фундаментных болтов Таблица 14 – Коэффициенты ,
Таблица 15 – Масса колпачковой тарелки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в каком виде выпускаются заготовки согласно гост, основные характеристики металла
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции.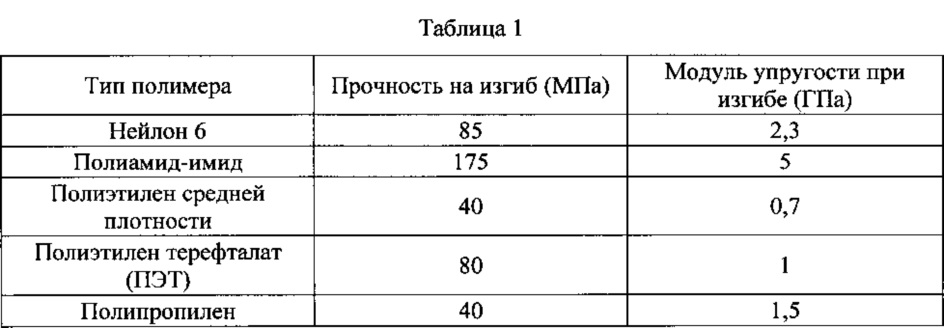 Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Этапы изменения структуры
При строительстве необходимо учитывать деформацию от приложенной нагрузки. В процессе эксплуатации бетонная структура деформируется в два этапа:
- Первый этап — краткосрочное изменение структуры. На этой стадии бетон сохраняет свою целостность и может восстанавливать исходное состояние. При этом во время растяжения, сжатия и изгибания возникает упругая деформация без необратимых разрушений.
- Второй этап — разрушения необратимого типа, которые происходят в результате внезапной и сильной нагрузки. Во время пластичной деформации появляются трещины, вследствие которых начинается постепенное разрушение бетонных конструкций.
Помимо деформации от приложенной нагрузки существует такое понятие, как коэффициент упругости. Такой показатель просто необходим для людей, занимающихся расчетом прочности бетонных зданий.
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Основное понятие
Важным параметром при выборе бетона является его упругость, которая показывает способность застывшей массы оставаться в целостности даже под воздействием деформации. Такие данные нужны проектировщикам для того, чтобы возводить прочные и долговечные конструкции.
Безусловно, главным достоинством материала является его твердость. Но из-за ползучести затвердевшая масса в процессе эксплуатации может деформироваться. Все это может происходить из-за воздействия нагрузки, если ее значение превысит допустимые нормы. Поэтому следует учитывать величину приложенной нагрузки и значение коэффициента ползучести, из-за которых структура затвердевшего изделия постепенно меняется.
Все это может происходить из-за воздействия нагрузки, если ее значение превысит допустимые нормы. Поэтому следует учитывать величину приложенной нагрузки и значение коэффициента ползучести, из-за которых структура затвердевшего изделия постепенно меняется.
Модуль Юнга в действии
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п — число пи, равное 3,14, а r — радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g — ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.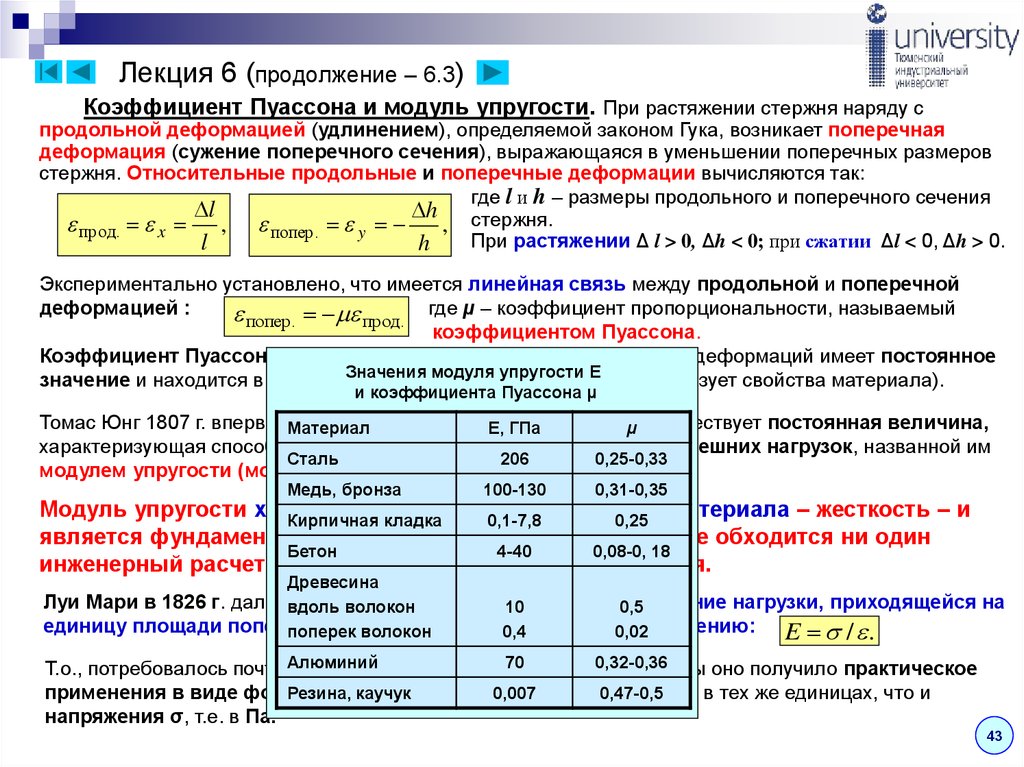
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d — относительная деформация в упругой области.
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия — явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления.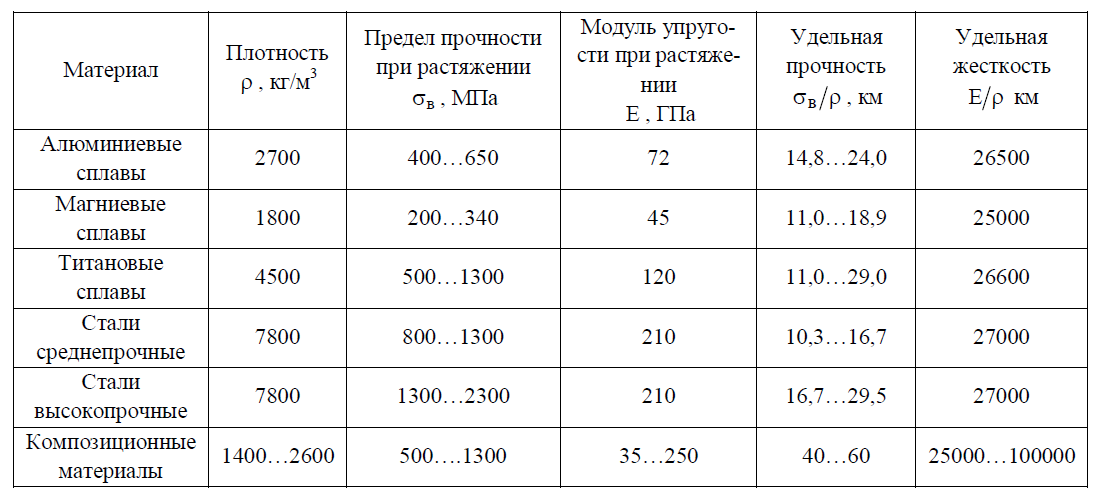 Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.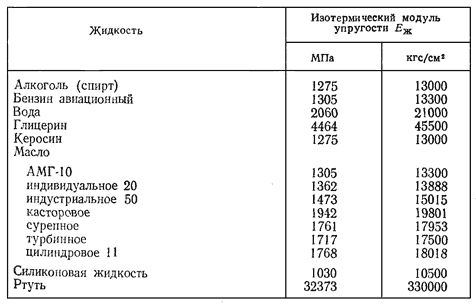
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля.
 По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы. - Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.

- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
- Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Модуль сдвига
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Модуль упругости дерева
Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления.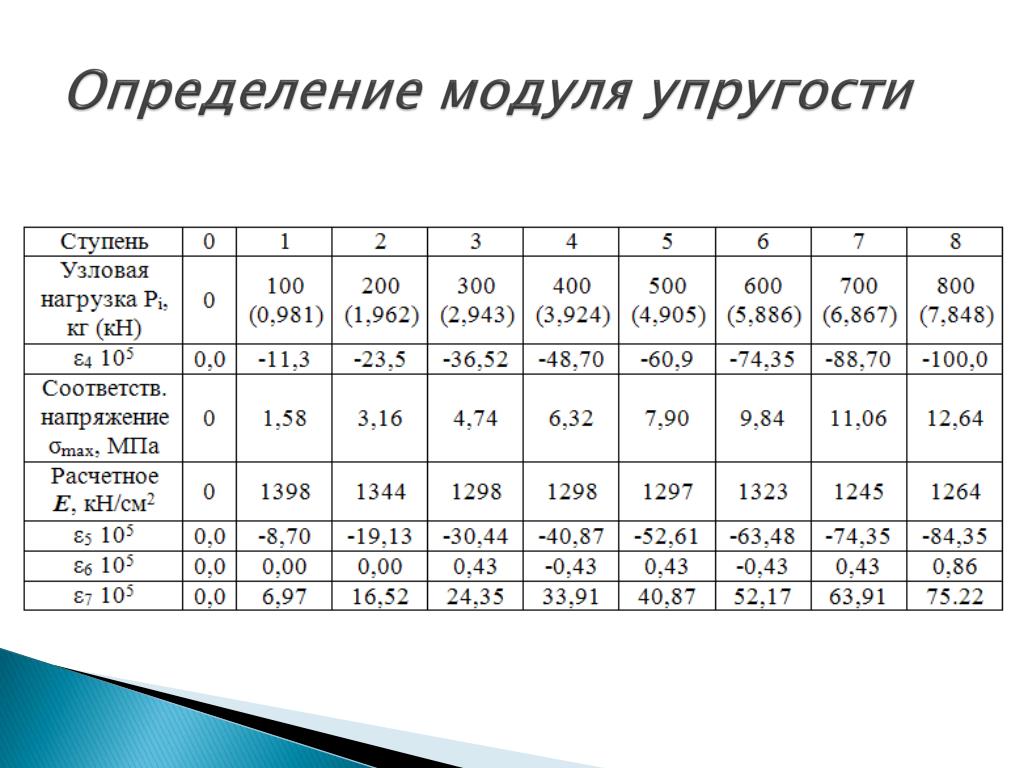 Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.
Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
Модуль упругости стали – это 200 ГПа?
Махендран, Махен (1996) Модуль упругости стали – 200 ГПа? В Недавние исследования и исследования Разработки в области проектирования и строительства из холодногнутой стали: 13-я Международная конференция по холодной штамповке. Университет Миссури-Ролла, Сент-Луис, Миссури.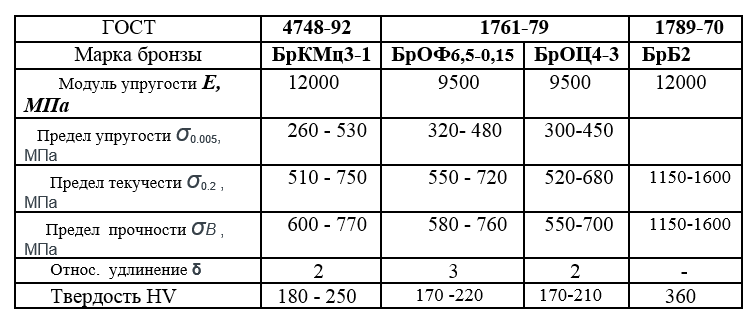
В конструкциях из холодногнутой стали в последнее время значительно увеличилось использование ряда тонких высокопрочных сталей (толщина 0,35 мм и предел текучести 550 МПа). Для удовлетворительного использования этих сталей необходимо хорошее знание основных механических свойств этих сталей. Что касается модуля упругости, то в настоящее время считается, что он составляет около 200 ГПа для всех марок стали. Однако испытания этих сталей на растяжение неизменно показывают, что модуль упругости изменяется в зависимости от сорта стали и толщины. Было обнаружено, что оно увеличивается до значений до 240 ГПа для меньших толщин и более высоких марок стали. В данной статье обсуждается эта тема, представлены результаты испытаний на растяжение для ряда марок стали и толщин, а также предпринимается попытка установить взаимосвязь между модулем упругости, пределом текучести и толщиной для рассматриваемых в данном исследовании марок стали.
Больше статистики…
| Идентификационный код: | 64377 | ||
|---|---|---|---|
| Тип товара: | Глава в книге, отчете или конференции (Вклад конференции) | ||
| ORCID ID: |
| ||
| Измерения или продолжительность: | 0 | ||
| Чистый ID: | 34360650 | ||
| Подразделения: | Прошлое > Факультеты и подразделения QUT > Факультет искусственной среды и инженерии ?? 1403 ?? Прошлое > Факультеты и подразделения QUT > Научно-технический факультет ?? 32 – ?? | ||
| Владелец авторских прав: | Проконсультируйтесь с автором(ами) по вопросам авторского права | ||
| Заявление об авторских правах: | Это произведение защищено авторским правом. Если документ не предоставляется в соответствии с лицензией Creative Commons, вы должны исходить из того, что повторное использование ограничено личным использованием и что для всех других видов использования необходимо получить разрешение от владельца авторских прав. Если документ доступен по лицензии Creative Commons (или другой указанной лицензии), обратитесь к лицензии для получения подробной информации о разрешенном повторном использовании. Условием доступа является то, что пользователи признают и соблюдают юридические требования, связанные с этими правами. Если вы считаете, что эта работа нарушает авторские права, сообщите подробности по электронной почте [email protected] Если документ доступен по лицензии Creative Commons (или другой указанной лицензии), обратитесь к лицензии для получения подробной информации о разрешенном повторном использовании. Условием доступа является то, что пользователи признают и соблюдают юридические требования, связанные с этими правами. Если вы считаете, что эта работа нарушает авторские права, сообщите подробности по электронной почте [email protected] | ||
| Депонировано: | 21 ноя 2013 00:55 | ||
| Последнее изменение: | 21 дек 2022 19:07 |
Эластичность. Почему модуль упругости бетона меньше, чем у стали?
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 4к раз
$\begingroup$
Я пытаюсь понять, что означает модуль упругости для различных материалов. Насколько я понимаю, поскольку
Насколько я понимаю, поскольку E = напряжение / деформация , более высокое значение E означает более жесткий материал, т. к. требуется больше силы для создания той же величины деформации.
С удивлением узнал, что Упругость бетона (24 ГПа) на порядок меньше, чем у стали (200 ГПа). Не означает ли это, что одна и та же сила вызовет в 10 раз большую деформацию бетона, чем стали? Это правда?
Линейное моделирование в SolidWorks показывает, что это действительно так:
Интуитивно кажется, что бетон должен быть более жестким (и, конечно, хрупким), чем сталь, однако эти результаты показывают, что это не так.
Почему?
- эластичность
- напряжение-деформация
$\endgroup$
$\begingroup$
Хрупкость и модуль упругости — две очень разные вещи.
Модуль упругости концептуально говорит о том, какое усилие вы можете приложить, чтобы получить определенную деформацию без разрушения материала. Точнее, модуль — это наклон графика деформации к напряжению в линейном режиме, который также можно назвать упругим режимом.
Точный способ, которым материал выйдет из строя, – это другой вопрос. Он не обязательно должен ломаться (как следует из размышлений о хрупкости), он также может, например, постоянно изгибаться.
На самом деле, например, в строительстве рабочие всегда гнут сталь, чтобы создать остаточную деформацию, чтобы получить стальные стержни под прямым углом.
Точнее, модуль — это наклон графика деформации к напряжению в линейном режиме, который также можно назвать упругим режимом.
Точный способ, которым материал выйдет из строя, – это другой вопрос. Он не обязательно должен ломаться (как следует из размышлений о хрупкости), он также может, например, постоянно изгибаться.
На самом деле, например, в строительстве рабочие всегда гнут сталь, чтобы создать остаточную деформацию, чтобы получить стальные стержни под прямым углом.
Кроме того, не рекомендуется пытаться определить поведение, близкое к разрушению, по модулю, так как все эти константы дают только линейное приближение, тогда как в действительности при больших деформациях поведение очень нелинейно и ближе к парабола с максимумами, говорящими нам, когда есть какой-то сбой.
При этом в SolidWorks вы провели линейный анализ. В то время как компьютер позволяет вам делать что угодно в реальности, бетонная балка находится далеко за пределом своей точки отказа, где линейный анализ не имеет ничего общего с реальностью.



 По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.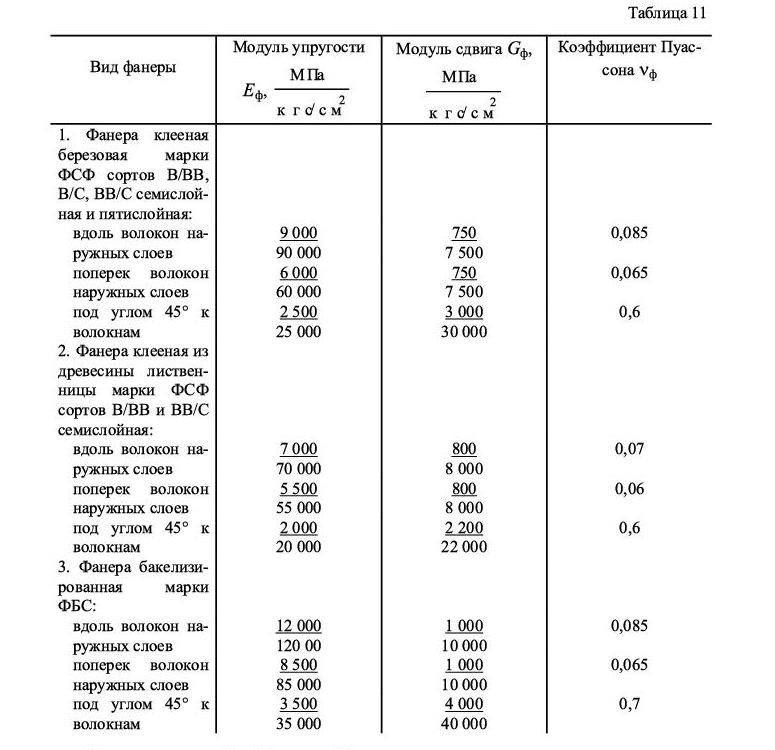
 org/0000-0001-7306-8821
org/0000-0001-7306-8821