Модуль упругости юнга: Модуль упругости (Модуль Юнга): понятие, формулы, как определить

alexxlab | 15.06.2018 | 0 | Разное

Содержание

Измерение модуля упругости

Приложение:

Измерение модуля продольной упругости, модуля сдвига и коэффициента Пуассона (поперечной деформации) в недисперсионных изотропных конструкционных материалах.

Общие сведения:

Модуль Юнга (модуль продольной упругости) определяется как отношение напряжения (сила на единицу площади) к деформации сжатия.

Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига.

Коэффициент Пуассона отношение относительного поперечного сжатия к относительному продольному растяжению.

Эти основные свойства материалов обязательно учитываются в производстве и в различных научных исследованиях, и определяются с помощью измеренных значений скорости звука и плотности материала. Скорость распространения звука легко вычисляется путем ультразвукового контроля в режиме импульс-эхо с использованием соответствующего оборудования. Представленная ниже процедура действительна для любого однородного, изотропного, недисперсионного материала (скорость звука не изменяется с частотой).

Сюда включены наиболее распространенные металлы, промышленная керамика и стекло, при условии, что размеры поперечного сечения не близки длине волны частоты контроля. Жесткие пластики, такие как полистирол и акрил, также могут быть измерены, несмотря на то, что они имеют высокий коэффициент затухания ультразвука.

Каучук не может быть измерен ультразвуковым методом по причине высокой степени дисперсии и нелинейно упругих свойств. Мягкие пластики точно так же показывают высокую степень затухания в режиме сдвиговых волн, и обычно не могут быть измерены. В случае анизотропных материалов, упругость варьируется в зависимости от направления, так же как и скорость распространения продольных волн и/или сдвиговых волн. Для генерации полной матрицы модуля упругости в анизотропных образцах обычно требуется шесть серий ультразвуковых измерений. Пористость или зернистость материала может влиять на точность измерения модуля упругости, поскольку вызывает колебания скорости звука исходя из размера и ориентации зерен или размера и распределения пор, вне зависимости от упругости материала.

Оборудование:

Для измерения скорости звука при расчете упругости обычно используются прецизионные толщиномеры 38DL PLUS или 45MG с ПО для одноэлементных ПЭП, или дефектоскопы с функцией измерения скорости звука (например, серии EPOCH). Генераторы/приемники модели 5072PR или 5077PR в комбинации с осциллографом или дискретизатором сигналов также могут использоваться для измерения времени распространения волн. Для данного теста потребуется два преобразователя, подходящих для эхо-импульсного измерения скорости звука в материале продольными и поперечными волнами. Среди наиболее используемых ПЭП: широкополосный преобразователь продольных волн M112 или V112 (10 МГц) и преобразователь поперечных волн с нормальным углом падения V156 (5 МГц). Они подходят для измерения наиболее распространенных металлов и обожженных керамических образцов. Для измерения очень толстых и очень тонких материалов или образцов с высоким затуханием ультразвука требуются специальные преобразователи.

В некоторых случаях применяется теневой метод контроля (метод сквозного прозвучивания) с использованием двух преобразователей, расположенных на одной оси, по разные стороны проверяемого изделия. При выборе преобразователя или настройке прибора необходимо проконсультироваться со специалистом Olympus.

Тестовый образец может быть любой формы, позволяющей выполнять эхо-импульсное измерение времени прохождения ультразвука через материал. Обычно, это образец толщиной 12,5 мм с ровными параллельными поверхностями, ширина или диаметр которого больше диаметра используемого преобразователя. Необходимо проявлять крайнюю осторожность при измерении узких образцов по причине возможных пограничных эффектов, которые могут повлиять на измеренное время прохождения импульса. При использовании сильно тонких образцов, разрешение будет ограничено из-за небольших колебаний во времени прохождения импульса через короткий УЗ-путь. Мы рекомендуем брать образцы толщиной минимум 5 мм, но желательно толще. Во всех случаях толщина тестового образца должна быть точно известна.

Процедура:

Измерьте скорость распространения продольных и сдвиговых волн тестового образца с использованием подходящих ПЭП и настроек прибора. Для измерения скорости сдвиговых волн потребуется специальная контактная жидкость высокой вязкости, как например SWC. Толщиномеры 38DL PLUS и 45MG могут напрямую измерять скорость звука в материале на основе введенной толщины образца, а дефектоскопы серии EPOCH измеряют скорость звука в ходе калибровки скорости звука. В обоих случаях, следуйте рекомендуемой процедуре измерения скорости звука, представленной в руководстве по эксплуатации прибора. При использовании генератора/приемника, зафиксируйте время прохождения сигнала туда и обратно через участок известной толщины с помощью преобразователей продольных и поперечных волн, и рассчитайте:

При необходимости, переведите единицы измерения скорости звука в дюйм/с или см/с. (Время обычно измеряется в микросекундах; для получения измерений в дюйм/с или см/с умножьте дюйм/мкс или см/мкс на 10⁶. ) Полученные значения скорости звука могут использоваться в следующих формулах.

Примечание: Если скорость звука выражена в см/с, а плотность – в г/см³, модуль упругости будет выражен в дин/см². Если вы используете английскую систему мер (дюйм/с и фунт/дюйм³) для расчета модуля упругости в фунтах на кв. дюйм (PSI), не путайте фунт (единицу измерения силы) с фунтом (единицей измерения массы). Поскольку модуль упругости выражен как сила на единицу площади, при расчете в английской системе мер необходимо умножить результат вышеуказанной формулы на коэффициент пересчета масса/сила (1 / ускорение свободного падения) для получения значения упругости в фунтах на кв. дюйм. Если исходные расчеты выполнены в метрических единицах, используйте коэффициент конверсии 1 psi = 6,89 x 10⁴ дин/см ². Вы также можете ввести скорость звука в дюймах/с, а плотность – в г/см ³, а затем разделить на коэффициент пересчета 1,07 x 10⁴ для получения упругости в PSI.

Для определения модуля сдвига умножьте квадрат скорости распространения поперечной волны на плотность.
Опять же, используйте единицы измерения см/с и г/см ³ для получения модуля упругости в дин/см² или английскую систему мер (дюйм/с и фунт/дюйм³) и умножьте результат на коэффициент пересчета масса/сила.

Библиография
Подробнее об измерении модулей упругости ультразвуковым методом см. в представленных ниже источниках:
1. Moore, P. (ed.), Nondestructive Testing Handbook, Volume 7, American Society for Nondestructive Testing, 2007, pp. 319-321.
2. Krautkramer, J., H. Krautkramer, Ultrasonic Testing of Materials, Berlin, Heidelberg, New York 1990 (Fourth Edition), pp. 13-14, 533-534.

Модуль упругости (модуль Юнга) | Мир сварки

Модуль упругости

Модуль упругости (модуль Юнга) E – характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению.

Часто модуль Юнга называют просто модулем упругости.

1 кгс/мм² = 10^-6 кгс/м² = 9,8·10⁶ Н/м² = 9,8·10⁷ дин/см² = 9,81·10⁶ Па = 9,81 МПа

Модуль упругости (модуль Юнга)
Материал	E
Материал	кгс/мм²	10⁷ Н/м²	МПа
Металлы
Алюминий	6300-7500	6180-7360	61800-73600
Алюминий отожженный	6980	6850	68500
Бериллий	30050	29500	295000
Бронза	10600	10400	104000
Бронза алюминиевая, литье	10500	10300	103000
Бронза фосфористая катаная	11520	11300	113000
Ванадий	13500	13250	132500
Ванадий отожженный	15080	14800	148000
Висмут	3200	3140	31400
Висмут литой	3250	3190	31900
Вольфрам	38100	37400	374000
Вольфрам отожженный	38800-40800	34200-40000	342000-400000
Гафний	14150	13900	139000
Дюралюминий	7000	6870	68700
Дюралюминий катаный	7140	7000	70000
Железо кованое	20000-22000	19620-21580	196200-215800
Железо литое	10200-13250	10000-13000	100000-130000
Золото	7000-8500	6870-8340	68700-83400
Золото отожженное	8200	8060	80600
Инвар	14000	13730	137300
Индий	5300	5200	52000
Иридий	5300	5200	52000
Кадмий	5300	5200	52000
Кадмий литой	5090	4990	49900
Кобальт отожженный	19980-21000	19600-20600	196000-206000
Константан	16600	16300	163000
Латунь	8000-10000	7850-9810	78500-98100
Латунь корабельная катаная	10000	9800	98000
Латунь холоднотянутая	9100-9890	8900-9700	89000-97000
Магний	4360	4280	42800
Манганин	12600	12360	123600
Медь	13120	12870	128700
Медь деформированная	11420	11200	112000
Медь литая	8360	8200	82000
Медь прокатанная	11000	10800	108000
Медь холоднотянутая	12950	12700	127000
Молибден	29150	28600	286000
Нейзильбер	11000	10790	107900
Никель	20000-22000	19620-21580	196200-215800
Никель отожженный	20600	20200	202000
Ниобий	9080	8910	89100
Олово	4000-5400	3920-5300	39200-53000
Олово литое	4140-5980	4060-5860	40600-58600
Осмий	56570	55500	555000
Палладий	10000-14000	9810-13730	98100-137300
Палладий литой	11520	11300	113000
Платина	17230	16900	169000
Платина отожженная	14980	14700	147000
Родий отожженный	28030	27500	275000
Рутений отожженный	43000	42200	422000
Свинец	1600	1570	15700
Свинец литой	1650	1620	16200
Серебро	8430	8270	82700
Серебро отожженное	8200	8050	80500
Сталь инструментальная	21000-22000	20600-21580	206000-215800
Сталь легированная	21000	20600	206000
Сталь специальная	22000-24000	21580-23540	215800-235400
Сталь углеродистая	19880-20900	19500-20500	195000-205000
Стальное литье	17330	17000	170000
Тантал	19000	18640	186400
Тантал отожженный	18960	18600	186000
Титан	11000	10800	108000
Хром	25000	24500	245000
Цинк	8000-10000	7850-9810	78500-98100
Цинк катаный	8360	8200	82000
Цинк литой	12950	12700	127000
Цирконий	8950	8780	87800
Чугун	7500-8500	7360-8340	73600-83400
Чугун белый, серый	11520-11830	11300-11600	113000-116000
Чугун ковкий	15290	15000	150000
Пластмассы
Плексиглас	535	525	5250
Целлулоид	173-194	170-190	1700-1900
Стекло органическое	300	295	2950
Резины
Каучук	0,80	0,79	7,9
Резина мягкая вулканизированная	0,15-0,51	0,15-0,50	1,5-5,0
Дерево
Бамбук	2000	1960	19600
Береза	1500	1470	14700
Бук	1600	1630	16300
Дуб	1600	1630	16300
Ель	900	880	8800
Железное дерево	2400	2350	32500
Сосна	900	880	8800
Минералы
Кварц	6800	6670	66700
Различные материалы
Бетон	1530-4100	1500-4000	15000-40000
Гранит	3570-5100	3500-5000	35000-50000
Известняк плотный	3570	3500	35000
Кварцевая нить (плавленая)	7440	7300	73000
Кетгут	300	295	2950
Лед (при -2 °С)	300	295	2950
Мрамор	3570-5100	3500-5000	35000-50000
Стекло	5000-7950	4900-7800	49000-78000
Стекло крон	7200	7060	70600
Стекло флинт	5500	5400	70600

Литература

Краткий физико-технический справочник. Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1981. 680 с.
Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.

Модуль упругости для стали, а также для других материалов

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Оцените статью: Поделитесь с друзьями!

Модуль упругости (Модуль Юнга): понятие, формулы, как определить

При проектировании строительной конструкции стоит задача спрогнозировать ее поведение при заданных нагрузках и внешних условиях. Бетон воспринимает значительные усилия, поэтому важный этап расчета — определение деформаций и прогибов при статическом нагружении.

В расчете железобетонных конструкций по второй группе предельных состояний применяют физическую величину, называемую модулем упругости бетона, или модулем Юнга. Он характеризует свойства твердого вещества в зоне упругих деформаций.

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

E=α/ε

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Способы определения

Модуль упругости бетона определяют:

механическим испытанием образцов;
неразрушающим ультразвуковым методом, основанным на сравнении скорости распространения волн в существующей конструкции и испытанном образце с заданными характеристиками.

Механический способ

Исследование первым методом проводят согласно ГОСТ 24452-80. Изготавливают образцы с сечением в виде квадрата или круга с соотношением высоты к диаметру (ширине), равным 4.

Образцы сериями по три штуки выбуривают, высверливают или выпиливают из готовых изделий, либо набивают формы согласно ГОСТ 10180-78. До начала испытаний призмы или цилиндры выдерживают под влажной тканью.

Для определения модуля упругости бетона используют прессы со специальными базами для измерения деформаций. Они состоят из приборов, расположенных под разными углами к граням образца. Индикаторы крепят к стальным рамкам или приклеенным опорным вставкам.

Если испытания проводят для конструкций, работающих при повышенной влажности или высокой температуре, выполняют специальную подготовку по ГОСТ 24452-80.

Испытания проводят по схеме:

Образцы с индикаторами помещают под пресс, совмещая ось заготовки с центром плиты оборудования. Величину разрушающей нагрузки назначают, исходя из марочной прочности бетона.
Нагрузку увеличивают постепенно, ступенями по 10% от разрушающей. Выдерживают интервалы 4-5 минут.
Доводят усилие до 40-45% от максимального. Если программа не предусматривает другие требования, приборы снимают. Дальнейшее нагружение проводят с постоянной скоростью.
Производят обработку результатов для каждого образца при нагрузке, равной 30% от разрушающей. Все данные заносят в журнал испытаний.

На основе исследований можно судить о начальном модуле упругости бетона. Эта величина характеризует свойства материала при нагрузке, в пределах которой в образцах возникают обратимые изменения. Показатель обозначается как Eb, его значение для каждого класса бетона внесено в таблицы строительных норм и маркировку изделий.

Так, модуль упругости бетона В15 естественного твердения составляет 23, а подвергнутого тепловой обработке 25 МПа*10-3.

Величина модуля упругости бетона для классов В20, В25, В30, В35 и В40 равна 27, 30, 32,5, 34,5 и 36 МПа*10-3. В пропаренных конструкциях она соответствует 24,5, 27, 29, 31 и 32,5 МПа*10-3.

Ультразвуковой способ

Применяется для исследования конструкций без их локального разрушения. При повышенной влажности такой метод определяет модуль упругости с погрешностью 15-75%, так как скорость распространения ультразвуковых колебаний в водной среде возрастает.

Чтобы избежать ошибок при измерениях, разработан метод определения модуля Юнга с учетом влажности бетона. Он основан на опытных испытаниях серий образцов с различной водонасыщенностью.

Нормативные и расчетные значения сопротивления бетона получают, используя корректирующие коэффициенты с учетом условий работы конструкции. Методика расчета описана в СП 63.13330.2012.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Виды деформации

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Δl = α * (lF) / S

Величину, обратную α, и называют модулем Юнга:

1/α = E

Относительная деформация:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

ε=α σ

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

σ = ε/α = E ε

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Источники и примечания

[www.physel.ru/mainmenu-4/-mainmenu-9/101-s-98—-.html Упругая деформация] (рус.). [www.webcitation.org/68nxdCgZR Архивировано из первоисточника 30 июня 2012].
Dieter Meschede, Christian Gerthsen.
Physik. — Springer, 2004. — P.
[books.google.com/books?id=pfpkxqB-jGoC&pg=PA181&dq=Federkonstante 181]
..
Bruno Assmann.
Technische Mechanik: Kinematik und Kinetik. — Oldenbourg, 2004. — P.
[books.google.com/books?id=NGu2K3eosMoC&pg=PA11&dq=Federkonstante 11]
..
[www.edu.yar.ru/projects/socnav/prep/phis001/dyn/dyn10.html Динамика, Сила упругости] (рус.). [www.webcitation.org/68nxeMf0N Архивировано из первоисточника 30 июня 2012].
[www.edu.delfa.net/CONSP/meh5.htm Механические свойства тел] (рус.). [www.webcitation.org/68nxfaOO5 Архивировано из первоисточника 30 июня 2012].

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Материал	модуль Юнга E, ГПа
Алюминий	70
Бронза	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лёд	3
Медь	110
Свинец	18
Серебро	80
Серый чугун	110
Сталь	200/210
Стекло	70

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

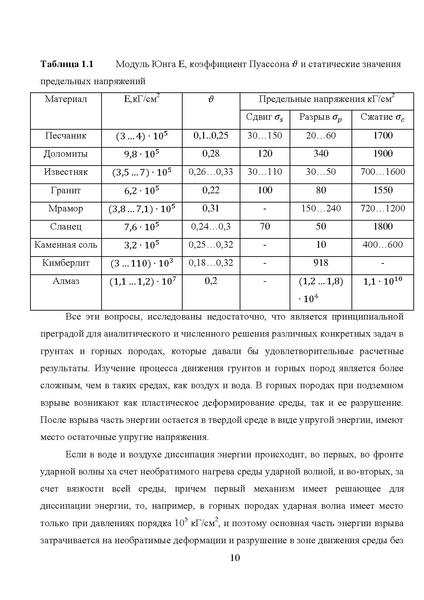
Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

Читать также: Какие бывают диодные ленты

Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Значения σраст в МПа:

Материалы	σраст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Общее понятие

Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).

В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.

Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.

Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.

Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.

Дополнительные характеристики механических свойств

Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:

Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. 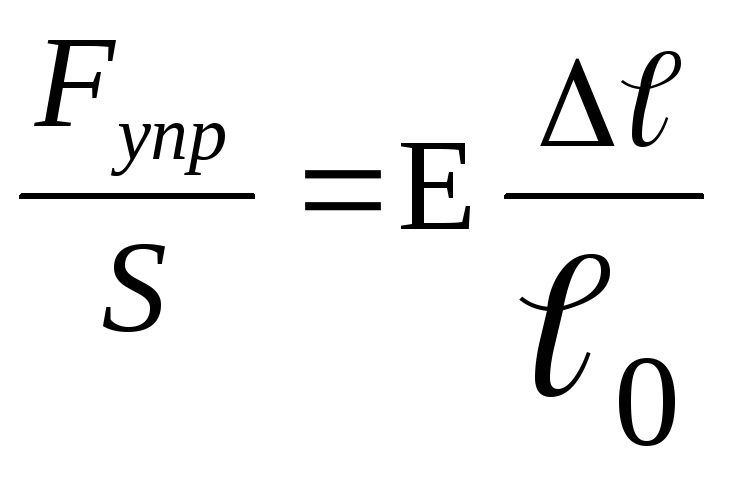Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.

Читать также: Неисправности магнетрона микроволновой печи

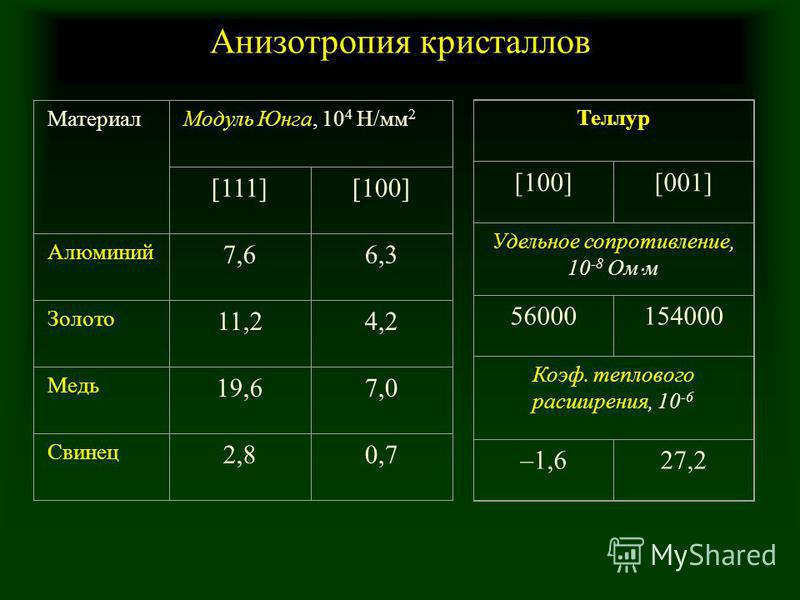
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.

У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)

Упругие свойства тел

Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.

Модуль Юнга или модуль продольной упругости в дин/см².

Модуль сдвига или модуль кручения G в дин/см².

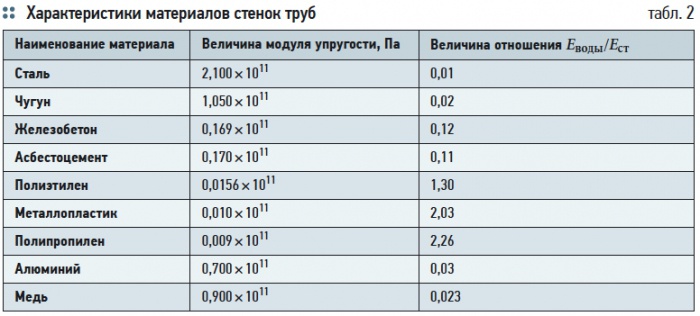
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см².

Объем сжимаемости k=1/K/.

Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.

Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:

G = E / 2(1 + μ) – (α)

μ = (E / 2G) – 1 – (b)

K = E / 3(1 – 2μ) – (c)

Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.

Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона

Курсивом даны значения, вычисленные из соотношений (a), (b), (c).

Материал при 18°С	Модуль Юнга E, 10¹¹дин/см².	Модуль сдвига G, 10¹¹дин/см².	Коэффициент Пуассона µ	Модуль объемной упругости К, 10¹¹дин/см².
Алюминий	7,05	2,62	0,345	7,58
Висмут	3,19	1,20	0,330	3,13
Железо	21,2	8,2	0,29	16,9
Золото	7,8	2,7	0,44	21,7
Кадмий	4,99	1,92	0,300	4,16
Медь	12,98	4,833	0,343	13,76
Никель	20,4	7,9	0,280	16,1
Платина	16,8	6,1	0,377	22,8
Свинец	1,62	0,562	0,441	4,6
Серебро	8,27	3,03	0,367	10,4
Титан	11,6	4,38	0,32	10,7
Цинк	9,0	3,6	0,25	6,0
Сталь (1% С) ¹⁾	21,0	8,10	0,293	16,88
(мягкая)	21,0	8,12	0,291	16,78
Константан ²⁾	16,3	6,11	0,327	15,7
Манганин	12,4	4,65	0,334	12,4
¹⁾ Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. ²⁾ 60% Cu, 40% Ni.

Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.

Вещество	Модуль Юнга E, 10¹¹дин/см².	Модуль сдвига G, 10¹¹дин/см².	Коэффициент Пуассона µ	Модуль объемной упругости К, 10¹¹дин/см².
Бронза (66% Cu)	-9,7-10,2	3,3-3,7	0,34-0,40	11,2
Медь	10,5-13,0	3,5-4,9	0,34	13,8
Нейзильбер¹⁾	11,6	4,3-4,7	0,37	–
Стекло	5,1-7,1	3,1	0,17-0,32	3,75
Стекло иенское крон	6,5-7,8	2,6-3,2	0,20-0,27	4,0-5,9
Стекло иенское флинт	5,0-6,0	2,0-2,5	0,22-0,26	3,6-3,8
Железо сварочное	19-20	7,7-8,3	0,29	16,9
Чугун	10-13	3,5-5,3	0,23-0,31	9,6
Магний	4,25	1,63	0,30	–
Бронза фосфористая²⁾	12,0	4,36	0,38	–
Платиноид³⁾	13,6	3,6	0,37	–
Кварцевые нити (плав. )	7,3	3,1	0,17	3,7
Резина мягкая вулканизированная	0,00015-0,0005	0,00005-0,00015	0,46-0,49	–
Сталь	20-21	7,9-8,9	0,25-0,33	16,8
Цинк	8,7	3,8	0,21	–
¹⁾ 60% Cu, 15% Ni, 25% Zn ²⁾ 92,5% Cu, 7% Sn, 0,5% P ³⁾ Нейзильбер с небольшим количеством вольфрама.

Вещество	Модуль Юнга E, 10¹¹дин/см².	Вещество	Модуль Юнга E, 10¹¹дин/см².
Цинк (чистый)	9,0	Дуб	1,3
Иридий	52,0	Сосна	0,9
Родий	29,0	Красное дерево	0,88
Тантал	18,6	Цирконий	7,4
Инвар	17,6	Титан	10,5-11,0
Сплав 90% Pt, 10% Ir	21,0	Кальций	2,0-2,5
Дюралюминий	7,1	Свинец	0,7-1,6
Шелковые нити¹	0,65	Тиковое дерево	1,66
Паутина²	0,3	Серебро	7,1-8,3
Кетгут	0,32	Пластмассы:
Лед (-2⁰С)	0,28	Термопластичные	0,14-0,28
Кварц	7,3	Термореактивные	0,35-1,1
Мрамор	3,0-4,0	Вольфрам	41,1
¹⁾ Быстро уменьшается с увеличением нагрузки ²⁾ Обнаруживает заметную упругую усталость

Температурный коэффициент (при 15⁰С) E_t=E₁₁(1-ɑ (t-15)), G_t=G₁₁(1-ɑ (t-15))			Сжимаемость k, бар^-1(при 7-11⁰С)
	ɑ^, для Е	ɑ^,для G
Алюминий	4,8*10^-4	5,2*10^-4	Алюминий	1,36*10^-6
Латунь	3,7*10^-4	4,6*10^-4	Медь	0,73*10^-6
Золото	4,8*10^-4	3,3*10^-4	Золото	0,61*10^-6
Железо	2,3*10^-4	2,8*10^-4	Свинец	2,1*10^-6
Сталь	2,4*10^-4	2,6*10^-4	Магний	2,8*10^-6
Платина	0,98*10^-4	1,0*10^-4	Платина	0,36*10^-6
Серебро	7,5*10^-4	4,5*10^-4	Стекло флинт	3,0*10^-6
Олово	–	5,9*10^-4	Стекло немецкое	2,57*10^-6
Медь	3,0*10^-4	3,1*10^-4	Сталь	0,59*10^-6
Нейзильбер	–	6,5*10^-4
Фосфористая бронза	–	3,0*10^-4
Кварцевые нити	-1,5*10^-4	-1,1*10^-4

Модуль нормальной упругости (модуль Юнга)

Сделаем некоторые замечания по поводу терминологии.

Мы приняли термин моду,ль продольной упругости как рекомендованный Комитетом по технической терминологии Академии наук. Наряду с ним применяют термины модуль нормальной упругости , модуль Юнга , модуль упругости первого рода . Полагаем, что предпочтителен термин, официально рекомендованный для краткости речи можно говорить просто модуль упругости . [c.67]
Е—модуль нормальной упругости (модуль Юнга). [c.5]

Упругие свойства тел характеризуются модулем нормальной упругости (модулем Юнга) и коэффициентом поперечного сжатия V (коэффициентом Пуассона). Сопротивляемость среды поперечной (сдвиговой) деформации связана с модулем сдвига, величина которого для больщинства металлов составляет 0,38…0,4 величины модуля Юнга. Эти физические константы связаны между собой соотношением [c.63]

Параметры упругости Е — модуль нормальной упругости (модуль Юнга) в кГ/мм G — модуль касательной упругости (модуль сдвига) в кГ мм р, — постоянная Пуассона. [c.194]

Модули упругости металлов находятся в указанных ниже пределах для стали разных марок модуль нормальной упругости (модуль Юнга) — = (2,0-4-2,2) МПа модуль сдвига (модуль касательной упругости) G = (8,0 -ь 8,5) 10 МПа. Для алюминиевых сплавов 0 = (7,0 -f- 7,5) 10 МПа G = 2,7-10 МПа. Для титановых сплавов 0 = (1,10-i-1,20) 10 МПа G — = (4,0 4-4,5)-104 МПа. Для меди ю= (1.13 1,32) 10 МПа 0 = = 4,24-10 МПа. Для никеля (чистого) =2,20-10 МПа. [c.226]

Нормальное и касательное напряжения о, ат, модуль продольной упругости (модуль Юнга) =о/Ео, модуль сдвига О=0т/д, модуль объемного сжатия — все эти величины имеют ту же размерность, что и давление, и выражаются в паскалях (вп — относительное удлинение, 0 — угол сдвига). [c.31]

Модуль Е, определяемый при растяжении, называется модулем нормальной упругости, или модулем Юнга, модуль G — модуль сдвига (касательной упругости) и К — модуль объемной упругости (Р — гидростатическое давление, и — уменьщение объема). Модули упругости определяют жесткость материала, т. е. интенсивность увеличения напряжения по мере упругой деформации. [c.28]

Известно, что отношение напряжения к относительному удлинению образца в упомянутом опыте называется модулем нормальной упругости (или модулем Юнга) и обозначается через Б отношение относительного удлинения в направлении действия нагрузки к относительному укорочению поперечных размеров обозначается через т и называется числом Пуассона часто применяется обратная величина а, [c.44]

При упругой деформации растяжение-сжатие модуль нормальной упругости или коэффициент пропорциональности характеризуется отношением напряжения к относительному удлинению и носит название модуля Юнга [c.14]

Измерение показателей упругих и релаксационных свойств Материалов динамическим методом чаще всего производится на цилиндрических образцах диаметром d = 8. 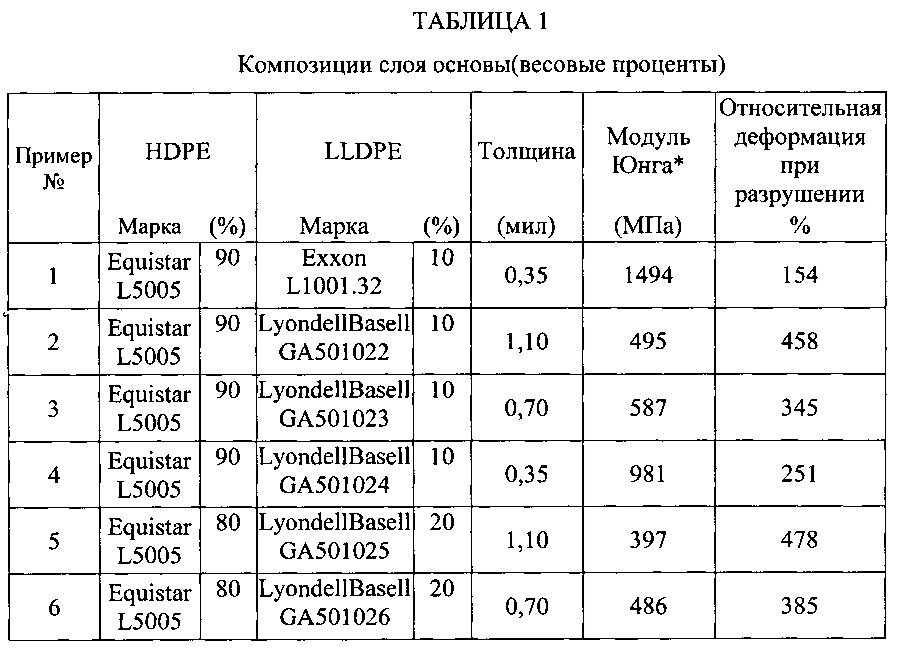.. 10 мм и длиной I = 200 мм. Измерив резонансную частоту (Гц) изгибных / и крутильных колебаний, а также массу т (кг) и размеры образца / и с/ (м), рассчитывают модуль нормальной упругости Юнга Е и модуль сдвига G (МПа) по формулам [c.463]

Через и V здесь обозначены упругие постоянные материала Е — модуль нормальной упругости или модуль Юнга v — коэффициент Пуассона. В каждом конкретном случае для того или иного нового материала эти параметры определяются экспериментально. [c.64]

Величина а = F / S называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций е соответствующим напряжениям выражает закон Гука. Коэффициент пропорциональности % называется коэффициентом удлинения и для каждого материала определяется опытным путем. Так как численные значения е гораздо меньше а, то % — весьма малая величина. Поэтому обычно вводят модуль упругости (модуль Юнга) Е = X , и закон Гука окончательно записывают в виде [c. 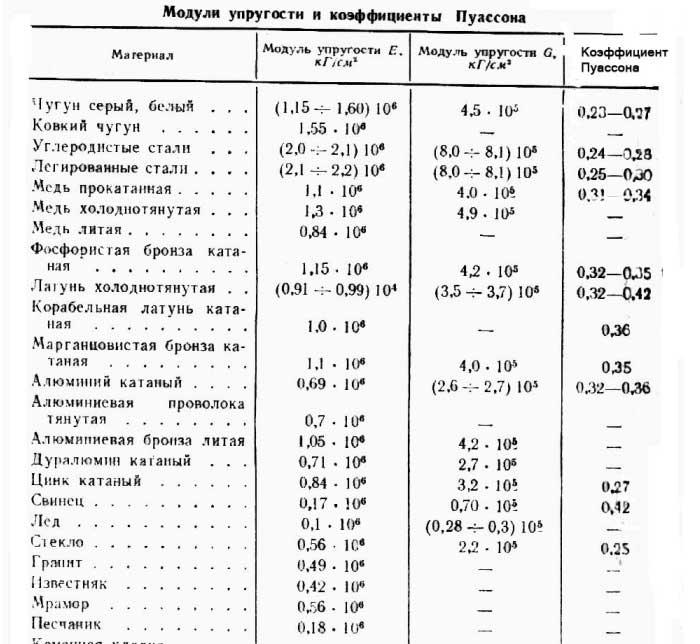11]

Как уже ранее было отмечено, материалы, упругие свойства которых не зависят от направления, называются изотропными. В этом случае будет минимальное количество упругих постоянных, характеризующих упругие свойства такого тела. Таких упругих постоянных будет три— нормальный модуль упругости Е (модуль Юнга), модуль сдвига О и коэффициент Пуассона р. Между этими тремя упругими постоянными имеется следующая зависимость [c.40]

Модулем упругости первого рода (модулем Юнга), или модулем нормальной упругости, называют величину, численно равную отношению напряжения к соответствующему относительному упругому удлинению [c.11]

Обозначения Ляме применяются преимущественно в теоретических работах, в технической литературе их заменяют другими модулями упругости, чаще всего модулем Юнга Е (модуль нормальной упругости) и коэффициентом Пуассона v. Чтобы ввести эти величины, выделим в формуле (3.1.6) для слагаемое Ох из суммы G. [c. 112]

Искажение или деформация некоторого типа, которую мы можем назвать е, создается в теле смеш,ениями. При этом возбуждается напряженное состояние или упругая сила, которую мы можем назвать s. Соотношение между напряжением и деформацией может быть записано так =ее, где е есть коэффициент упругости для конкретного вида деформирования. Этот коэффициент есть модуль Юнга Е, если S и е являются нормальными напряжениями, и модуль сдвига, если они являются касательными напряжениями и деформациями . В твердом теле, свободном от релаксации, S будет оставаться равным е е, и [c.152]

Последние три соотношения в (2.4.1) показывают, что нормальные напряжения не вызывают сдвиговых деформаций подобно тому, как первые три из этих соотношений показывают, что касательные деформации не вызывают нормальных деформаций. Более того, все касательные напряжения (и сдвиговые деформации) независимы и каждая компонента сдвиговой деформации связана с соответствующей компонентой касательного напряжения модулем сдвига G. Модуль сдвига не является независимой упругой постоянной он связан с модулем Юнга и коэффициентом Пуассона следующим образом [53, стр. 29] [c.24]

Ортотропный материал имеет девять независимых упругих постоянных. Три из этих постоянных связывают нормальные деформации вхх, Syy и с нормальными напряжениями о х, (Ууу и Огг- постоянные называют модулями Юнга. Три другие независимые упругие постоянные называются коэффициентами Пуассона. Они связывают нормальные деформации в одном направлении, скажем вхх, с нормальными деформациями в другом направлении, например Три упругие постоянные для ортотропного материала связывают деформации сдвига вху, вхг и ву с вызывающими их касательными напряжениями Оху, a z и Оу . Эти постоянные называют модулями сдвига. [c.188]

МПа и ударную вязкость а >250 Дж/см . Упругие характеристики иодидного титана таковы модуль объемной упругости /С=123-10 МПа модуль нормальной упругости, или модуль Юнга, = 10,6-10 МПа модуль сдвига 0=40-10 МПа коэффициент Пуассона [х=0,34 [4]. [c.7]

По мнению зарубежных специалистов материал прочных корпусов подводных лодок должен обладать высокой уделыной прочностью (отношение предела текучести к удельному весу) высоким модулем нормальной упругости (модулем Юнга) высокой пластичностью основного материала и соединительных элементов (например, сварных швов) высокой усталостной и динамической прочностью коррозионной стойкостью и устойчивостью физических свойств в диапазоне температур, встречающихся при эксплуатации подводной лодки (от —35 до +50°С) технологичностью и возможностью соединения отдельных элементов конструкции по возможности немагнитностью приемлемой стоимостью. [c.143]

Модуль продольной упругости (модуль Юнга) Е—величина, равная отношению нормального напряжения о к относител П1эму удлинению (или укорочению) е==А/// [c.67]

Все сплавы направленной кристаллизации обладают преимущественной кристаллографической ориентировкой по крайней мере в одном направлении. Модуль нормальной упругости (Юнга) Е анизотропен его значение будет различным в зависимости от того, по какой из ориентировок нагружен суперсплав направленной кристаллизации. Для монокристалли-ческих суперсплавов модуль нормальной упругости в пределах стандартного стереографического треугольника можно выразить как [c.263]

Для обоснования того, что эта интерпретация является законной в некотором вполне определенном смысле, а также для получения оценок толщин слоев концентрации напряжений Эверстайн и Пипкин [12] проанализировали некоторые точные решения теории упругих трансверсально изотропных материалов. Предполагалось, что модуль Юнга Е вдоль волокон много больше модуля сдвига G. Коэффициент Пуассона v, определяющий уменьшение поперечных размеров в направлении, перпендикулярном волокнам, при приложении растягивающей нагрузки, также перпендикулярной волокнам, выбирался близким к единице. Оказалось, что теория упругости действительно предсказывает существование тонких слоев с высокой концентрацией напряжений там, где они должны быть согласно идеализированной теории. Было найдено, что толщина слоев концентрации напряжений вдоль волокон имеет порядок (G/ ) / L, где L — характерная длина слоя. Было установлено также, что толщина слоев концентрации напряжений вдоль нормальных линий, существование которых обусловлено малой сжимаемостью материала, имеет порядок (1—v) i L. В обоих случаях было показано, что максимум растягивающих напряжений с удовлетворительной точностью определяется делением результирующей силы, найденной по идеализированной теории, на, приближенное значение толщины. [c.298]

МОДУЛЬ [продольной упругости определяется отношением нормального напряжения в поперечном сечении цилиндрического образца к относительному удлинению при его растяжении сдвига измеряется отношением касательного напряжения в поперечном сечении трубчатого тонкостенного образца к деформации сдвига при его кручении Юнга равен нормальному напряжению, при котором линейный размер тела изменяется в два раза] МОДУЛЯЦИЯ [есть изменение по заданному во времени величин, характеризующих какой-либо регулярный физический процесс колебаний определенному закону какого-либо из параметров периодических колебаний, осуществляемое за время, значительно большее, чем период колебаний амплитудная выражается в изменении амплитуды фазовая указывает на изменение их фазы частотная состоит в изменении их частоты) пространственная заключается в изменении в пространстве характеристик постоянного во времени колебательного процесса] МОЛЕКУЛА [есть наименьшая устойчивая частица данного вещества, обладающая его химическими свойствами атомная (гомеополярная) возникает в результате взаимного притяжения нейтральных атомов ионная (гетерополярная) образуется в результате превращения взаимодействующих атомов в противоположно электрически заряженные и взаимно притягивающиеся ионы эксимерная является корот-коживущим соединением атомов инертных газов друг с другом, с галогенами или кислородом, существующим только в возбужденном состоянии и входящим в состав активной среды лазеров некоторых типов МОЛНИЯ электрический разряд между облаками или между облаками и землей линейная является гигантским электрическим искровым разрядом в атмосфере с диаметром канала от 10 до 25 см и длиной до нескольких километров при максимальной силе тока до ЮОкА) [c. 250]

Определение остаточных напряжений. Ревтгеногра-фич. определение механич. напряжений в простейшем случае сводится к измерению смещения дебаевской линии Ад. При нормальных напряжениях о смещение Дв связано с о выражением а = i tgd-Дв/р, где Е — модуль Юнга, р — коэф. Пуассона (см. Модули упругости). Микронапряжения, как и измельчение блоков мозаики, приводят к уширению дебаевских линий. [c.377]

Начальной стадией деформации металла является упругая деформация (участок АВ рис. 2.8). С точки зрения кристаллического строения, упругая деформация проявляется в некотором увеличении расстояния между атомами в кристаллической решетке. После снятия нафузки атомы возвращаются в прежнее положение и деформация исчезает. Другими словами, упругая деформация не вызывает никаких последствий в металле. Чем меньшую деформацию вызывают напряжения, тем более жесткий и более упругий металл. Характеристикой упругости металла являются дна вида модуля упругости модуль нормальной упругости (модуль Юкга) – характеризует силы, стремящиеся оторвать атомы друг от друга, и модуль касательной упругости (модуль Гука) – характеризует силы, стремящиеся сдвинуть атомы относительно друг друга. Значения модулей упругости являются константами материала и зависят от сил межатомного взаимодействия. Все конструкции и изделия из металлов эксплуатируются, как правило, в упругой области. Таким образом, упругость – это свойство твердого тела восстанавливать свою первоначальнуто фор.му и объем после прекращения действия внешней нагрузки. Модуль упругости практически не зависит от структуры металла и определяется, в основном, типом кристаллической решетки. Так, например, модуль Юнга для магния (кристаллическая решетка ГП% ) равен 45-10 Па, для меди (ГКЦ) – 105-10 Па, для железа (ОЦК) – 21010 Па. [c.28]

Соотношения (5-12) и (5-13) являются обобщенной формой закона Гука для упругого твердого тела. Они содержат два модуля упругости модуль упругости при сдвиге и модуль унр угости при растяжении (модуль Юнга). Так как эти величины связаны между собой, то можно преобразовать формулы (5-12) так, чтобы выразить соотношение между нормальными напряжениями и деформациями через модуль сдвига. [c.107]

В состоянии простого растяжения, при котором обычно определяют модуль Юнга путем вытягивания упругой полосы, напряжение поверхностной силы нормально к одной из плоскостей и равно по величине Т. В то же время напряжения на площадках, перпендикулярных к отмеченной плоскости, будут равны нулю. Декартовы компоненты напряжения по отношению к ортонормаль-иому базису, где вектор е служит нормалью к площад- [c.80]

Коэффициент пропорциональности Е называют модулем продольной упругости (другие названия модуль нормальной упругости модуль упругости модуль упругости 1-го рода модуль Юнга). Очевидно, Е имеет ty же размерность, что и напряжение, т. е. измеряется в н м , или Мн1м , или н мм , или кПсм , или кПмм и т. п., [c.38]

Коэффициент пропорциональности Е, связывающ.и нормальное напряжение и продольную деформацию, на зывается модулем упругости при растяжении—сжатий материала. Этот коэффициент имеет и другие названия модуль упругости 1-го рода, модуль Юнга. Модуль упругости Е является одной из важнейших физических постоянных, характеризующих способность материала сопротивляться упругому деформированию. Чем больше эта величина, тем менее растягивается или сжимается брус при приложении одной и той же силы Р. [c.69]

Модуль упругости алюминия

Модуль упругости = Модуль Юнга

На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза. Наклон этой части кривой определяет характеристику материала – модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.

Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа.
См. Модуль упругости различных алюминиевых сплавов

Рисунок

Ясно, что если стальную балку заменить на идентичную по форме балку из алюминиевого сплава, то вес ее будет в три раза меньше, но и ее упругий прогиб под той же нагрузкой будет приблизительно в три раза больше. 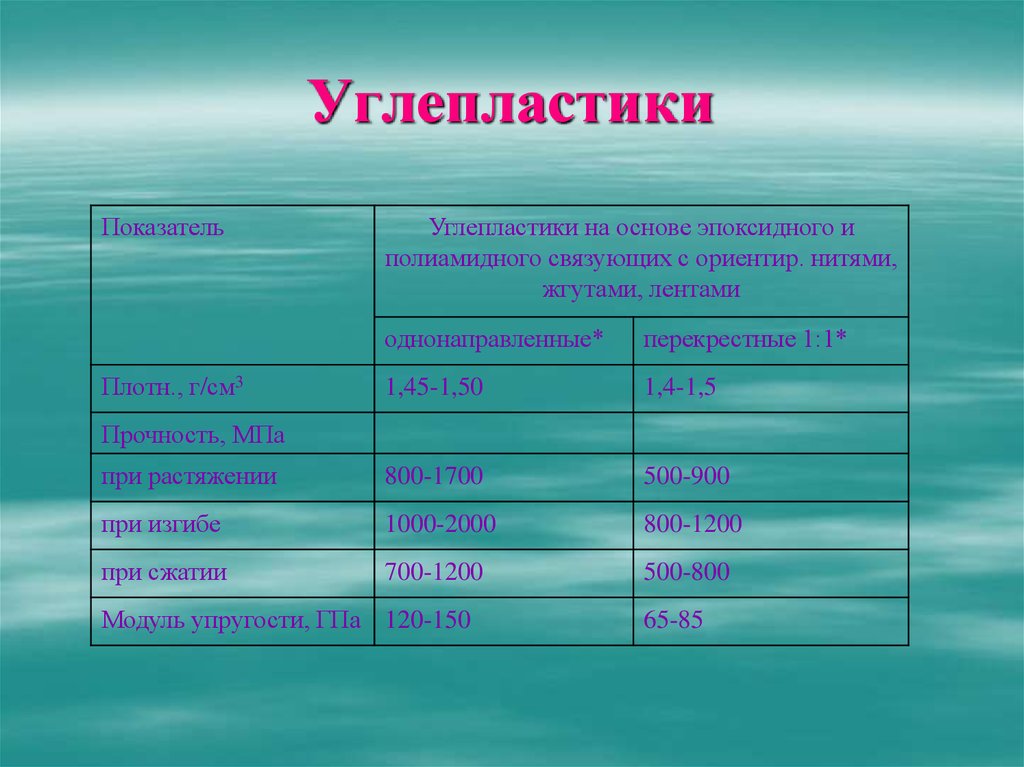Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.

В таблице ниже представлены величины модулей упругости алюминия и различных металлов.

Жесткость алюминиевых профилей

Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки. Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений.

Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение. В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.

Модуль упругости (модуль Юнга) | Мир сварки

Модуль упругости

Модуль упругости (модуль Юнга) E – показывает сопротивление материала растяжению / сжатию при упругой деформации, или свойства объекта деформироваться вдоль оси при воздействии силы вдоль оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.

1 кгс / мм ² = 10 ^-6 кгс / м ² = 9,8 · 10 ⁶ Н / м ² = 9,8 · 10 ⁷ дин / см ² = 9,81 · 10 ⁶ Па = 9,81 МПа

Модуль упругости (модуль Юнга)
Материал	E
Материал	кгс / мм ²	10 ⁷ Н / м ²	МПа
Металлы
Алюминий	6300-7500	6180-7360	61800-73600
Алюминий отожженный	6980	6850	68500
Бериллий	30050	29500	295000
Бронза	10600	10400	104000
Бронза алюминиевая, литье	10500	10300	103000
Бронза фосфористая катаная	11520	11300	113000
Ванадий	13500	13250	132500
Ванадий отожженный	15080	14800	148000
Висмут	3200	3140	31400
Висмут литой	3250	3190	31900
Вольфрам	38100	37400	374000
Вольфрам отожженный	38800-40800	34200-40000	342000-400000
Гафний	14150	13900	139000
Дюралюминий	7000	6870	68700
Дюралюминий катаный	7140	7000	70000
Железо кованое	20000-22000	19620-21580	196200-215800
Железо литое	10200-13250	10000-13000	100000-130000
Золото	7000-8500	6870-8340	68700-83400
Золото отожженное	8200	8060	80600
Инвар	14000	13730	137300
Индий	5300	5200	52000
Иридий	5300	5200	52000
Кадмий	5300	5200	52000
Кадмий литой	5090	4990	49900
Кобальт отожженный	19980-21000	19600-20600	196000-206000
Константан	16600	16300	163000
Латунь	8000–10000	7850-9810	78500-98100
Латунь корабельная катаная	10000	9800	98000
Латунь холоднотянутая	9100-9890	8900-9700	89000-97000
Магний	4360	4280	42800
Манганин	12600	12360	123600
Медь	13120	12870	128700
Медь деформированная	11420	11200	112000
Медь литая	8360	8200	82000
Медь прокатанная	11000	10800	108000
Медь холоднотянутая	12950	12700	127000
Молибден	29150	28600	286000
Нейзильбер	11000	10790	107900
Никель	20000-22000	19620-21580	196200-215800
Никель отожженный	20600	20200	202000
Ниобий	9080	8910	89100
Олово	4000-5400	3920-5300	39200-53000
Олово литое	4140-5980	4060-5860	40600-58600
Осмий	56570	55500	555000
Палладий	10000-14000	9810-13730	98100-137300
Палладий литой	11520	11300	113000
Платина	17230	16900	169000
Платина отожженная	14980	14700	147000
Родий отожженный	28030	27500	275000
Рутений отожженный	43000	42200	422000
Свинец	1600	1570	15700
Свинец литой	1650	1620	16200
Серебро	8430	8270	82700
Серебро отожженное	8200	8050	80500
Сталь инструментальная	21000-22000	20600-21580	206000-215800
Сталь легированная	21000	20600	206000
Сталь специальная	22000-24000	21580-23540	215800-235400
Сталь углеродистая	19880-20900	19500-20500	195000-205000
Стальное литье	17330	17000	170000
Тантал	19000	18640	186400
Тантал отожженный	18960	18600	186000
Титан	11000	10800	108000
Хром	25000	24500	245000
Цинк	8000–10000	7850-9810	78500-98100
Цинк катаный	8360	8200	82000
Цинк литой	12950	12700	127000
Цирконий	8950	8780	87800
Чугун	7500-8500	7360-8340	73600-83400
Чугун белый, серый	11520-11830	11300-11600	113000-116000
Чугун ковкий	15290	15000	150000
Пластмассы
Плексиглас	535	525	5250
Целлулоид	173-194	170-190	1700-1900
Стекло органическое	300	295	2950
Резины
Каучук	0,80	0,79	7,9
Резина мягкая вулканизированная	0,15-0,51	0,15-0,50	1,5-5,0
Дерево
Бамбук	2000	1960	19600
Береза	1500	1470	14700
Бук	1600	1630	16300
Дуб	1600	1630	16300
Ель	900	880	8800
Железное дерево	2400	2350	32500
Сосна	900	880	8800
Минералы
Кварц	6800	6670	66700
Различные материалы
Бетон	1530-4100	1500-4000	15000-40000
Гранит	3570-5100	3500-5000	35000-50000
Известняк плотный	3570	3500	35000
Кварцевая нить (плавленая)	7440	7300	73000
Кетгут	300	295	2950
Лед (при -2 ° С)	300	295	2950
Мрамор	3570-5100	3500-5000	35000-50000
Стекло	5000-7950	4900-7800	49000-78000
Стекло кроны	7200	7060	70600
Стекло флинт	5500	5400	70600

Литература

Краткий физико-технический справочник. Т.1 / Под общ. ред. К.П. Яковлева. М .: ФИЗМАТГИЗ. 1960. – 446 с.
Справочник по сварке цветных металлов / С.М. Гуревич. Киев .: Наукова думка. 1981. 680 с.
Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.

Модуль упругости для стали, а также другие материалы

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать, как с ним обращаться, какое механическое воздействие будет для ему приемлемым, и так далее.Одной из важных характеристик, на которую очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эти отношения по отношению к одному из самых популярных в строительстве и ремонтных работах материалу – стали. Также будут рассмотрены эти показатели у других материалов, ради пример.

Модуль упругости – что это?

Модулем упругости какого-либо материала называют совокупность физических величин , которые характеризуют способность-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы.Выражается она буквой Е. Так она будет подключена во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ утверждения упругости. Различные подходы к изучению этой возможности привести к тому, что существует сразу несколько разных подходов. Ниже представлены три основных метода расчёта показателей этих характеристик для разных материалов:

Модуль Юнга (Е) сопротивления материала любому растяжению или сжатию при упругой деформации.Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно его называют просто модулем упругости.
Модуль сдвига (G) , называемый также модулем жёсткости . Этот способ выявляет способность материала сопротивления любому изменению формы, но в условиях им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, который определяет в виде изменения угла прямого между соответствующими плоскостями, подвергающимися воздействию касательных напряжений.Модуль сдвига, кстати, является одним из составляющих такого явления, как вязкость.
Модуль объёмной упругости (К) , который также именуется модулем объёмного сжатия . Данный вариант обозначает способность объекта из какого-либо эксперта свой объём в случае воздействия всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношения величины объёмного напряжения к величине относительного объёмного сжатия.
Существуют также другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными методами упругости являются параметров Ламе или же коэффициент Пуассона .

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве дополнительной информации, таблицу, содержащую данные об величине по отношению к другим материалам. Данные измеряются в МПа .

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателю разнятся, если учитывать или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга.2.

И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведенные для стали и стальных изделий. Каждая величина высчитано согласно всем физическим правилам и с учётом всех видов отношений, которые используются для выведения этих характеристик.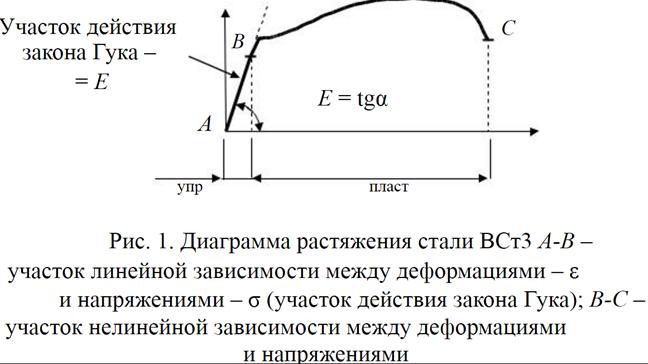

Ниже приведена вся общая информация об этой характеристике стали. Значения будут даваться как п о модулю Юнга , так и по модулю сдвига, как в единицах измерения (МПа), так и в других (кг / см2, ньютон * м2).4 МПа

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей , которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Согласно расчетам, следует выбрать правильное значение упругости.2 .

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с использованием значений данных характеристик для стали, стальных изделий, а также для нескольких других материалов.

следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного.Величина модуля упругости стали практически зависит от структуры. а также от углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Оцените статью: Поделитесь с друзьями!

Модуль упругости разных материалов, включая сталь

Перед тем, как использовать какой-либо материал в строительных работах, использовать его физическими характеристиками для того, чтобы использовать его, какое механическое воздействие будет для него приемлемым, и так далее.Одной из важных характеристик, на которую очень часто обращают внимание, является модуль упругости.

Блок: 1/3 | Кол-во символов: 563
Источник: https://stanok. guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html

Связь с другими модулями упругости

В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями

где – коэффициент Пуассона.

Блок: 2/8 | Кол-во символов: 176
Источник: https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE% D0% BD% D0% B3% D0% B0

Модуль упругости – что это?

Модулем упругости какого-либо материала представляют собой совокупность физических величин , которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в приложении к нему силы. Выражается она буквой Е. Так она будет подключена во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ значения упругости. Различные подходы к изучению этой возможности привести к тому, что существует сразу несколько разных подходов. Ниже приведены три основных метода расчёта этих характеристик для разных материалов:

Модуль Юнга (Е) сопротивления материала растяжению или силе упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия.Обычно его называют просто модулем упругости.
Модуль сдвига (G) , называемый также модулем жёсткости . Этот способ выявляет способность материала сопротивления любому изменению формы, но в условиях им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, который определяет в виде изменения угла прямого между соответствующими плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одним из составляющих такого явления, как вязкость.
Модуль объёмной упругости (К) , который также именуется модулем объёмного сжатия . Данный вариант обозначает способность объекта из какого-либо эксперта свой объём в случае воздействия всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношения величины объёмного напряжения к величине относительного объёмного сжатия.
Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями.Другими ещё очень известными и популярными методами упругости являются параметров Ламе или же коэффициент Пуассона .

Блок: 2/3 | Кол-во символов: 1976
Источник: https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html

Температурная зависимость модуля Юнга

Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости определяется как вторая производная от внутренней энергии по форме деформации.Поэтому при температурех (- температуре Дебая) температурная зависимость модуля упругости определяется основанием

где – адиабатический модуль упругости идеального кристалла при; – дефект модуля, обусловленный тепловыми фононами; – дефект модуля, обусловленный тепловым движением электронов проводимости

Блок: 3/8 | Кол-во символов: 578
Источник: https://ru. wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE% D0% BD% D0% B3% D0% B0

Механические свойства

Только при работе на растяжение или сжатие Модуль (Юнга) упругости помогает угадать поведение того или иного материала .А вот при изгибе, срезе, смятии и прочих нагрузках потребуется дополнительные параметры:

Жёсткость называют произведением поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения килограммы силы.
Продольное относительное удлинение – это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу.В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
Коэффициент Пуассона.Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
Модуль сдвига упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером таких нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки.Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.

Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства . Подобные материалы называются анизотропными. Примерами подобного являются ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.

У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам защиты металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.

Блок: 3/4 | Кол-во символов: 2487
Источник: https://tokar.guru/metally/stal/modul-deformacii-stali-i-ee-uprugosti.html

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой информации, рассмотрим для начала, в примере и дополнительной информации, таблице, содержащей данные об величине по другим к другим материалам. Данные измеряются в МПа .

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателю разнятся, если учитывать тот или иной вариант этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга.2.

И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведенные для видов стали и стальных изделий. Каждая величина высчитано согласно всем физическим правилам и с учётом всех видов отношений, которые используются для выведения этих характеристик.

Ниже будет приведена вся информация об этой характеристике стали. Значения будут даваться как п о модулю Юнга , так и по модулю сдвига, как в единицах измерения (МПа), так и в других (кг / см2, ньютон * м2).

Сталь и несколько разных её марок

Значения упругости стали разнятся, так как существуют сразу несколько модулей , которые исчисляются и высчитываются по-разному.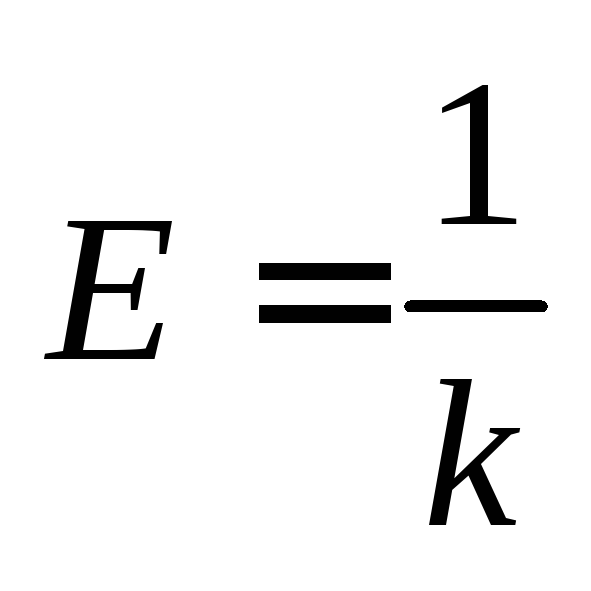 Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Согласно расчетам, следует выбрать правильное значение упругости.2 .

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомьтесь с заданными значениями характеристик для стали, стальных изделий, а также для нескольких других материалов.

Блок: 3/3 | Кол-во символов: 3589
Источник: https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal. html

Модуль упругости для разных марок стали

Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности.В таблице 2 показаны характеристики для наиболее распространенных сталей.

Таблица 2: Упругость сталей

Наименование стали	Значение модуля упругости, 10¹² · Па
Сталь низкоуглеродистая	165… 180
Сталь 3	179… 189
Сталь 30	194… 205
Сталь 45	211… 223
Сталь 40Х	240… 260
65Г	235… 275
Х12МФ	310… 320
9ХС, ХВГ	275… 302
4Х5МФС	305… 315
3Х3М3Ф	285… 310
Р6М5	305… 320
Р9	320… 330
Р18	325… 340
Р12МФ5	297… 310
У7, У8	302… 315
У9, У10	320… 330
У11	325… 340
У12, У13	310… 315

Видео: закон Гука, модуль упругости.

Блок: 4/5 | Кол-во символов: 686
Источник: https://metmastanki.ru/modul-uprugosti-stali-i-metallov

Прочность

Кроме нормального нагружения, другие другие силовые воздействия на материалы.

Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.

Модуль объемной упругости К упругие свойства материала изменить объем.При любом деформации происходит изменение формы предмета.

Коэффициент Пуассона μ определяет изменение отношения величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.

Для разных значений стали указанные модули в таблице 3.

Таблица 3: Модули прочности для сталей

Наименование стали	Модуль упругости Юнга, 10¹² · Па	Модуль сдвига G, 10² · Па	Модуль объемной упругости, 10¹² · Па	Коэффициент Пуассона, 10¹² · Па
Сталь низкоуглеродистая	165… 180	87… 91	45… 49	154… 168
Сталь 3	179… 189	93… 102	49… 52	164… 172
Сталь 30	194… 205	105… 108	72… 77	182… 184
Сталь 45	211… 223	115… 130	76… 81	192… 197
Сталь 40Х	240… 260	118… 125	84… 87	210… 218
65Г	235… 275	112… 124	81… 85	208… 214
Х12МФ	310… 320	143… 150	94… 98	285… 290
9ХС, ХВГ	275… 302	135… 145	87… 92	264… 270
4Х5МФС	305… 315	147… 160	96… 100	291… 295
3Х3М3Ф	285… 310	135… 150	92… 97	268… 273
Р6М5	305… 320	147… 151	98… 102	294… 300
Р9	320… 330	155… 162	104… 110	301… 312
Р18	325… 340	140… 149	105… 108	308… 318
Р12МФ5	297… 310	147… 152	98… 102	276… 280
У7, У8	302… 315	154… 160	100… 106	286… 294
У9, У10	320… 330	160… 165	104… 112	305… 311
У11	325… 340	162… 170	98… 104	306… 314
У12, У13	310… 315	155… 160	99… 106	298… 304

Для других материалов прочностных характеристик указать в специальной литературе. Однако в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводятся испытания по определению предельных значений.

Блок: 5/5 | Кол-во символов: 1940
Источник: https://metmastanki.ru/modul-uprugosti-stali-i-metallov

Литература

Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл.ред.). – 3-е изд. – М .: Сов. энциклопедия, 1974. – Т. XVI. – С. 406. – 616 с.
Г. Мавко, Т. Мукерджи, Я. Дворкин. Справочник по физике горных пород . Cambridge University Press 2003 (мягкая обложка). ISBN 0-521-54344-4

Эта страница в последний раз была отредактирована 21 февраля 2019 в 15:38.

Блок: 4/4 | Кол-во символов: 427
Источник: https://wiki2.org/ru/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%83%D0% BF% D1% 80% D1% 83% D0% B3% D0% BE% D1% 81% D1% 82% D0% B8

Кол-во блоков: 15 | Общее кол-во символов: 15444
Количество используемых доноров: 5
Информация по каждому донору:

https: // ru. wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0: занято 2 блока из 8, кол-во символов 754 (5%)
https://wiki2.org/ru/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%83%D0%BF%D1%80%D1% 83% D0% B3% D0% BE% D1% 81% D1% 82% D0% B8: 1 блок из 4, кол-во символов 427 (3%)
https://metmastanki.ru/modul-uprugosti-stali-i-metallov: использовано 3 блока из 5, кол-во символов 4379 (28%)
https://tokar.guru/metally/stal/modul-deformacii-stali-i-ee-uprugosti.html: использовано 2 блока из 4, кол-во символов 3756 (24%)
https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html: использовано 3 блока из 3, кол-во символов 6128 (40%)

Таблица Модуль Юнга. Модуль упругости. Определение Модуля Юнга.

ЗАДАЧНИК ОНЛ @ ЙН
БИБЛИОТЕКА 1 БИБЛИОТЕКА 2

Примечание. Значение модуля упругости зависит от структуры, химического состава и метода обработки материила. Поэтому значения E могут отличаться от средних значений, приведенных в таблице.

Таблица модуля Юнга. Модуль упругости. Определение модуля Юнга. Коэффицент запаса прочности.

Таблица модуля Юнга

Материал	E		Материал	E
Материал	ГПа	кгс / мм ²	Материал	ГПа	кгс / мм ²
Алюминий	70	7000	Стали легированные	210-220	21000-22000
Бетон	3000		Стали углеродистые	200-210	20000-2100
Древесина (вдоль волокон)	10–12	1000-1200	Стекло	56	5600
Древесина (поперечное волокно)	0,5-1,0	50–100	Стекло органическое	2,9	290
Железо	200	2000	Титан	112	11200
Золото	79	7900	Хром	240–250	24000-25000
Магний	44	4400	Цинк	80	8000
Медь	110	11000	Чугун серый	115-150	11500-15000
Свинец	17	1700

Предел прочности материала

Материал	σ _пч		Материал	σ _пч
Материал	ГПа	кгс / мм ²	Материал	ГПа	кгс / мм ²
Алюминий	0,05-0,11	5-11	Сталь (марки Ст3)	0,38-0,47	38-47
Бетон прочный	0,048	4,8	Сталь легированная	0,8-1,0	80-100
Железо	0,17-0,21	17–21	Стекло	0,06-0,12	6–12
Золото	0,14	14	Стекло органическое	0,08	8
Олово	0,027	2,7	Цинк	0,11	11
Свинец	0,016	1,6	Чугун серый	0,25-0,55	25-55
Серебро	0,14	14

Допускаемое механическое напряжение в некоторых метериалах (при растяжении)

Материал	σ _доп		Материал	σ _доп
Материал	ГПа	кгс / мм ²	Материал	ГПа	кгс / мм ²
Алюминий	0,03-0,08	3-8	Сталь (марки Ст3)	0,16	16
Бетон	0,0003–0,0015	0,03-0,15	Сталь углеродистая	0,06-0,25	6-25
Медь	0,03-0,12	3-12	Чугун серый	0,028–0,080	2,8-8,0
Стал легированный	0,1-0,4	10-40

Коэффициент запаса прочности

Стал при переменных нагрузке	5-15
Стал при длительной нагрузке	2,4-2,6
Сталь при ударной нагрузке	2,8-5,0
Чугун, бетон, деревисина при постоянной длительной нагрузке	3-9

Продолжение будет. ..

Измерение модуля упругости

Приложение:

Измерение модуля продольной упругости, модуля сдвига и коэффициента Пуассона (поперечной деформации) в недисперс изотропных конструкционных материалов.

Общие сведения:

Модуль Юнга (модуль продольной упругости) определяет как отношение напряжения (сила на единицу площади) к деформации сжатия.

Модуль сдвига определяет как отношение напряжения сдвига к деформации сдвига.

Эти основные свойства материалов обязательно учитываются в различных научных исследованиях, и измеряются значениями скорости звука и плотности материала. Скорость распространения звука легко вычисляется посредством ультразвукового контроля в режиме импульс-эхо с использованием соответствующего оборудования. Представленная ниже процедура действительна для любого однородного, изотропного, недисперсионного материала (скорость звука не изменяется с параметром).Сюда включены наиболее распространенные металлы, промышленная керамика и стекло, при условии, что размеры поперечного сечения не близки длины волны контроля частоты. Жесткие пластики, такие как полистирол и акрил, также могут быть измерены, несмотря на то, что они имеют высокий коэффициент затухания ультразвуковой.

Каучук не может быть измерен ультразвуковым методом по высокой степени дисперсии и нелинейно упругих свойств. Мягкие пластики точно так же высокая степень затухания в режиме сдвиговых волн, и обычно не могут быть измерены.В случае анизотропных материалов, упругость меняется в зависимости от направления, так же происходит и распространение продольных волн и / или сдвиговых волн. Для генерации матрицы полной упругости в анизотропных образцах обычно требуется шесть серий ультразвуковых измерений. Пористость или зернистость материала вызывает колебания скорости звука на основе размера и ориентации зерен или размера и распределения.

Оборудование:

Для измерения скорости звука при расчете упругости обычно используются прецизионные толщиномеры 38DL PLUS или 45MG с ПО для одноэлементных ПЭП, или дефектоскопы с функцией измерения скорости звука (например, серии EPOCH). Генераторы / приемники модели 5072PR или 5077PR в комбинации с осциллографом или дискретизатором сигналов также измерения времени распространения. Для данного теста требуется два преобразователя, подход для эхо-импульсного измерения скорости звука в материале продольными и поперечными волнами.Среди наиболее используемых ПЭП: широкополосный преобразователь продольных волн M112 или V112 (10 МГц) и преобразователь поперечных волн с нормальным углом падения V156 (5 МГц). Они подходят для измерения наиболее распространенных металлов и обожженных керамических образцов. Требуются специальные преобразователи для измерения очень толстых и очень тонких материалов. В некоторых вариантах применения теневой метод контроля (метод сквозного прозвучивания) с использованием двух преобразователей, применяемых на одной оси, по разные стороны проверяемого изделия.При выборе преобразователя или настройки прибора необходимо проконсультироваться со специалистом Olympus.

Тестовый образец может быть любой формы, позволяющей выполнять эхо-импульсное измерение времени прохождения ультразвука через материал. Обычно это толщина 12,5 мм с ровными параллельными поверхностями, ширина или диаметр которого больше диаметра используемого преобразователя. Необходимо проявлять крайнюю осторожность при измерении узких образцов по задействованию пограничных эффектов, которые могут повлиять на измеренное прохождения импульса.При использовании сильно тонких образцов, разрешение будет ограничено из-за небольших колебаний времени прохождения импульса через короткий УЗ-путь. Мы рекомендуем брать образцы толщиной минимум 5 мм, но желательно толще. Во всех случаях толщина тестового образца должна быть точно известна.

Процедура:

Измерение скорости распространения продольных и сдвиговых волн тестового образца с использованием подходящих ПЭП и настроек прибора. Для измерения скорости сдвиговых волн потребуется специальная контактная жидкость высокой вязкости, как например SWC.Толщиномеры 38DL PLUS и 45MG могут напрямую измерять скорость звука в материале на основе введенной толщины образца, а дефектоскопы серии EPOCH измеряют скорость звука в ходе калибровки скорости звука. В случаях, следуя рекомендуемой процедуре измерения скорости звука, представленной в случае использования прибора. При использовании генератора / приемника зафиксируйте время прохождения сигнала туда и обратно через участок известной толщины с помощью преобразователей продольных и поперечных волн, и рассчитайте:

При необходимости переведите единицы измерения скорости звука в дюйм / с или см / с.(Время обычно измеряется в микросекундах; для получения измерений в дюйм / с или см / с умножьте дюйм / мкс или см / мкс на 10 ⁶.) Полученные значения скорости звука могут использовать в следующих формулах.

Примечание: Если скорость звука выражена в см / с, а плотность – в г / см ³, модуль упругости будет выражен в дин / см ². Если вы используете английскую систему мер (дюйм / с и фунт / дюйм ³) для расчета модуля упругости в фунтах на кв.дюйм (PSI), не путайте фунт (единицу измерения силы) с фунтом (единицы измерения массы). Для упругости в фунтах на кв. М. Требуется упругость в фунтах на кв. дюйм. Если исходные расчеты выполнены в метрических единицах, используйте коэффициент конверсии 1 psi = 6,89 x 10 ⁴ дин / см ².Вы также можете увеличить скорость звука в дюймах / с, плотность – в г / см ³, а затем разделить коэффициент пересчета 1,07 x 10 ⁴ для упругости в PSI.

Для определения модуля сдвига умножьте квадрат скорости поперечной волны на плотность.
Опять же, используйте единицу измерения см / с и г / см ³ для модуля упругости в дин / см ² или английскую систему мер (дюйм / с и фунт / дюйм ³) и умножьте результат на коэффициент пересчета масса / сила.

Библиография
Подробнее об измерении модулей упругости ультразвуковым методом см. в представленных ниже источниках:
1. Мур П. (ред.), Справочник по неразрушающему контролю, том 7, Американское общество неразрушающего контроля, 2007, стр. 319-321.
2. Крауткрамер, Дж., Х. Крауткрамер, Ультразвуковой контроль материалов , Берлин, Гейдельберг, Нью-Йорк 1990 (четвертое издание), стр. 13-14, 533-534.

Модуль упругости (Модуль Юнга): концепция, формулы, как определить

При проектировании строительной конструкции стоит задача спрогнозировать ее поведение при заданных нагрузках и внешних условиях.Бетон воспринимает большие усилия, поэтому важный этап расчета – определение деформаций и прогибов при статическом нагружении.

В расчете железобетонных конструкций по второй группе предельных положений применяют физическую информацию, называемую модулем упругости бетона, или модулем Юнга. Он описывает свойства твердого вещества в упругих деформаций.

Основные сведения

Модуль Юнга, называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества.Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н / м2 или в Па.

Это важный коэффициент применения при расчетах жесткости заготовок, узлов и конструкций, в применении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графики, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

E = α / ε

Закон Гука также можно указать и с использованием модуля Юнга.

Способы определения

Модуль упругости бетона определяет:

механическим испытанием образцов;
неразрушающим ультразвуковым методом, основанным на сравнении скорости распространения волн в существующей конструкции и испытанном образце с заданными характеристиками.

Механический способ

Исследование первым методом проводят согласно ГОСТ 24452-80. Изготавливают образцы сечением в виде квадрата или круга с использованием высоты до диаметра (ширины), равным 4.

Образцы сериями по три штуки выбуривают, высверливают или выпиливают из готовых изделий, либо набивают из готовых изделий, либо набивают согласно ГОСТ 10180-78. До начала испытаний призмы или цилиндры выдерживают под влажной тканью.

Для определения модуля упругости бетона использовать прессы со специальными базами для измерения деформаций.Они состоят из приборов, отдельных под разными углами к граням образца. Индикаторы крепят к стальным рамкам или приклеенным опорным вставкам.

Если испытания конструкций, работающих при повышенном уровне или высокой температуре, выполняют специальную подготовку по ГОСТ 24452-80.

Испытания проводят по схеме:

Образцы с индикаторами помещают под пресс, совмещают ось заготовки для плиты оборудования. Величину разрушающую нагрузку назначают, исходя из марочной прочности бетона.
Нагрузку увеличивают постепенно, ступенями по 10% от разрушающей. Выдерживают интервалы 4-5 минут.
Доводят усилие до 40-45% от размера. Если программа не предусматривает другие требования, приборы снимают. Дальнейшее нагружение проводят с постоянной скоростью.
Производит обработку результатов для каждого образца при нагрузке, равной 30% от разрушающей. Все данные заносят в журнал испытаний.

На основе исследований можно судить о начальном модуле упругости бетона.Эта величина характеризует материал при нагрузке, в пределах которой в образцах представлены обратимые изменения. Показатель обозначается как Eb, его значение для каждого класса бетона вносится в таблицы строительных норм и маркировку изделий.

Так, модуль упругости бетона В15 естественного твердения составляет 23, а подвергнутого термической обработке 25 МПа * 10-3.

Величина модуля упругости бетона для классов В20, В25, В30, В35 и В40 равна 27, 30, 32,5, 34,5 и 36 МПа * 10-3.В пропаренных конструкциях она соответствует 24,5, 27, 29, 31 и 32,5 МПа * 10-3.

Ультразвуковой способ

Применяется для исследования конструкций без их локального разрушения. При повышенной температуре такой метод определяет упругость с погрешностью 15-75%, так как скорость распространения ультразвуковых колебаний в водной среде возрастает.

Чтобы избежать ошибок при измерениях, разработан метод определения модуля Юнга с учетом условий бетона.Он основан на опытных испытаниях серий образцов с различной водонасыщенностью.

Нормативные и расчетные значения сопротивления получаютона, используя корректирующие коэффициенты с учетом условий работы конструкции. Методика расчета описана в СП 63.13330.2012.

Физический смысл модуля Юнга

Если же тело не оказывает сопротивление изменению формы и по окончанию воздействия в сформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Виды деформации

Р. Гук исследовал удлинениережней из различных веществ, под воздействием подвешенных к свободному концу гирь. Положительным выражением степени формы считается относительное удлинение, равное относительное удлинение и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение усиливает упругость исходной длины и деформирующую силу F и обратно пропорционально площади этого стержня S:

Δl = α * (lF) / S

Величину, обратную α, и называют модулем Юнга:

1 / α = E

Относительная деформация:

ε = (Δl) / l = α * (F / S)

Отношение растягивающей силы F к S Называют упругим напряжением σ:

ε = α σ

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

σ = ε / α = E ε

Теперь можно определить физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство разрушается до того, как растянутся вдвое от первоначальной длины. Значение E определяют с помощью косвенного метода деформаций.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определения потенциальной энергии тел или сред, подвергшихся упругой деформации.

Источники и примечания

[www.physel.ru/mainmenu-4/-mainmenu-9/101-s-98—-.html Упругая деформация] (рус.). [www.webcitation.org/68nxdCgZR Архивировано из первоисточника 30 июня 2012].
Дитер Мешеде, Кристиан Гертсен.
Physik. – Springer, 2004. – P.
[books.google.com/books?id=pfpkxqB-jGoC&pg=PA181&dq=Federkonstante 181]
..
Бруно Ассманн.
Technische Mechanik: Kinematik und Kinetik. – Oldenbourg, 2004. – P.
[books.google.com/books?id=NGu2K3eosMoC&pg=PA11&dq=Federkonstante 11]
..
[www.edu.yar.ru/projects/socnav/prep/phis001/dyn/dyn10.html Динамика, Сила упругости] (рус.). [www.webcitation.org/68nxeMf0N Архивировано из первоисточника 30 июня 2012].
[www.edu.delfa.net/CONSP/meh5.htm Механические свойства тел] (рус.). [www.webcitation.org/68nxfaOO5 Архивировано из первоисточника 30 июня 2012].

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Материал	Модуль Юнга E, ГПа
Алюминий	70
Бронза	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лёд	3
Медь	110
Свинец	18
Серебро	80
Серый чугун	110
	200/210
Стекло	70

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна.Модуль Юнга используемая формула прочлахностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел высокого напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический – при кратковременном, ударном характере усилия. Для размеров веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, пределы прочности на сжатие материала и на растяжение.Они на испытательных стенда опытным путем при растягивании или испытании образцов мощными гидравлическими машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения необходимого давления гидравлическим способом иногда применяется направленный взрыв в герметичной капсуле.

Виды нагрузок

Сжатие – действующая сила сдавливающего предмета, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающие устанавливающий вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном напряжении.

Растяжение – усилие стремится удлинить тело в определенном направлении.Подъемно-транспортные машины и испытывают испытывают нагружения при подъеме и переноске грузов.

Читать также: Какие бывают диодные ленты

Сдвиг и срез – такое нагружение происходит в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузки подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин имеются соединительные детали.От их прочности зависит работоспособность устройств.

Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей.Мосты, перекладины, консоли, подъемно-механизмы и другие детали испытывают подобное нагружение.

Допускаемое механическое напряжение в некоторых материалах известно при растяжении

Из жизненного опыта, что разные материалы формы по-разному сопротивляются изменению. Прочностные характеристики кристаллических и других твердых тел силы межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу.Эти силы достигают максимума при величине напряжения одной десятой от модуля Юнга.

Испытание на растяжение

Это называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности начинается при меньших значениях, поскольку строение реальных раз неоднородно. Это неравномерное начинается напряжений, и разрушение с тех участков, где напряжения максимальны.

Значения σраст в МПа:

0,038

Материалы	σраст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе деталей будущего изделия.С их использованием также прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз на десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Общее понятие

Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения.Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем меньше будет растягиваться какой-либо стержень при равных условиях (величина нагрузки, площадь сечения и прочее).

В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закон о деформации упругих тел). Связывает напряжение, развивающее в материале, и его деформацию.

Согласно международной стандартной системе измеряется в МПа.На практике инженеры предпочитают использовать размерность кгс / см2.

Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного метода заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.

Отметим сразу, таким методом упругости пластичных материалов: сталь, медь и прочее.Хрупкие материалы – чугун, бетон – сжимают до появления трещин.

Дополнительные характеристики механических свойств

Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее введение дополнительных параметров:

Жесткость есть модуль упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узел конструкции в целом.Измеряется в килограммах силы.
Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо этого здесь диаметр диаметра стержня.Опыты показывают, что для большого поперечного удлинения в 3-4 раза меньше, чем продольное.
Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение под воздействием нагрузки.
Модуль сдвига проверяет упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела.Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
Модуль объемной упругости характеризует объем материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.

Читать также: Неисправности магнетрона оборудования печи

Помимо вышесказанного необходимо упомянуть, что некоторые материалы имеют различные механические свойства в зависимости от нагрузки.Такие материалы характеризуются как анизотропные. Яркими примерами древесины, слоистые пластмассы, некоторые виды камня, ткани и прочее.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяется коэффициент запаса прочности.Он оценивает способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных деталей и деталей, могущих при разрушении узлов опасности для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшение ее эксплуатационных характеристик. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение.Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Упругость модуль Юнга – Справочник химика 21

Модуль упругости (модуль Юнга) для различных материалов, кг / мм [c.372]

Модуль упругости, сдвига, коэффициент Пуассона. Модуль упругости (модуль Юнга) Е = [c.499]

Самым прочным металлом 1г, если оценивать его прочность по модулю нормальной упругости (модуль Юнга). [c.378]

ГУКА ЗАКОН устанавливает линейную зависимость между упругой деформацией твердого тела и приложенным мех напряжением Напр, если стержень длиной I и поперечным сечением S растянуть продольной силой F, то удлинение Д / = FI / ES, где -модуль упругости (модуль Юнга), зависящий от материала стержня Для деформации сдвига (см рис) Г имеет вид т = Гр, где [c.618]

Модуль продольной упругости (модуль Юнга) Сосредоточенная сила воздействия вообще Модуль упругости при сдвиге постоянная нагрузка (вес) [c.375]

Величина Однозначно связано с модулем упругости (модулем Юнга) Е по сдвиге [c.77]

В работе [228] исследовали эволюцию и упругие свойства Си, подвергнутой интенсивной деформации РКУ-прессованием при комнатной температуре и последующему отжигу при температурех до 500 ° С.Упругие модули Юнга Е и сдвига вычисляли из величин скоростей VI и VI соответственно продольных и поперечных ультразвуковых волн по известным соотношениям [c.169]

Упругие характеристики изотропных твердых тел двумя независимыми параметрами Ламе Л и модулем упругости при сдвиге Сили жесткость) ц. В – [c.283]

Начальной стадией деформации металла является упругая деформация (участок АВ рис. 2.8). С точки зрения кристаллической строения. Упругая деформация проявляется в некотором увеличении расстояния между атомами в кристаллической решетке. После снятия нафузки атомы возвращаются в прежнее положение и деформация исчезает. Другими словами, упругая деформация не вызывает никаких последствий в металле. Чем меньщую деформацию вызывает напряжение, тем более жесткая и более упругий металл.Характеристика упругости нового металла модуля упругости Модуль упругости (модуль Юнга) – обеспечивает силы, стремящиеся оторвать атомы друг от друга, и модуль касательной упругости (модуль Гука) – показывает силы, стремящиеся сдвинуть атомы относительно друг друга. Значения упругости являются константами материала и зависят от сил межатомного взаимодействия. Все конструкции и изделия из металлов эксплуатируются, как правило, в упругой области. Таким образом, упругость – это свойство твердого тела восстанавливать свою первоначальнуто фор.му и объем после прекращения действия внешней нафузки. Модуль упругости практически не зависит от структуры металла и определяется, в основном, типом кристаллической решетки. Так, например, модуль Юнга для магния (кристаллическая решетка ГП%) равенство 45-10 Па, для меди (ГКЦ) – 105-10 Па, для железа (ОЦК) – 210-10 Па. [c.28]

X – степень кристалличности полимера У – модуль упругости (модуль Юнга) [c.6]

Термостойкость стекла зависит от целого ряда его свойств, определяющих коэффициент термического расширения, прочность на разрыв и модуль упругости (модуль Юнга) . [c.19]

Модуль продольной упругости (модуль Юнга) Е и [c.37]

Модуль упругости (модуль Юнга) – одна из существенных характеристик эластомеров. Этот параметр коррелирует с молекулярной массой между узлами поперечной сшивки [76, с. 165] по кинетике изменений с наибольшей достоверностью можно судить о степени завершенности процесса структурирования. Значение модуля упругости является определяющим при расчете конструкций ряда изделий из эластомеров, например шин, акустических устройств и т.д. Представляет интерес по изменению модуля упругости исследовать поведение эластомеров при воздействии температуры в различных средах. [c.116]

Пластич. деформация твердого тола всегда сопровождается его упрочнением, т. е. ростом напряжения по мере роста пластич. деформации. У п р о ч н е-н и е в процессе пластич. деформации характеризует коэфф. упрочнения к = йР1модулем нормальной пластичности. Его величина на 2—3 порядка меньше модуля упругости (модуля Юнга). [c.34]

Кристаллические твердые вещества обладают модулем продольной упругости (модулем Юнга) порядка 10 —10 дин1см и очень малым конечным удлинением. При сохранении той же длины тела, то непрерывно возрастает. По ур. (XVII, 3) это означает, что изменение внутренней энергии, связано- [c.576]

. , а не к ее скорости.Типичная кривая деформации от напряжения для физического тел на рис. VII. 15. Пряолинейный участок кривой ОА включает пропорциональности напряжению сдвига в соответствии с законом Гука (VII. 3). До напряжения Ри отвечающего точке А, размер и форма тела восстанавливаются после снятия нагрузки. Важными элементами такой системы являются модули упругости (модуль Юнга) и модуль эластической деформации. Считает, что в суспензиях с прослойками дисперсионной среды (возможно скольжение частиц относительно друг друга без разрывают связей).Напряжение Р соответствует пределу текучести (правильнее – пределу упругости). С напряжения напряжения проявляется пластичность, а после его снятия – остаточные деформации. При напряжении Рг (точка) происходит течение твердообразной системы. При увеличении напряжения до величины Рз (точка В), предел прочности, обычно наблюдается негупрочнение тела, затем наступает разрушение системы. [c.380]

Удобным методом определения упругости жестких материало в со слабым поглощением является возбуждение свободных колебаний и определенных частот, которые завмодуля упругости (модуля Юнга Е) материала.При динамического измерениях модуля Юнга заменяется модулем накопления при растяжении Е. [c.148]

Обозначения основных величин, принятых ниже, следующие р – плотность (объемная масса) Ею – модуль упругости (модуль Юнга) 8 – диэлектрическая проницаемость tg б – тангенс угла диэлектрических потерь Q – добротность / – частота А /// о – уход резонансной частоты в указанном интервале температур Сзв – скорость звука d – пьезоэлектрический модуль 33 – пьезоэлектрический модуль продольных колебаний 31 – пьезоэлектрический модуль радиальных колебаний d / e, d / Y – характеристики эффективности в режиме приема iotgS.ro / etg6 – характеристики эффективности в режиме излучения [c.339]

Кристаллические твердые вещества обладают модулем продольной упругости (модулем Юнга) порядка 10 —дин / см и очень малым конечным удлинением. При сохранении той же длины тела, то непрерывно возрастает. По ур. (XVII, 3) это означает, что изменение внутренней энергии, связанное с напряжением dUldl) T, v, значительно по величине и положительно по знаку, т.е. внутренняя энергия тела возрастает. [c.568]

С коэфф. т.ер.чического расширения 8,28 10 ко градэфф. теплопроводности 0,0218 кал см X X сек град теплоемкость 6,56 кал г-атом – электрическое сопротивление 140,5 мком см. Отличается самым поперечным сечением захвата тепловых нейтронов – 460С0 барн. Работа выхода электронов – 3,07 эв. Кюри точка 17 ° С (290 К). Модуль норм, упругости (модуль Юнга) 5730 кгс предел прочности 18,6 кгс мм НВ = = 60. Легко поддается мех.обработка. Химически активен. При высоких т-рах активно взаимодействует с кислородом, галогенами, серой, азотом, углеродом и др. неметаллами. Во время длительного хранения в воздухе при наличии водяных паров подвергается коррозии (см. Коррозия). Г. сплавляется [c.240]