Модуль юнга алюминий: Модуль упругости алюминия
alexxlab | 07.06.1986 | 0 | Разное
| Модуль упругости алюминия кг см2. Модуль упругости разных материалов, включая сталь | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем. Общие понятияМодуль упругости (модуль Юнга) – это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения
. Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию. Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях) . Но инженеры на практике больше склоняются к применению размерности кгс/см2. Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости. Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. Механические свойстваТолько при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала . А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры: Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства . Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее. У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые. Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Некоторые значения (величина представлена в миллионах кгс/см2) :
Разница в показателях модулей упругости для сталей в зависимости от их марок: Ещё это значение изменяется в зависимости от вида проката:
Как видно, отклонения в значениях модулей упругой деформации стали незначительны.
Примечание : 1. Для определения модуля упругости в кгс/см 2 табличное значение умножается на 10 (более точно на 10.1937) 2. Значения модулей упругости Е для металлов, древесины , каменной кладки следует уточнять по соответствующим СНиПам. Нормативные данные для расчетов железобетонных конструкций:Таблица 2. Начальные модули упругости бетона (согласно СП 52-101-2003)Таблица 2.1. Начальные модули упругости бетона согласно СНиП 2.03.01-84*(1996)Примечания : 1. Над чертой указаны значения в МПа, под чертой – в кгс/см 2 . 2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции. 3. Для ячеистого бетона неавтоклавного твердения значения Е b принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8. 4. Для напрягающего бетона значения Е b принимают как для тяжелого бетона с умножением на коэффициент a = 0,56 + 0,006В. 5. Приведенные в скобках марки бетона не точно соответствуют указанным классам бетона. Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)Таблица 4. Расчетные значения сопротивления бетона (согласно СП 52-101-2003)Таблица 4.1. Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)Таблица 6.2. Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)Таблица 7. Расчетные сопротивления для арматуры(согласно СП 52-101-2003)Таблица 7.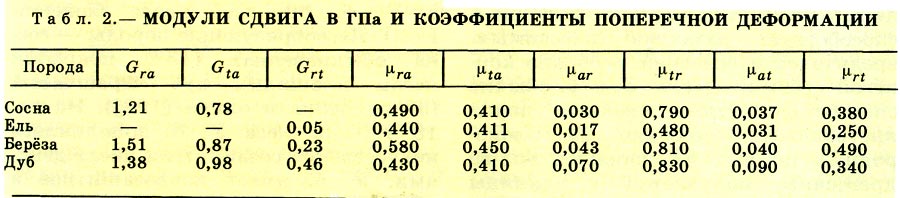 Таблица 7.2. Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)Нормативные данные для расчетов металлических конструкций:Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990))листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений Примечания : 1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм). 2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88. 3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см 2). Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))Примечания : 1. Расчетные сопротивления для стали, используемой для производства профилированных листов, приводятся отдельно . Список использованной литературы: 1. СНиП 2.03.01-84 “Бетонные и железобетонные конструкции” 2. СП 52-101-2003 3. СНиП II-23-81 (1990) “Стальные конструкции” 4. Александров А.В. Сопротивление материалов. Москва: Высшая школа. – 2003. 5. Фесик С.П. Справочник по сопротивлению материалов. Киев: Будiвельник. – 1982. Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Общие понятияМодуль упругости (модуль Юнга) – это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения . Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие). Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию. Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях) . Но инженеры на практике больше склоняются к применению размерности кгс/см2. Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости. Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные. Механические свойстваТолько при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала . А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры: Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства
. У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые. Модуль упругостиСтоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь. А есть и такие ситуации, когда эта величина измеряется формой профиля. Некоторые значения (величина представлена в миллионах кгс/см2) :
Разница в показателях модулей упругости для сталей в зависимости от их марок: Ещё это значение изменяется в зависимости от вида проката:
Как видно, отклонения в значениях модулей упругой деформации стали незначительны. Именно по этой причине большинство инженеров, проводя свои расчёты, пренебрегают погрешностями и берут значение, равное 2,00. Физические характеристики материалов для стальных конструкций | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Материал | Модуль упругости Е, МПа | Чугун белый, серый | (1,15…1,60) · 10 5 |
| Чугун ковкий | 1,55 · 10 5 |
| Сталь углеродистая | (2,0…2,1) · 10 5 |
| Сталь легированная | (2,1…2,2) · 10 5 |
| Медь прокатная | 1,1 · 10 5 |
| Медь холоднотянутая | 1,3 · 10 3 |
| Медь литая | 0,84 · 10 5 |
| Бронза фосфористая катанная | 1,15 · 10 5 |
| Бронза марганцевая катанная | 1,1 · 10 5 |
| Бронза алюминиевая литая | 1,05 · 10 5 |
| Латунь холоднотянутая | (0,91. ..0,99) · 10 5 ..0,99) · 10 5 |
| Латунь корабельная катанная | 1,0 · 10 5 |
| Алюминий катанный | 0,69 · 10 5 |
| Проволока алюминиевая тянутая | 0,7 · 10 5 |
| Дюралюминий катанный | 0,71 · 10 5 |
| Цинк катанный | 0,84 · 10 5 |
| Свинец | 0,17 · 10 5 |
| Лед | 0,1 · 10 5 |
| Стекло | 0,56 · 10 5 |
| Гранит | 0,49 · 10 5 |
| Известь | 0,42 · 10 5 |
| Мрамор | 0,56 · 10 5 |
| Песчаник | 0,18 · 10 5 |
| Каменная кладка из гранита | (0,09…0,1) · 10 5 |
| Каменная кладка из кирпича | (0,027…0,030) · 10 5 |
| Бетон (см. таблицу 2) | |
| Древесина вдоль волокон | (0,1…0,12) · 10 5 |
| Древесина поперек волокон | (0,005. ..0,01) · 10 5 ..0,01) · 10 5 |
| Каучук | 0,00008 · 10 5 |
| Текстолит | (0,06…0,1) · 10 5 |
| Гетинакс | (0,1…0,17) · 10 5 |
| Бакелит | (2…3) · 10 3 |
| Целлулоид | (14,3…27,5) · 10 2 |
Нормативные данные для рассчетов железобетонных конструкций
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)
Примечания:
1. Над чертой указаны значения в МПа, под чертой – в кгс/см².
2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции.
3. Для ячеистого бетона неавтоклавного твердения значения Е b принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8.
4. Для напрягающего бетона значения Е b принимают как для тяжелого бетона с умножением на коэффициент
a = 0,56 + 0,006В.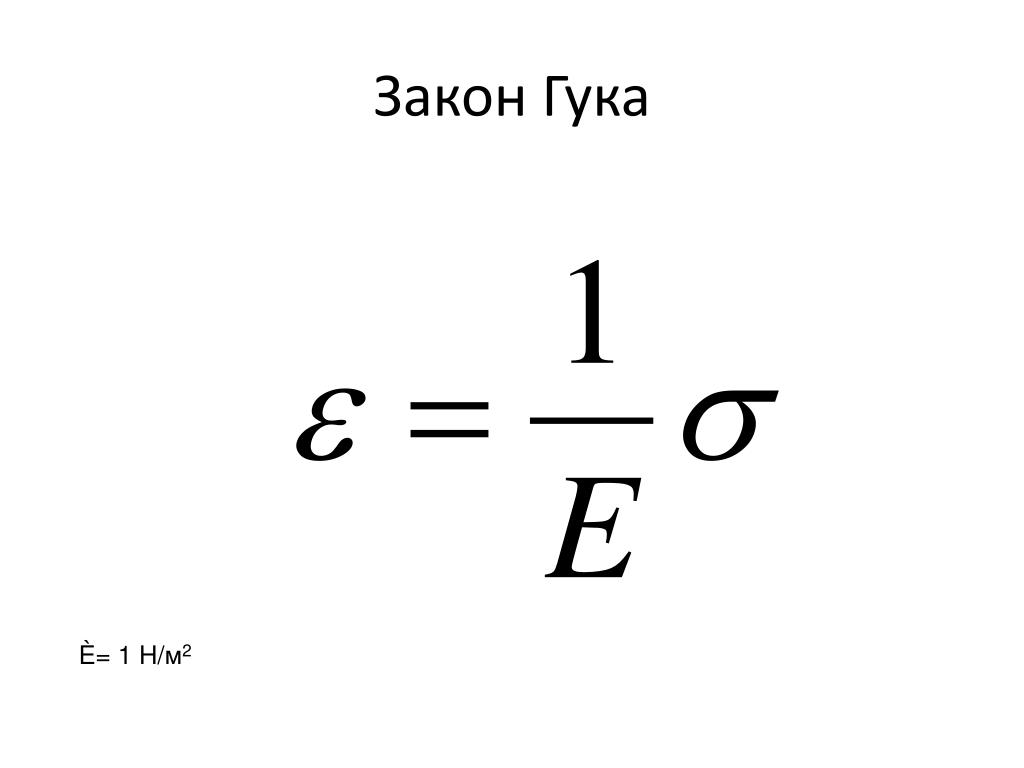
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)
Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2. 03.01-84* (1996)
03.01-84* (1996)
Нормативные данные для расчетов металлических контрукций
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
Примечания:
1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм).
2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88.
3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
Примечания:
1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*.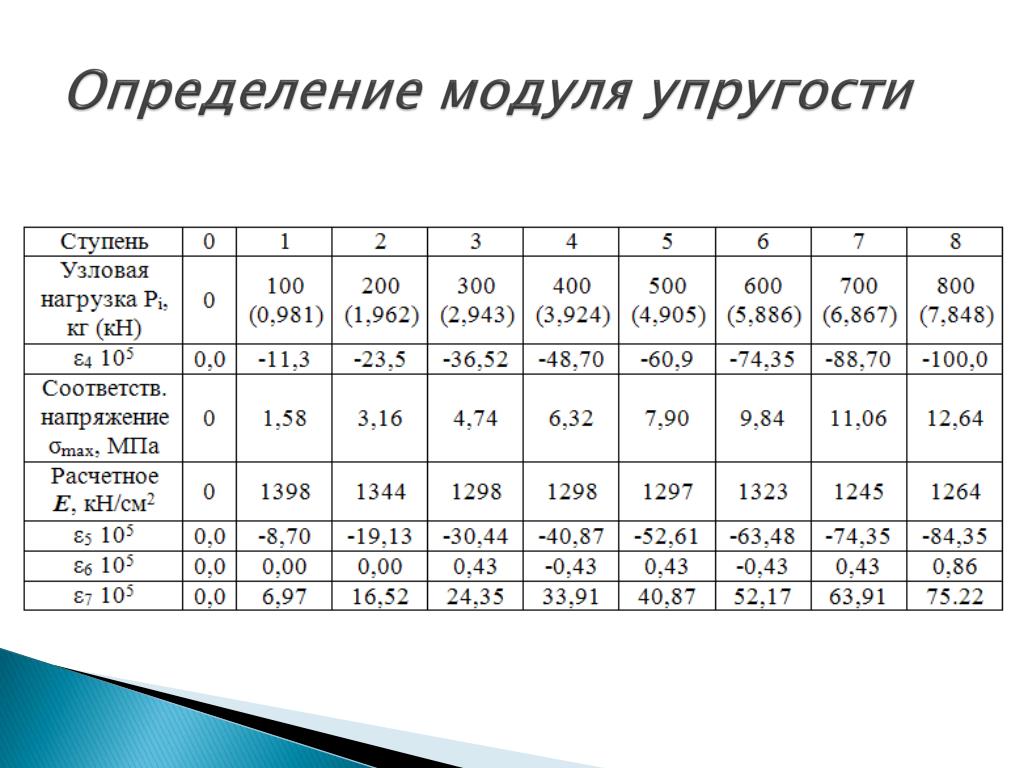
2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице.
3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.
Модуль упругости для стали, а также для других материалов
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу – стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости – что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
- Модуль сдвига (G), называемый также модулем жёсткости.
 Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость. - Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.
После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.
Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:
- Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.
 2 .
2 . - И напоследок коэффициент Пуассона для стали равен значению 0,3
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него. 2.
2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
stanok.guru
Таблица. Значения модулей продольных упругостей Е, модулей сдвигов G и коэффициентов Пуассона µ (при температуре 20oC).
| |||
tehtab. ru
ru
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) – (α)
μ = (E / 2G) – 1 – (b)
K = E / 3(1 – 2μ) – (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Коэффициент Пуассона µ | ||
Алюминий | ||||
Сталь (1% С) 1) | ||||
Константан 2) | ||||
Манганин | ||||
1) Для стали, содержащий около 1% С, упругие константы, как известно, меняются при термообработке. 2) 60% Cu, 40% Ni. | ||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
Бронза (66% Cu) | ||||
Нейзильбер1) | ||||
Стекло иенское крон | ||||
Стекло иенское флинт | ||||
Железо сварочное | ||||
Бронза фосфористая2) | ||||
Платиноид3) | ||||
Кварцевые нити (плав. | ||||
Резина мягкая вулканизированная | ||||
1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. | ||||
Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
Цинк (чистый) | |||
Красное дерево | |||
Цирконий | |||
Сплав 90% Pt, 10% Ir | |||
Дюралюминий | |||
Шелковые нити1 | Тиковое дерево | ||
Пластмассы: | |||
Термопластичные | |||
Термореактивные | |||
Вольфрам | |||
1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость | |||
Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 (при 7-110С) | |||
Алюминий | Алюминий | |||
Стекло флинт | ||||
Стекло немецкое | ||||
Нейзильбер | ||||
Фосфористая бронза | ||||
Кварцевые нити | ||||
infotables. ru
ru
Модуль упругости (модуль Юнга) | Мир сварки
Модуль упругости
Модуль упругости (модуль Юнга) E – характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к удлинению. Часто модуль Юнга называют просто модулем упругости.
1 кгс/мм2 = 10-6 кгс/м2 = 9,8·106 Н/м2 = 9,8·107 дин/см2 = 9,81·106 Па = 9,81 МПа
| Металлы | |||
| Алюминий | 6300-7500 | 6180-7360 | 61800-73600 |
| Алюминий отожженный | 6980 | 6850 | 68500 |
| Бериллий | 30050 | 29500 | 295000 |
| Бронза | 10600 | 10400 | 104000 |
| Бронза алюминиевая, литье | 10500 | 10300 | 103000 |
| Бронза фосфористая катаная | 11520 | 11300 | 113000 |
| Ванадий | 13500 | 13250 | 132500 |
| Ванадий отожженный | 15080 | 14800 | 148000 |
| Висмут | 3200 | 3140 | 31400 |
| Висмут литой | 3250 | 3190 | 31900 |
| Вольфрам | 38100 | 37400 | 374000 |
| Вольфрам отожженный | 38800-40800 | 34200-40000 | 342000-400000 |
| Гафний | 14150 | 13900 | 139000 |
| Дюралюминий | 7000 | 6870 | 68700 |
| Дюралюминий катаный | 7140 | 7000 | 70000 |
| Железо кованое | 20000-22000 | 19620-21580 | 196200-215800 |
| Железо литое | 10200-13250 | 10000-13000 | 100000-130000 |
| Золото | 7000-8500 | 6870-8340 | 68700-83400 |
| Золото отожженное | 8200 | 8060 | 80600 |
| Инвар | 14000 | 13730 | 137300 |
| Индий | 5300 | 5200 | 52000 |
| Иридий | 5300 | 5200 | 52000 |
| Кадмий | 5300 | 5200 | 52000 |
| Кадмий литой | 5090 | 4990 | 49900 |
| Кобальт отожженный | 19980-21000 | 19600-20600 | 196000-206000 |
| Константан | 16600 | 16300 | 163000 |
| Латунь | 8000-10000 | 7850-9810 | 78500-98100 |
| Латунь корабельная катаная | 10000 | 9800 | 98000 |
| Латунь холоднотянутая | 9100-9890 | 8900-9700 | 89000-97000 |
| Магний | 4360 | 4280 | 42800 |
| Манганин | 12600 | 12360 | 123600 |
| Медь | 13120 | 12870 | 128700 |
| Медь деформированная | 11420 | 11200 | 112000 |
| Медь литая | 8360 | 8200 | 82000 |
| Медь прокатанная | 11000 | 10800 | 108000 |
| Медь холоднотянутая | 12950 | 12700 | 127000 |
| Молибден | 29150 | 28600 | 286000 |
| Нейзильбер | 11000 | 10790 | 107900 |
| Никель | 20000-22000 | 19620-21580 | 196200-215800 |
| Никель отожженный | 20600 | 20200 | 202000 |
| Ниобий | 9080 | 8910 | 89100 |
| Олово | 4000-5400 | 3920-5300 | 39200-53000 |
| Олово литое | 4140-5980 | 4060-5860 | 40600-58600 |
| Осмий | 56570 | 55500 | 555000 |
| Палладий | 10000-14000 | 9810-13730 | 98100-137300 |
| Палладий литой | 11520 | 11300 | 113000 |
| Платина | 17230 | 16900 | 169000 |
| Платина отожженная | 14980 | 14700 | 147000 |
| Родий отожженный | 28030 | 27500 | 275000 |
| Рутений отожженный | 43000 | 42200 | 422000 |
| Свинец | 1600 | 1570 | 15700 |
| Свинец литой | 1650 | 1620 | 16200 |
| Серебро | 8430 | 8270 | 82700 |
| Серебро отожженное | 8200 | 8050 | 80500 |
| Сталь инструментальная | 21000-22000 | 20600-21580 | 206000-215800 |
| Сталь легированная | 21000 | 20600 | 206000 |
| Сталь специальная | 22000-24000 | 21580-23540 | 215800-235400 |
| Сталь углеродистая | 19880-20900 | 19500-20500 | 195000-205000 |
| Стальное литье | 17330 | 17000 | 170000 |
| Тантал | 19000 | 18640 | 186400 |
| Тантал отожженный | 18960 | 18600 | 186000 |
| Титан | 11000 | 10800 | 108000 |
| Хром | 25000 | 24500 | 245000 |
| Цинк | 8000-10000 | 7850-9810 | 78500-98100 |
| Цинк катаный | 8360 | 8200 | 82000 |
| Цинк литой | 12950 | 12700 | 127000 |
| Цирконий | 8950 | 8780 | 87800 |
| Чугун | 7500-8500 | 7360-8340 | 73600-83400 |
| Чугун белый, серый | 11520-11830 | 11300-11600 | 113000-116000 |
| Чугун ковкий | 15290 | 15000 | 150000 |
| Пластмассы | |||
| Плексиглас | 535 | 525 | 5250 |
| Целлулоид | 173-194 | 170-190 | 1700-1900 |
| Стекло органическое | 300 | 295 | 2950 |
| Резины | |||
| Каучук | 0,80 | 0,79 | 7,9 |
| Резина мягкая вулканизированная | 0,15-0,51 | 0,15-0,50 | 1,5-5,0 |
| Дерево | |||
| Бамбук | 2000 | 1960 | 19600 |
| Береза | 1500 | 1470 | 14700 |
| Бук | 1600 | 1630 | 16300 |
| Дуб | 1600 | 1630 | 16300 |
| Ель | 900 | 880 | 8800 |
| Железное дерево | 2400 | 2350 | 32500 |
| Сосна | 900 | 880 | 8800 |
| Минералы | |||
| Кварц | 6800 | 6670 | 66700 |
| Различные материалы | |||
| Бетон | 1530-4100 | 1500-4000 | 15000-40000 |
| Гранит | 3570-5100 | 3500-5000 | 35000-50000 |
| Известняк плотный | 3570 | 3500 | 35000 |
| Кварцевая нить (плавленая) | 7440 | 7300 | 73000 |
| Кетгут | 300 | 295 | 2950 |
| Лед (при -2 °С) | 300 | 295 | 2950 |
| Мрамор | 3570-5100 | 3500-5000 | 35000-50000 |
| Стекло | 5000-7950 | 4900-7800 | 49000-78000 |
| Стекло крон | 7200 | 7060 | 70600 |
| Стекло флинт | 5500 | 5400 | 70600 |
Литература
- Краткий физико-технический справочник.
 Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с. - Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1981. 680 с.
- Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
- Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.
weldworld.ru
МЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА | Энциклопедия Кругосвет
Содержание статьиМЕТАЛЛОВ МЕХАНИЧЕСКИЕ СВОЙСТВА. Когда на металлический образец действует сила или система сил, он реагирует на это, изменяя свою форму (деформируется). Различные характеристики, которыми определяются поведение и конечное состояние металлического образца в зависимости от вида и интенсивности сил, называются механическими свойствами металла.
Интенсивность силы, действующей на образец, называется напряжением и измеряется как полная сила, отнесенная к площади, на которую она действует. Под деформацией понимается относительное изменение размеров образца, вызванное приложенными напряжениями.
УПРУГАЯ И ПЛАСТИЧЕСКАЯ ДЕФОРМАЦИЯ, РАЗРУШЕНИЕ
Если напряжение, приложенное к металлическому образцу, не слишком велико, то его деформация оказывается упругой – стоит снять напряжение, как его форма восстанавливается. Некоторые металлические конструкции намеренно проектируют так, чтобы они упруго деформировались. Так, от пружин обычно требуется довольно большая упругая деформация. В других случаях упругую деформацию сводят к минимуму. Мосты, балки, механизмы, приборы делают по возможности более жесткими. Упругая деформация металлического образца пропорциональна силе или сумме сил, действующих на него. Это выражается законом Гука, согласно которому напряжение равно упругой деформации, умноженной на постоянный коэффициент пропорциональности, называемый модулем упругости: s = eY, где s – напряжение, e – упругая деформация, а Y – модуль упругости (модуль Юнга). Модули упругости ряда металлов представлены в табл. 1.
Пользуясь данными этой таблицы, можно вычислить, например, силу, необходимую для того, чтобы растянуть стальной стержень квадратного поперечного сечения со стороной 1 см на 0,1% его длины:
F = YґAґDL/L = 200 000 МПа ґ 1 см2ґ0,001 = 20 000 Н (= 20 кН)
Когда к металлическому образцу прикладываются напряжения, превышающие его предел упругости, они вызывают пластическую (необратимую) деформацию, приводящую к необратимому изменению его формы. Более высокие напряжения могут вызвать разрушение материала.
Более высокие напряжения могут вызвать разрушение материала.
Важнейшим критерием при выборе металлического материала, от которого требуется высокая упругость, является предел текучести. У самых лучших пружинных сталей практически такой же модуль упругости, как и у самых дешевых строительных, но пружинные стали способны выдерживать гораздо большие напряжения, а следовательно, и гораздо большие упругие деформации без пластической деформации, поскольку у них выше предел текучести.
Пластические свойства металлического материала (в отличие от упругих) можно изменять путем сплавления и термообработки. Так, предел текучести железа подобными методами можно повысить в 50 раз. Чистое железо переходит в состояние текучести уже при напряжениях порядка 40 МПа, тогда как предел текучести сталей, содержащих 0,5% углерода и несколько процентов хрома и никеля, после нагревания до 950° С и закалки может достигать 2000 МПа.
Когда металлический материал нагружен с превышением предела текучести, он продолжает деформироваться пластически, но в процессе деформирования становится более твердым, так что для дальнейшего увеличения деформации требуется все больше повышать напряжение. Такое явление называется деформационным или механическим упрочнением (а также наклепом). Его можно продемонстрировать, скручивая или многократно перегибая металлическую проволоку. Деформационное упрочнение металлических изделий часто осуществляется на заводах. Листовую латунь, медную проволоку, алюминиевые стержни можно холодной прокаткой или холодным волочением довести до уровня твердости, который требуется от окончательной продукции.
Такое явление называется деформационным или механическим упрочнением (а также наклепом). Его можно продемонстрировать, скручивая или многократно перегибая металлическую проволоку. Деформационное упрочнение металлических изделий часто осуществляется на заводах. Листовую латунь, медную проволоку, алюминиевые стержни можно холодной прокаткой или холодным волочением довести до уровня твердости, который требуется от окончательной продукции.
Растяжение.
Соотношение между напряжением и деформацией для материалов часто исследуют, проводя испытания на растяжение, и при этом получают диаграмму растяжения – график, по горизонтальной оси которого откладывается деформация, а по вертикальной – напряжение (рис. 1). Хотя при растяжении поперечное сечение образца уменьшается (а длина увеличивается), напряжение обычно вычисляют, относя силу к исходной площади поперечного сечения, а не к уменьшенной, которая давала бы истинное напряжение. При малых деформациях это не имеет особого значения, но при больших может приводить к заметной разнице. На рис. 1 представлены кривые деформация – напряжение для двух материалов с неодинаковой пластичностью. (Пластичность – это способность материала удлиняться без разрушения, но и без возврата к первоначальной форме после снятия нагрузки.) Начальный линейный участок как той, так и другой кривой заканчивается в точке предела текучести, где начинается пластическое течение. Для менее пластичного материала высшая точка диаграммы, его предел прочности на растяжение, соответствует разрушению. Для более пластичного материала предел прочности на растяжение достигается тогда, когда скорость уменьшения поперечного сечения при деформировании становится больше скорости деформационного упрочнения. На этой стадии в ходе испытания начинается образование «шейки» (локальное ускоренное уменьшение поперечного сечения). Хотя способность образца выдерживать нагрузку уменьшается, материал в шейке продолжает упрочняться. Испытание заканчивается разрывом шейки.
На рис. 1 представлены кривые деформация – напряжение для двух материалов с неодинаковой пластичностью. (Пластичность – это способность материала удлиняться без разрушения, но и без возврата к первоначальной форме после снятия нагрузки.) Начальный линейный участок как той, так и другой кривой заканчивается в точке предела текучести, где начинается пластическое течение. Для менее пластичного материала высшая точка диаграммы, его предел прочности на растяжение, соответствует разрушению. Для более пластичного материала предел прочности на растяжение достигается тогда, когда скорость уменьшения поперечного сечения при деформировании становится больше скорости деформационного упрочнения. На этой стадии в ходе испытания начинается образование «шейки» (локальное ускоренное уменьшение поперечного сечения). Хотя способность образца выдерживать нагрузку уменьшается, материал в шейке продолжает упрочняться. Испытание заканчивается разрывом шейки.
Типичные значения величин, характеризующих прочность на растяжение ряда металлов и сплавов, представлены в табл. 2. Нетрудно видеть, что эти значения для одного и того же материала могут сильно различаться в зависимости от обработки.
2. Нетрудно видеть, что эти значения для одного и того же материала могут сильно различаться в зависимости от обработки.
| Таблица 2 | ||||
| Металлы и сплавы | Состояние | Предел текучести, МПа | Предел прочности на растяжение, МПа | Удлинение, % |
| Малоуглеродистая сталь (0,2% С) | Горячекатанная | 300 | 450 | 35 |
| Среднеуглеродистая сталь (0,4% С,0,5% Mn) | Упрочненная и отпущенная | 450 | 700 | 21 |
| Высокопрочная сталь (0,4% С, 1,0% Mn,1,5% Si, 2,0% Cr,0,5% Мo) | Упрочненная и отпущенная | 1750 | 2300 | 11 |
| Серый чугун | После литья | – | 175–300 | 0,4 |
| Алюминий технически чистый | Отожженный | 35 | 90 | 45 |
| Алюминий технически чистый | Деформационно-упрочненный | 150 | 170 | 15 |
| Алюминиевый сплав (4,5% Cu, 1,5% Mg,0,6% Mn) | Упрочненный старением | 360 | 500 | 13 |
| Полностью отожженная | 80 | 300 | 66 | |
| Латунь листовая (70% Cu, 30% Zn) | Деформационно-упрочненная | 500 | 530 | 8 |
| Вольфрам, проволока | Тянутая до диаметра 0,63 мм | 2200 | 2300 | 2,5 |
| Свинец | После литья | 0,006 | 12 | 30 |
Сжатие.

Упругие и пластические свойства при сжатии обычно весьма сходны с тем, что наблюдается при растяжении (рис. 2). Кривая соотношения между условным напряжением и условной деформацией при сжатии проходит выше соответствующей кривой для растяжения только потому, что при сжатии поперечное сечение образца не уменьшается, а увеличивается. Если же по осям графика откладывать истинное напряжение и истинную деформацию, то кривые практически совпадают, хотя при растяжении разрушение происходит раньше.
Твердость.
Твердость материала – это его способность сопротивляться пластической деформации. Поскольку испытания на растяжение требуют дорогостоящего оборудования и больших затрат времени, часто прибегают к более простым испытаниям на твердость. При испытаниях по методам Бринелля и Роквелла в поверхность металла при заданных нагрузке и скорости нагружения вдавливают «индентор» (наконечник, имеющий форму шара или пирамиды). Затем измеряют (часто это делается автоматически) размер отпечатка, и по нему определяют показатель (число) твердости. Чем меньше отпечаток, тем больше твердость. Твердость и предел текучести – это в какой-то мере сравнимые характеристики: обычно при увеличении одной из них увеличивается и другая.
Чем меньше отпечаток, тем больше твердость. Твердость и предел текучести – это в какой-то мере сравнимые характеристики: обычно при увеличении одной из них увеличивается и другая.
Может сложиться впечатление, что в металлических материалах всегда желательны максимальные предел текучести и твердость. На самом деле это не так, и не только по экономическим соображениям (процессы упрочнения требуют дополнительных затрат).
Во-первых, материалам необходимо придавать форму различных изделий, а это обычно осуществляется с применением процессов (прокатки, штамповки, прессования), в которых важную роль играет пластическая деформация. Даже при обработке на металлорежущем станке очень существенна пластическая деформация. Если твердость материала слишком велика, то для придания ему нужной формы требуются слишком большие силы, вследствие чего режущие инструменты быстро изнашиваются. Такого рода трудности можно уменьшить, обрабатывая металлы при повышенной температуре, когда они становятся мягче. Если же горячая обработка невозможна, то используется отжиг металла (медленные нагрев и охлаждение).
Если же горячая обработка невозможна, то используется отжиг металла (медленные нагрев и охлаждение).
Во-вторых, по мере того как металлический материал становится тверже, он обычно теряет пластичность. Иначе говоря, материал становится хрупким, если его предел текучести столь велик, что пластическая деформация не происходит вплоть до тех напряжений, которые сразу же вызывают разрушение. Конструктору обычно приходится выбирать какие-то промежуточные уровни твердости и пластичности.
Ударная вязкость и хрупкость.
Вязкость противоположна хрупкости. Это способность материала сопротивляться разрушению, поглощая энергию удара. Например, стекло хрупкое, потому что оно не способно поглощать энергию за счет пластической деформации. При столь же резком ударе по листу мягкого алюминия не возникают большие напряжения, так как алюминий способен к пластической деформации, поглощающей энергию удара.
Существует много разных методов испытания металлов на ударную вязкость. При использовании метода Шарпи призматический образец металла с надрезом подставляют под удар отведенного маятника. Работу, затраченную на разрушение образца, определяют по расстоянию, на которое маятник отклоняется после удара. Такие испытания показывают, что стали и многие металлы ведут себя как хрупкие при пониженных температурах, но как вязкие – при повышенных. Переход от хрупкого поведения к вязкому часто происходит в довольно узком температурном диапазоне, среднюю точку которого называют температурой хрупко-вязкого перехода. Другие испытания на ударную вязкость тоже указывают на наличие такого перехода, но измеренная температура перехода изменяется от испытания к испытанию в зависимости от глубины надреза, размеров и формы образца, а также от метода и скорости ударного нагружения. Поскольку ни в одном из видов испытаний не воспроизводится весь диапазон рабочих условий, испытания на ударную вязкость ценны лишь тем, что позволяют сравнивать разные материалы. Тем не менее они дали много важной информации о влиянии сплавления, технологии изготовления и термообработки на склонность к хрупкому разрушению.
Работу, затраченную на разрушение образца, определяют по расстоянию, на которое маятник отклоняется после удара. Такие испытания показывают, что стали и многие металлы ведут себя как хрупкие при пониженных температурах, но как вязкие – при повышенных. Переход от хрупкого поведения к вязкому часто происходит в довольно узком температурном диапазоне, среднюю точку которого называют температурой хрупко-вязкого перехода. Другие испытания на ударную вязкость тоже указывают на наличие такого перехода, но измеренная температура перехода изменяется от испытания к испытанию в зависимости от глубины надреза, размеров и формы образца, а также от метода и скорости ударного нагружения. Поскольку ни в одном из видов испытаний не воспроизводится весь диапазон рабочих условий, испытания на ударную вязкость ценны лишь тем, что позволяют сравнивать разные материалы. Тем не менее они дали много важной информации о влиянии сплавления, технологии изготовления и термообработки на склонность к хрупкому разрушению. Температура перехода для сталей, измеренная по методу Шарпи с V-образным надрезом, может достигать +90° С, но соответствующими легирующими присадками и термообработкой ее можно понизить до -130° С.
Температура перехода для сталей, измеренная по методу Шарпи с V-образным надрезом, может достигать +90° С, но соответствующими легирующими присадками и термообработкой ее можно понизить до -130° С.
Хрупкое разрушение стали было причиной многочисленных аварий, таких, как неожиданные прорывы трубопроводов, взрывы сосудов давления и складских резервуаров, обвалы мостов. Среди самых известных примеров – большое количество морских судов типа «Либерти», обшивка которых неожиданно расходилась во время плавания. Как показало расследование, выход из строя судов «Либерти» был обусловлен, в частности, неправильной технологией сварки, оставлявшей внутренние напряжения, плохим контролем за составом сварного шва и дефектами конструкции. Сведения, полученные в результате лабораторных испытаний, позволили существенно уменьшить вероятность таких аварий. Температура хрупко-вязкого перехода некоторых материалов, например вольфрама, кремния и хрома, в обычных условиях значительно выше комнатной. Такие материалы обычно считаются хрупкими, и придавать им нужную форму за счет пластической деформации можно только при нагреве. В то же время медь, алюминий, свинец, никель, некоторые марки нержавеющих сталей и другие металлы и сплавы вообще не становятся хрупкими при понижении температуры. Хотя многое уже известно о хрупком разрушении, это явление нельзя еще считать полностью изученным.
В то же время медь, алюминий, свинец, никель, некоторые марки нержавеющих сталей и другие металлы и сплавы вообще не становятся хрупкими при понижении температуры. Хотя многое уже известно о хрупком разрушении, это явление нельзя еще считать полностью изученным.
Усталость.
Усталостью называется разрушение конструкции под действием циклических нагрузок. Когда деталь изгибается то в одну, то в другую сторону, ее поверхности поочередно подвергаются то сжатию, то растяжению. При достаточно большом числе циклов нагружения разрушение могут вызывать напряжения, значительно более низкие, чем те, при которых происходит разрушение в случае однократного нагружения. Знакопеременные напряжения вызывают локализованные пластическую деформацию и деформационное упрочнение материала, в результате чего с течением времени возникают малые трещины. Концентрация напряжений вблизи концов таких трещин заставляет их расти. Сначала трещины растут медленно, но по мере уменьшения поперечного сечения, на которое приходится нагрузка, напряжения у концов трещин увеличиваются. При этом трещины растут все быстрее и, наконец, мгновенно распространяются на все сечение детали. См. также РАЗРУШЕНИЯ МЕХАНИЗМЫ.
При этом трещины растут все быстрее и, наконец, мгновенно распространяются на все сечение детали. См. также РАЗРУШЕНИЯ МЕХАНИЗМЫ.
Усталость, несомненно, является самой распространенной причиной выхода конструкций из строя в условиях эксплуатации. Особенно подвержены этому детали машин, работающие в условиях циклического нагружения. В авиастроении усталость оказывается очень важной проблемой из-за вибрации. Во избежание усталостного разрушения приходится часто проверять и заменять детали самолетов и вертолетов.
Ползучесть.
Ползучестью (или крипом) называется медленное нарастание пластической деформации металла под действием постоянной нагрузки. С появлением воздушно-реактивных двигателей, газовых турбин и ракет стали приобретать все более важное значение свойства материалов при повышенных температурах. Во многих областях техники дальнейшее развитие сдерживается ограничениями, связанными с высокотемпературными механическими свойствами материалов.
При нормальных температурах пластическая деформация устанавливается почти мгновенно, как только прикладывается соответствующее напряжение, и в дальнейшем мало увеличивается. При повышенных же температурах металлы не только становятся мягче, но и деформируются так, что деформация продолжает нарастать со временем. Такая зависящая от времени деформация, или ползучесть, может ограничивать срок службы конструкций, которые должны длительное время работать при повышенных температурах.
При повышенных же температурах металлы не только становятся мягче, но и деформируются так, что деформация продолжает нарастать со временем. Такая зависящая от времени деформация, или ползучесть, может ограничивать срок службы конструкций, которые должны длительное время работать при повышенных температурах.
Чем больше напряжения и чем выше температура, тем больше скорость ползучести. Типичные кривые ползучести представлены на рис. 3. После начальной стадии быстрой (неустановившейся) ползучести эта скорость уменьшается и становится почти постоянной. Перед разрушением скорость ползучести вновь увеличивается. Температура, при которой ползучесть становится критической, неодинакова для разных металлов. Предметом забот телефонных компаний является ползучесть подвесных кабелей в свинцовой оболочке, работающих при обычных температурах окружающей среды; в то же время некоторые специальные сплавы могут работать при 800° С, не обнаруживая чрезмерной ползучести.
Срок службы деталей в условиях ползучести может определяться либо предельно допустимой деформацией, либо разрушением, и конструктор должен всегда иметь в виду эти два возможных варианта. Пригодность материалов для изготовления изделий, рассчитанных на длительную работу при повышенных температурах, например лопаток турбин, трудно оценить заранее. Испытания за время, равное предполагаемому сроку службы, зачастую практически невозможны, а результаты кратковременных (ускоренных) испытаний не так просто экстраполировать на более длительные сроки, поскольку может измениться характер разрушения. Хотя механические свойства жаропрочных сплавов постоянно улучшаются, перед металлофизиками и материаловедами всегда будет стоять задача создания материалов, способных выдерживать еще более высокие температуры. См. также МЕТАЛЛОВЕДЕНИЕ ФИЗИЧЕСКОЕ.
Пригодность материалов для изготовления изделий, рассчитанных на длительную работу при повышенных температурах, например лопаток турбин, трудно оценить заранее. Испытания за время, равное предполагаемому сроку службы, зачастую практически невозможны, а результаты кратковременных (ускоренных) испытаний не так просто экстраполировать на более длительные сроки, поскольку может измениться характер разрушения. Хотя механические свойства жаропрочных сплавов постоянно улучшаются, перед металлофизиками и материаловедами всегда будет стоять задача создания материалов, способных выдерживать еще более высокие температуры. См. также МЕТАЛЛОВЕДЕНИЕ ФИЗИЧЕСКОЕ.
КРИСТАЛЛИЧЕСКАЯ СТРУКТУРА
Выше речь шла об общих закономерностях поведения металлов под действием механических нагрузок. Чтобы лучше понять соответствующие явления, нужно рассмотреть атомное строение металлов. Все твердые металлы – кристаллические вещества. Они состоят из кристаллов, или зерен, расположение атомов в которых соответствует правильной трехмерной решетке. Кристаллическую структуру металла можно представить как состоящую из атомных плоскостей, или слоев. Когда прикладывается напряжение сдвига (сила, заставляющая две соседние плоскости металлического образца скользить друг по другу в противоположных направлениях), один слой атомов может сдвинуться на целое межатомное расстояние. Такой сдвиг скажется на форме поверхности, но не на кристаллической структуре. Если один слой сдвинется на много межатомных расстояний, то на поверхности образуется «ступенька». Хотя отдельные атомы слишком малы, чтобы их можно было увидеть под микроскопом, ступеньки, образовавшиеся за счет скольжения, хорошо видны под микроскопом и названы линиями скольжения.
Кристаллическую структуру металла можно представить как состоящую из атомных плоскостей, или слоев. Когда прикладывается напряжение сдвига (сила, заставляющая две соседние плоскости металлического образца скользить друг по другу в противоположных направлениях), один слой атомов может сдвинуться на целое межатомное расстояние. Такой сдвиг скажется на форме поверхности, но не на кристаллической структуре. Если один слой сдвинется на много межатомных расстояний, то на поверхности образуется «ступенька». Хотя отдельные атомы слишком малы, чтобы их можно было увидеть под микроскопом, ступеньки, образовавшиеся за счет скольжения, хорошо видны под микроскопом и названы линиями скольжения.
Обычные металлические предметы, встречающиеся нам ежедневно, являются поликристаллическими, т.е. состоят из большого числа кристаллов, в каждом из которых своя ориентация атомных плоскостей. Деформация обычного поликристаллического металла имеет с деформацией монокристалла то общее, что она происходит за счет скольжения по атомным плоскостям в каждом кристалле.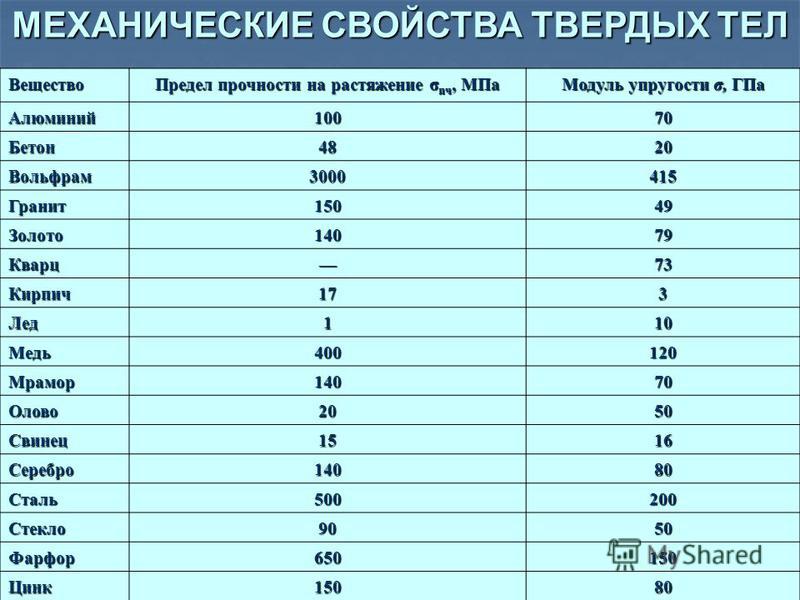 Заметное же скольжение целых кристаллов по их границам наблюдается только в условиях ползучести при повышенных температурах. Средний размер одного кристалла, или зерна, может составлять от нескольких тысячных до нескольких десятых долей сантиметра. Желательна более мелкая зернистость, так как механические характеристики мелкозернистого металла лучше, чем у крупнозернистого. Кроме того, мелкозернистые металлы менее хрупки.
Заметное же скольжение целых кристаллов по их границам наблюдается только в условиях ползучести при повышенных температурах. Средний размер одного кристалла, или зерна, может составлять от нескольких тысячных до нескольких десятых долей сантиметра. Желательна более мелкая зернистость, так как механические характеристики мелкозернистого металла лучше, чем у крупнозернистого. Кроме того, мелкозернистые металлы менее хрупки.
Скольжение и дислокации.
Процессы скольжения удалось подробнее исследовать на монокристаллах металлов, выращенных в лаборатории. При этом выяснилось не только то, что скольжение происходит в некоторых определенных направлениях и обычно по вполне определенным плоскостям, но и то, что монокристаллы деформируются при очень малых напряжениях. Переход монокристаллов в состояние текучести начинается для алюминия при 1, а для железа – при 15–25 МПа. Теоретически же этот переход в обоих случаях должен происходить при напряжениях ок. 10 000 МПа. Такое расхождение между экспериментальными данными и теоретическими расчетами на протяжении многих лет оставалось важной проблемой.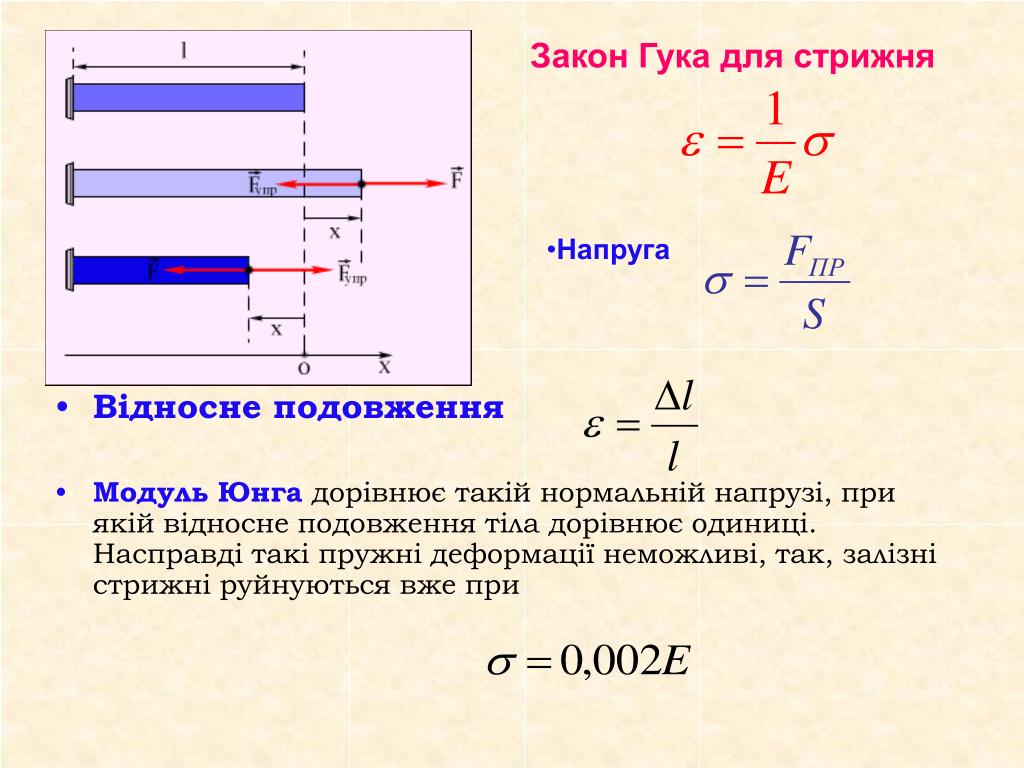 В 1934 Тейлор, Полани и Орован предложили объяснение, основанное на представлении о дефектах кристаллической структуры. Они высказали предположение, что при скольжении сначала происходит смещение в какой-то точке атомной плоскости, которое затем распространяется по кристаллу. Граница между сдвинувшейся и несдвинувшейся областями (рис. 4) представляет собой линейный дефект кристаллической структуры, названный дислокацией (на рисунке эта линия уходит в кристалл перпендикулярно плоскости рисунка). Когда к кристаллу прикладывается напряжение сдвига, дислокация движется, вызывая скольжение по плоскости, в которой она находится. После того как дислокации образовались, они очень легко движутся по кристаллу, чем и объясняется «мягкость» монокристаллов.
В 1934 Тейлор, Полани и Орован предложили объяснение, основанное на представлении о дефектах кристаллической структуры. Они высказали предположение, что при скольжении сначала происходит смещение в какой-то точке атомной плоскости, которое затем распространяется по кристаллу. Граница между сдвинувшейся и несдвинувшейся областями (рис. 4) представляет собой линейный дефект кристаллической структуры, названный дислокацией (на рисунке эта линия уходит в кристалл перпендикулярно плоскости рисунка). Когда к кристаллу прикладывается напряжение сдвига, дислокация движется, вызывая скольжение по плоскости, в которой она находится. После того как дислокации образовались, они очень легко движутся по кристаллу, чем и объясняется «мягкость» монокристаллов.
В кристаллах металлов обычно имеется множество дислокаций (общая длина дислокаций в одном кубическом сантиметре отожженного металлического кристалла может составлять более 10 км). Но в 1952 научные сотрудники лабораторий корпорации «Белл телефон», испытывая на изгиб очень тонкие нитевидные кристаллы («усы») олова, обнаружили, к своему удивлению, что изгибная прочность таких кристаллов близка к теоретическому значению для совершенных кристаллов. Позднее были обнаружены чрезвычайно прочные нитевидные кристаллы и многих других металлов. Как предполагают, столь высокая прочность обусловлена тем, что в таких кристаллах либо вообще нет дислокаций, либо имеется одна, идущая по всей длине кристалла.
Позднее были обнаружены чрезвычайно прочные нитевидные кристаллы и многих других металлов. Как предполагают, столь высокая прочность обусловлена тем, что в таких кристаллах либо вообще нет дислокаций, либо имеется одна, идущая по всей длине кристалла.
Температурные эффекты.
Влияние повышенных температур можно объяснить, исходя из представлений о дислокациях и зеренной структуре. Многочисленные дислокации в кристаллах деформационно-упрочненного металла искажают кристаллическую решетку и увеличивают энергию кристалла. Когда же металл нагревается, атомы становятся подвижными и перестраиваются в новые, более совершенные кристаллы, содержащие меньше дислокаций. С такой рекристаллизацией и связано разупрочнение, которое наблюдается при отжиге металлов.
www.krugosvet.ru
| ЗАДАЧНИК ОНЛ@ЙН БИБЛИОТЕКА 1 БИБЛИОТЕКА 2 Примечание. Значение модуля упругости зависит от структуры, химическая состава и способа обрабртки материила. | Таблица модуль Юнга. Модуль упругости. Определение модуля Юнга. Коэффицент запаса прочности.Таблица модуль Юнга
Предел прочности материалаДопускаемое механическое напряжение в некоторых метериалах (при растяжении)Коэффициент запаса прочностиПродолжение будет. | ||||
www.kilomol.ru
| Материал | Модули упругости, МПа | Коэффициент Пуассона | |
| Модуль ЮнгаE | Модуль сдвигаG | ||
| Чугун белый, серый Чугун ковкий | (1,15…1,60)·105 1,55·105 | 4,5·104 – | 0,23…0,27 – |
| Сталь углеродистая Сталь легированная | (2,0…2,1)·105 (2,1…2,2)·105 | (8,0…8,1)·104 (8,0…8,1)·104 | 0,24…0,28 0,25…0,30 |
| Медь прокатная Медь холоднотянутая Медь литая | 1,1·105 1,3·105 0,84·105 | 4,0·104 4,9·104 – | 0,31…0,34 – – |
| Бронза фосфористая катаная Бронза марганцовистой катаная Бронза алюминиевая литая | 1,15·105 1,1·105 1,05·105 | 4,2·104 4,0·104 4,2·104 | 0,32. ..0,35
0,35
– ..0,35
0,35
– |
| Латунь холоднотянутая Латунь корабельная катаная | (0,91…0,99)·105 1,0·105 | (3,5…3,7)·104 – | 0,32…0,42 0,36 |
| Алюминий катаный Проволока алюминиевая тянутая Дюралюминий катаный | 0,69·105 0,7·105 0,71·105 | (2,6…2,7)·104 – 2,7·104 | 0,32…0,36 – – |
| Цинк катаный | 0,84·105 | 3,2·104 | 0,27 |
| Свинец | 0,17·105 | 0,7·104 | 0,42 |
| Лед | 0,1·105 | (0,28…0,3)·104 | – |
| Стекло | 0,56·105 | 0,22·104 | 0,25 |
| Гранит | 0,49·105 | – | – |
| Известняк | 0,42·105 | – | – |
| Мрамор | 0,56·105 | – | – |
| Песчаник | 0,18·105 | – | – |
| Каменная кладка из гранита Каменная кладка из известняка Каменная кладка из кирпича | (0,09. ..0,1)·105
0,06·105
(0,027…0,030)·105 ..0,1)·105
0,06·105
(0,027…0,030)·105 | – – – | – – – |
| Бетон при пределе прочности, МПа: 10 15 20 | (0,146…0,196)·105 (0,164…0,214)·105 (0,182…0,232)·105 | – – – | 0,16…0,18 0,16…0,18 0,16…0,18 |
| Древесина вдоль волокон Древесина поперек волокон | Мобильный бетонный завод на шасси|||
Модуль упругости стали в кгс\см2, примеры
Модуль упругости стали в кгс\см2, примеры- Статьи
- Обновлено 10 октября 2020 г.
Одной из главных задач инженерного проектирования является выбор материала конструкции и оптимального сечения профиля. Необходимо найти тот размер, который при минимально возможной массе будет обеспечивать сохранение формы системы под воздействием нагрузки.
Например, какой номер стального двутавра использовать в качестве пролетной балки сооружения? Если взять профиль размерами ниже требуемого, то гарантировано получим разрушение строения. Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Если больше, то это ведет к нерациональному использованию металла, а, следовательно, утяжелению конструкции, усложнению монтажа, увеличению финансовых затрат. Знание такого понятия как модуль упругости стали даст ответ на вышепоставленный вопрос, и позволит избежать появления данных проблем на самом раннем этапе производства.
Общее понятие
Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).
В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.
Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.
Но на практике инженеры предпочитают использовать размерность кгс/см2.
Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.
Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.
Дополнительные характеристики механических свойств
Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:
- Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом.
 Измеряется в килограммах силы.
Измеряется в килограммах силы. - Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
- Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
- Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
- Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т.
 е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла. - Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.
Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.
У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.
Значение модуля упругости
Необходимо заметить, что модуль Юнга не является постоянной величиной. Даже для одного и того же материала он может колебаться в зависимости от точек приложения силы.
Некоторые упруго – пластичные материалы обладают более или менее постоянным модулем упругости при работе как на сжатие, так и на растяжение: медь, алюминий, сталь. В других случаях упругость может изменяться исходя из формы профиля.
Вот примеры значений модуля Юнга (в миллионах кгс\см2) некоторых материалов:
- Чугун белый – 1,15.
- Чугун серый -1,16.
- Латунь – 1,01.
- Бронза – 1,00.
- Кирпичная каменная кладка – 0,03.
- Гранитная каменная кладка – 0,09.
- Бетон – 0,02.
- Древесина вдоль волокон – 0,1.
- Древесина поперек волокон – 0,005.
- Алюминий – 0,7.
Рассмотрим разницу в показаниях между модулями упругости для сталей в зависимости от марки:
- Стали конструкционные высокого качества (20, 45) – 2,01.

- Стали обычного качества (Ст.3, Ст.6) – 2,00.
- Стали низколегированные (30ХГСА, 40Х) – 2,05.
- Стали нержавеющие (12Х18Н10Т) – 2,1.
- Стали штамповые (9ХМФ) – 2,03.
- Стали пружинные (60С2) – 2,03.
- Стали подшипниковые (ШХ15) – 2,1.
Также значение модуля упругости для сталей изменяется исходя из вида проката:
- Проволока высокой прочности – 2,1.
- Плетенный канат – 1,9.
- Трос с металлическим сердечником – 1,95.
Как видим, отклонения между сталями в значениях модулей упругой деформации имеют небольшую величину. Поэтому в большинстве инженерных расчетов можно пренебречь погрешностями и брать значение Е=2,0.
Оцените статью:
Рейтинг: 0/5 – 0 голосов
Ещё статьи по теме:
Модуль юнга для стали и других материалов
ПОИСК
Е — приведенный модуль Юнга, принятый равным модулю упругости стали [c. 71]
71]
Деформационные свойства. Модуль Р. (Е) при небольшом растяжении на 4—5 десятичных порядков ниже модуля Юнга для стали [соответственно 0,5— [c.158]
МОДУЛЬ ЮНГА УГЛЕРОДИСТОЙ И ЛЕГИРОВАННОЙ СТАЛЕЙ ПРИ РАЗНЫХ ТЕМПЕРАТУРАХ [c.16]
Следует отметить, что высокая эластичность каучука совершенно отлична от упругих деформаций кристаллических веществ или металлов, составляющих всего несколько процентов от исходных размеров, тогда как каучук можно растягивать в 10 раз.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20000 кг/мм , для стекла около 6000 кг/мм , а для каучука лишь около [c.228]
При конструировании важно установить распределение деформаций конструкции, возникающих в процессе эксплуатации под влиянием приложенных напряжений. Напряжения могут возникать из-за давления, создаваемого жидкостью или газом, течением жидкости или неоднородным температурным расширением при изменениях температуры. Упругие свойства часто считают не зависящими от структуры, но существуют ситуации, когда такое утверждение становится неверным. Отдельные зерна металлических кристаллов в отношении упругих свойств анизотропны. Таким образом, упругие постоянные зависят от ориентации зерна по отношению к ориентации приложенных напряжений. В процессе производства деталей может возникнуть преимущественная ориентация отдельных зерен, что и создает упругую анизотропию. Весьма вероятно, что различные степени преимущественной ориентации приводят к довольно широкому разбросу данных по упругим свойствам металлов и сплавов. Вследствие того что этот разброс может вызывать появление погрешности, достигающей в некоторых случаях при расчетах деформаций 20 %, эта тема детально рассматривается в настоящем параграфе. Таблица 3, 4.5,8 — лишь пример того типа информации, которая встречается в литературе.
Напряжения могут возникать из-за давления, создаваемого жидкостью или газом, течением жидкости или неоднородным температурным расширением при изменениях температуры. Упругие свойства часто считают не зависящими от структуры, но существуют ситуации, когда такое утверждение становится неверным. Отдельные зерна металлических кристаллов в отношении упругих свойств анизотропны. Таким образом, упругие постоянные зависят от ориентации зерна по отношению к ориентации приложенных напряжений. В процессе производства деталей может возникнуть преимущественная ориентация отдельных зерен, что и создает упругую анизотропию. Весьма вероятно, что различные степени преимущественной ориентации приводят к довольно широкому разбросу данных по упругим свойствам металлов и сплавов. Вследствие того что этот разброс может вызывать появление погрешности, достигающей в некоторых случаях при расчетах деформаций 20 %, эта тема детально рассматривается в настоящем параграфе. Таблица 3, 4.5,8 — лишь пример того типа информации, которая встречается в литературе. Можно полагать, например, что стали с 5—9 %-ным содержанием хрома должны иметь примерно те же значения модуля Юнга, что и стали, содержание хрома в которых близко к указанному. [c.196]
Можно полагать, например, что стали с 5—9 %-ным содержанием хрома должны иметь примерно те же значения модуля Юнга, что и стали, содержание хрома в которых близко к указанному. [c.196]
Прочность сталей значительно изменяется при переходе к высоким температурам. Так, предел прочности при растяжении хромоникелевой стали типа 18-8 падает с 7000 до 4000 кгс/см при 700 °С до 2000 кгс/см при 800 °С. Модуль Юнга углеродистой и легированной сталей уменьшается при нагревании от 20 до 500 °С на 30%. [c.19]
Иногда для повышения прочности между двумя пьезоэлементами помещают металлическую пластину [318].
Собственная частота преобразователя может быть повышена расположением двух пассивных (например, стальных) пластин по обе стороны от биморфного преобразователя из двух пьезопластин.
Это объясняется тем, что модуль Юнга стали много больше, чем у пьезокерамики, а изгибная жесткость конструкции определяется в основном ее [c. 70]
70]
Твердость вещества можно оценить при помощи модуля Юнга, представляющего собой отношение приложенного напряжения (или силы, отнесенной к единице площади) и соответствующей ему деформации или удлинения.
Типичные значения модуля Юнга для различных материалов представлены на рис. 7.1. На одном конце шкалы расположены неорганические кристаллические материалы, такие, как алмаз, кварц, сталь и т. д., модули которых [c.
131]
Еще большее впечатление производит различие в силе, необходимой для осуществления деформации.
Для удлинения стальной проволоки диаметром 1 мм на 1% требуется нагрузка в 1600 Н (двукратный средний вес человека), а для удлинения каучуковой нити того же диаметра на ту же величину необходима нагрузка меньше Ю Н.
Так называемый модуль Юнга (отношение напряжения к удлинению) для стали в 100 000 раз больше, чем для каучука. [c.45]
Характеристика сталей и сплавов при комнатной температуре и частоте колебаний 20 кгц (р — плотность Е — модуль Юнга Спр — скорость звука рс — волновое сопротивление [c. 115]
115]
Следует отметить, что для коммуникаций часто применяют титан неоправданно большой толщины, что не вызывается ни прочностными, ни коррозионными требованиями. Часто на титан как конструкционный материал переносятся представления, сложившиеся в результате многолетней работы со сталью.
Так, при замене коммуникаций из стали на титановые используют титан той же толщины, что и сталь. Большой расход титана именно на коммуникации объясняется в некоторой степени и этой причиной.
Например, коллекторы влажного хлора на заводах делают из листов титана толщиной 3—5 мм (только на двух предприятиях эти коллекторы сделаны из листов толщиной 2 мм, но и это значительная толщина). За рубежом для данных целей используют титан толщиной 0,8—1,0 мм.
В связи с тем, что модуль Юнга у титана незначителен, при расчетах следует обращать внимание на возможный прогиб труб, а при монтаже — на крепление трубопроводов. [c.156]
Любопытные наблюдения публикует Фирс-Виккерс, утверждая, что нержавеющие аустенитовые стали (хромовые и хромоникелевые) дают падение модуля Юнга приблизительно на 1% на каждые 30° повыщения температуры.
В случае особенно тяжелых условий работы лучше всего обратиться за информацией к поставщикам стали. [c.670]
Вулканизованный каучук способен испытывать обратимые деформации на сотни процентов при весьма малом значении модуля упругости. (Модуль Юнга для стали 20 000—22 000 кг/см , для каучука [c.10]
Следует отметить, что высокая эластичность каучука совершенно отличается от упругих деформаций кристаллических веществ или металлов, которые составляют всего несколько процентов от исходных размеров, тогда как каучук можно растягивать до десятикратных удлинений.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20 ООО кг/мм», для стекла—около 6000 кг/мм , а для каучука—лишь около 0,1 кг/мм». Эти различия объясняются тем, что нри упругой деформации кристаллов происходят лишь небольшие изменения средних расстояний между молекулами и валентных расстояний между атомами, связанные со значительными изменениями внутренней энергии напротив, при чистой высоко-эластической деформации большие удлинения происходят без изменения валентных расстояний нри постоянстве внутренней энергии. [c.272]
[c.272]
На практике все большее применение стали получать ОВ с двуслойным покрытием, в которых первый слой выполнен мягким (буферным) с низким (1—2 МПа) модулем Юнга, а второй—с высоким модулем Юнга от 0,1 до 4 ГПа [52] [c.101]
В формуле (П1.2) за начальную деформацию 5 обычно (но не обязательно) принимается величина некоторой условно упругой деформации, которая определяет начало пластического течения материала.
Так, если известен модуль Юнга Е или условный предел текучести сг (стандартные справочные характеристики конструкционных сталей), то 0 определяется через любую из этих характеристик с помощью очевидных соотношений [c.572]
Относительный вклад в полную деформацию атомов, совершающих большие перемещения, увеличивается при больших напряжениях и повышенных температурах.
Зависимость упругих свойств от структуры и времени при этих условиях становится еще более очевидной.
Значения модуля Юнга стали при 600 «С могут отличаться примерно вдвое для квазистатических и иысокочастот]1ых нагрузок или для ползучестойкой и мягкой стали [1]. [c.197]
По М.с. различают след. осн. типы материалов 1) жесткие и хрупкие (чугуны, высокоориентир. волокна, камни и др.), для них характерны модули Юнга > 10 ГПа и низкие разрывные удлинения (до неск. %) 2) твердые и пластичные (мн.
пластмассы, мягкие стали, нек-рые цветные металлы), для них характерен модуль Юнга > 2 ГПа и большие разрывные удлинения 3) эластомеры (резины)-низкомодульные в-ва (мвновесный модуль высокоэластичности порядка 0,1-2 МПа), способные к огромнььм обратимым деформациям (сотни %) 4) вязкопластичные среды, способные к неограниченным деформациям и сохраняющие приданную им форму после снятия нагрузки (глины, пластичные смазки, бетонные смеси), 5) жидкости, расплавы солей, металлов, полимеров и т п., способные к необратимым деформациям (течению) и принимающие заданную форму. Возможны также разнообразные промежут. случаи проявления М. с. [c.76]
Возможны также разнообразные промежут. случаи проявления М. с. [c.76]
При проведении теоретических расчетов анизотропии модуля Юнга считается, что упругие свойства поликристаллических материалов определяются константами упругости монокристаллов и преимущественными ориентировками зерен в пространстве [299, 301-305, 307].
При этом обычно пренебрегают взаимодействием между соседними зернами и пользуются различными аппроксимациями.
Наиболее близкой к эксперименту является аппроксимация Хилла, который предложил брать среднее от аппроксимаций Фойгта (одинаковая деформация всех зерен) и Ройсса (одинаковое напряжение во всех зернах).
Бунге в работе [292] рассчитал зависимость величины модуля Юнга от ориентации в плоскости прокатки для холоднокатаной Си. При этом полученная зависимость аналогична по форме экспериментальным данным и ощибка не превышает 7%. Аналогичные исследования были выполнены для Fe промышленной чистоты и Nb [293], стали [294], Си [295]. [c.175]
[c.175]
Следует отметить, что высокая эластичность каучука совершенно отлична от упругих деформаций кристаллических веществ или металлов, составляющих всего несколько процентов от исходных размеров, тогда как каучук можно растягивать в 10 раз.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением-и относительным удлинением образца, составляет для стали около 20000 кг мм , для стекла около 6000 кгЬш , а для каучука лишь около 0,1 кг/мм .
Эти различия объясняются тем, что при упругой деформации кристаллов происходят небольшие изменения средних расстояний между молекулами и валентных расстояний между атомами, связанные со значительными изменениями внутренней энергии.
Напротив, при чистой высокоэластической деформации большие удлинения происходят без изменения валентных расстояний, при постоянстве внутренней энергии (во всяком случае, при удлинениях до 3 раз). Лишь у идеальных газов можно также осуществить большие обратимые сжатия под действием небольших напряжений без изменения внутренней энергии.
Лишь у идеальных газов можно также осуществить большие обратимые сжатия под действием небольших напряжений без изменения внутренней энергии.
Сжатый газ в замкнутом пространстве после снятия давления вновь возвращается к первоначальному объему благодаря тому, что этот процесс соответствует переходу в наиболее вероятное состояние и происходит с увеличением энтропии. Легко видеть, что механизм упругих деформаций газа, несмотря на внешнее несходство, вполне аналогичен механизму эластической деформации каучука, причем модуль [c.228]
Поражает разнообразие применений, которые уже придуманы для нанотрубок. Первое, это использование нанотрубок в качестве очень прочных микроскопических стержней, нитей, волокон.
Как показывают результаты экспериментов и численного моделирования, модуль Юнга однослойной нанотрубки достигает величин порядка 1-5 ТПа, что на порядок больше, че.м у стали Правда, в настоящее время максимальная длина нанотрубок составляет десятки и сотни. микронов — что, конечно, очень велико по ато.
микронов — что, конечно, очень велико по ато.
мным масштабам, но слишком мало для широкого использования. Однако длина нанотрубок, получаемых в лаборатории, постепенно увеличивается — сейчас ученые уже подошли к миллиметровому рубежу. Поэтов есть все основания надеяться, что в скоро.м будуще.м научатся вьфащивать нанотрубки длиной в сантиметры и даже метры.
Безусловно, это сильно повлияет на будущие технологии ведь «трос» толщиной с человеческий волос, способный удерживать груз в сотни килoфa.vIм, найдет себе бесчисленное множество при.менений. [c.175]
В стеклообразном состоянии (см. рис. 29) при малых напряжениях в полимере возникает только упругая деформация с модулем Юнга 200—600 кгс/мм (для стали модуль Юига равен 20 ООО кгс/мм—). При больших напряжениях деформационные свойства.
аморфных полимеров сложнее В стеклообразном состоянии, в котором пластмас-сы находятся при обычных, а каучуки и резины при низких температурах, растяжение аморфного полимера (рис.
33) внешне пронсходит так же, как и кристаллического, Когда условное напряжение достигает так называемого предела вынужденной эластичности (точка А), в наиболее слабом месте образца образуется шейка , в которую постепенно переходит весь образец (участок А Б). Затем тонкий образец еиде несколько растягивается до разрыва (участок ББ). [c.69]
Коэффициент пропорциональности Е называется модулем упругости, или модулем Юнга. Выше предела применимости закона Гука зависимость деформации от напряжения носит сложный характер.
На примере кривой для стали видно, что нри значительных деформа1(иях может возникать упрочнение деформируемого тела (уменьшение зависимости удлинения от напряжения).
В конце концов напряжение достигает критического значения, и деформируемое тело разрушается при удлинении — разрывается (рис.
73). [c.338]
Е — модуль Юнга материала, фунт/дюйм (0,07 кГ/см ) р — плотность материала, фунт/фут (0,016 г см ) 8 = 30-106 фунт дюйм — иолуяъ Юнга для стали [c.356]
Коэффициент пропорциональности Е называется модулем упругости или модулем Юнга. Выше предела применимости закона Гука зависимость деформации от напряжения носит сложный характер.
На примере кривой для стали видно, что при значительных деформациях может возникать упрочнение деформируемого тела (уменьшение зависимости удлинения от напряжения). В конце концов напряжение достигает критического значения и деформируемое тело разрушается при удлинении (рис. 1,1Х)—разрывается.
Значение критического напряжения и предельной величины удлинения — важные показатели механических свойств технических полимеров. [c.249]
Опытные данные показывают [124], что трубные стали обладают свойством изотропии своих физико-механических свойств в достаточно хорошем приближении. Кроме того, при малых деформациях они, как и большинство конструкционных материалов, следуют закону Гука.
Кроме того, при малых деформациях они, как и большинство конструкционных материалов, следуют закону Гука.
Поэтому, в случае физического обоснования малости ожидаемых деформаций, либо в других строго обоснованных случаях, при анализе НДС промышленной трубопроводной системы можно использовать линейно-упругую модель материала труб, не снижая точности результатов и существенно уменьшая трудоемкость и время проведения расчетов. В качестве независимых параметров упругих свойств материала удобно использовать стандартные технические характеристики модуль Юнга Е коэффициент Пуассона V (либо модуль сдвига О). Эти характеристики связаны между собой соотношением [123] [c.278]
Источник: http://chem21.info/info/390636/
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
| Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
| Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
| Железо | 21,2 | 8,2 | 0,29 | 16,9 |
| Золото | 7,8 | 2,7 | 0,44 | 21,7 |
| Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
| Медь | 12,98 | 4,833 | 0,343 | 13,76 |
| Никель | 20,4 | 7,9 | 0,280 | 16,1 |
| Платина | 16,8 | 6,1 | 0,377 | 22,8 |
| Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
| Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
| Титан | 11,6 | 4,38 | 0,32 | 10,7 |
| Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
| Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
| (мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
| Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
| Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. 2) 60% Cu, 40% Ni. |
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
| Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
| Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
| Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
| Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | — |
| Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
| Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
| Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
| Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
| Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
| Магний | 4,25 | 1,63 | 0,30 | — |
| Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | — |
| Платиноид3) | 13,6 | 3,6 | 0,37 | — |
Кварцевые нити (плав. ) ) | 7,3 | 3,1 | 0,17 | 3,7 |
| Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | — |
| Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
| Цинк | 8,7 | 3,8 | 0,21 | — |
| 1) 60% Cu, 15% Ni, 25% Zn2) 92,5% Cu, 7% Sn, 0,5% P3) Нейзильбер с небольшим количеством вольфрама. |
| Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
| Цинк (чистый) | 9,0 | Дуб | 1,3 |
| Иридий | 52,0 | Сосна | 0,9 |
| Родий | 29,0 | Красное дерево | 0,88 |
| Тантал | 18,6 | Цирконий | 7,4 |
| Инвар | 17,6 | Титан | 10,5-11,0 |
| Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
| Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
| Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
| Паутина2 | 0,3 | Серебро | 7,1-8,3 |
| Кетгут | 0,32 | Пластмассы: | |
| Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
| Кварц | 7,3 | Термореактивные | 0,35-1,1 |
| Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
| 1) Быстро уменьшается с увеличением нагрузки2) Обнаруживает заметную упругую усталость |
| Температурный коэффициент (при 150С)Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1(при 7-110С) | |||
| ɑ, для Е | ɑ, для G | |||
| Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
| Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
| Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
| Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
| Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
| Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
| Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
| Олово | — | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
| Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
| Нейзильбер | — | 6,5*10-4 | ||
| Фосфористая бронза | — | 3,0*10-4 | ||
| Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
Источник: http://infotables. ru/fizika/295-uprugie-svojstva-tel
ru/fizika/295-uprugie-svojstva-tel
Модуль Юнга для стали
Под термином модуля Юнга или продольной упругости конструкционного материала принято понимать физическую величину, которая показывает определенное свойство материалов. Свойство это обеспечивает их сопротивление, действующим деформациям в продольном направлении. Иными словами, этот показатель говорит о степени жесткости какого-либо конкретного материала.
Свое название данный модуль получил, благодаря Томасу Юнгу, который и работал над выявлением данного феномена. Такая физическая величина выражается в Паскалях и обозначается буквой латинского алфавита – Е.
Область применения
Основной сферой применения данного показателя является испытание всевозможных материалов.
Благодаря этой величине можно судить о степени деформации материала во время его растяжения, сжатия и изгиба. В строительстве крайне важно знать модуль Юнга всех материалов, использующихся в работе.
В строительстве крайне важно знать модуль Юнга всех материалов, использующихся в работе.
Именно от него, в большей степени, зависит уровень прочности, долговечности и надежности возведенных зданий.
Нередко можно заметить, что при выражении этой величины, существует приставка «гига». Это делается по той причине, что у многих материалов модуль Юнга имеет достаточно высокую характеристику, доходящую до порядка 109 Па. Для облегчения выражения и добавляется эта приставка, выражающаяся на письме следующим образом «ГПА».
Существует специальная таблица, согласно которой, можно найти показатель модуля Юнга того или иного материала. Так, модуль Юнга для стали равняется 200 Е, (ГПА), что может считаться достаточно высокой цифрой. а наименьшим показателем обладает дерево — всего 10 Е, (ГПА).
Формула модуля Юнга
Если модуль Юнга нужно показать графически, то следует изобразить специальную диаграмму напряжения. На ней будут изображены кривые, которые получались при многократном испытании на прочность одного и того же вещества.
Тогда модуль Юнга можно выразить отношением нормального напряжения к показателю деформации на каком-то участке диаграммы.
Таким образом, математическое выражение можно записать следующим способом E=σ/ε=tgα.
При этом следует помнить, что этот модуль может рассматриваться в виде коэффициента пропорциональности в описании закона Гука, имеющего следующее значение σ=Eε.
Тогда, модуль продольной упругости и показатели поперечных сечений оказываются в непосредственной связи. Зависимость эта может выражаться, как ЕА и Е1.
ЕА является показателем жесткости при сжатии и растяжении материала на его поперечном сечении. Площадь сечения в этом выражении обозначается буквой «А».
Е1 означает показатель жесткости во время изгиба поперечного сечения материала. В этой формуле «1» означает осевой момент инерции, появляющийся в сечении изгибаемого материала.
Самые высокие показатели модуля Юнга имеют:
• Хром – 300 Е, (ГПА)
• Никель – 210 Е, (ГПА)
• Сталь — 200 Е, (ГПА)
• Чугун – 120 Е, (ГПА)
• Хром – 110 Е, (ГПА)
• Кремний – 110 Е, (ГПА).
Среди материалов с самым низким значением модуля Юнга можно отметить:
• Олово – 35 Е, (ГПА)
• Бетон – 20 Е, (ГПА)
• Свинец – 18 Е, (ГПА)
• Древесина – 10 Е, (ГПА).
Источник: http://specural.com/articles/5/modul-yunga-dlya-stali.html
Модуль упругости алюминия и алюминиевых сплавов
Модуль упругости = Модуль Юнга
На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза.
Наклон этой части кривой определяет характеристику материала — модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.
Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа.
См. Модуль упругости различных алюминиевых сплавов
Модуль упругости различных алюминиевых сплавов
Ясно, что если стальную балку заменить на идентичную по форме балку из алюминиевого сплава, то вес ее будет в три раза меньше, но и ее упругий прогиб под той же нагрузкой будет приблизительно в три раза больше.
Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.
Жесткость алюминиевых профилей
Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки.
Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений. Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение.
Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение.
В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.
В таблицах представлены типичные прочностные характеристики популярных деформируемыхалюминиевых сплавов: предел прочности, предел текучести и удлинение при испытаниях на растяжение, а также усталостная прочность, твердость и модуль упругости – отдельно для сплавов, упрочняемых нагартовкой, и сплавов, упрочняемые термической обработкой. Как типичные свойства они годятся только для сравнительных целей, а не для инженерных расчетов. В большинстве случаев они являются средними значениями для различных размеров изделий, их форм и методов изготовления.
Источник: Aluminium and Aluminium Alloys. — ASM International, 1993.
Источник: http://uvakin.ru/modul-uprugosti-alyuminiya-i-alyuminievyx-splavov/
Модуль Юнга
модуль юнга, модуль юнга вікіпедія
L−1MT−2
Па
дин·см-2
Модуль Юнга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
где:
- F — нормальная составляющая силы,
- S — площадь поверхности, по которой распределено действие силы,
- l — длина деформируемого стержня,
- — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где — плотность вещества.
Содержание
- 1 Связь с другими модулями упругости
- 2 Значения модуля Юнга для некоторых материалов
- 3 См. также
- 4 Примечания
- 5 Литература
- 6 Ссылки
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями
и
где — коэффициент Пуассона.
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Германий | 83 |
| Дюралюминий | 74 |
| Иридий | 520 |
| Кадмий | 50 |
| Кобальт | 210 |
| Константан | 163 |
| Кремний | 109 |
| Латунь | 95 |
| Лёд | 3 |
| Магний | 45 |
| Манганин | 124 |
| Медь | 110 |
| Никель | 210 |
| Олово | 35 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 210 |
| Стекло | 70 |
| Титан | 112 |
| Фарфор | 59 |
| Цинк | 120 |
| Хром | 300 |
См.
 также
такжеПримечания
- ↑ Модули упругости – Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
Литература
- Волькенштейн, В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
- Квазистатический модуль Юнга (код на Mathcad).
- Модуль упругости I рода
Объёмный модуль упругости () | Модуль Юнга () | Параметры Ламе () | Модуль сдвига () | Коэффициент Пуассона () | en:P-wave modulus () |
модуль юнга, модуль юнга вікіпедія, модуль юнга деформация, модуль юнга н/мм2, модуль юнга стали, модуль юнга формула, модуль юнга это
Модуль Юнга Информацию О
Модуль Юнга
Модуль Юнга
Модуль Юнга Вы просматриваете субъект
Модуль Юнга что, Модуль Юнга кто, Модуль Юнга описание
There are excerpts from wikipedia on . postlight.com»>
postlight.com»>
Источник: https://www.turkaramamotoru.com/ru/-90808.html
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) – (α)
μ = (E / 2G) – 1 – (b)
K = E / 3(1 – 2μ) – (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
|
Материал при 18°С |
Модуль Юнга E, 1011 дин/см2. |
Модуль сдвига G, 1011 дин/см2. |
Коэффициент Пуассона µ |
Модуль объемной упругости К, 1011 дин/см2. |
|
Алюминий |
7,05 |
2,62 |
0,345 |
7,58 |
|
Висмут |
3,19 |
1,20 |
0,330 |
3,13 |
|
Железо |
21,2 |
8,2 |
0,29 |
16,9 |
|
Золото |
7,8 |
2,7 |
0,44 |
21,7 |
|
Кадмий |
4,99 |
1,92 |
0,300 |
4,16 |
|
Медь |
12,98 |
4,833 |
0,343 |
13,76 |
|
Никель |
20,4 |
7,9 |
0,280 |
16,1 |
|
Платина |
16,8 |
6,1 |
0,377 |
22,8 |
|
Свинец |
1,62 |
0,562 |
0,441 |
4,6 |
|
Серебро |
8,27 |
3,03 |
0,367 |
10,4 |
|
Титан |
11,6 |
4,38 |
0,32 |
10,7 |
|
Цинк |
9,0 |
3,6 |
0,25 |
6,0 |
|
Сталь (1% С) 1) |
21,0 |
8,10 |
0,293 |
16,88 |
|
(мягкая) |
21,0 |
8,12 |
0,291 |
16,78 |
|
Константан 2) |
16,3 |
6,11 |
0,327 |
15,7 |
|
Манганин |
12,4 |
4,65 |
0,334 |
12,4 |
|
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
|
Вещество |
Модуль Юнга E, 1011 дин/см2. |
Модуль сдвига G, 1011 дин/см2. |
Коэффициент Пуассона µ |
Модуль объемной упругости К, 1011 дин/см2. |
|
Бронза (66% Cu) |
-9,7-10,2 |
3,3-3,7 |
0,34-0,40 |
11,2 |
|
Медь |
10,5-13,0 |
3,5-4,9 |
0,34 |
13,8 |
|
Нейзильбер1) |
11,6 |
4,3-4,7 |
0,37 |
– |
|
Стекло |
5,1-7,1 |
3,1 |
0,17-0,32 |
3,75 |
|
Стекло иенское крон |
6,5-7,8 |
2,6-3,2 |
0,20-0,27 |
4,0-5,9 |
|
Стекло иенское флинт |
5,0-6,0 |
2,0-2,5 |
0,22-0,26 |
3,6-3,8 |
|
Железо сварочное |
19-20 |
7,7-8,3 |
0,29 |
16,9 |
|
Чугун |
10-13 |
3,5-5,3 |
0,23-0,31 |
9,6 |
|
Магний |
4,25 |
1,63 |
0,30 |
– |
|
Бронза фосфористая2) |
12,0 |
4,36 |
0,38 |
– |
|
Платиноид3) |
13,6 |
3,6 |
0,37 |
– |
|
Кварцевые нити (плав. |
7,3 |
3,1 |
0,17 |
3,7 |
|
Резина мягкая вулканизированная |
0,00015-0,0005 |
0,00005-0,00015 |
0,46-0,49 |
– |
|
Сталь |
20-21 |
7,9-8,9 |
0,25-0,33 |
16,8 |
|
Цинк |
8,7 |
3,8 |
0,21 |
– |
|
1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
||||
|
Вещество |
Модуль Юнга E, 1011 дин/см2. |
Вещество |
Модуль Юнга E, 1011 дин/см2. |
|
Цинк (чистый) |
9,0 |
Дуб |
1,3 |
|
Иридий |
52,0 |
Сосна |
0,9 |
|
Родий |
29,0 |
Красное дерево |
0,88 |
|
Тантал |
18,6 |
Цирконий |
7,4 |
|
Инвар |
17,6 |
Титан |
10,5-11,0 |
|
Сплав 90% Pt, 10% Ir |
21,0 |
Кальций |
2,0-2,5 |
|
Дюралюминий |
7,1 |
Свинец |
0,7-1,6 |
|
Шелковые нити1 |
0,65 |
Тиковое дерево |
1,66 |
|
Паутина2 |
0,3 |
Серебро |
7,1-8,3 |
|
Кетгут |
0,32 |
Пластмассы: |
|
|
Лед (-20С) |
0,28 |
Термопластичные |
0,14-0,28 |
|
Кварц |
7,3 |
Термореактивные |
0,35-1,1 |
|
Мрамор |
3,0-4,0 |
Вольфрам |
41,1 |
|
1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
|||
|
Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) |
Сжимаемость k, бар-1 |
|||
|
|
ɑ, для Е |
ɑ, для G |
|
|
|
Алюминий |
4,8*10-4 |
5,2*10-4 |
Алюминий |
1,36*10-6 |
|
Латунь |
3,7*10-4 |
4,6*10-4 |
Медь |
0,73*10-6 |
|
Золото |
4,8*10-4 |
3,3*10-4 |
Золото |
0,61*10-6 |
|
Железо |
2,3*10-4 |
2,8*10-4 |
Свинец |
2,1*10-6 |
|
Сталь |
2,4*10-4 |
2,6*10-4 |
Магний |
2,8*10-6 |
|
Платина |
0,98*10-4 |
1,0*10-4 |
Платина |
0,36*10-6 |
|
Серебро |
7,5*10-4 |
4,5*10-4 |
Стекло флинт |
3,0*10-6 |
|
Олово |
– |
5,9*10-4 |
Стекло немецкое |
2,57*10-6 |
|
Медь |
3,0*10-4 |
3,1*10-4 |
Сталь |
0,59*10-6 |
|
Нейзильбер |
– |
6,5*10-4 |
|
|
|
Фосфористая бронза |
– |
3,0*10-4 |
|
|
|
Кварцевые нити |
-1,5*10-4 |
-1,1*10-4 |
|
|
Модуль Юнга (упругости) для стали и других материалов: определение, смысл
Основные сведения
Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м2 или в Па.
Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (1012Па)
Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.
Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.
График теста на растяжение
E- это частное от деления нормальных напряжений σ на относительное удлинение ε.
E=α/ε
Закон Гука также можно сформулировать и с использованием модуля Юнга.
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.
Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.
С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
Физический смысл модуля Юнга
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Влияние температуры на изменение механических свойств материалов
Твердое состояние — не единственное агрегатное состояние вещества. Твердые тела существуют только в определенном интервале температур и давлений. Повышение температуры приводит к фазовому переходу из твердого состояния в жидкое, а сам процесс перехода называется плавлением. Температуры плавления, как и другие физические характеристики материалов, зависят от множества факторов и также определяются опытным путем.
Таблица 318.6. Температуры плавления некоторых веществ
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20оС. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35оС.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Характеристики пластичности меди, медных сплавов и магния с ростом температуры уменьшаются, а алюминия — увеличиваются. При нагреве пластмасс и резины их предел прочности резко снижается, а при охлаждении эти материалы становятся очень хрупкими.
Значения модуля юнга для некоторых материалов
В таблице показаны значения E ряда распространенных веществ.
| Материал | модуль Юнга E, ГПа |
| Алюминий | 70 |
| Бронза | 75-125 |
| Вольфрам | 350 |
| Графен | 1000 |
| Латунь | 95 |
| Лёд | 3 |
| Медь | 110 |
| Свинец | 18 |
| Серебро | 80 |
| Серый чугун | 110 |
| Сталь | 200/210 |
| Стекло | 70 |
Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Предел прочности материала
Это предел возникающего напряжения, после которого образец начинает разрушаться.
Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.
Инструмент для определения предела прочности
Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.
Допускаемое механическое напряжение в некоторых материалах при растяжении
Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.
Испытание на растяжение
Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.
Значения σраст в МПа:
| Материалы | σраст | |
| Бор | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловолокно | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.
Запасы прочности, закладываемые в ответственные конструкции, также многократны.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. 2.
2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Коэффициент запаса прочности
Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.
Запас прочности
Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.
Расчетные сопротивления и модули упругости для различных строительных материалов. Модуль упругости разных материалов, включая сталь Модуль упругости алюминия кг см2
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Общие понятия
Модуль упругости (модуль Юнга) – это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения . Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях) . Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала . А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства . Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Модуль упругости
Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь. А есть и такие ситуации, когда эта величина измеряется формой профиля.
Некоторые значения (величина представлена в миллионах кгс/см2) :
- Алюминий – 0,7.
- Древесина поперёк волокон – 0,005.
- Древесина вдоль волокон – 0,1.
- Бетон – 0,02.
- Каменная гранитная кладка – 0,09.
- Каменная кирпичная кладка – 0,03.
- Бронза – 1,00.
- Латунь – 1,01.
- Чугун серый – 1,16.
- Чугун белый – 1,15.
Разница в показателях модулей упругости для сталей в зависимости от их марок:
Ещё это значение изменяется в зависимости от вида проката:
- Трос с сердечником металлическим – 1,95.

- Канат плетёный – 1,9.
- Проволока высокой прочности – 2,1.
Как видно, отклонения в значениях модулей упругой деформации стали незначительны. Именно по этой причине большинство инженеров, проводя свои расчёты, пренебрегают погрешностями и берут значение, равное 2,00.
Физические характеристики материалов для стальных конструкций
2,06 · 10 5 (2,1 · 10 6)
0,83 · 10 5 (0,85 · 10 6)
0,98 · 10 5 (1,0 · 10 6)
1,96 · 10 5 (2,0 · 10 6)
1,67 · 10 5 (1,7 · 10 6)
1,47 · 10 5 (1,5 · 10 6)
1,27 · 10 5 (1,3 · 10 6)
0,78 · 10 5 (0,81 · 10 6)
Примечание. Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом.
Физические характеристики проводов и проволоки
Модуль упругости – общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
E = def d σ d ε > >
В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука):
E = σ ε >> .
Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости – это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
Здесь даны три основных модуля:
Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
или второй параметр Ламе
Модули упругости (Е) для некоторых веществ.
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу – стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости – что это?
Модулем упругости какого-либо материала называют совокупность физических величин , которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали , рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. 2 .
2 .
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга , так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей , которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него. 2 .
2 .
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Основной главной задачей инженерного проектирования служит выбор оптимального сечения профиля и материала конструкции. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Общие понятия
Модуль упругости (модуль Юнга) – это показатель механического свойства материала, характеризующий его сопротивляемость деформации растяжения . Иными словами, это значение пластичности материала. Чем выше значения модуля упругости, тем меньше будет какой-либо стержень растягиваться при иных равных нагрузках (площадь сечения, величина нагрузки и другие).
Модуль Юнга в теории упругости обозначается буквой Е. Он является составляющей закона Гука (о деформации упругих тел). Эта величина связывает возникающее в образце напряжение и его деформацию.
Измеряется эта величина согласно стандартной международной системе единиц в МПа (Мегапаскалях) . Но инженеры на практике больше склоняются к применению размерности кгс/см2.
Опытным путём осуществляется определение этого показателя в научных лабораториях. Сутью этого метода является разрыв гантелеобразных образцов материала на специальном оборудовании. Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Узнав удлинение и натяжение, при которых образец разрушился, делят переменные данные друг на друга. Полученная величина и является модулем (Юнга) упругости.
Таким образом определяется только модуль Юнга материалов упругих: медь, сталь и прочее. А материалы хрупкие сжимают до того момента, пока не появятся трещины: бетон, чугун и им подобные.
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала . А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства . Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Модуль упругости
Стоит отметить, что эта величина непостоянная. Даже для одного материала она может иметь разное значение в зависимости от того, в какие точки была приложена сила. Кое-какие пластично-упругие материалы имеют практически постоянное значение модуля упругости при работе как на растяжение, так и на сжатие: сталь, алюминий, медь. А есть и такие ситуации, когда эта величина измеряется формой профиля.
Некоторые значения (величина представлена в миллионах кгс/см2) :
- Алюминий – 0,7.
- Древесина поперёк волокон – 0,005.
- Древесина вдоль волокон – 0,1.
- Бетон – 0,02.
- Каменная гранитная кладка – 0,09.
- Каменная кирпичная кладка – 0,03.
- Бронза – 1,00.
- Латунь – 1,01.
- Чугун серый – 1,16.
- Чугун белый – 1,15.
Разница в показателях модулей упругости для сталей в зависимости от их марок:
Ещё это значение изменяется в зависимости от вида проката:
- Трос с сердечником металлическим – 1,95.

- Канат плетёный – 1,9.
- Проволока высокой прочности – 2,1.
Как видно, отклонения в значениях модулей упругой деформации стали незначительны. Именно по этой причине большинство инженеров, проводя свои расчёты, пренебрегают погрешностями и берут значение, равное 2,00.
Перевод единиц измерения модулей упругости, модулей Юнга (E), предела прочности, модулей сдвига (G), предела текучести
 0197
0197Подробный список единиц давления (да, эти единицы совпадают с единицами измерения давления по размерности, но не совпадают по смыслу:)
- 1 Па (Н/м 2) = 0.0000102 Атмосфера “метрическая” / Atmosphere (metric)
- 1 Па (Н/м 2) = 0.0000099 Атмосфера стандартная Atmosphere (standard) = Standard atmosphere
- 1 Па (Н/м 2) = 0.00001 Бар / Bar
- 1 Па (Н/м 2) = 10 Барад / Barad
- 1 Па (Н/м 2) = 0.
 0007501 Сантиметров рт. ст. (0 °C)
0007501 Сантиметров рт. ст. (0 °C) - 1 Па (Н/м 2) = 0.0101974 Сантиметров во. ст. (4 °C)
- 1 Па (Н/м 2) = 10 Дин/квадратный сантиметр
- 1 Па (Н/м 2) = 0.0003346 Футов водяного столба / Foot of water (4 °C)
- 1 Па (Н/м 2) = 10 -9 Гигапаскалей
- 1 Па (Н/м 2) = 0.01 Гектопаскалей
- 1 Па (Н/м 2) = 0.0002953 Дюмов рт.ст. / Inch of mercury (0 °C)
- 1 Па (Н/м 2) = 0.0002961 Дюймов рт. ст. / Inch of mercury (15.56 °C)
- 1 Па (Н/м 2) = 0.0040186 Дюмов в.ст. / Inch of water (15.56 °C)
- 1 Па (Н/м 2) = 0.0040147 Дюмов в.ст. / Inch of water (4 °C)
- 1 Па (Н/м 2) = 0.0000102 кгс/см 2 / Kilogram force/centimetre 2
- 1 Па (Н/м 2) = 0.0010197 кгс/дм 2 / Kilogram force/decimetre 2
- 1 Па (Н/м 2) = 0.101972 кгс/м 2 / Kilogram force/meter 2
- 1 Па (Н/м 2) = 10 -7 кгс/мм 2 / Kilogram force/millimeter 2
- 1 Па (Н/м 2) = 10 -3 кПа
- 1 Па (Н/м 2) = 10 -7 Килофунтов силы/ квадратный дюйм / Kilopound force/square inch
- 1 Па (Н/м 2) = 10 -6 МПа
- 1 Па (Н/м 2) = 0.
 000102 Метров в.ст. / Meter of water (4 °C)
000102 Метров в.ст. / Meter of water (4 °C) - 1 Па (Н/м 2) = 10 Микробар / Microbar (barye, barrie)
- 1 Па (Н/м 2) = 7.50062 Микронов рт.ст. / Micron of mercury (millitorr)
- 1 Па (Н/м 2) = 0.01 Милибар / Millibar
- 1 Па (Н/м 2) = 0.0075006 Миллиметров рт.ст / Millimeter of mercury (0 °C)
- 1 Па (Н/м 2) = 0.10207 Миллиметров в.ст. / Millimeter of water (15.56 °C)
- 1 Па (Н/м 2) = 0.10197 Миллиметров в.ст. / Millimeter of water (4 °C)
- 1 Па (Н/м 2) =7.5006 Миллиторр / Millitorr
- 1 Па (Н/м 2) = 1Н/м 2 / Newton/square meter
- 1 Па (Н/м 2) = 32.1507 Повседневных унций / кв. дюйм / Ounce force (avdp)/square inch
- 1 Па (Н/м 2) = 0.0208854 Фунтов силы на кв. фут / Pound force/square foot
- 1 Па (Н/м 2) = 0.000145 Фунтов силы на кв. дюйм / Pound force/square inch
- 1 Па (Н/м 2) = 0.671969 Паундалов на кв. фут / Poundal/square foot
- 1 Па (Н/м 2) = 0.0046665 Паундалов на кв. дюйм / Poundal/square inch
- 1 Па (Н/м 2) = 0.
 0000093 Длинных тонн на кв. фут / Ton (long)/foot 2
0000093 Длинных тонн на кв. фут / Ton (long)/foot 2 - 1 Па (Н/м 2) = 10 -7 Длинных тонн на кв. дюйм / Ton (long)/inch 2
- 1 Па (Н/м 2) = 0.0000104 Коротких тонн на кв. фут / Ton (short)/foot 2
- 1 Па (Н/м 2) = 10 -7 Тонн на кв. дюйм / Ton/inch 2
- 1 Па (Н/м 2) = 0.0075006 Торр / Torr
Физические характеристики материалов для стальных конструкций
проката и стальных отливок
отливок из чугуна
Коэффициент линейного расширения α , ºC -1
прокатной стали и стальных отливок
отливок из чугуна марок:
пучков и прядей параллельных проволок
спиральных и закрытых несущих
двойной свивки с неметаллическим сердечником
Модуль сдвига прокатной стали и стальных отливок G , МПа (кгс/см 2 )
Коэффициент поперечной деформации (Пуассона) ν
Примечание . Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом.
Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом.
Физические характеристики проводов и проволоки
Марка и номинальное сечение, мм 2
Коэффициент линейного расширения α; ºС -1
Алюминиевые провода по ГОСТ 839-80 *Е
При расчете строительных конструкций нужно знать расчетное сопротивление и модуль упругости для того или иного материала. Здесь представлены данные по основным строительным материалам.
Таблица 1. Модули упругости для основных строительных материалов
| Материал | Модуль упругости Е, МПа | Чугун белый, серый | (1,15…1,60) · 10 5 |
| Чугун ковкий | 1,55 · 10 5 |
| Сталь углеродистая | (2,0. ..2,1) · 10 5 ..2,1) · 10 5 |
| Сталь легированная | (2,1…2,2) · 10 5 |
| Медь прокатная | 1,1 · 10 5 |
| Медь холоднотянутая | 1,3 · 10 3 |
| Медь литая | 0,84 · 10 5 |
| Бронза фосфористая катанная | 1,15 · 10 5 |
| Бронза марганцевая катанная | 1,1 · 10 5 |
| Бронза алюминиевая литая | 1,05 · 10 5 |
| Латунь холоднотянутая | (0,91…0,99) · 10 5 |
| Латунь корабельная катанная | 1,0 · 10 5 |
| Алюминий катанный | 0,69 · 10 5 |
| Проволока алюминиевая тянутая | 0,7 · 10 5 |
| Дюралюминий катанный | 0,71 · 10 5 |
| Цинк катанный | 0,84 · 10 5 |
| Свинец | 0,17 · 10 5 |
| Лед | 0,1 · 10 5 |
| Стекло | 0,56 · 10 5 |
| Гранит | 0,49 · 10 5 |
| Известь | 0,42 · 10 5 |
| Мрамор | 0,56 · 10 5 |
| Песчаник | 0,18 · 10 5 |
| Каменная кладка из гранита | (0,09. ..0,1) · 10 5 ..0,1) · 10 5 |
| Каменная кладка из кирпича | (0,027…0,030) · 10 5 |
| Бетон (см. таблицу 2) | |
| Древесина вдоль волокон | (0,1…0,12) · 10 5 |
| Древесина поперек волокон | (0,005…0,01) · 10 5 |
| Каучук | 0,00008 · 10 5 |
| Текстолит | (0,06…0,1) · 10 5 |
| Гетинакс | (0,1…0,17) · 10 5 |
| Бакелит | (2…3) · 10 3 |
| Целлулоид | (14,3…27,5) · 10 2 |
Нормативные данные для рассчетов железобетонных конструкций
Таблица 2. Модули упругости бетона (согласно СП 52-101-2003)
Таблица 2.1 Модули упругости бетона согласно СНиП 2.03.01-84*(1996)
Примечания:
1. Над чертой указаны значения в МПа, под чертой – в кгс/см².
2. Для легкого, ячеистого и поризованного бетонов при промежуточных значениях плотности бетона начальные модули упругости принимают по линейной интерполяции.
3. Для ячеистого бетона неавтоклавного твердения значения Е b принимают как для бетона автоклавного твердения с умножением на коэффициент 0,8.
4. Для напрягающего бетона значения Е b принимают как для тяжелого бетона с умножением на коэффициент
a = 0,56 + 0,006В.
Таблица 3. Нормативные значения сопротивления бетона (согласно СП 52-101-2003)
Таблица 4. Расчетные значения сопротивления бетона сжатию (согласно СП 52-101-2003)
Таблица 4.1 Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 6.2 Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Таблица 7. Расчетные сопротивления для арматуры (согласно СП 52-101-2003)
Расчетные сопротивления для арматуры (согласно СП 52-101-2003)
Таблица 7.1 Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Таблица 7.2 Расчетные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
Нормативные данные для расчетов металлических контрукций
Таблица 8. Нормативные и расчетные сопротивления при растяжении, сжатии и изгибе (согласно СНиП II-23-81 (1990)) листового, широкополосного универсального и фасонного проката по ГОСТ 27772-88 для стальных конструкций зданий и сооружений
Примечания:
1. За толщину фасонного проката следует принимать толщину полки (минимальная его толщина 4 мм).
2. За нормативное сопротивление приняты нормативные значения предела текучести и временного сопротивления по ГОСТ 27772-88.
3. Значения расчетных сопротивлений получены делением нормативных сопротивлений на коэффициенты надежности по материалу, с округлением до 5 МПа (50 кгс/см²).
Таблица 9. Марки стали, заменяемые сталями по ГОСТ 27772-88 (согласно СНиП II-23-81 (1990))
Примечания:
1. Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*.
2. Стали С345К, С390, С390К, С440, С590, С590К по ГОСТ 27772-88 заменяют соответствующие марки стали категорий 1-15 по ГОСТ 19281-73* и ГОСТ 19282-73*, указанные в настоящей таблице.
3. Замена сталей по ГОСТ 27772-88 сталями, поставляемыми по другим государственным общесоюзным стандартам и техническим условиям, не предусмотрена.
Расчетные сопротивления для стали, используемой для производства профилированных листов здесь не показаны.
3Справочник CRC по материаловедению и инженерии, стр. 46
http://www.memsnet.org/material/aluminumalbulk/
Янга модуль
70 ГПа
Тонкие твердые пленки, 270 (1995), стр. 263
263
http://www.memsnet.org/material/aluminumalbulk/
Коэффициент Пуассона
0,33
Микрозондовое измерение модуля Юнга и Пуассона коэффициент с помощью определения глубины вдавливания и акустической микроскопии, Comte, C. von Stebut, J. Surface & Coatings Technology, v 154, n 1, 1 May 2002, p. 42-8
Жесткость Константы
Растяжение или прочность на излом
Чистый алюминий: 47 МПа
Пленка в артикуле: 70 МПа
Алюминий
осаждение с использованием MOCVD на углеродных волокнах на основе пека, Suzuki, T. , Materials
Общество служения науке и технике. Материалы Третьего Окинагского симпозиума по материаловедению и инженерии
Общество служения, 1998, стр. 210-13
, Materials
Общество служения науке и технике. Материалы Третьего Окинагского симпозиума по материаловедению и инженерии
Общество служения, 1998, стр. 210-13
Остаток нагрузка на кремний
от -20 до -30 МПа неотожженный от 120 до 140 МПа отожженный при 450С
Рентген определение остаточных напряжений в тонких алюминиевых пленках, нанесенных на кремниевые подложки, Корхонен, М.А., Пашкиет, К.А., Scripta Metallurgica, т. 23, № 8, август 1989 г., стр. 1449-53
Удельная теплоемкость
898,7 Дж/кг/К
Справочник CRC по материаловедению и инженерии, стр. 260
http://www.memsnet.org/material/aluminumalbulk/
Термальный проводимость
237 Вт/м/К
Справочник CRC по материаловедению и инженерии, стр. 270-274
270-274
http://www.memsnet.org/material/aluminumalbulk/
Диэлектрик константа
Алюминиевый порошок 1,6-1,8
Справочное руководство по диэлектрической проницаемости
http://www.asiinstr.com/dc1.html#List
Индекс преломление
1,44
Справочник по химическим свойствам
Под редакцией Yaws, C.L. 1999 г.; Макгроу-Хилл
Электрика проводимость
3,538×10 7 Ш/м
ResourceCenter по неразрушающему контролю
http://www.ndt-ed.org/GeneralResources/MaterialProperties/ET/ET_matlprop_Aluminum.htm
Магнитный проходимость
мк r =1
Восприимчивость = 6×10-7 сгс
Базовый анализ металлоискателя Yamazaki, S. ; Накане,
ЧАС.; Танака, А., IEEE
Сделки по инструментам
и измерения, Том: 51, Выпуск: 4, Год: август 2002 г., Страниц: 810-
814
; Накане,
ЧАС.; Танака, А., IEEE
Сделки по инструментам
и измерения, Том: 51, Выпуск: 4, Год: август 2002 г., Страниц: 810-
814
Восприимчивость с http://www.matweb.com/search/SpecificMaterial.asp?bassnum=MEAl00
Пьезосопротивление
2×10-5 Ом-см
Определение
коэффициент пьезосопротивления в алюминии
межблочные конструкции из сплава
Reilly,
CJ, Санчес,
Дж. Э., младший, материалы
Надежность в микроэлектронике IX. Симпозиум, 1999, стр. 213-18
Пьезоэлектричество
Мокрое травление метод
85 мас.% раствор фосфорной кислоты
Механизмы жидкостного травления алюминия
электроды под низким давлением-ширина линии
явления сужения
Утияма,
М. ; Накамура,
М. Денки Кагаку, v
56, № 7, июль 1988 г., стр. 563-8
; Накамура,
М. Денки Кагаку, v
56, № 7, июль 1988 г., стр. 563-8
Плазменное травление метод
Cl 2 , BCl 3 /Cl 2
Ленгмюровские исследования плазмы с трансформаторной связью,
травитель алюминия
Малышев М.В.; Доннелли,
В.М.; Корнблит, А .; Чиампа, Н.А.; Полковник, JI; Ли, JTC
Источник: Journal of Vacuum Science & Technology A (Вакуум, поверхности и
Фильмы), т. 17, № 2, 19 марта99, стр. 480-92
Адгезия к диоксид кремния
хорошо
Реакция Al
со стекловидным кварцем
Черный, J.R., 15th
Ежегодные труды по физике надежности, 1977 г., стр. 257-61
Биосовместимость
№
Зависимость биосовместимости иономерных цементов in vitro от высвобождения ионов, A. J. Devlin,
J. Devlin,
Journal of Materials Science: Materials in Medicine 9(12): 737-741; декабрь 1998 г.
Ссылка на медицинское устройство — MDDI, июль 2002 г.
Металлообработка: будущее завтра, сегодня Медицинское устройство…
Гидрофобность
90 градусов ниже 120°C
Угол контакта
температурная зависимость капель воды на практических алюминиевых поверхностях
Bernardin, J.D.; Мудавар, И.; Уолш, CB;
Франсес, E.I.International Journal of Heat and Mass Transfer,
т. 40, № 5, март 1997 г., стр. 1017-33
Все о 6061 Алюминий (свойства, прочность и применение)
Металлический алюминий и его сплавы используются в большинстве, если не во всех современных промышленных процессах из-за его широкой доступности и огромного количества применений. Сплав — это металл, полученный путем объединения двух или более металлических элементов для достижения улучшенных свойств материала. Процесс легирования включает добавление определенных металлических «легирующих» элементов в основной металл, чтобы придать ему определенные свойства, такие как повышенная прочность, коррозионная стойкость, проводимость, ударная вязкость и т. д., или желаемую комбинацию этих характеристик. Сплавы с низким процентным содержанием легирующих элементов (около <4%) классифицируются как деформируемые и пригодны для обработки, тогда как сплавы с более высоким процентным содержанием (до 22%) классифицируются как литейные сплавы и обычно являются хрупкими. Алюминиевая ассоциация (AA Inc.) является передовым авторитетом в области алюминиевых сплавов и разработала четырехзначную систему наименования, используемую для характеристики отличающихся друг от друга деформируемых сплавов на основе их основных легирующих элементов. В этой статье будет подробно рассмотрен алюминиевый сплав 6061 с акцентом на его физические свойства, а также общие области применения этого очень полезного материала.
Сплав — это металл, полученный путем объединения двух или более металлических элементов для достижения улучшенных свойств материала. Процесс легирования включает добавление определенных металлических «легирующих» элементов в основной металл, чтобы придать ему определенные свойства, такие как повышенная прочность, коррозионная стойкость, проводимость, ударная вязкость и т. д., или желаемую комбинацию этих характеристик. Сплавы с низким процентным содержанием легирующих элементов (около <4%) классифицируются как деформируемые и пригодны для обработки, тогда как сплавы с более высоким процентным содержанием (до 22%) классифицируются как литейные сплавы и обычно являются хрупкими. Алюминиевая ассоциация (AA Inc.) является передовым авторитетом в области алюминиевых сплавов и разработала четырехзначную систему наименования, используемую для характеристики отличающихся друг от друга деформируемых сплавов на основе их основных легирующих элементов. В этой статье будет подробно рассмотрен алюминиевый сплав 6061 с акцентом на его физические свойства, а также общие области применения этого очень полезного материала.
типа 6061 относится к алюминиевым сплавам 6ххх, что влечет за собой те смеси, в которых магний и кремний используются в качестве основных легирующих элементов. Вторая цифра указывает на степень контроля примесей для основного алюминия. Когда эта вторая цифра равна «0», это указывает на то, что основная часть сплава представляет собой коммерческий алюминий, содержащий существующие уровни примесей, и не требуется особого внимания для ужесточения контроля. Третья и четвертая цифры — это просто обозначения отдельных сплавов (обратите внимание, что это не относится к алюминиевым сплавам 1xxx). Номинальный состав алюминия марки 6061: 97,9% Al, 0,6% Si, 1,0% Mg, 0,2% Cr и 0,28% Cu. Плотность алюминиевого сплава 6061 составляет 2,7 г/см 3 (0,0975 фунта/дюйм 3 ). Алюминиевый сплав 6061 поддается термообработке, легко формуется, поддается сварке и хорошо сопротивляется коррозии.
Механические свойства
Механические свойства алюминиевого сплава 6061 различаются в зависимости от того, как он подвергается термообработке или становится более прочным в процессе отпуска. Чтобы упростить эту статью, значения прочности для этого сплава будут взяты из отпущенного алюминиевого сплава 6061 T6 (6061-T6), который является обычным отпуском для алюминиевых листов и прутков. Его модуль упругости равен 68,9.ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм). Эти значения измеряют жесткость сплава или устойчивость к деформации и приведены в таблице 1. Как правило, этот сплав легко соединяется с помощью сварки и легко деформируется в наиболее желаемые формы, что делает его универсальным производственным материалом.
Чтобы упростить эту статью, значения прочности для этого сплава будут взяты из отпущенного алюминиевого сплава 6061 T6 (6061-T6), который является обычным отпуском для алюминиевых листов и прутков. Его модуль упругости равен 68,9.ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм). Эти значения измеряют жесткость сплава или устойчивость к деформации и приведены в таблице 1. Как правило, этот сплав легко соединяется с помощью сварки и легко деформируется в наиболее желаемые формы, что делает его универсальным производственным материалом.
Двумя важными факторами при рассмотрении механических свойств являются предел текучести и предел прочности. Предел текучести описывает максимальную величину напряжения, необходимого для упругой деформации детали при данном нагружении (растяжение, сжатие, скручивание и т. д.). С другой стороны, предел прочности описывает максимальное напряжение, которое материал может выдержать до разрушения (претерпевая пластическую или необратимую деформацию). Для статических приложений предел текучести является более важным конструктивным ограничением в соответствии со стандартными отраслевыми методами проектирования; однако предельная прочность может быть полезна для определенных приложений, которые требуют этого. Алюминиевый сплав 6061 имеет предел текучести при растяжении 276 МПа (40000 фунтов на квадратный дюйм) и предел прочности при растяжении 310 МПа (45000 фунтов на квадратный дюйм). Эти значения приведены в таблице 1.
Для статических приложений предел текучести является более важным конструктивным ограничением в соответствии со стандартными отраслевыми методами проектирования; однако предельная прочность может быть полезна для определенных приложений, которые требуют этого. Алюминиевый сплав 6061 имеет предел текучести при растяжении 276 МПа (40000 фунтов на квадратный дюйм) и предел прочности при растяжении 310 МПа (45000 фунтов на квадратный дюйм). Эти значения приведены в таблице 1.
Прочность на сдвиг — это способность материала сопротивляться сдвигу под действием противоположных сил вдоль плоскости, подобно тому, как ножницы разрезают бумагу. Когда два лезвия ножниц смыкаются, их противоположные силы действуют на плоскость поперечного сечения бумаги и заставляют ее разрушаться «при сдвиге». Это значение полезно при кручении (валы, стержни и т. д.), где скручивание может вызвать такое напряжение сдвига материала. Прочность на сдвиг алюминиевого сплава 6061 составляет 207 МПа (30000 фунтов на кв. дюйм), и эти значения приведены в таблице 1.
дюйм), и эти значения приведены в таблице 1.
Усталостная прочность — это способность материала сопротивляться разрушению при циклической нагрузке, когда к материалу многократно воздействуют небольшие нагрузки с течением времени. Это значение полезно для приложений, в которых деталь подвергается повторяющимся циклам нагрузки, например, оси автомобиля или поршни. Усталостная прочность алюминиевого сплава 6061 составляет 96,5 МПа (14000 фунтов на квадратный дюйм), что рассчитывается с использованием 500 000 000 циклов непрерывной циклической нагрузки ниже предела текучести. Эти значения приведены в таблице 1.
Таблица 1: Сводка механических свойств алюминиевого сплава 6061.
Механические свойства | Метрическая система | Английский |
Предельная прочность на растяжение | 310 МПа | 45000 фунтов на кв. |
Предел текучести при растяжении | 276 МПа | 40000 фунтов на кв. дюйм |
Прочность на сдвиг | 207 МПа | 30000 фунтов на кв. дюйм |
Усталостная прочность | 96,5 МПа | 14000 фунтов на кв. дюйм |
Модуль упругости | 68,9 ГПа | 10000 тысяч фунтов на квадратный дюйм |
Модуль сдвига | 26 ГПа | 3770 тысяч фунтов на квадратный дюйм |
Коррозионная стойкость
При воздействии воздуха или воды алюминиевый сплав 6061 образует слой оксида, который делает его нереактивным с элементами, вызывающими коррозию основного металла. Степень коррозионной стойкости зависит от атмосферных/водных условий; однако при температуре окружающей среды коррозионное воздействие в воздухе/воде обычно незначительно. Важно отметить, что из-за содержания меди в 6061 он немного менее устойчив к коррозии, чем другие типы сплавов (например, алюминиевый сплав 5052, который не содержит меди). При контакте с щелочной почвой могут возникать некоторые коррозионные эффекты, такие как точечная коррозия, но это сильно зависит от состояния почвы. 6061 особенно хорошо противостоит коррозии от концентрированной азотной кислоты, а также аммиака и гидроксида аммония. Коррозионное воздействие можно полностью устранить, покрыв сплав защитным слоем, на который хорошо реагирует сплав 6061.
Важно отметить, что из-за содержания меди в 6061 он немного менее устойчив к коррозии, чем другие типы сплавов (например, алюминиевый сплав 5052, который не содержит меди). При контакте с щелочной почвой могут возникать некоторые коррозионные эффекты, такие как точечная коррозия, но это сильно зависит от состояния почвы. 6061 особенно хорошо противостоит коррозии от концентрированной азотной кислоты, а также аммиака и гидроксида аммония. Коррозионное воздействие можно полностью устранить, покрыв сплав защитным слоем, на который хорошо реагирует сплав 6061.
Применение алюминия типа 6061
АлюминийТип 6061 является одним из наиболее широко используемых алюминиевых сплавов. Его способность к сварке и формованию делает его пригодным для многих применений общего назначения. Его высокая прочность и коррозионная стойкость делают сплав типа 6061 особенно полезным в архитектурных, конструкционных и автомобильных применениях. Список его применений является исчерпывающим, но некоторые основные области применения алюминиевого сплава 6061 включают:
- Сварные узлы
- Морские рамы
- Рамы самолетов и грузовиков
- Химическое оборудование
- Электронные детали
- Мебель
- Крепеж
- Теплообменники
- Радиаторы
Резюме
В этой статье представлен краткий обзор свойств, прочности и применения алюминия 6061. Для получения информации о других продуктах обратитесь к нашим дополнительным руководствам или посетите платформу поиска поставщиков Thomas, чтобы найти потенциальные источники поставок или просмотреть подробную информацию о конкретных продуктах. У нас также есть руководства по другим типам алюминия, включая алюминий 5052, алюминий 3003 и алюминий 7075.
Для получения информации о других продуктах обратитесь к нашим дополнительным руководствам или посетите платформу поиска поставщиков Thomas, чтобы найти потенциальные источники поставок или просмотреть подробную информацию о конкретных продуктах. У нас также есть руководства по другим типам алюминия, включая алюминий 5052, алюминий 3003 и алюминий 7075.
Другие изделия из алюминия
- Ведущие поставщики и производители алюминия в США
- Различные типы марок алюминия (свойства и применение)
- Все об алюминии 7075 (свойства, прочность и применение)
- Все об алюминии 5052 (свойства, прочность и применение)
- Все об алюминии 2024 (свойства, прочность и применение)
- Все об алюминии 6063 (свойства, прочность и применение)
- Все об алюминии 3003 (свойства, прочность и применение) Алюминий
- 6061 и алюминий 7075 — различия в свойствах, прочности и использовании Алюминий
- 6061 и алюминий 6063 — различия в свойствах, прочности и использовании Алюминий
- 6061 и алюминий 5052 — различия в свойствах, прочности и использовании Алюминий
- 6061 и алюминий 2024 — различия в свойствах, прочности и использовании Алюминий
- 3003 и алюминий 6061 — различия в свойствах, прочности и использовании
Источники:
- https://materialsdata.
 nist.gov/bitstream/handle/11115/173/Aluminum%20and%20Aluminum%20Alloys%20Davis.pdf?sequence=3&isAllowed=y
nist.gov/bitstream/handle/11115/173/Aluminum%20and%20Aluminum%20Alloys%20Davis.pdf?sequence=3&isAllowed=y - https://sites.esm.psu.edu
- https://www.nrc.gov/docs/ML0633/ML0633.pdf
- https://materialsdata.nist.gov/bitstream/handle/11115/185/Understanding%20Wrought%20and%20Cast%20Al%20Alloy%20Designations.pdf?isAllowed=y&sequence=3
Больше из Металлы и изделия из металла
Модуль упругости Модуль упругости Юнга для металлов
Модуль упругости, модуль Юнга для обычных технических материалов Таблица
Технические металлы и материалы Содержание
Связанные:
Технические свойства металлов
Обзор предела текучести и таблица материалов
Модуль упругости, средние свойства конструкционных материалов, модуль сдвига, коэффициент Пуассона, плотность
Тепловые свойства металлов, проводимость, тепловое расширение, удельная теплоемкость
В следующей таблице приведены данные по предельной прочности, пределу текучести и модулю упругости для стали и чугуна.
Технические материалы | Модуль упругости | Максимальное растяжение | Предел текучести | |
x 10 6 psi | x ГПа | |||
АБС-пластик | – | 1,45 – 3,15 | 40 | – |
A53 Бесшовные и сварные стальные трубы | – | – | 331 | 207 |
A53 Бесшовные и сварные стальные трубы | – | – | 414 | 241 |
А106 безшовная труба из углеродистой стали | – | – | 400 | 248 |
А106 безшовная труба из углеродистой стали | – | – | 483 | 345 |
А106 безшовная труба из углеродистой стали | – | – | 483 | 276 |
А252 Сваебойная стальная труба | – | – | 345 | 207 |
А252 Свайная стальная труба | – | – | 414 | 241 |
А252 Свайная стальная труба | – | – | 455 | 310 |
A501 Горячедеформированная углеродистая сталь | – | – | 400 | 248 |
A501 Горячедеформированная углеродистая сталь | – | – | 483 | 345 |
Ранг а | стальных трубопроводов цепи кабеля А523 – | – | 331 | 207 |
ранг б | трубопровода цепи кабеля А523 стальной – | – | 414 | 241 |
A618 Горячеформованные | – | – | 483 | 345 |
A618 Горячедеформированные | – | – | 414 | 345 |
A618 Горячедеформированные | – | – | 448 | 345 |
Линейная труба API 5L | – | – | 310 – 1145 | 175 – 1048 |
Ацетали | – | 2,78 | 65 | – |
Акрил | – | 3. | 70 | – |
Алюминий Бронза | – | 118 | – | – |
Алюминий | 10,0 | 67 | 110 | 95 |
Алюминиевые сплавы | 10,2 | – | – | – |
Сурьма | 11,3 | – | – | – |
Арамид | – | 70 – 112 | – | – |
Бериллий (Be) | 42 | 287 | – | – |
Бериллиевая медь | 18,0 | – | – | – |
Висмут | 4,6 | – | – | – |
Кость губчатая | – | 76 | – | – |
Бор | – | – | – | 3100 |
Латунь | – | 102 – 125 | 250 | – |
Латунь, морской | – | 100 | – | – |
Бронза | – | 96 – 120 | – | – |
КАБ | – | 0,8 | – | – |
Кадмий | 4,6 | – | – | – |
Пластик, армированный углеродным волокном | – | 150 | – | – |
Углеродная нанотрубка, одностенная | – | 1000+ | – | – |
Чугун 4,5% C, ASTM A-48 | – | – | 170 | – |
Целлюлоза, хлопок, древесная масса | – | – | 80 – 240 | – |
Ацетат целлюлозы формованный | – | – | 12 – 58 | – |
Ацетат целлюлозы, лист | – | – | 30 – 52 | – |
Нитрат целлюлозы, целлулоид | – | – | 50 | – |
Хлорированный полиэфир | – | 1. | 39 | – |
Хлорированный ПВХ (ХПВХ) | – | 2,9 | – | – |
Хром | 36 | – | – | – |
Кобальт | 30 | – | – | – |
Бетон | – | 17 | – | – |
Бетон, высокопрочный | – | 30 | 40 | – |
Медь | 17 | 117 | 220 | 70 |
Алмаз (С) | – | 1220 | – | – |
Древесина пихты Дугласа | – | 13 | 50 | – |
Эпоксидные смолы | – | 3-2 | 26 – 85 | – |
Древесноволокнистая плита средней плотности | – | 4 | – | – |
Льняное волокно | – | 58 | – | – |
Стекло | – | 50 – 90 | 50 | – |
Матрица из полиэстера, армированного стекловолокном | – | 17 | – | – |
Золото | 10,8 | 74 | – | – |
Гранит | – | 52 | – | – |
Графен | – | 1000 | – | – |
Серый чугун | – | 130 | – | – |
Пеньковое волокно | – | 35 | – | – |
Инконель | 31 | – | – | – |
Иридий | 75 | – | – | – |
Железо | 28,5 | 210 | – | – |
Свинец | 2,0 | – | – | – |
Металлический магний (Mg) | 6,4 | 45 | – | – |
Марганец | 23 | – | – | – |
Мрамор | – | – | 15 | – |
Древесноволокнистая плита средней плотности | – | 4 | – | – |
Меркурий | – | – | – | – |
Молибден (Mo) | 40 | 329 | – | – |
Монель-металл | 26 | – | – | – |
Никель | 31 | 170 | – | – |
Нейзильбер | 18,5 | – | – | – |
Никелированная сталь | 29 | – | – | – |
Ниобий (Колумбий) | 15 | – | – | – |
Нейлон-6 | – | 2 – 4 | 45 – 90 | 45 |
Нейлон-66 | – | – | 60 – 80 | – |
Древесина дуба (вдоль волокон) | – | 11 | – | – |
Осмий | 80 | 550 | – | – |
Фенольные литые смолы | – | – | 33 – 59 | – |
Фенолформальдегид | – | – | 45 – 52 | – |
Фосфорная бронза | – | 116 | – | – |
Древесина сосны (вдоль волокон) | – | 9 | 40 | – |
Платина | 21,3 | – | – | – |
Плутоний | 14 | 97 | – | – |
Полиакрилонитрил, волокна | – | – | 200 | – |
Полибензоксазол | – | 3,5 | – | – |
Поликарбонаты | – | 2,6 | 52 – 62 | – |
Полиэтилен HDPE (высокой плотности) | – | 0,8 | 15 | – |
Полиэтилентерефталат, ПЭТ | – | 2 – 2,7 | 55 | – |
Полиамид | – | 2,5 | 85 | – |
Полиизопрен, твердая резина | – | – | 39 | – |
Полиметилметакрилат (ПММА) | – | 2,4 – 3,4 | – | – |
Полиимидные ароматические соединения | – | 3. | 68 | – |
Полипропилен, ПП | – | 1,5 – 2 | 28 – 36 | – |
Полистирол, полистирол | – | 3 – 3,5 | 30 – 100 | – |
Полиэтилен, LDPE (низкой плотности) | – | 0,11 – 0,45 | – | – |
Политетрафторэтилен (ПТФЭ) | – | 0,4 | – | – |
Полиуретановая заливочная жидкость | – | – | 10 – 20 | – |
Полиуретановый эластомер | – | – | 29 – 55 | – |
Поливинилхлорид (ПВХ) | – | 2,4 – 4,1 | – | – |
Калий | – | – | – | – |
Родий | 42 | – | – | – |
Резина, малая деформация | – | 0,01 – 0,1 | – | – |
Сапфир | – | 435 | – | – |
Селен | 8,4 | – | – | – |
Кремний | 16 | 130 – 185 | – | – |
Карбид кремния | – | 450 | – | 3440 |
Серебро | 10,5 | – | – | – |
Натрий | – | – | – | – |
Сталь, высокопрочный сплав | – | – | 755 | 670 |
Сталь нержавеющая AISI 302 | – | 184 | 850 | 506 |
Сталь, конструкционная ASTM-A36 | – | 24 | 403 | 245 |
Тантал | 27 | – | – | – |
Политетрафторэтилен | – | 0,5 | – | – |
Торий | 8,5 | – | – | – |
Олово | – | 47 | – | – |
Титан | 16 | – | – | – |
Титановый сплав | – | 105 – 120 | 900 | 730 |
Зубная эмаль | – | 83 | – | – |
Вольфрам (W) | – | 400 – 410 | – | – |
Карбид вольфрама (WC) | – | 450 – 650 | – | – |
Уран | 24 | 170 | – | – |
Ванадий | 19 | – | – | – |
Кованое железо | – | 190 – 210 | – | – |
Цинк | 12 | – | – | – |
| Материал
| Окончательный Прочность | Выход
Наконечник X 1000/дюйм 2 | Модуль эластичности | |||
(Т)
Натяжение | Компрессионный, | Сдвиг в пересчете на Т | дюймов
Напряжение (E) x 10 6 psi | в
Ножницы, | ||
| Чугун серый, класс 20 | 20 и | 3,6 т – 4,4 т | 1,6 т | . …… …… | 11,6 | 0,40 Е |
класс 25 | 25 а | 3,6 Т – 4,4 Т | 1.4 Т | ……. | 14,2 | 0,40 Е |
класс 30 | 30 а | 3,6 Т – 4,4 Т | 1,4 Т | . | 14,5 | 0,40 Е |
класс 35 | 35 и | 3,6 Т – 4,4 Т | 1.4 Т | ……. | 16,0 | 0,40 Е |
класс 40 | 40 и | 3,6 Т – 4,4 Т | 1. | ……. | 17 | 0,40 Е |
класс 50 | 50 и | 3,6 Т – 4,4 Т | 1.3 Т | . | 18 | 0,40 Е |
класс 60 | 60 а | 2,8 Т | 1.О Т | ……. | 19,9 | 0,40 Е |
Ковкий | 40 до 100 | . | ……. | 30 до 80 | 25 | 0,43 Е |
узловатый (ковкий чугун) | 60 до 120 | ……. | . | 40 до 90 | 23 | …… |
В ролях Сталь углеродистая | 60 до 100 | Т | 0,75 Т | 30 до 70 | 30 | 0,38 Е |
низкий сплав | 70 до 200 | Т | 0,75 Т | 45 до 170 | 30 | 0,38 Е |
Сталь, САЕ 950 | 66 до 70 | Т | 0,75 Т | 45 до 50- | 30 | 0,38 Е |
1025 (низкоуглеродистый) | 60 до 103 | Т | 0,75 Т | 40 до 90 | 30 | 0,38 Е |
1045 (среднеуглеродистый) | 80 до 182 | Т | 0,75 Т | 50 до 162 | 30 | 0,38 Е |
1095 (с высоким содержанием углерода) | 90 до 213 | Т | 0,75 Т | 20 до 150 | 30 | 0,38 Е |
1112 (свободная резка) | 60 до 100 | Т | 0,75 Т | 30 до 95 | 30 | 0,38 Е |
1212 (свободная резка) | 57 до 80 | Т | 0,75 Т | 25 до 72 | 30 | 0,38 Е |
1330 (сплав) | 90 до 162 | Т | 0,75 Т | 27 до 149 | 30 | 0,38 Е |
2517 (сплав) | 88 до 190 | Т | 0,75 Т | 60 до 155 | 30 | 0,38 Е |
3140 (сплав) | 93 – 188 | Т | 0,75 Т | 62 до 162 | 30 | 0,38 Е |
3310 (сплав) | 104 до 172 | Т | 0,75 Т | 56 до 142 | 30 | 0,38 Е |
4023 (сплав) | 105 до 170 | Т | 0,75 Т | 60 до 114 | 30 | 0,38 Е |
4130 (сплав) | 81 до 179 | Т | 0,75 Т | 46 до 161 | 30 | 0,38 Е |
4340 (сплав) | 109 до 220 | Т | 0,75 Т | 68 до 200 | 30 | 0,38 Е |
4640 (сплав) | 98 до 192 | Т | 0,75 Т | 62 до 169 | 30 | 0,38 Е |
4820 (сплав) | 98 до 209 | Т | 0,75 Т | 68 до 184 | 30 | 0,38 Е |
5150 (сплав) | 98 до 210 | Т | 0,75 Т | 51 до 190 | 30 | 0,38 Е |
52100 (сплав) | 100 до 238 | Т | 0,75 Т | 81 до 228 | 30 | 0,38 Е |
6150 (сплав) | 96 до 228 | Т | 0,75 Т | 59 до 210 | 30 | 0,38 Е |
| 8650 (сплав) | 110 до 228 | Т | 0,75 Т | 69 до 206 | 30 | 0,38 Е |
| 8740 (сплав) | 100 до 179 | Т | 0,75 Т | 60 до 165 | 30 | 0,38 Е |
| 9310 (сплав) | 117 до 187 | Т | 0,75 Т | 63 до 162 | 30 | 0,38 Е |
| 9840 (сплав) | 120 к 285 | Т | 0,75 Т | 45 до 50 | 30 | 0,38 Е |
| Хромовый сплав 13 | 65 тысяч фунтов/кв. дюйм дюйм 449 МПа | – | 40 тысяч фунтов/кв. дюйм 276 МПа | |||
Сталь Нержавеющая сталь, SAE | ||||||
| 30302 ф | 85 до 125 | Т | ……. | 35 до 95 | 28 | 0,45 Е |
| 30321 ф | 85 до 95 | Т | . …… …… | 30 до 60 | 28 | ……. |
| 30347 ф | 90 до 100 | Т | ……. | 35 до 65 | 28 | 0,40 Е |
| 51420 ф | 95 до 230 | Т | . …… …… | 50 до 195 | 29 | ……. |
| 51430 ф | 75 до 85 | Т | ……. | 40 до 70 | 29 | . …… …… |
| 51446 ф | 80 до 85 | Т | ……. | 50 до 70 | 29 | ……. |
| 51501 ф | 70 до 175 | Т | . …… …… | 30 до 135 | 29 | ……. |
| Структурный Сталь | ||||||
| Общий | 60 до 75 | Т | 0,75 Т | 33 | 29 | 0,41 Е |
| Заклепка | 52 до 62 | Т | 0,75 Т | 28 | 29 | . …… …… |
| заклепка, высокая прочность | 68 до 82 | Т | 0,75 Т | 38 | 29 | ……. |
| Кованый железо | 34 до 54 | Т | 0,75 Т | 23 до 32 | 28 | . …… …… |
а – Минимальное заданное значение Американское общество тестирования материалов. Ссылки irom, ASTM A48, конструкционная сталь для мостов и конструкций, АСТМ А7. Конструкционная заклепочная сталь, ASTM A141; высокая сила конструкционная заклепочная сталь, ASTM A195
Преобразования
- 1 Па (Н/м 2 ) = 1×10 -6 Н/мм 2 = 1,4504×10 -4 1 psi
- 1 МПа = 10 6 Н/м 2 = 0,145×10 3 фунтов на квадратный дюйм (фунт-сила/дюйм 2 ) = 0,145 тысяч фунтов на квадратный дюйм
- 1 ГПа = 10 9 Н/м 2 = 10 6 Н/см 2 = 10 3 Н/мм 2 = 0,145×10 6 фунтов на кв. дюйм (фунт-сила/дюйм 2 )
- 1 psi (фунт/дюйм 2 ) = 0,001 ksi = 144 фунтов на квадратный фут (фунт-сила/фут 2 ) = 6894,8 Па (Н/м 2 ) = 6,895×10 -3 Н/мм 2
Каков модуль Юнга алюминия 6061 T6?
Какова прочность на растяжение алюминия 6061?
6061-Т4. T4 закалка 6061 имеет предел прочности при растяжении не менее 30 000 фунтов на кв. дюйм (207 МПа) и предел текучести не менее 16 000 фунтов на кв. дюйм (110 МПа).
T4 закалка 6061 имеет предел прочности при растяжении не менее 30 000 фунтов на кв. дюйм (207 МПа) и предел текучести не менее 16 000 фунтов на кв. дюйм (110 МПа).
Модуль упругости равен модулю Юнга?
17.6. 1 Модуль упругости (модуль Юнга или модуль упругости) Модуль Юнга описывает относительную жесткость материала, который измеряется наклоном упругой кривой напряжения и деформации. Он рассчитывается как отношение значения напряжения к соответствующему значению деформации.
Можно ли согнуть алюминий 6061?
6061. Это один из самых универсальных сплавов, поддающихся термообработке. В отожженном состоянии его можно использовать для изгиба , так как разница между пределом текучести и пределом прочности составляет 10 Ksi, а относительное удлинение составляет до 18%. Однако при переходе к состояниям Т4 и Т6 способность к изгибу имеет тенденцию к снижению. 10 мая 2015 г.
Это один из самых универсальных сплавов, поддающихся термообработке. В отожженном состоянии его можно использовать для изгиба , так как разница между пределом текучести и пределом прочности составляет 10 Ksi, а относительное удлинение составляет до 18%. Однако при переходе к состояниям Т4 и Т6 способность к изгибу имеет тенденцию к снижению. 10 мая 2015 г.
Как рассчитать модуль упругости?
Модуль упругости (Е) — это наклон начального линейного участка кривой напряжения-деформации в упругой области — изменение напряжения (Δσ), деленное на изменение деформации (Δϵ) .17 сентября 2021 г.
Родственные
Что такое модуль сдвига алюминия?
Значение модуля сдвига для алюминия составляет примерно 3,5 × 10 6 фунтов на квадратный дюйм или 2,4 × 10 1 0 Н/м 2 .
Родственные
Как изготавливается алюминий 6061 T6?
Глинозем или оксид алюминия извлекают из бокситов в процессе очистки с использованием каустической соды и извести. … Разработанный в 1935 году алюминий 6061-T6 представляет собой дисперсионно-твердеющий алюминий . Дисперсионное твердение использует высокие температуры для увеличения предела текучести алюминия.
Родственные
Что такое модуль упругости алюминия PSI?
Модуль упругости алюминия составляет 69 ГПа (10 000 000 фунтов на кв. дюйм) .9 октября 2020 г.
Какова теоретическая ценность алюминия?
Принятое значение плотности алюминия 2,699 г/см3 .
Родственные
Соответствует ли алюминий 6061 RoHS?
Сюда входят обычные аэрокосмические и коммерческие алюминиевые сплавы, такие как 6061, 7075, 2024, 6063, 3003, 5052, 5083, 5086. … Сплавы из нержавеющей стали не содержат свинца и должны обеспечивать соответствие деталей RoHS при условии, что они не подвергаются обработке поверхности, не соответствующей требованиям RoHS. 4 декабря 2017 г.
… Сплавы из нержавеющей стали не содержат свинца и должны обеспечивать соответствие деталей RoHS при условии, что они не подвергаются обработке поверхности, не соответствующей требованиям RoHS. 4 декабря 2017 г.
Связанные
Является ли алюминий 6061 пластичным или хрупким?
(2) Алюминиевые сплавы 5052 и 6061 подлежат смешанный вязкий и хрупкий излом ; вязкое разрушение играет основную роль для AA5052, тогда как хрупкое разрушение играет основную роль для AA6061.
Родственные
Что такое рама из алюминия 6061?
6061 – это сплав , состоящий из алюминия, магния и силикона , и считается, что он превосходит сплав 7005, сделанный из алюминия и цинка, хотя последний кажется более стойким. …28 декабря 2020 г.
Родственный
Каков модуль упругости алюминиевого сплава 6061?
Модуль упругости Юнга Модуль упругости Юнга алюминиевого сплава 6061 составляет около 69 ГПа.
 Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Связанные
Какова прочность на растяжение алюминия 6061?
Алюминий 6061 Типичные механические свойства при различных температурах. Сплав и закалка. Температура, °C (°F) Предел прочности при растяжении, МПа (ksi) Предел текучести при смещении 0,2 %. Удлинение в 50 мм (2 д.), %, АЛ 6061-Т6, 6061-Т651. -195 (-320)
Связанные
Что такое модуль упругости стали?
Его модуль упругости составляет 68,9 ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм). Эти значения измеряют жесткость сплава или устойчивость к деформации и приведены в таблице 1.

Для чего используется алюминий марки 6061?
Тип 6061 алюминий является одним из наиболее широко используемых алюминиевых сплавов . Его способность к сварке и формованию делает его пригодным для многих применений общего назначения. Его высокая прочность и коррозионная стойкость делают сплав типа 6061 особенно полезным в архитектурных, структурных и автомобильных приложениях.
Родственные
Каков модуль упругости алюминиевого сплава 6061? Каков модуль упругости алюминиевого сплава 6061?
Модуль упругости Юнга Модуль упругости Юнга алюминиевого сплава 6061 составляет около 69 ГПа. Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.

Родственные
Какова прочность на растяжение алюминия 6061? Какова прочность на растяжение алюминия 6061?
Алюминий 6061 Типичные механические свойства при различных температурах. Сплав и закалка. Температура, °C (°F) Предел прочности при растяжении, МПа (ksi) Предел текучести при смещении 0,2 %. Удлинение в 50 мм (2 д.), %, АЛ 6061-Т6, 6061-Т651. -195 (-320)
Родственный
Что такое алюминиевый сплав алал-6061? Что такое алюминиевый сплав алал-6061?
Алюминиевый сплав AL-6061 — конструкционный сплав общего назначения, разработанный компанией Alcoa в 1935. Обозначения отпуска в основном имеют 6061-Т4, Т451, АЛ 6061-Т6, 6061-Т651 и др. Это один из наиболее широко используемых сплавов. Основными легирующими элементами являются магний (Mg) и кремний (Si).
Родственные
Что такое модуль упругости стали? Что такое модуль упругости стали?
Его модуль упругости составляет 68,9 ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм).
 Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1.
Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1.общий Информация СМИ Нажмите галерея иллюстрация
Поделиться этой записью:
Изменение модуля Юнга холоднодеформированного алюминия AA 1050 и AA 2024 (T65): сравнительное исследование
[1] Д.Дж. Мак: Пер. АЙМЕ Том. 166 (1946), стр. 68.
[2] Дж.А. Бенито, Дж. М. Манеро, Дж.
 Джорба и А. Рока: Мет. и мат. Транс. Том. 36А (2005), стр. 3317.
Джорба и А. Рока: Мет. и мат. Транс. Том. 36А (2005), стр. 3317.[3] Х.М. Ледбеттер, С.А. Ким: Матер. науч. англ. Том. 101 (1988) стр. 87.
[4] Ф. Морестин и М. Бойвин: Nuclear Eng. и Дизайн Том. 162 (1996), с.107.
[5] К. Ямагути, Х. Адачи и Н. Такакура: Мет. и мат. Том. 4, 3 (1998) стр. 420.
[6] Дж.
 А. Бенито, Дж. Джорба и А. Рока: Матем. науч. Форум Том. 426-432 (2003), стр. 4435.
А. Бенито, Дж. Джорба и А. Рока: Матем. науч. Форум Том. 426-432 (2003), стр. 4435.[7] Дж. Джорба, Р. Понс, Дж.А. Бенито и А. Рока: специальный выпуск J. Mater. Технология обработки. Том. 117, 3, Thermec’00-Proc. Междунар. конф. Об обработке и производстве передовых материалов, Лас-Вегас, Невада, CDROM.
[8] Дж.А. Бенито: докторская диссертация, Барселонский университет, Испания (2001).
[9] В.
 Кестер и К. Розенталь: Zisch. Металлкунде Том. 30 (1938), стр. 345.
Кестер и К. Розенталь: Zisch. Металлкунде Том. 30 (1938), стр. 345.[10] С. Сима и М. Ян: J. Soc. Мат. науч. Япония Том. 44, 500 (1995) с.578.
[11] Э.П. Пападакис: J. Appl. физ. Том. 35 (1964) стр. 1474.
[12] Справочник Smithells Metals, 7 th. Эд., Э.А. Брандес, Г.Б. Брук (ред.) 1992, с.15. 2.
[13] И.
 Фонсека, Х.А. Бенито, И. Мехиа, Х. Джорба и А. Рока: Rev. Metal. Мадрид Том. 38 (2002), стр. 249.
Фонсека, Х.А. Бенито, И. Мехиа, Х. Джорба и А. Рока: Rev. Metal. Мадрид Том. 38 (2002), стр. 249.[14] Э.П. Пападакис, К.А. Стикелс и Р.К. Иннес: SAE Trans. Коврики JNL. Производитель Том. 104 (1995), с.830.
[15] М. Лусена, Дж.А. Бенито, А. Рока и Дж. Джорба: Rev. Metal. Мадрид Том. 34 (1998), стр. 310.
[16] Дж.
 Калле, Дж.А. Бенито, Дж. Джорба и А. Рока: Proc. V Congreso Nacional de Propiedades Mecánicas de Sólidos UPC Vol. 1 (1996), с.314.
Калле, Дж.А. Бенито, Дж. Джорба и А. Рока: Proc. V Congreso Nacional de Propiedades Mecánicas de Sólidos UPC Vol. 1 (1996), с.314.[17] Н.Ф. Мотт: Фил. Маг. Том 43 (1952), стр. 1151.
[18] Дж. Фридель: Фил. Маг. Том. 44 (1953), с.444.
Узнать о модуле упругости алюминия
Модуль упругости алюминия Определение
Модуль упругости можно определить как константу, которая представляет собой количественную меру сопротивления объекта приложенному к нему напряжению.
 Математически он представляется в виде наклона кривой напряжения-деформации, построенной для конкретного объекта.
Математически он представляется в виде наклона кривой напряжения-деформации, построенной для конкретного объекта.Обзор модуля упругости алюминия
Концепция модулей упругости очень важна в практическом мире. Мы определяем полезность того или иного материала на основе значения его модулей упругости.
Существует три основных типа модулей упругости, а именно модуль Юнга, модуль сдвига и объемный модуль. Все три из них количественно определяют сопротивляемость различным видам стресса. Математически модули упругости представлены как отношение напряжения растяжения к деформации растяжения.
σ∝ε\sigma \propto \varepsilonσ∝ε
σ=Eε\sigma =E\varepsilonσ=Eε
E=σ/εE = \sigma /\varepsilonE=σ/ε
Есть вопрос по этой теме?
Что вы узнаете:
- Определение модуля упругости алюминия
- Обзор модуля упругости алюминия
- Три вида модулей упругости
- Модуль упругости для алюминия
- Кривая напряжения-деформации для алюминия
- 1
- 1 модулей упругости
Обсудим подробно все ранее упомянутые виды модулей.
 Как упоминалось ранее, существует три вида модулей упругости : –
Как упоминалось ранее, существует три вида модулей упругости : – Модуль Юнга
Упругость при растяжении представлена с использованием модуля Юнга. Это тенденция деформации вдоль оси, проявляемая объектом при приложении противоположных сил вдоль указанной оси.
Модуль сдвига
Он также известен как модуль жесткости, и он количественно определяет сопротивление, оказываемое объектом и при постоянном объеме, при приложении противоположных сил для деформации его формы.
Объемный модуль
Этот модуль представляет собой объемную эластичность, которая проявляется, когда объект подвергается воздействию противоположных сил от всех задержаний. Это сопротивление объекта деформации в вышеизложенном сценарии.
Модуль упругости для алюминия
Значение модуля упругости для алюминия составляет 69 ГПа (или 10 000 000 фунтов на квадратный дюйм).
 Это означает, что 692}1м2.
Это означает, что 692}1м2.Как видно, это очень большое значение. Следовательно. Алюминий имеет разнообразное и широкое применение в строительных конструкциях, где требуется, чтобы материал был прочным.
Кривая напряжения-деформации для алюминия
На рисунке выше показана типичная кривая напряжения-деформации. Давайте посмотрим глубже и проанализируем некоторые его части
Максимальное безопасное напряжение, которое можно приложить к объекту без его разрушения, известно как предел прочности. Чтобы признать материал хрупким или пластичным, сравнивают его предел прочности и предел текучести. В случае пластичных металлов предел прочности может быть выше, чем предел текучести; для хрупких материалов эти два значения близки. Предел прочности алюминия составляет 310 МПа.
Предел текучести (B)
Это значение, соответствующее пределу текучести материала, т.
 е. значение, при котором приложенное напряжение упругой деформации начинает пластически деформировать материал, а не пластически. Предел текучести алюминия составляет 276 МПа. Алюминий пластичен по своей природе, так как это значение ниже, чем предел прочности.
е. значение, при котором приложенное напряжение упругой деформации начинает пластически деформировать материал, а не пластически. Предел текучести алюминия составляет 276 МПа. Алюминий пластичен по своей природе, так как это значение ниже, чем предел прочности.На кривой напряжение-деформация пропорциональным предельным напряжением является значение, соответствующее точке, в которой график перестает быть линейным и переходит в пластическую область из упругой области. Аналогичным этой концепции является предел эластичности; предел упругости можно определить как максимальное безопасное напряжение, которое может выдержать материал, прежде чем он окончательно деформируется. Обычно используемые алюминиевые сплавы имеют диапазон предела упругости от 30 до 280 МПа. 9Разрыв (D)
Деформация при смещении (E)
Также известная как предел текучести при смещении, деформация при смещении представляет собой точку, в которой приблизительно определяется предел упругости материала.



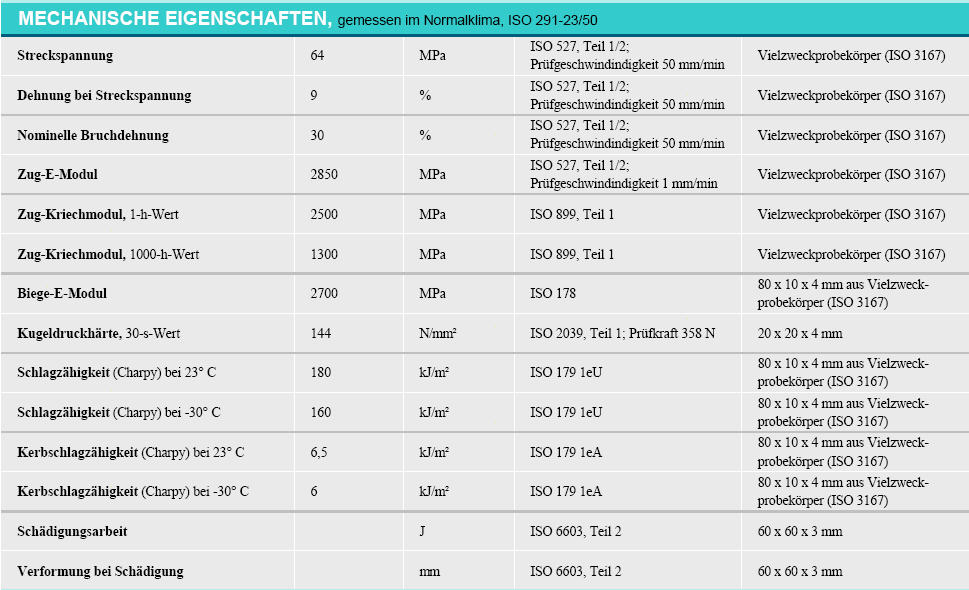

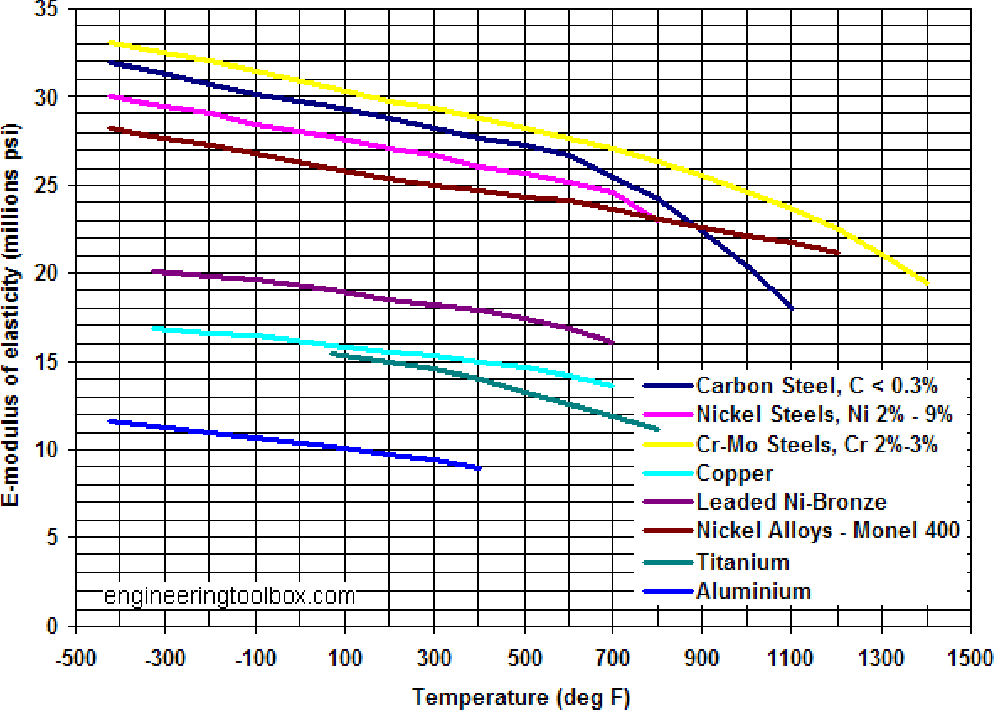 10 5
10 5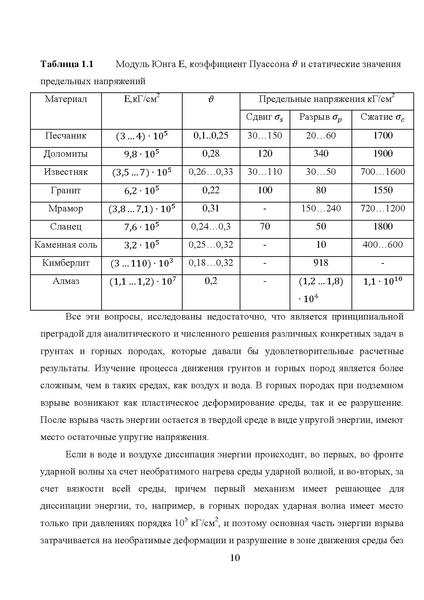 ..0,1) . 10 5
..0,1) . 10 5
 Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*.
Стали С345 и С375 категорий 1, 2, 3, 4 по ГОСТ 27772-88 заменяют стали категорий соответственно 6, 7 и 9, 12, 13 и 15 по ГОСТ 19281-73* и ГОСТ 19282-73*. Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
Нужно найти именно тот размер, который обеспечит сохранение формы системы при минимальной возможной массе под влиянием нагрузки. К примеру, какую именно сталь следует применять в качестве пролётной балки сооружения? Материал может использоваться нерационально, усложнится монтаж и утяжелится конструкция, увеличатся финансовые затраты. На этот вопрос ответит такое понятие как модуль упругости стали. Он же позволит на самой ранней стадии избежать появления этих проблем.
 Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.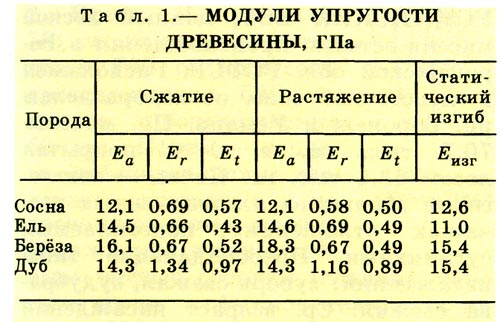
 Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом.
Значения модуля упругости даны для канатов, предварительно вытянутых усилием не менее 60 % разрывного усилия для каната в целом. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
 Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
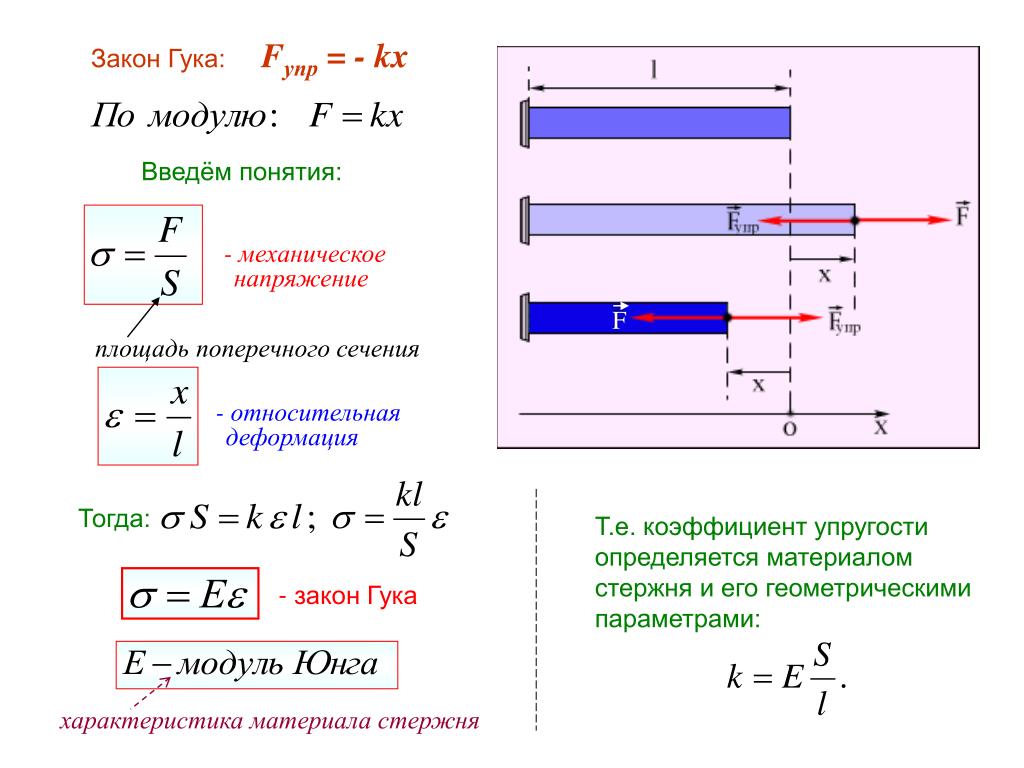 2 .
2 .
 )
) Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с.
Т.1 / Под общ. ред. К.П. Яковлева. М.: ФИЗМАТГИЗ. 1960. – 446 с. Поэтому значения E могут отличаться от средних значений, приведенных в таблице.
Поэтому значения E могут отличаться от средних значений, приведенных в таблице. ..
.. Измеряется в килограммах силы.
Измеряется в килограммах силы. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.