Модуль юнга через закон гука: Механическое напряжение. Модуль Юнга. Закон Гука — урок. Физика, 10 класс.
alexxlab | 25.05.2023 | 0 | Разное
ОглавлениеВВЕДЕНИЕ§ 1.2. Физика и техника. § 1.3. Понятие о величине и измерении. Физические величины. § 1.4. Прямое и косвенное измерения. § 1.5. Звездное небо и его видимое вращение. § 1.6. Угловые измерения на небе. § 1.7. Определение расстояний до небесных тел на основе измерения параллаксов. § 1.8. Основные единицы времени и их связь с движением Земли. § 1.9. Правило вывода единиц физических величин из формул. Международная система единиц СИ. § 1.10. Плотность вещества. Раздел I. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА Глава 2. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА § 2.2. Диффузия. § 2.3. Силы молекулярного взаимодействия. § 2.4. Кинетическая и потенциальная энергия молекул. § 2.5. Агрегатное состояние вещества. § 2.6. Понятие о температуре и внутренней энергии тела. Глава 3. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗООБРАЗНОГО СОСТОЯНИЯ ВЕЩЕСТВА § 3.  2. Броуновское движение.§ 3.3. Измерение скорости движения молекул газа. Опыт Штерна. § 3.4. Распределение молекул по скоростям их хаотического движения. § 3.5. Размеры и массы молекул и атомов. § 3.6. Постоянная Авогадро и постоянная Лошмидта. § 3.7. Число столкновений и длина свободного пробега молекул в газе. § 3.8. Давление газа. Манометры. § 3.9. Понятие вакуума. § 3.10. Межзвездный газ. Глава 4. ИДЕАЛЬНЫЙ ГАЗ. АБСОЛЮТНАЯ ТЕМПЕРАТУРА И ЕЕ СВЯЗЬ С ЭНЕРГИЕЙ МОЛЕКУЛ ГАЗА § 4.2. Основное уравнение молекулярно-кинетической теории газов. § 4.3. Зависимость давления газа от температуры при постоянном объеме. § 4.4. Абсолютный нуль. § 4.5. Термодинамическая шкала температур. Абсолютная температура. § 4.6. Связь между температурой и кинетической энергией молекул газа. Постоянная Больцмана. Глава 5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА § 5.3. Молярная газовая постоянная.  Определение числового значения постоянной Больцмана.§ 5.4. Уравнение Клапейрона — Менделеева. Плотность газа. § 5.5. Зависимость средней квадратичной скорости молекул газа от температуры. § 5.6. Изохорический процесс. § 5.7. Изобарический процесс. § 5.8. Изотермический процесс. § 5.9. Внутренняя энергия идеального газа. § 5.10. Работа газа при изменении его объема. Физический смысл молярной газовой постоянной. Глава 6. ИЗМЕНЕНИЕ ВНУТРЕННЕЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ § 6.2. Теплообмен. § 6.3. Виды теплообмена. § 6.4. Изменение внутренней энергии при нагревании и охлаждении. § 6.5. Уравнение теплового баланса при теплообмене. § 6.6. Подсчет теплоты, выделяемой при сжигании топлива. К. п. д. нагревателя. § 6.7. Изменение внутренней энергии при выполнении механической работы. Опыт Джоуля. § 6.8. Закон сохранения и превращения энергии в механике. § 6.9. Закон сохранения и превращения энергии в механических и тепловых процессах.  § 6.10. Первое начало термодинамики. § 6.11. Применение первого начала термодинамики к изопроцессам в идеальном газе. § 6.12. Адиабатный процесс. § 6.13. Понятие о строении Солнца и звезд. Глава 7. ПЕРЕХОД ВЕЩЕСТВА ИЗ ЖИДКОГО СОСТОЯНИЯ В ГАЗООБРАЗНОЕ И ОБРАТНО § 7.2. Испарение. § 7.3. Теплота парообразования. Глава 8. СВОЙСТВА ПАРОВ. КИПЕНИЕ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ВЕЩЕСТВА § 8.2. Свойства паров, насыщающих пространство. § 8.3. Свойства паров, не насыщающих пространство. § 8.4. Процесс кипения жидкости. § 8.5. Зависимость температуры кипения жидкости от внешнего давления. Точка кипения. § 8.6. Уравнение теплового баланса при парообразовании и конденсации. § 8.8. Критическое состояние вещества. § 8.9. Сжижение газов и использование жидких газов в технике. Глава 9. ВОДЯНОЙ ПАР В АТМОСФЕРЕ § 9.2. Абсолютная и относительная влажность воздуха. Точка росы. § 9.3. Приборы для определения влажности воздуха.  § 9.4. Понятие об атмосферах планет. Глава 10. СВОЙСТВА ЖИДКОСТЕЙ § 10.2. Поверхностный слой жидкости. § 10.3. Энергия поверхностного слоя жидкости. Поверхностное натяжение. § 10.4. Сила поверхностного натяжения. § 10.5. Смачивание. Краевой угол. § 10.6. Мениск. Давление, создаваемое искривленной поверхностью жидкости. § 10.7. Капиллярность. Капиллярные явления в природе и технике. § 10.8. Понятие о вязкости среды. Ламинарное течение жидкости. § 10.9. Закон Ньютона для внутреннего трения. Динамическая вязкость. § 10.10. Аморфные вещества. Глава 11. СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДЕФОРМАЦИИ § 11.2. Анизотропия кристаллов. Пространственная решетка и ее дефекты. § 11.3. Виды кристаллических структур. § 11.4. Виды деформаций. § 11.5. Механическое напряжение. § 11.6. Упругость, пластичность, хрупкость и твердость. § 11.7. Закон Гука. Модуль упругости. § 11.8. Энергия упруго деформированного тела. Глава 12. ПЛАВЛЕНИЕ И КРИСТАЛЛИЗАЦИЯ.  СУБЛИМАЦИЯ. ДИАГРАММА СОСТОЯНИЙ ВЕЩЕСТВА§ 12.2. Удельная теплота плавления. § 12.3. Изменение объема и плотности вещества при плавлении и отвердевании. § 12.4. Зависимость температуры и теплоты плавления от давления. Точка плавления. § 12.5. Уравнение теплового баланса при плавлении и кристаллизации. § 12.6. Растворы и сплавы. Охлаждающие смеси. § 12.8. Диаграмма состоянии вещества. Тройная точка. Глава 13. ТЕПЛОВОЕ РАСШИРЕНИЕ ТЕЛ § 13.2. Линейное расширение твердых тел при нагревании. § 13.3. Объемное расширение тел при нагревании. Зависимость плотности вещества от температуры. § 13.4. Особенности теплового расширения твердых тел. § 13.5. Некоторые особенности теплового расширения жидкостей. § 13.6. Значение теплового расширения тел в природе и технике. Раздел II. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ Глава 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ЗАКОН КУЛОНА § 14.2. Явления, подтверждающие сложное строение атома.  § 14.3. Опыты Резерфорда. Ядерная модель строения атома. § 14.4. Понятие о строении атомов различных химических элементов. § 14.5. Электризация при соприкосновении незаряженных тел. § 14.6. Сила взаимодействия электрических зарядов. Закон Кулона. § 14.7. Диэлектрическая проницаемость среды. § 14.8. Международная система единиц СИ в электричестве. Электрическая постоянная. § 14.9. Электроскоп. Глава 15. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 15.2. Напряженность электрического поля. § 15.3. Линии напряженности электрического поля. § 15.4. Однородное поле. Поверхностная плотность заряда. § 15.5. Работа электрического поля при перемещении заряда. Потенциальная энергия заряда. § 15.6. Потенциал. Разность потенциалов и напряжение. Эквипотенциальные поверхности. § 15.7. Связь между напряженностью поля и напряжением. Градиент потенциала. § 15.8. Проводник в электрическом поле. § 15.9. Электрометр. § 15.10. Диэлектрик в электрическом поле. Поляризация диэлектрика.  § 15.11. Понятие о сегнетоэлектриках. § 15.12. Пьезоэлектрический эффект. § 15.13. Электроемкость проводника. § 15.14. Условия, от которых зависит электроемкость проводника. § 15.15. Конденсаторы. § 15.16. Соединение конденсаторов в батарею. § 15.17. Энергия заряженного конденсатора. Плотность энергии электрического поля. § 15.18. Опыт Милликена. Глава 16. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА § 16.2. Сила тока и плотность тока в проводнике. § 16.3. Замкнутая электрическая цепь. § 16.4. Электродвижущая сила источника электрической энергии. § 16.5. Внешняя и внутренняя части цепи. § 16.6. Закон Ома для участка цепи без э. д. с. Сопротивление проводника. Падение напряжения. § 16.7. Зависимость сопротивления от материала, длины и площади поперечного сечения проводника. § 16.8. Зависимость сопротивления от температуры. § 16.9. Сверхпроводимость. § 16.10. Эквивалентное сопротивление. § 16.11. Последовательное соединение потребителей энергии тока.  § 16.12. Параллельное соединение потребителей энергии тока § 16.13. Закон Ома для всей цепи. § 16.14. Соединение одинаковых источников электрической энергии в батарею. § 16.15. Закон Ома для участка цепи с э. д. с. и для всей цепи при нескольких э. д. с. Глава 17. РАБОТА, МОЩНОСТЬ И ТЕПЛОВОЕ ДЕЙСТВИЕ ЭЛЕКТРИЧЕСКОГО ТОКА § 17.2. Мощность электрического тока. § 17.3. Тепловое действие электрического тока. Закон Джоуля — Ленца. § 17.4. Короткое замыкание. Практическое применение теплового действия тока. Глава 18. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ § 18.2. Контактная разность потенциалов. § 18.3. Термоэлектродвижущая сила. § 18.4. Явление Пельтье. § 18.5. Применение термоэлектрических явлений в науке и технике. Глава 19. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ § 19.3. Электролиз, сопровождающийся растворением анода. § 19.4. Количество вещества, выделяющегося при электролизе. Первый закон Фарадея. § 19.5. Второй закон Фарадея.  Определение заряда иона.§ 19.6. Использование электролиза в технике. § 19.7. Гальванические элементы. § 19.8. Аккумуляторы. § 19.9. Применение гальванических элементов и аккумуляторов в технике. Явление электрокоррозии. Глава 20. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ И В ВАКУУМЕ § 20.2. Зависимость силы тока в газе от напряжения. § 20.3. Электрический разряд в газе при атмосферном давлении. § 20.4. Электрический разряд в разреженных газах. Газосветные трубки и лампы дневного света. § 20.5. Излучение и поглощение энергии атомом. § 20.6. Катодные лучи. § 20.7. Понятие о плазме. § 20.8. Электрический ток в вакууме. § 20.9. Двухэлектродная лампа (диод). § 20.10. Трехэлектродная лампа (триод). § 20.11. Электронно-лучевая трубка. Глава 21. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ § 21.2. Чистые (беспримесные) полупроводники. Термисторы. § 21.3. Примесные полупроводники. § 21.4. Электронно-дырочный переход. § 21.5. Полупроводниковый диод.  § 21.6. Полупроводниковый триод (транзистор). Глава 22. ЭЛЕКТРОМАГНЕТИЗМ § 22.2. Магнитное поле как особый вид материи. § 22.3. Магниты. § 22.4. Линии магнитной индукции. Понятие о вихревом поле. § 22.5. Магнитное поле прямолинейного тока, кругового тока и соленоида. § 22.6. Сравнение магнитных свойств соленоида и постоянного магнита. § 22.7. Сила взаимодействия параллельных токов. Магнитная проницаемость среды. § 22.8. Определение ампера. Магнитная постоянная. § 22.9. Действие магнитного поля на прямолинейный проводник с током. § 22.10. Однородное магнитное поле. § 22.11. Магнитный момент контура с током. § 22.12. Работа при перемещении проводника с током в магнитном поле. Магнитный поток. § 22.13. Индукция магнитного поля, создаваемая в веществе проводниками с током различной формы. § 22.14. Напряженность магнитного поля и ее связь с индукцией и магнитной проницаемостью среды. § 22.15. Парамагнитные, диамагнитные и ферромагнитные вещества.  § 22.16. Намагничивание ферромагнетиков. Электромагнит. § 22.17. Работа и устройство амперметра и вольтметра. § 22.18. Сила Лоренца. Движение заряда в магнитном поле. § 22.19. Постоянное и переменное магнитные поля. Глава 23. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 23.2. Явление электромагнитной индукции. § 23.3. Э. д. с. индукции, возникающая в прямолинейном проводнике при его движении в магнитном поле. Правило правой руки. § 23.4. Опыты Фарадея. § 23.5. Закон Ленца для электромагнитной индукции. Объяснение диамагнитных явлений. § 23.6. Величина э. д. с. индукции. § 23.7. Вихревое электрическое поле и его связь с магнитным полем. § 23.8. Вихревые токи. § 23.9. Роль магнитных полей в явлениях, происходящих на Солнце и в космосе. § 23.10. Явление самоиндукции. Э. д. с. самоиндукции. § 23.11. Энергия магнитного поля. Раздел III. КОЛЕБАНИЯ И ВОЛНЫ Глава 24. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ § 24.2. Условия возникновения колебаний. § 24.  3. Классификация колебательных движений тела в зависимости от действующей на него силы.§ 24.4. Параметры колебательного движения. § 24.5. Величины, характеризующие мгновенное состояние колеблющейся точки. § 24.6. Гармоническое колебание. § 24.7. Уравнение гармонического колебания и его график. § 24.8. Математический маятник. § 24.9. Законы колебания математического маятника. Формула маятника. § 24.10. Физический маятник. § 24.11. Практические применения маятников. § 24.12. Упругие колебания. Превращение энергии при колебательном движении. § 24.13. Распространение колебательного движения в упругой среде. § 24.14. Перенос энергии бегущей волной. § 24.15. Поперечные и продольные волны. § 24.16. Волна и луч. Длина волны. § 24.17. Скорость распространения волн и ее связь с длиной волны и периодом (частотой) колебаний. § 24.18. Сложение колебаний, происходящих по одной прямой. § 24.19. Отражение волн. § 24.20. Стоячие волны.  § 24.21. Интерференция волн. § 24.22. Сложение колебаний с кратными частотами. Разложение сложного колебания на гармонические составляющие. § 24.23. Вынужденные колебания. Механический резонанс и его роль в технике. Глава 25. ЗВУК И УЛЬТРАЗВУК § 25.3. Громкость и интенсивность звука. § 25.4. Высота тона и тембр звука. § 25.5. Интерференция звуковых волн. § 25.6. Отражение и поглощение звука. § 25.7. Звуковой резонанс. § 25.8. Ультразвук и его применение в технике. Глава 26. ПЕРЕМЕННЫЙ ТОК § 26.2. Понятие об устройстве индукционных генераторов. § 26.3. Действующие значения э. д. с., напряжения и силы переменного тока. § 26.4. Индуктивность и емкость в цепи переменного тока. § 26.5. Преобразование переменного тока. Трансформатор. § 26.6. Индукционная катушка. § 26.7. Трехфазный ток. § 26.8. Получение, передача и распределение электрической энергии в народном хозяйстве СССР. Глава 27. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 27.  2. Затухающие электромагнитные колебания. Электрический резонанс.§ 27.3. Получение незатухающих колебаний с помощью лампового генератора. § 27.4. Токи высокой частоты и их применение. § 27.5. Электромагнитное поле как особый вид материи. § 27.6. Открытый колебательный контур. Излучение. § 27.7. Электромагнитные волны. Скорость их распространения. § 27.8. Опыты Герца. § 27.9. Изобретение радио А С. Поповым. Радиотелеграфная связь. § 27.10. Радиотелефонная связь. Амплитудная модуляция. § 27.11. Устройство простейшего лампового радиоприемника с усилителем низкой частоты. § 27.12. Понятие о радиолокации. Раздел IV. ОПТИКА. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ Глава 28. ПРИРОДА СВЕТА. РАСПРОСТРАНЕНИЕ СВЕТА § 28.2. Понятие об электромагнитной теории света. Диапазон световых волн. § 28.3. Понятие о квантовой теории света. Постоянная Планка. § 28.4. Источники света. § 28.5. Принцип Гюйгенса. Световые лучи. § 28.6. Скорость распространения света в вакууме. 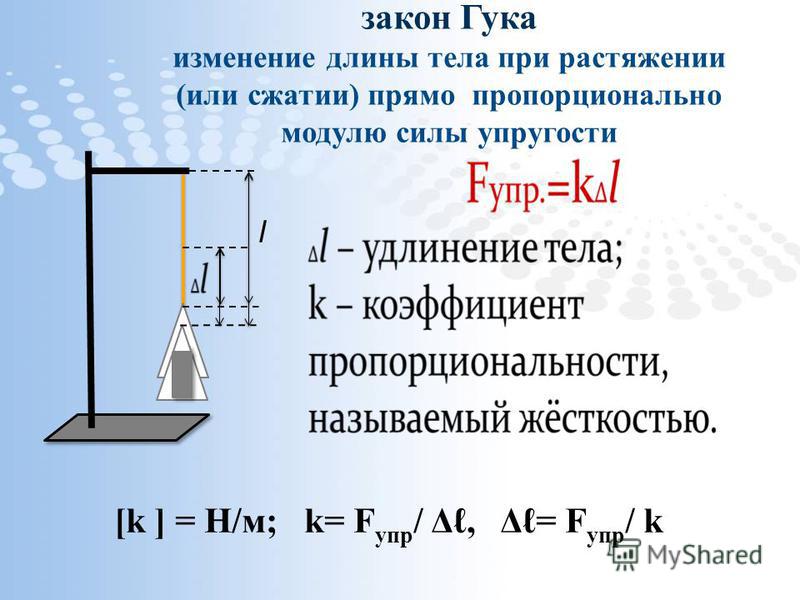 Опыт Майкельсона.§ 28.7. Скорость распространения света в различных средах. Глава 29. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА § 29.2. Законы отражения света. § 29.3. Зеркальное и диффузное отражение. Плоское зеркало. § 29.4. Сферические зеркала. § 29.5. Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала. § 29.6. Законы преломления света. § 29.7. Абсолютный показатель преломления и его связь с относительным показателем преломления. § 29.8. Полное отражение света. Предельный угол. § 29.9. Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением. Глава 30. ЛИНЗЫ. ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ С ПОМОЩЬЮ ЛИНЗ § 30.2. Главные фокусы и фокальные плоскости линзы. § 30.3. Оптическая сила линзы. § 30.4. Построение изображения светящейся точки, расположенной на главной оптической оси линзы. § 30.5. Вывод формулы для сопряжеппых точек тонкой линзы. § 30.  6. Построение изображения светящейся точки, расположенной на побочной оптической оси линзы.§ 30.7. Построение изображений предмета, создаваемых линзой. § 30.8. Линейное увеличение, полученное с помощью линзы. § 30.9. Недостатки линз. Выясним, какие существенные недостатки встречаются у линз. Глава 31. ОПТИЧЕСКИЕ ПРИБОРЫ. ГЛАЗ § 31.2. Фотографический аппарат. § 31.3. Глаз как оптическая система. § 31.4, Длительность зрительного ощущения. § 31.5. Угол зрения. § 31.6. Расстояние наилучшего зрения. Оптические дефекты глаза. § 31.7. Увеличение оптического прибора. Лупа. § 31.8. Микроскоп. § 31.9. Труба Кеплера. Телескопы. § 31.10. Труба Галилея. Бинокль. Глава 32. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ ВОЛНОВЫМИ СВОЙСТВАМИ СВЕТА § 32.2. Цвета тонких пленок. § 32.3. Интерференция в клинообразной пленке. Кольца Ньютона. § 32.4. Интерференция света в природе и технике. § 32.5. Дифракция света. § 32.6. Дифракционная решетка и дифракционный спектр.  Измерение длины световой волны.§ 32.7. Поляризация волн. § 32.8. Поляризация света. Поляроиды. § 32.9. Поляризация при отражении и преломлении света. Глава 33. ФОТОМЕТРИЯ § 33.2. Световой поток. § 33.3. Сила света. Единицы силы света и светового потока. § 33.4. Освещенность. § 33.5. Яркость. § 33.6. Законы освещенности. § 33.7. Сравнение силы света двух источников. Фотометр. Люксметр. Глава 34. ИЗЛУЧЕНИЕ И СПЕКТРЫ. РЕНТГЕНОВСКИЕ ЛУЧИ § 34.2. Разложение белого света призмой. Сплошной спектр. § 34.3. Сложение спектральных цветов. Дополнительные цвета. § 34.4. Цвета тел. § 34.5. Ультрафиолетовая и инфракрасная части спектра. § 34.6. Роль ультрафиолетовых и инфракрасных лучей в природе. Их применение в технике. § 34.7. Приборы для получения и исследования спектров. § 34.8. Виды спектров. § 34.9. Спектры поглощения газов. Опыты Кирхгофа. § 34.10. Закон теплового излучения Кирхгофа. § 34.11. Законы теплового излучения Стефана — Больцмана, Вина, Планка.  § 34.12. Спектры Солнца и звезд. Их связь с температурой. § 34.13. Спектральный анализ. § 34.14. Понятие о принципе Доплера. § 34.15. Рентгеновские лучи и их практическое применение. § 34.16. Шкала электромагнитных волн. § 34.17. Виды космического излучения. Глава 35. ЯВЛЕНИЯ, ОБЪЯСНЯЕМЫЕ КВАНТОВЫМИ СВОЙСТВАМИ ИЗЛУЧЕНИЯ § 35.2. Давление световых лучей. Опыты П. Н. Лебедева. § 35.3. Тепловое действие света. § 35.4. Химическое действие света. § 35.5. Использование химического действия света при фотографировании. Понятие о квантовой природе химического действия излучения. § 35.6. Внешний фотоэлектрический эффект. Опыты Столетова. § 35.7. Законы внешнего фотоэффекта. § 35.8. Объяснение фотоэффекта на основе квантовой теории. § 35.9. Фотоэлементы с внешним фотоэффектом. § 35.10. Внутренний фотоэффект. § 35.11. Фотосопротивления. § 35.12. Фотоэлементы с внутренним фотоэффектом. § 35.13. Использование фотоэлементов в науке и технике.  § 35.14. Понятие о телевидении. § 35.15. Понятие о теории Бора. Строение атома водорода. § 35.16. Излучение и поглощение энергии атомами. § 35.17. Явление люминесценции. § 35.18. Понятие о квантовых генераторах. Глава 36. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 36.2. Экспериментальные основы специальной теории относительности Эйнштейна. Постулаты Эйнштейна. § 36.3. Понятие одновременности. § 36.4. Относительность понятий длины и промежутка времени § 36.5. Теорема сложения скоростей Эйнштейна. § 36.6. Масса и импульс в специальной теории относительности. § 36.7. Связь между массой и энергией. Уравнение Эйнштейна. § 36.8. Связь между импульсом и энергией. Импульс и энергия фотонов. Раздел V. ФИЗИКА АТОМНОГО ЯДРА Глава 37. СТРОЕНИЕ АТОМНОГО ЯДРА § 37.2. Радиоактивность. § 37.3. Понятие о превращении химических элементов. § 37.4. Понятие об энергии и проникающей способности радиоактивного излучения. § 37.5. Эффект Вавилова — Черенкова.  § 37.6. Открытие искусственного превращения атомных ядер. § 37.7. Открытие нейтрона. § 37.8. Состав атомного ядра. Запись ядерных реакций. § 37.9. Изотопы. § 37.10. Понятие о ядерных силах. § 37.11. Дефект массы атомных ядер. Энергия связи. Глава 38. КОСМИЧЕСКИЕ ЛУЧИ. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 38.2. Открытие позитрона. § 38.3. Нейтрино. § 38.4. Открытие новых элементарных частиц. § 38.5. Классификация элементарных частиц. § 38.6. Античастицы. Взаимные превращения вещества и поля. § 38.7. Гипотеза кварков. Глава 39. АТОМНАЯ ЭНЕРГИЯ И ЕЕ ИСПОЛЬЗОВАНИЕ § 39.2. Деление тяжелых атомных ядер. § 39.3. Цепная реакция деления. Ядерный взрыв. § 39.4. Ядерный реактор. § 39.5. Развитие ядерной энергетики в СССР. § 39.6. Понятие о термоядерной реакции. Энергия Солнца и звезд. § 39.7. Понятие об управляемой термоядерной реакции. § 39.8. Получение радиоактивных изотопов и их применение. Раздел VI. ОСНОВНЫЕ СВЕДЕНИЯ ПО АСТРОНОМИИ Глава 40.  СТРОЕНИЕ И РАЗВИТИЕ ВСЕЛЕННОЙ§ 40.2. Происхождение и развитие небесных тел. § 40.3. Понятие о космологии. |
Уточнение закона физики – Наука – Коммерсантъ
Упругие свойства материалов интересовали человечество с древнейших времен. Существенный прогресс в понимании упругости был достигнут в работах Роберта Гука, английского исследователя, работавшего во второй половине XVII века. Считается, что наряду с Исааком Ньютоном Гук «ответственен» за закон всемирного тяготения.
Фото: Getty Images
Фото: Getty Images
В теории упругости он известен открытием закона Гука, который гласит, что сила, которая требуется, чтобы растянуть материал (см. рисунок), оказывается пропорциональна величине растяжения. Коэффициент пропорциональности характеризует конкретный материал и называется объемным модулем Юнга. Для тонких пластин удобно работать с модулем Юнга Y, который получается умножением объемного модуля Юнга на толщину пластины.
(Модуль Юнга в системе единиц СИ измеряется в ньютонах на метр (н/м).) Кроме растяжения или сжатия в плоскости у тонких пластин возникает возможность изгиба. Энергия, связанная с изгибом, определяется величиной изгибной жесткости. (В системе СИ изгибная жесткость измеряется в джоулях.)
Возникающий при уменьшении толщины пластины до одного атомарного слоя объект принято называть кристаллической мембраной. Самый известный пример — это графен, который представляет собой один слой атомов углерода, расположенных в узлах шестигранных (сотовых) ячеек. Графен был получен в лаборатории Андреем Геймом и Константином Новоселовым в 2004 году. За это открытие им обоим была присуждена Нобелевская премия по физике в 2010 году. В настоящее время графен находит широкое применение в различных областях, включая биомедицину (сенсоры молекул), химию (молекулярные фильтры) и электронику (графеновые конденсаторы и транзисторы). Часто можно встретить утверждение, что графен является очень прочным материалом.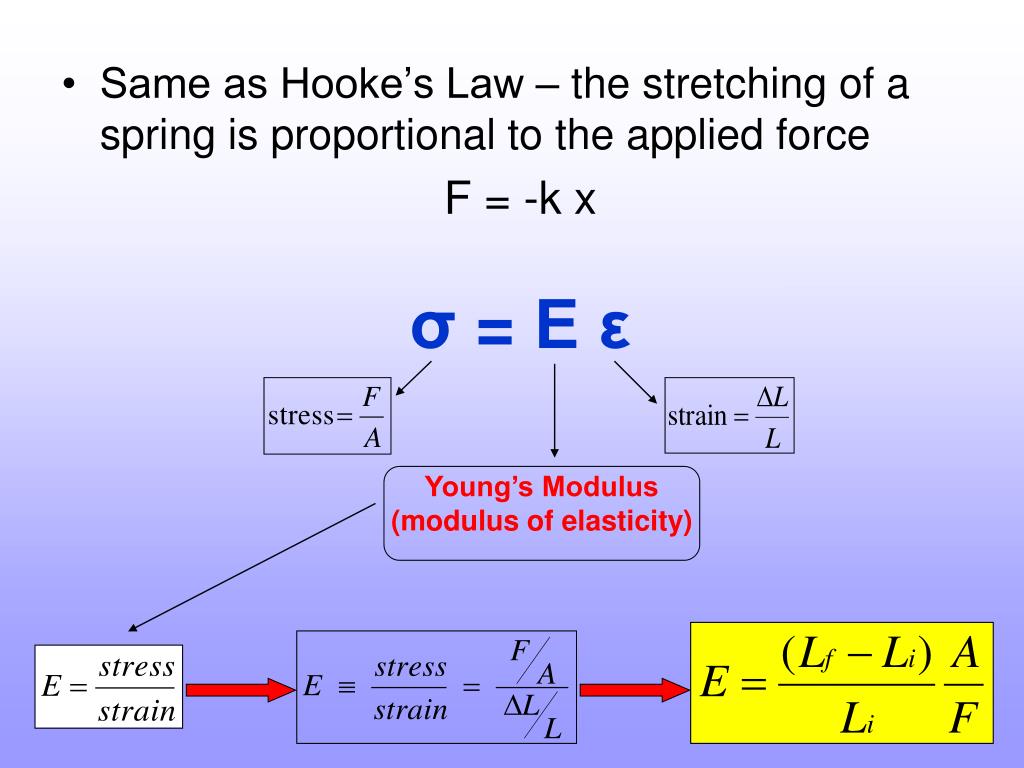
–19 джоулей.
Брусок, к одному концу которого приложена растягивающая сила F. Эта сила приводит к продольному растяжению бруска. Модуль Юнга Y связан c объемным модулем Юнга E как Y=E t
Брусок, к одному концу которого приложена растягивающая сила F. Эта сила приводит к продольному растяжению бруска. Модуль Юнга Y связан c объемным модулем Юнга E как Y=E t
Как известно из школьного курса физики, атомы в кристаллах совершают тепловые колебания около своих положений равновесия. Эти же тепловые колебания могут вызывать изгибные деформации мембраны. Можно оценить, как величина изгибных деформаций, вызванных тепловыми флуктуациями, растет с увеличением продольного размера мембраны, и найти, при каком размере она сравнивается с толщиной мембраны. Последняя для одноатомного слоя имеет порядок долей нанометра (нм). Соответствующая длина, называемая длиной Гинзбурга, оказывается для графена исключительно маленькой.
Она равна 1 нм при комнатной температуре. Поэтому для всех исследуемых в лабораториях образцах графена тепловые изгибные флуктуации оказываются принципиально важны. Для сравнения можно оценить длину Гинзбурга для листа бумаги толщиной 1 мм. Она оказывается равной 1000 км при комнатной температуре! Именно поэтому в обычной жизни мы, как правило, не встречаемся с проявлением тепловых изгибных флуктуаций.
Несмотря на то что роль длины Гинзбурга в физике кристаллических мембран была осознана только в середине 1980-х годов, важность тепловых изгибных флуктуаций была понятна еще с 1930-х годов. В это время Лев Ландау и Рудольф Пайерлс, английский физик-теоретик, один из пионеров концепции дырочной проводимости в полупроводниках и теории экситонов, независимо друг от друга показали, что бесконечные кристаллические мембраны из-за тепловых изгибных флуктуаций должны разрушаться, превращаясь в бесформенный комок атомов. Другими словами, получается, что их результат, который до сих пор входит в стандартные учебники по теоретической физике, например, в курс Ландау и Лифшица, запрещает существование графена!
Как же примерить ставшее классическим утверждение Ландау—Пайерлса и чешуйки графена, имеющиеся в настоящее время во многих лабораториях мира.
Как это обычно бывает для многих вопросов, разгадка скрыта в деталях. Обратим внимание на то, что, согласно результату Ландау—Пайерлса, не существует кристаллических мембран бесконечных размеров. При любой заданной температуре существует предельный продольный размер мембраны, когда изгибных тепловых флуктуаций недостаточно для разрушения мембраны. Подчеркнем, что этот размер не нужно путать с длиной Гинзбурга! Если оценить такой предельный размер для графена при комнатной температуре, то получится гигантская длина. Так как в лабораториях чешуйки графена обычно имеют размер всего несколько микрометров, то, казалось бы, разгадка найдена!
Как это часто бывает в физике, самое простое объяснение явления не всегда оказывается правильным. Утверждение Ландау—Пайерлса основано на предположении, что изгибные тепловые флуктуации не взаимодействуют друг с другом, как говорят, являются гармоническими. Оказывается, что для графена такая идеализация справедлива только для очень маленьких размеров, меньше длины Гинзбурга.
Для графена микронного размера игнорировать взаимодействие изгибных флуктуаций между собой оказывается принципиально неправильным. Их взаимодействие приводит к тому, что изгибная жесткость мембраны начинает расти степенным образом с увеличением продольного размера, то есть чем больше размер мембраны, тем все труднее становится ее изогнуть. Этот эффект был теоретически предсказан в середине 80-х годов прошлого века. Он приводит к тому, что бесконечная кристаллическая мембрана оказывается устойчивой при температурах ниже некоторой критической. Для графена критическая температура оказывается выше 10 тыс. градусов Кельвина. Такая высокая критическая температура означает, что тепловые изгибные флуктуации никогда не разрушают графен, так как при таких высоких температурах уже расплавится кристаллическая решетка.
Взаимодействие изгибных флуктуаций приводит к ряду интересных явлений в кристаллических мембранах, которые называют термином аномальная упругость. В области малых продольных деформаций нарушается закон Гука: деформация мембраны как целого становится степенной функцией приложенной силы со значением показателя степени меньше единицы, который к тому же не зависит от типа атомов мембраны, то есть является универсальным.
Линейный закон Гука восстанавливается только при достаточно больших значениях деформации. Недавно такой нелинейный закон Гука для графена был измерен экспериментально. Также у графена в широкой области параметров оказывается отрицательным коэффициент Пуассона. Напомним, что положительный коэффициент Пуассона характеризует, как при растяжении в одном направлении материал сжимается в поперечном направлении. У графена вместо сжатия в поперечном направлении происходит растяжение! Наконец, вплоть до ультранизких температур коэффициент теплового расширения графена оказывается отрицательным, то есть графен при нагреве сжимается, вместо того чтобы расширяться, как это делает большинство веществ.
В заключение можно сказать, что физика кристаллических мембран, в частности графена, в очередной раз подтверждает, что в настоящей науке не бывает абсолютных истин: все законы выводятся в рамках некоторых предположений, о которых не стоит забывать. В теории кристаллических мембран все еще осталось значительное количество вопросов, связанных с аномальной упругостью, требующих теоретического и экспериментального изучения.
В частности, этим занимаются ученые из Физико-технического института им. А. Ф. Иоффе РАН, Института теоретической физики им. Л. Д. Ландау РАН и Сколковского института науки и технологий в рамках гранта РФФИ 20-52-12019.
Игорь Бурмистров, доктор физико-математических наук, заместитель директора Института теоретической физики им. Л. Д. Ландау РАН
Понимание эластичных свойств кожи
КОНТЕКСТНа протяжении веков было изобретено множество устройств, в основном понимающих механику , прежде чем она сможет быть так широко понята и изучена. Глубокое понимание механики кожи открывает путь к характеристике механических свойств кожи человека и позволяет наблюдать за ее поведением в соответствии с законами упругости*, кручения и силы, которые вместе известны как «закон Гука» .
Определение
Закон Гука, применяемый к коже, представляет собой принцип физики, моделирующий ее деформацию* при внешнем растяжении, сжатии или изгибе.
Этот закон упругости является связующим звеном между смещением или величиной деформации и деформирующей силой или нагрузкой. Вот почему кожа возвращается к своей первоначальной форме после снятия нагрузки .
Эта способность возвращаться к нормальной форме после искажения называется «восстанавливающая сила» . Ссылаясь на закон Гука, эта восстанавливающая сила обычно пропорциональна степени растяжения * кожи. Закон также может быть выражен в терминах напряжения и напряжения.
Закон Гука можно сформулировать так:
F = -kx
Где :
- F есть сила
- X is длина растяжения/сжатия*
- k — это константа пропорциональности, которая обычно выражается в Н/м. Его значение зависит не только от типа рассматриваемого эластичного материала, но также от его размера и формы.
Рис.
1: Иллюстрация закона Гука, показывающая взаимосвязь между силой и расстоянием при приложении к пружине.
История закона Гука
За этим законом стоит Роберт Гук, британский физик 17-го века, давший ему свое имя, продемонстрировавший взаимосвязь между силами, приложенными к пружине, и ее упругостью. Благодаря этому опыту он заметил, что кривая зависимости напряжения от деформации для таких материалов, как кожа, имеет линейная область . Этот закон был впервые извлечен в 1660 году из латинской анаграммы, а затем использован как решение в 1678 году под формой «ut tensio, sic vis» , что означает по-английски «as the extension, so the force» или . «расширение пропорционально силе» .
Спустя столетие закон Гука смог связать деформацию с напряжением в области линейной упругости благодаря модулю, называемому… модулем Юнга.
Модуль Юнга
Модуль Юнга — это числовая константа , названная английским врачом 18 века Томасом Юнгом.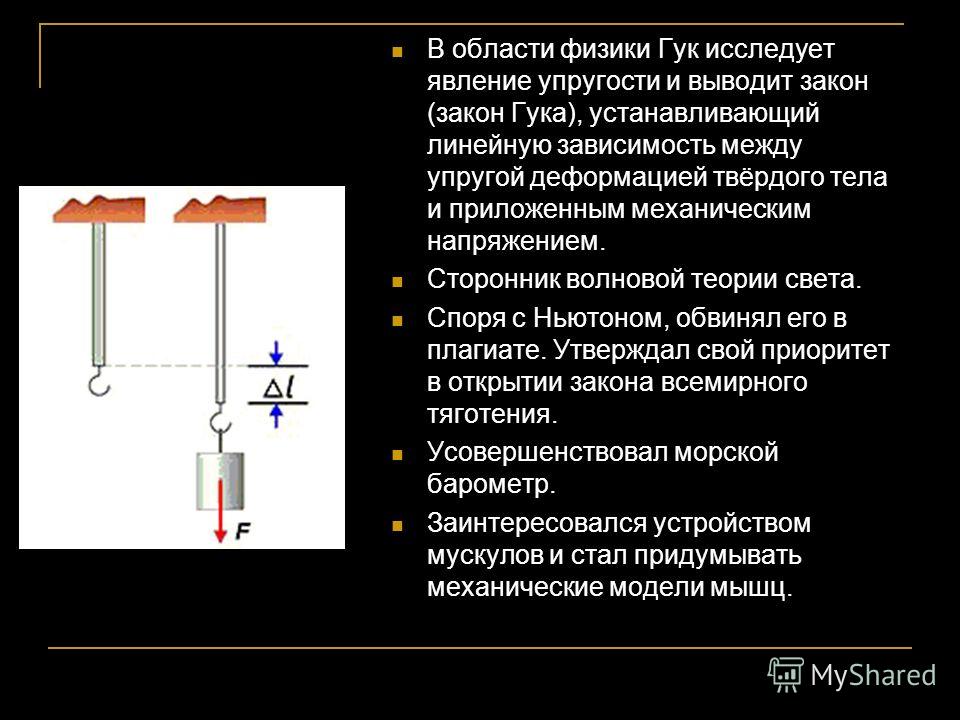
Он описывает сопротивление объекта упругой деформации при приложении к нему внешней силы. Модуль Юнга равен продольному напряжению, деленному на деформацию.
В чем разница между законом Гука и модулем Юнга?
Закон Гука — это основное эмпирическое правило, применяемое к коже и описывающее Связь прямой пропорциональности между силой, приложенной к объекту, и индуцированной деформацией. Модуль Юнга — это постоянный коэффициент жесткости*, обозначаемый k, который описывает жесткость кожи или вероятность ее деформации. Модуль Юнга может быть получен путем сжатия кожи с последующим измерением напряжения и деформации.
Рис. 2: Кривая напряжения и деформации в масштабе закона Гука.
Нанесение на кожу
По закону Гука эластичность материала равна отчасти из-за небольших смещений составляющих его молекул. Эти смещения также пропорциональны силе, вызванной самими смещениями.
Кожа определяется как идеально эластичная, так как она возвращается к своей первоначальной форме после приложения силы. Тогда кожа играет по механическим законам, которые могут переопределить ее собственные свойства.
ПОЧЕМУ АСМ?
АСМ собирает любую информацию о механических свойствах кожи, измеренных с помощью оптической системы, установленной на кантилевере. По отклонению АСМ силу можно рассчитать по закону Гука, если известна жесткость пружины.
В масштабе закона, которому более 300 лет, АСМ представляет собой один из самых современных и эффективных методов характеристики упругих свойств кожи.
Два известных физика 17-го и 18-го веков соответственно, множество разработок в области исследований кожи и яркая команда BioMeca, чтобы предоставить вам мощные инструменты, чтобы революционизировать тесты эффективности in vitro и ex vivo.
ЛЕКСИЧЕСКИЙ
- Деформация: изменение размера или формы объекта.
- Эластичность (или упругая деформация): временное изменение длины, объема или формы, возникающее в упругом веществе под действием напряжения.
- Жесткость (или жесткость): степень, в которой объект сопротивляется деформации в ответ на приложенную силу (измеряется в Н/м).
- Растягивание: делают материал длиннее или шире, чем обычно, в результате натяжения краев.
- Сжатие: процесс вдавливания материала в меньшее пространство или давления на него с разных сторон до тех пор, пока он не станет меньше.
Чтобы пойти дальше
Откройте для себя наши учебные примеры
Тематические исследования
Эффект натяжения
Дерма в основном состоит из плотного богатого коллагеном внеклеточного матрикса (ECM). Дермальный коллаген представляет собой наиболее распространенный белок внеклеточного матрикса и составляет основную часть кожи.
См. исследование
Тематические исследования
Разглаживающий эффект
Мобилизация кожи является результатом различной подвижности кожи и нижележащих структур. При растяжении и мобилизации кожи возникает упругая восстанавливающая сила, противоположная оси натяжения, стремящаяся вернуть кожу в прежнее состояние.
См. исследование
Тематические исследования
Кожный барьер
Эпидермальная дифференцировка приводит к образованию апоптотических клеток, более или менее сплоченных корнеоцитов. Одной из основных функций этих клеток является регулирование проницаемости эпидермиса. Кожный барьер обусловлен накоплением липидов.
См. исследование
НИЧЕГО НЕ ПРОПУСТИТЕ
Следите за другими нашими новостями
Новости
Месяц осведомленности о раке поджелудочной железы подходит к концу, и что может быть лучше, чем закончить его хорошим чтением о влиянии табака на кожу? Если вы курите или даже планируете бросить, уверяем вас, эта статья поможет вам принять решение бросить курить
Подробнее
29 ноября 2022
Новости
Температура падает с каждым днем все больше, и мы часто забываем, что наша кожа нуждается в защите от этих климатических изменений.
Если вы хотите, чтобы ваша кожа выглядела идеально этой зимой, не забудьте прочитать эту статью!
Подробнее
18 ноября 2022
Новости
Меньше значит больше становится все более и более источником вдохновения на многих рынках по всему миру. На этот раз мы говорим о рынке красоты и о том, как простота и многофункциональность стали важным фактом, который следует учитывать при создании формул их продуктов.
Подробнее
19 октября 2022 г.
модуль Юнга, закон Гука и свойства материала. От Physclips
 В этом разделе мы объясним происхождение упругих свойств и закон Гука, рассматривая силы и энергии между атомами или молекулами в твердом теле. Но сначала эксперимент.Пример закона Гука и его ограничений
Силы притяжения и отталкивания между атомами
 Возьмите короткий кусок металлической проволоки (например, распрямленную канцелярскую скрепку) и попробуйте растянуть ее по всей длине. Если проволока не очень тонкая или вы не очень сильны, количество стежков будет небольшим, и проволока не порвется. Здесь произошло то, что вы немного увеличили среднее расстояние r между атомами. Однако сила притяжения между парами атомов смогла противостоять силе растяжения, которую вы приложили. Теперь попробуйте укоротить металл, прикладывая сжимающее усилие по его длине. Здесь вы немного уменьшили среднее расстояние между атомами, но сила отталкивания между парами атомов смогла противостоять приложенной вами сжимающей силе. Из этого можно сделать вывод, что (i) когда расстояние между атомами больше, чем его безударное значение, силы притяжения между атомами должны быть больше, чем силы отталкивания (силы притяжения уравновешивают как силы отталкивания, так и силы, которые вы прикладываете). И наоборот, (ii) когда межатомное расстояние меньше его ненапряженного значения, силы отталкивания между атомами должны быть больше, чем силы притяжения. Еще два наблюдения. Во-первых, сжать металл чрезвычайно трудно, поэтому (iii) силы отталкивания должны стать очень даже при малых уменьшениях r. Во-вторых, после того как вы разбили кусок металла, он не может автоматически снова собраться вместе: (iv) если атомы отделены друг от друга даже на расстоянии, намного меньшем миллиметра, силы притяжения фактически равны нулю. Из всех этих наблюдений мы можем сделать вывод, что межатомные силы отталкивания и притяжения в зависимости от межатомного расстояния должны качественно выглядеть так, как показано на графике внизу слева.
 На этих графиках это происходит при r = r 0 = 1,12σ, а значение характерной длины σ будет объяснено позже.
Притяжение сильнее отталкивания при растяжении (справа от вертикальной линии, r > 1,12σ) и слабее отталкивания при сжатии. Заметим также, что, как того требуют наши наблюдения, приведенные выше, сила отталкивания очень быстро возрастает при сжатии (r < 1,12σ) и что обе силы быстро стремятся к нулю по мере увеличения расстояния.Разделение сил на компоненты притяжения и отталкивания, по крайней мере, немного условно: что действительно важно, так это общая сила и энергия, которые мы можем реально измерить. Это показано фиолетовой кривой в следующей версии этих графиков. Опять же, вертикальная серая линия отмечает ненагруженное значение r и, конечно же, определяет расстояние, при котором общая сила равна нулю. Это также точка, в которой потенциальная энергия U имеет минимум, поскольку полная сила F r = −dU/dr. (См. Наша цель здесь состоит в том, чтобы связать эти кривые с модулем Юнга и законом Гука. Но как такие кривые могут дать линейную зависимость между приложенной силой и растяжением межатомных связей? Ответ заключается в том, что закон Гука применим только к ограниченному диапазону деформации. Он соответствует линейной аппроксимации F(r), проходящей через точку (r 0 ,0), где r 0 — ненапряженная длина. Интегрирование закона Гука дает потенциальную энергию U(r), параболическую относительно минимума при r 0 . Таким образом, закон Гука соответствует зеленой линии на графике F(r) и зеленой параболе на графике U(r). Вставки на каждом графике показывают эти аппроксимации крупным планом и показывают, что аппроксимации плохи для деформаций, превышающих несколько процентов. (Обсуждая этот график, заметим, что хотя аппроксимация закона Гука для U(r) симметрична относительно своего минимума, эти кривые (и более реалистичные кривые) таковыми не являются. Получение модуля Юнга из атомных сил
 Назовем это значение разделения r 0 . Используя (2) и переставляя:Мы можем подставить это значение в (1), чтобы получить минимальное значение U(r 0 ). (Для двухатомной молекулы это значение дало бы оценку энергии связи, но поскольку для кристалла это сложнее, мы оставим этот расчет в стороне.)
Подставляя r = r 0 из (3) и используя определение Y: где A, n и m — константы в уравнении (1), r 0 и y — межатомные расстояния в продольном и поперечном направлениях. Потенциал U(r), который я использовал для построения приведенных выше кривых, представляет собой потенциал Леннарда-Джонса
, поэтому на предыдущих графиках использовалась характеристическая длина σ. Можно возразить, что r −6 представляет запаздывающие силы Ван-дер-Ваальса. Однако член отталкивания — это просто удобная дифференцируемая функция, дающая очень сильное отталкивание. Итак, мы связали модуль Юнга с отдельными атомными силами и энергиями: m, n, A и B в более общей эмпирической форме или, подстановкой, ε и σ в потенциале Леннарда-Джонса (положим A = 4εσ 6 , B = 4εσ 12 , n = 6 и m = 12). Чтобы связать закон Гука с модулем Юнга в приведенном выше эксперименте, необходимо рассмотреть изгиб проволоки. При сгибании одна сторона предмета растягивается, а другая сжимается. Это также требует учета геометрии пружины. Хотя длина пружины может изменяться на много процентов, нигде сталь не сжимается и не растягивается более чем на один процент. Полимеры и энтропийные силы Многие полимерные материалы, такие как каучук, имеют гораздо более низкие значения модуля Юнга, чем другие твердые вещества. Механизм растяжения здесь иной, поскольку растяжение в значительной степени выпрямляет молекулы полимера, а не изменяет среднее расстояние между ними. Чтобы проанализировать это, нужно учитывать не только потенциальную энергию, но и свободную энергию, U − TS, где T — (абсолютная) температура, а S — энтропия. Полностью выпрямленная молекула полимера имеет только одну возможную конфигурацию. Изогнутая (и, следовательно, более короткая) молекула имеет по крайней мере один изгиб. Перегибы могут возникать во многих различных местах, поэтому обычно существует множество возможных конфигураций, соответствующих определенной укороченной длине. Следовательно, энтропия сжатого состояния выше, чем у выпрямленного состояния. Когда вы растягиваете резину, большая часть выполняемой вами работы приходится на член свободной энергии −TS, так что это энтропийная сила. (Подробнее о термических свойствах: при повышении температуры -TS вносит больший вклад в свободную энергию, и обнаруживается больше молекул с большим количеством изгибов и, следовательно, они короче. Как следствие, полимеры часто сжимаются при повышении температуры. |
потенциальную энергию.)
Эта асимметрия относительно минимума U(r) равна отвечает за тепловое расширение (большинства) конденсированных фаз: при конечных температурах атомы не находятся точно в минимуме U, потому что они имеют конечную кинетическую энергию из-за их теплового движения.Упрощая в интересах краткости, мы можем утверждать что среднее значение U при значении выше минимума лежит правее минимума и увеличивается по мере добавления тепловой энергии.)
Подстановка в (3) дает r 0 = 2 1/6 σ = 1,12σ, откуда приведенное выше значение.
