Модуль юнга для алюминия: Модуль упругости алюминия
alexxlab | 21.01.2023 | 0 | Разное
Модуль упругости для стали, а также для других материалов
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
- Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.

- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Физический смысл модуля Юнга
Сталь 9хс и хвг: характеристика, термообработка и применение
Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.
Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.
Виды деформации
Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.
В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:
Δl = α * (lF) / S
Величину, обратную α, и называют модулем Юнга:
1/α = E
Относительная деформация:
ε = (Δl) / l = α * (F/S)
Отношение растягивающей силы F к S называют упругим напряжением σ:
ε=α σ
Закон Гука, записанный с использованием модуля Юнга, выглядит так:
σ = ε/α = E ε
Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.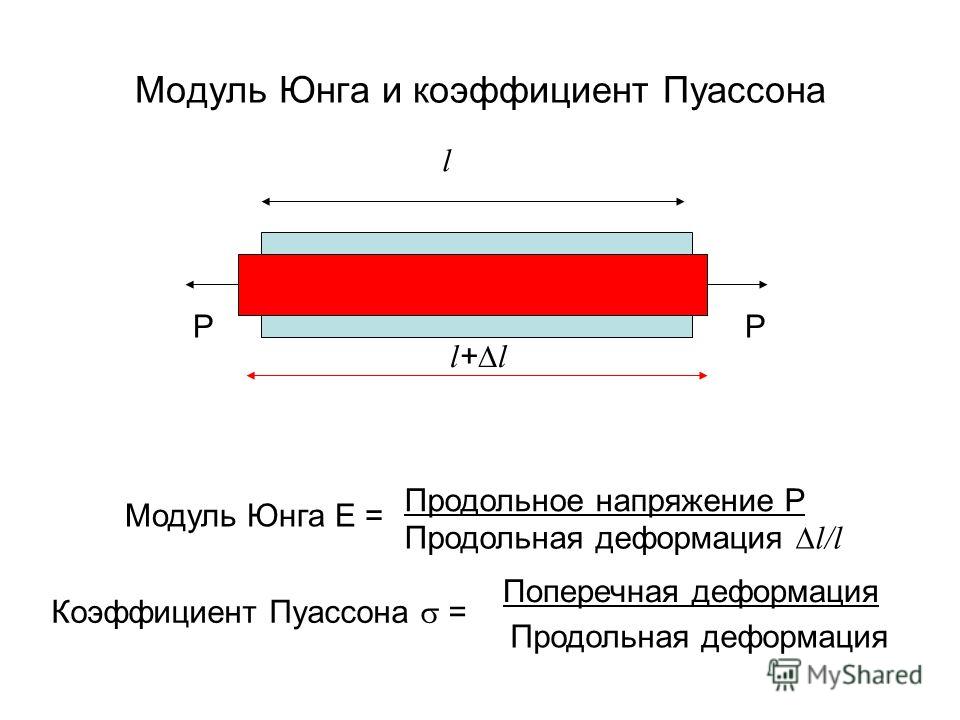
В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.
Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l
Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.
Модуль упругости различных материалов
Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. 2 .
2 .
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь 45
Общие данные
| Заменитель |
| Сталь 40Х, Сталь 50, Сталь 50Г2 |
| Вид поставки |
| Сортовой прокат, в том числе фасонный: ГОСТ 1050-74, ГОСТ 2590-71, ГОСТ 2591-71, ГОСТ 2879-69, ГОСТ 8509-86, ГОСТ 8510-86, ГОСТ 8239-72, ГОСТ 8240-72, ГОСТ 10702-78. Калиброванный пруток ГОСТ 1050-74, ГОСТ 7414-75, ГОСТ 8559-75, ГОСТ 8560-78, ГОСТ 10702-78. Лист толстый ГОСТ 1577-81, ГОСТ 19903-74.  Лист тонкий ГОСТ 16523-70. Лента ГОСТ 2284-79. Полоса ГОСТ 1577-81, ГОСТ 103-76, ГОСТ 82-70. Проволока ГОСТ 17305-71, ГОСТ 5663-79. Поковки и кованые заготовки ГОСТ 8479-70, ГОСТ 1131-71. Трубы ГОСТ 8732-78, ГОСТ 8733-87, ГОСТ 8734-75, ГОСТ 8731-87, ГОСТ 21729-78. |
| Назначение |
| Вал-шестерни, коленчатые и распределительные валы, шестерни, шпиндели, бандажи, цилиндры, кулачки и другие нормализованные, улучшаемые и подвергаемые поверхности термообработке детали, от которых требуется повышенная прочность. |
Химический состав (по ГОСТ 1050-2013)
| Химический элемент | % |
| Углерод (C) | 0.42-0.50 |
| Кремний (Si) | 0.17-0.37 |
| Медь (Cu), не более | 0.25 |
| Мышьяк (As), не более | 0.08 |
| Марганец (Mn) | 0.50-0.80 |
| Никель (Ni), не более | 0.25 |
| Фосфор (P), не более | 0. 035 035 |
| Хром (Cr), не более | 0.25 |
| Сера (S), не более | 0.04 |
Механические свойства
Механические свойства при повышенных температурах
| t испытания, °C | σ0,2, МПа | σB, МПа | δ5, % | δ, % | ψ, % | KCU, Дж/м2 |
| Нормализация | ||||||
| 200 | 340 | 690 | 10 | 36 | 64 | |
| 300 | 255 | 710 | 22 | 44 | 66 | |
| 400 | 225 | 560 | 21 | 65 | 55 | |
| 500 | 175 | 370 | 23 | 67 | 39 | |
| 600 | 78 | 215 | 33 | 90 | 59 | |
| Образец диаметром 6 мм и длиной 30 мм, кованый и нормализованный. Скорость деформирования 16 мм/мин. Скорость деформации 0,009 1/с. | ||||||
| 700 | 140 | 170 | 43 | 96 | ||
| 800 | 64 | 110 | 58 | 98 | ||
| 900 | 54 | 76 | 62 | 100 | ||
| 1000 | 34 | 50 | 72 | 100 | ||
| 1100 | 22 | 34 | 81 | 100 | ||
| 1200 | 15 | 27 | 90 | 100 | ||
Механические свойства проката
| Термообработка, состояние поставки | Сечение, мм | σB, МПа | δ5, % | δ4, % | ψ, % |
| Сталь горячекатаная, кованая, калиброванная и серебрянка 2-й категории после нормализации | 25 | 600 | 16 | 40 | |
| Сталь калиброванная 5-й категории после нагартовки | 640 | 6 | 30 | ||
| Сталь калиброванная и калиброванная со специальной отделкой после отпуска или отжига | <590 | 40 | |||
| Листы нормализованные и горячекатаные | 80 | 590 | 18 | ||
| Полосы нормализованные или горячекатаные | 6-25 | 600 | 16 | 40 | |
| Лист горячекатаный | <2 | 550-690 | 14 | ||
| Лист горячекатаный | 2-3,9 | 550-690 | 15 | ||
| Лист холоднокатаный | <2 | 550-690 | 15 | ||
| Лист холоднокатаный | 2-3,9 | 550-690 | 16 |
Механические свойства поковок
| Сечение, мм | σ0,2, МПа | σB, МПа | δ5, % | ψ, % | HB |
| Нормализация | |||||
| 100-300 | 245 | 470 | 19 | 42 | 143-179 |
| 300-500 | 245 | 470 | 17 | 35 | 143-179 |
| 500-800 | 245 | 470 | 15 | 30 | 143-179 |
| <100 | 275 | 530 | 20 | 44 | 156-197 |
| 100-300 | 275 | 530 | 17 | 34 | 156-197 |
Закалка. Отпуск Отпуск | |||||
| 300-500 | 275 | 530 | 15 | 29 | 156-197 |
| Нормализация. Закалка. Отпуск. | |||||
| <100 | 315 | 570 | 17 | 39 | 167-207 |
| 100-300 | 315 | 570 | 14 | 34 | 167-207 |
| 300-500 | 315 | 570 | 12 | 29 | 167-207 |
| <100 | 345 | 590 | 18 | 59 | 174-217 |
| 100-300 | 345 | 590 | 17 | 54 | 174-217 |
| <100 | 395 | 620 | 17 | 59 | 187-229 |
Механические свойства в зависимости от температуры отпуска
| t отпуска, °С | σ0,2, МПа | σB, МПа | δ5, % | ψ, % | KCU, Дж/м2 | HB |
| Закалка 850 °С, вода. Образцы диаметром 15 мм | ||||||
| 450 | 830 | 980 | 10 | 40 | 59 | |
| 500 | 730 | 830 | 12 | 45 | 78 | |
| 550 | 640 | 780 | 16 | 50 | 98 | |
| 600 | 590 | 730 | 25 | 55 | 118 | |
Закалка 840 °С, вода. Диаметр заготовки 60 мм Диаметр заготовки 60 мм | ||||||
| 400 | 520-590 | 730-840 | 12-14 | 46-50 | 50-70 | 202-234 |
| 500 | 470-520 | 680-770 | 14-16 | 52-58 | 60-90 | 185-210 |
| 600 | 410-440 | 610-680 | 18-20 | 61-64 | 90-120 | 168-190 |
Механические свойства в зависимости от сечения
| Сечение, мм | σ0,2, МПа | σB, МПа | δ5, % | ψ, % | KCU, Дж/м2 |
| Закалка 850 °С, отпуск 550 °С. Образцы вырезались из центра заготовок. | |||||
| 15 | 640 | 780 | 16 | 50 | 98 |
| 30 | 540 | 730 | 15 | 45 | 78 |
| 75 | 440 | 690 | 14 | 40 | 59 |
| 100 | 440 | 690 | 13 | 40 | 49 |
Технологические свойства
| Температура ковки |
Начала 1250, конца 700. Сечения до 400 мм охлаждаются на воздухе. Сечения до 400 мм охлаждаются на воздухе. |
| Свариваемость |
| Трудносвариваемая. Способы сварки: РДС и КТС. Необходим подогрев и последующая термообработка. |
| Обрабатываемость резанием |
| В горячекатаном состоянии при НВ 170-179 и sB = 640 МПа Ku тв.спл. = 1, Ku б.ст. = 1. |
| Склонность к отпускной способности |
| Не склонна. |
| Флокеночувствительность |
| Малочувствительна. |
Температура критических точек
| Критическая точка | °С |
| Ac1 | 730 |
| Ac3 | 755 |
| Ar3 | 690 |
| Ar1 | 780 |
| Mn | 350 |
Ударная вязкость
Ударная вязкость, KCU, Дж/см2
| Состояние поставки, термообработка | +20 | -20 | -40 | -60 |
| Пруток диаметром 25 мм. Горячекатаное состояние. | 14-15 | 10-14 | 5-14 | 3-8 |
Пруток диаметром 25 мм. Отжиг Отжиг | 42-47 | 27-34 | 27-31 | 13 |
| Пруток диаметром 25 мм. Нормализация | 49-52 | 37-42 | 33-37 | 29 |
| Пруток диаметром 25 мм. Закалка. Отпуск | 110-123 | 72-88 | 36-95 | 31-63 |
| Пруток диаметром 120 мм. Горячекатаное состояние | 42-47 | 24-26 | 15-33 | 12 |
| Пруток диаметром 120 мм. Отжиг | 47-52 | 32 | 17-33 | 9 |
| Пруток диаметром 120 мм. Нормализация | 76-80 | 45-55 | 49-56 | 47 |
| Пруток диаметром 120 мм. Закалка. Отпуск | 112-164 | 81 | 80 | 70 |
Предел выносливости
| σ-1, МПа | τ-1, МПа | σB, МПа | σ0,2, МПа |
| 245 | 157 | 590 | 310 |
| 421 | 880 | 680 | |
| 231 | 520 | 270 | |
| 331 | 660 | 480 |
Прокаливаемость
Твердость для полос прокаливаемости HRCэ (HRB).
| Расстояние от торца, мм / HRC э | |||||||||
| 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 12 | 16.5 | 24 | 30 |
| 50.5-59 | 41.5-57 | 29-54 | 25-42.5 | 23-36.5 | 22-33 | 20-31 | (92)-29 | (88)-26 | (86)-24 |
| Термообработка | Кол-во мартенсита, % | Крит.диам. в воде, мм | Крит.диам. в масле, мм |
| Закалка | 50 | 15-35 | 6-12 |
Физические свойства
| Температура испытания, °С | 20 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
| Модуль нормальной упругости, Е, ГПа | 200 | 201 | 193 | 190 | 172 | |||||
| Модуль упругости при сдвиге кручением G, ГПа | 78 | 69 | 59 | |||||||
| Плотность, ρn, кг/см3 | 7826 | 7799 | 7769 | 7735 | 7698 | 7662 | 7625 | 7587 | 7595 | |
| Коэффициент теплопроводности Вт/(м ·°С) | 48 | 47 | 44 | 41 | 39 | 36 | 31 | 27 | 26 | |
| Температура испытания, °С | 20- 100 | 20- 200 | 20- 300 | 20- 400 | 20- 500 | 20- 600 | 20- 700 | 20- 800 | 20- 900 | 20- 1000 |
| Коэффициент линейного расширения (α, 10-6 1/°С) | 11. 9 9 | 12.7 | 13.4 | 14.1 | 14.6 | 14.9 | 15.2 | |||
| Удельная теплоемкость (с, Дж/(кг · °С)) | 473 | 498 | 515 | 536 | 583 | 578 | 611 | 720 | 708 |
Зарубежные аналоги Стали 45
| США | Германия | Япония | Франция | Англия | Евросоюз | Италия | Бельгия | Испания | Китай |
| — | DIN,WNr | JIS | AFNOR | BS | EN | UNI | NBN | UNE | GB |
| 1044 | 1,0503 | S45C | 1C45 | 060A47 | 1,0503 | 1C45 | C45-1 | C45 | 45 |
| 1045 | 1,1191 | S48C | 2C45 | 080M | 1,1191 | C43 | C45-2 | C45E | 45H |
| 1045H | 1,1193 | SWRCh55K | AF65 | 080M46 | 1,1192 | C45 | C46 | C45k | ML45 |
| G10420 | C45 | SWRCh58K | C40E | 1449-50CS | 2C45 | C45E | C48k | SM45 | |
| G10430 | C45E | C45 | 1449-50HS | C45 | C45R | F. 114 114 | ZG310-570 | ||
| G10440 | C45R | C45E | 50HS | C45E | C46 | F.1140 | ZGD345-570 | ||
| G10450 | Cf45 | C45RR | C45 | C45EC | F.1142 | ||||
| M1044 | Ck45 | CC45 | C45E | C46 | |||||
| Cm45 | XC42h2 | ||||||||
| Cq45 | XC42h2TS | ||||||||
| XC45 | |||||||||
| XC45h2 | |||||||||
| XC48 | |||||||||
| XC48h2 | |||||||||
| Швеция | Болгария | Венгрия | Польша | Румыния | Чехия | Австрия | Австралия | Швейцария | Юж.Корея |
| SS | BDS | MSZ | PN | STAS | CSN | ONORM | AS | SNV | KS |
| 1650 | 45 | A3 | 45 | OLC45 | 12050 | C45SW | 1045 | C45 | SM45C |
| 1672 | C45 | C45E | OLC45q | 12056 | HK1042 | Ck45 | SM48C | ||
| C45E | OLC45X | K1042 |
Условные обозначения
| Механические свойства | |
| σB | временное сопротивление разрыву (предел прочности при растяжении), МПа |
| σ0,2 | предел текучести условный, МПа |
| σсж | предел прочности при сжатии, МПа |
| σсж0,2 | предел текучести при сжатии, МПа |
| σ0,05 | предел упругости, МПа |
| σизг | предел прочности при изгибе, МПа |
| σ-1 | предел выносливости при испытании на изгиб с симметричным циклом нагружения, МПа |
| δ5 , δ4 , δ10 | относительное удлинение после разрыва, % |
| ψ | относительное сужение, % |
| ν | относительный сдвиг, % |
| ε | относительная осадка при появлении первой трещины, % |
| τК | предел прочности при кручении, максимальное касательное напряжение, МПа |
| τ-1 | предел выносливости при испытании на кручение с симметричным циклом нагружения, МПа |
| KCU и KCV | ударная вязкость, определенная на образце с концентраторами вида U и V, Дж/см2 |
| HRCэ и HRB | твёрдость по Роквеллу (шкала C и B соответственно) |
| HB | твёрдость по Бринеллю |
| HV | твёрдость по Виккерсу |
| HSD | твёрдость по Шору |
| Физические свойства | |
| E | модуль упругости нормальный, ГПа |
| G | модуль упругости при сдвиге кручением, ГПа |
| ρn | плотность, кг/м3 |
| λ | коэффициент теплопроводности, Вт/(м∙°C) |
| ρ | удельное электросопротивление, Ом∙м |
| α | коэффициент линейного теплового расширения, 10-61/°С |
| с | удельная теплоёмкость, Дж/(кг∙°С) |
Поделиться:
969
Факторы, влияющие на упругость
Чтобы понять, от чего зависит модуль упругости бетона В25, В20, В15 и других классов, нужно рассмотреть все причины. На эту величину влияет очень много факторов, но самыми распространенными являются:
На эту величину влияет очень много факторов, но самыми распространенными являются:
- Свойства наполнителя. Если изделие имеет низкую плотность, то и модуль упругости у него небольшой. При использовании тяжелых наполнителей упругость возрастает в несколько раз.
- Классность. Чем выше класс, тем больше и упругость. Например, модуль упругости В30 равен 32,5, а у класса В10 он составляет всего лишь 19.
- Продолжительность использования. Бетонные конструкции становятся крепче со временем, поэтому специалисты используют таблицы для таких целей.
- Особенности производства. В процессе изготовления могут использоваться разные обработки бетона. Некоторые применяют высокую температуру и давление. Другие же проводят обработку при атмосферном давлении и дают строительному материалу затвердевать естественным путем. Все эти особенности изготовления напрямую влияют на показатель прочности и упругости.
- Время нахождения под давлением и нагрузкой. Для расчета используются специальные таблицы, из которых берется значение и умножается на корректирующий коэффициент.

- Влажность воздуха. Температура и влажность также влияют на значение упругости.
- Арматура. Использование стальной арматуры помогает противостоять различным нагрузкам и сопротивляться деформациям. Необходимые значения находятся в нормативных документах.
Способы определения и контроля показателей прочности металлов
Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.
Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.
Виды нагрузок
При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.
- Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.
- Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.
- Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида.
 В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
- Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.
- Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.
В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:
Введены и понятия:
- Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
- Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).
Формула по закону Гука записывается в виде ε = σz/E, где:
- ε – относительное удлинение;
- σz – нормальное напряжение.
Демонстрация закона Гука для упругих тел:
Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.
Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.
В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.
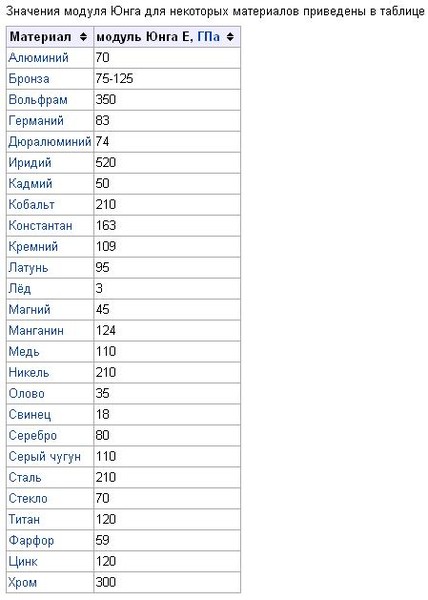
Значения модуля упругости для некоторых материалов приведены в таблице 1.
Таблица 1: Модуль упругости для металлов и сплавов
| Наименование материала | Значение модуля упругости, 10¹²·Па |
| Алюминий | 65…72 |
| Дюралюминий | 69…76 |
| Железо, содержание углерода менее 0,08 % | 165…186 |
| Латунь | 88…99 |
| Медь (Cu, 99 %) | 107…110 |
| Никель | 200…210 |
| Олово | 32…38 |
| Свинец | 14…19 |
| Серебро | 78…84 |
| Серый чугун | 110…130 |
| Сталь | 190…210 |
| Стекло | 65…72 |
| Титан | 112…120 |
| Хром | 300…310 |
АК6М2 / Алюминиевый литейный сплав / Алюминий, сплав алюминия / Материалы / Информация / ТехноСтали
| Марка : | АК6М2 |
| Классификация : | Алюминиевый литейный сплав |
| Применение: | для изготовления чушек и фасонных отливок различными способами литья (в песчаные формы, по выплавляемым моделям, в кокиль) |
| Зарубежные аналоги: | Нет данных |
Химический состав в % материала АК6М2 ГОСТ 1583- 93
| Fe | Si | Mn | Ni | Ti | Al | Cu | Mg | Zn | Примесей |
до 0. 6 6 | 5.5- 6.5 | до 0.1 | до 0.05 | 0.1- 0.2 | 89.79- 92.3 | 1.8- 2.3 | 0.3- 0.45 | до 0.06 | всего 0.7 |
Примечание: Al-основа. процентное содержание Al дано приблизительно
| Примечание: В чушках содержание магния 0.35-0.5 % |
Механические свойства при Т=20oС материала АК6М2 .
| Сортамент | Размер | Напр. | sв | sT | d5 | y | KCU | Термообр. |
| – | мм | – | МПа | МПа | % | % | кДж / м2 | – |
| Отливки, ГОСТ 1583-93 | 196-294 | 1-2 |
| Твердость АК6М2 , Отливки ГОСТ 1583-93 | HB 10 -1 = 70-75 МПа |
Обозначения:
| Механические свойства : | |
| sв | -Предел кратковременной прочности , [МПа] |
| sT | -Предел пропорциональности (предел текучести для остаточной деформации), [МПа] |
| d5 | -Относительное удлинение при разрыве , [ % ] |
| y | -Относительное сужение , [ % ] |
| KCU | -Ударная вязкость , [ кДж / м2] |
| HB | -Твердость по Бринеллю , [МПа] |
Физические свойства : | |
| T | |
| E | -Модуль упругости первого рода , [МПа] |
| a | -Коэффициент температурного (линейного) расширения (диапазон 20o-T ) , [1/Град] |
| l | -Коэффициент теплопроводности (теплоемкость материала) , [Вт/(м·град)] |
| r | -Плотность материала , [кг/м3] |
| C | -Удельная теплоемкость материала (диапазон 20o-T ), [Дж/(кг·град)] |
| R | -Удельное электросопротивление, [Ом·м] |
АК6М2-Алюминиевый литейный сплав
АК6М2-химический состав, механические, физические и технологические свойства, плотность, твердость, применение
Каков модуль Юнга алюминия 6061 Т6?
Какова прочность на растяжение алюминия 6061?
6061-Т4. Состояние T4 6061 имеет предел прочности при растяжении не менее 30 000 фунтов на квадратный дюйм (207 МПа) и предел текучести не менее 16 000 фунтов на квадратный дюйм (110 МПа).
Состояние T4 6061 имеет предел прочности при растяжении не менее 30 000 фунтов на квадратный дюйм (207 МПа) и предел текучести не менее 16 000 фунтов на квадратный дюйм (110 МПа).
Модуль упругости равен модулю Юнга?
17.6. 1 Модуль упругости (модуль Юнга или модуль упругости) Модуль Юнга описывает относительную жесткость материала, которая измеряется наклоном упругости графика напряжений и деформаций. Он рассчитывается как отношение значения напряжения к соответствующему значению деформации.
Можно ли согнуть алюминий 6061?
6061.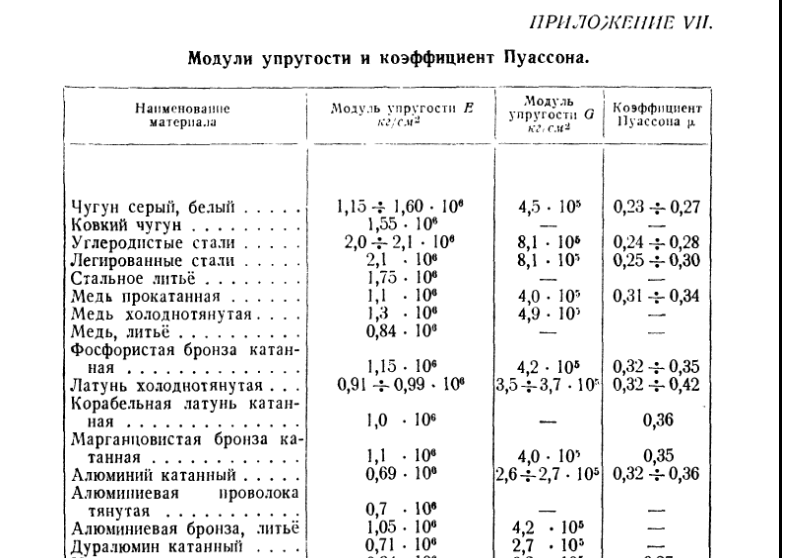 Это один из самых универсальных сплавов, поддающихся термообработке. В отожженном состоянии может быть использован для гибки , так как разница между пределом текучести и пределом прочности составляет 10 Ksi, а относительное удлинение составляет до 18%. Однако при переходе к состояниям Т4 и Т6 способность к изгибу имеет тенденцию к снижению. 10 мая 2015 г.
Это один из самых универсальных сплавов, поддающихся термообработке. В отожженном состоянии может быть использован для гибки , так как разница между пределом текучести и пределом прочности составляет 10 Ksi, а относительное удлинение составляет до 18%. Однако при переходе к состояниям Т4 и Т6 способность к изгибу имеет тенденцию к снижению. 10 мая 2015 г.
Как рассчитать модуль упругости?
Модуль упругости (E) представляет собой наклон начального линейного участка кривой напряжение-деформация в упругой области — изменение напряжения (Δσ), деленное на изменение деформации (Δϵ) . 17 сентября 2021 г.
Что такое модуль сдвига алюминия?
Значение модуля сдвига для алюминия составляет примерно 3,5 × 10 6 фунтов на квадратный дюйм или 2,4 × 10 1 0 Н/м 2 .
Как производится алюминий 6061 T6?
Глинозем или оксид алюминия извлекают из бокситов в процессе очистки с использованием каустической соды и извести. … Разработан в 1935, алюминий 6061-T6 представляет собой дисперсионно-твердеющий алюминий . Дисперсионное твердение использует высокие температуры для увеличения предела текучести алюминия.
Каков модуль упругости алюминия PSI?
Модуль упругости алюминия составляет 69 ГПа (10 000 000 фунтов на квадратный дюйм)9. 0008 .9 окт. 2020 г.
0008 .9 окт. 2020 г.
Какова теоретическая ценность алюминия?
Принятое значение плотности алюминия 2,699 г/см3 .
Соответствует ли алюминий 6061 RoHS?
Это включает в себя обычные аэрокосмические и коммерческие алюминиевые сплавы, такие как 6061, 7075, 2024, 6063, 3003, 5052, 5083, 5086. … Сплавы из нержавеющей стали не содержат свинца и должны обеспечивать детали, соответствующие требованиям RoHS, если они не подвергается обработке поверхности, не соответствующей требованиям RoHS.
Связанные
Является ли алюминий 6061 пластичным или хрупким?
(2) Алюминиевые сплавы 5052 и 6061 подвержены смешанному вязкому разрушению и хрупкому разрушению ; вязкое разрушение играет основную роль для AA5052, тогда как хрупкое разрушение играет основную роль для AA6061.
Связанные
Что такое рама из алюминия 6061?
6061 это сплав алюминия, магния и силикона и считается превосходящим 7005, изготовленным из алюминия и цинка, хотя последний кажется более стойким. …28 декабря 2020 г.
Похожие
Каков модуль упругости алюминиевого сплава 6061?
Модуль упругости Юнга Модуль упругости Юнга алюминиевого сплава 6061 составляет около 69 ГПа.
 Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Родственный
Какова прочность на растяжение алюминия 6061?
Алюминий 6061 Типичные механические свойства при различных температурах. Сплав и закалка. Температура, °C (°F) Предел прочности при растяжении, МПа (ksi) Предел текучести при смещении 0,2 %. Удлинение в 50 мм (2 д.), %, АЛ 6061-Т6, 6061-Т651. -195 (-320)
Связанные
Что такое модуль упругости стали?
Его модуль упругости составляет 68,9 ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм). Эти значения измеряют жесткость сплава или устойчивость к деформации и приведены в таблице 1.

Для чего используется алюминий марки 6061?
Тип 6061 алюминий является одним из наиболее широко используемых
Связанные
Каков модуль упругости алюминиевого сплава 6061? Каков модуль упругости алюминиевого сплава 6061?
Модуль упругости Юнга Модуль упругости Юнга алюминиевого сплава 6061 составляет около 69 ГПа. Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.

Связанные
Какова прочность на растяжение алюминия 6061? Какова прочность на растяжение алюминия 6061?
Алюминий 6061 Типичные механические свойства при различных температурах. Сплав и закалка. Температура, °C (°F) Предел прочности при растяжении, МПа (ksi) Предел текучести при смещении 0,2 %. Удлинение в 50 мм (2 д.), %, АЛ 6061-Т6, 6061-Т651. -195 (-320)
Родственный
Что такое алюминиевый сплав alal-6061? Что такое алюминиевый сплав alal-6061?
Алюминиевый сплав AL-6061 — конструкционный сплав общего назначения, разработанный компанией Alcoa в 1935. Обозначения отпуска в основном имеют 6061-Т4, Т451, АЛ 6061-Т6, 6061-Т651 и др. Это один из наиболее широко используемых сплавов. Основными легирующими элементами являются магний (Mg) и кремний (Si).
Связанные
Что такое модуль упругости стали? Что такое модуль упругости стали?
Его модуль упругости составляет 68,9 ГПа (10 000 тысяч фунтов на квадратный дюйм), а его модуль сдвига составляет 26 ГПа (3770 тысяч фунтов на квадратный дюйм).
 Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1.
Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1.общий Информация СМИ Нажмите галерея иллюстрация
Поделиться этой записью:
Определение модуля Юнга сплавов алюминия, меди, железа, латуни и стали с использованием метода голографической интерферометрии с двойной экспозицией (DEHI) – Material Science Research India
Determination of Young’s Modulus of Aluminium, Copper, Iron, Brass and Steel Alloys by Using Double Exposure Holographic Interferometry (DEHI) Technique
H. R. Kulkarni 1 , S. N. Shukla 2 and M. B. Dongare 3
1 Колледж инженерных и управленческих исследований KJEI, Пуна, Махараштра, Индия
2 Колледж инженерии и исследований Матошри, Эклахар Насик, Махараштра, Индия
3 Факультет физики, Университет Шиваджи, Колхапур, Махараштра, Индия
Автор, ответственный за переписку Электронная почта: hrkulkarni@rediffmail.
 com
comИстория публикации статьи
Статья получена : 22 сентября 2017 г.
Статья принята : 04 октября 2017 г.
Статья опубликована : 13 октября 2017 г.0204АННОТАЦИЯ:
Метод голографической интерферометрии с двойной экспозицией (DEHI) имеет широкое применение в области науки и техники. DEHI можно использовать для определения очень малых изменений поверхности объекта за очень небольшой интервал времени.
В данном случае метод DEHI используется для записи голограммы одного и того же объекта в разное время при различных нагрузках. Этот метод успешно используется для определения модуля Юнга (Y) алюминия, меди, железа, латуни и некоторых стальных сплавов. Установлено, что значения Y, полученные методом ДЭГИ, хорошо согласуются со стандартными значениями Y, доступными для соответствующих металлов и их сплавов. Этот метод также используется для установления стандартной зависимости между влиянием состава углерода и Y стальных сплавов.

КЛЮЧЕВЫЕ СЛОВА: ДЕХИ; Голографическая интерферометрия с двойной экспозицией; Модуль для младших
Скопируйте следующее, чтобы процитировать эту статью: Кулкарни Х. Р., Шукла С. Н., Донгаре М. Б. Определение модуля Юнга сплавов алюминия, меди, железа, латуни и стали с помощью голографической интерферометрии с двойной экспозицией ( ДЭХИ) Техника. Mat.Sci.Res.India;14(2)
Скопируйте следующее, чтобы процитировать этот URL-адрес: Кулкарни Х. Р., Шукла С. Н., Донгаре М. Б. Определение модуля Юнга сплавов алюминия, меди, железа, латуни и стали с использованием метода голографической интерферометрии с двойной экспозицией (DEHI). Mat.Sci.Res.India;14(2). Доступно по адресу: http://www.materialsciencejournal.org/?p=6086
.Введение
Техника DEHI используется для записи голограмм одних и тех же объектов в разное время.
 1 У этого метода есть некоторые преимущества перед другими методами, особенно при изучении переходных явлений. Анализ, конечно, существенно не отличается от анализа, проведенного для метода однократного воздействия, и результирующая интерференционная картина определяется разностью фаз между объектной волной в первом положении и объектной волной во втором положении. 2 Этот метод может быть использован при изучении зависимости напряжения от деформации и механики жидкости, 3 механики разрушения для неразрушающего контроля. 4 Голографическая интерферометрия также может использоваться для демонстрации изменений формы образца. 5
1 У этого метода есть некоторые преимущества перед другими методами, особенно при изучении переходных явлений. Анализ, конечно, существенно не отличается от анализа, проведенного для метода однократного воздействия, и результирующая интерференционная картина определяется разностью фаз между объектной волной в первом положении и объектной волной во втором положении. 2 Этот метод может быть использован при изучении зависимости напряжения от деформации и механики жидкости, 3 механики разрушения для неразрушающего контроля. 4 Голографическая интерферометрия также может использоваться для демонстрации изменений формы образца. 5 Качественное определение механической деформации[6] на поверхности объекта произвольной формы методом голографической интерферометрии требует решения следующих трех основных задач.
- Связь между поверхностной деформацией и поверхностным смещением;
- Связь между выводом смещения поверхности и интерференционными полосами в плоскости изображения;
- Интерполяция картины интерференционных полос и количественное определение интерференционной фазы.

Разработка практического метода получения количественной информации 7 из голограммы с двойной экспозицией до сих пор остается одной из наиболее интересных задач голографической интерферометрии. Применение методов голографической интерферометрии в неразрушающем контроле привлекло большое внимание в последние годы. Благодаря своей чрезвычайной чувствительности голографическая интерферометрия позволяет обнаруживать небольшие дефекты и аномалии в диффузных трехмерных объектах. 7-9 Описаны различные голографические методы 10-12 для измерения трехмерных перемещений объекта под нагрузкой. К ним относятся просмотр поверхности объекта через разные точки голограммы под разными углами и подсчет количества полос, проходящих через рассматриваемую точку между двумя экспозициями, очень мало или меньше одной полосы. Однако успех голографического неразрушающего контроля 13 материала зависит от принятого метода воздействия. Напряжение должно деформировать испытуемое тело таким образом, чтобы «хорошие» области отличались от «плохих» просто путем изучения интерференции, генерируемой на голографической интерферограмме.

Измерение модуля Юнга 14
Модуль Юнга материала можно рассчитать с помощью уравнения прогиба кантилевера. Уравнение прогиба кантилевера задается следующим образом:
ΔZ = (WL 3 ) / (3YI) …..(1)
Где
W = действующая нагрузка в пролете, кг
Y = модуль Юнга в кгс/см 2
I = момент инерции в см 4 , можно получить из физических размеров консоли
. Его значение для прямоугольной балки шириной «a» и толщиной «b»
равно ab 3 / 12 . где
Пусть θ i и θ o — угол, определяющий направления освещения и наблюдения соответственно. Они измеряются по геометрии фигуры, как показано на рисунке 2. Разность хода Δ между двумя лучами, рассеянными из двух идентичных точек на объекте, определяется выражением
Δ = ΔZ. н. (Cos θ i + Cos θ o )………………………..(3)
Где, n = показатель преломления, обычно 1 для воздуха.

Если на длину пролета L консоли, считая от неподвижного конца, изготовлено N полос, то
ΔZ = Nλ / (Cos θ i + Cos θ o ) ……………… …(4).
Подставив значение ΔZ в уравнение 2. Затем можно рассчитать значение модуля Юнга из
Y = WL 3 (Cos θ i + Cos θ o ) / (3 I Nλ)……………(5)
Экспериментальные результаты Y для металлов и сплавов
Модуль Юнга определен для алюминий, медь, железо, латунь и некоторые стальные сплавы с использованием технологии DEHI. Образцы для этой цели были получены от Mayura Steel Industries, Колхапур. Состав сплава и их состав, а также их размеры приведены в таблице 1 .
Экспериментальная установка для записи голограммы с двойной экспозицией с загруженными объектами показана на рис. 1.
Рис. 1. Экспериментальная установка для DEHI
Голограммы с двойной экспозицией соответствующих объектов были записаны в двух различных ситуациях.
 Один в нормальном состоянии, а другой в деформированном состоянии из-за приложения нагрузки. Для приложения нагрузки использовалось расположение струны и шкива, как показано на рис. 3 . Рис. 2. Измерение углов Для записи голограмм использовался двухлучевой внеосевой метод. Голограммы обрабатывались обычным образом. Восстановленные голограммы выявили количество полос, расположенных на поверхности металлических пластин. Время экспозиции по 7 секунд было дано для обеих экспозиций. Размеры объекта были точно измерены и представлены в таблице 2. Точно подсчитано количество полос. Они показаны на фотографиях 1-7. Используя уравнение (5), был определен модуль Юнга материала объекта. Значения Y, рассчитанные этим методом, занесены в таблицу 2 вместе с размерами объекта и углом освещения и рассеиванием света от поверхности объекта.
Один в нормальном состоянии, а другой в деформированном состоянии из-за приложения нагрузки. Для приложения нагрузки использовалось расположение струны и шкива, как показано на рис. 3 . Рис. 2. Измерение углов Для записи голограмм использовался двухлучевой внеосевой метод. Голограммы обрабатывались обычным образом. Восстановленные голограммы выявили количество полос, расположенных на поверхности металлических пластин. Время экспозиции по 7 секунд было дано для обеих экспозиций. Размеры объекта были точно измерены и представлены в таблице 2. Точно подсчитано количество полос. Они показаны на фотографиях 1-7. Используя уравнение (5), был определен модуль Юнга материала объекта. Значения Y, рассчитанные этим методом, занесены в таблицу 2 вместе с размерами объекта и углом освещения и рассеиванием света от поверхности объекта.Рисунок 3: Объект при применении нагрузки
Фото 1: Механически напряженная Al Plate
Фото 2: Механически напряженная тарелка Cu
Фото 3: Механически напряженная железная пластина.

Фото 4: Механически напряженная латунная пластина
ФОТО 5: МЕХАНИЧЕСКИЙ СТАРШИЙ K 1 ПЛАТА
Фото 6: Механически стресс K 2 Пластинка
Фото 70360.
Результаты и обсуждение
С помощью метода DEHI рассчитанные значения Y для пластин из сплавов алюминия, меди, латуни, железа и стали приведены в таблице 2. Установлено, что рассчитанные значения Y равны в близком соответствии со стандартными значениями.
В случае стальных сплавов K 1 , K 2 и K 3 (даны общие названия) найденное значение Y выше, чем у железа. Это в основном зависит от процентного содержания углерода в этом сплаве. Процент углерода указан в таблице 1. Содержание углерода в K 1 , K 2 и K 3 находится в порядке возрастания, что приводит к увеличению их модуля Юнга. Для образца К 1 она в 1,04 раза больше, чем у железа и К 2 наблюдается в 1,08 раза больше, а у К 3 в 1,19 раза больше, чем у железа.
 Значения, определенные для образцов К 1 , К 2 и К 3 , нигде не доступны. Значения Y, определенные для алюминия, меди, латуни и железа, полностью соответствуют имеющимся стандартным значениям. Эти результаты показывают, что метод DEHI можно использовать для определения стандартных значений модуля Юнга упругого материала. Этот результат подтверждает, что значения Y, определенные для образцов K 1 , K 2 и K 3 верны.
Значения, определенные для образцов К 1 , К 2 и К 3 , нигде не доступны. Значения Y, определенные для алюминия, меди, латуни и железа, полностью соответствуют имеющимся стандартным значениям. Эти результаты показывают, что метод DEHI можно использовать для определения стандартных значений модуля Юнга упругого материала. Этот результат подтверждает, что значения Y, определенные для образцов K 1 , K 2 и K 3 верны.Таблица 1: Составные части стальных сплавов
Составляющие %
Стальные образцы
К 1
К 2
К 3
С
0,184
0,40
1,17
Мн
0,93
0,090
13.
 15
15Си
0,41
0,42
0,42
С
0,037
0,039
0,004
Р
0,030
0,038
0,066
Кр
0,099
0,763
0,23
Ni
—
3.
 258
2580,038
Пн
30.00
0,231
—
Таблица 2: Определенные значения Y
Объектная пластина
Длина L в см
Ширина «а» в см
Глубина ‘b’ в см
Приложенная нагрузка Вт в кг
Количество полос, расположенных на объекте
Угол (в градусах)
Модуль Юнга Y в кгс/см 2
Освещение
θ и
Рассеяние
θ или
Определенные значения
Стандартные значения
Ал
3,00
3,00
0,110
0,007
10
6˚ 30’
46˚
0,672 x 10 6
0,70 x 10 6
Медь
1,80
3,00
0,110
0,650
11
6˚ 00’
44˚ 30’
1,240 x 10 6
1,240 x 10 6
Железо
3,00
3,00
0,120
0,140
36
5˚ 30’
48˚
2,130 x 10 6
2,00 x 10 6
Латунь
3,00
3,00
.
 011
0110,015
15
6˚ 30’
44˚ 30’
0,970 x 10 6
0,9от 0 до 1 x 10 6
К 1
2,40
3,00
0,380
3,00
12
4˚ 30’
48˚
2,230 x 10 6
——
К 2
2,40
2,90
0,353
3,00
15
7˚ 00’
46˚
2,311 x 10 6
——
К 3
2,50
3,00
0,310
1.
 800
80013
4˚ 30’
48˚
2,549 x 10 6
——
Ссылки
- Helfinger L. O., Brooks R. E и Wuerker R. F. J. Appl. Физ . 1966; 37:642.
- Tanner L. H. J. Sci. Инструм . 1967; 44:1015.
Перекрёстная ссылка - Дуддерар Т. Д. Exp. Мех . 1969; 9:281.
Перекрёстная ссылка - Steel WH Interferometry, Cambridge University Press. 1968; 188.
- Дандликер Р., Элиассон Б., Инейхен Б., Моттерер Ф. М. Инженерное использование когерентной оптики, Издательство Кембриджского университета, Кембридж. 1976; 99-117.
- Маром Э., Фризем А. А., Авниар В. Е. Приложения голографии и оптической обработки данных, Pergamon Press, Лондон.





 В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.
В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.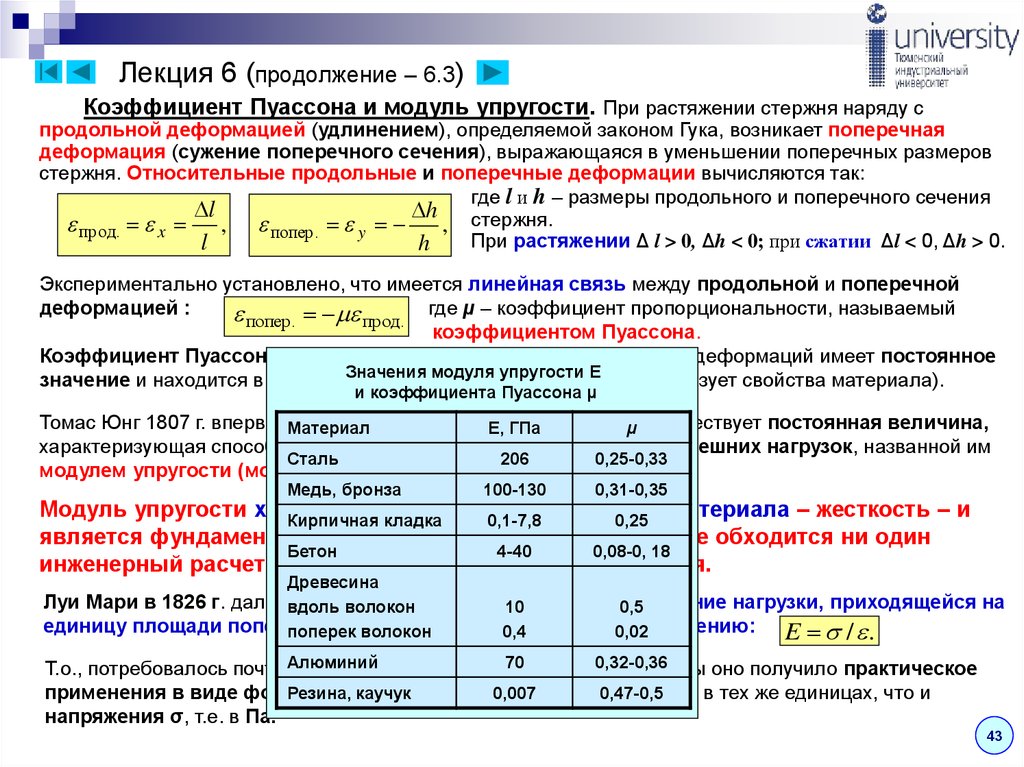 Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.
Модуль упругости Юнга представляет собой модуль упругости при растягивающем и сжимающем напряжении в режиме линейной упругости при одноосной деформации и обычно оценивается испытаниями на растяжение.

 Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1.
Эти значения измеряют жесткость сплава или сопротивление деформации и приведены в таблице 1. com
com
 1 У этого метода есть некоторые преимущества перед другими методами, особенно при изучении переходных явлений. Анализ, конечно, существенно не отличается от анализа, проведенного для метода однократного воздействия, и результирующая интерференционная картина определяется разностью фаз между объектной волной в первом положении и объектной волной во втором положении. 2 Этот метод может быть использован при изучении зависимости напряжения от деформации и механики жидкости, 3 механики разрушения для неразрушающего контроля. 4 Голографическая интерферометрия также может использоваться для демонстрации изменений формы образца. 5
1 У этого метода есть некоторые преимущества перед другими методами, особенно при изучении переходных явлений. Анализ, конечно, существенно не отличается от анализа, проведенного для метода однократного воздействия, и результирующая интерференционная картина определяется разностью фаз между объектной волной в первом положении и объектной волной во втором положении. 2 Этот метод может быть использован при изучении зависимости напряжения от деформации и механики жидкости, 3 механики разрушения для неразрушающего контроля. 4 Голографическая интерферометрия также может использоваться для демонстрации изменений формы образца. 5 


 Один в нормальном состоянии, а другой в деформированном состоянии из-за приложения нагрузки. Для приложения нагрузки использовалось расположение струны и шкива, как показано на рис. 3 . Рис. 2. Измерение углов Для записи голограмм использовался двухлучевой внеосевой метод. Голограммы обрабатывались обычным образом. Восстановленные голограммы выявили количество полос, расположенных на поверхности металлических пластин. Время экспозиции по 7 секунд было дано для обеих экспозиций. Размеры объекта были точно измерены и представлены в таблице 2. Точно подсчитано количество полос. Они показаны на фотографиях 1-7. Используя уравнение (5), был определен модуль Юнга материала объекта. Значения Y, рассчитанные этим методом, занесены в таблицу 2 вместе с размерами объекта и углом освещения и рассеиванием света от поверхности объекта.
Один в нормальном состоянии, а другой в деформированном состоянии из-за приложения нагрузки. Для приложения нагрузки использовалось расположение струны и шкива, как показано на рис. 3 . Рис. 2. Измерение углов Для записи голограмм использовался двухлучевой внеосевой метод. Голограммы обрабатывались обычным образом. Восстановленные голограммы выявили количество полос, расположенных на поверхности металлических пластин. Время экспозиции по 7 секунд было дано для обеих экспозиций. Размеры объекта были точно измерены и представлены в таблице 2. Точно подсчитано количество полос. Они показаны на фотографиях 1-7. Используя уравнение (5), был определен модуль Юнга материала объекта. Значения Y, рассчитанные этим методом, занесены в таблицу 2 вместе с размерами объекта и углом освещения и рассеиванием света от поверхности объекта.
 Значения, определенные для образцов К 1 , К 2 и К 3 , нигде не доступны. Значения Y, определенные для алюминия, меди, латуни и железа, полностью соответствуют имеющимся стандартным значениям. Эти результаты показывают, что метод DEHI можно использовать для определения стандартных значений модуля Юнга упругого материала. Этот результат подтверждает, что значения Y, определенные для образцов K 1 , K 2 и K 3 верны.
Значения, определенные для образцов К 1 , К 2 и К 3 , нигде не доступны. Значения Y, определенные для алюминия, меди, латуни и железа, полностью соответствуют имеющимся стандартным значениям. Эти результаты показывают, что метод DEHI можно использовать для определения стандартных значений модуля Юнга упругого материала. Этот результат подтверждает, что значения Y, определенные для образцов K 1 , K 2 и K 3 верны. 15
15 258
258 011
011 800
800