Модуль юнга это: Модуль Юнга | это… Что такое Модуль Юнга?
alexxlab | 12.02.2023 | 0 | Разное
Модуль Юнга | это… Что такое Модуль Юнга?
ТолкованиеПеревод
- Модуль Юнга
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:
где:
- E — модуль упругости,
- F — сила,
- S — площадь поверхности, по которой распределено действие силы,
- l — длина деформируемого стержня,
- x — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
где — плотность вещества.
Содержание
- 1 Значения модуля Юнга для некоторых материалов
- 2 Примечания
- 3 Примечания
- 4 См. также
- 5 Литература
- 6 Ссылки
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице [2]
Материал модуль Юнга E, ГПа Алюминий 70 Бронза 75-125 Вольфрам 350 Германий 83 Дюралюминий 74 Иридий 520 Кадмий 50 Кобальт 210 Константан 163 Кремний 109 Латунь 95 Лёд 3 Магний 45 Манганин 124 Медь 110 Никель 210 Олово 35 Свинец 18 Серебро 80 Серый чугун 110 Сталь 210 Стекло 70 Титан 120 Фарфор 59 Цинк 120 Хром 300 Примечания
- ↑ Модули упругости – Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.

- ↑ Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
Примечания
См. также
- Закон Гука
Литература
- Волькенштейн, В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
- Квазистатический модуль Юнга (код на Mathcad).
Модули упругости для гомогенных изотропных материалов Модуль объёмной упругости () | Модуль Юнга () | Параметры Ламе () | Модуль сдвига () | Коэффициент Пуассона () | en:P-wave modulus ()
Wikimedia Foundation. 2010.
Игры ⚽ Нужна курсовая?
- Артикуляция
- Лагор (голубь)
Полезное
Испытания на эластичность – EUROLAB
- Вы находитесь здесь:
- Eurolab
- Отраслевые тесты и анализ
- Испытания строительных материалов
- Испытания на эластичность
Модуль упругости (или модуль Юнга) является мерой скорости изменения напряжения как функции напряжения. Представляет наклон прямой части кривой напряжение-деформация.
Представляет наклон прямой части кривой напряжение-деформация.
Этот метод испытаний используется для определения поведения образца при осевой растягивающей нагрузке. Общие результаты испытаний на растяжение включают предел упругости, предел прочности, предел текучести, предел текучести, удлинение и модуль Юнга. Модуль Юнга, обычно N / mm2 (фунты / in2), указывается как MPA (фунт / кв.дюйм).
Модуль упругости несколько ниже, чем у контрольного бетона, изготовленного с таким же соотношением веса / см, как у бетона HVNP, изготовленного с использованием цеолита природного пуццолана (Uzal 2007). Однако известно, что модуль упругости бетона HVFA выше, чем у бетона из портландцемента, который имеет сопоставимую прочность (Malhotra and Ramezanianpour, 1994). Это различие между бетонными смесями HVFA и HVNP может быть связано с различиями в микроструктуре межфазной переходной зоны, но требует дальнейшего изучения. В обоих типах пуццоланового бетона большого объема модуль упругости при 28 близок к 30 ГПа или выше.
Модуль упругости или «модуль Юнга» является мерой скорости изменения напряжения в зависимости от напряжения. Что касается испытания на растяжение, его можно назвать модулем растяжения. Представляет наклон линейного участка кривой напряжения-деформации.
Испытание на растяжение, также известное как испытание на расплавление, является, вероятно, самым основным типом механических испытаний, которые вы можете провести на материале. Испытания на растяжение просты, относительно недороги и полностью стандартизированы. Потянув вещи, вы быстро определите, как материал будет реагировать на силы, приложенные к растяжению. Когда материал нарисован, вы увидите, как долго он будет увеличивать свою прочность.
Этот метод испытаний используется для определения поведения образца при осевой растягивающей нагрузке. Общие результаты испытаний на растяжение включают предел упругости, предел прочности, предел текучести, предел текучести, удлинение и модуль Юнга.
 Модуль Юнга, обычно N / mm2 (фунты / in2), указывается как MPA (фунт / кв.дюйм).
Модуль Юнга, обычно N / mm2 (фунты / in2), указывается как MPA (фунт / кв.дюйм).Твердый материал, такой как алмаз, имеет высокий модуль Юнга и слегка изменяет свою форму при упругой нагрузке. Упругий материал, такой как резина, имеет низкий модуль Юнга и значительно меняет свою форму. Твердый материал требует высоких нагрузок, чтобы упруго деформироваться – его не следует путать с прочным материалом, который требует высоких нагрузок, чтобы постоянно деформироваться или ломаться. Твердость компонента означает, насколько он отклоняется при данной нагрузке. Это зависит от модуля Юнга материала, а также от нагрузки (растяжение или изгиб) и формы и размера компонента. Удельная жесткость представляет собой деление модуля Юнга на плотность (но более точно его следует называть «удельным модулем»).
 Для транспортных применений (например, самолетов, гоночных велосипедов) требуется минимальный вес жесткости. В этих случаях материалы с большой твердостью являются лучшими.
Для транспортных применений (например, самолетов, гоночных велосипедов) требуется минимальный вес жесткости. В этих случаях материалы с большой твердостью являются лучшими.Вы можете работать с нашей лабораторией EUROLAB для тестирования модуля упругости.
Лаборатория строительных материалов
- ASTM E119 Строительство зданий и огнестойкие испытания материалов
- ASTM E84 Лаборатория испытаний на воспламеняемость строительных материалов
- Испытание на прочность при сжатии
- Измерения стабильности и изменения размеров
- Стекло Тесты
- Тесты на огнестойкость стекла
- Тесты на преодоление трещин
- Испытания на огнестойкость по немецким стандартам DIN 4102
- Испытания на эластичность
- Тесты на гибкость
- Газобетон Ytong Тесты
- ИМО Тесты
- Дверные тесты
- Маркировка CE и испытания на дверях и окнах
- Тесты на огнестойкость дверей
- Тесты средств индивидуальной защиты
- Тесты на устойчивость к корням
- M1 M2 M3 M4 Испытания на воспламеняемость (NF P 92-5XX)
- TS EN 13501-1 Испытания на огнестойкость
- TSCA Carb II Тесты на токсические вещества
- Испытания на устойчивость к дождю и ветру
- Акустические испытания строительных изделий
Калькулятор модуля Юнга – EngineerExcel
Модуль Юнга является важным физическим свойством любого материала. Он описывает, насколько легко материал растягивается или изгибается. Когда к материалу прикладывается сила, этот материал меняет форму. Каждый материал будет иметь внутреннюю величину, которую он может изменить, прежде чем начнет деформироваться. Эта величина изменения является модулем Юнга материала.
Он описывает, насколько легко материал растягивается или изгибается. Когда к материалу прикладывается сила, этот материал меняет форму. Каждый материал будет иметь внутреннюю величину, которую он может изменить, прежде чем начнет деформироваться. Эта величина изменения является модулем Юнга материала.
Модуль Юнга материала является постоянной величиной при заданных параметрах окружающей среды. При поиске материала с определенными свойствами важно понимать среду, в которой будет использоваться материал, поскольку различные температуры или давления будут влиять на свойства материала, а не только на модуль Юнга.
Contents
- Understanding Young’s modulus
- Young’s modulus components
- Stress
- Strain
- Applying Young’s modulus
- High Young’s modulus materials
- Low Young’s modulus materials
- Determining Young’s modulus
- Extended applications Модуль Юнга
Понимание модуля Юнга
Модуль Юнга, E , рассчитывается по следующей формуле: 92 в СИ)
 е. отношение изменения длины к исходной длине
е. отношение изменения длины к исходной длинеПоскольку деформация является безразмерной величиной, единицы модуля Юнга такие же, как и для напряжения. На изображении ниже показана зависимость между напряжением и деформацией материала при приложении силы.
На приведенном выше изображении при приложении силы материал растягивается или изгибается, пока не достигнет своего предела текучести. Если сила устранена до достижения предела текучести, материал вернется к своим первоначальным размерам и форме. Однако, если сила продолжает применяться, внутренняя структура материала будет необратимо изменена.
Хороший способ понять, что происходит, когда к материалу прилагается сила, — это резиновая лента, имеющая высокий модуль Юнга. Резиновую ленту можно растянуть, и она возвращается к своей первоначальной форме, когда растяжение прекращается. Однако, если резиновая лента растянута слишком сильно, она превысит свой модуль Юнга, достигнув предела текучести и быстро превысив предел прочности до разрушения.
Компоненты модуля Юнга
Как уже говорилось, модуль Юнга представляет собой отношение величины напряжения к величине деформации, испытываемой материалом до того, как он начнет деформироваться.
Напряжение
Когда к конструкции прикладывается сила, эта сила вызывает напряжение в материале конструкции. Напряжение рассчитывается по следующей формуле:
где:
- F приложенная сила (Н в СИ)
- A — площадь поперечного сечения, на которое действует сила (м 2 в СИ)
На рисунке ниже показан пример силы, действующей параллельно концу балки.
Штамм
Кроме того, когда к конструкции прилагается сила, эта конструкция испытывает деформацию. Эта деформация является мерой того, насколько структура изменяется по отношению к ее первоначальной форме. Деформация конструкции рассчитывается по следующей формуле:
где:
- ΔL изменение длины (м в СИ)
- L первоначальная длина (м в СИ)
Применение модуля Юнга
Модуль Юнга используется для определения подходящих материалов для конструкции. Поскольку каждый материал имеет свой модуль Юнга, необходимо понимать, что означают разные значения.
Поскольку каждый материал имеет свой модуль Юнга, необходимо понимать, что означают разные значения.
Материалы с высоким модулем Юнга
Материал с высоким модулем Юнга считается жестким материалом. Эти материалы, в том числе сталь и титан, могут выдерживать большие нагрузки и демонстрируют очень небольшие изменения формы. Чтобы спроектировать конструкцию, которая не изменит свою форму или не деформируется под действием больших приложенных сил, например, при проектировании моста или здания, рассмотрите материалы с высоким модулем Юнга.
Материалы с низким модулем Юнга
Материал с низким модулем Юнга считается эластичным материалом. Эти материалы, в том числе резина и пенопласт, претерпевают значительные изменения формы при приложении силы. При разработке чего-либо для накопления упругой энергии, например пружины, рассмотрите материалы с низким модулем Юнга.
Материалы с различными значениями модуля Юнга показаны на графике ниже:
Определение модуля Юнга
Несмотря на то, что модуль Юнга для многих материалов был определен, новые сплавы и разработанные материалы могут проявлять разные свойства, поэтому их необходимо оценивать независимо.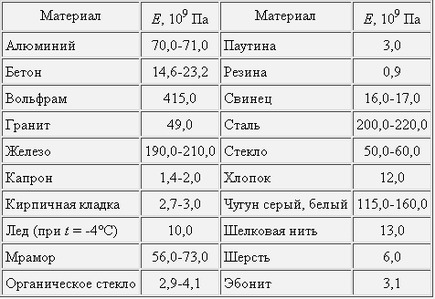 Наиболее распространенным методом определения модуля Юнга материала является испытание на растяжение. В этом испытании образец материала подвергается растягивающей нагрузке при измерении его удлинения. На основе собранных данных можно построить кривую напряжения-деформации при разрушении материала.
Наиболее распространенным методом определения модуля Юнга материала является испытание на растяжение. В этом испытании образец материала подвергается растягивающей нагрузке при измерении его удлинения. На основе собранных данных можно построить кривую напряжения-деформации при разрушении материала.
Поскольку разные материалы будут использоваться в разных условиях, инженеру может быть полезно определить модуль Юнга с помощью чего-то другого, кроме испытания на растяжение. Хотя свойства материала постоянны, использование испытания на сжатие громоздких материалов, которые, скорее всего, будут подвергаться сжатию, а не растяжению, может оказаться выгодным. Это испытание аналогично испытанию на растяжение, за исключением того, что образец сжимают и измеряют его укорочение.
Расширенные применения модуля Юнга
Хотя знание и понимание модуля Юнга материала важно для инженера, существуют и другие свойства, которые можно рассчитать по модулю Юнга, которые также могут оказаться полезными. Примером одного из таких свойств является удельная жесткость материала.
Примером одного из таких свойств является удельная жесткость материала.
Удельная жесткость представляет собой модуль Юнга, деленный на плотность материала, и может называться удельным модулем. Удельная жесткость используется, когда важен вес материала, например, в конструкции самолета, где требуется прочный, но легкий материал. Удельную жесткость различных материалов можно легко сравнить, чтобы определить материал, который будет соответствовать требованиям проекта по прочности и весу.
Модуль Юнга – физика Хоффнера
Модуль Юнга
Автор: Джейкоб Хоффнер
Партнеры лаборатории: Зак Кристофф и Алисса Джордан
Дата: апрель 2016 г. .
Теория
Мы должны найти модуль Юнга, E. Для этого мы должны определить напряжение и деформацию используемого материала. Напряжение и деформация будут использоваться на графике зависимости напряжения от деформации, а наклон этой линии будет равен E, модулю Юнга. В этой лаборатории мы будем использовать оптический рычаг для обнаружения измерений. Лазер, отражающийся от патрона, несущего латунную проволоку, покажет изменение длины, дельта l, увеличивая незначительные изменения в проволоке. Будут использованы два подобных треугольника. Длина от цилиндрического патрона до линейки, где лазерный луч находится в одном треугольнике, связанном с изменением положения лазерного луча, составляет один треугольник. Второй треугольник будет радиусом патрона по отношению к длине, созданной на краю патрона изменением положения, которое будет вдвое больше изменения l. Стресс и деформация Чтобы найти модуль Юнга, необходимо найти напряжения и деформации. Напряжение — это общая площадь поперечного сечения провода. Напряжение – это сила над площадью, а площадь основана на цилиндрической форме проволоки. Сила будет приложена подвешенной массой. Деформация – это изменение длины проволоки по отношению к исходной длине проволоки. Изменение длины будет определяться с помощью пропорционального уравнения, найденного с помощью FBD. Эта величина будет подставлена в это уравнение деформации: | Прочность на растяжение и модуль Юнга Прочность на растяжение (предельная прочность) также будет определяться силой над площадью, однако сила определяется максимальным количеством силы, используемой в системе, или максимальной массой, умноженной на гравитацию. Прочность на растяжение Модуль Юнга затем определяется наклоном линии графика, сравнивающего напряжение и деформацию, поскольку E равно напряжению относительно деформации (подъем относительно пробега). |
Экспериментальная техника
Чтобы измерить модуль Юнга, мы должны сначала провести начальные испытания выбранного материала проволоки, чтобы определить, какой вес материал может выдержать. Я использовал латунную проволоку. Установка этой лаборатории состояла из стойки, удерживающей проволочную подвеску вверху, и держателя груза, подвешенного к проволоке внизу. Эта установка использовалась, чтобы выяснить, какой вес может выдержать проволока до разрушения, путем постепенного размещения грузов на держателе грузов.
Я использовал латунную проволоку. Установка этой лаборатории состояла из стойки, удерживающей проволочную подвеску вверху, и держателя груза, подвешенного к проволоке внизу. Эта установка использовалась, чтобы выяснить, какой вес может выдержать проволока до разрушения, путем постепенного размещения грузов на держателе грузов.
Затем проволока была намотана на патрон с зеркалом, используемым для отражения лазера для оптического рычага. Лазер располагался на дальнем конце стола вдали от аппарата. Лазерная подставка имеет линейку, обращенную к проволочной подставке. Лазер был направлен на зеркало патрона, и лазер отражался обратно на линейку рядом с лазером. Незначительные изменения в проволоке будут перемещать цилиндрический патрон, что приводит к перемещению зеркала и лазерного луча. Созданный оптический рычаг позволяет нам видеть, как лазер перемещается по линейке с каждым приращением веса, добавляемого к держателю массы и, в конечном итоге, к проволоке.
Собранная информация, наряду с измерениями расстояний между всеми объектами, будет использоваться для создания графика зависимости деформации от напряжения для определения модуля Юнга. Используя информацию из теоретического раздела, мы построим диаграмму, показывающую значения, обнаруженные в тестируемой латунной проволоке. Диаграмма будет преобразована в график, где найденная информация и наклон линии графика найдут наш окончательный ответ.
Используя информацию из теоретического раздела, мы построим диаграмму, показывающую значения, обнаруженные в тестируемой латунной проволоке. Диаграмма будет преобразована в график, где найденная информация и наклон линии графика найдут наш окончательный ответ.
Микрометр для определения ширины латунной проволоки.
Данные
Ниже приведены данные для поиска измерений лаборатории:
Измерения, которые были необходимы, чтобы найти: | Собранные данные и полученные значения деформации и напряжения: |
Анализ
Ниже приведены примеры расчетов напряжения, деформации, предела прочности при растяжении и процентной ошибки:
На основании графика мы можем сравнить наш модуль Юнга E с принятым значением, а затем найти процент ошибки.
Далее находим предел прочности латуни. | Мы измеряем процентную погрешность прочности на растяжение. |
Заключение
В этой лаборатории мы должны были исследовать эластичность и прочность на растяжение латунной проволоки. Эта лабораторная работа включала большую процентную ошибку, так как некоторые измерения было трудно поддерживать последовательными и точными. Ошибка параллакса может быть проблемой из-за нашей прямой видимости лазерного луча. Постоянное растяжение и растяжка проволоки могло сделать ее более хрупкой и изменить положение оптического рычага. Каждое измерение могло быть выполнено с разными интервалами от предыдущего из-за того, насколько сильно растянулся провод за это время. Найдя модуль Юнга, я обнаружил ошибку -80% от принятого значения. Было трудно найти точную точку разрыва латунной проволоки, о чем свидетельствует процентная ошибка в найденном значении предела прочности при растяжении, равная 324%.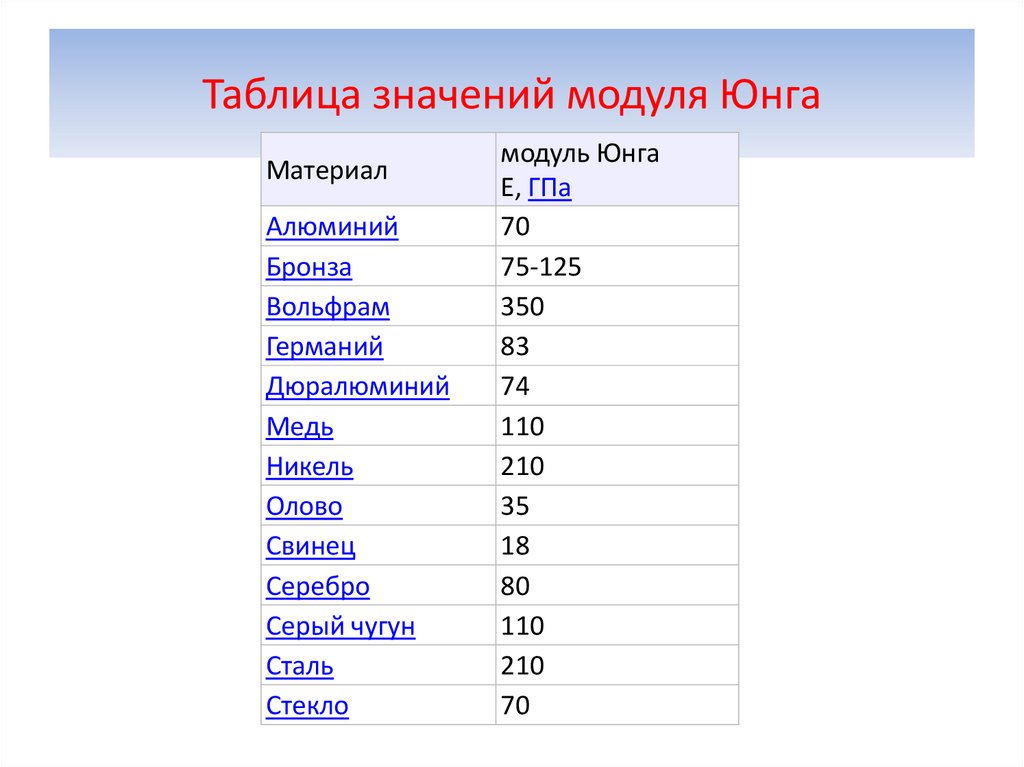




 Чтобы определить предел прочности на разрыв измеряемого латунного материала, мы должны определить, какую максимальную массу латунная проволока может выдержать до разрушения. На графике справа показан пример графика зависимости напряжения от деформации и показано, как материал, измеряемый для модуля Юнга, будет действовать в таких условиях.
Чтобы определить предел прочности на разрыв измеряемого латунного материала, мы должны определить, какую максимальную массу латунная проволока может выдержать до разрушения. На графике справа показан пример графика зависимости напряжения от деформации и показано, как материал, измеряемый для модуля Юнга, будет действовать в таких условиях.