Модуль юнга формула – Модуль упругости (Модуль Юнга): понятие, формулы, как определить
alexxlab | 29.08.2019 | 0 | Разное
Упругие деформации. Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.
Все тела деформируемы. Изменения, вызванные действиями приложенных сил, при которых тела меняют форму и объем – деформации.
Упругие деформации – деформации, которые исчезают, после прекращения действия приложенной силы.
Пластические деформации (остаточные деформации) – деформации, которые сохраняются в теле (частично или полностью) после прекращения действия приложенной силы.
Если напряжение (сила, отнесенная к единице площади) не превышает некоторой величины (предел упругости), то деформация будет упругой.
Идеально упругие тела – тела, которые могут претерпевать только упругие деформации. Для таких тел существует однозначная зависимость между силами и вызываемыми ими деформациями.
Пусть есть два стержня. Один сжимаем, а другой сдавливаем с силой (как на рисунке). Перпендикулярно к оси стержня проведем сечение . Для равновесия стержня , на его нижнее основание должна действовать сила . Нижняя и верхняя части стержня действуют друг на друга с равной силой , т.к. они деформированы. Отношение силы к площади поперечного сечения – напряжение.
Натяжение – напряжение при натяжении, .
Давление – напряжение при сжатии , где площадь сечения. Давление – отрицательное напряжение и наоборот .
– длина недеформированного стержня. – приращение длины, после приложения силы . Значит полная длина . – относительное удлинение стержня (если – относительное сжатие).
Для малых упругих деформаций натяжение (давление ) пропорционально относительному удлинению (относительному сжатию) — (),
где – модуль Юнга (постоянная, зависящая только от материала стержня и его физического состояния).
Модуль Юнга – натяжение, которое необходимо приложить к стержню, чтобы его длина увеличилась в два раза. А две формулы выше – закон Гука.
Вычислим упругую энергию растянутого стержня. Приложим к стержню растягивающую силу и будем постепенно (непрерывно и медленно) увеличивать ее от до . Удлинение будет меняться от до . По закону Гука ,
Вся работа по растяжению стержня пойдет на увеличение его упругой энергии . Т.к. в конечном состоянии , то , то для энергии получим .
Под действием растягивающей или сжимающей силы изменяются не только продольные, но и поперечные размеры стержня. Если сила растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. – толщина стержня до деформации (диаметр, если стержень круглый, одна из сторон, если прямоугольный). – толщина стержня после деформации. Если растягиваем стержень, то – относительное поперечное сжатие ().
– коэффициент Пуассона.
Он зависит только от материала рассматриваемого тела. Модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства изотропного материала. Все остальные упругие деформации можно выразить через эти коэффициенты.
Post Views: 4 220
Похожее
optoelectrosys.ru
Модуль упругости (модуль Юнга)
Модуль упругости (модуль Юнга) — коэффициент, характеризующий сопротивление материала растяжению или сжатию при упругой деформации
С помощью легких преобразований, данная формула получается из Закона Гука.
Закон Гука: механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации этого тела.
σ =k·ε
Другая форма записи закона Гука:
Коэффициент E в этом соотношении и есть модуль Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E≈2·1011 Н/м2, а для резины E≈2·106 Н/м
Модуль упругости, или модуль продольной деформации Е, показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения.
Таблица значений Модуля Юнга (модуля упругости) для некоторых материалов

Физический смысл Модуля Юнга: он показывает напряжение, которое необходимо приложить к телу, чтобы увеличить его длину в два раза
Обозначения:
E — модуль упругости (Модуль Юнга)
σp— критическое напряжение
ε — относительное удлинение
F — сила, действующая на стержень
l — длина деформируемого стержня
x — модуль изменения длины стержня в результате упругой деформации
S — площадь поверхности, по которой распределено действие силы
infofiz.ruЛабораторнаяработа № m-4
ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ИЗ ПРОГИБА СТЕРЖНЯ
1 Цель работы
Целью работы является изучение зависимости прогиба стержня от величины действующей на него силы; определение модуля Юнга материала стержня.
2 Оборудование и принадлежности
Прибор для определения модуля Юнга, набор грузов.
3 Теоретическая часть
3.1 Основные понятия и определения
Деформация– изменение относительного положения частиц тела, связанное с ихперемещением.Все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.
Деформации разделяют на упругие и пластические.
Упругие деформации– это деформации, исчезающие после снятия нагрузки. Т.е. после прекращения действия силы тело принимает первоначальные форму и размеры. В основе упругих деформаций лежат обратимые смещения атомов вещества от положения равновесия
Пластические деформации– это деформации, которые остаются после окончания действия приложенных сил. В основе пластических деформаций лежат необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.
Наиболее простые виды деформации тела в целом:
растяжение,
сжатие,
сдвиг,
изгиб,
кручение.
В теории упругости доказывается, что все виды деформаций могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига.
Рассмотрим
простейшую деформацию продольного
растяжения (рисунок 1). К
концам
однородного стержень длиной l с площадью поперечного сечения S приложены силы  и
и 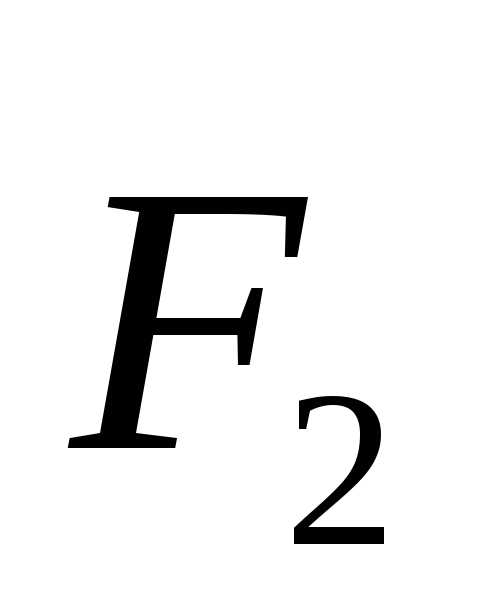 .
В результате действия этих сил длина
стержня меняется на величину
.
В результате действия этих сил длина
стержня меняется на величину l.
l.
 l – абсолютное
удлинение стержня;
l – абсолютное
удлинение стержня;
 –относительное
удлинение (относительная деформация).
–относительное
удлинение (относительная деформация).
Рисунок 1 – Схема продольного растяжения
Сила, действующая на единицу площади поперечного сечения, называется напряжением:
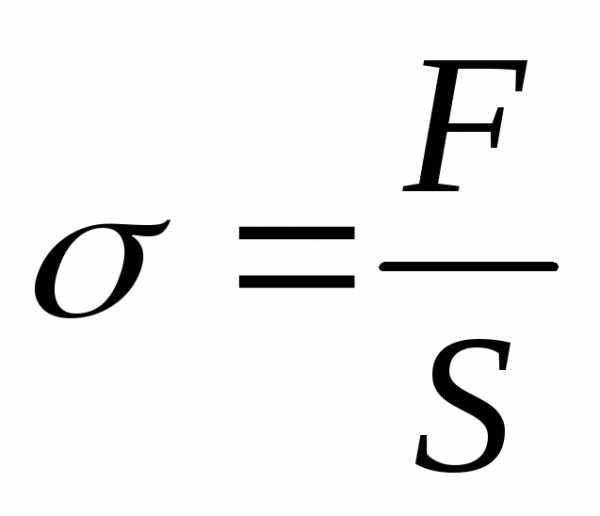 . (1)
. (1)
Если
сила направлена по нормали к поверхности,
напряжение называется
Закон Гука: для малых деформаций относительное удлинение прямо пропорционально вызывающему его напряжению :
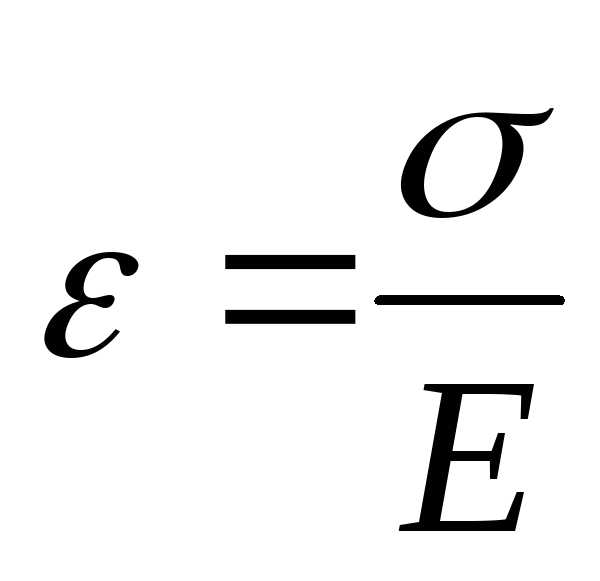 (2)
(2)
где Е – коэффициент пропорциональности, называется модулем Юнга.
Физический
смысл модуля Юнга:
модуль Юнга численно
равен напряжению, вызывающему
относительное удлинение, равное единице.
При относительном удлинении, равном
единице 
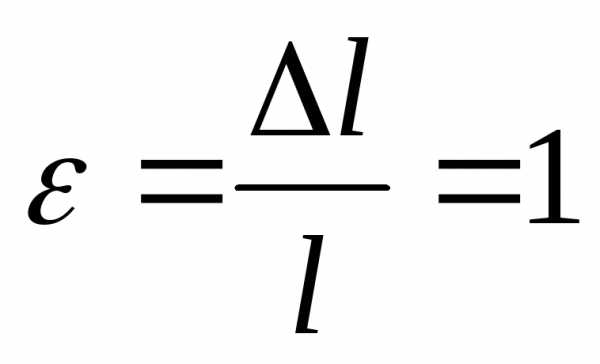 ,
абсолютное удлинение
,
абсолютное удлинение  l = l, откуда
получаем: модуль Юнга численно равен
тому напряжению, которое растягивает
стержень вдвое. На самом деле большинство
материалов разрушается раньше, чем они
будут растянуты вдвое, поэтому фактически
нельзя приложить к стержню напряжение
численно равное модулю Юнга.
l = l, откуда
получаем: модуль Юнга численно равен
тому напряжению, которое растягивает
стержень вдвое. На самом деле большинство
материалов разрушается раньше, чем они
будут растянуты вдвое, поэтому фактически
нельзя приложить к стержню напряжение
численно равное модулю Юнга.
Выразим
относительное удлинение с учетом (1) и
(2): 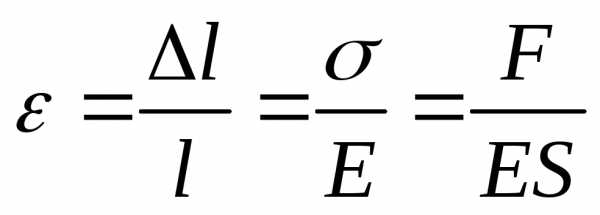 ,
отсюда
,
отсюда 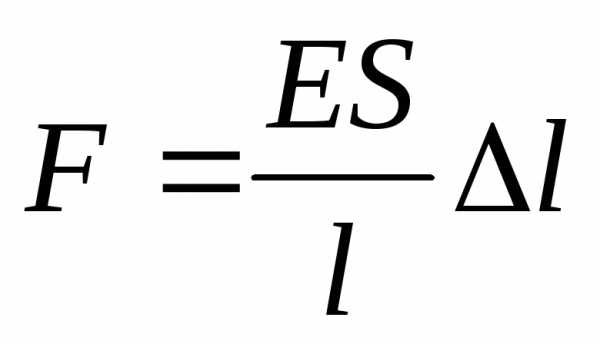 или
или
 , (3)
, (3)
где k – коэффициент упругости.
Выражение (3) также задает закон Гука: при упругой деформации абсолютное удлинение стержня пропорционально действующей силе.
Закон Гука справедлив только при невысоких напряжениях. При больших напряжениях закон Гука нарушается. Связь между деформацией и напряжением представляется в виде диаграммы напряжений (рисунок 2).
Рисунок 2 – Диаграмма напряжений малоуглеродистой стали
Из рисунка видно, что линейная зависимость (), установленная Гуком, выполняется лишь в очень узких пределах до так называемого предела пропорциональности (п). При дальнейшем увеличении напряжения деформация еще упругая (хотя зависимость () уже не линейна) и до предела упругости (у) остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, а параллельной ей – CF. Напряжение, при котором появляется заметная остаточная деформация (0,2 %), называется пределом текучести (т) – точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, для которых же она практически отсутствует хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности (p).
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рисунок 3).
Рисунок 3 – Деформация изгиба
При изгибе на выпуклой стороне тело подвергается растяжению, а на вогнутой – сжатию. Внутри изгибаемого тела находится слой, не испытывающий ни растяжения, ни сжатия, называемый нейтральным слоем. Около него при деформации возникают лишь ничтожно малые упругие силы. Слои балки испытывают тем большее напряжение, чем дальше они находятся от нейтрального слоя. На рисунке 3 показана деформация изгиба. Пунктирная линия – нейтральный слой, стрелками показаны силы, действующие в некотором сечении ab.
Для деформации изгиба стержня с круглыми поперечным сечением, имеющим две точки опоры, когда сила приложена в середине расстояния между опорами, расчеты дают следующее выражение:
 , (4)
, (4)
где k– коэффициент упругости при изгибе, пропорциональный приложенной силе,
l – расстояние между опорами;
D – диаметр стержня;
 –
стрела прогиба (рисунок 3),
–
стрела прогиба (рисунок 3), 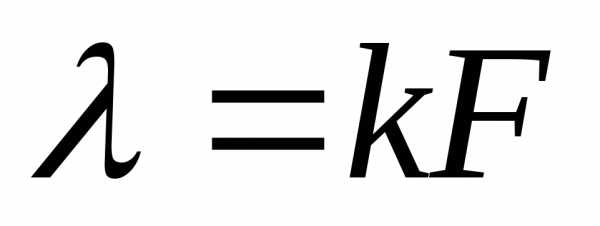 .
.
Вычислив коэффициент упругости
, (5)
по (4) определим модуль Юнга:
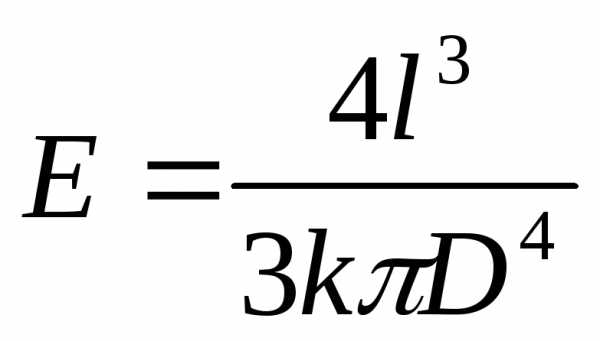 . (6)
. (6)
studfiles.net
Коэффициент упругости, формула и примеры
Определение и формула коэффициента упругости
Если под воздействием внешних сил на твердое тело оно деформируется, то в нем происходят смещения частиц узлов кристаллической решетки. Этому сдвигу противостоят силы взаимодействия частиц. Так возникают силы упругости, которые приложены к телу, подвергшемуся деформации. Модуль силы упругости пропорционален деформации:
где — напряжение при упругой деформации, K — модуль упругости, который равен напряжению при относительной деформации, равной единице. где — относительная деформация, — абсолютная деформация, — первоначальное значение величины, которая характеризовала форму или размеры тела.
Коэффициент упругости зависит от материала тела, его размеров. Так при увеличении длины пружины и уменьшении ее толщины коэффициент упругости уменьшается.
Модуль Юнга и коэффициент упругости
При продольной деформации, в одностороннем растяжении (сжатии) мерой деформации служит относительное удлинение, которое обозначают или . При этом модуль силы упругости определяют как:
где — модуль Юнга, который в рассматриваемом случае равен модулю упругости () и характеризующий упругие свойства тела; — первоначальная длина тела; — изменение длины при нагрузке . При S — площадь поперечного сечения образца.
Коэффициент упругости растянутой (сжатой) пружины
При растяжении (сжатии) пружины вдоль оси X закон Гука записывается как:
где — модуль проекции силы упругости; — коэффициент упругости пружины, — удлинение пружины. Тогда коэффициент упругости — это сила, которую следует приложить к пружине, чтобы изменить ее длину на единицу.
Единицы измерения
Основной единицей измерения коэффициента упругости в системе СИ является:
Примеры решения задач
ru.solverbook.com
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) – (α)
μ = (E / 2G) – 1 – (b)
K = E / 3(1 – 2μ) – (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
Материал при 18°С | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
Алюминий | 7,05 | 2,62 | 0,345 | 7,58 |
Висмут | 3,19 | 1,20 | 0,330 | 3,13 |
Железо | 21,2 | 8,2 | 0,29 | 16,9 |
Золото | 7,8 | 2,7 | 0,44 | 21,7 |
Кадмий | 4,99 | 1,92 | 0,300 | 4,16 |
Медь | 12,98 | 4,833 | 0,343 | 13,76 |
Никель | 20,4 | 7,9 | 0,280 | 16,1 |
Платина | 16,8 | 6,1 | 0,377 | 22,8 |
Свинец | 1,62 | 0,562 | 0,441 | 4,6 |
Серебро | 8,27 | 3,03 | 0,367 | 10,4 |
Титан | 11,6 | 4,38 | 0,32 | 10,7 |
Цинк | 9,0 | 3,6 | 0,25 | 6,0 |
Сталь (1% С) 1) | 21,0 | 8,10 | 0,293 | 16,88 |
(мягкая) | 21,0 | 8,12 | 0,291 | 16,78 |
Константан 2) | 16,3 | 6,11 | 0,327 | 15,7 |
Манганин | 12,4 | 4,65 | 0,334 | 12,4 |
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. | ||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
Вещество | Модуль Юнга E, 1011 дин/см2. | Модуль сдвига G, 1011 дин/см2. | Коэффициент Пуассона µ | Модуль объемной упругости К, 1011 дин/см2. |
Бронза (66% Cu) | -9,7-10,2 | 3,3-3,7 | 0,34-0,40 | 11,2 |
Медь | 10,5-13,0 | 3,5-4,9 | 0,34 | 13,8 |
Нейзильбер1) | 11,6 | 4,3-4,7 | 0,37 | – |
Стекло | 5,1-7,1 | 3,1 | 0,17-0,32 | 3,75 |
Стекло иенское крон | 6,5-7,8 | 2,6-3,2 | 0,20-0,27 | 4,0-5,9 |
Стекло иенское флинт | 5,0-6,0 | 2,0-2,5 | 0,22-0,26 | 3,6-3,8 |
Железо сварочное | 19-20 | 7,7-8,3 | 0,29 | 16,9 |
Чугун | 10-13 | 3,5-5,3 | 0,23-0,31 | 9,6 |
Магний | 4,25 | 1,63 | 0,30 | – |
Бронза фосфористая2) | 12,0 | 4,36 | 0,38 | – |
Платиноид3) | 13,6 | 3,6 | 0,37 | – |
Кварцевые нити (плав.) | 7,3 | 3,1 | 0,17 | 3,7 |
Резина мягкая вулканизированная | 0,00015-0,0005 | 0,00005-0,00015 | 0,46-0,49 | – |
Сталь | 20-21 | 7,9-8,9 | 0,25-0,33 | 16,8 |
Цинк | 8,7 | 3,8 | 0,21 | – |
1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. | ||||
Вещество | Модуль Юнга E, 1011 дин/см2. | Вещество | Модуль Юнга E, 1011 дин/см2. |
Цинк (чистый) | 9,0 | Дуб | 1,3 |
Иридий | 52,0 | Сосна | 0,9 |
Родий | 29,0 | Красное дерево | 0,88 |
Тантал | 18,6 | Цирконий | 7,4 |
Инвар | 17,6 | Титан | 10,5-11,0 |
Сплав 90% Pt, 10% Ir | 21,0 | Кальций | 2,0-2,5 |
Дюралюминий | 7,1 | Свинец | 0,7-1,6 |
Шелковые нити1 | 0,65 | Тиковое дерево | 1,66 |
Паутина2 | 0,3 | Серебро | 7,1-8,3 |
Кетгут | 0,32 | Пластмассы: |
|
Лед (-20С) | 0,28 | Термопластичные | 0,14-0,28 |
Кварц | 7,3 | Термореактивные | 0,35-1,1 |
Мрамор | 3,0-4,0 | Вольфрам | 41,1 |
1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость | |||
Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) | Сжимаемость k, бар-1 | |||
| ɑ, для Е | ɑ, для G |
|
|
Алюминий | 4,8*10-4 | 5,2*10-4 | Алюминий | 1,36*10-6 |
Латунь | 3,7*10-4 | 4,6*10-4 | Медь | 0,73*10-6 |
Золото | 4,8*10-4 | 3,3*10-4 | Золото | 0,61*10-6 |
Железо | 2,3*10-4 | 2,8*10-4 | Свинец | 2,1*10-6 |
Сталь | 2,4*10-4 | 2,6*10-4 | Магний | 2,8*10-6 |
Платина | 0,98*10-4 | 1,0*10-4 | Платина | 0,36*10-6 |
Серебро | 7,5*10-4 | 4,5*10-4 | Стекло флинт | 3,0*10-6 |
Олово | – | 5,9*10-4 | Стекло немецкое | 2,57*10-6 |
Медь | 3,0*10-4 | 3,1*10-4 | Сталь | 0,59*10-6 |
Нейзильбер | – | 6,5*10-4 |
|
|
Фосфористая бронза | – | 3,0*10-4 |
|
|
Кварцевые нити | -1,5*10-4 | -1,1*10-4 |
|
|
infotables.ru
Модуль Юнга
Компьютерная модель позволяет провести ряд экспериментов по теме «Сила упругости. Закон Гука». Экспериментальная установка представляет собой штатив с подвешенным на металлической проволоке телом. Можно изменять материал, из которого изготовлена проволока, площадь ее сечения, начальную длину, а также массу подвешенного груза. В информационном окне выводится информация об удлинении проволоки.
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
| Fx = Fупр = –kx. |
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение:
| σ = F / S = –Fупр / S, |
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2∙1011 Н/м2, а для резины E ≈ 2∙106 Н/м2, то есть на пять порядков меньше.
В рамках эксперимента можно выбирать материал проволоки (сталь, железо, медь, латунь, алюминий, свинец), площадь ее сечения (от 1 до 5 мм2 с шагом 0,5 мм2), массу груза (от 1 до 10 кг с шагом 0,5 кг).
Задав исходные условия эксперимента можно пронаблюдать результат, считывая показания удлинения проволоки по увеличенному участку измерительной шкалы.
Модель может стать основой исследовательских работ по данной учебной теме, т. к. допускает широкую вариативность исходных условий.
files.school-collection.edu.ru
Модуль упругости (модуль Юнга)
Модуль упругости (модуль Юнга) — коэффициент, характеризующий сопротивление материала растяжению или сжатию при упругой деформации
С помощью легких преобразований, данная формула получается из Закона Гука.
Закон Гука: механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации этого тела.
σ =k·ε
Другая форма записи закона Гука:
Коэффициент E в этом соотношении и есть модуль Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E≈2·1011 Н/м2, а для резины E≈2·106 Н/м2, то есть на пять порядков меньше.
Модуль упругости, или модуль продольной деформации Е, показывает критическое напряжение, которое может иметь структура материала при максимальной ее деформации до разрушения.
Таблица значений Модуля Юнга (модуля упругости) для некоторых материалов

Физический смысл Модуля Юнга: он показывает напряжение, которое необходимо приложить к телу, чтобы увеличить его длину в два раза
Обозначения:
E — модуль упругости (Модуль Юнга)
σp— критическое напряжение
ε — относительное удлинение
F — сила, действующая на стержень
l — длина деформируемого стержня
x — модуль изменения длины стержня в результате упругой деформации
S — площадь поверхности, по которой распределено действие силы
infofiz.ru

