Модуль юнга формула: Модуль упругости (модуль Юнга)
alexxlab | 21.01.1991 | 0 | Разное
15.Рассчитайте модуль Юнга для каждой нагрузки по формуле
Е = (F/k) .
16.Окончательный результат для е запишите в виде , где– абсолютная погрешность; – среднее арифметическое значение модуля Юнга.
Таблица 1
m, кг | 0,4 | 0,3 | 0,2 | 0,15 | 0,1 | 0,05 | 0 |
F=mg, Н | |||||||
, мм | |||||||
k=/∆X | |||||||
F/k | |||||||
Е, Н/м2 |
Задание 2.
Определение
показателя преломления воздуха
Показатель преломления является важной характеристикой среды. Различают абсолютный и относительный показатели преломления. Абсолютным показателем преломления среды называется отношение скорости распространения света в вакууме (с) к скорости ее распространения в данной среде ():
.
Относительный показатель преломления определяется для двух сред с различными абсолютными показателями преломления. Относительный показатель преломления второй среды относительно первой равен
.
Таким образом, показатель преломления связан со скоростью распространения света в среде и зависит от физического состояния среды (от температуры, плотности, наличия упругих напряжений, а также от длины волны света).
В
настоящей работе предлагается
интерферометрическим методом исследовать
зависимость между давлением газа в
кювете и его показателем преломления.
Для этого в один из пучков излучения в
интерферометре помещают кювету длиной
Установите в кронштейнах поворотного столика (4) интерферометра (рис.2) кювету для воздуха (5), соединенную с пневмоблоком. Манометр пневмоблока (5-1) должен показывать нуль (если не показывает, то настройте нуль манометра).
Закройте кран насоса пневмоблока (5-2) и создайте в кювете насосом избыточное давление 250-300 мм ртутного столба.
Отметьте на экране положение какой-либо интерференционной полосы. Аккуратно приоткрывая кран насоса пневмоблока, снижайте давление и следите за смещением интерференционной картины. Фиксируйте одновременно число пройденных через отметку полос N и величину соответствующего давления р1.
Данные занесите в таблицу 2.
Данные занесите в таблицу 2.Число смещенных интерференционных полос рассчитайте следующим образом. Если, например, при давлении 280 мм рт.ст. смещение произошло на 5 полос, а дальнейшее падение давления до 250 привело к смещению еще на 4 полосы, то общее число смещенных полос для давления 250 мм рт. ст. будет 5+ 4 = 9.
Постройте график зависимости числа смещенных интерференционных полос ΔN от разности избыточного давления∆p1и убедитесь в его линейности.
Определите по графику зависимости угловой коэффициентΔN/Δp = ΔN/Δp1 и затем найдите зависимость показателя преломления от давления по формуле
1.
6. Показатель преломления воздуха в кювете рассчитайте по формуле
,
где p0 = 720 мм рт.
ст – атмосферное давление.
Удобно измерять p0 и ∆p1 в одних и тех же (любых) единицах.
Длина кюветы = 120 мм;
Длина волны λ0 =0,652 мкм;
Давление в кювете p = po + p1, где p1 – избыточное давление, определяемое манометром.
7. Окончательный результат представьте в виде
ΔN/Δp = ΔN/Δp1= ___________________полос/мм.рт.ст.
n -1=) =_______________________________
Смещение N, полос | ||||||||
Избыточное
давление p1, мм
рт. |
ст.Таблица 2
Модуль Юнга Калькулятор | Вычислить Модуль Юнга
✖Напряжение, приложенное к материалу, – это сила, приложенная к материалу на единицу площади. Максимальное напряжение, которое может выдержать материал до разрушения, называется разрывным напряжением или пределом прочности при растяжении.ⓘ стресс [σ] | Атмосфера ТехническийАттопаскальБармикробарСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)сантипаскальдекапаскальдесятипаскальДайн / кв.смэкса паскаль Фемто паскаль Морская вода для ног (15 °C)Вода для ног (4 °C)Вода для ног (60 ° F)ГигапаскальГрамм-сила на квадратный сантиметргектопаскальДюйм ртутного столба (32 ° F)Дюйм ртутного столба (60 ° F)Дюйм водяного столба (4 °C)Дюйм воды (60 ° F)кгс / кв. | +10% -10% | |
✖Деформация – это просто мера того, насколько объект растягивается или деформируется.ⓘ Напряжение [ε] | +10% -10% |
смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыМетр воды (4 °C)МикробармикропаскальМиллибарМиллиметр ртутного столба (0 °C)Миллиметр воды (4 ° C)миллипаскальнанопаскальНьютон / кв.смНьютон / квадратный метрНьютон / квадратный миллиметрпаскальПета паскаль Пико паскаль пьезаФунт на квадратный дюймПаундаль / квадратный футПаундаль / квадратный футФунт-сила / квадратный футФунт-сила / квадратный дюймФунты / квадратная ногаСтандартная атмосфераТерапаскальТонна-сила (длинная) на квадратный футТон-сила (длинный) / квадратный дюймТонна-сила (короткая) на квадратный футТонна-сила (короткая) на квадратный дюймторр|
✖Модуль Юнга — это механическое свойство линейно-упругих твердых тел. |
Атмосфера ТехническийАттопаскальБармикробарСантиметр ртутного столба (0 °C)Сантиметр водяного столба (4 °C)сантипаскальдекапаскальдесятипаскальДайн / кв.смэкса паскаль Фемто паскаль Морская вода для ног (15 °C)Вода для ног (4 °C)Вода для ног (60 ° F)ГигапаскальГрамм-сила на квадратный сантиметргектопаскальДюйм ртутного столба (32 ° F)Дюйм ртутного столба (60 ° F)Дюйм водяного столба (4 °C)Дюйм воды (60 ° F)кгс / кв. смКилограмм-сила / квадратный метрКилограмм-сила / кв. миллиметрКилоньютон / квадратный метркилопаскальКило фунт на квадратный дюймКип-сила / квадратный дюймМегапаскальИзмеритель морской водыМетр воды (4 °C)МикробармикропаскальМиллибарМиллиметр ртутного столба (0 °C)Миллиметр воды (4 ° C)миллипаскальнанопаскальНьютон / кв. |
⎘ копия |
👎
Формула
сбросить
👍
Модуль Юнга Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
стресс: 12000 паскаль –> 12000 паскаль Конверсия не требуется
Напряжение: 0.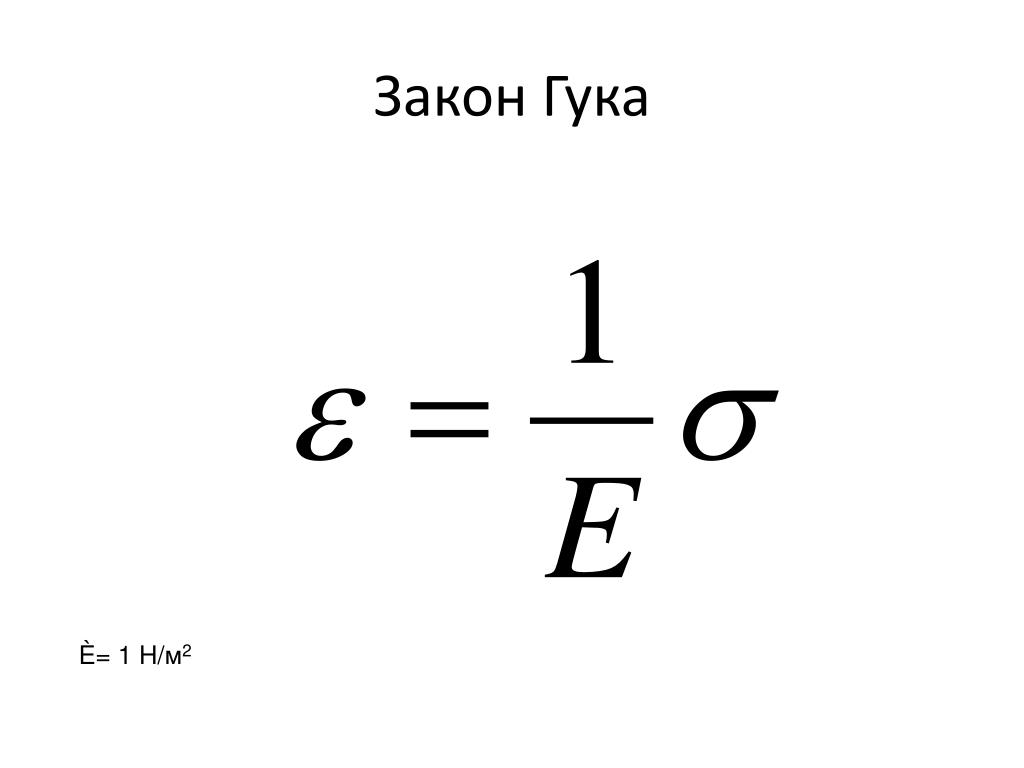
5 –> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
24000 паскаль –> Конверсия не требуется
< 10+ физика Калькуляторы
< 10+ Сопротивление материалов Калькуляторы
< 10+ Равновесный метод Калькуляторы
Статическое отклонение
Статическое отклонение = (Нагрузка, прикрепленная к свободному концу ограничения*Длина ограничения)/(Модуль для младших*Площадь поперечного сечения) Идти
Нагрузка прикреплена к свободному концу ограничения
Нагрузка, прикрепленная к свободному концу ограничения = (Статическое отклонение*Модуль для младших*Площадь поперечного сечения)/Длина ограничения Идти
Временной период свободных продольных колебаний
Временной период = 2*pi*sqrt(Нагрузка, прикрепленная к свободному концу ограничения/Жесткость ограничения) Идти
Угловая скорость свободных продольных колебаний
Естественная круговая частота = sqrt(Жесткость ограничения/Нагрузка, прикрепленная к свободному концу ограничения) Идти
Перемещение тела при заданной жесткости связи
Смещение тела = (-Нагрузка, прикрепленная к свободному концу ограничения*Ускорение тела)/Жесткость ограничения Идти
Ускорение тела при заданной жесткости связи
Ускорение тела = (-Жесткость ограничения*Смещение тела)/Нагрузка, прикрепленная к свободному концу ограничения Идти
Собственная частота свободных продольных колебаний
Частота = (sqrt(Ускорение силы тяжести/Статическое отклонение))/(2*pi) Идти
Гравитационное притяжение уравновешивается силой пружины
Сила = Жесткость ограничения*Статическое отклонение Идти
Восстанавливающая сила
Сила = -Жесткость ограничения*Смещение тела Идти
Модуль Юнга
Модуль для младших = стресс/Напряжение Идти
Модуль Юнга формула
Модуль для младших = стресс/Напряжение
E = σ/ε
Share
Copied!
Графен оказался прочнее всех • Юрий Ерин • Новости науки на «Элементах» • Физика, Нанотехнологии
Измерения, сделанные американскими учеными из Колумбийского университета, говорят о том, что графен — самое прочное из известных на сегодняшний день веществ.
Правда, полученные данные относятся к «идеальному» графену, в котором очень мало примесей и кристаллическая структура однородна.
Графен продолжает преподносить сюрпризы. С момента его открытия в 2004 году физикам уже удалось достоверно установить, что графен обладает высокой подвижностью зарядов (приблизительно в 100 раз выше, чем у кремния, и в 20 раз выше, чем у арсенида галлия; с прикладной точки зрения это означает возможность создания в будущем более совершенных электронных устройств, таких как транзисторы, например), наименьшим среди всех проводников удельным сопротивлением, а также что графен лучший проводник тепла (его коэффициент теплопроводности приблизительно равен 5000 Вт/м·К).
И вот в одном из последних номеров журнала Science появилась статья Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, в которой исследуются характеристики графена при его деформации. Авторы работы, ученые из Колумбийского университета США, выяснили, что, помимо указанных выше «рекордов», графен еще и самый прочный материал из известных на данный момент веществ.
Что подразумевается под этими словами? Известно, что в области малых по величине продольных деформаций выполняется закон Гука — возникающее удлинение образца Δl под действием внешней силы F пропорционально величине действующей силы, первоначальной длине l и обратно пропорционально площади поперечного сечения S:
.
Закон Гука можно переписать в более привычной, известной из школьного курса физики, форме:
,
где k — коэффициент жесткости, а величину E называют модулем Юнга или модулем упругости первого порядка. Именно модуль Юнга и служит своеобразной численной характеристикой, которая позволяет судить о прочности того или иного материала. Всё очень просто: чем больше модуль Юнга, тем прочнее материал.
Отношение обозначают обычно через σ — механическое напряжение, а через ε — относительная деформация. В этих терминах закон Гука можно переписать следующим образом:
σ = Eε.
Важно заметить, что данное соотношение работает, когда деформация упругая (то есть исчезающая с прекращением действия силы). Сложнее выглядит ситуация, когда прикладываемая сила такова, что деформация перестает быть упругой и закон Гука уже не выполняется. В этом случае можно воспользоваться таким соотношением:
σ = Eε + Dε2.
Здесь D обозначает модуль упругости третьего порядка. Как правило, D является отрицательной величиной.
Приведенная выше формула указывает путь для измерения модуля Юнга. Но как быть с графеном, который представляет собой, по сути, атомарную плоскость графита? Ведь в этом случае измерение величины деформации должно быть невероятно точным, а прикладываемая сила очень малой. Чтобы справиться с этой задачей, исследователи прибегли к помощи атомно-силового микроскопа, предварительно приготовив лист графена размером 5 на 5 мм с массивом «вырезанных» в нём отверстий (рис. 1A). Диаметры отверстий были составляли 1,5 и 1 мкм, а их глубина была равна 500 нм.
Схема эксперимента показана на рис. 1C. Алмазная игла (применялось два вида игл: одна с диаметром наконечника 27,5 нм, другая 16,5 нм) атомно-силового микроскопа оказывает давление на центр графенной мембраны, подвергая, таким образом, ее деформации (рис. 2). Было установлено, что при деформациях, превышающих 100 нм, и при значениях сил 1,8 и 2,9 мкН для маленькой и большой иглы микроскопа соответственно мембрана рвется (рис. 1D).
Дополнительные исследования с помощью просвечивающего туннельного микроскопа показали, что разрушения алмазной иглы при прогибе графенной пленки не происходит. Также удалось выяснить, что для графена существует область упругих деформаций, когда закон Гука выполняется, а значит, измеряя величину прогиба мембраны Δl, с помощью формулы F = kΔl можно измерить коэффициент жесткости k данного вещества. Но как от коэффициента жесткости перейти к искомому модулю Юнга? Ведь, строго говоря, графен — это двумерная структура, а поэтому связь k и E здесь просто некорректна.
Что, например, следует подразумевать под длиной образца l?
Авторы решают этот вопрос так: чтобы получить модуль Юнга E, коэффициент жесткости k, который в их статье обозначается как Е2D (под 2D здесь подразумевается не степень, а верхний индекс размерности), должен быть разделен на расстояние h = 0,335 нм между атомными плоскостями в графите, в котором, как известно, каждая плоскость как раз и представляет собой графен. Проще говоря, связь между E и Е2Dосуществляется с помощью формулы:
.
В эксперименте величина прогиба графенной мембраны изменялась в интервале от 20 до 100 нм. Проведя 67 измерений, ученые построили гистограмму (рис. 3) распределения коэффициента жесткости Е2Dи значения модуля Юнга Е.
Таким образом, рис. 3 можно назвать основным результатом проведенной работы: измеренный коэффициент жесткости для графена составил Е2D = 340 ± 50 Н/м, что отвечает модулю Юнга Е = 1,0 ± 0,1 ТПа (терапаскаля, 1 Тпа = 1012 Па).
Поскольку мы упоминали модуль упругости третьего порядка D (для ситуаций, когда деформация перестает быть упругой), то приведем и его значение для графена: D = –2 ± 0,4 ТПа.
А теперь сравним измеренный модуль Юнга графена с другими веществами. На рис. 4 приведена диаграмма «модуль Юнга — плотность» для некоторых веществ. Красным кружком отмечено положение на этой диаграмме графена (значение плотности указано для графита).
Как видно из диаграммы, прочность графена на порядок и более превосходит прочность всех известных в настоящее время веществ. Однако важно понимать, что полученные данные относятся к «идеальному» графену, в котором очень мало примесей и кристаллическая структура однородна; поэтому авторы работы для «чистоты эксперимента» и разработали во избежание этих проблем столь сложную методику измерений.
Источник: Changgu Lee, Xiaoding Wei, Jeffrey W. Kysar, James Hone. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene // Science.
2008. V. 321. P. 385–388.
Юрий Ерин
| (VP, VS) {\ displaystyle (V _ {\ mathrm {P}}, \, V _ {\ mathrm {S}})} | (μ, λ) {\ Displaystyle (\ му, \, \ лямбда)} | (Е, λ) † {\ Displaystyle (Е, \, \ лямбда) \, \ кинжал} | (Е, μ) {\ Displaystyle (Е, \, \ му)} | (К, λ) {\ Displaystyle (К, \, \ лямбда)} | (К, μ) {\ Displaystyle (К, \, \ му)} | (К, Е) {\ Displaystyle (К, \, Е)} | (ν, λ) {\ Displaystyle (\ ню, \, \ лямбда)} | (ν, μ) {\ Displaystyle (\ ню, \, \ му)} | (ν, E) {\ Displaystyle (\ ню, \, E)} | (ν, K) {\ displaystyle (\ nu, \, K)} | |||||||||||||||||||||||||||||||||||||||||||||||
| Скорость P-волны VP = {\ displaystyle V _ {\ mathrm {P}} = \,} | ВП {\ displaystyle V _ {\ mathrm {P}}} | λ + 2μρ {\ displaystyle {\ sqrt {\ tfrac {\ lambda + 2 \ mu} {\ rho}}}} | E-λ + X2ρ {\ displaystyle {\ sqrt {\ tfrac {E- \ lambda + X} {2 \ rho}}}} | μ (E−4μ) ρ (E−3μ) {\ displaystyle {\ sqrt {\ tfrac {\ mu \, (E-4 \ mu)} {\ rho \, (E-3 \ mu)}}} } | 3K−2λρ{\ displaystyle {\ sqrt {\ tfrac {3K-2 \ lambda} {\ rho}}}} | К + 43μρ {\ displaystyle {\ sqrt {\ tfrac {K + {\ frac {4} {3}} \ mu {\ rho}}}} | 3K (3K + E) ρ (9K−E) {\ displaystyle {\ sqrt {\ tfrac {3K \ влево (3K + E \ вправо)} {\ rho \ влево (9K-E \ вправо)}}}} | λ (1−ν) ρν {\ displaystyle {\ sqrt {\ tfrac {\ lambda (1- \ nu)} {\ rho \ nu}}}} | 2μ (1−ν) ρ (1−2ν) {\ displaystyle {\ sqrt {\ tfrac {2 \ mu (1- \ nu)} {\ rho (1-2 \ nu)}}}} | E (1−ν) ρ (1 + ν) (1−2ν) {\ displaystyle {\ sqrt {\ tfrac {E (1- \ nu)} {\ rho (1+ \ nu) (1-2 \ ну )}}}} | 3K (1−ν) ρ (1 + ν) {\ displaystyle {\ sqrt {\ tfrac {3K (1- \ nu)} {\ rho (1+ \ nu)}}}}} | ||||||||||||||||||||||||||||||||||||||||||||||
| S -скорость волны VS = {\ displaystyle V _ {\ mathrm {S}} = \,} | VS {\ displaystyle V _ {\ mathrm {S}}} | μρ{\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | E−3λ + X4ρ {\ displaystyle {\ sqrt {\ tfrac {E-3 \ lambda + X} {4 \ rho}}}} | μρ{\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | 3 (K−λ) 2ρ {\ displaystyle {\ sqrt {\ tfrac {3 (K- \ lambda)}} {2 \ rho}}}} | μρ{\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | -3EKρ (E-9K) {\ displaystyle {\ sqrt {- {\ tfrac {3EK} {\ rho \ left (E-9K \ right)}}}}} | λ2νρ−λρ{\ displaystyle {\ sqrt {{\ tfrac {\ lambda} {2 \ nu \ rho}} – {\ tfrac {\ lambda} {\ rho}}}}} | μρ{\ displaystyle {\ sqrt {\ tfrac {\ mu} {\ rho}}}} | E2ρ (1 + ν) {\ displaystyle {\ sqrt {\ tfrac {E} {2 \ rho (1+ \ nu)}}}} | -3K (2ν−1) 2ρ (ν + 1) {\ displaystyle {\ sqrt {- {\ tfrac {3K (2 \ nu -1)} {2 \ rho (\ nu + 1)}}}}} | ||||||||||||||||||||||||||||||||||||||||||||||
| Коэффициент скорости Γ = {\ displaystyle \ Gamma = \,} | VPVS{\ displaystyle {\ frac {V _ {\ mathrm {P}}} {V _ {\ mathrm {S}}}}} | λ + 2μμ {\ displaystyle {\ sqrt {\ tfrac {\ lambda + 2 \ mu} {\ mu}}}} | 3E + 3λ + X2E {\ displaystyle {\ sqrt {\ tfrac {3E + 3 \ lambda + X} {2E}}}} | E−4μE−3μ{\ displaystyle {\ sqrt {\ tfrac {E-4 \ mu} {E-3 \ mu}}}} | 43λ−2Kλ−K {\ displaystyle {\ sqrt {\ tfrac {{\ tfrac {4}} {3}} \ lambda -2K} {\ lambda -K}}}} | K + 43μμ {\ displaystyle {\ sqrt {\ tfrac {K + {\ frac {4} {3}} \ mu {\ mu}}}} | E + 3KE {\ displaystyle {\ sqrt {\ tfrac {E + 3K} {E}}}} | 2ν−22ν−1 {\ displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν−22ν−1 {\ displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν−22ν−1 {\ displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | 2ν−22ν−1 {\ displaystyle {\ sqrt {\ tfrac {2 \ nu -2} {2 \ nu -1}}}} | ||||||||||||||||||||||||||||||||||||||||||||||
| 1-й параметр Ламе λ = {\ displaystyle \ lambda = \,} | ρ (VP2−2VS2) {\ displaystyle \ rho (V _ {\ mathrm {P}} ^ {2} -2V _ {\ mathrm {S}} ^ {2})} | λ {\ Displaystyle \ лямбда} | λ {\ Displaystyle \ лямбда} | μ (E−2μ) 3μ−E {\ displaystyle {\ tfrac {\ mu (E-2 \ mu)} {3 \ mu -E}}} | λ {\ Displaystyle \ лямбда} | К−2μ3{\ displaystyle K – {\ tfrac {2 \ mu} {3}}} | 3K (3K-E) 9K-E {\ displaystyle {\ tfrac {3K (3K-E)} {9K-E}}} | λ {\ Displaystyle \ лямбда} | 2μν1−2ν{\ displaystyle {\ tfrac {2 \ mu \ nu} {1-2 \ nu}}} | Eν (1 + ν) (1−2ν) {\ displaystyle {\ tfrac {E \ nu} {(1+ \ nu) (1-2 \ nu)}}} 9{2}} | μ{\ displaystyle \ mu} | E−3λ + X4 {\ displaystyle {\ tfrac {E-3 \ lambda + X} {4}}} | μ{\ displaystyle \ mu} | 3 (К-λ) 2 {\ displaystyle {\ tfrac {3 (K- \ lambda)} {2}}} | μ{\ displaystyle \ mu} | 3KE9K−E {\ displaystyle {\ tfrac {3KE} {9K-E}}} | λ (1−2ν) 2ν {\ displaystyle {\ tfrac {\ lambda (1-2 \ nu)} {2 \ nu}}} | μ{\ displaystyle \ mu} | E2 (1 + ν) {\ displaystyle {\ tfrac {E} {2 (1+ \ nu)}}} | 3K (1−2ν) 2 (1 + ν) {\ displaystyle {\ tfrac {3K (1-2 \ nu)} {2 (1+ \ nu)}}} 9{2}}}} | μ (3λ + 2μ) λ + μ {\ displaystyle {\ tfrac {\ mu (3 \ lambda + 2 \ mu)} {\ lambda + \ mu}}} | Е {\ Displaystyle Е \} | Е {\ displaystyle E} | 9K (K-λ) 3K-λ {\ displaystyle {\ tfrac {9K (K- \ lambda)} {3K- \ lambda}}} | 9Kμ3K + μ{\ displaystyle {\ tfrac {9K \ mu} {3K+ \ mu}}} | Е {\ Displaystyle Е \} | λ (1 + ν) (1−2ν) ν {\ displaystyle {\ tfrac {\ lambda (1+ \ nu) (1-2 \ nu)} {\ nu}}} | 2μ (1 + ν) {\ Displaystyle 2 \ му (1+ \ ню) \,} | Е {\ displaystyle E \ } 9{2})} | λ + 2μ3 {\ displaystyle \ lambda + {\ tfrac {2 \ mu} {3}}} | E + 3λ + X6 {\ displaystyle {\ tfrac {E + 3 \ lambda + X} {6}}} | Eμ3 (3μ−E) {\ displaystyle {\ tfrac {E \ mu} {3 (3 \ mu -E)}}} | К {\ Displaystyle К} | К {\ Displaystyle К} | К {\ Displaystyle К} | λ (1 + ν) 3ν {\ displaystyle {\ tfrac {\ lambda (1+ \ nu)} {3 \ nu}}} | 2μ (1 + ν) 3 (1−2ν) {\ displaystyle {\ tfrac {2 \ mu (1+ \ nu)} {3 (1-2 \ nu)}}} | E3 (1−2ν) {\ displaystyle {\ tfrac {E} {3 (1-2 \ nu)}}} 9{2})}}} | λ2 (λ + μ) {\ displaystyle {\ tfrac {\ lambda} {2 (\ lambda + \ mu)}}} | -E-λ + X4λ {\ displaystyle {\ tfrac {-E- \ lambda + X} {4 \ lambda}}} | E2μ−1 {\ displaystyle {\ tfrac {E} {2 \ mu}} -1} | λ3K−λ{\displaystyle {\tfrac {\lambda}{3K-\lambda}}} | 3K−2μ2 (3K + μ) {\ displaystyle {\ tfrac {3K-2 \ mu} {2 (3K + \ mu)}}} | 3K−E6K{\displaystyle {\tfrac {3K-E}{6K}}} | ν {\ Displaystyle \ ню} | ν {\ Displaystyle \ ню} | ν {\ Displaystyle \ ню} 9{2}} | λ + 2μ {\ Displaystyle \ лямбда + 2 \ мю \,} | E-λ + X2 {\ displaystyle {\ tfrac {E- \ lambda + X} {2}}} | μ (4μ−E) 3μ−E {\ displaystyle {\ tfrac {\ mu (4 \ mu -E)} {3 \ mu -E}}} | 3K−2λ {\ displaystyle 3K-2 \ lambda \,} | К + 4μ3 {\ displaystyle K + {\ tfrac {4 \ mu} {3}}} | 3K (3K + E) 9K−E {\ displaystyle {\ tfrac {3K (3K + E)} {9K-E}}} | λ (1−ν) ν {\ displaystyle {\ tfrac {\ lambda (1- \ nu)} {\ nu}}} | 2μ (1−ν) 1−2ν {\ displaystyle {\ tfrac {2 \ mu (1- \ nu)} {1-2 \ nu}}} | E (1−ν) (1 + ν) (1−2ν) {\ displaystyle {\ tfrac {E (1- \ nu)} {(1+ \ nu) (1-2 \ nu)}}} | 3K(1−ν)1+ν{\displaystyle {\tfrac {3K(1-\nu)}{1+\nu}}} |
Модуль Юнга: формула, эксперимент, единица измерения, график
Модуль Юнга или модуль упругости описывает способность материалов сопротивляться изменению длины при растяжении или сжатии.
Этот модуль очень полезен в инженерии, поскольку он предоставляет подробную информацию об упругих свойствах материалов, таких как их прочность на растяжение и жесткость.
Определение модуля Юнга
Модуль Юнга равен приложенному продольному напряжению, деленному на деформацию. Напряжение и деформация объекта, подвергающегося растяжению, также могут быть выражены следующим образом: когда металлический объект тянется с силой F на каждом конце, объект будет растягиваться от исходной длины L 0 до новой растянутой длины L н .
Поскольку объект растягивается, площадь поперечного сечения уменьшается. Напряжение можно выразить как приложенную растягивающую силу (F), измеренную в ньютонах (Н), деленную на площадь поперечного сечения (A), измеренную в м 2 , , как показано в уравнении ниже. Полученная единица напряжения равна Н/м 2 .
Деформация, также известная как относительная деформация, представляет собой изменение длины, вызванное растяжением или сжатием, деленное на исходную длину L 0 .
Деформация безразмерна, так как оба члена дроби измеряются в метрах и могут быть рассчитаны по следующему уравнению.
Формула модуля Юнга
Модуль упругости E можно выразить как напряжение, деленное на деформацию, как показано в формуле ниже.
Единицы модуля Юнга такие же, как и напряжение, Н/м 2 , что эквивалентно Па (паскаль). Поскольку модуль упругости обычно представляет собой очень большое число величины 10 9 , его часто выражают в гигапаскалях, отображаемых как ГПа.
Металлический стержень испытывает нагрузку 60 N применяется в конце. Металлический стержень имеет цилиндрическую форму и площадь поперечного сечения 0,02 мм 2 . Длина полосы увеличивается на 0,30 процента. Найдите модуль упругости стержня.
Решение:
Поскольку требуется модуль Юнга, нам нужно сначала найти напряжение и деформацию (помните, модуль Юнга – это отношение напряжения к деформации).
Применим формулу напряжения, чтобы найти напряжение.
Затем мы применяем формулу деформации, чтобы найти деформацию:
Затем, наконец, мы делим напряжение на деформацию, чтобы найти модуль Юнга.
Как модуль Юнга связан с законом Гука?
Закон Гука гласит, что сила, действующая на тело или пружину, создающая смещение Δx, линейна по отношению к смещению, создаваемому в соответствии с приведенным ниже уравнением, где k — константа, относящаяся к жесткости пружины. Закон Гука можно применить к ситуациям, когда тело упруго деформируется.
Аналогично закону Гука, где растяжение или сжатие пружины линейно пропорционально приложенной силе; напряжение, приложенное к телу, линейно пропорционально модулю Юнга E, как показано в приведенном ниже преобразованном уравнении.
Графический расчет модуля Юнга
Поскольку модуль упругости материала линейно пропорционален приложенному напряжению, деленному на деформацию, модуль Юнга также можно рассчитать по графику напряжение-деформация, который описывает линейную деформацию, как показано ниже. по закону Гука. Модуль Юнга равен наклону линейного участка кривой зависимости напряжения от деформации, как показано на рисунке ниже.
Расчет модуля Юнга по графику напряжения-деформации
Эксперименты для определения модуля Юнга
Чтобы измерить модуль Юнга металла, можно провести несколько экспериментов. К медному проводу будут прикладываться различные нагрузки — полученное удлинение будет измерено для построения графика напряжения-деформации. В соответствии с уравнениями напряжений и деформаций требуемые параметры будут измеряться с помощью следующего оборудования.
Проволока
Микрометр
Шкив
Metre ruler
Caliper
Weights
Clamp
Wooden block
Bench
Methodology
Using the ruler, we measure the initial length of провод.
Мы используем микрометр для измерения диаметра проволоки в трех точках по ее длине. Это для среднего диаметра, который будет использоваться в расчете площади.Один конец провода присоединяем к шкиву, который зажат к скамье, а другой конец к зажатому деревянному бруску.
Удлинение проволоки под действием груза измеряется и регистрируется. Разница между новой длиной и исходной длиной до удлинения используется при расчете деформации.
Повторите процесс, чтобы получить еще от 5 до 10 показаний. Для уменьшения ошибок рекомендуется проводить различные измерения с различными весами.
Затем постройте график зависимости напряжения от деформации и найдите модуль упругости, взяв градиент линии.
Мы используем микрометр для измерения диаметра проволоки в трех точках по ее длине. Это для среднего диаметра, который будет использоваться в расчете площади.Анализ результатов
Целью эксперимента является оценка модуля Юнга.
Это можно найти, оценив напряжение и деформацию. Следующие шаги необходимы, чтобы найти напряжение и деформацию.
Найдите площадь провода, используя измеренный диаметр и уравнение A=πr 2 , где r=R/2.
Измените формулу модуля Юнга и решите ее для F. Это даст нам F=((E⋅A)/L)⋅ΔL.
Перестроенное уравнение аналогично уравнению прямой вида y = ax, , где y равно F , а наклон является коэффициентом ΔL.
График зависимости силы от ΔL строится по зарегистрированным точкам силы и растяжения, чтобы можно было найти наклон. Находится наклон ΔF/ΔL и умножается на исходную длину L 0 и разделить на площадь A, для оценки значения модуля Юнга.
График напряжения-деформации и характеристики материалов
Некоторые важные характеристики материалов показаны на рисунке ниже.
Красная область указывает на упругую область, где она деформируется в соответствии с законом Гука, а напряжение и деформация пропорциональны друг другу. Красная точка указывает предел упругости или предел текучести. Это точка, в которой материал может сохранять свою первоначальную длину после приложения нагрузки.
Зеленая область указывает на область пластичности, в которой материал не может вернуться в исходное состояние и подвергся необратимой деформации. Зеленая точка указывает предел прочности при растяжении, до которого материал может выдерживать максимальную нагрузку на единицу без разрушения.
Синяя точка указывает точку разрыва или предел прочности при разрыве материала.
График напряжения-деформации предела упругости материала, области пластичности и точек разрыва
Модуль Юнга — основные выводы
Модуль Юнга — это способность материала сопротивляться изменению длины при растяжении или сжатии.
Модуль Юнга можно рассчитать графически, используя график напряжения-деформации.
Экспериментальный расчет модуля Юнга возможен путем построения разности длины нагрузки.
Используя график напряжений и деформаций, можно определить прочность материала на растяжение и предел прочности.
Модуль Юнга – GeeksforGeeks
Модуль Юнга назван в честь Томаса Янга , британского физика. Связь между напряжением (силой на единицу площади) и деформацией (пропорциональной деформацией объекта) определяется модулем Юнга.
Когда к жесткому материалу добавляется определенная нагрузка, он деформируется. Когда груз снимается с эластичного материала, тело возвращается в свою первоначальную форму. За пределами минимальной степени деформации материалы часто не являются линейными и эластичными. Только линейные упругие поверхности имеют устойчивый модуль Юнга.
Как и модуль объемного сжатия, коэффициент Пуассона и модуль сдвига, модуль Юнга также является константой упругости. Поэтому, прежде чем понять концепцию модуля Юнга, давайте сначала узнаем о константах упругости.
Постоянные упругости
Постоянные упругости – это константы, определяющие деформацию, вызываемую данной системой напряжений, действующих на материал. Существует много типов констант упругости, таких как объемный модуль, модуль Юнга или модуль упругости, коэффициент Пуассона и модуль сдвига или модуль жесткости. Когда деформирующая сила действует на объект, она вызывает сдвиг исходного размера твердого тела. В таких ситуациях связь между константами упругости может быть использована для определения степень деформации .
Ниже приведены основные константы упругости, которые необходимо изучить:
1. Объемный модуль: Он определяется отношением давления (P), приложенного к соответствующему относительному уменьшению объема или объемной деформации ( ∈ V ) материала. Математически это определяется как:
K = P / ∈ V = P / -(∆V/V 0 )
где ∆V — изменение объема материала в результате сжатия и В 0 Начальный объем материала.
Значение обозначается символом K и имеет размерность силы на единицу площади.
Выражается в единицах на квадратный дюйм (psi) в английской системе и в ньютонах на квадратный метр (Н/м 2 ) в метрической системе.
2. Модуль Юнга: Это мера жесткости твердого тела или сопротивления упругой деформации под нагрузкой. Он связывает напряжение (силу на единицу площади) с деформацией (пропорциональной деформацией) вдоль оси или линии.
Y = (F/A) / -(∆L/L 0 )
где ∆L — изменение длины материала в результате сжатия, а L 0 — начальная длина материал.
Значение обозначается символом Y и имеет размерность силы на единицу площади.
Единицей СИ для модуля Юнга является Паскаль (Па), значения чаще всего выражаются в мегапаскалях (МПа) или ньютонах на квадратный миллиметр (Н/мм 2 ).
3. Модуль сдвига или модуль жесткости: T Отношение касательного напряжения (или) касательного напряжения и касательной деформации (или) касательной деформации называется модулем жесткости. Математически это определяется как:
η = (F/A) / ∅
, где F — сила, приложенная к единице площади поверхности тела A, а ∅ — деформация при сдвиге.
Значение обозначается символом η.
Выражается в Паскалях (Па) в системе СИ.
Математически это определяется как:Теперь давайте обсудим модуль упругости Юнга более подробно:
Модуль упругости Юнга Модуль Юнга является математической константой.
Он был назван в честь Томаса Янга , английского врача и ученого 18-го века. Он определяет упругие характеристики твердого тела, которое подвергается растяжению или сжатию только в одном направлении. В качестве примера рассмотрим металлический стержень, который возвращается к своей первоначальной длине после растяжения или сжатия в продольном направлении.
Измерение способности материала выдерживать изменения длины при продольном растяжении или сжатии. Он также известен как модуль упругости. Мы вычисляем его путем деления. Он рассчитывается как продольное напряжение, деленное на деформацию. В случае натянутого металлического стержня можно указать как напряжение, так и деформацию.
Модуль Юнга, также известный как Модуль упругости или Модуль упругости при растяжении , представляет собой измерение механических свойств линейных упругих твердых тел, таких как стержни, проволоки и т. д. Существуют и другие числа, которые дают нам меру упругих характеристик материала.
Объемный модуль и модуль сдвига являются двумя примерами. Однако чаще всего используется значение модуля Юнга. Это связано с тем, что он предоставляет информацию об эластичности материала при растяжении.
Когда материал сжимается или растягивается, он испытывает упругую деформацию и возвращается к своей первоначальной форме при снятии нагрузки. Когда гибкий материал деформируется, он деформируется больше, чем когда деформируется жесткое вещество. Другими словами, это можно интерпретировать как:
- Твердое тело с низким значением модуля Юнга упруго.
- Твердое тело с высоким значением модуля Юнга является неупругим или жестким.
Модуль Юнга описывается как механическая способность материала выдерживать сжатие или удлинение относительно его начальной длины.
Формула для модуля Юнга:
Математически модуль Юнга определяется как отношение напряжения, приложенного к материалу, и деформации, соответствующей приложенному к материалу напряжению, как показано ниже:
Модуль Юнга = Напряжение / Деформация
или
Y = σ / ϵ
где Y — модуль Юнга материала, σ — напряжение, приложенное к материалу, а ε — деформация, соответствующая приложенному напряжение в материале.
Единицы модуля Юнга:
Единицей модуля Юнга в системе СИ является Паскаль (Па) .
Размерная формула для Y: [ML -1 T -2 ] .
Значения чаще всего выражаются в мегапаскалях (МПа), ньютонах на квадратный миллиметр (Н/мм 2 ), гигапаскалях (ГПа) или килоньютонах на квадратный миллиметр (кН/мм 2 ).
Young’s Modulus of some materials are as follows:
| Materials | Young’s Modulus (Y) in Nm -2 |
|---|---|---|
1. | Rubber | 5 × 10 8 |
2. | Bone | 1.4 × 10 10 |
3. | Lead | 1. |
4. | Aluminum | 7.0 × 10 10 |
5. | Brass | 9.0 × 10 10 |
6. | Copper | 11.0 × 10 10 |
7. | Iron | 19,0 × 10 10 |
6 × 10 10 Математическая интерпретация молодых. по его длине, т. е. по нормали к поверхности провода, как показано на рисунке. Если △L — изменение длины проволоки, то растягивающее напряжение (σ = F/A), где A — площадь поперечного сечения проволоки, и продольная деформация (ϵ = △L/L).
Таким образом, модуль Юнга для этого случая определяется как:
Y = (F/A) / (△L/L)
= (F × L) / (A × △L)
Если растяжение производится грузом массы m, то Сила F равна mg , где m — масса, а g — ускорение свободного падения.
А площадь поперечного сечения провода, A, равна πr 2 , где r — радиус провода.
Таким образом, приведенное выше выражение можно записать как:
Y = (m × g × L) / (πr 2 × △L)
Следовательно, Факторы, от которых зависит модуль Юнга материала: :
- модуля материала, тем больше значение силы , необходимой для изменения длины материала .
- Модуль Юнга объекта зависит от природы материала объекта .
- Модуль Юнга объекта не зависит от размеры (т. е. длина, ширина, площадь и т. д.) объекта.
- Модуль Юнга вещества уменьшается с увеличением температуры .
- Модуль упругости Юнга абсолютно твердого тела бесконечен.
Таким образом, из приведенного выше выражения наклон, построенный для изменения длины (△L) и массы объекта (м), показан ниже как:
График между △L и m.
Примеры задач
Задача 1. Кабель обрезан на половину своей длины. Почему это изменение не влияет на опору кабины при максимальной нагрузке?
Решение:
Максимальная нагрузка, которую может выдержать кабель, определяется по формуле:
F = (YA△L) / L
Здесь Y и A постоянные, значение △ не изменяется. л/л.
Следовательно, не влияет на на максимальную нагрузку.
Задача 2. Чему равен модуль Юнга абсолютно твердого тела?
Решение:
Модуль Юнга для материала равен
Y=(F/A) / (△L/L)
Здесь △L = 0 для твердого тела. Следовательно, модуль Юнга равен бесконечным .
Задача 3. Модуль Юнга стали намного больше, чем у резины. Если продольная деформация одинакова, какой из них будет иметь большее растягивающее напряжение?
Решение:
Поскольку растягивающее напряжение материала равно произведению модуля Юнга (Y) на продольную деформацию.
