Модуль юнга латуни: Модуль упругости (Модуль Юнга): понятие, формулы, как определить

alexxlab | 17.04.2023 | 0 | Разное

Содержание

Определение модуля Юнга по изгибу стержня.

Министерство образования Российской Федерации

Тверской государственный университет

Кафедра общей физики

Лаборатория механики

Лабораторная работа №10

Тверь

2000

Цель работы: определить модуль Юнга для латуни и стали.

Оборудование: стойка с 2-мя опорами, стержни из латуни и стали,

ИЧ-1,набор грузов

Под деформацией понимается изменение положения точек тела при котором меняется взаимное расстояние между ними. Изменение формы и размеров тела может быть следствием теплового расширения, воздействия магнитного и электрического полей, а также внешнего механического воздействия. Деформация называется упругой, если она исчезает после удаления вызвавшей ее нагрузки, и пластической, если после снятия нагрузки она полностью не исчезает.

Мысленно рассечем упруго деформированное тело на две части. Две смежных части одного тела можно рассматривать как два различных тела, связанных друг с другом силами молекулярного взаимодействия. Пусть стержень AB растягивается силами ии находится в равновесии (Рис.1).

A B

Рис. 1

Тогда . Можно считать, что часть B действует на часть А с силой , часть А действует на часть В с силой, так как в противном случае части А и В не были бы в равновесии. Эти внутренние силы, действующие между отдельными частями одного и того же тела, рассчитанные на единицу площади сечения, называются внутренними напряжениями. Таким образом, если площадь сечения стержняS, то напряжение , в общем случае.

Пусть некоторая величина характеризует форму или размеры тела(для стержня в качестве

x обычно рассматривается его длина l).

Величина деформации в результате действия на тело силы задается абсолютной деформацией или относительной.Для упругих деформаций, согласно закону Гука, , где носит название коэффициента упругости (жесткости). Для внутреннего напряжения опыт дает [1, стр. 62-63]:

где коэффициент Е носит название модуля упругости. Он определяется свойствами материала, из которого изготовлено тело. Е зависит от вида деформации. Модуль упругости имеет различные наименования, обозначения и численные значения. При продольном (одноосном) растяжении ,,.

Модуль упругости называется также модулем Юнга. Таким образом, модуль Юнга определяется как коэффициент пропорциональности между напряжением и относительной деформацией стержня. Можно также сказать, что

модуль Юнга равен тому внутреннему напряжению, которое возникло бы в образце с относительной деформацией , что означает: длина образца увеличилась в два раза.

Любую сложную деформацию твердого тела можно представить как наложение более простых деформаций одностороннего растяжения (сжатия), всестороннего растяжения (сжатия), сдвига.

Деформация «плоский изгиб». В процессе плоского поперечного изгиба все передвижения различных точек тела совершаются в различных плоскостях, называемых плоскостями изгиба. Деформация плоского поперечного изгиба вызывается такой системой, которая может быть сведена к двум парам сил, лежащим в плоскости изгиба. Они дают противоположные вращающие моменты, действующие на разные части тела.

Так в случае, представленном на рис.2, силы иобразуют пару с моментомM

1, поворачивающим левый конец стержня по часовой стрелке, а силыи- пару с моментомM₂, оказывающую противоположное действие на правый конец стержня:

M₂= -M₁

M₁ M₂

Рис. 2

Силы и , если их точки приложения сблизятся до совпадения, могут быть заменены одной силой , как это изображено на Рис.3.

M₁ M₁

Рис.3

Каждая из частей изгибаемого тела находится под воздействием неуравнавешенного момента внешних сил, то есть сил, действующих со стороны других частей данного тела, распределенных по поверхности раздела этих частей. Например, если провести в середине изогнутого стержня (Рис.3) перпендикулярное сечение кроме момента M

2 кроме внешних сил действует еще и момент внутренних сил M.

Рис. 4

Силы и,действующие на правую часть стержня со стороны левой, суммируется из сил, приложенных к различным участкам площади поперечного сеченияS (рис.5).

N₁

N₂

Рис.5

Возникновение этих сил связано с продольным сжатием верхней части стержня, расположенной над слоем N₁N₂ и растяжением нижней, лкжащей под этим слоем. Линия N₁N₂ отмечает положение слоя, не испытывающего при изгибе ни растяжения,ни сжатия, и поэтому называемого нейтральным.

Чем дальше удалены слои от нейтрального, тем значительнее напряжение, возникающее в этих слоях. Таким образом, поперечный изгиб- сложная деформация, сводящаяся к продльным деформациям, различным в различных частях тела.

За меру деформации при изгибе принимают так называемую “стрелу прогиба” .“Стрела прогиба” задает расстояние, на которое перемещается точка приложения силы при деформации

. Стрела прогиба зависит от способа закрепления стержня.

Характер деформации изгиба зависит от способа закрепления концов стержня.

I. Оба конца стержня свободно лежат на подставке (рис.6). Сила P приложена к середине стержня.

Рис.6

II. Стержень закреплен одним концом. Сила приложена к другому концу.

Рис.7

III. Оба конца стержня закреплены неподвижно. Сила приложена к середине стержня.

Рис.8

Модуль упругости стали и формулы его расчета

О чем речь? Модуль упругости стали требуется при проектировании стальных изделий и элементов конструкций. Он показывает стойкость материала к разнонаправленным нагрузкам. Это одна из важнейших характеристик металла.

Как определять? Показатель рассчитывается по определенной формуле и зависит от вида стали и добавок в нее. Помимо этого, для расчетов используются специальные нормативы и практические испытания материала. Требуются точные вычисления, так как в противном случае изделию грозит деформация, способная привести к его разрушению.

Вопросы, рассмотренные в материале:

Формула модуля упругости стали
Типы модулей упругости стали
Особенности модуля упругости стали

Определение модуля упругости стали
Другие коэффициенты для оценки свойств стали

Формула модуля упругости стали

Инженерное проектирование является направлением в сфере строительства, призванным решить целый ряд задач. Так, возведению любых объектов предшествует подготовка проекта. На данном этапе необходимо провести расчеты, чтобы подобрать оптимальное сечение профиля стальных конструкций и избежать разрушения готового здания.

Важным показателем, обеспечивающим прочность будущего объекта, считается модуль упругости стали. Его использование в расчетах позволяет защитить здание от преждевременных деформаций металлопроката. Сила упругости проявляется при деформации тела – она стремится восстановить его прежние размеры и форму и является следствием электромагнитного взаимодействия атомов и молекул.

Благодаря модулю упругости как физической величине (Е) описывают упругую сопротивляемость материала изделия приложенным нагрузкам. В случае с модулем упругости стали и других материалов нагрузки могут быть:

продольные – растягивающие и сжимающие;
поперечные, то есть изгибающие или на сдвиг;
объемные или скручивающие.

Данный показатель принято измерять в паскалях, мегапаскалях (МПа) и кгс/см2. От его значения напрямую зависит сопротивляемость материала нагрузкам, прочность предмета и предел разрушения. Так, у стали модуль упругости равен до 220 ГПа, у алюминия он находится на уровне в 70 ГПа, у чугуна – 120 ГПа, железа – 190 ГПа.

Для его вычисления используют формулу: E= σ / ε, где σ – напряжение, соответствующее силе, поделенной на площадь ее воздействия; ε – упругая деформация, определяемая как отношение удлинения образца с начала деформации к сжатию при завершении воздействия.

Рекомендуем статьи

Титан и его сплавы: свойства, применение
Сплавы черных металлов: классификация и особенности производства
Плавление латуни в различных условиях

Коэффициент E иначе обозначают как модуль Юнга в честь Томаса Юнга, английского физика XIX века. Модуль Юнга определяется свойствами материала, тогда как размеры и форма объекта не оказывают на него влияния. Показатель меняется в широких пределах в зависимости от конкретного материала. Допустим, у стали он равен ≈ 2·1011 Н/м2, а для резины он в пять раз меньше ≈ 2·106 Н/м2.

Напряжение измеряется в паскалях, а раз деформация считается безразмерной величиной, то Е принято указывать в паскалях.

Существует альтернативное определение, согласно которому модуль упругости представляет собой напряжение, которое достаточно, чтобы увеличить длину образца вдвое. Для подавляющего числа материалов эта формулировка является неточной. Дело в том, что данное значение значительно больше предела текучести материала или значения, когда удлинение делается нелинейным, но при этом оказывается более интуитивным.

Типы модулей упругости стали

Есть множество способов изменения напряжения и деформации, в том числе применение различных направлений действия силы. В связи с этим существует большое количество типов модулей упругости, среди которых основными считаются:

Модуль Юнга, обозначаемый символом E. Является показателем сопротивления материала растяжению или сжатию при упругой деформации. Характеризует способность предмета деформироваться вдоль оси под действием силы, приложенной вдоль данной оси. Определяется как отношение напряжения к деформации сжатия или удлинения. Нередко данный модуль обозначают просто как модуль упругости.
Модуль сдвига или модуль жесткости. Обозначается символом G и описывает способность материала сопротивляться изменению формы при сохранении объема. Вычисляется как отношение напряжения сдвига к деформации сдвига. Последнюю определяют как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига входит в число составляющих вязкости.
Модуль объемной упругости или объемного сжатия. Для его обозначения используют символ K. Показатель позволяет определить способность объекта изменять объем под воздействием всестороннего нормального напряжения (объемного), которое является одинаковым по всем направлениям.

Допустим, такое напряжение может появляться под действием гидростатического давления. Данный модуль вычисляется как отношение величины объемного напряжения к величине относительного объемного сжатия. K отличается от E и G тем, что для невязкой жидкости он не равен нулю, а для несжимаемой жидкости – бесконечен.

Это далеко не весь перечень модулей упругости, также существуют коэффициент Пуассона, параметры Ламе.

Описанная методика определения показателя применяется при вычислении Е для:

стальных изделий;
медных предметов;
прочих упругих образцов.

Особенности модуля упругости стали

Сталь является прочным материалом с высоким модулем упругости. Самые высокие показатели устойчивости к воздействиям имеют стальные сплавы с измененной кристаллической решеткой. Они отличаются значительным пределом текучести, определяемым опытным путем.

Особенности упругого поведения стальных изделий зависят от того, насколько сложны связи в кристаллической решетке. Решетка формируется в соответствии с типом материала – легирующей сталью. Благодаря наличию углерода решетка становится более твердой, но избыточное количество данного компонента негативно сказывается на пластичности и пружинистых свойствах сплава, влияет на значение модуля упругости стали. Не допустить подобного эффекта удается за счет внесения легирующих добавок, к которым относятся:

кремний;
никель;
вольфрам;
марганец.

Хотя указанные элементы повышают упругость, не всегда с их помощью можно обеспечить требуемый результат. Тогда прибегают к термообработке, поскольку под влиянием температуры свойства стали меняются: пропадают слабые участки, выравнивается показатель текучести отдельных фрагментов.

На данный момент существует свыше нескольких сотен марок стали, каждая из которых имеет свои свойства. Далее приведены популярные марки стали и соответствующий им модуль упругости E:

Низкоуглеродистая

В пределах 180

Ст3

В пределах 189

Ст10

В пределах 192

Ст45

В пределах 223

Ст40Х

В пределах 260

65Г

В пределах 275

Х12МФ

В пределах 320

9ХС

В пределах 302

ХВГ

В пределах 302

4Х5МФС

В пределах 315

3Х3М3Ф

В пределах 310

Р6М5

В пределах 320

Р9

В пределах 330

Р18

В пределах 340

Р12МФ5

В пределах 310

У7

В пределах 315

У8

В пределах 315

У9

В пределах 330

У10

В пределах 330

У11

В пределах 340

У12

В пределах 315

У13

В пределах 315

Модуль упругости не относится к постоянным величинам, так как зависит от места воздействия нагрузки. Правда, для некоторых материалов, например, стали 3 или 10 первого и второго рода, алюминия, меди, показатель сохраняется при растяжении и сжатии. Для разных марок стали модуль упругости отличается незначительно. По этой причине в процессе подготовки проекта E округляют, а подобные погрешности не учитывают.

Определение модуля упругости стали

Хотя твердые тела справляются с воздействием больших нагрузок, однако как только достигнуты определенные значения, они меняют форму и резко разрушаются. Чтобы определить момент, в который появятся трещины, разрыв, узнают модуль упругости стали посредством простых испытаний.

Госстандарты предлагают несколько возможных видов лабораторных исследований материала:

нагружение в течение продолжительного периода времени;
быстрые и длительные удары;
воздействие на растягивание и сжатие;
давление посредством гидравлики.

По модулю упругости стали удается понять, насколько жесткой и устойчивой будет оставаться конструкция, когда на нее будут воздействовать определенные нагрузки.

Чтобы узнать приблизительный показатель, прибегают к детальному изучению, выведению диаграммы напряжений. Для этого во время испытаний образец на специальных установках медленно растягивают до определенного предела. После этого результаты нормальных и относительных напряжений делят – итоговый показатель и является искомой величиной.

Модуль упругости ряда материалов содержится в нормативных документах. Так, определить его для конкретной марки стали можно, используя специальные таблицы, которые входят в состав нормативных документов в области строительства. Речь идет о строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ), указывающих искомые модули упругости стали.

Так, модуль упругости Юнга для белого и серого чугуна составляет 115–160 ГПа, а для ковкого находится на уровне 155. Модуль упругости углеродистой стали С245 может быть 200–210 ГПа. У легированной он немного выше: 210–220 ГПа. Для рядовых марок стали Ст. 3 и Ст.5 он равен 210 ГПа, а сталь Ст.45, 25Г2С и 30ХГС имеет показатель 200 ГПа.

Получается, у различных марок стали модуль упругости мало отличается, чего нельзя сказать о готовых изделиях. Рассмотрим в качестве примера аналогичный показатель для канатов:

пряди и свивки проволоки, обладающие высокой прочностью – 200 ГПа;
стальные тросы, имеющие металлический стержень – 150 ГПа;
стальные канаты, в которых предусмотрен органический сердечник – 130 ГПа.

Модуль сдвига или жесткости (G) обычно имеет меньшие значения, которые указываются в тех же таблицах. Для прокатной стали этот модуль составляет 84 ГПа, для углеродистой и легированной 80-81 ГПа, а для типов стали Ст.3 и Ст.45 – 80 ГПа.

Значения параметра упругости отличаются, поскольку наблюдается одновременное действие сразу трех основных модулей – каждый из них вычисляют отдельным методом. При этом разница небольшая, а значит, можно считать, что достигается достаточно высокая точность определения упругости.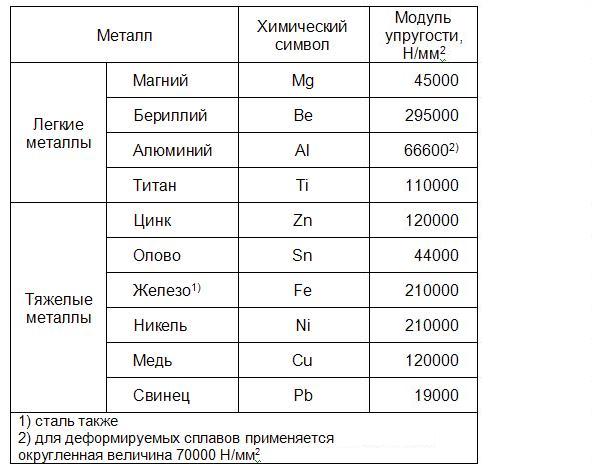 Нет смысла концентрироваться только на вычислениях и формулах – разумнее принять за константу конкретную величину упругости.

Комплексный расчет вместо вычисления по отдельным модулям позволяет получить значение Е = 200 ГПа. Показатель будет отличаться в зависимости от присадок, использованных в стали, а также особенностей изделия, например, наличия элементов из других веществ. Однако разница окажется невелика. Модуль упругости стали зависит в первую очередь от доли углерода. Тогда как задействованный способ обработки, то есть горячий прокат либо холодная штамповка, мало воздействует на показатель.

Выбирая стальные изделия, важно опираться также на расчетное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Данный показатель регламентируется наравне с модулем упругости стали и других материалов таблицами ГОСТов и СНиПов. Он имеет аналогичную размерность, что и модуль упругости, но его значения на три порядка меньше.

Для показателя принимают во внимание расчетное и нормативное сопротивление. Первое необходимо для выполнения расчетов прочности конструкций. Например, для стали С255 при толщине проката 10–20 мм оно составляет 240 МПа, тогда как нормативное находится на уровне 245 МПа. Для проката 20–30 мм расчетное сопротивление равно 230 МПа.

Другие коэффициенты для оценки свойств стали

Благодаря модулю упругости удается заранее понять, как различные типы стали и другие материалы будут вести себя в определенной ситуации. Однако с его помощью нельзя определить, как изменится вещество в иных обстоятельствах. Чтобы расчеты были более эффективны, прибегают к следующим показателям:

Коэффициент жесткости – свидетельствует об уровне пластичности материала, исчисляется в килограмм-силах (кгс).
Относительное продольное удлинение – измеряется в процентах. Формула для его вычисления предполагает учет длины образца и ее абсолютное изменение.
Относительное поперечное удлинение – определяется по аналогии с предыдущим показателем с тем отличием, что для расчетов нужна не длина, а диаметр.
Коэффициент Пуассона – представляет собой соотношение продольного относительного удлинения к поперечному. Позволяет определить, каким образом изменится форма заготовки в зависимости от разных значений силы и мест ее приложения.
Модуль сдвига – свидетельствует о поведении упругих материалов, подвергаемых воздействию усилий по касательной. Показатель необходим, чтобы оценить воздействие ветра с перпендикулярным направлением и предельной величиной усилия.
Модуль объемной упругости – демонстрирует изменение объема тела в случае равномерного, но при этом разностороннего приложения усилий.

Определить возможности применения стали позволяет предел упругости, исчисляемый в паскалях. По нему можно понять напряжение, которое вызовет разрушение, необратимую деформацию изделия.

При подготовке проекта конструкций важно использовать минимум два разных модуля упругости стали. Опираясь на коэффициент жесткости, проектировщик получает возможность перейти к другим видам сопротивления внешнему воздействию: упругости при изгибе и объемной упругости.

Строительство любого объекта предполагает использование набора конструкторских расчетов и грамотный подбор материалов в соответствии с их прочностью. Обеспечить безопасность зданий можно лишь при наличии у проектировщиков наиболее полных представлений о процессах, протекающих внутри материалов.

(-2). Латунная и стальная проволоки одинаковой длины растягиваются на 1 мм каждая под действием одинаковой силы. Если радиусы бюстгальтеров и стальной проволоки равны R(B) и R(s) соответственно, то

MHTCET ДОКУМЕНТЫ ПРЕДЫДУЩЕГО ГОДА И ПРАКТИЧЕСКИЕ ДОКУМЕНТЫ-ЭЛАСТИЧНОСТЬ-УПРАЖНЕНИЕ 1

20 видео

Ab Padhai karo bina ads ke

Khareedo DN Pro и дехо сари видео бина kisi ad ki rukaavat ke!

Дата обновления: 27 июня 2022 г.

Текстовое решение

RS = √2RB

RS = RB√2

RS = 4RB

RS = RB2

Ответ

Правильный ответ – B

. (11) Па. 9(2) . Соответственно . Латунная проволока и стальная проволока одинаковой длины удлиняются на 1 мм под действием одной и той же силы. Радиусы из латунных и стальных проводов – R_ (B) и R_ (S) соответственно, их

18254302

0,25 सेमी व्यास के त त जिनमे एक इस्50 0,25 बिना भार लटकाये इस्पात तथा पीतल के तारो की लमшить यदि इस्पात तथ|

94856580

Модуль Юнга латуни и стали составляет соответственно 1,0×1011 Н/м2 и 2,0×1011 Н/м2. Латунная и стальная проволоки одинаковой длины удлиняются на 1 мм каждая под действием одной и той же силы. Если радиусы латунной и стальной проволоки соответственно RB и RS, затем

95416810

Стальную проволоку длиной 4,0 м натягивают на 2,0 мм. Площадь поперечного сечения провода 2,0 мм2. Если модуль Юнга стали 2,0×1011 Нм-2, то найти плотность энергии проволоки.

112984461

Модули Юнга латуни и стали находятся в соотношении 1:2. Латунная проволока и стальная проволока одинаковой длины удлиняются на одинаковую величину под действием одинаковой деформирующей силы. Если rB и rS — радиусы латунной и стальной проволоки соответственно, то две проволоки диаметром 0,25 см, одна из стали, а другая из латуни, нагружены, как показано на рисунке. Ненагруженная длина стальной проволоки 1,5 м, латунной проволоки 1,0 м. Вычислите удлинение стальной и латунной проволоки. Модуль Юнга стали равен 2,0×1011 Па, а латуни — 9..1×1011 Па.

236919064

Если отношение длин, радиусов и модуль Юнга стальной и латунной проволоки, показанные на рисунке, равны a, b и c соответственно, то отношение между увеличением длины латунной и стальной проволоки проволока будет латунной, а стальная проволока будет

261057879

Модуль Юнга стали в два раза больше, чем у латуни. К одной и той же крыше подвешены две проволоки одинаковой длины и площади поперечного сечения, одна из стали, а другая из латуни. Тогда веса, добавленные к стальной и латунной проволоке, должны быть в соотношении 9(-2) соответственно. Латунная проволока и стальная проволока одинаковой длины удлиняются на 1 мм под действием одной и той же силы. Если радиусы латунной и стальной проволоки равны R_(B) и R_(S) соответственно, то .. .

621574595

Медная проволока и стальная проволока с радиусами в соотношении 1:2 и длинами в соотношении 2:1 растягиваются с одинаковой силой. Если модуль Юнга меди = 1,1×1011 Нм-2, найти отношение их удлинений (модуль Юнга стали =2×1011 Н/м2).

642668663

Модуль Юнга латуни и стали соответственно 10×1010 Н/м2. А 2×1010 Н/м2 Латунная проволока и стальная проволока одинаковой длины растягиваются на 1 мм под действием одной и той же силы, радиусы латунной и стальной проволок ar RBиRSсоответственно. Затем 9(2) Латунная проволока и стальная проволока одинаковой длины растягиваются на 1 мм под действием одинаковой силы, радиусы латунной и стальной проволок равны R(B) и R(S) соответственно. Затем

ИКСЕ-КОНКУРС УХОД БЛОК-СВОЙСТВА МАТЕРИИ (УПРУГОСТЬ )

20 видео

Аб Падхай каро бина адс ке

Хариэдо Д.Н. Про и дехо сари видео бина киси ад ки рукаават ке!

Обновлено: 27-06-2022

Text Solution

RS=√2RB

RS = RB/√2

RS = 4RB

RS = RB/4

Ответ

Правильный ответ – B

Решение

R2 = fl/yπl, R2B=FL/YBπl
R2S=FL/YSπl, R2B/R2S=YS/YB=2, RS=RB/√2.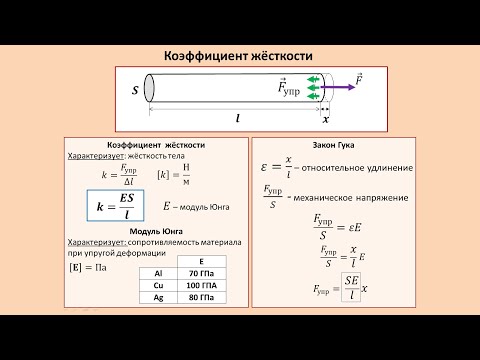

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

Стенограмма

сегодня вопрос Модуль Юнга латуни и стали соответственно затем в 10 поднять до Hotel Newton на квадратный метр на террасу Hotel терме параметры которые расширены на 1 мм в те же радиусы и стальная проволока ka rbns ожидаемые 10 которые вариант сохранен от вопроса что мы дали что имеем мы дали модуль Юнга латуни равный 10 в 10 поднять на 10 ньютонов на метр квадратный модуль Юнга стали привести в 10 в степени 10 ньютон на метр квадратный ок вам же дается исходная длина стальной проволоки и латунной проволоки обидно что оригинальная длина

децибел равно исходной функции длины, учитывая, что их удлинение на 1 мм расширено на 1 предел в разделе, поскольку это означает, что приложенная сила также такая же, также такое же изменение длины. Винод, что этот модуль Юнга равен напряжению на струне

ok Y равен напряжению при бронировании поезда, что является исходной и изменением единицы силы и площади поперечного сечения a можно прочитать здесь вы можете записать это как Y равно Apple bi Pi R Square tan tan ОК, где вы будете, каков будет радиус проволоки, теперь примените эту формулу для латунной проволоки DY, латунь и меньшие saptraas, равные f bi R bi ka Square в векторном приложении примените ту же формулу для Toshiba, вот почему сталь равна f

Pi R Квадратное время теперь сначала / у нас есть один модуль Юнга, равный квадрату Rs, и теперь мы знаем, почему латунный молодой белый осадок является вибрацией, заданной процессом, является стандартным для компьютеров 11 M и почему сталь 2 в 10 поднять до мощности 10 SSC Киран ке гана теперь мы дали близко, чтобы найти соотношение

радиусов отношения приемопередатчика между ними, и все в порядке, я думаю, что это одна ошибка в этом вопросе 10 возвести в степень 11 10 возвести в степень обед извините 10 возвести в степень 11 Янга модуль стали, где 2 на 10 Ашок 11 ньютонов на квадратный метр – это вызов для 11-го, это будут тендеры на 11, поэтому оба будут компенсировать друг друга, и, наконец, у нас есть r r b равно 1 на 2, чтобы можно было сказать, что Rs равно на РРБ так что это будет правильный вариант это наше слово ответ 9(2) . Соответственно . Латунная проволока и стальная проволока одинаковой длины удлиняются на 1 мм под действием одной и той же силы. Его радиусы латунной и стальной проволоки равны R_(B) и R_(S) соответственно, их

18254302

Модуль Юнга латуни и стали соответственно 1,0×1011 Н/м2 и 2,0×1011 Н/м2. Латунная и стальная проволоки одинаковой длины удлиняются на 1 мм каждая под действием одной и той же силы. Если радиусы латунной и стальной проволоки соответственно RB и RS, затем

95416810

Модуль Юнга латуни и стали составляет соответственно 1,0×1011 Нм-2 и 2,0×1011 Нм-2. Латунная и стальная проволоки одинаковой длины растягиваются на 1 мм каждая под действием одинаковой силы. Если радиусы латуни и стальной проволоки равны RB и Rs соответственно, то

112984475

(модуль Юнга для латуни =10×1010 Н/м2)

121606220

131204735

Две проволоки диаметром 0,25 см, одна из стали, а другая из латуни, нагружены, как показано на рисунке. Ненагруженная длина стальной проволоки 1,5 м, латунной проволоки 1,0 м. Вычислите удлинение стальной и латунной проволоки. Модуль Юнга для стали равен 2,0×1011 Па, а для латуни — 9,1×1011 Па.

236919064

показаны на рисунке a, b и c соответственно, соотношение между увеличением длины латунной и стальной проволоки будет равно 9.0039

261057879

Модуль Юнга стали в два раза больше, чем у латуни. К одной и той же крыше подвешены две проволоки одинаковой длины и площади поперечного сечения, одна из стали, а другая из латуни. Если тогда веса, добавленные к стальным и латунным проводам, должны находиться в соотношении

342578462

Текстовое решение

पीतल व स स के यंग प्रत्यास=F यह पीतल व स्टील के तारों पर (समान लम्बाई) समान बल लगाने पर, 1 मिमी ज जाते हैं।।।।।।। हैं मिमी मिमी ज ज ज हैं पीतल व स्टील के तारों की त्रिज्याएं RB व RS है तो 9(-2) соответственно.

TOP HEADLINES