Модуль юнга таблица для металлов – Модуль упругости (Модуль Юнга): понятие, формулы, как определить
alexxlab | 22.10.2019 | 0 | Разное
Модуль Юнга – Howling Pixel
Мо́дуль Ю́нга (модуль продольной упругости) — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации[1]. Обозначается большой буквой Е.
Назван в честь английского физика XIX века Томаса Юнга.
В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал деформируемой среды и процесса.
В Международной системе единиц (СИ) измеряется в ньютонах на квадратный метр или в паскалях. Является одним из модулей упругости.
Модуль Юнга рассчитывается следующим образом:
- E=F/SΔl/l=FlSΔl,{\displaystyle E={\frac {F/S}{\Delta l/l}}={\frac {Fl}{S\Delta l}},}
где:
Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:
- c=Eρ,{\displaystyle c={\sqrt {\frac {E}{\rho }}},}
где ρ{\displaystyle \rho } — плотность вещества.
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига G{\displaystyle G} и модулем объёмной упругости K{\displaystyle K} соотношениями
- G=E2(1+ν){\displaystyle G={\frac {E}{2(1+\nu )}}}
и
- K=E3(1−2ν),{\displaystyle K={\frac {E}{3(1-2\nu )}},}
где ν{\displaystyle \nu } — коэффициент Пуассона.
Температурная зависимость модуля Юнга
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости M(T){\displaystyle M(T)} определяется как вторая производная от внутренней энергии W(T){\displaystyle W(T)} по соответствующей деформации E(T)=d2W(T)dε2{\displaystyle E(T)={d^{2}W(T) \over d\varepsilon ^{2}}} . Поэтому при температурах T≤ΘD{\displaystyle T\leq \Theta _{D}} (ΘD{\displaystyle \Theta _{D}} — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением
- M(T)=M0−M1T−M2T2{\displaystyle M(T)=M_{0}-M_{1}T-M_{2}T^{2}}
где M0{\displaystyle M_{0}} — адиабатический модуль упругости идеального кристалла при T⟶0K{\displaystyle T\longrightarrow 0K}; M1T{\displaystyle M_{1}T} — дефект модуля, обусловленный тепловыми фононами; M2T2{\displaystyle M_{2}T^{2}} — дефект модуля, обусловленный тепловым движением электронов проводимости[2]
Значения модуля Юнга для некоторых материалов
Значения модуля Юнга для некоторых материалов приведены в таблице
См. также
Примечания
- ↑ Модули упругости — Статьи в Физическом энциклопедическом словаре и Физической энциклопедии.
- ↑ Л.Н. Паль-Валь, Ю.А. Семеренко, П.П. Паль-Валь, Л.В. Скибина, Г.Н. Грикуров. Исследование акустических и резистивных свойств перспективных хромо-марганцевых аустенитных сталей в области температур 5-300 К // Конденсированные среды и межфазные границы. — 2008. — Т. 10, вып. 3. — С. 226—235.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Анурьев В. И. Справочник конструктора-машиностроителя в 3т. Т. 1/В. И. Анурьев; 8-е изд., перераб и доп. Под ред. И. Н. Жестковой — М.: Машиностроение, 2001. — С. 34. ISBN 5-217-02963-3
- ↑ Галашев А. Е., Рахманова О. Р. Устойчивость графена и материалов на его основе при механических и термических воздействиях // Успехи физических наук. — М.: РАН, ФИАН, 2014. — Т. 184, вып. 10. — С. 1051.
- ↑ В.Д. Нацик, П.П. Паль-Валь, Л.Н. Паль-Валь, Ю.А. Семеренко. Низкотемпературный a-пик внутреннего трения в ниобии и его связь с релаксацией кинков на дислокациях // ФНТ. — 2001. — Т. 27, вып. 5. — С. 547—557.
- ↑ П.П. Паль-Валь, В.Д. Нацик, Л.Н. Паль-Валь, Ю.А. Семеренко. Нелинейные акустические эффекты в монокристаллах ниобия, обусловленные дислокациями // ФНТ. — 2004. — Т. 30, вып. 1. — С. 115—125.
Литература
- Волькенштейн В. С. Сборник задач по общему курсу физики / В. С. Волькенштейн. — СПб.: Лань, 1999. — 328 с.
Ссылки
ВиброскопВиброскоп (лат. vibrare ‘вибрировать’ + греч. σκοπέω ‘исследовать, изучать’) — измерительный инструмент для наблюдения и обнаружения источника (и иногда записывания) вибраций.Например, примитивный механический виброскоп содержит вибрирующую палочку с заострённым концом, который оставляет волновой след на поверхности вращающегося цилиндра.Виброскопы применяются для изучения свойств веществ. Например, коэффициет кручения и модуль Юнга полимеров можно определить по замерам их частоты вибрации под действием заданных приложенных сил. Подобный подход позволяет определить линейную плотность — плотность на единицу длины — нитевидных объектов, таких как волокна, текстильные волокна, пряжа.Виброскопы также применяются для изучения звука во рту во время речи.
Динамо́ме́тр (от др.-греч. δύναμις — «сила» и μέτρεω — «измеряю») — прибор для измерения силы или момента силы, состоит из силового звена (упругого элемента) и отсчётного устройства. В силовом звене измеряемое усилие вызывает деформацию, которая непосредственно или через передачу сообщается отсчётному устройству. Существующими динамометрами можно измерять усилия от долей ньютонов (н, долей кгс) до 20 Мн (2000 тс). По принципу действия различают динамометры механические (пружинные или рычажные), гидравлические и электронные. Иногда в одном динамометре используют два принципа.
ДунитДунит (др.-англ. dūn — возвышенность, холм, по горе Дун, Новая Зеландия) — магматическая плутоническая горная порода ультраосновного состава, нормального ряда щелочности из семейства дунитов. Более чем на 90 % состоит из оливина с примесью хромита, чем отличается от оливинита, в котором вместо хромита присутствует магнетит. Различают хромитовый дунит (70 % оливина, 30 % хромита), ильменитовый дунит (60 % оливина, 36 % ильменита, остальное — акцессорные минералы) и магнетитовый дунит (70 % оливина, 30 % титаномагнетита). В незначительном количестве в дунитах могут присутствовать клинопироксен, ортопироксен, плагиоклаз и т. д. Цвет чёрный, тёмно- и светло-зелёный. Текстура массивная.
Средний химический состав: SiO2 35-40 %, ТіO2 до 0.02 %, Al2O3 до 2.5 %, Fe2O3 0.5-7 %, FeO 3-6 %, MgO 38-50 %, CaO до 1.5 %, Na2O до 0.3 %, К2О до 0.25 %.
Закон ГукаЗако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским учёным Робертом Гуком.
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.
Кантиле́вер (англ. cantilever — кронштейн, консоль) — устоявшееся название наиболее распространенной в сканирующей атомно-силовой микроскопии конструкции микромеханического зонда.
Карбидкремниевое волокноКарбидкремниевое волокно (англ. silicon carbide fibres) — конструкционное волокно, состоящее из нанокристаллического карбида кремния.
КоварКова́р — прецизионный сплав с заданным коэффициентом линейного теплового расширения, обычно состоящий из 29 % никеля (Ni), 17 % кобальта (Co) и 54 % железа (Fe) с примесями кремния, углерода, марганца.
Имеет коэффициент теплового расширения близкий в широком диапазоне температур к коэффициенту теплового расширения боросиликатного стекла, используемого для изготовления баллонов ламп накаливания, люминесцентных ламп, электровакуумных приборов, металлостеклянных изоляторов и металлокерамических корпусов микросхем.
Отличается высокой адгезией к расплавленному стеклу, поэтому широко используется для изготовления проходящих через стекло электрических выводов вакуумных, газонаполненных и герметизированных приборов и различных ламп.
Название сплава «ковар» является зарегистрированной торговой маркой фирмы Carpenter Technology Corporation CRS Holdings, inc., Delaware. В СССР и России имеет наименование «сплав НК29» и «сплав НК29-ВИ».
Коэффициент ПуассонаКоэффициент Пуассона (обозначается как ν{\displaystyle \nu } или μ{\displaystyle \mu }) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.
Коэффицие́нт упру́гости (иногда называют коэффициентом Гука, коэффициентом жёсткости или жёсткостью пружины) — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой k, иногда D или c. Имеет единицу измерения Н/м или кг/с2 (в СИ), дин/см или г/с2 (в СГС).
Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.
Механические свойства волоконМеханические свойства волокон — комплекс характеристик, определяющих механическое поведение волокон при действии на них внешних сил.
МодульМодуль (от лат. modulus — «маленькая мера»):
Модуль — функционально завершённый узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельный продукт. См. также: унификация.
Модуль (космонавтика) — конструктивно законченная составная часть орбитального средства, предназначенная для реализации целевых, управляющих и/или обеспечивающих функций самостоятельно или в составе орбитального средства.
Модуль (архитектура) — предварительно заданная величина, размер, кратным которому принимаются остальные размеры при разработке или при оценке проекта здания.
Модуль — шаг сетки, основа композиции полос и разворотов в модульной системе вёрстки.
Модуль — произведение длины между перпендикулярами, ширины и высоты борта судна в судостроении.
Модуль (реклама) — размеры графики для печатной рекламы.
Модуль зубчатого колеса — основной параметр зубчатой передачи.
НТЦ «Модуль» — компания, учреждённая в 1990 году предприятиями НПО «Вымпел» и НИИ Радиоприборостроения.Информатика
Модуль (программирование) — функционально законченный фрагмент программы, оформленный в виде отдельного файла с исходным кодом или поименованной непрерывной её части.
Исполнимый модуль — файл, содержащий программу в виде, в котором она может быть исполнена компьютером.
Объектный модуль — файл с промежуточным представлением отдельного модуля программы, полученный в результате обработки исходного кода компилятором.
Модуль ядра — объект, содержащий код, который расширяет функциональность запущенного или т. н. базового ядра ОС.Математика
Абсолютная величина
Модуль вектора
Модули римановой поверхности
Модуль над кольцом, в частности Нётеров модуль.
проективный модуль
инъективный модуль
конечнопорождённый модуль
артинов модуль
Модуль непрерывности
Сравнение по модулю
Модуль перехода (логарифмы)
Модуль автоморфизмаМеханика твёрдого тела
Модуль потерь
Модуль упругости
Модуль Юнга
Модуль сдвига
Объёмный модуль упругости
Модуль сдвига Модуль сдвига — физическая величина, характеризующая способность материала сопротивляться сдвиговой деформации. Является вторым параметром Ламе (μ{\textstyle \mu }). Модуль сдвига определяется следующим соотношением:- G=τxyγxy=F/AΔx/I=FIAΔx,{\displaystyle G={\frac {\tau _{xy}}{\gamma _{xy}}}={\frac {F/A}{\Delta x/I}}={\frac {FI}{A\Delta x}},}
где
- τxy=F/A{\displaystyle \tau _{xy}=F/A} — касательное напряжение;
- F{\displaystyle F} — действующая сила;
- A{\displaystyle A} — площадь, на которую действует сила;
- γxy=Δx/I=tgθ{\displaystyle \gamma _{xy}=\Delta x/I=\operatorname {tg} \theta } — сдвиговая деформация;
- Δx{\displaystyle \Delta x} — смещение;
- I{\displaystyle I} — начальная длина.
В международной системе единиц (СИ) модуль сдвига измеряется в паскалях (на практике —- в гигапаскалях).
Модуль сдвига — одна из нескольких величин, характеризующих упругие свойства материала. Все они возникают в обобщённом законе Гука:
У однородного изотропного материала модуль сдвига связан с модулем Юнга через коэффициент Пуассона:
G=E2(1+ν),{\displaystyle G={\frac {E}{2(1+\nu )}},}
где ν{\displaystyle \nu } — значение коэффициента Пуассона для данного материала.
Предел прочностиПреде́л про́чности — механическое напряжение σB{\displaystyle \sigma _{B}}, выше которого происходит разрушение материала. Иначе говоря, это пороговая величина, превышая которую механическое напряжение разрушит некое тело из конкретного материала. Следует различать статический и динамический пределы прочности. Также различают пределы прочности на сжатие и растяжение.
ПружинаПружина — упругий элемент машин и различных механизмов, накапливающий и отдающий, или поглощающий механическую энергию.
СтекловолокноСтекловолокно́ (стеклонить) — волокно или комплексная нить, формируемые из стекла. В такой форме стекло демонстрирует необычные для себя свойства: не бьётся и не ломается, а вместо этого легко гнётся без разрушения. Это позволяет ткать из него стеклоткань.
Стекловолокна естественного происхождения встречаются в местах, где в прошлом происходили извержения вулканов, название данного вида волокон — волосы Пеле. Волосы Пеле имеют химический состав базальтовых пород, имеют включения кристаллов и по физико-механическим свойствам не являются аналогами стекловолокна.
ФононФоно́н — квазичастица, введённая советским учёным Игорем Таммом. Фонон представляет собой квант колебательного движения атомов кристалла.
ЭбонитЭбонит (от др.-греч. ἔβενος, ebenos — чёрное дерево) — высоко-вулканизированный каучук с большим содержанием серы (30–50 % в расчёте на массу каучука), обычно тёмно-бурого или чёрного цвета; химически инертен, имеет высокие электроизоляционные свойства.
На других языках
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
| Алюминий модуль упругости алюминия | 7.1 · 1010 (Ньютон / Метр2) |
| Вольфрам модуль упругости вольфрама | 39 · 1010 (Ньютон / Метр2) |
| Германий модуль упругости германия | 8.1 · 1010 (Ньютон / Метр2) |
| Дюралюминий модуль упругости дюралюминия | 7.3 · 1010 (Ньютон / Метр2) |
| Иридий модуль упругости иридия | 52.8 · 1010 (Ньютон / Метр2) |
| Константан модуль упругости константана | 16.3 · 1010 (Ньютон / Метр2) |
| Латунь модуль упругости латуни | 9.8 · 1010 (Ньютон / Метр2) |
| Марганец модуль упругости марганца | 12.4 · 1010 (Ньютон / Метр2) |
| Медь модуль упругости меди | 12.3 · 1010 (Ньютон / Метр2) |
| Плексиглас модуль упругости плексигласа | 0.32 · 1010 (Ньютон / Метр2) |
| Полистирол модуль упругости полистирола | 0.32 · 1010 (Ньютон / Метр2) |
| Свинец модуль упругости свинца | 1.6 · 1010 (Ньютон / Метр2) |
| Серебро модуль упругости серебра | 7.9 · 1010 (Ньютон / Метр2) |
| Сталь модуль упругости стали | 20.6 · 1010 (Ньютон / Метр2) |
| Стекло кварцевое модуль упругости кварцевого стекла | 7.5 · 1010 (Ньютон / Метр2) |
| Стекло оконное модуль упругости оконного стекла | 7 · 1010 (Ньютон / Метр2) |
| Фарфор модуль упругости фарфора | 5.8 · 1010 (Ньютон / Метр2) |
| Чугун модуль упругости чугуна | 10.8 · 1010 (Ньютон / Метр2) |
www.fxyz.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Материалы / / Сопротивление материалов. Сопромат. Таблицы строительных конструкций. / / Перевод единиц измерения модулей упругости, модулей Юнга (E), предела прочности, модулей сдвига (G), предела текучести.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dpva.ru
Показатель предела нагрузки на сталь — модуль упругости Юнга
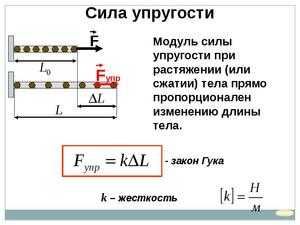До того, как взять в работу какой-то строительный материал, необходимо изучить его прочностные данные и возможное взаимодействие с другими веществами и материалами, их сочетаемость в плане адекватного поведения при одинаковых нагрузках на конструкцию. Определяющая роль для решения этой задачи отводится модулю упругости – его называют ещё модулем Юнга.
Высокая прочность стали позволяет использовать её при строительстве высотных зданий и ажурных конструкций стадионов и мостов. Добавки в сталь некоторых веществ, влияющих на её качество, называют легированием, и эти добавки могут увеличить прочность стали в два раза. Модуль упругости стали легированной гораздо выше, чем обычной. Прочность в строительстве, как правило, достигается подбором площади сечения профиля в силу экономических причин: высоколегированные стали имеют более высокую стоимость.
Далее, будет рассмотрено значение термина, изменчивость его для стали различных сортов. Для сравнения будут приведены значения модуля других материалов.
Физический смысл
Обозначение модуля упругости как физической величины – (Е), этот показатель характеризует упругую сопротивляемость материала изделия прилагаемым к нему деформирующим нагрузкам:
- продольным – растягивающим и сжимающим;
- поперечным – изгибающим или исполненным в виде сдвига;
- объёмным – скручивающим.
Чем выше значение (Е), тем выше сопротивляемость материала нагрузкам, тем прочнее будет изделие из этого материала и тем выше будет предел разрушения. Например, для алюминия эта величина составляет 70 ГПа, для чугуна – 120, железа – 190, а для стали до 220 ГПа.
Определение
Модуль упругости – сводный термин, вобравший в себя другие физические показатели свойства упругости твёрдых материалов – под воздействием силы изменяться и обретать прежнюю форму после её прекращения, то есть, упруго деформироваться. Это отношение напряжения в изделии – давление силы на единицу площади, к упругой деформации (безразмерная величина, определяемая отношением размера изделия к его изначальному размеру). Отсюда и его размерность, как и у напряжения – отношение силы к единице площади. Поскольку напряжение в метрической СИ принято измерять в Паскалях, то и показатель прочности – тоже.
Существует и другое, не очень корректное определение: модуль упругости – это давление, способное удлинить изделие вдвое. Но предел текучести большого количества материалов значительно ниже прилагаемого давления.
Модули упругости, их виды
Способов изменения условий приложения силы и вызываемых при этом деформаций много, и это предполагает и большое количество видов модулей упругости, но на практике сообразно деформирующим нагрузкам выделяют три основных:
Юнга (Е) представляет упругую сопротивляемость растягивающим и сжимающим нагрузкам – собственно, именно этим термином пользуются, когда говорят о модуле упругости;- модуль сдвига (G) характеризует сопротивляемость любому нарушению формы без её разрушения или изменения нормы – это отношение сдвигающей нагрузки к деформации, проявляющейся в виде изменчивости прямого угла между двумя половинами плоскости, подвергшейся нагрузке. Второе название этого термина – жёсткости, он же представляет и вязкость материала;
- модуль объёмной упругости (К) – сопротивляемость изменению объёма при разносторонних нормально приложенных напряжениях, имеющих равную величину по всем векторам. Его называют ещё модулем объёмного сжатия, выражается отношением объёмного давления к объёмной деформации сжатия.
Юнга (Е) представляет упругую сопротивляемость растягивающим и сжимающим нагрузкам – собственно, именно этим термином пользуются, когда говорят о модуле упругости;Этими показателями характеристики упругости не исчерпываются, есть и другие, которые несут другую информацию, имеют иную размерность и смысл. Это также широко известные среди специалистов показатели упругости Ламе и коэффициент Пуассона.
Как определить модуль упругости стали
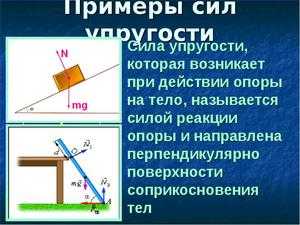Для определения параметров различных марок стали существуют специальные таблицы в составе нормативных документов в области строительства – в строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ). Так, модуль упругости (Е) или Юнга, у чугуна белого и серого от 115 до 160 ГПа, ковкого – 155. Что касается стали, то модуль упругости стали С245 – углеродистой имеет значения от 200 до 210 ГПа. Легированная сталь имеет показатели несколько выше – от 210 до 220 ГПа.
Та же самая характеристика у рядовых марок стали Ст.3 и Ст.5 имеет то же значение – 210 ГПа, а у стали Ст.45, 25Г2С и 30ХГС – 200 ГПа. Как видим, изменчивость (Е) для различных марок стали незначительна, а вот в изделиях, например, в канатах – другая картина:
- у прядей и свивок проволоки высокой прочности 200 ГПа;
- стальные тросы с металлическим стержнем 150 ГПа;
- стальные канаты с органическим сердечником 130 ГПа.
Как можно заметить, разница значительная.
Значения модуля сдвига или жёсткости (G) можно увидеть в тех же таблицах, они имеют меньшие значения, для прокатной стали – 84 ГПа, углеродистой и легированной – от 80 до 81 гпа, а для сталей Ст.3 и Ст.45–80 ГПа. Причиной различия значений параметра упругости является одновременное действие сразу трёх основных модулей, рассчитываемых по разным методикам. Однако разница между ними небольшая, что говорит о достаточной точности изучения упругости. Поэтому не стоит зацикливаться на вычислениях и формулах, а следует принять конкретную величину упругости и пользоваться ей как константой. Если не производить вычисления по отдельным модулям, а сделать расчёт комплексно, значение (Е) будет составлять 200 ГПа.
Необходимо понимать, значения эти разнятся для сталей с разными присадками и стальных изделий, включающих детали из других веществ, но разнятся эти значения незначительно. Основное влияние на показатель упругости оказывает содержание углерода, а вот способ обработки стали – горячий прокат или холодная штамповка, значительного влияния не оказывает.
При выборе стальных изделий пользуются также и ещё одним показателем, который регламентируется так же, как и модуль упругости в таблицах изданий ГОСТ и СНиП – это расчётное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Размерность у этого показателя та же, что и у модуля упругости, но значения на три порядка меньше. Этот показатель имеет два назначения: нормативное и расчётное сопротивление, названия сами говорят за себя – расчётное сопротивление применяется при выполнении расчётов прочности конструкций. Так, расчётное сопротивление стали С255 при толщине проката от 10 до 20 мм – 240 МПа, при нормативном 245 МПа. Расчётное сопротивление проката от 20 до 30 мм чуть ниже и составляет 230 МПа.
instrument.guru
Модуль упругости алюминия и алюминиевых сплавов
Модуль упругости = Модуль Юнга
На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза. Наклон этой части кривой определяет характеристику материала — модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.
Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа.
См. Модуль упругости различных алюминиевых сплавов
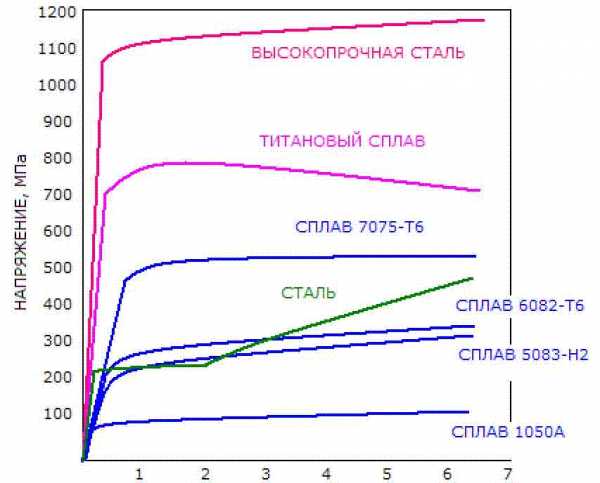
Ясно, что если стальную балку заменить на идентичную по форме балку из алюминиевого сплава, то вес ее будет в три раза меньше, но и ее упругий прогиб под той же нагрузкой будет приблизительно в три раза больше. Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.
Жесткость алюминиевых профилей
Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки. Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений. Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение. В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.
В таблицах представлены типичные прочностные характеристики популярных деформируемыхалюминиевых сплавов: предел прочности, предел текучести и удлинение при испытаниях на растяжение, а также усталостная прочность, твердость и модуль упругости – отдельно для сплавов, упрочняемых нагартовкой, и сплавов, упрочняемые термической обработкой. Как типичные свойства они годятся только для сравнительных целей, а не для инженерных расчетов. В большинстве случаев они являются средними значениями для различных размеров изделий, их форм и методов изготовления.
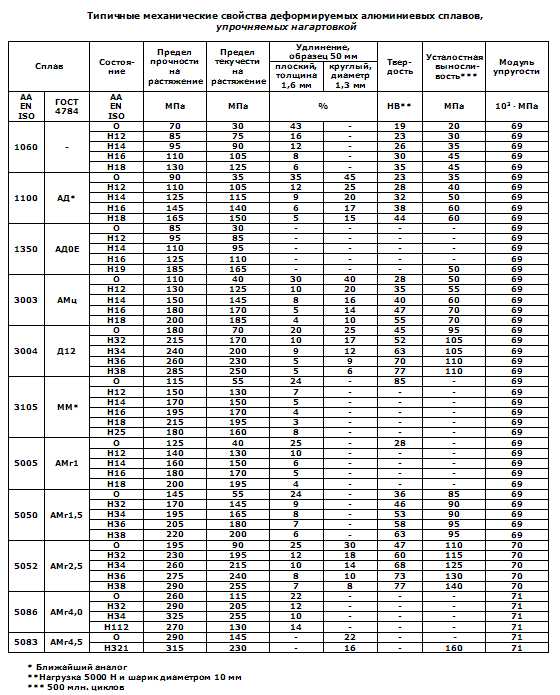
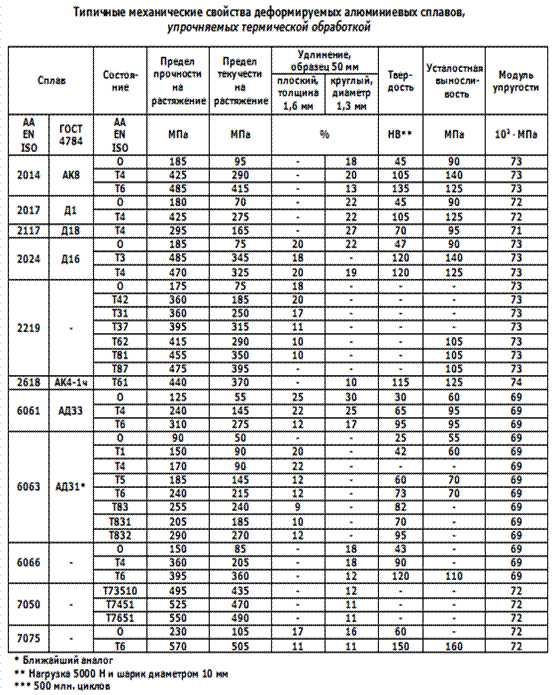
Источник: Aluminium and Aluminium Alloys. — ASM International, 1993.
uvakin.ru
| Материал | Модули упругости, МПа |
Коэффициент Пуассона |
|
|
Модуль Юнга E |
Модуль сдвига G |
||
|
Чугун белый, серый Чугун ковкий |
(1,15…1,60)·105 1,55·105 |
4,5·104 – |
0,23…0,27 – |
|
Сталь углеродистая Сталь легированная |
(2,0…2,1)·105 (2,1…2,2)·105 |
(8,0…8,1)·104 (8,0…8,1)·104 |
0,24…0,28 0,25…0,30 |
|
Медь прокатная Медь холоднотянутая Медь литая |
1,1·105 1,3·105 0,84·105 |
4,0·104 4,9·104 – |
0,31…0,34 – – |
|
Бронза фосфористая катаная Бронза марганцовистой катаная Бронза алюминиевая литая |
1,15·105 1,1·105 1,05·105 |
4,2·104 4,0·104 4,2·104 |
0,32…0,35 0,35 – |
|
Латунь холоднотянутая Латунь корабельная катаная |
(0,91…0,99)·105 1,0·105 |
(3,5…3,7)·104 – |
0,32…0,42 0,36 |
|
Алюминий катаный Проволока алюминиевая тянутая Дюралюминий катаный |
0,69·105 0,7·105 0,71·105 |
(2,6…2,7)·104 – 2,7·104 |
0,32…0,36 – – |
| Цинк катаный | 0,84·105 | 3,2·104 | 0,27 |
| Свинец | 0,17·105 | 0,7·104 | 0,42 |
| Лед | 0,1·105 | (0,28…0,3)·104 | – |
| Стекло | 0,56·105 | 0,22·104 | 0,25 |
| Гранит | 0,49·105 | – | – |
| Известняк | 0,42·105 | – | – |
| Мрамор | 0,56·105 | – | – |
| Песчаник | 0,18·105 | – | – |
|
Каменная кладка из гранита Каменная кладка из известняка Каменная кладка из кирпича |
(0,09…0,1)·105 0,06·105 (0,027…0,030)·105 |
– – – |
– – – |
|
Бетон при пределе прочности, МПа: 10 15 20 |
(0,146…0,196)·105 (0,164…0,214)·105 (0,182…0,232)·105 |
– – – |
0,16…0,18 0,16…0,18 0,16…0,18 |
|
Древесина вдоль волокон Древесина поперек волокон |
(0,1…0,12)·105 (0,005…0,01)·105 |
0,055·104 – |
– – |
| Каучук | 0,00008·105 | – | 0,47 |
| Текстолит | (0,06…0,1)·105 | – | – |
| Гетинакс | (0,1…0,17)·105 | – | – |
| Бакелит | (2…3)·103 | – | 0,36 |
| Висхомлит (ИМ-44) | (4,0…4,2)·103 | – | 0,37 |
| Целлулоид | (1,43…2,75)·103 | – | 0,33…0,38 |
www.sopromat.info
Модуль упругости – что это такое? Определение модуля упругости для материалов
Модуль упругости – это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.
История исследования упругости материалов
Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.
Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.
Физическая природа упругости
Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.
В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).
Предел упругости
Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.
Модуль Юнга в действии
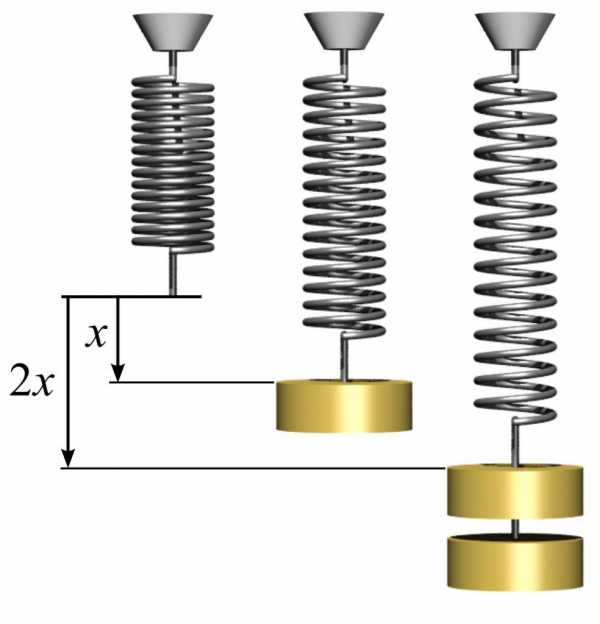
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п – число пи, равное 3,14, а r – радиус витка пружины.
Далее следует замерить длину пружины l0 без нагрузки. Если повесить какой-либо груз массой m1 на пружину, тогда она увеличит свою длину до некоторой величины l1. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m1gl0/(S(l1-l0)), где g – ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.
Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m2, получим следующую величину относительной деформации: d = m2g/(SE), где d – относительная деформация в упругой области.
Изотропия и анизотропия
Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.
Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.
Анизотропия – явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.
Модуль сдвига
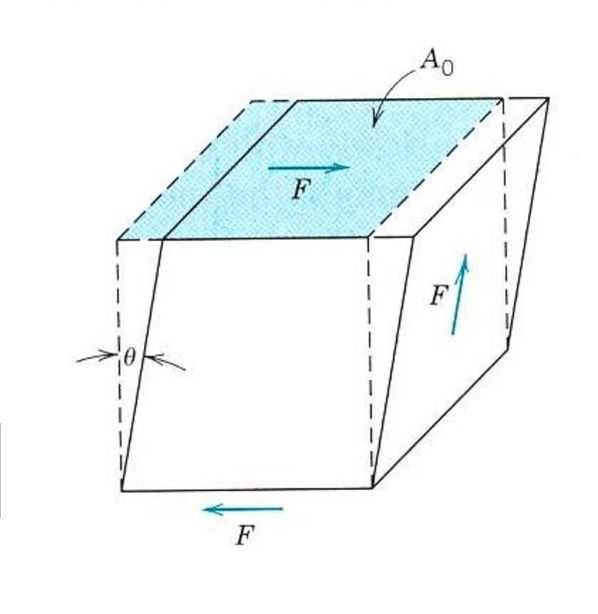
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.
Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.
Модуль упругости дерева
Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.
Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.
| Вид дерева | Модуль Юнга в ГПа |
| Лавровое дерево | 14 |
| Эвкалипт | 18 |
| Кедр | 8 |
| Ель | 11 |
| Сосна | 10 |
| Дуб | 12 |
Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.
Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.
Характеристики упругости металлов
Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.
| Металл | Модуль Юнга в ГПа |
| Бронза | 120 |
| Медь | 110 |
| Сталь | 210 |
| Титан | 107 |
| Никель | 204 |
Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.
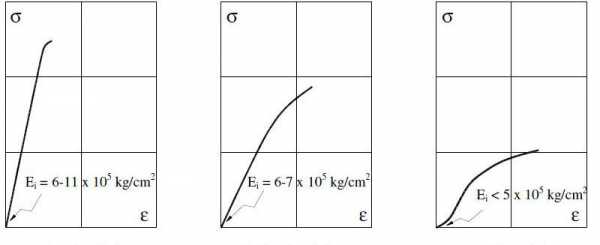
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.
fb.ru