Модуль зацепления нормальный – Нормальный модуль зацепления принимаем по следующей рекомендации

alexxlab | 23.02.2020 | 0 | Разное

Содержание

Нормальный модуль зацепления принимаем по следующей рекомендации

[1, с.36]:

;

принимаем по ГОСТ 9563-80 m_n = 2,5 (мм).

Примем предварительно угол наклона зубьев [1, с.37]  = 10 ⁰ и определим числа зубьев шестерни и колеса:

;

примем Z₁ = 25, тогда Z₂ = Z₁∙U_p = 25∙4 = 100;

примем Z₂ = 100.

Уточненное значение угла наклона зубьев:

,  = 12⁰34^/.

Основные размеры шестерни и колеса:

диаметры делительные:

проверка:

диаметры вершин зубьев:

ширина колеса:

ширина шестерни:

Определяем коэффициент ширины шестерни по диаметру:

Окружная скорость колес и степень точности передачи:

при такой скорости для косозубых колес следует принять 8-ю степень точности [1, с.32].

Коэффициент нагрузки.

При _bd = 1,08, твердости менее 350 и несимметричном расположении колес относительно опор с учетом изгиба ведомого вала от напряжения шатунной передачи К_Н_ = 1,044 [1, с.39]. При

v = 1,6 (м/с) и восьмой степени точности

К_Н_ = 1,0651 [1, с.39]. Для косозубых колес при v < 5 м/с имеем К_Н_v = 1,0 [1, с.40].

Таким образом, коэффициент нагрузки равен:

Проверка контактных напряжений [1, с.31]:

Силы, действующие в зацеплении [1, с.294]:

окружная:

радиальная:

осевая:

Проверяем зубья на выносливость по напряжениям изгиба [1, с. 46]:

Коэффициент нагрузки

Здесь

K_F_ = 1,112; K_FV = 1,1 [1, c.43].

Y_F – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев Z_v_.

для шестерни

для колеса

При этом Y_F₁ = 3,86; Y_F₂ = 3,6 [1, c. 42].

Допускаемое напряжение при проверке зубьев на выносливость по напряжениям изгиба [1, c. 43]

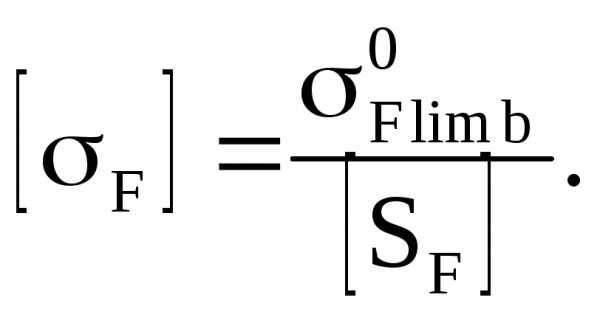
Для стали 45 нормализованной при твердости НВ меньше 350 [2, c. 295] предел выносливости при отнулевом цикле изгиба ;

для шестерни ;

для колеса

Коэффициент безопасности .для поковок и штамповок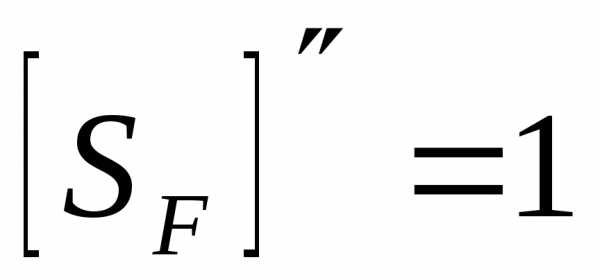[1,c.45]. Таким образом,

Допускаемые напряжения при расчете зубьев на выносливость:

для шестерни

для колеса

Для шестерни отношение

для колеса

Коэффициент Y_ учитывает повышение прочности косых зубьев по сравнению с прямыми:

Коэффициент К_F_ учитывает распределение нагрузки между зубьями.

где _ – коэффициент торцового перекрытия и n – степень точности зубчатых колес.

_= 1,5; n = 8 [2, c.47].

Проверяем прочность зуба колеса [2, c. 46]:

_F2 = F_tK_FY_FY_K_F_ /b₂m_n  [_F];

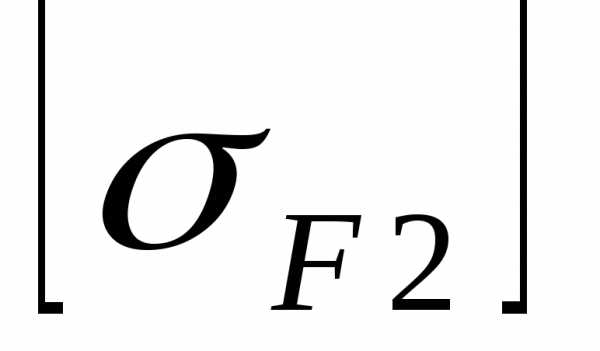= 206 (МПа) – условие прочности выполнено.

3. Расчёт клиноремённой передачи

Исходные данные для расчёта: передаваемая мощность Р_тр = 4,98 кВт; частота вращения ведущего (меньшего) шкива n_дв = 1445 об/мин; передаточное отношение U_рем= 2,5; скольжение ремня  = 0,015.

По номограмме принимаем сечение клинового ремня О [1, c.134].

Вращающий момент

Диаметр меньшего шкива [1, c.130]

Принимаем d₁ = 125 мм.

Диаметр большего шкива [1, c.120]

d₂ = U_ремd₁(1 – ) = 2,5∙125(1 – 0,015) = 307,8 мм;

Принимаем d₂ = 310 мм.

Уточняем передаточное отношение

При этом угловая скорость вала В будет

Расхождение с тем, что было получено по первоначальному расчёту,

что менее допускаемого –  3 %.

studfiles.net

Нормальный модуль зацепления — КиберПедия

Нормальный модуль зацепления принимаем по следующей рекомендации:

m_n = (0.01 ÷ 0.02) а_W = (0.01 ÷ 0.02) ^. 160 =1.6÷3.2 мм.

Принимаем по ГОСТ 9563-60* m

n = 2 мм (см. с. 36 [1]).

Примем предварительно угол наклона зубьев в = 10^о и определим число зубьев шестерни и колеса (см. формулы (3.12) и (3.13) [1]):

Принимаем z₁ = 31, тогда z₁ = z₁^. u = 31 ^. 4 = 124.

Уточненное значение угла наклона зубьев

Основные размеры шестерни и колеса

Диаметры делительные (см. формулу (3.17), с. 37 [1]):

;

Проверка:

Диаметры вершин зубьев:

d_a₁=d₁+ 2m_n= 64+ 2^.2 = 68 мм;

d_a₂ = d₂ + 2m_n = 256 + 2 ^. 2 = 260 мм;

ширина колеса: b₂= y_baa_W=0,4 ^. 160 = 64 мм;

ширина шестерни: b₁=b₂ + 5 = 69мм.

Определяем коэффициент ширины шестерни по диаметру:

Окружная скорость колес и степень точности передачи:

Для косозубых колес при v до 10 м/с назначаем 8-ю степень точности и принимаем К_H_х=1,0¸1,05.

Силы, действующие в зацеплении

Окружная сила

;

Радиальная сила

;

Осевая сила

Проверочный расчет зубьев на контактную выносливость

Коэффициент нагрузки

К_Н = К_Н_a^. К_Н_b^. К_Н_u.

При y_bd=1,0, твердости НВ 350 и симметричном расположении колес относительно опор принимаем К_H_b≈1,04.

При u= 4,88м/с и 8-й степени точности К_H_a≈1,09 (см. табл. 3.4 [1]).

Для косозубых колес при u£ 5м/с К_H_u=1,0 (см. табл. 3.6 [1]).

Таким образом, К

H = 1,04 ^. 1,09 ^. 1,0 = 1,526.

Проверка контактных напряжений по формуле (3.6) [1]:

Проверочный расчет на контактную статическую прочность

При пиковой нагрузке

Расчетные контактные напряжения по формуле 3.21 [1]

Допускаемое контактное напряжение при действии пиковой нагрузки для стальных колес с улучшением

где предел текучести для стали 45 и диаметра заготовки свыше 120 мм s_т=340 МПа (табл.3.3 [1])

Условие прочности выполняется.

Проверка зубьев на выносливость по напряжениям изгиба

По формуле (3.25) [1, с.41]

Коэффициент нагрузки [1, с.42].

По табл. 3.7 [1] при y_bd=1,1, твердости HВ £ 350 и симметричном расположении зубчатых колес относительно опор К_F_b =1,1; К_F

u = 1,3 (см. табл. 3.8 [1]). Таким образом, коэффициент k_f=1,1×1,3=1,43.

К_F_a – коэффициент, учитывающий неравномерность распределения нагрузки между зубьями. При среднем значении коэффициента торцового перекрытия e_a = 1,5 и 8-й степени точности

Y_F – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев z_u(см. гл. III, пояснения к формуле (3.25) [1]):

– у шестерни ;

– у колеса .

и Y_F₂=3,6 [1, с. 42].

Допускаемое напряжение определяем по формуле (3.24) [1]

По табл. 3.9 [1] для стали 45 улучшенной при НВ £ 350 предел выносливости при изгибе s⁰_Flimb=1,8 НВ.

Для шестерни s⁰_Flimb=1,8×230=415 МПа, для колеса s⁰_Flimb= 1,8×200 = =360 МПа.

[s_f]= [S_F]’

.[S_F]” – коэффициент безопасности (см. пояснения к формуле (3.24) [1]), где [S_F]¢=1,75 (по табл. 3.9 [1]) и [S_F]”=1 (для поковок и штамповок). Следовательно, [S_F] = 1,75.

Допускаемые напряжения:

– для шестерни МПа;

– колеса МПа.

Находим отношения :

– для шестерни МПа;

– колеса МПа.

Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.

Определяем коэффициент Y_b , учитывающий наклон зубьев:

Y_b = 1 – = 1 – = 0,88.

Проверяем прочность зуба по формуле (3.25) [1]:

;

Условие прочности выполнено.

Проверочный расчет на изгибную статическую прочность

При пиковой нагрузке

Расчетные изгибные напряжения

Допускаемые изгибные напряжения при действии пиковой нагрузки для стальных колес с улучшением:

Условие прочности выполнено.

ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ ВАЛОВ РЕДУКТОРА

Предварительный расчет проведем на кручение по пониженным допускаемым напряжениям.

Ведущий вал. Диаметр выходного конца при допускаемом напряжении [t_K]= 25 МПа (по формуле (8.16) [1])

мм.

Так как вал редуктора соединен муфтой с валом электродвигателя, то необходимо согласовать диаметры ротора d_ДВ и вала d_В1. У выбранного двигателя диаметр вала d_ДВ=38 мм. Выбираем МУВП по ГОСТ 21424-75 с расточками полумуфт под d_ДВ=38 мм и d_В1=32мм (округляем d_B₁ из формулы до ближайшего числа из ряда на с. 161 [1]). Примем под подшипниками d_п=40 мм.

Ведомый вал. Принимаем [t_K]= 25 МПа.

Диаметр выходного конца вала (см. формулу (8.16) [1])

Принимаем ближайшее большее значение из стандартного ряда d_B₁ = 42 мм (см. гл. VIII, пояснения к формуле (8.16) [1]). Диаметр вала под подшипниками принимаем d_n₂= 45 мм, под зубчатым колесом d_к2 = 50мм .

Диаметры остальных участков вала назначаем исходя из конструктивных соображений при компоновке редуктора.

cyberpedia.su

Модуль зацепления нормальный – Энциклопедия по машиностроению XXL

Модули зацепления нормальный торцовый ms —….. os — угол наклона по делительному цилиндру [c.357]

Модуль зацепления Нормальный (или торцовый) модуль Радиус окружности выступов Радиус окружности впадин [c.18]

Частота враш,ения шестерни косозубой цилиндрической передачи, имеющей 60 зубьев, 1450 об мин. Частота вращения колеса 630 об мин. Определить модуль зацепления (нормальный и торцовый), если межосевое расстояние передачи 400 м и угол наклона зубьев 8° 06 34″. Каково число зубьев колеса [c.384]

Модуль зацепления (нормальный) т в мм. [c.507]

Нормальный модуль зацепления [c.160]

Проверку на выносливость по напряжениям изгиба также можно выполнять по формуле (3.47), подставляя в нее нормальный модуль зацепления т и вводя в знаменатель указанный выше коэффициент /г . Кроме того, коэффициент формы зуба у надо определять не по действительному, а по так называемому фиктивному числу зубьев 2ф, связанному с действительным числом зубьев г формулой [c.361]

Параметры косозубого колеса определяются также в соответствии с величиной модуля зацепления, причем шаг зацепления, устанавливающий величину модуля, можно измерять по трем направлениям (рис. 30). Шаг, по которому устанавливается стандартная величина модуля, измеряется в нормальной плоскости к боковой поверхности зуба. Такие шаг и модуль называются нормальными и обозначаются через и / г . Шаг, измеряемый в торцовой плоскости, называется торцовым или окружным, обозначается он через ts. Соответствующий ему торцовый модуль обозначается через т . Наконец, измеряя шаг в направлении образующей цилиндра, получаем осевой шаг 1а, определяющий осевой модуль Ша- Бее указанные шаги равны соответствующим им модулям, умноженным на число п. [c.57]

У косозубого колеса (рис. 10.2) расстояние между зубьями можно измерить в торцовом, или окружном i — t),и нормальном (п — п) направлениях. В первом случае получим окружной шаг р/, во втором — нормальный шаг р. Различными в этих направлениях будут и модули зацепления [c.150]

Нормальный модуль зацепления [формула (9.14)]. Для косозубой передачи коэффициент /( = 5,8. [c.156]

Размеры передачи и элементов зацепления межцентровое расстояние А в см, рабочая ширина зубчатых колёс Ь в см, угол наклона зубьев по начальному цилиндру р, угол зацепления в нормальном сечении а , модуль в нормальном сечении т , коэфициент высоты головки зуба основной рейки [c.286]

Для косых и шевронных зубьев нормальный модуль зацепления т равен (рис. 65 и 66) [c.132]

Для профилирования зубьев зацепления М. Л. Новикова проф. В. Н. Кудрявцевым разработан исходный ксн-тур, представленный на рис. 81 (а — для выпуклых зубьев, б— для вогнутых зубьев), в котором за исходный параметр принят нормальный модуль зацепления т . Остальные геометрические параметры этого контура указаны на рис. 81. [c.167]

Потом вычисляется нормальный модуль зацепления по формуле [c.170]

Для шестерен с нормальным эвольвентным некорригированным зацеплением A Ds mz, высота головки зуба h=m и Dr=m z+2), где т. — модуль зацепления и г —число зубьев шестерни. Для таких шестерен формула (16.5) принимает вид [c.230]

Примечание. В чертежах косозубых конических колес указывается модуль в нормальном сечении и в характеристику зацепления дополнительно вводятся графы Направление наклона зуба ,. Эксцентриситет (е =. i sin и. Угол наклона зуба р . [c.156]

Проектировочный расчет. Аналогично расчету прямозубой передачи [см. формулу (4.28)1 нормальный модуль зацепления [c.121]

Модуль зацепления измеряется в миллиметрах. Нормальные значения величин модуля в СССР утверждены Общесоюзным Стандартом (ОСТ 1597). [c.198]

Модуль зацепления измеряется в миллиметрах. В СССР нормальные значения величин модуля утверждены Общесоюзным стандартом (ОСТ 1597). [c.209]

Задавшись модулем зацепления (он же будет и нормальным модулем исходного контура), следует вычислить радиусы окруж[c.231]

Нормальный модуль зацепления принимаем по следующей рекомендации [c.293]

Модуль зацепления в нормальном сечении 3 4 мм [c.286]

Модуль зацепления Нормальный(илиторцевой)модуль Радиус окружности выступов Радиус окружности впадин Радиус начальной окружности (начального цилиндра) [c.216]

Обозначения о — допустимая относительная norpeujHO Tb в передаточном отношении А — допустимая погрешность в логарифме передаточного отношения р —постоянная цепи деления (для многоэаходных фрез всюду множить на число заходов) А — постоянная цепи подач г — постоянная цепи диференциала р, — постоянная цепи обкатки О — диаметр делительной окружности m – модуль зацепления нормальный —ширина заготовки Р — угол наклона зуба f – угол начального конуса у — угол ножки зуба а — угол зацепления t — шаг винтовой нарезки Г — шаг винтовой линии зуба Л — подача на 1 оборот заготовки — изменение толщины одного из зубьев А — отклонение направления зуба в мм на ширине заготовки ht – погрешность в шаге нарезки в мм на длине 1000 мх ifi — изменение угла наклона линии зуба в минутах Да — изменение угла зацепления в минутах х – передаточное число цепи деления — передаточное число цепи подач — передаточное число цепи обкатки i—передаточное число цепи диференциала п – число заходов червячной фрезы А — произвольное [c.64]

Цилинд ш- ческие Угол наклона зуба Модуль зацепления (нормальный) д т град мм [c.438]

Принимаем ближайшее стандартное значение а=125мм и определяем нормальный модуль зацепления [c.155]

Особенности определения модуля зацепления косозубых цилиндрических колес. При изучении конструкции и расчета косозубых колес приходится рассматривать геометрию зацепления в торцевой и нормальной плоскостях (рис. 16.5, б). Угол, составленный этими плоскостями, равен 90°—р. Величина шага зубьев в плоскости торца связана с величиной шага в нормальном сечении зависимостью pt — pj os p. Аналогичная зависимость су-ЩбСТВуеТ И МбЖДу значениями модуля в торцевом ш/ и нормальном гпп сечениях rtit = m / os p. [c.307]

Модуль нсрнальийш Угол зацепления нормальный Угол зацеплена торцовый [c.561]

Модуль зацепления в нормальном сечении зуба колеса при твердости Н 45НЯСэ — ffг = (0,016-0,0315) г , и округляют до стандартного значения. Ширину зубчатых колес Ь выражают через коэффициент ширины зубчатого венца = bja ,. Для зубчатых колес из улучшенных сталей с Н [c.243]

Для установленных ГОСТом межосевых расстояний в табл. 60 приведены суммарные числа зубьев и углы наклона зубьев Р на делительном цилиндре при определенных интервалах передаточных чисел и модулей в нормальном сечении. Эти значения рекомендуются при коэффициенте ширины 0,4 при неКор-ригированном и корригированном зацеплении с коэффициентом сдвига Xi = -Х2 соответственно для теории и колеса, но могут быть использованы и при Фьа [c.92]

Маркировать на заднем торце модуль торцевой, число зубьев, угол зацепления нормальный, угол наклона зубьев, шаг винтовой поверх-ности зубьев, номер долбяка, марку стали, марку завода и год изготовления. [c.221]

Р — угол наклона зуба (для прямозубых колео 3 = 0) z — число зубьев проверяемого колеса m — модуль зацепления, мм (для косозубых колео следует подставлять нормальный модуль tnn) knp — коэффициент, учитывающий повышение прочности на изгиб косозубых колее по сравнению с прямозубыми для прямозубых колес knff — 1 для косозубых kaptt 1,2. .. 1,4 [а ] — допускаемое напряжение при изгибе, МПа. [c.159]

Конусы с вершинами в точках и 0 и образующими, нормальными к образующим делительных конусов, называются дополнительными. Точки пересечения делительных и дополнительных конусов определяют диаметры внешних делительных окружностей колес и 2- По этим окружностям определяют внешний окружной модуль зацепления, стандартизованный к1ак и модуль цилиндрических зубчатых колес по ГОСТ 9563—60 (СТ СЭВ 310—76). Для конических колес модуль не является постоянным по длине зуба и уменьшается по мере продвижения вдоль образующей к центру делительных конусов. Передаточное отношение ортогональной конической передачи, для которой 61 + 62 = 90°, можно выразить через углы делительных конусов [c.92]

mash-xxl.info

Нормальный модуль зацепления – Архитектура

Нормальный модуль зацепления принимаем по следующей рекомендации:

m_n = (0.01 ÷ 0.02) а_W = (0.01 ÷ 0.02) ^. 160 =1.6÷3.2 мм.

Принимаем по ГОСТ 9563-60* m_n = 2 мм (см. с. 36 [1]).

Принимаем z₁ = 31, тогда z₁ = z₁^. u = 31 ^. 4 = 124.

Уточненное значение угла наклона зубьев

Основные размеры шестерни и колеса

Диаметры делительные (см. формулу (3.17), с. 37 [1]):

;

Проверка:

Диаметры вершин зубьев:

d_a₁=d₁+ 2m_n= 64+ 2^.2 = 68 мм;

d_a₂ = d₂ + 2m_n = 256 + 2 ^. 2 = 260 мм;

ширина колеса: b₂ = y_baa_W=0,4 ^. 160 = 64 мм;

ширина шестерни: b₁=b₂ + 5 = 69мм.

Определяем коэффициент ширины шестерни по диаметру:

Окружная скорость колес и степень точности передачи:

Для косозубых колес при v до 10 м/с назначаем 8-ю степень точности и принимаем К_H_х=1,0¸1,05.

Силы, действующие в зацеплении

Окружная сила

;

Радиальная сила

;

Осевая сила

Проверочный расчет зубьев на контактную выносливость

Коэффициент нагрузки

К_Н = К_Н_a^. К_Н_b^. К_Н_u.

При y_bd=1,0, твердости НВ 350 и симметричном расположении колес относительно опор принимаем К_H_b≈1,04.

При u= 4,88м/с и 8-й степени точности К_H_a≈1,09 (см. табл. 3.4 [1]).

Для косозубых колес при u£ 5м/с К_H_u=1,0 (см. табл. 3.6 [1]).

Таким образом, К_H = 1,04 ^. 1,09 ^. 1,0 = 1,526.

Проверка контактных напряжений по формуле (3.6) [1]:

Проверочный расчет на контактную статическую прочность

При пиковой нагрузке

Расчетные контактные напряжения по формуле 3.21 [1]

Допускаемое контактное напряжение при действии пиковой нагрузки для стальных колес с улучшением

где предел текучести для стали 45 и диаметра заготовки свыше 120 мм s_т=340 МПа (табл.3.3 [1])

Условие прочности выполняется.

Проверка зубьев на выносливость по напряжениям изгиба

По формуле (3.25) [1, с.41]

Коэффициент нагрузки [1, с.42].

По табл. 3.7 [1] при y_bd=1,1, твердости HВ £ 350 и симметричном расположении зубчатых колес относительно опор К_F_b =1,1; К_F_u = 1,3 (см. табл. 3.8 [1]). Таким образом, коэффициент k_f=1,1×1,3=1,43.

– у шестерни ;

– у колеса .

и Y_F₂=3,6 [1, с. 42].

Допускаемое напряжение определяем по формуле (3.24) [1]

По табл. 3.9 [1] для стали 45 улучшенной при НВ £ 350 предел выносливости при изгибе s⁰_Flimb=1,8 НВ.

Для шестерни s⁰_Flimb=1,8×230=415 МПа, для колеса s⁰_Flimb= 1,8×200 = =360 МПа.

[s_f]= [S_F]’^.[S_F]” – коэффициент безопасности (см. пояснения к формуле (3.24) [1]), где [S_F]¢=1,75 (по табл. 3.9 [1]) и [S_F]”=1 (для поковок и штамповок). Следовательно, [S_F] = 1,75.

Допускаемые напряжения:

– для шестерни МПа;

– колеса МПа.

Находим отношения :

– для шестерни МПа;

– колеса МПа.

Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.

Определяем коэффициент Y_b , учитывающий наклон зубьев:

Y_b = 1 – = 1 – = 0,88.

Проверяем прочность зуба по формуле (3.25) [1]:

;

Условие прочности выполнено.

Проверочный расчет на изгибную статическую прочность

При пиковой нагрузке

Расчетные изгибные напряжения

Допускаемые изгибные напряжения при действии пиковой нагрузки для стальных колес с улучшением:

Условие прочности выполнено.

ПРЕДВАРИТЕЛЬНЫЙ РАСЧЕТ ВАЛОВ РЕДУКТОРА

Предварительный расчет проведем на кручение по пониженным допускаемым напряжениям.

Ведущий вал. Диаметр выходного конца при допускаемом напряжении [t_K]= 25 МПа (по формуле (8.16) [1])

мм.

Ведомый вал. Принимаем [t_K]= 25 МПа.

Диаметр выходного конца вала (см. формулу (8.16) [1])

Диаметры остальных участков вала назначаем исходя из конструктивных соображений при компоновке редуктора.

student2.ru

Нормальный модуль зацепления – Механика

=2,5…3,0 мм;

Принимаем: = 3,0; = 3,0; = 2,75; = 2,5; = 2,5.

Угол наклона зубьев

Принимаем: ; ; ; ;

Суммарное число зубьев

Принимаем: z = 46; z =46; z =51; z =66 ;z =58.

Начальные параметры передачи

ПГУ 1.03-07.190201.003.001 ПЗ

Принимаем число зубьев шестерни первой передачи таким, чтобы не было подрезания ножки зуба. Для косозубой передачи .

Принимаем =14;

=2.886

Передаточное число сведущего на промежуточный

Для остальных передач

Суммарный коэффициент смещения первой передачи

;

где коэффициенты смещения шестерни и колеса.

Суммарный коэффициент смещения второй передачи

Корректировка параметров передач

Диаметры делительных окружностей:

Диаметры впадин зубьев:

Диаметры вершин зубьев

где =0,25

Результаты расчётов приведены в таблице 9.

ПГУ 1.03-07.190201.003.001 ПЗ

Таблица 9

Переда-ча	,мм	,мм	,мм	,мм	,мм	,мм
I	37,4147	43,4147	29,9147	136,053	142,053	128,5535
II	52,5661	58,5661	45,0661	119,0468	125,0486	111,5468
III	76,522	81,7289	69,3539	99,478	106,122	93,7472
V	95,1431	100,1431	88,8931	81,5526	86,551	75,3012

Расчет промежуточной шестерни заднего хода

Выбираем диаметр промежуточной шестерни из условия отсутствия подрезания зубьев в зацеплении

ПГУ 1.03-07.190201.003.001 ПЗ

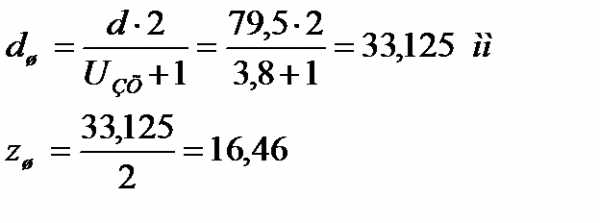
Принимаем по условию ,

Тогда

Получаем

Из условия отсутствия подрезания зубьев в зацеплении назначаем для шестерни положительное смещение , а для колеса отрицательное смещение

Диаметр окружности впадин

;

Определим координаты центра оси паразитной шестерни.

Расстояние между осью паразитной шестерни и осью первичного вала

;

Диаметр окружности выступов

;

Расстояние между осью паразитной шестерни и осью вторичного вала

Расстояние между осью первичного вала и осью вторичного вала

ПГУ 1.03-07.190201.003.001 ПЗ

Обозначим угол между сторонами a и b через α. Этот угол найдем с помощью теоремы косинусов:

Координаты относительно центра оси промежуточного вала обозначим через x и y:

;

3 Проверочный расчёт на прочность зубчатых передач

3.1 Расчётные предельные относительные силы тяги

По двигателю

;

Средние значения удельных окружных сил на передачах определяются сопротивлением движению. В общем виде

где – удельное сопротивление дороги;

– среднее удельное сопротивление воздуха;

– среднее удельное сопротивление разгону.

Сила сопротивления воздуха

где – средние значения скорости на каждой передаче;

– среднее значение скорости движения автомобиля;

ПГУ 1.03-07.190201.003.001 ПЗ

где x_i– относительная доля пробега на i передаче.

По отношению g_pi/g_mi из графика находим коэффициенты пробега

, .

Полученные значения представлены в таблице 10.

Таблица 10

Передача					g_pi/g_mi			,км/ч
I	0,34056	0,00084	0,0641	0,0842	4,045	0,048	0,0065	7,6257	0,01
II	0,202	0,000269	0,036	0,05796	3,484	0,065	0,01	13,6598	0,03
III	0,1234	0,000843	0,01915	0,04684	2,6354	0,15	0,035	24,1675	0,06
IV	0,0785	0,001612	0,00863	0,04402	1,7847	0,22	0,06	33,4231	0,15
V	0,056	0,001971	0,00343	0,0424	1,3233	0,28	0,08	36,9921	0,75

student2.ru

Модуль зубчатого зацепления – Энциклопедия по машиностроению XXL

Что называется модулем зубчатою зацепления [c.239]

Коэффициент неравномерности движения 6 Перемещение толкателя кулачка h, мм Номер закона движения толкателя Модуль зубчатого зацепления т, мм Число зубьев колеса Частота вращения вала электродвигателя об/мин [c.259]

В планетарном механизме (рис. 8.10) с плавающим води-лом Н количество зубьев у колес 2i = 20, 2а = 30, 2з = 80, 22 = 25 и 24 = 75 колесо 3 неподвижно угол зацепления у всех колес а = 20″ модуль зубчатого зацепления /п = 5 на колесо 1 действует движущий момент Mi = 20 Н м. Определить реакции в кинематических парах и момент сопротивления на колесо 4. [c.141]

Отношение величины шага / к числу я называется модулем зубчатого зацепления и обозначается буквой т [c.30]

Модуль зубчатого зацепления 30 [c.383]

Рассчитанный модуль зубчатого зацепления необходимо согласовать с ГОСТ 9563—60 на ассортимент зуборезного инструмента, изготовляемого со стандартными модулями, краткая выдержка из которого приводится в таблице. [c.208]

Нормальный модуль имеет стандартное значение, определяемое режущим инструментом. При этом торцовый модуль или модуль зубчатого зацепления может иметь самые различные значения в зависимости от угла 5°. [c.242]

Модуль. Зубчатое зацепление характеризуется шагом этого [c.265]

И. Что называется щагом и модулем зубчатого зацепления [c.131]

Модуль зубчатого зацепления представляет собой количество единиц длины делительного диаметра, приходяш,ееся на один зуб. [c.280]

Модуль зубчатого зацепления в зависимости от давления рк и диаметра D может быть определен по формуле [c.140]

Величину т (м) – часть диаметра делительной окружности зубчатого колеса, приходящуюся на один зуб, называют. модулем зубчатого зацепления. Его значения стандартизованы. [c.45]

Микро-экскаваторы 223 Мини-экскаваторы 222 Модель машины 11 Модуль зубчатого зацепления 44 Мозаично-шлифовальные машины 332 Мойки вибрационные 305 Молотки монтажные сборочные 347 [c.367]

Из приведенных соотношений видно, что шаг зацепления выражается через диаметр делительной окружности несоизмеримым числом, так как в формулы входит трансцендентное число п. По этой причине для удобства определения основных размеров зубчатых колес и возможности их измерения вводится основной расчетный параметр, который назван модулем зубчатого зацепления. [c.250]

Следовательно, под модулем зубчатого зацепления понимается шаг зацепления, деленный на число я, а делительную окружность можно охарактеризовать как окружность стандартного модуля. [c.250]

При проектировании зубчатых передач важное значение имеет длина зуба Ь (см. рис. 9). В зависимости от назначения зубчатой передачи длину зуба принимают в пределах от десятых долей m до 50 т, где т—модуль зубчатого зацепления. Для зубчатых колес редукторов величина Ь может быть еще большей. На судовых редукторах Ь достигает 3D, где D —диаметр делительной (начальной) окружности меньшего зубчатого колеса. [c.251]

Затем определяют модуль зубчатого зацепления из соотношения [c.307]

Определяем модуль зубчатого зацепления по формуле (49) [c.330]

Зубчатые зацепления. Исходный контур зубчатых колес с большим модулем Зубчатые зацепления. Исходный контур зубчатых мелкомодульных колес Зубчатые колеса. Допуски на изготовление и классификация зубьев цилиндрических зубчатых колес [c.132]

Модуль зубчатого зацепления можно определять по формуле [c.26]

В зависимости от величины передаваемой мощности по табл. 26 выбирают марку редуктора и модули зубчатых зацеплений. [c.32]

Расчет зубчатой передачи Модуль зубчатого зацепления [c.170]

Отсюда видно, что диаметр О и шаг t выражаются несоизмеримыми числами, так как в правую часть входит трансцендентное число Для облегчения расчетов, измерения и изготовления зубчатых колес отношение стандартизовано и выражается целыми числами или числами с простой десятичной дробью. Это отношение шага зубчатого зацепления t к числу – называется модулем зубчатого зацепления и обозначается буквой т [c.132]

Для удобства определения основных размеров зубчатых колес введен основной расчетный параметр, который называют модулем зубчатого зацепления и обозначают т [c.412]

Передачи зубчатые цилиндрические. Допуски Передачи зубчатые конические. Допуски Передачи червячные. Допуски Зубчатые, зацепления. Исходный контур зубчатых колес Зубчатые колеса. Модули Зубчатые зацепления. Основные термины, обозначения и определения Соединения зубчатые (шлицевые) эвольвентные Соединения зубчатые (шлицевые) прямобочные. Размеры, допуски и посадки [c.267]

Модулем зубчатого зацепления называют величину, численно равную отношению диаметра делительной окружности к числу зубьев колеса нли в я раз меньшую шага зубьев колеса [c.175]

Модули зубчатых зацеплений (ГОСТ 9863—60) [c.176]

Модуль зубчатого зацепления 175. [c.236]

Ills — торцовый модуль зубчатого зацепления осевой модуль червячного зацепления [c.6]

Индикаторы (рис. 6.3) бывают рычажные (а), рычажно-вин-товые (б), рычажно-пружинные (в), рычажно-зубчатые ( ), зубчатые (()). Их передаточные отношения i для индикаторов следующие рычажный i=L/A = R/a, рычажно-винтоной i = = L/s = 2K(R/a) l/s), рычажно-пружинный i = L/A = R/a, рычажно-зубчатый i = L/A = Rl/ar, зубчатый i = IR jm = Iz , где m- модуль зубчатого зацепления, 2,, Zj- числа чубьев колес остальные параметры показаны на рис. 6.3. [c.71]

Зубчатые колеса внешнего зацепления имеют число зубьев 2х = 8 и 22=16. Модуль зубчатого зацепления /и=10мм. Определить аналитически угол зацепления, при котором зубчатые колеса могут работать без подрезания. Разобрать и сравнить между собой два случая 1) ft = ha/m =1 и 2) ha = halm—0,8, где /ifl —высота головки зуба. [c.102]

В процессе исследования модели системы было проанализировано также влияние на динамическую нагрузку и на длительность выстоя основных конструктивных параметров (длины стойки AD, жесткостей Ср, q, с , момента инерции Jg, зазоров Д , Aj, величины тормозного момента Мтор)- Такая оценка влияния отдельных параметров на основные характеристики механизма дала возможность уточнить конструкцию экспериментального стенда для натурных исследований устройства углового позиционирования. Основные параметры и результаты исследования экспериментальной установки с параметрами Zi = = Zg = 18, модулем зубчатых зацеплений m = 3, длинами ЛВ = 34 мм, ВС = D = 108 мм приведены в табл. 1. [c.52]

Лшах = 0,01 0,03 т, где т — модуль зубчатого зацепления смонтированных колес. [c.425]

Распространена норма [/] = (2 ч-З) 10 /, где I — расстояние между опорамрг. Для зубчатых передач часто принимают, что прогиб под серединой колеса не должен превышать 0,01—0,03 от модуля зубчатого зацепления. Напомним, что при больших прогибах возрастает концентрация нагрузки по длине зубьев и, как следствие, снижается нагрузочная способность передачи. [c.371]

mash-xxl.info

Модуль зацепления – Энциклопедия по машиностроению XXL

Отсюда видно, что шаг зацепления всегда выражается через радиус НЛП через диаметр окружности несоизмеримым числом, так как в правую часть входит трансцендентное число л. Это затрудняет подбор размеров зубчатых колес % при проектировании колес и практическое их измерение. Поэтому для определения основных размеров зубчатых колес в качестве основной единицы принят некоторый параметр, называемый модулем зацепления. Модуль зацепления измеряется в миллиметрах и обозначается буквой т. Величина модуля равна [c.429]
Расстояние a , между центрами Oj и Oa колес (рис. 22.5) может также быть выражено через число зубьев и модуль зацепления. [c.431]

Все размеры и параметры привести в соответствие с такими же, приведенными в соответствующих стандартах (например, длины, диаметры, параметры и размеры резьб, модули зацеплений, размеры элементов зубчатых соединений и т. п.). [c.256]

Модули зацепления колес механизма т, мм [c.273]

Острые кромки на торцах венца притупляют фасками / х0,5 щ, где т — модуль зацепления, с округлением до стандартного значения (см. табл. 4.1). [c.72]

Расстояние от поверхности наружного цилиндра червяка (рис. 17.30) или колеса (рис. 17.31) до дна корпуса зависит от соотношения размеров /г,, в редукторе и в сопряженных узлах (электродвигатель, приводной вал и др.). Чтобы не происходило перемешивания осевшей на дно грязи с маслом, должно быть Ь бт, где т — модуль зацепления. [c.249]

Допустимые уровни погружения колес цилиндрического редуктора в масляную ванну (рис. 11.1) Л (2т…0,25 /2т). Здесь т —модуль зацепления. Наибольшая допустимая глубина погружения зависит от окружной скорости колеса. Чем медленнее вращение колеса, тем на большую глубину оно может быть погружено. [c.173]

Модуль зацепления из условия прочности зубьев колеса на изгиб [c.156]

Нормальный модуль зацепления [c.160]

Определить модуль зацепления и основные размеры косозубых цилиндрических колес одноступенчатого редуктора (см. рис. 9.16) yv, = 8,62 квт = 76,4 рад сек i = 6 р = lO [c.162]

Определить модуль зацепления и основные размеры прямозубых колес одноступенчатого редуктора (рис. 9.19) по следующим данным [c.162]

Определить модуль зацепления и основные размеры шевронных колес одноступенчатого редуктора по следующим данным Л, = 200 л. с. til — 3000 об/мин-, i = 7. Передача нереверсивная, недостающими данными задаться самостоятельно. Срок службы передачи неограничен. [c.162]

Определить модуль зацепления и основные размеры [c.172]

Определить модуль зацепления и основные размеры конических зубчатых колес редуктора (см. рис. 9.31) с передаточным числом i — 2. Передаваемая ведущим валом мощность /V, = 20 кет при угловой скорости этого вала п- = 940 об/мин. Передача нереверсивная. Срок службы передачи неограничен. [c.175]

А. Определение требуемого модуля зацепления [c.178]

На рис. 12.22 дан вид сверху промежуточного вала комбинированного червячно-зубчатого редуктора. Червячное колесо / получает мощность Л/ = 2,8 кет при со = 7,2 рад сек 40% этой мощности передается шестерней 2 ведомому валу редуктора и 60/i) шестерней 3 второму ведомому валу. Число зубьев колеса = 41 модуль зацепления гп = 6 л л число заходов червяка 2 червяк правый угол зацепления а = 20° угол подъема винтовой линии X = 12°13 44″ коэффициент трения в червячном зацеплении / = 0,05. Требуется а) определить усилия, действующие в червячном и зубчатом зацеплениях б) принимая, что червяк располо- [c.209]

Определить реакции в кинематических парах А и В одноступенчатой зубчатой передачи, если к колесу 2 приложен момент М = 5 нм, а к колесу / — уравновешиваюш,ий момент Му. Модуль зацепления т = 10 мм, числа зубьев колес = 20 и = 80, угол зацепления = 2(f. [c.116]

Определить реакции в кинематических парах Л, В и С и уравновешивающий момент Му, приложенный к колесу 1 двухсту-пенчг1Той передачи с зубчатыми колесами, если к колесу 3 приложен момелт Мз = 3 нм. Модуль зацепления т = 20 мм, числа зубьея колес 2 = 20, 2а = 50 и = 40, угол зацепления = 15°. [c.117]

Определить реакцию в кинематической паре В и уравновешивающий момент Му, приложенный к водилу Н планетарного одгюступенчатого редуктора, если к колесу 1 приложен момент Ml == 2 нм. Модуль зацепления т — 2.0 мм, числа зубьев колес Zj == = 20, = 20 и 2з = 60, угол зацепления Kq = 20°. [c.117]

Для трехзвенной зубчатой передачи с внешним зацеплением зубьев, у которой профили зубьев очерчены эвольвентами окружностей, определить степень перекрытия е, если число зубьев колес z- == 22, 2.2 = 30, модуль зацепления m = 10 мм, угол зацеп-ЛС1Н1Я при сборке а б = 20 и высота головок зубьев = т. [c.210]

Предельно допусгимые уровни погружения колес цилиг -дрического редуктора в масляную ванну приведены на рис. 8.1. При этом 2ш 0,25( 2, где ш – модуль зацепления. [c.135]

Червячные колеса вращаются с небольшой скоростью н, как правило, не требуют балансировки, поэтому нерабочие поверхности обода, диска, ступицы колеса оставляют необработанными и делают конустлми с большими радиусами закруглений. Острые кромки на торцах вецца притупляют фасками / 0,5щ, где /71 — модуль зацепления с округлением до стандартного значения (см. с. 42). Размеры других основных конструктивных элементов принимают но соотношениям 5 2,5т 5(1= (1,2…1,3)5 С=(1,2…1,3)5о /г [c.52]

Частота вращения червячных колес, как правило, невелика, и их балансировку не проводят. Поэтому нерабочие поверхности обода, диска, ступицы колеса оставляют необработанными и делают конусными с больишми радиусами закруглений. Острые кромки на торцах венца притупляют фасками / я 0,5от с округлением до стандартного значения (см. стр. 63), где т — модуль зацепления. Размеры других основных конструктивных элементов [c.73]

Скорость скольжения пропорциональна расстоянию е точки контакта от полюса. В полюсе она равна нулю, а при переходе через полюс меняется знак. Переходя от линии зацепления к поверхности зубьев (рис. 8.6, б), от.метим, что максимальное скольжение наблюдается на ножках и головках зубьев, на начальной окружности оно равно нулю и изменяет направление. Скольжение сопровождается 1рением. Трение является причиной потерь в зацеплении и износа зубьев. У ведущи.ч зубьев силы трения направлены от начальной окружности, а у ведомых — наоборот. При постоянных диаметрах колес расстояние точек начала и конца зацепления от полюса, а следовательно, и скорост , скольжения увеличива отся с увеличением вь[соты зуба и модуля зацепления. У мелкомодульных колес с большим числом зубьев скольжение меньше, а к. и. д. выше, чем у крупномодульных с малым числом зубьев [см. формулу (8.52)1. [c.101]

Определить диаметр вала d под серединой колеса и диаметр выходного конца вала d . Принять, что выходной конец вала работает только на кручение и (т] = 30 М.н м . Диаметр d определить из расчета на изгиб с кручением, приняв [сг] = 50 Мн/м и применив гипотезу наибольших касательных напряжений. Число зубьев колеса = 70 модуль зацепления = 9 мм число заходов червяка 2., = 3, диаметр делительного цилиндра червяка = 72мм к. п. д. червячного зацепления ц = 0,82. [c.208]

Выходной вал червячного редуктора смонтирован на конических роликоподшипниках (рис. 13.9). Определить требуемые коэффициенты работоспособности и выбрать подшипники по каталогу по следующим данным N = 3,3 квт м = 3,7 рад1сек модуль зацепления = 6 мм число зубьев колеса 2, == 41 /г = 15 ООО ч К/ = 1,3 расстояние между серединами опор L = 140 мм осевое усилие колеса = 1960 н. [c.224]

Венец червячного колеса скреплен с колесным центром тремя чистыми болтами с резьбой М14, поставленными в отверстия из-под развертки (рис. 16.1). Центры болтов расположены на окружности диаметра = 430 мм, диаметр отверстия = 15 мм. Определить напряжения среза в болтах. Зубья червячного колеса рассчитаны на контактную прочность при допускаемом напряжении [а] = 220 УИн/ж число зубьев колеса = 52 модуль зацепления rtis = 10 мм червяк двухзаходный с отношением диаметра делительного цилиндра к модулю q = 8. Коэффициент нагрузки принят равным единице. [c.259]

Винт домкрата путеукладочной машины приводится в движение через червячный редуктор (рис. 16.4). Выяснить исходя из приведенных ниже данных, что ограничивает предельную нагрузку рассматри ваемой конструкции прочность винта, его устойчивость, контактная прочность зубьев червячного колеса или их прочность на изгиб. Винт изготовлен из стали Ст.4, резьба винта трапецеидальная однозаходная по ГОСТу 9484—60, наружным диаметром 44 мм и шагом 8 мм. Свободная длина винта 1,8 м, коэффициент запаса устойчивости [п ] — 4 (при расчете на устойчивость рассматривать винт как стойку, имеющую один конец, защемленный жестко, а второй свободный). Червячное колесо изготовлено из чугуна СЧ 18-36 число зубьев 2 = 38 модуль зацепления = = 5 мм. Червяк однозаходный диаметр делительного цилиндра = 50 мм угловая скорость вала червяка = 48 рад1сек. Недостающие для расчета данные выбрать самостоятельно. [c.262]

Зубчатая передача лебедки, общий вид которой показан на рис. 16.6, имеет числа зубьев шестерни = 16, колеса 2 = 80 модуль зацепления m = 8 ширину колес В = 100 мм. Шестерня изготовлена из стали Ст.6, а колесо — из стального литья 25Л. Червячная передача характеризуется следующими параметрами число заходов червяка = 2 передаточное число i,, = 18 диаметр делительного цилиндра червяка = 80 мм модудь зацепления [c.264]

mash-xxl.info

TOP HEADLINES