Модули зубчатых колес – Стандартные модули зубчатых колес
alexxlab | 16.02.2020 | 0 | Разное
Стандартные модули зубчатых колес
ГОСТ 9563 – 60
Зубчатая передача – это кинематическая схема, которая позволяет передавать усилия от ведущего элемента механизма к ведомому. Наиболее распространённое соединение, применяемое в технике, где происходит подобная передача, является эвольвентное зубчатое зацепление, где профили зубьев в сечении составлены из двух эвольвентных кривых симметрично расположенных по отношению друг к другу.

Зубчатые передачи бывают: цилиндрические, конические, червячные, реечные. Основные параметры в передачах с эвольвентным зацеплением являются: количество зубьев, диаметр зубчатого колеса и модуль. При расчёте схемы передачи модуль берётся за основу, по которому рассчитываются параметры, зубчатых колёс, реек и червяков.
| Модули для цилиндрических и конических зубчатых колёс | |||
| 1-й ряд | 2-й ряд | 1-й ряд | 2-й ряд |
|---|---|---|---|
| 0.05 | 0.055 | 2.5 | 2.75 |
| 0.06 | 0.07 | 3 | 3.5 |
| 0.08 | 0.09 | 4 | 4.5 |
| 0.1 | 0.11 | 5 | 5.5 |
| 0.12 | 0.14 | 6 | 7 |
| 0.15 | 0.18 | 8 | 9 |
| 0.2 | 0.22 | 10 | 11 |
| 0.25 | 0.28 | 12 | 14 |
| 0.3 | 0.35 | 16 | 18 |
| 0.4 | 0.45 | 20 | 22 |
| 0.5 | 0.55 | 25 | 28 |
| 0.6 | 0.7 | 32 | 36 |
| 0.8 | 0.9 | 40 | 45 |
| 1 | 1.125 | 50 | 55 |
| 1.25 | 1.375 | 60 | 70 |
| 1.5 | 1.75 | 80 | 90 |
| 2 | 2.25 | 100 | |
| Modules of gears | Модули, данной таблицы, выбираемые из ячеек первого ряда, следует использовать в приоритетном порядке. | ||
Формулы расчёта элементов зубчатого колеса

De– диаметр окружности выступовd– диаметр начальной окружностиD1– диаметр окружности впадинh– высота зубаh′– высота головки зубаh″– высота ножки зубаt –шаг зацепленияZ– число зубьев
gk-drawing.ru
модуль зубчатого колеса – это… Что такое модуль зубчатого колеса?
- модуль зубчатого колеса
- мо́дуль зубча́того колеса́
отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально модулю.
Энциклопедический словарь. 2009.
- модули упругости
- модус
Смотреть что такое “модуль зубчатого колеса” в других словарях:
МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
Модуль зубчатого колеса — геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π. Для … Большая советская энциклопедия
нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
Что такое модуль зубчатого колеса?
Зубча́тое колесо́, шестерня́ — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. В машиностроении принято малое зубчатое колесо с меньшим числом зубьев называть шестернёй, а большое — колесом. Однако часто все зубчатые колёса называют шестерня́ми. Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов валов на входе и выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то вращающий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.
Толщина средней части зуба. Подробнее в википедии.
Диаметр делительной окружности разделит на число зубьев. Делительная окр. это диаметр шестерни по средней части зуба
в таком возросте такие интересы, зачем тебе? однофамилица??
Модуль – величина связывающая делительный диаметр и число зубьев. Модуль- толщина зуба по делительному диаметру ( для колес без смещения)
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач (смотри _http://stankiexpert.ru/tehnologii/modul-zubev-zubchatogo-kolesa.html)
touch.otvet.mail.ru
Зубчатые передачи | Автомобильный справочник

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Содержание
Типы зубчатых передач

Эвольвентное зацепление
 Эвольвентное зацепление — это зубчатые передачи, которые нечувствительны к изменению межосевого расстояния. Ее изготавливается методом обкатки.
Эвольвентное зацепление — это зубчатые передачи, которые нечувствительны к изменению межосевого расстояния. Ее изготавливается методом обкатки.
Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
 |  |
Форма зубьев
 Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30\ 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
 |  |
Коррегирование зубчатого зацепления
 Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи. Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес. Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Степени точности зубчатых передач (DIN 3961…..3964)

Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модули зубчатых передач стартеров

Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
Р = z/d = z/(z • m/25,4) =25,4/m
Для перевода стандарта США в европейский стандарт служит зависимость:
m = 25,4 мм / P
Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
CP = (25,4 мм / P) π.
Табл. Стандарты зубчатых передач
 |  |
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
Обозначение (пример): Р 5 /7
Р = 7 для расчета головки зуба,
Р = 5 для расчета других параметров.
Система обозначений и преобразований
Диаметр окружности выступов: OD = da.
Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
Диаметр окружности впадин: RD = df
Начальный диаметр:
LD =(N+2x) / P (в дюймах)
или
LD= (N+2x)·m (в мм).
LD ≈ dw,
где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
 |  |
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1. В случае зубчатого зацепления с z1< 20 следует принимать Sw ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления. Поскольку контактные давления равны по величине для обоих колес, значение kperm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n2, пользуясь помещаемой ниже таблицей.
Формулы для расчета наибольшего допустимого давления

Содержащиеся в таблице значения коэффициента &Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых колес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент kperm следует увеличить примерно в 1,8 раза. Для зубчатого зацепления лишь с одним поверхностно упрочненным колесом, коэффициент kperm для незакаленного колеса необходимо увеличить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы Lh = 5000 ч. При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч

Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.

- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба

Коэффициент профиля зуба YFa

Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
В следующей статье я расскажу об электрических свойствах материалов.
Рекомендую еще почитать:
press.ocenin.ru
Выбор модуля зубчатой передачи. — Студопедия.Нет
В формулу для межосевого расстояния aw величина модуля m непосредственно не входит. Таким образом, величина aw, определяемая из условия контактной прочности, не зависит от m. Существует два основных способа определения модуля.
I способ
Экспериментально установлено, что рациональные значения модуля лежат в пределах
m = (0,01…0,02)aw, HB1,2 <= 350,
m = (0,0125…0,025)aw, HB1 > 350, HB2 <= 350,
m = (0,016…0,0315)aw, HB1,2 > 350.
II способ
Задаются числом зубьев на шестерни z1. Минимально число z1, при котором отсутствует подрезание зубьев: z1 > 17. Для снижения шума в зацеплении обычно задают z1 = 20 … 25 зубьев, соответственно z2 = z1*u.
Далее из зависимости d1 + d2 = m* z1 + m* z2 = 2aw получимm= 2aw /(z1+z2)
Полученное значение m округляем до ближайшего стандартного значения.
III способ
Вычисляем модуль m по формуле и округляем до большего стандартного значения.
Расчет зубьев и прямозубых цилиндрических колес на изгиб. Вывод формул для проверочного проектного расчета.
Наибольшие напряжения изгиба возникают у основания зуба в зоне перехода эвольвентной поверхности в галтель. Здесь же наблюдается концентрация напряжений. Допущения:
1. в зацеплении находится одна пара зубьев; 2. сила приложена к вершине зуба; 3. силами трения на поверхности зуба пренебрегаем; 4. радиальной силой Fr в расчете пренебрегаем 5. зуб рассматриваем как консольно закрепленную балку, для которой справедлива гипотеза плоских сечений.
Напряжения изгиба в опасном сечении, расположенном вблизи хорды основной окружности db
осевой момент сопротивлен
b – ширина зубчатого венца, s – толщина основания зуба в опасном сечении, l – расстояние от опасного сечения до места приложения нагрузки
Расчет зубьев на изгиб проводят по условию
KT – теоретический коэффициент концентрации нагрузки KF – коэффициент расчетной нагрузки
действительные напряжения изгиба в опасном сечении
безразмерные коэффициенты:
где YF – коэффициент формы зуба
Проектный расчет
выразим окружную силу Ft через мощность P
коэффициент ширины зуба
Условие равной прочности зубьев колес и шестерни по напряжениям изгиба.
Условие равной прочности по напряжению изгиба
m≥267
Известно, что в условиях равной прочности геометрические размеры должны быть одинаковыми,
m1=m2; P1=P2; KF1=KF2; z1n1»z2n2; YF 1/[σF]1= YF 2/[σF]2 – условие, обеспечивающее равную прочность
Тот из зубьев у которого отношение YF/[sF] больше и есть менее прочный по напряжению изгиба. его и следует взять за основу при расчете m
YF – коэффициент формы зуба; z- количество зубьев; m- модуль; KF – коэффициент расчетной нагрузки;
Косозубые цилиндрические колеса. Геометрические параметры. Силы действующие в косозубой передаче.
У косозубых колес зубья расположены не по образующей делительного цилиндра, а составляют с ней угол β
Профиль косого зуба в нормальном сечении n-n совпадает с профилем прямого зуба. Модуль в этом сечении должен быть так же стандартным. В торцевом сечении t-t или окружном направлении параметры косового зуба изменяются в зависимости от угла β:
· Окружной шаг pt=pn/cos β, Окружной модуль mt=mn/cos β, Диаметр делительной окружности d=mtz=mnz/cos β.
Силы действующие в косозубых передачах:
Здесь силу Fn раскладывают на три составляющие:
· Окружную силу Ft=2T/d
· Осевую силу Fa=Ft tg β
· Радиальную силу
· Нормальная сила
В косозубом цилиндрическом колесе линия контакта расположена наклонно, а нагрузка по линии контакта распределяется неравномерно. Наибольшая нагрузка наблюдается при зацеплении зубьев в средней части линии контакта в связи с тем, что в этом случае суммарная жесткость взаимодействующих зубьев наибольшая.
Прямозубое цилиндрическое колесо, эквивалентное косозубому. Вывод формулы для эквивалентного диаметра и числа зубьев. Расчет косозубой передачи на прочность по контактным напряжениям и по напряжениям изгиба.
Эквивалентным называется такое воображаемое прямозубое цилиндрическое колесо, форма и размеры зуба которого соответственно совпадают с формой и размерами зуба реального косозубого колеса в его нормальном сечении.
Нормальное сечение n–n косозубого колеса имеет форму эллипса с полуосями a и b’
Радиус кривизны эллипса
диаметр эквивалентного колеса
число зубьев
По контактным напряжениям
Коэффициент повышения прочности
KHa – коэффициент учитывающий неравномерность распределения нагрузки ea – коэффициент торцевого перекрытия
значения ZНb в формуле предварительно оценивают приближенно; при некоторых средних значениях: b = 12°; ea = 1,5; KHa = 1,1, получим ZНb = 0,85.
или
По напряжениям изгиба.
YF – коэффициент формы зуба KF = KFβ*KFν – коэффициент расчетной нагрузки; b – ширина колеса; mn – модуль в нормальном сечении; ZFb – коэффициент повышения
прочности по напряжению изгиба
Yb – коэффициент учитывающий повышение изгибной прочности
при b > 40° принимают Yb = 0,7; Ea – коэффициент торцевого перекрытия, учитывает уменьшение нагрузки ввиду многопарности зацепления
studopedia.net
6.6 Нормальный модуль зубчатых колес.
По табл. 6.4 определяем коэффициент ширины зубчатого венца по отношению к модулю: для случая.
Величина модуля должна удовлетворять условию: , согласно форм. 6.8.;.
Минимальный потребный модуль из условия прочности зубьев колеса по напряжениям изгиба по формуле (6.9):
,
где
– для случая косозубой передачи;
Максимальный допустимый модуль из условия отсутствия подрезания зубьев шестерни по форм. (6.10): .
Удовлетворяя двум полученным диапазонам модулей, назначаем стандартную величину нормального модуля .
6.7 Числа зубьев шестерни и колеса.
Суммарное число зубьев шестерни и колеса согласно форм. 6.11: ;
> ,
согласно форм. 6.12;
,
согласно форм. 6.12;
.
Округлим 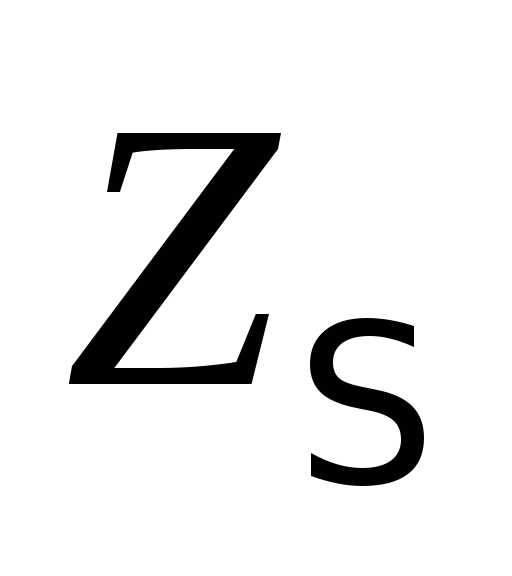 в меньшую сторону. Желательно, чтобы
число
в меньшую сторону. Желательно, чтобы
число было нечётным, поэтому принимаем
было нечётным, поэтому принимаем .
.
Уточним величину наклона зуба: , при этом.
Число зубьев
шестерни:
;.
Условие выполняется. Назначаем
выполняется. Назначаем =24.
Число зубьев колеса:.
=24.
Число зубьев колеса:.
6.8 Передаточное число передачи.
. Отклонение передаточного числа от заданной величины составляет: , что допустимо, так как не превышает 4%.
6.9 Уточнение
величины коэффициента нагрузки –  .
.
Фактическая
окружная скорость в зацеплении:
,
где =2880
=2880 – частота вращения шестерни. Используя
табл. 5.1 для заданной 7-ой степени точности,
при соотношении твердостей шестерни и
колеса типаB
из знаменателя и делая интерполяцию,
выбираем:
– частота вращения шестерни. Используя
табл. 5.1 для заданной 7-ой степени точности,
при соотношении твердостей шестерни и
колеса типаB
из знаменателя и делая интерполяцию,
выбираем:
.Следовательно, .
6.10 Проверочный расчет зубьев на сопротивление контактной усталости.
В связи с наличием
отклонения фактического передаточного
числа от заданного требуется уточнить
величину вращающегося момента на
шестерне  .
.
Контактные напряжения в зацеплении:
,
согласно форм. 6.17, где  =8400.
=8400.
Условие прочности выполняется.
Отклонение расчетного напряжения от допускаемого напряжения составляет:
, что меньше предельной недогрузки 20%.
6.11 Проверочный расчет зубьев на сопротивление изгибной усталости.
Условие прочности по напряжениям изгиба для зубьев шестерни и колеса,
согласно форм. 6.18:
Коэффициент
расчетной нагрузки  рассчитывается аналогично
рассчитывается аналогично .
.
; согласно рис.5,2 б, при и.
Используя табл. 5.1 для заданной 7-ой степени точности, при соотношении твердостей шестерни и колеса типа B из знаменателя и делая интерполяцию, выбираем:
Следовательно, .
Окружная сила в зацеплении: .
Приведенные числа зубьев:
шестерни – .
колеса – .
Находим коэффициент: согласно форм. 6.20.
Коэффициент,
учитывающий влияние формы зубьев на
величину напряжений изгиба,  зависит от приведенного числа зубьев
и коэффициента смещения инструмента
зависит от приведенного числа зубьев
и коэффициента смещения инструмента .
Принимаем коэффициент смещения
.
Принимаем коэффициент смещения .
.
Согласно рис. 6.1
при  находими
находими .
.
Коэффициент,
учитывающий наклон зубьев:  >0,7.>0,7
>0,7.>0,7
Коэффициент,
учитывающий торцевое перекрытие  соответственно для косозубых и шевронных
передач.
соответственно для косозубых и шевронных
передач.
Для шестерни: .
Для колеса: .
Напряжения изгиба в зубьях:
Шестерни:
<;
Колеса: <.
Условия прочности для зубьев шестерни и колеса выполняются.
6.12 Геометрические размеры передачи.
Делительные диаметры:
Шестерня: .
Колесо: .
Условие выполняется.
Диаметры вершин зубьев:
Шестерня: .
Колесо: .
х– коэффициент смещения инструмента при изготовлении зубьев.
Диаметры впадин зубьев:
Шестерня: .
Колесо: .
6.13 Расчет сил в зацеплении.
Схема сил.

Окружная сила: .
Радиальная сила:
,
где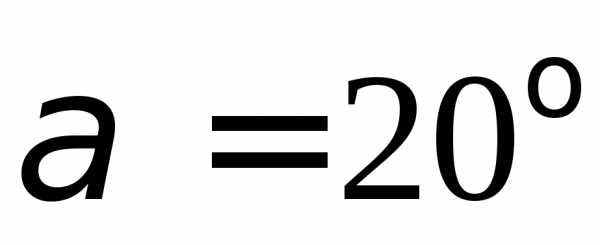 .
.
Осевая сила в одном зацеплении:
Суммарная осевая сила равна нулю, так как они взаимны в косозубом зацеплении.
Нормальная сила: .
6.14 Расчет перегрузочной способности передачи.
Перегрузочная способность по контактным напряжениям:
.
Перегрузочная способность по напряжениям изгиба:
Для шестерни: .
Для колеса: .
Рассчитанная передача может выдерживать кратковременную нагрузку, превышающую номинальную в 5,05 раз.
7. Схема передачи.
8. Литература.
Финогенов В.А. Проектировочный расчет зубчатых и червячных передач. 2008.
Иванов М.Н., Финогенов В.А. Детали машин. -М.: Высшая школа, 2002.
14
studfiles.net
Модуль – зубчатое колесо – Большая Энциклопедия Нефти и Газа, статья, страница 1
Модуль – зубчатое колесо
Cтраница 1
Модули зубчатых колес выбираются по ОСТ 1597 ( см. стр. Основные параметры зубчатых цилиндрических редукторов даны в ГОСТ 2185 – 43 Редукторы зубчатые цилиндрические. Основные параметры, которым следует пользоваться при проектировании. [1]
Модули зубчатых колес, которые можно контролировать на этом приборе, находятся в зависимости от измеряемого показателя точности. В частности, при измерении накопленной погрешности шага по зубчатому колесу ( Fpr) и на & шагов ( Fpkr), отклонений шага ( fp ( r) и радиального биения зубчатого колеса ( F r) на приборе можно контролировать зубчатые колеса модулем от 0 3 до 16 мм. Wm) и отклонений шага зацепления ( fpbr) возможен для зубчатых колес модулем от 1 до 10 мм. [2]
Модуль зубчатых колес рекомендуется брать возможно малым для снижения шума во время работы. [3]
Модули зубчатых колес дифференциала одинаковы. [4]
Обычно модуль готового зубчатого колеса определяется вычислением после замеров наружного диаметра, числа зубьев, шага и высоты зуба по известным формулам. Однако этот способ дает правильные результаты, если зубчатая пара некорригирована и зубчатый венец не нарушен. В противном случае расчеты и измерения значительно усложняются, отнимают много времени и нередко приводят к существенным ошибкам. [6]
Для определения модуля зубчатых колес необходимо измерить наружный диаметр колеса и произвести подсчет зубьев. [7]
При неравенстве модулей зубчатых колес не равны и шаги, и зацепление зубчатых колес невозможно. [8]
Допускается применение модулей зубчатых колес 3 25; 3 75; 4 25 мм для автомобильной промышленности и модуля 6 5 мм для тракторной промышленности. [9]
Что называется модулем зубчатого колеса. [11]
Что называется модулем зубчатого колеса. [12]
В скобках указан модуль зубчатых колес, применяемых в кранах последних образцов. [13]
Стандарт распространяется на модули зубчатых колес цилиндрических, конических и червячных ( с цилиндрическим червяком) передач. [14]
Настоящая таблица распространяется на модули зубчатых колес цилиндрических, конических и червячных с цилиндрическим червяком. [15]
Страницы: 1 2 3 4
www.ngpedia.ru

