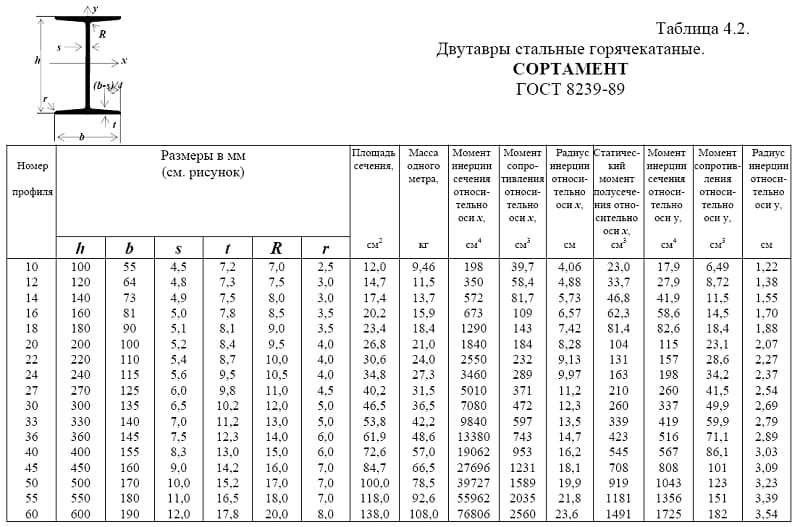
Момент сопротивления равнополочного уголка: Уголок равнополочный по ГОСТ 8509-93*
alexxlab | 23.04.2023 | 0 | Разное
Уголок 125x125x8 равнополочный по ГОСТ 8509-93. Размеры и геометрические характеристики
- Сортамент
- ГОСТ 8509-93
- Уголок равнополочный
- 125x125x8
Размеры профиля
Геометрические характеристики
Высота сечения
h=125,0мм
Ширина сечения
b=125,0мм
Толщина стенки
s=8,0мм
Толщина полки
t=8,0мм
Радиус сопряжения
R=14,0мм
Площадь сечения
A=19,69см2
Масса одного метра сечения
M=15,46кг
Момент инреции относительно оси “x”
Ix=294,36см4
Момент сопротивления относительно оси “x”
Wx=32,2см3
Статический момент половины сечения
Sx=см3
Радиус инерции относительно оси “x”
ix=38,7см
Момент инерции относительно оси “y”
Iy=294,36 см4
Момент сопротивления относительно оси “y”
Wy=32,2 см3
Радиус инерции относительно оси “y”
iy=38,7 см
Момент инерции относительно оси “u”
Iu=466,76 см4
Другие названия:
L125x125x8
Поделиться/сохранить:
Отправить ссылку:
К таблице
20x20x3
20x20x4
25x25x3
25x25x4
25x25x5
28x28x3
30x30x3
30x30x4
30x30x5
32x32x3
32x32x4
35x35x3
35x35x4
35x35x5
40x40x3
40x40x4
40x40x5
40x40x6
45x45x3
45x45x4
45x45x5
45x45x6
50x50x3
50x50x4
50x50x5
50x50x6
50x50x7
50x50x8
56x56x4
56x56x5
60x60x4
60x60x5
60x60x6
60x60x8
60x60x10
63x63x4
63x63x5
63x63x6
65x65x6
65x65x8
70x70x4
70x70x5
70x70x6
70x70x7
70x70x8
70x70x10
75x75x5
75x75x6
75x75x7
75x75x8
75x75x9
80x80x5
80x80x6
80x80x7
80x80x8
80x80x10
80x80x12
90x90x6
90x90x7
90x90x8
90x90x9
90x90x10
90x90x12
100x100x6. 5
5
100x100x7
100x100x8
100x100x10
100x100x12
100x100x14
100x100x15
100x100x16
110x110x7
110x110x8
120x120x8
120x120x10
120x120x12
120x120x15
125x125x8
125x125x9
125x125x10
125x125x12
125x125x14
125x125x16
140x140x9
140x140x10
140x140x12
150x150x10
150x150x12
150x150x15
150x150x18
160x160x10
160x160x11
160x160x12
160x160x14
160x160x16
160x160x18
160x160x20
180x180x11
180x180x12
180x180x15
180x180x18
180x180x20
200x200x12
200x200x13
200x200x14
200x200x16
200x200x18
200x200x20
200x200x24
200x200x25
200x200x30
220x220x14
220x220x16
250x250x16
250x250x18
250x250x20
250x250x22
250x250x25
250x250x28
250x250x30
250x250x35
- Все профили
- Нормальный (балочный)
- Широкополочный
- Колонный
- Балочный нормальный
- Балочный широкополочный
- Колонный
- Свайный
- Дополнительной серии балочный
- Дополнительной серии колонный
- Нормальный (балочный)
- Широкополочный
- Колонный
- Дополнительной серии
- С уклоном полок
- С уклоном полок
- Квадратная
- Прямоугольная
- Квадратная
- Прямоугольная
- Квадратная
- Прямоугольная
- Квадратная
- Прямоугольная
- Квадратная
- Квадратная специального размера
- Равнополочный
- Неравнополочный
- С параллельными гранями полок
- С уклоном полок
- С параллельными гранями полок
- С уклоном полок
- Экономичный с параллельными гранями полок
- Легкой серии с параллельными гранями полок
- Специальный
- С уклоном полок
- С уклоном полок
Уголок 56х56х4 – вес, размеры, характеристики » Металлобазы.
 ру
руВыбор металлопрокатаАрматураБалка двутавроваяКатанкаКвадратКругЛентаЛистПолосаПроволокаСеткаТруба профильнаяТруба круглаяТруба чугуннаяУголокШвеллерШестигранникШпунтТипРазмер
По всей РоссииСанкт-Петербург
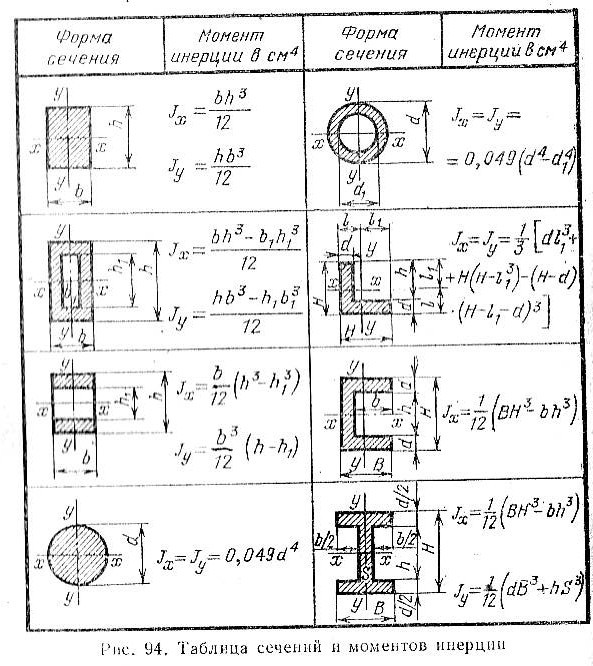
Чертёж сечений равнополочного уголка 56х56х4
Уголок 56х56х4 – первый из двух в номерном ряде №5,6.
Входит в тип стальных «равнополочных» уголков, производимых «горячекатаным» методом.
- Стандарт: ГОСТ 8509;
- Вес погонного метра: 3,44 кг;
- Площадь поперечного сечения (F): 4,38 cm2;
- Ближайшие типоразмеры: 56х56х5;
- Заводы-производители равнополочных уголков: смотреть.
Размеры профиля |
||
| Участок профиля уголка | Значение | |
| Ширина полки (b): | ||
| Толщина полки (t): | 4 mm | |
| Радиус внутреннего закругления (R): | 6,0 mm | |
| Радиус закругления полок (r): | 2,0 mm | |
Допустимые отклонения |
||
| Участок уголка | Значение | |
| Ширина полки (h): | ±1,5 mm | |
| Толщина полки (t): | А (высокая точность) | +0,2 mm -0,4 mm |
| Б (обычная точность) | +0,3 mm -0,5 mm |
|
| * Вес уголка | 1 класс | +3 % -5 % |
| 2 класс | +3 % -5 % |
|
* Отклонения по весу допустимы в замен отклонений толщины полки.
|
||
Величины и значения в осях |
||
| Величины профиля в оси x-x | Значение | |
| Момент инерции (Ix): | 13,10 cm4 | |
| Момент сопротивления (Wx): | 3,21 cm3 | |
| Радиус инерции (ix): | 1,73 cm | |
| Величины профиля в оси x0-x0 | Значение | |
| Момент инерции (Ix0 |
max 20,79 cm4 | |
| Радиус инерции (ix0): | max 2,18 cm3 | |
| Величины профиля в оси y0-y0 | Значение | |
| Момент инерции (Iy0): | min 5,41 cm4 | |
| Момент сопротивления (Wy0): | 2,52 cm3 | |
| Радиус инерции (iy0): | min 1,11 cm | |
Уголок 56х56х4 – двадцать третий по списку из восьмидесяти девяти в ГОСТ 8509. Первый профиль из двух в размерном ряде №5,6.
Первый профиль из двух в размерном ряде №5,6.
Таблицы с параметрами «равнополочного», «горячекатаного» уголка созданы на основе стандарта качества ГОСТ 8509-93 Уголки стальные горячекатаные равнополочные.
Проектирование одинарного уголка Рабочий пример
Проектирование одинарного уголка с использованием EN 1993-1-1 обсуждается в этой статье на рабочем примере. Угловое сечение, подверженное сжимающей силе, рассчитано со ссылкой на соответствующий раздел в нормах.
Процедура проектирования сжатых элементов такая же, как описано в статье Расчет стальных колонн с использованием Еврокода 3.
Давайте обсудим расчет на рабочем примере.
Данные дизайна
- Angle section 60x60x6
- Lenght of the angle section 600mm
- Applied Load 100kN
- Single raw of bolts
- Steel grade S275
Classification of the Sections
Let’s find the material data
Thickness of section = 6 мм ≤ 40 мм и
Марка стали S275
Из таблицы 3. 1 EN 1993-1-1,
1 EN 1993-1-1,
fy = 275 Н/мм 2
Из таблицы 5.2 (лист 3 из 3)
ε = √(235/f y ) = √(235/275) = 0,924Из табл. 5.2 (лист 3 из 3) = 13,86
(b+h) / 2t = (60+60) / (2×6) = 10 ≤ 11,5ε = 11,5 x 0,924 = 10,626
Следовательно, сечение относится к классу 3
Прочность поперечного сечения на сжатие
N Ed / N c,Rd ≤ 1,0
N c,Rd = Af y / 4 γ07
γ M0 = 1.0 from Clause 6.1
A = 695 mm 2
N c,Rd = Af y / γ M0 = 695 x 275 / 1.0 = 191.1 kN
N Ed / N c,Rd = 100 / 191,1 = 0,524 < 1
Секция удовлетворяет сжимающей способности.
Сопротивление продольному изгибу
N Ed / N b,Rd ≤ 1,0
Расчет длины потери устойчивости, L cr
Нам необходимо проверить устойчивость к потере устойчивости по критической оси. Поэтому мы рассматриваем оси Y-Y, Z-Z и V-V и находим критический коэффициент уменьшения (за вычетом значения, превышающего уменьшение изгибающего момента. Это необходимо при проектировании углового сечения.
Поэтому мы рассматриваем оси Y-Y, Z-Z и V-V и находим критический коэффициент уменьшения (за вычетом значения, превышающего уменьшение изгибающего момента. Это необходимо при проектировании углового сечения.
Найдите длину потери устойчивости по каждой оси. длину можно считать указанной в BS 5950.
Ось Y-Y: 0,85 x 600 = 510 мм
Ось Z-Z; 1,0 x 600 = 600 мм
Ось V-V; 0,85 x 600 = 510 мм
Из данных свойств сечения определите радиус инерции (i)
i – ось Y-Y = 18,3 мм
i – ось Z-Z = 18,3 мм
i- ось V-V = 11,8 мм
3
3
λ1 = 93,9ε = 93,9 x 0,924 = 86,4
λ‾ = (Lcr / i)( 1 / λ1)
Примечание: символ λ должен быть таким, как указано в коде. Есть небольшая разница в символе по сравнению с кодом.
Рассчитайте для каждого направления, чтобы получить критический коэффициент.
λ‾ ось Y-Y = (510 / 18,5)( 1 / 86,4) = 0,323
λ‾ ось Z-Z = (600 / 18,5)( 1 / 86,4) = 0,379 ( 1 / 86,4) = 0,5
Если в конструкции с одним уголком соединение выполняется одним болтом, следует учитывать λ¯ eff . При наличии двух и более болтов эксцентриситетами можно пренебречь.
При наличии двух и более болтов эксцентриситетами можно пренебречь.
В этом примере рассмотрим угол, соединенный одной стороной. Поэтому рассмотрим, λ¯ eff
Ось Y-Y; λ¯ эфф = 0,5 + 0,7λ‾ = 0,5 + 0,7×0,323 = 0,726
Ось Z-Z; λ¯ эфф = 0,5 + 0,7λ‾ = 0,5 + 0,7×0,379 = 0,765
ось В-В; λ¯ эфф = 0,35 + 0,7λ‾ = 0,35 0,7×0,5 = 0,7
Критический коэффициент уменьшения – это меньшее значение «χ». Это значение становится меньше, когда Ø больше. Это значение становится больше, когда λ¯ eff выше. Поэтому выбираем
λ¯ эфф = 0,765
Теперь получите кривую потери устойчивости из таблицы 6.2 EN 1993-1-1.
Для угловых профилей кривая потери устойчивости имеет вид «b».
Получите значение α из таблицы 6.1 стандарта EN 1993-1-1.
α = 0,34
Теперь вычислите Ø из Cl. 6.3.1.2
Ø = 0,5[ 1 + 0,34(λ¯0,2 ) + λ¯ 2 ] = 0,5 [1 + 0,34 (0,765 – 0,2) + 0,765 2
χ = 1 / [ Ø + √(Ø 2 – λ¯ 2 )] = 1 / [0,889 + √ (0,889 2 + 0,765 2 )] = 0,742
Теперь рассчитывайте Brackling
N B, RD = χaf 4444444444. y / γ M1
y / γ M1
N b,Rd = 0.742 x 695 x 275 / 1.0 = 141.8 kN
N Ed / N b,Rd < 1.0
N Ed / N b, Rd = 100 / 141,8 = 0,7 < 1
Раздел соответствует требованиям.
Дополнительные сведения о конструкционной стали можно найти в статье Википедии.
Свойства поперечного сечения угла (L) | Calcresource
Соглашение
-Геометрия
-Момент инерции
-Основные оси
-момент инерции и изгиба
-Полярный момент инерции L -Section
-Эластичный раздельный модуль
-пластиковый модуль сечения
– Вокруг оси x
– Вокруг оси Y
– Радиус вращения
– Формулы сечения угла (L)
– Связанные страницы
Геометрия
Площадь A и периметр P угла можно найти по следующим формулам:
\begin{split} & A & = (h+b-t)t \\ & P & = 2b + 2h \end{split}
Расстояние центра тяжести от левого края сечения x_c и от нижнего края y_c можно найти, используя первые моменты площади двух ветвей: 92\right) \right) \end{split}
У нас есть специальная статья о центроиде сложных областей и о том, как его вычислить. Если вам нужна дополнительная информация, вы можете найти ее здесь.
Если вам нужна дополнительная информация, вы можете найти ее здесь.
Момент инерции
Момент инерции углового поперечного сечения можно найти, если всю площадь разделить на три меньшие, A, B, C, как показано на рисунке ниже. Конечную область можно рассматривать как аддитивную комбинацию A+B+C. Тем не менее, более простой расчет может быть достигнут комбинацией (A+C)+(B+C)-C. Кроме того, расчет лучше проводить вокруг нецентроидальных осей x0,y0 с последующим применением теоремы о параллельных осях. 92 \\ & I_{xy} & = I_{x0y0} – A x_c y_c \end{split}
где x_c расстояние от центра тяжести до оси y0 и x_c расстояние от центра тяжести до оси x0. Выражения для этих расстояний приведены в предыдущем разделе.
Имейте в виду, что оси x, y не являются естественными, L-образное сечение предпочло бы изгибаться, если его не ограничивать. Это будут главные оси, наклоненные относительно геометрических осей x, y, как описано в следующем разделе.
Главные оси
Главные оси – те, для которых произведение инерции I xy поперечного сечения становится равным нулю. Обычно главные оси обозначаются буквами I и II и перпендикулярны друг другу. Моменты инерции, заданные вокруг главных осей, называются главными моментами инерции и являются максимальным и минимальным. В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split}
Обычно главные оси обозначаются буквами I и II и перпендикулярны друг другу. Моменты инерции, заданные вокруг главных осей, называются главными моментами инерции и являются максимальным и минимальным. В частности, момент инерции вокруг главной оси I максимален, а момент инерции вокруг главной оси II минимален по сравнению с любой другой осью поперечного сечения. Для симметричных сечений главные оси совпадают с осями симметрии. Однако в L-образном сечении нет оси симметрии (за исключением особого случая угла с равными сторонами), и в результате главные оси не видны только при осмотре. Их необходимо вычислить и, в частности, определить их наклон относительно какой-либо удобной геометрической оси (например, x, y). 92} \\ & \tan 2\theta & = -\frac{2I_{xy}}{I_x-I_y} \end{split}
По определению I_I считается главным главным моментом (максимальным) и I_{ II} второстепенный главный момент (минимальный). Отсюда следует, что: I_I>I_{II}.
Момент инерции и изгиб
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:0003
Изгибающий момент M, приложенный к поперечному сечению, связан с его моментом инерции следующим уравнением:0003
M = E\times I \times \kappa
где E — модуль Юнга, свойство материала, а \kappa — кривизна балки из-за приложенной нагрузки. Таким образом, из предыдущего уравнения видно, что когда определенный изгибающий момент M прикладывается к поперечному сечению балки, развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции L-образного сечения
Полярный момент инерции описывает жесткость поперечного сечения по отношению к крутящему моменту, так же как описанные выше плоские моменты инерции относятся к изгибному изгибу. Расчет полярного момента инерции I_z вокруг оси z-z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях: 94 .
Модуль упругости сечения
Модуль упругости сечения S_x любого поперечного сечения вокруг центральной оси x-x описывает реакцию сечения на упругий изгиб при изгибе. Он определяется как:
Он определяется как:
S_x = \frac{I_x}{Y}
, где I_x, момент инерции сечения вокруг оси x-x и Y, расстояние от центра тяжести волокна данного сечения (параллельного ось). Для углового сечения из-за его несимметричности S_x отличается для верхнего волокна (на конце вертикального участка) или нижнего волокна (в основании горизонтального участка). Обычно при нахождении модуля упругости учитывается более удаленное волокно (от центра тяжести). Это происходит на кончике вертикальной ноги (для изгиба вокруг х-х). Используя, возможно, большее значение Y, мы получаем меньшее значение S_x, что приводит к более высоким расчетам напряжения, как будет показано вскоре после этого. Обычно это предпочтительнее для дизайна раздела. Следовательно:
S_{x,\textit{min}} = \frac{I_x}{h-y_c}
S_{x,\textit{max}} = \frac{I_x}{y_c}
, где «min Обозначения ” или “max” основаны на предположении, что y_c \lt h-y_c , что справедливо для любого углового сечения.
Аналогично, для модуля упругого сечения S_y относительно оси y-y минимальный модуль упругого сечения находится с помощью:
S_{y,\textit{min}} = \frac{I_y}{b-x_c}
, где обозначение «min» основано на допущении, что x_c \lt b-x_c , что опять-таки справедливо для любого углового сечения.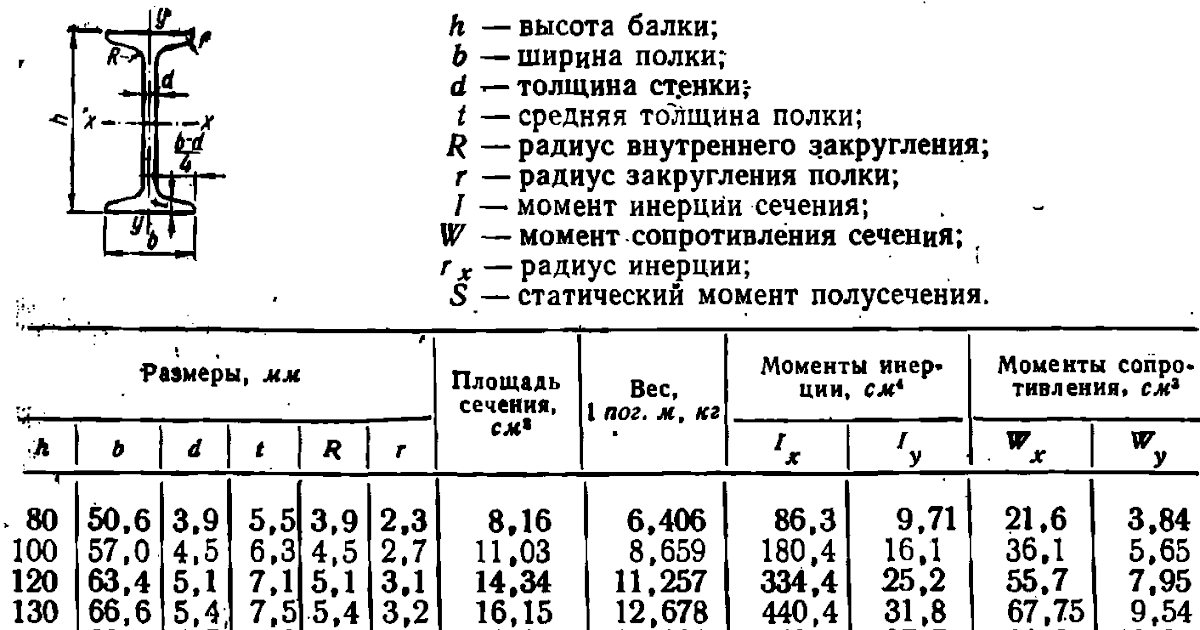
Если к оси x-x приложен изгибающий момент M_x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которая в упругом режиме совпадает с центроидальной осью x-x). Над нейтральной осью напряжения по определению равны нулю. Абсолютное максимальное напряжение будет возникать на самом удаленном волокне, величина которого определяется формулой: аналогично поперечному сечению А для осевой нагрузки. Для последнего нормальным напряжением является F/A. 93 .
Модуль пластического сечения
Модуль пластического сечения аналогичен упругому, но определяется в предположении полной пластической текучести поперечного сечения вследствие изгибного изгиба. В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится в однородном поле напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t, при растяжении и A_c, при сжатии, разделенные нейтральной осью.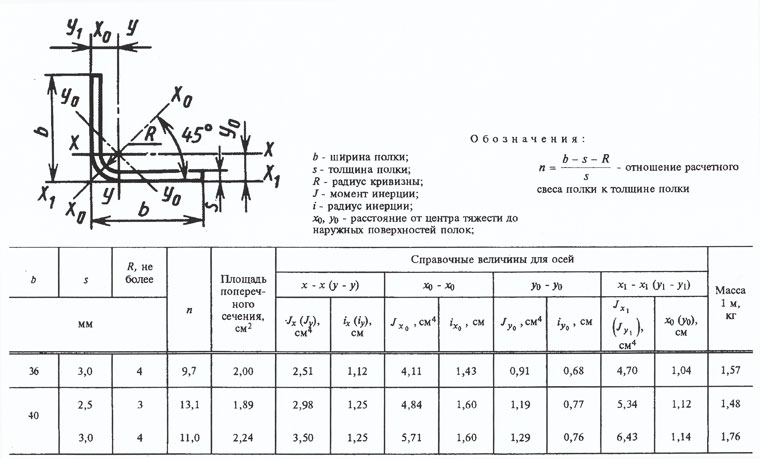 Эта ось называется пластическая нейтральная ось и для несимметричных сечений не совпадает с упругой нейтральной осью (которая снова является центроидальной). Модуль пластического сечения задается общей формулой:
Эта ось называется пластическая нейтральная ось и для несимметричных сечений не совпадает с упругой нейтральной осью (которая снова является центроидальной). Модуль пластического сечения задается общей формулой:
Z = A_c Y_c + A_t Y_t
, где Y_c — расстояние от центра тяжести области сжатия A_c до нейтральной пластической оси, а Y_t — соответствующее расстояние от центра тяжести зоны растяжения. площадь А_т.
Вокруг оси x
В случае углового поперечного сечения пластическая нейтральная ось для изгиба x-x может быть найдена одним из следующих двух уравнений:
\left \{ \begin{array}{ll} (h-y_{pna})t = \frac{A}{2} & \text{ , if } y_{pna} \ge t \\ y_{ pna} b = \frac{A}{2} & \text{ , if } y_{pna} \lt t \\ \end{array} \right.
, который становится:
y_{pna} =\left \{ \begin{array}{ll} h- \frac{A}{2t} & \text{ , если: } t \le {A\over2 b } \\ \frac{A}{2b} & \text{ , если: } t \gt {A\over2 b} \\ \end{array} \right.
где y_\textit{pna}, расстояние пластической нейтральной оси от нижнего конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через вертикальную ветвь, а второе — когда она проходит через горизонтальную ветвь. Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b}
Первое уравнение справедливо, когда пластическая нейтральная ось проходит через вертикальную ветвь, а второе — когда она проходит через горизонтальную ветвь. Как правило, нельзя заранее знать, какое уравнение является релевантным. 92 \over4b} \quad , t \gt {A\over2 b}
где h_1=h-t.
Вокруг оси y
Аналогичным образом можно найти модуль пластического сечения вокруг оси y. Если сориентировать Г-образное сечение так, чтобы вертикальная ветвь стала горизонтальной, то получившаяся фигура по форме подобна первоначально ориентированной. Таким образом, полученные уравнения должны иметь тот же вид, что и для оси абсцисс. Нам нужно только поменять местами h на b и наоборот. Таким образом, точное положение пластической нейтральной оси определяется следующей формулой:
x_{pna} =\left \{ \begin{array}{ll} b- \frac{A}{2t} & \text{ , если: } t \le {A\over2 h} \\ \frac {A}{2h} & \text{ , если: } t \gt {A\over2 h} \\ \end{массив} \right.
где x_\textit{pna}, расстояние пластической нейтральной оси от левого конца сечения. Первое уравнение справедливо, когда пластическая нейтральная ось проходит через горизонтальную ветвь, а вторая — когда она проходит через вертикальную ветвь (см. рисунок ниже).
Первое уравнение справедливо, когда пластическая нейтральная ось проходит через горизонтальную ветвь, а вторая — когда она проходит через вертикальную ветвь (см. рисунок ниже).
Для первого случая, т.е. когда ось y пересекает горизонтальную ветвь, модуль пластичности находится по формуле: 92 \over4h} \quad , t \gt {A\over2 h}
, где b_1=b-t.
Радиус вращения
Радиус вращения R g поперечного сечения относительно оси определяется по формуле: I момент инерции поперечного сечения вокруг той же оси и A его площадь. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг — это форма с минимальным радиусом вращения по сравнению с любым другим сечением той же площади A.
Формулы углового сечения (L)
В следующей таблице перечислены основные формулы для механических свойств углового (L) поперечного сечения.
Angle (L) section formulas | |
|---|---|
| Quantity | Formula |
| Area: | A = (h+b-t)t |
| Perimeter: | P = 2b + 2h |
| Центроид: | x_c = \frac{t}{2A}\left( b^2 + h t – t^2\right) 92 \over4h} & \quad , t \gt {A\over2 h} \end{массив}\right. |