Момент сопротивления швеллера 10: Слишком много запросов
alexxlab | 01.03.2023 | 0 | Разное
Гнутый швеллер. Расчет в Excel геометрических характеристик.
Опубликовано 07 Июл 2013
Рубрика: Механика | 8 комментариев
Швеллер – это один из профилей металлопроката, имеющий в поперечном сечении «П» — образный вид. В отличие от уголка швеллер хорошо воспринимает поперечные нагрузки, то есть хорошо «работает» на изгиб. Именно это качество и технологичность изготовления и…
…обусловили высочайшую популярность этому профилю.
Швеллеры изготавливают из пластмасс, цветных металлов и сплавов, но, безусловно, основным материалом является сталь. Основная масса швеллеров производится на сортовых станах методом горячей прокатки — горячекатаные швеллеры. Швеллеры, изготовленные из стальной «холодной» полосы на специальных профилегибочных станах, называются холодногнутыми или чаще просто – гнутыми. На машиностроительных заводах и заводах металлоконструкций гнутые швеллеры часто изготавливают «V» — образной гибкой на листогибах (листогибочных прессах) из прямоугольных листовых заготовок, вырубленных на гильотинных ножницах или вырезанных на газорежущих или плазморежущих машинах.
Хотя по характеристикам гнутый швеллер и уступает прокатному, распространенность он имеет не меньшую.
В этой статье представлена программа в MS Excel расчета геометрических характеристик поперечного сечения гнутого равнополочного швеллера.
Гнутый швеллер любых произвольных размеров, в том числе отличных от размеров по ГОСТ 8278-75, может быть без труда рассчитан в этой программе.
Расчет в Excel можно заменить расчетом в программе Calc из свободно распространяемого пакета Open Office.
Исходные данные записываем в ячейки со светло-бирюзовой заливкой. Результаты расчетов считываем в ячейках со светло-желтой заливкой.
Как видно из рисунка – исходных данных всего четыре.
Заполняем ячейки исходными данными:
1. Высоту швеллера H в миллиметрах заносим
в ячейку D3: 200
2. Ширину полок швеллера В в миллиметрах пишем
в ячейку D4: 80
3.
Толщину стенки и полок S в миллиметрах пишем
в ячейку D5: 4
4. Внутренний радиус сгибов R в миллиметрах записываем
в ячейку D6: 6
Всё, далее весь расчет Excel выполнит без нашего участия и выдаст все геометрические характеристики заданного сечения.
Тем, кому нужен результат и не интересны формулы, рекомендую сразу перейти к концу статьи – там ссылка на скачивание программы. Для тех, кто желает сам увидеть и разобраться, как это все рассчитывается, ниже представлено подробное описание.
Сначала проведем расчет характеристик элементов сечения – прямоугольников №1, №3, №3’ и кольцевых сегментов в углах сгибов №2 и №2’. Эти данные являются вспомогательными для расчетов сечения в целом.
Геометрические характеристики элемента №1 рассчитываются по формулам:
5., 6. Координаты центра тяжести относительно осей x* и y* xc1 и yc1 в миллиметрах рассчитываем
в ячейке D8: =D5/2=2,000 xc1=S/2
и в ячейке D9: 0,000 yc1=0
7.
2/12
Выполнив предварительные вспомогательные расчеты характеристик элементов сечения гнутого швеллера, приступаем к основным расчетам сечения целиком.
Расчет в Excel выполняется по формулам:
20. Площадь сечения A в квадратных сантиметрах рассчитываем
в ячейке D26: =D10+2*D16+2*D22=13,805 A=A1+2*A2+2*A3
21., 22. Статические моменты инерции Sx и Sy в сантиметрах в третьей степени считаем
в ячейке D27: 0,000 Sx=0
и в ячейке D28: =D8/10*D10+2*D14/10*D16+2*D20/10*D22=27,123 Sy=xc1*A1+2*xc2*A2+2*xc3*A3
23., 24. Координаты центра тяжести сечения относительно осей x* и y* xc и yc в миллиметрах рассчитываем
в ячейке D29: =D28/D26*10=19,647 xc=Sy/A
и в ячейке D30: 0,000 yc=0
25.
0,5
32. Масса погонного метра швеллера из стали M в килограммах рассчитываем
в ячейке D38: =0,785*D26=10,837 M=0,785*A
33. Длина развертки сечения L в миллиметрах считаем
в ячейке D39: =2*(D4-D5-D6)+D3-2*(D5+D6)+ПИ()*(D5/LN (1+ D5/D6))=344,600 L=2*(B-R-S)+H-2*(R+S)+3,14*(S/ln (1+S/R))
34. Расстояние до линии сгиба от края заготовки a в миллиметрах считаем
в ячейке D40: =D4-D6-D5+ПИ()/4*(D5/LN (1+D5/ D6))=76,150 a=H-R-S+3,14/4*(S/ln (1+S/R))
На этом расчет в Excel характеристик гнутого швеллера завершен.
Выборочное тестирование результатов расчетов показало полное соответствие со значениями из ГОСТа. Отклонения не превысили 0,05%, то есть не превысили погрешности округления.
Очень близки затронутой теме статьи «Расчет усилия листогиба» и «Расчет длины развертки» – рекомендую посмотреть!
Ссылка на скачивание файла: gnutyy-shveller (xls 37,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
Швеллер гнутый ГОСТ 8278-83 » Металлургпром
МЕЖГОСУДАРСТВЕННЫЙСТАНДАРТ
ШВЕЛЛЕРЫ СТАЛЬНЫЕ ГНУТЫЕ РАВНОПОЛОЧНЫЕ Сортамент | ГОСТ 8278-83 |
Срок действия с 01.01.84
до 01.01.99
1. Настоящий стандарт распространяется на стальные гнутые равнополочные швеллеры, изготовляемые на профилегибочных станах из холоднокатаной и горячекатаной, рулонной стали обыкновенного качества, углеродистой качественной конструкционной и низколегированной.
Показатели технического уровня, установленные настоящим стандартом, предусмотрены для высшей и первой категории качества.
(Измененная редакция, Изм. № 1, 2).
1a. По точности профилирования швеллеры изготовляют:
высокой точности – А;
повышенной точности – Б;
обычной точности – В.
Требования высокой и повышенной точности профилирования соответствуют высшей категории качества.
(Введен дополнительно, Изм. № 1).
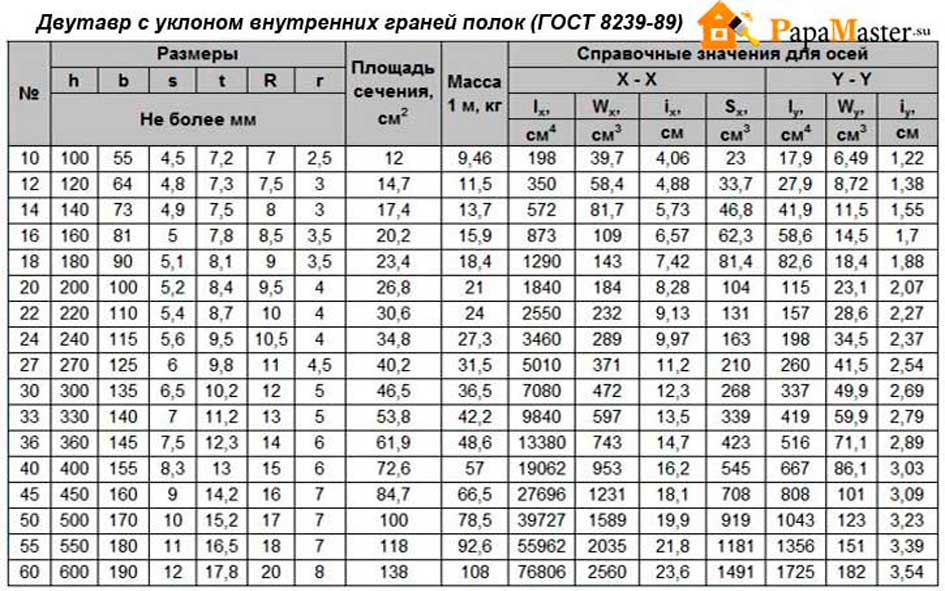
2. Поверочное сечение швеллеров должно соответствовать указанному на чертеже.
h – высота стенки; b – ширина полки; s – толщина швеллера; R – радиус
кривизны; W -момент сопротивления; I – момент инерции; i -радиус инерции; Sx – статический момент полусечения, x0 –расстояние от оси у – у до наружной поверхности стенки; – отношение расчетного свеса полки к толщине швеллера; – отношение расчетной высоты к толщине швеллера
3. Размеры швеллеров, площадь поперечного сечения, справочные значения величин для осей и масса 1 м швеллера должны соответствовать:
для швеллеров из углеродистой кипящей и полуспокойной стали -указанным в табл.
1;
для швеллеров из углеродистой спокойной и низколегированной стали – указанным в табл. 2.
Таблица 1
h
| b
| s
| R, не |
n
|
n1
| Площадь поперечного сечения, см2 | Справочные величины для осей | Масса 1 м, кг
| |||||||
х- х | у у | x 0, см | |||||||||||||
мм | Ix,см4 | Wx,см3 | ix, см | sx,см3 | Iу,см4 | Wу,см3 | iу, см | ||||||||
25 | 26 | 2 | 3 | 10,5 | 7,5 | 1,39 | 1,43 | 1,14 | 1,01 | 0,67 | 0,96 | 0,60 | 0,83 | 1,00 | 1,09 |
25 | 30 | 2 | 3 | 12,5 | 7,5 | 1,55 | 1,64 | 1,31 | 1,03 | 0,76 | 1,42 | 0,78 | 0,96 | 1,19 | 1,22 |
28 | 27 | 2,5 | 4 | 8,2 | 6,0 | 1,81 | 2,24 | 1,60 | 1,11 | 0,95 | 1,32 | 0,80 | 0,85 | 0,04 | 1,42 |
30 | 25 | 3 | 5 | 5,7 | 4,7 | 2,05 | 2,73 | 1,82 | 1,15 | 1,10 | 1,24 | 0,78 | 0,96 | 1,61 | |
30 | 30 | 2 | 3 | 12,5 | 10,0 | 1,65 | 2,50 | 1,67 | 1,23 | 0,96 | 1,53 | 0,82 | 0,96 | 1,12 | 1,30 |
32 | 25 | 3 | 5 | 5,7 | 5,3 | 2,11 | 3,20 | 2,00 | 1,23 | 1,23 | 1,28 | 0,82 | 0,78 | 0,94 | 1,66 |
32 | 32 | 2 | 3 | 13,5 | 11,0 | 1,77 | 3,08 | 1,92 | 1,31 | 1,10 | 1,88 | 0,93 | 1,03 | 1,29 | 1,39 |
38 | 95 | 2,5 | 3 | 35,8 | 10,8 | 5,48 | 15,42 | 8,12 | 1,68 | 4,47 | 49,26 | 9,18 | 3,00 | 4,13 | 4,30 |
40 | 20 | 2 | 3 | 7,5 | 15,0 | 1,45 | 3,40 | 1,70 | 1,53 | 1,02 | 0,35 | 0,40 | 0,62 | 0,60 | 1,14 |
40 | 20 | 3 | 5 | 4,0 | 8,0 | 2,05 | 4,45 | 2,23 | 1,47 | 1,38 | 0,75 | 0,56 | 0,60 | 0,66 | 1,61 |
40 | 30 | 2 | 3 | 12,5 | 15,0 | 1,85 | 4,85 | 2,42 | 1,62 | 1,40 | 1,72 | 0,86 | 0,96 | 1,01 | 1,45 |
40 | 30 | 2,5 | 3 | 9,8 | 11,6 | 2,28 | 5,83 | 2,91 | 1,60 | 1,66 | 2,09 | 1,06 | 0,96 | 1,03 | 1,79 |
40 | 40 | 2 | 3 | 17,5 | 15,0 | 2,25 | 6,29 | 3,15 | 1,67 | 1,78 | 3,79 | 1,49 | 1,30 | 1,45 | 1,77 |
40 | 40 | 2,5 | 3 | 13,8 | 11,6 | 2,78 | 7,58 | 3,79 | 1,65 | 2,17 | 4,63 | 1,83 | 1,29 | 1,47 | 2,18 |
40 | 40 | 3 | 5 | 10,7 | 8,0 | 3,25 | 8,57 | 4,28 | 1,62 | 2,51 | 5,31 | 2,14 | 1,28 | 1,52 | 2,55 |
42 | 42 | 4 | 6 | 8,0 | 5,5 | 4,45 | 12,34 | 5,88 | 1,67 | 3,49 | 7,80 | 3,05 | 1,32 | 1,65 | 3,49 |
43 | 45 | 2 | 3 | 20,0 | 16,5 | 2,51 | 8,25 | 3,84 | 1,81 | 2,15 | 5,38 | 1,88 | 1,46 | 1,64 | 1,97 |
45 | 25 | 3 | 5 | 5,7 | 9,7 | 2,50 | 7,29 | 3,24 | 1,71 | 1,99 | 1,49 | 0,89 | 0,77 | 0,82 | 1,96 |
45 | 31 | 2 | 3 | 13,0 | 17,5 | 1,99 | 6,55 | 2,91 | 1,81 | 1,68 | 1,97 | 0,94 | 0,99 | 1,01 | 1,56 |
48 | 70 | 5 | 7 | 11,6 | 4,8 | 8,49 | 32,60 | 13,58 | 1,96 | 7,95 | 41,22 | 10,15 | 2,20 | 2,94 | 6,67 |
50 | 30 | 2 | 3 | 12,5 | 20,0 | 2,05 | 8,12 | 3,25 | 1,99 | 1,88 | 1,87 | 0,90 | 0,96 | 0,92 | 1,61 |
50 | 30 | 2,5 | 3 | 9,8 | 15,6 | 2,53 | 9,82 | 3,93 | 1,97 | 2,30 | 2,28 | 1,11 | 0,95 | 0,94 | 1,99 |
50 | 32 | 2,5 | 3 | 10,6 | 15,6 | 2,63 | 10,38 | 4,15 | 1,98 | 2,42 | 2,72 | 1,25 | 1,02 | 1,02 | 2,07 |
50 | 40 | 2 | 3 | 17,5 | 20,0 | 2,45 | 10,42 | 4,17 | 2,06 | 2,36 | 4,13 | 1,55 | 1,30 | 1,34 | 1,92 |
50 | 40 | 2,5 | 3 | 13,8 | 15,6 | 3,03 | 12,64 | 5,06 | 2,04 | 2,90 | 5,05 | 1,92 | 1,29 | 1,36 | 2,38 |
50 | 40 | 3 | 4 | 11,0 | 12,0 | 3,58 | 14,55 | 5,82 | 2,02 | 3,37 | 5,88 | 2,26 | 1,28 | 1,39 | 2,81 |
50 | 40 | 4 | 6 | 7,5 | 7,5 | 4,61 | 17,80 | 7,12 | 1,97 | 4,23 | 7,35 | 2,89 | 1,26 | 1,48 | 3,62 |
50 | 47 | 6 | 9 | 5,3 | 3,3 | 7,30 | 26,62 | 10,65 | 1,91 | 6,54 | 15,42 | 5,51 | 1,45 | 1,90 | 5,73 |
50 | 50 | 2,5 | 3 | 17,8 | 15,6 | 3,53 | 15,46 | 6,18 | 2,09 | 3,49 | 9,31 | 2,92 | 1,62 | 1,81 | 2,77 |
50 | 50 | 3 | 4 | 14,3 | 12,0 | 4,18 | 17,87 | 7,15 | 2,07 | 4,08 | 10,89 | 3,44 | 1,61 | 1,84 | 3,28 |
Уравнения модуля сечения и калькуляторы Общие формы
Связанные ресурсы: Материаловедение
Уравнения модуля сечения и калькуляторы Общие формы
Сопротивление материалов | Прогиб и напряжение балки
Модуль упругости — это геометрическое свойство заданного поперечного сечения, используемое при расчете балок или изгибаемых элементов.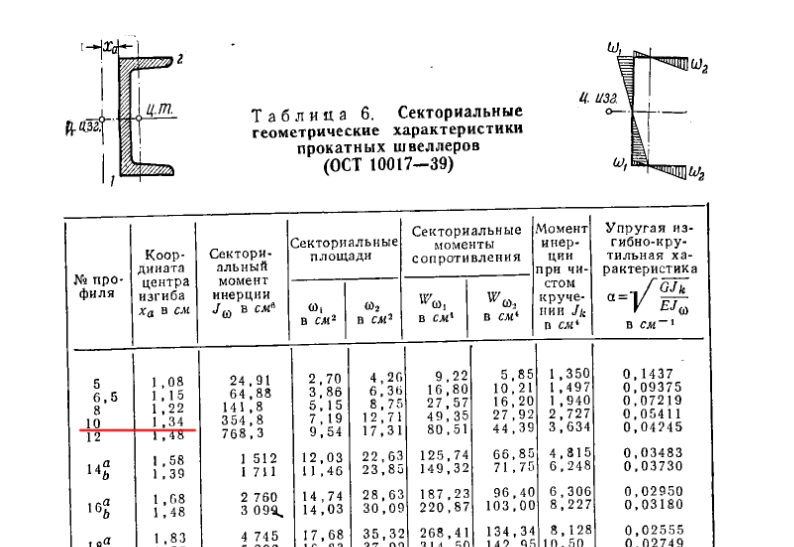
Другие геометрические свойства, используемые в конструкции, включают площадь для растяжения, радиус вращения для сжатия и момент инерции для жесткости. Любая связь между этими свойствами сильно зависит от рассматриваемой формы. Уравнения для модулей сечения обычных форм приведены ниже. Существует два типа модулей сечения: модуль упругого сечения (S) и модуль пластического сечения (Z).
Для общего расчета используется модуль упругого сечения, применяемый до предела текучести для большинства металлов и других распространенных материалов.
Модуль упругого сечения определяется как S = I / y, где I — второй момент площади (или момент инерции), а y — расстояние от нейтральной оси до любого заданного волокна. Об этом часто сообщают, используя y = c, где c — расстояние от нейтральной оси до самого крайнего волокна, как показано в таблице ниже. Он также часто используется для определения момента текучести (M y ), так что M y = S × σ y , где σ y — предел текучести материала.
Расширенный список: Модуль сечения, Момент инерции площади, Уравнения и калькуляторы
| Форма поперечного сечения | Уравнение | Комментарий |
Калькулятор: Калькулятор прямоугольника модуля сечения | Сплошная стрелка представляет нейтральную ось | |
Калькулятор: Модуль упругости двутавровой балки Универсальный калькулятор | NA указывает нейтральную ось | |
Калькулятор: Калькулятор удельного веса I балки по центру нейтральной оси | NA указывает нейтральную ось | |
Калькулятор: Модуль модуля сечения, окружность, центр, нейтральная ось, калькулятор | Сплошная стрелка представляет нейтральную ось | |
Калькулятор: Калькулятор удельного веса полого круглого центра нейтральной оси | NA указывает нейтральную ось | |
Калькулятор: Модуль модуля сечения полого прямоугольника, квадрата, центра, нейтральной оси, калькулятор | NA указывает нейтральную ось | |
Калькулятор: Модуль модуля сечения ромбовидной формы, центр нейтральной оси, калькулятор | NA указывает нейтральную ось | |
Калькулятор: Калькулятор центра нейтральной оси формы канала по модулю сечения | NA указывает нейтральную ось |
Модуль пластического сечения (PNA)
Модуль пластического сечения используется для материалов, в которых преобладает (необратимое) пластическое поведение.
Большинство проектов намеренно не сталкиваются с таким поведением.
Модуль упругости пластического сечения зависит от положения нейтральной оси пластичности (PNA). PNA определяется как ось, которая разделяет поперечное сечение таким образом, что сила сжатия от области, находящейся в состоянии сжатия, равна силе растяжения, создаваемой областью, находящейся в состоянии растяжения. Так, для сечений с постоянным пределом текучести площадь над и под ПНА будет равна, а для составных сечений это не обязательно.
Модуль пластического сечения представляет собой сумму площадей поперечного сечения с каждой стороны PNA (которые могут быть равными, а могут и не быть равными), умноженные на расстояние от локальных центров тяжести двух площадей до PNA:
- Уравнения модуля сечения и калькуляторы
- Свойства сечения Радиус инерции Варианты 1–10
- Свойства сечения Радиус инерции Варианты 11–16
- Свойства сечения Радиус инерции Случаи 17 – 22
- Свойства сечения Радиус инерции Случаи 23 – 27
- Свойства сечения Радиус инерции Случаи 28 – 31
- Свойства сечения Радиус инерции Случаи 32 – 34
- Свойства сечения Радиус инерции Случаи 35 – 37
Формулы модуля сечения для различных форм
Модуль сечения обычно используется при расчете напряжений в поперечных сечениях, однако вместо него часто используется момент инерции, вероятно, потому, что конструкторы лучше знакомы с формулами момента инерции.