Момент сопротивления швеллера: Момент сопротивления швеллер таблица | ТРАСТ МЕТАЛЛ

alexxlab | 23.03.1989 | 0 | Разное

Учебное пособие для студентов заочной формы обучения, страница 8

Пример решения задачи

Исходные данные приведены на рис. 3.11.

1.  Определение грузоподъемности стержня.

Грузоподъемность центрально сжатого стержня определяется по формуле

,                                        (3.19)

где  – коэффициент понижения основного допускаемого напряжения.

Коэффициент  зависит от , то есть . Гибкость вычисляется по формуле

,                                                   (3.20)

где

–  μ – коэффициент приведения длины стержня,

–   ‑ минимальный радиус инерции поперечного сечения стержня

Величина  определяется по сортаменту “Балки двутавровые” (Приложение 1). Для заданного номера двутавра № 36 в сортаменте находим , , следовательно . При шарнирном опирании стержня коэффициент приведения длины .

Гибкость стержня .

а)
б)
Рис. 3.10

Рис.3.11

По таблице коэффициента продольного изгиба (Приложение 3) для  и стали марки Ст. 4, 3, 2 определяется значение коэффициента  понижения основного допускаемого напряжения. В таблице зависимости  от  значения гибкости кратны 10. Поэтому, из таблицы берутся два ближайших к найденному значения гибкости  и соответствующие им два значения :

,  

,   .

Для определения искомого значения коэффициента  выполняется линейная интерполяция:

Величина допускаемой нагрузки на устойчивость

где

–   см² ‑ площадь поперечного сечения двутавра № 36 (берется по сортаменту).

2.  Подбор рационального поперечного сечения стержня.

Рациональным поперечным сечением является сечение, у которого главные моменты инерции одинаковые . У стандартных прокатных профилей моменты инерции  и  значительно отличаются (например, для двутавра I № 36 , ). В расчетах на устойчивость используется минимальный момент инерции . Максимальный момент инерции , не используемый в расчетах на устойчивость, косвенно свидетельствует о наличии перерасхода материала.

Рациональное поперечное сечение может быть сконструировано с помощью двух одинаковых прокатных профилей. (рис. 3.11,б). Варьируя значение величины а (или с), можно для любого номера швеллера добиться выполнения условия  . Момент инерции  двух швеллеров равен  ( – осевой момент инерции швеллера, определяется по номеру швеллера).

При подборе рационального поперечного сечения стержня, определенная ранее величина допускаемой нагрузки , принимается в качестве исходной

Формула (3.19) переписывается в виде

                                                    (3. 21)

В правую часть формулы (3.21) входит коэффициент , который зависит от площади , так как , а . Такие уравнения решаются методом последовательных приближений.

На первом шаге назначается среднее значение коэффициента . Подстановка  в формулу (3.21) дает величину требуемой площади поперечного сечения .

Площадь одного швеллера

По сортаменту “Швеллеры” (Приложение 2) по величине  подбирается номер прокатного профиля, площадь поперечного сечения которого , это швеллер [ № 27 (, ).

Осевые моменты инерции рационального поперечного сечения одинаковые . Вычисляется минимальный радиус инерции рационального сечения

Определяется гибкость стержня

По таблице “Коэффициент продольного изгиба ” (Приложение 3) для  и материала Ст. 4, 3, 2 находится . Допускаемые напряжения на устойчивость .

Вычисляются нормальные напряжения

Эти напряжения сравниваются с . Недонапряжение составляет

Необходимо продолжить подбор.

В начале второго шага приближения выбираем

,

затем из (3.21) определяем площадь, выбираем швеллер, определяем гибкость стержня, определяем , вычисляем  и , проверяем выполнение условия

.

Если оно верно, то подбор сечения закончен, если нет – необходимо переходить к следующему шагу приближения, который выполняется аналогично.

В данном примере необходимо сделать четыре шага приближения. В результате выбираем швеллер № 16   (,). В этом случае

Перенапряжение . Так как величина перенапряжения составляет менее , то расчет можно считать выполненным.

Таким образом, выбрано рациональное сечение стержня в виде двух швеллеров № 16.

За счет рационального проектирования поперечного сечения стержня достигнут экономический эффект, который может быть оценен путем сравнения начальной площади  поперечного сечения и конечной :

Для определения линейного размера c (рис. 3.11, б) составляется выражение осевого момента инерции рационального сечения стержня относительно оси

y

Так как

,

то

,

В результате решения данного квадратного уравнения определяется значение .

Таким образом, выполнены расчет и проектирование рационального поперечного сечения центрально сжатого стержня.

4.  ЛАБОРАТОРНЫЙ ПРАКТИКУМ

4.1.  Лабораторная работа №5. “Определение реакции лишней связи в статически неопределимой балке”

Цель опыта: сравнение теоретической и опытной величин реакции лишней связи.

Постановка опыта.

Рис.4.1

Методика проведения опыта.

После ознакомления с опытной установкой в журнал наблюдений записываются величины l, c, P.

Фиксируется начальный отсчет  прибора (рис.4.1). К балке прикладывается груз P заданной величины. Под действием груза P происходит искривление оси балки, что приводит к изменению показания прибора. С помощью коромысла к балке прикладывается второй груз Q. Варьированием величины груза Q можно изменять показания прибора. В опыте требуется подобрать такую величину  груза, при котором прибор будет показывать начальный отсчет . Найденное значение  соответствует искомой величине реакции лишней связи.

Теоретический расчет.

Реакция  лишней связи определяется из канонического уравнения метода сил

Коэффициенты  и  определяются по формуле Симпсона

Ординаты определяются с помощью грузовой и единичной эпюр изгибающего момента (рис.4.2).

Геометрические характеристики плоского поперечного сечения 3 элемента (полоса, швеллер, уголок) 024

Рис. 1

Дано схему поперечного сечения, составленную из трех элементов (рис. 1). Определить геометрические характеристики составного сечения. Площадь, центр тяжести, положение главных осей, главные моменты инерции, главные радиусы инерции, главные моменты сопротивления и построить эллипс инерции. План выполнения задачи: 1) Геометрические характеристики элементов сечения. 2) Положение центра тяжести сечения. 3) Моменты инерции относительно центральных осей. 4) Положение главных осей. 5) Определение главных моментов инерции. 6) Главные радиусы инерции. 7) Определение главных моментов сопротивления.

1) Выписываем из таблицы сортамента (ГОСТ 8240-72 и ГОСТ 8509-86) необходимые геометрические характеристики для швеллера, уголка и вычисляем по формулам прямоугольника:

а) Полоса (прямоугольник) 240Х18

см 2, см 4, см 4,

 

б) Швеллер №33

см 2, см 4, см 4, см, см, см.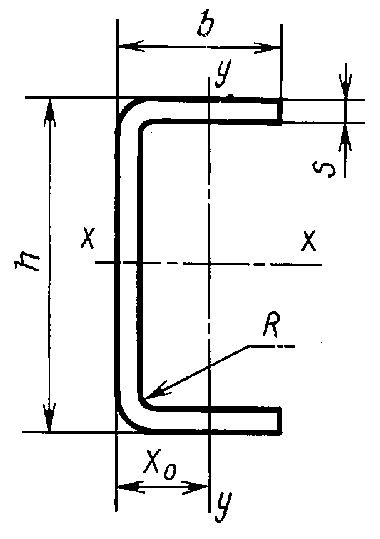

 

в) Уголок 50Х5

см 2, см 4, см 4, см 4, см, см.

 

2) Определяем положение центра тяжести сечения относительно начальных осей (осей полосы)

На отдельном листе бумаги в масштабе чертим схему поперечного сечения (рис. 2) и указываем положение центральных осей каждого элемента. Выполняем привязку (указываем расстояния) центров тяжести каждого элемента относительно начальных осей

Координаты центров тяжести элементов в осях

см,

см,

см,

см.

Рис. 2

Площадь поперечного сечения:

см ²,

Координаты центра тяжести сечения:

см,

см.

Откладываем на рисунке координаты и с учетом знаков, обозначаем положение центра тяжести (точка С) и проводим центральные оси

Контролируем достоверность определения положения центра тяжести сложного сечения. Для этого вычисляем координаты центров тяжести элементов сечения в координатных осях и (расстояния между собственными центральными осями отдельных элементов и центральными осями сечения):

см, см, см.

см, см, см.

и статические моменты площади сечения относительно центральных осей:

см ³,

погрешность:

см ³,

погрешность:

3) На основании формул параллельного перехода вычисляем моменты инерции сечения относительно центральных осей и

– осевые

см ⁴,

см ⁴,

– центробежный

см ⁴.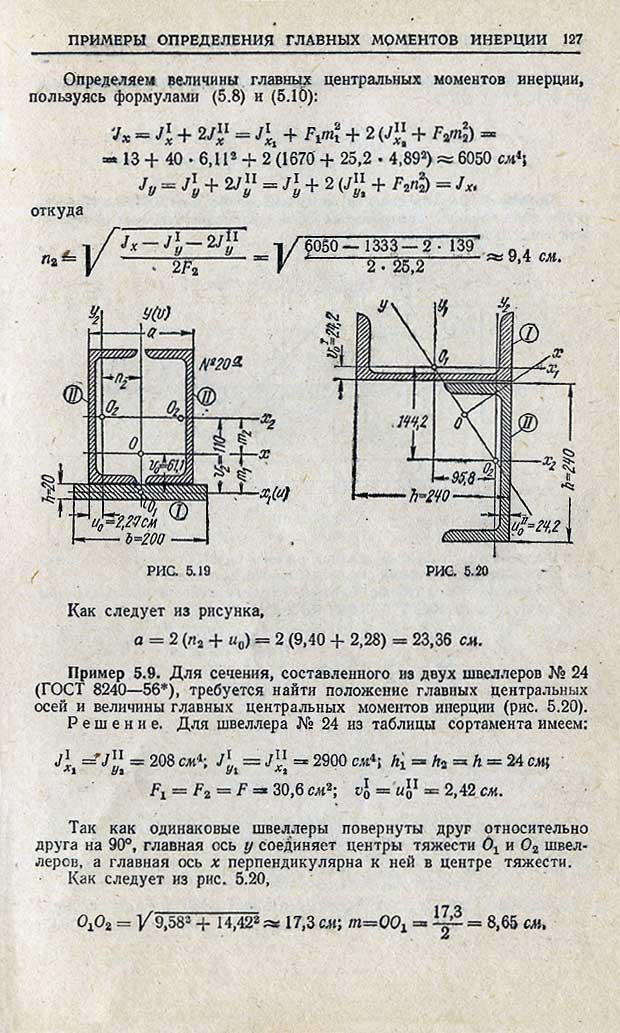

4) Определяем положение главных центральных осей инерции:

Отсюда

На рисунке откладываем положительный угол против часовой стрелки и чертим главные центральные оси инерции (рис. 3).

5) Для определения величин главных центральных моментов инерции используем три вида формул.

а)

см ⁴,

см ⁴,

Для проверки правильности нахождения главных моментов инерции, определяем центробежный момент инерции относительно главных осей:

,

погрешность:

б)

см ⁴,

см ⁴,

в)

.

Поскольку , то

см ⁴,

см ⁴.

Проверяем условие инвариантности осевых моментов инерции:

см ⁴,

см ⁴.

6) Вычисляем главные радиусы инерции:

см,

см,

и строим эллипс инерции (рис. 3). Определяем графически радиусы инерции относительно осей

см, см.

Вычисляем моменты инерции относительно этих осей:

см ⁴,

см ⁴,

и сравниваем с ранее вычисленными значениями:

см ⁴, см ⁴.

7) Определяем главные моменты сопротивления и

Наиболее удаленной точкой от оси является точка а от оси – точка Измеряя на рисунке расстояния до этих точек от соответствующих главных осей, находим: см, см.

Проверяем по формулам:

см,

см.

Главные моменты сопротивления:

см ³,

см ³.

Рис. 3

Понравилась статья! Поддержи проект! Ставь ЛАЙК!

Задача на подбор сечения и проверку прочности. Касательное напряжение и энергетический критерий прочности

Проектный и проверочный расчеты. Для балки с построенными эпюрами внутренних усилий  подобрать сечение в виде двух швеллеров из условия прочности по нормальным напряжениям. Проверить прочность  балки, используя условие прочности по касательным напряжениям и энергетический критерий прочности. Дано:

Покажем балку с построенными эпюрами Q и М

Согласно эпюре изгибающих моментов опасным является сечение С, в котором М_С=М_max=48,3кНм.

Условие прочности по нормальным напряжениям для данной балки имеет вид σ_max=M_C/W_X≤σ_adm. Требуется подобрать сечение из двух швеллеров.

Определим необходимое расчетное значение осевого момента сопротивления сечения:

Для сечения в виде двух швеллеров согласно сортаменту прокатной стали принимаем два швеллера №20а, момент инерции каждого швеллера I_x=1670см⁴, тогда осевой момент сопротивления всего сечения:

Перенапряжение (недонапряжение) в опасных точках  посчитаем по формуле: Тогда получим недонапряжение:

Теперь проверим прочность балки, исходя из условия прочности по касательным напряжениям.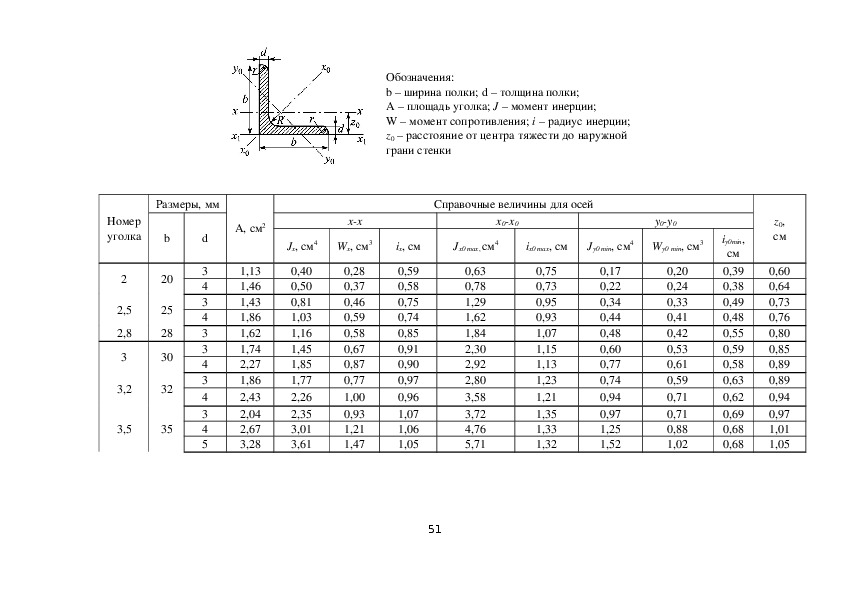  Согласно эпюре поперечных сил  опасными являются сечения на участке ВС и сечение D. Как видно из эпюры,  Q_max=48,9 кН.

Условие прочности по касательным напряжениям имеет вид:

Для швеллера №20 а:  статический момент площади S_x1=95,9 см³, момент инерции сечения I_x1=1670 см⁴, толщина стенки d₁=5,2 мм, средняя толщина полки t₁=9,7 мм, высота швеллера h₁=20 см, ширина полки b₁=8 см.

Для поперечного сечения из двух швеллеров:

S_x= 2S_x1=2·95,9=191,8 см³,

I_x=2I_x1=2·1670=3340 см⁴,

b=2d₁=2·0,52=1,04 см.

Определяем значение максимального касательного  напряжения:

τ_max=48,9·10³·191,8·10⁻⁶/3340·10⁻⁸·1,04·10⁻²=27МПа.

Как видно, τ_max <τ_adm (27МПа<75МПа).

Следовательно, условие прочности выполняется.

Проверяем прочность балки по энергетическому критерию.

Из рассмотрения эпюр Q и М следует, что опасным является сечение С, в котором действуют M_C=M_max=48,3 кНм и Q_C=Q_max=48,9 кН.

Проведем анализ напряженного состояния в точках сечения С 

Схема сечения балки и эпюры напряжений для анализа напряженного состояния

Определим нормальные и касательные напряжения на нескольких уровнях (отмечены на схеме сечения)

Уровень 1-1: y_1-1=h₁/2=20/2=10см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 2−2: y_2-2=h₁/2−t₁=20/2−0,97=9,03см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 3−3: y_3-3=h₁/2−t₁=20/2−0,97=9,03см.

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 4−4:    y_4-4=0.

Нормальные и касательные напряжения:(в середине нормальные напряжения равны нулю, касательные максимальны, их находили в проверке прочности по касательным напряжениям)

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 5−5:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

Уровень 6−6:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

 Уровень 7−7:

Нормальные и касательные напряжения:

Главные напряжения:

Экстремальные касательные напряжения:

В соответствии с выполненными расчетами эпюры напряжений σ, τ, σ₁, σ₃, τ_max и τ_min представлены на рис. Схема сечения балки и эпюры напряжений для анализа напряженного состояния

Анализ этих эпюр показывает, что в сечении балки опасными являются точки на уровне 3-3 (или 5-5), в которых: 

Используя энергетический критерий прочности, получим

Из сравнения эквивалентного и допускаемого напряжений следует, что условие прочности также выполняется  

 (135,3 МПа<150 МПа).

 

 

 

3.

Существует два типа модулей сечения: модуль упругого сечения и модуль пластического сечения. Модуль упругости сечения применяется к конструкциям, которые находятся в пределах предела упругости материала, что является наиболее распространенным случаем. Часто «модуль упругости сечения» называют просто «модулем сечения».

Модуль сопротивления сечения используется в проектировании конструкций для расчета изгибающего момента, который приводит к деформации балки, по следующему уравнению:

где

• S = момент сопротивления
• σ _y = предел текучести материала

Балки при изгибе испытывают напряжения как растяжения, так и сжатия.

Содержание

• Секционные модуль Калькуляторы
  • Секция модуля секции прямоугольного калькулятора
  • Секционные модуль калькулятора I-лучи
  • Секция модуля Circle Calculator
  • SECE SECT Калькулятор полых прямоугольников
  • Калькулятор модуля сечения C-канала
• Какова формула модуля сечения?
• Каков требуемый модуль сопротивления сечения?
• Как найти момент сопротивления неправильной формы?
• В чем разница между модулем сопротивления и модулем пластичности?
• В чем разница между моментом инерции и модулем сечения?
• Как увеличить момент сопротивления?

Калькуляторы модуля упругости

Используйте приведенные ниже калькуляторы для расчета модулей упругого сечения обычных форм, таких как прямоугольники, двутавровые балки, круги, трубы, полые прямоугольники и с-образные каналы, которые подвергаются изгибу. Постоянные единицы необходимы для каждого калькулятора, чтобы получить правильные результаты.

Калькулятор модуля сечения прямоугольника

Уравнение для расчета модуля упругости сечения прямоугольника:

где

• b = ширина сечения
• h = высота секции

Калькулятор модуля упругости двутавровой балки

Модуль упругости двутавровой балки рассчитывается по следующему уравнению:

H = высота двутавровой балки

b = ширина полки минус ширина стенки

h = высота стенки

Калькулятор модуля сечения окружности

Приведенное ниже уравнение используется для расчета модуля упругости сечения окружности:

, где

D = диаметр круга

Секция модуля секции калькулятора с полым кружком

Формула для расчета модуля упругости для трубы показана ниже:

, где

• . d1 = внутренний диаметр = 2 x внутренний радиус
• d2 = внешний диаметр = 2 x внешний радиус

Калькулятор модуля сечения полого прямоугольника

Для полого прямоугольника модуль упругого сечения можно определить по следующей формуле:

где

• B = внешняя ширина
• H = внешняя высота
• b = внутренняя (полая) ширина
• h = внутренняя (полая) высота

Калькулятор модуля сечения С-канала

Модуль упругости сечения С-канала рассчитывается по следующему уравнению:

где

• B = ширина полки
• H = общая высота
• b = ширина полки минус толщина стенки
• h = высота стенки

Какова формула модуля сечения?

Общая формула модуля упругости поперечного сечения:

где

I = момент инерции площади (или второй момент площади)

y = расстояние от нейтральной оси наружу край балки

Какой требуемый модуль упругости?

Требуемый модуль упругости можно рассчитать, если известны изгибающий момент и предел текучести материала. Рассмотрим следующий пример:

Балка из стали A36 должна подвергаться нагрузке в 120 000 фунт-сила-дюйм. Рассчитайте необходимый модуль сопротивления сечения с запасом прочности 2.

Перепишите уравнение из начала этого поста в следующий вид:

Допустимое напряжение в

Сталь A36 имеет предел текучести 36 000 фунтов на квадратный дюйм. Таким образом, требуемый модуль сопротивления сечения для достижения коэффициента запаса прочности 2 при изгибе рассчитывается, как показано ниже:

Для этого примера задачи требуемый модуль сопротивления составляет 6,67 дюйма3.

Как найти момент сопротивления неправильной формы?

Даже если форма не имеет предварительно заданного уравнения модуля сечения, все равно можно рассчитать модуль ее сечения.

Напомним, что модуль сопротивления равен I/y, где I — момент инерции площади. Определение момента инерции:

, где

дА = площадь элемента площади поперечного сечения неправильной формы

l = перпендикулярное расстояние от элемента до нейтральной оси, проходящей через центр тяжести

Таким образом, модуль сечения неправильной формы может быть определен как

Это может быть очень сложной задачей для выполнения с высоким уровнем точности для неправильной формы. По этой причине в таких случаях обычно используют специализированное программное обеспечение для расчета модуля сечения.

В чем разница между модулем упругости и модулем упругости?

Когда используется термин модуль упругости, он обычно относится к модулю упругости. Это наиболее распространенное использование, поскольку оно имеет дело с материалами, которые находятся в пределах своего предела упругости или имеют напряжения меньше, чем предел текучести.

Модуль пластического сечения, однако, используется, когда материалу позволено поддаваться текучести и пластически деформироваться. Очень редко секции допускают текучесть, поэтому модуль пластического сечения используется редко.

В чем разница между моментом инерции и модулем сечения?

Термин «момент инерции» используется в двух случаях:

• Момент инерции площади: геометрическое свойство поперечного сечения (также известное как второй момент площади)
• Момент инерции массы или полярный момент инерции: сопротивление массы изменению скорости вращения

Модуль упругости и момент инерции площади тесно связаны между собой, поскольку оба они являются свойствами площади поперечного сечения балки.

Момент инерции площади можно использовать для расчета напряжения в балке из-за приложенного изгибающего момента на любом расстоянии от нейтральной оси с использованием следующего уравнения:

где σ — напряжение в балке, y — расстояние от нейтральной оси, проходящей через центр тяжести, а I — момент инерции площади. 92.

Как увеличить модуль сопротивления?

Модуль упругости можно увеличить вместе с площадью поперечного сечения, хотя некоторые методы более эффективны, чем другие. Возьмем, к примеру, прямоугольное поперечное сечение, модуль сечения которого определяется следующим уравнением:

Удвоение ширины прямоугольника b увеличит модуль сечения в 2 раза. Однако удвоение высоты креста -section увеличит модуль сечения в 4 раза. Это был бы гораздо более эффективный способ использования материала для увеличения модуля сечения.

Определение, типы, формула с выводом

В этой статье вы узнаете полный обзор модуля сечения, такой как его определение, типы, формула с выводом для различных сечений и многое другое.

Давайте подробно узнаем о каждом из аспектов, связанных с модулем сечения.

Модуль сопротивления сечения

Модуль сопротивления сечения — это геометрическое свойство, используемое для расчета изгибающих напряжений в элементе конструкции.

Математически,

Определяется как отношение момента инерции сечения относительно его центральной оси к расстоянию крайнего слоя от нейтральной оси.

Обозначается Z.

Z = I/ymax

Математически По уравнению напряжения изгиба

M/I = σmax/ymax

M = σmax × (I/ymax) =

σmax × Z

Где,

I = момент инерции (м⁴)

y = расстояние от северной широты до крайнего слоя (м)

Единицей модуля упругости является м³.

Типы модуля упругости сечения

Существует два типа модуля сечения:

• Модуль упругости сечения
• Модуль упругости сечения

Модуль упругости сечения

Модуль упругости сечения, пока мы не вычислим поведение материала, пока не будет рассчитано поведение материала. предел текучести.

В целях общего проектирования мы используем модуль упругости сечения.

Обычно модуль упругого сечения обозначается Zₑ.

Итак,

Zₑ = I/ymax

Где,

I = Момент инерции 

ymax = Расстояние от Северной Америки до крайнего слоя модуль:

Прямоугольное сечение

Поскольку мы знаем момент инерции прямоугольного сечения, 

I = bd³/12

И расстояние от нейтральной оси,

ymax = d/2

Итак,

Zₑ = I/ymax

Zₑ = (bd³/12)/(d/2)

После их расчета,

Момент сопротивления прямоугольного сечения,

50/ Zₑ = b²

Полое прямоугольное сечение

Как мы знаем момент инерции полого прямоугольного сечения,

I = (BD³/12) – (bd³/12)

ymax = D/2

После подстановки этих значений,

Zₑ = I/ymax

(BD³/12) – (bd³/12)/(D/2)

9Тогда {(π/64) × d⁴}/(d/2)

После расчета найти значения момента сопротивления сплошного круга

Zₑ = (π/32) × d³

Полый круг

Момент инерция полого круга,

I = (π/64) × (D⁴ – d⁴)

А,

ymax = D/2

После ввода этих значений

Zₑ = (π/64) × (D⁴ – d⁴)/(D/2)

Zₑ = π/32 × {(D⁴ – d⁴)/D}

Симметричный Секция КИПиА

Момент инерции секции КИПиА,

I = (BD³/12) – {(B – b)d³}/12

ymax = D/2

Итак,

Zₑ = [(BD³/12) – {(B – b)d³}/12]/(D/2)

Zₑ = {BD³ – (B – b)d³}/6D

Алмаз

Эластичная секция модуль для алмаза,

Zₑ = bd²/24

Модуль пластического сечения

Модуль пластического сечения используется для материалов, для которых предел текучести является приемлемым, а пластическое поведение считается приемлемым диапазоном.

Зависит от расположения пластиковой нейтральной оси. PNA – это ось, которая делит поперечное сечение пополам так, что сжимающая сила со стороны сжимаемой области равна силе растяжения со стороны растягиваемой области. Так, для сечений с постоянным пределом текучести площади над и под ПНА будут равны, а для смешанных сечений это не обязательно.

Математически,

Модуль пластического сечения представляет собой сумму площадей поперечных сечений по обе стороны от нейтральной пластической оси, которые могут быть равны или не равны, и умножить на расстояние от местного центра тяжести двух областей до пластиковая нейтральная ось.

Zₚ = (Ac × yc) + (Aₜ + yₜ)

Где,

Ac = площадь поперечного сечения при сжатии.

Aₜ = площадь поперечного сечения под напряжением.

yc = Расстояние от нейтральной пластической оси до центра тяжести сжимаемых областей.

yₜ = Расстояние от нейтральной пластической оси до центра тяжести областей, находящихся под напряжением.

Так как на нейтральной оси площадь при сжатии равна площади при растяжении.

So,

Ac = Aₜ

And,

yc = yₜ

Plastic Section Modulus of Different Section

There are following section modulus for different section:

Rectangular Section

As we know ,

на нейтральной оси площадь при сжатии равна площади при растяжении.

SO,

AC = Aₜ

и,

YC = Yₜ

AC = Aₜ = BD/2

YC = Yₜ = D/4

SO,

Zₚ = (AC × YC) + + (Aₜ + yₜ)

Zₚ = (bd/2 × d/4) + (bd/2 × d/4))

После вычисления

Zₚ = bd²/4

момент сопротивления прямоугольного полого профиля,

Zₚ = (bd²/4) – (b- 2t) × {(b/2) – t}²

Круговое сечение

Как мы знаем, на нейтральной оси площадь сжатия равна участок под напряжением.

Итак,

Ac = Aₜ = πd²/8

yc = yₜ = 2d/3π

Zₚ = (πd²/8 × 2d/3π) + (πd²/8 × 2d/3π) 

После

Zₚ = d³/6

Аналогичным образом можно рассчитать момент сопротивления круглого полого сечения,

Круглое полое сечение,

Zₚ = (D³ – D ним)/6

Связанная статья:

Buckling

Модуль устойчиво аспекты, связанные с модулем сечения . Если у вас есть какие-либо сомнения, вы можете задать их мне по почте или на странице контактов.

Спасибо.

Свойства поперечного сечения | MechaniCalc

База данных

ИнструкцииСправочник

База данных поперечных сечений

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

---

Поведение элемента конструкции определяется его материалом и геометрией. Эта ссылка посвящена влиянию геометрии на поведение элемента конструкции. Поперечное сечение и длина элемента конструкции влияют на то, насколько этот элемент прогибается под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе под данной нагрузкой.

Свойства областей

Центроид

Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения. Если область дважды симметрична относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центроид лежит где-то вдоль этой оси (необходимо вычислить другую координату). Если точное местоположение центроида не может быть определено осмотром, его можно рассчитать следующим образом:

где dA представляет собой площадь бесконечно малого элемента, A представляет собой общую площадь поперечного сечения, а x и y представляют собой координаты элемента dA относительно оси интереса.

Центроидальное расположение общих поперечных сечений хорошо задокументировано, поэтому обычно нет необходимости вычислять местоположение с помощью приведенных выше уравнений.

Если поперечное сечение состоит из набора основных форм, центральные положения которых известны относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:

где x _c,i и y _c,i — прямоугольные координаты центра тяжести сечения i ^th относительно опорной точки, а A _i — площадь i ^th раздел.

Центральное расстояние

центроидальное расстояние , с, представляет собой расстояние от центра тяжести поперечного сечения до крайней точки волокна. Центроидальное расстояние в направлении Y для прямоугольного поперечного сечения показано на рисунке ниже:

Общие способы использования центроидального расстояния включают:

• расчет максимального напряжения изгиба в поперечном сечении
• вычисление значения первого момента площади Q над точкой в ​​поперечном сечении для определения напряжения сдвига в этой точке

---

---

Первый момент области

Первый момент площади указывает распределение площади относительно некоторой оси. Первый момент площади относительно интересующей оси рассчитывается как:

Q x = ∫ y дА

Q y = ∫ x dA

где Q _x — первый момент относительно оси x, а Q _y — первый момент относительно оси y.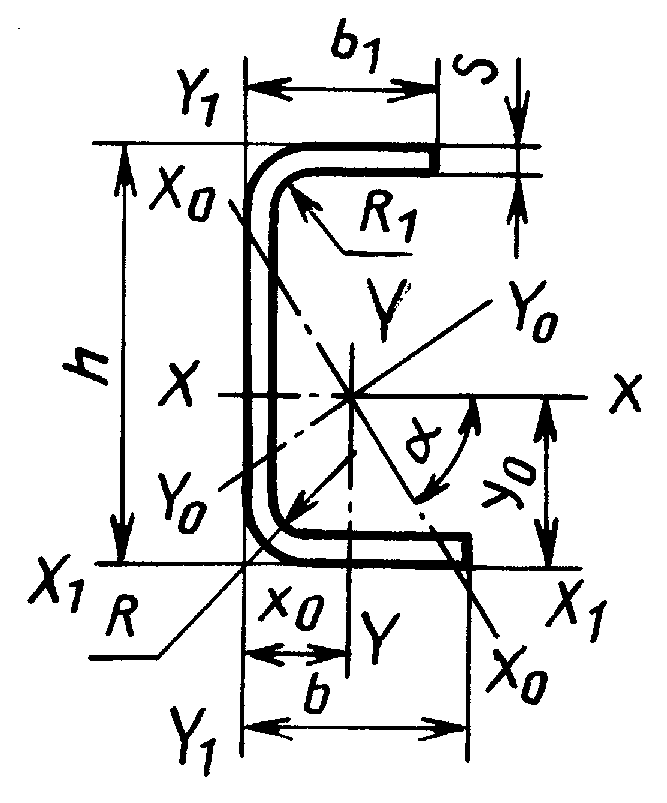 Значения x и y указывают положение относительно оси интереса бесконечно малых площадей dA каждого элемента при выполнении интегрирования.

Если область состоит из набора основных форм, центральные положения которых известны относительно оси интереса, то первый момент составной области можно рассчитать как:

Если вы сравните приведенные выше уравнения для Q с уравнениями для расчета центроида (обсуждаемыми в предыдущем разделе), вы увидите, что мы фактически используем первый момент площади при расчете центроидального местоположения относительно интересующего источника.

Первый момент также используется при расчете величины касательного напряжения в той или иной точке поперечного сечения. Напомним, что касательное напряжение в любой точке, расположенной на расстоянии y ₁ от центра тяжести поперечного сечения рассчитывается как:

где Q — первый момент площади между точкой y ₁ и крайним волокном (верхним или нижним) сечения. Рассмотрим рисунок ниже. Нас интересует расчет касательного напряжения в точке, расположенной на расстоянии y ₁ от центра тяжести поперечного сечения. Мы можем рассчитать первый момент площади выше или ниже этого местоположения. В этом случае точка интереса находится выше нейтральной оси, поэтому проще рассмотреть верхнюю область, которая на рисунке ниже заштрихована синим цветом. Эта область простирается от точки y ₁ до крайнего волокна в верхней части поперечного сечения.

Первый момент относительно оси x области, заштрихованной синим цветом на рисунке выше, рассчитывается относительно центра тяжести поперечного сечения (точка O на рисунке) как:

Если центроидальное расположение интересующей области известно, то первый момент области относительно центроида упрощается до (см. Рисунок выше):

Q _сх = у _с1 А ₁

Следует отметить, что первый момент области может быть либо положительным, либо отрицательным в зависимости от положения области относительно оси интереса. Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида равен нулю.

Площадь момента инерции

Второй момент площади, более известный как момент инерции , I поперечного сечения, является показателем способности элемента конструкции сопротивляться изгибу. ^{(Примечание 1)} I _x и I _y — моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:

I x = ∫ y 2 дА

I y = ∫ x 2 дА

где x и y — координаты элемента dA относительно оси интереса.

Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения. В этом случае они обозначаются как центроидальные моменты инерции и обозначаются как I _cx для инерции относительно оси x и I _cy для инерции относительно оси y.

Моменты инерции обычных поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений.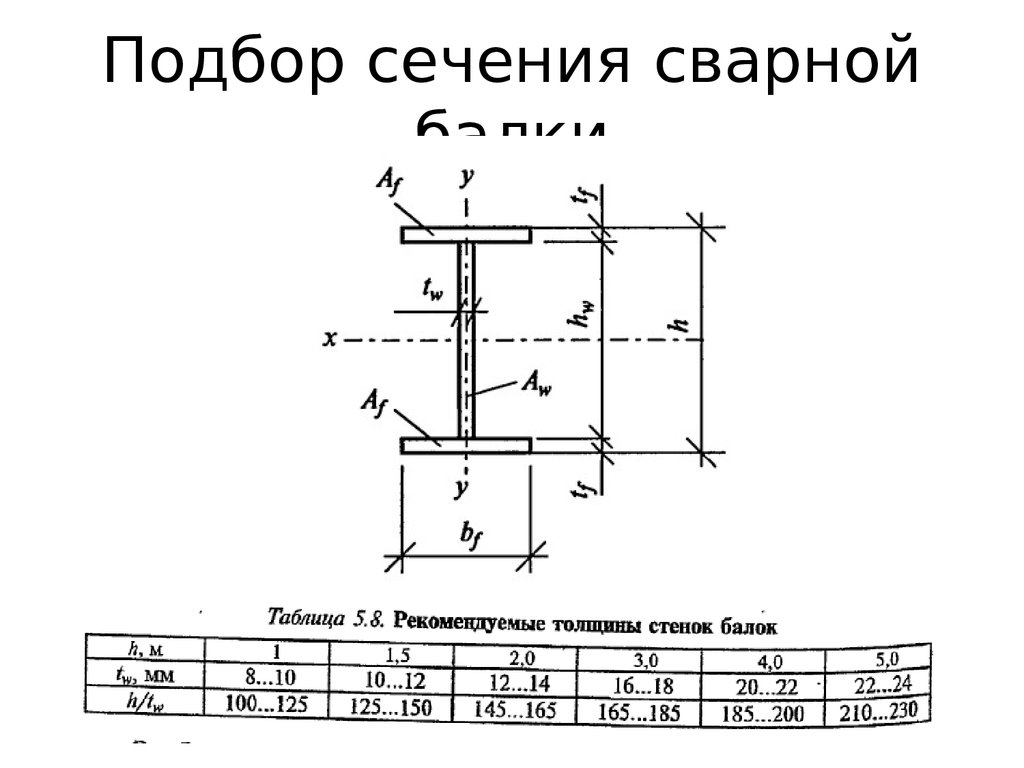 Свойства нескольких общих сечений приведены в конце этой страницы.

Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения представляет собой просто сумму отдельных моментов инерции. Примером этого является коробчатая балка, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя секция имеет «положительную площадь», а внутренняя секция имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней секции из внешней секции.

В случае более сложного составного поперечного сечения, в котором положения центров не совпадают, момент инерции можно рассчитать с помощью теоремы о параллельности осей .

Важно не путать момент инерции площади с моментом инерции массы твердого тела. Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.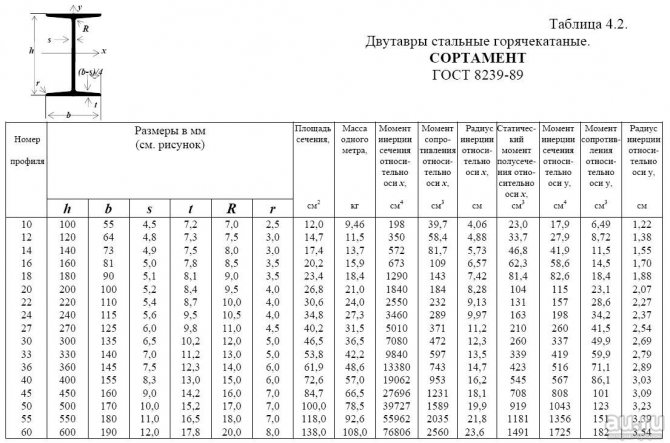

---

---

Теорема о параллельных осях

Если известен момент инерции поперечного сечения относительно центральной оси, то можно использовать теорему о параллельной оси для расчета момента инерции относительно любой параллельной оси:

I _{параллельная ось} = I _c +; А д ²

где I _c — момент инерции относительно центральной оси, d — расстояние между центральной осью и параллельной осью, а A — площадь поперечного сечения.

Если поперечное сечение состоит из набора основных форм, центральные моменты инерции которых известны вместе с расстояниями от центроидов до некоторой контрольной точки, то теорему о параллельных осях можно использовать для расчета момента инерции составного поперечного сечения.

Например, двутавровая балка может быть аппроксимирована тремя прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения может быть расположен путем осмотра на пересечении этих осей. Центроид расположен в начале координат O на рисунке.

Момент инерции составного сечения можно рассчитать, используя теорему о параллельных осях. Центроидальный момент инерции секции относительно оси x I _cx рассчитывается как:

I _cx.IBeam = I _cx.W +плюс; ( I _cx.F1 + A _F1 d ₁ ² ) + ( I _cx.F2 + A _F2 d ₂ ² )

где я 9Члены 0018 cx представляют собой моменты инерции отдельных сечений относительно их собственных центроидов при ориентации оси x, члены d представляют собой расстояния центроидов отдельных сечений до центроида составного сечения, а члены A равны площади отдельных секций. Поскольку центроид сечения W и центроид составного сечения совпадают, d равно нулю для этого сечения, и поэтому член Ad ² отсутствует.

Важно отметить, что следствие теоремы о параллельности осей заключается в том, что по мере удаления отдельной секции от центра тяжести составной секции вклад этой секции в момент инерции составной секции увеличивается в d 9 раз.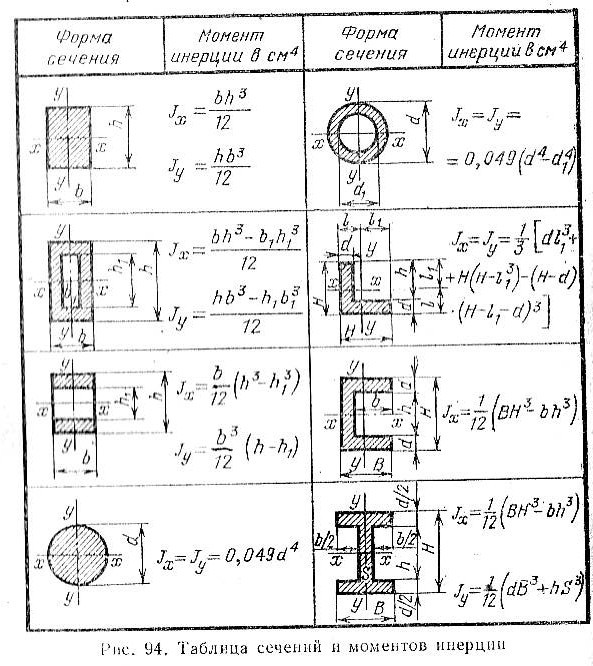 0637 2 . Поэтому, если целью является увеличение момента инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси. Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако перемычка должна сохранять некоторую толщину, чтобы избежать коробления, а также потому, что перемычка принимает на себя значительную часть напряжения сдвига в сечении.

Полярный момент инерции

Полярный момент инерции , Дж, поперечного сечения является показателем способности элемента конструкции сопротивляться кручению вокруг оси, перпендикулярной сечению. Полярный момент инерции сечения относительно оси можно рассчитать по формуле:

J = ∫ r ² dA = ∫ (x ² + y ² ) dA

где x и y — координаты элемента dA относительно оси интереса, а r — расстояние между элементом dA и осью интереса.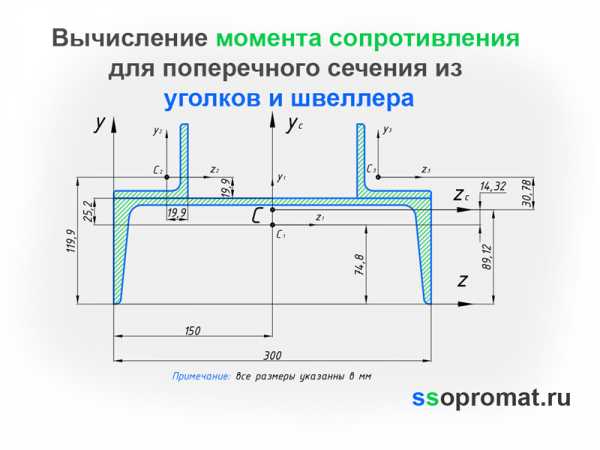

Хотя полярный момент инерции можно рассчитать с помощью приведенного выше уравнения, обычно удобнее вычислять его с помощью теоремы о перпендикулярной оси , которая утверждает, что полярный момент инерции площади представляет собой сумму моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:

Дж = I _x + я _г

Чаще всего ось интереса проходит через центр тяжести поперечного сечения.

Модуль упругости сечения

Максимальное напряжение изгиба в балке рассчитывается как σ _b = Mc / I _c , где c — расстояние от нейтральной оси до крайней оси, I _c — центроидальный момент инерции, а M — изгибающий момент. Модуль сопротивления объединяет члены c и I _c в уравнении напряжения изгиба:

S = I _с / с

Используя модуль сечения, напряжение изгиба рассчитывается как σ _b = M / S. Полезность модуля сечения заключается в том, что он характеризует сопротивление поперечного сечения изгибу в одном выражении. Это позволяет оптимизировать поперечное сечение балки для сопротивления изгибу за счет максимизации одного параметра.

Радиус вращения

Радиус вращения представляет собой расстояние от центра тяжести сечения, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется выражением:

Полярный радиус вращения также можно рассчитать для задач, связанных с кручением вокруг центральной оси:

Прямоугольные радиусы вращения также можно использовать для расчета полярного радиуса вращения:

r _p ² = r _x ² +плюс; г _г ²

---

PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице поперечных сечений. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!

Просмотреть курс сейчас:

Просмотреть курс

Свойства общих сечений

В таблице ниже приведены свойства обычных поперечных сечений. Более подробные таблицы можно найти в перечисленных ссылках.

Свойства, рассчитанные в таблице, включают площадь, центральный момент инерции, модуль сечения и радиус вращения.

Форма	Представительство	Свойства
Прямоугольник		А = чб
Круг
Круглая трубка
Двутавровая балка

---

---

Примечания

Примечание 1: Прогиб балки

Прогиб балки при изгибе определяется моментом инерции поперечного сечения, длиной балки и модулем упругости материала.