Нормальные колебания: НОРМАЛЬНЫЕ КОЛЕБАНИЯ • Большая российская энциклопедия
alexxlab | 11.04.2023 | 0 | Разное
Нормальные колебания (моды). Связанные колебательные системы
Под нормальными колебаниями (нормальными модами) понимают собственные (свободные) незатухающие гармонические колебания в замкнутых линейных колебательных системах (в них отсутствуют как потери энергии, так и приток извне колебательной энергии).
Каждое нормальное колебание характеризуется определенным значением частоты. Эти частоты называются собственными частотами системы.
Вводится
понятие степеней свободы системы. Под степенями
свободы системы понимают число независимых параметров,
описывающих возможные изменения
состояния системы. Линейные колебательные
системы (они представляют собой
гармонические осцилляторы, такие как
колебательный контур, пружинный маятник,
математический маятник) являются
системами с одной степенью свободы.
Действительно, для описания их движения
необходимо задать только один параметр.
Связанные колебательные системы представляют собой системы с двумя и более степенями свободы, рассматриваемые как совокупность систем с одной степенью свободы, взаимодействующих между собой. Колебания, возникающие в связанных системах, называют связанными колебаниями.
В дискретных
связанных системах, состоящих
из
связанных гармонических осцилляторов
(например, механических маятников,
колебательных контуров), число нормальных
колебаний равно.
Примером связанных систем могут служить два колебательных контура, связанных между собой индуктивной связью (рис. 5.27,а). Колебания в одном контуре из-за наличия связи вызывают колебания в другом, т.е. происходит переход энергии из одного контура в другой. Число нормальных колебаний для таких контуров равно двум.
Рис. 5.27
В линейных распределенных системах (струна, мембрана, резонатор) существует бесконечное, но счетное множество нормальных колебаний.
Произвольное свободное колебание системы может быть представлено в виде суперпозиции нормальных колебаний. При этом полная энергия движения распадается на сумму энергий отдельных нормальных колебаний.
Примером
такой системы являются колебания струны,
закрепленной на концах. Возбуждение в
ней поперечных колебаний приводит к
образованию стоячей волны, узлы которой
приходятся на закрепленные концы (рис.
5.27,в). На длине струны
укладывается целое число полуволн
, , n=1,2,3,… . (5.92)
Все частоты представляют собой частоты нормальных колебаний струны, частота, соответствующаяn=1, называется основной частотой. Основную частоту можно изменить, уменьшая или увеличивая натяжение струны
, (5.93)
где F – сила натяжения струны; ρ, S – плотность материала струны и площадь ее поперечного сечения соответственно.Любое колебание струны можно представить в виде суммы ее нормальных колебаний. Таким образом, линейная распределенная система ведет себя как набор независимых гармонических осцилляторов.
Полученная
формула (5.92) используется, в частности,
для определения спектра частот нормальных
колебаний кристаллической решетки,
связанных с тепловыми колебаниями
атомов.
Резонанс в системах с несколькими степенями свободы. При внешнем возбуждении системы нормальные колебания в значительной мере определяют ее резонансные свойства. Резонанс может возникнуть лишь в том случае, когда частота гармонического внешнего воздействия близка к одной из собственных частот системы, либо к их линейной комбинации, если внешнее воздействие меняет параметры системы (параметрический резонанс).
В линейном приближении собственные колебания этих систем представляют собой набор нормальных колебаний (мод). Если отклик системы представляет собой суммарный отклик всех степеней свободы, то тогда резонансная кривая будет наложением резонансных кривых отдельных нормальных колебаний и может иметь сложный характер.
Так,
в системе с двумя степенями свободы,
ввиду того, что собственные колебания
могут происходить с двумя различными
частотами, резонанс наступает при
совпадении частоты гармонического
внешнего воздействия как с одной, так
и с другой нормальной частотой системы.
Подбором параметров нормальных колебаний
можно создать резонансную кривую любой
формы, что широко используется, например,
в радиотехнике для создания фильтрации
частот (рис. 5.27,б).
Наличие связи изменяет характер резонансных явлений в связанных системах по сравнению с одиночным контуром. В связанных системах резонанс наступает всякий раз, когда частота внешнего воздействия совпадает с одной из частот собственных колебаний всей системы, отличающихся от собственных частот отдельных контуров. Например, в связанных системах, состоящих из двух контуров, резонанс наступает на двух резонансных частотах. При этом для двух слабо взаимодействующих систем с близкими собственными частотами колебаний может происходить резонансная перекачка энергии из одной подсистемы в другую.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А
%PDF-1.6 % 1 0 obj > /Outlines 2 0 R /Metadata 3 0 R /AcroForm 4 0 R /Pages 5 0 R /StructTreeRoot 6 0 R /Type /Catalog /Lang (ru-RU) >> endobj 7 0 obj /Creator /Producer /ModDate (D:20140523145532+06’00’) /Title >> endobj 2 0 obj > endobj 3 0 obj > stream application/pdf
Шариков
64 595.32]
/Parent 14 0 R
/Resources >
/Font >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XObject >
>>
/Rotate 0
/StructParents 10
/Tabs /S
/Type /Page
>>
endobj
30 0 obj
>
/MediaBox [0 0 419.64 595.32]
/Parent 14 0 R
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XObject >
>>
/Rotate 0
/StructParents 11
/Tabs /S
/Type /Page
>>
endobj
31 0 obj
>
/MediaBox [0 0 419.64 595.32]
/Parent 14 0 R
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Rotate 0
/StructParents 12
/Tabs /S
/Type /Page
>>
endobj
32 0 obj
>
/MediaBox [0 0 419.64 595.32]
/Parent 14 0 R
/Resources >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
/XObject >
>>
/Rotate 0
/StructParents 13
/Tabs /S
/Type /Page
>>
endobj
33 0 obj
>
endobj
34 0 obj
>
endobj
35 0 obj
>
endobj
36 0 obj
>
endobj
37 0 obj
>
endobj
38 0 obj
>
endobj
39 0 obj
>
endobj
40 0 obj
>
endobj
41 0 obj
>
endobj
42 0 obj
>
endobj
43 0 obj
>
endobj
44 0 obj
>
endobj
45 0 obj
>
endobj
46 0 obj
>
endobj
47 0 obj
>
endobj
48 0 obj
>
endobj
49 0 obj
>
endobj
50 0 obj
>
endobj
51 0 obj
>
endobj
52 0 obj
>
endobj
53 0 obj
>
endobj
54 0 obj
>
endobj
55 0 obj
>
endobj
56 0 obj
>
endobj
57 0 obj
>
endobj
58 0 obj
>
endobj
59 0 obj
>
endobj
60 0 obj
>
endobj
61 0 obj
>
endobj
62 0 obj
>
endobj
63 0 obj
>
endobj
64 0 obj
>
endobj
65 0 obj
>
endobj
66 0 obj
>
endobj
67 0 obj
>
endobj
68 0 obj
>
endobj
69 0 obj
>
endobj
70 0 obj
>
endobj
71 0 obj
>
endobj
72 0 obj
>
endobj
73 0 obj
>
endobj
74 0 obj
>
endobj
75 0 obj
>
endobj
76 0 obj
>
endobj
77 0 obj
>
endobj
78 0 obj
>
endobj
79 0 obj
>
endobj
80 0 obj
>
endobj
81 0 obj
>
endobj
82 0 obj
>
endobj
83 0 obj
>
endobj
84 0 obj
>
endobj
85 0 obj
>
endobj
86 0 obj
>
endobj
87 0 obj
>
endobj
88 0 obj
>
endobj
89 0 obj
>
endobj
90 0 obj
>
endobj
91 0 obj
>
endobj
92 0 obj
>
endobj
93 0 obj
>
endobj
94 0 obj
>
endobj
95 0 obj
>
endobj
96 0 obj
>
endobj
97 0 obj
>
endobj
98 0 obj
>
endobj
99 0 obj
>
endobj
100 0 obj
>
endobj
101 0 obj
>
endobj
102 0 obj
>
endobj
103 0 obj
>
endobj
104 0 obj
>
endobj
105 0 obj
>
endobj
106 0 obj
>
endobj
107 0 obj
>
endobj
108 0 obj
>
endobj
109 0 obj
>
endobj
110 0 obj
>
endobj
111 0 obj
>
endobj
112 0 obj
>
endobj
113 0 obj
>
endobj
114 0 obj
>
endobj
115 0 obj
>
endobj
116 0 obj
>
endobj
117 0 obj
>
endobj
118 0 obj
>
endobj
119 0 obj
>
endobj
120 0 obj
>
endobj
121 0 obj
>
endobj
122 0 obj
>
endobj
123 0 obj
>
endobj
124 0 obj
>
endobj
125 0 obj
>
endobj
126 0 obj
>
endobj
127 0 obj
>
endobj
128 0 obj
>
endobj
129 0 obj
>
endobj
130 0 obj
>
endobj
131 0 obj
>
endobj
132 0 obj
>
endobj
133 0 obj
>
endobj
134 0 obj
>
endobj
135 0 obj
>
endobj
136 0 obj
>
endobj
137 0 obj
>
endobj
138 0 obj
>
endobj
139 0 obj
>
endobj
140 0 obj
>
endobj
141 0 obj
>
endobj
142 0 obj
>
endobj
143 0 obj
>
endobj
144 0 obj
>
endobj
145 0 obj
>
endobj
146 0 obj
>
endobj
147 0 obj
>
endobj
148 0 obj
>
endobj
149 0 obj
>
endobj
150 0 obj
>
endobj
151 0 obj
>
endobj
152 0 obj
>
endobj
153 0 obj
>
endobj
154 0 obj
>
endobj
155 0 obj
/K [1]
/P 47 0 R
/S /Span
/Pg 23 0 R
/Type /StructElem
>>
endobj
156 0 obj
>
endobj
157 0 obj
/K [3]
/P 47 0 R
/S /Span
/Pg 23 0 R
/Type /StructElem
>>
endobj
158 0 obj
>
endobj
159 0 obj
>
endobj
160 0 obj
>
endobj
161 0 obj
>
endobj
162 0 obj
>
endobj
163 0 obj
>
endobj
164 0 obj
>
endobj
165 0 obj
>
endobj
166 0 obj
/K [12]
/P 48 0 R
/S /Span
/Pg 23 0 R
/Type /StructElem
>>
endobj
167 0 obj
>
endobj
168 0 obj
>
endobj
169 0 obj
>
endobj
170 0 obj
>
endobj
171 0 obj
>
endobj
172 0 obj
>
endobj
173 0 obj
>
endobj
174 0 obj
>
endobj
175 0 obj
>
endobj
176 0 obj
>
endobj
177 0 obj
>
endobj
178 0 obj
>
endobj
179 0 obj
>
endobj
180 0 obj
>
endobj
181 0 obj
>
endobj
182 0 obj
>
endobj
183 0 obj
>
endobj
184 0 obj
>
endobj
185 0 obj
>
endobj
186 0 obj
>
endobj
187 0 obj
>
endobj
188 0 obj
>
endobj
189 0 obj
>
endobj
190 0 obj
/K [25]
/P 65 0 R
/S /Span
/Pg 24 0 R
/Type /StructElem
>>
endobj
191 0 obj
>
endobj
192 0 obj
>
endobj
193 0 obj
>
endobj
194 0 obj
>
endobj
195 0 obj
>
endobj
196 0 obj
>
endobj
197 0 obj
>
endobj
198 0 obj
>
endobj
199 0 obj
>
endobj
200 0 obj
>
endobj
201 0 obj
>
endobj
202 0 obj
>
endobj
203 0 obj
>
endobj
204 0 obj
>
endobj
205 0 obj
>
endobj
206 0 obj
>
endobj
207 0 obj
>
endobj
208 0 obj
>
endobj
209 0 obj
>
endobj
210 0 obj
>
endobj
211 0 obj
>
endobj
212 0 obj
>
endobj
213 0 obj
/K [3]
/P 84 0 R
/S /Span
/Pg 26 0 R
/Type /StructElem
>>
endobj
214 0 obj
>
endobj
215 0 obj
/K [5]
/P 84 0 R
/S /Span
/Pg 26 0 R
/Type /StructElem
>>
endobj
216 0 obj
>
endobj
217 0 obj
>
endobj
218 0 obj
>
endobj
219 0 obj
>
endobj
220 0 obj
>
endobj
221 0 obj
>
endobj
222 0 obj
>
endobj
223 0 obj
>
endobj
224 0 obj
>
endobj
225 0 obj
>
endobj
226 0 obj
>
endobj
227 0 obj
>
endobj
228 0 obj
>
endobj
229 0 obj
>
endobj
230 0 obj
>
endobj
231 0 obj
>
endobj
232 0 obj
>
endobj
233 0 obj
>
endobj
234 0 obj
/K [26]
/P 90 0 R
/S /Span
/Pg 26 0 R
/Type /StructElem
>>
endobj
235 0 obj
>
endobj
236 0 obj
>
endobj
237 0 obj
>
endobj
238 0 obj
>
endobj
239 0 obj
>
endobj
240 0 obj
>
endobj
241 0 obj
>
endobj
242 0 obj
>
endobj
243 0 obj
>
endobj
244 0 obj
>
endobj
245 0 obj
>
endobj
246 0 obj
/K [13]
/P 97 0 R
/S /Span
/Pg 27 0 R
/Type /StructElem
>>
endobj
247 0 obj
>
endobj
248 0 obj
/K [15]
/P 97 0 R
/S /Span
/Pg 27 0 R
/Type /StructElem
>>
endobj
249 0 obj
>
endobj
250 0 obj
/K [17]
/P 97 0 R
/S /Span
/Pg 27 0 R
/Type /StructElem
>>
endobj
251 0 obj
>
endobj
252 0 obj
>
endobj
253 0 obj
>
endobj
254 0 obj
>
endobj
255 0 obj
/K [1]
/P 102 0 R
/S /Span
/Pg 28 0 R
/Type /StructElem
>>
endobj
256 0 obj
>
endobj
257 0 obj
>
endobj
258 0 obj
>
endobj
259 0 obj
>
endobj
260 0 obj
>
endobj
261 0 obj
>
endobj
262 0 obj
>
endobj
263 0 obj
>
endobj
264 0 obj
>
endobj
265 0 obj
>
endobj
266 0 obj
/K [13]
/P 106 0 R
/S /Span
/Pg 28 0 R
/Type /StructElem
>>
endobj
267 0 obj
>
endobj
268 0 obj
/K [15]
/P 106 0 R
/S /Span
/Pg 28 0 R
/Type /StructElem
>>
endobj
269 0 obj
>
endobj
270 0 obj
>
endobj
271 0 obj
>
endobj
272 0 obj
>
endobj
273 0 obj
>
endobj
274 0 obj
>
endobj
275 0 obj
>
endobj
276 0 obj
>
endobj
277 0 obj
>
endobj
278 0 obj
>
endobj
279 0 obj
>
endobj
280 0 obj
>
endobj
281 0 obj
>
endobj
282 0 obj
>
endobj
283 0 obj
>
endobj
284 0 obj
>
endobj
285 0 obj
>
endobj
286 0 obj
>
endobj
287 0 obj
>
endobj
288 0 obj
>
endobj
289 0 obj
>
endobj
290 0 obj
>
endobj
291 0 obj
>
endobj
292 0 obj
>
endobj
293 0 obj
>
endobj
294 0 obj
>
endobj
295 0 obj
/K [1]
/P 122 0 R
/S /Span
/Pg 30 0 R
/Type /StructElem
>>
endobj
296 0 obj
>
endobj
297 0 obj
/K [3]
/P 122 0 R
/S /Span
/Pg 30 0 R
/Type /StructElem
>>
endobj
298 0 obj
>
endobj
299 0 obj
>
endobj
300 0 obj
>
endobj
301 0 obj
>
endobj
302 0 obj
>
endobj
303 0 obj
>
endobj
304 0 obj
>
endobj
305 0 obj
>
endobj
306 0 obj
>
endobj
307 0 obj
>
endobj
308 0 obj
>
endobj
309 0 obj
>
endobj
310 0 obj
>
endobj
311 0 obj
>
endobj
312 0 obj
>
endobj
313 0 obj
>
endobj
314 0 obj
>
endobj
315 0 obj
>
endobj
316 0 obj
/K [9]
/P 441 0 R
/Pg 32 0 R
/S /Span
/Type /StructElem
>>
endobj
317 0 obj
>
endobj
318 0 obj
>
endobj
319 0 obj
>
endobj
320 0 obj
>
endobj
321 0 obj
>
endobj
322 0 obj
>
endobj
323 0 obj
>
endobj
324 0 obj
>
endobj
325 0 obj
>
/Rotate 0
/Type /Page
>>
endobj
326 0 obj
>
stream
HWˎ7W1>fwКоличество мод колебаний в молекуле
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1857
Принцип неопределенности Гейзенберга утверждает, что все атомы в молекуле постоянно находятся в движении (иначе мы бы точно знали положение и импульс).
Для молекул они демонстрируют три основных типа движения: поступательное (внешнее), вращение (внутреннее) и колебания (внутреннее). Двухатомная молекула содержит только одно движение, в то время как многоатомные молекулы демонстрируют более сложные колебания, известные как нормальные моды.
Молекулярные колебания
Молекула в целом имеет поступательное и вращательное движение, в то время как каждый атом имеет свое собственное движение. Колебательные моды могут быть ИК или рамановскими активными. Чтобы мода наблюдалась в ИК-спектре, изменения должны происходить в постоянном диполе (т.е. не в двухатомных молекулах). Двухатомные молекулы наблюдаются в спектрах КР, но не наблюдаются в ИК-спектрах. Это связано с тем, что двухатомные молекулы имеют одну полосу и не имеют постоянного диполя, а, следовательно, одно единственное колебание. Примером этого может быть \(\ce{O2}\) или \(\ce{N2}\). Однако несимметричные двухатомные молекулы (т. Е. \ (\ ce {CN} \)) действительно поглощают в ИК-спектрах.
Многоатомные молекулы испытывают более сложные колебания, которые можно суммировать или разложить на нормальные колебания.
Нормальные формы вибрации: асимметричная, симметричная, виляющая, скручивающая, ножничная и раскачивающаяся для многоатомных молекул.
| Симметричное растяжение | Асимметричное растяжение | Виляние |
|---|---|---|
| Скручивание | Ножницы | R упор |
Рисунок \(\PageIndex{1}\): Шесть типов режимов вибрации.
Изображения использованы с разрешения (общественное достояние; Тьяго Бесерра Паолини).
Вычислить количество мод колебаний
Степень свободы — это количество переменных, необходимых для полного описания движения частицы. Для атома, движущегося в трехмерном пространстве, достаточно трех координат, поэтому его степень свободы равна трем. Его движение чисто поступательное. Если у нас есть молекула, состоящая из N атомов (или ионов), степень свободы становится равной 3N, потому что каждый атом имеет 3 степени свободы. Кроме того, поскольку эти атомы связаны друг с другом, все движения не являются поступательными; некоторые становятся вращательными, некоторые другие вибрируют. Для нелинейных молекул все вращательные движения можно описать в терминах вращения вокруг 3 осей, вращательная степень свободы равна 3, а остальные 3N-6 степеней свободы составляют колебательное движение. Однако для линейной молекулы вращение вокруг собственной оси не является вращением, потому что оно оставляет молекулу неизменной.
Таким образом, для любой линейной молекулы существует только 2 вращательных степени свободы, оставляя 3N-5 степеней свободы для колебаний.
Степени мод колебаний для линейных молекул можно рассчитать по формуле:
\[3N-5 \label{1}\]
Степени свободы для нелинейных молекул можно рассчитать по формуле :
\[3N-6 \label{2}\]
\(n\) равно количеству атомов в интересующей молекуле. При попытке подсчитать количество колебательных мод следует придерживаться следующей процедуры:
- Определите, является ли молекула линейной или нелинейной (т. е. нарисуйте молекулу, используя VSEPR). Если линейно, используйте уравнение \ref{1}. Если нелинейный, используйте уравнение \ref{2}
- Подсчитайте, сколько атомов в вашей молекуле. Это ваше значение \(N\).
- Подставьте свое значение \(N\) и решите.
Пример \(\PageIndex{1}\): Углекислый газ
Сколько колебательных мод имеется в линейной молекуле \(\ce{CO_2}\) ?
- Ответить
Всего в этой молекуле \(3\) атомов.
Это линейная молекула, поэтому мы используем уравнение \ref{1}. В \(\ce{CO_2}\) имеется \[3(3)-5 = 4 \нечисло\] мод колебаний.Могут ли \(\ce{CO_2}\) и \(\ce{SO_2}\) иметь разное число степеней колебательной свободы? Следуя описанной выше процедуре, становится ясно, что \(\ce{CO_2}\) является линейной молекулой, а \(\ce{SO_2}\) – нелинейной. \(\ce{SO_2}\) содержит неподеленную пару, из-за которой молекула изгибается по форме, тогда как \(\ce{CO_2}\) не имеет неподеленных пар. Очень важно иметь представление о том, как устроена молекула. Следовательно, \(\ce{CO_2}\) имеет 4 формы колебаний, а \(\ce{SO_2}\) – 3 формы свободы.
Это линейная молекула, поэтому мы используем уравнение \ref{1}. В \(\ce{CO_2}\) имеется \[3(3)-5 = 4 \нечисло\] мод колебаний.- Последующие действия ( \(\ce{SO_2}\))
Могут ли \(\ce{CO_2}\) и \(\ce{SO_2}\) иметь разное число степеней колебательной свободы? Следуя описанной выше процедуре, становится ясно, что \(\ce{CO_2}\) является линейной молекулой, а \(\ce{SO_2}\) – нелинейной. \(\ce{SO_2}\) содержит неподеленную пару, из-за которой молекула изгибается по форме, тогда как \(\ce{CO_2}\) не имеет неподеленных пар.
Очень важно иметь представление о том, как устроена молекула. Следовательно, \(\ce{CO_2}\) имеет 4 формы колебаний, а \(\ce{SO_2}\) – 3 формы свободы.
Очень важно иметь представление о том, как устроена молекула. Следовательно, \(\ce{CO_2}\) имеет 4 формы колебаний, а \(\ce{SO_2}\) – 3 формы свободы.Пример \(\PageIndex{2}\): Метан
Сколько мод колебаний имеется в тетраэдрической молекуле \(\ce{CH_4}\) ?
- Ответить
В этой молекуле всего 5 атомов. Это нелинейная молекула, поэтому мы используем уравнение \ref{2}. В \(\ce{CH_4}\) имеется \[3(5)-6 = 9\нечисло\] мод колебаний.
Пример \(\PageIndex{3}\): Buckyballs
Сколько мод колебаний существует в нелинейной молекуле \(\ce{C_{60}}\) ?
- Ответить
В этой молекуле всего 60 атомов углерода. Это нелинейная молекула, поэтому мы используем уравнение \ref{2}. В \(\ce{C_60}\) имеется \[3(60)-6 = 174\нечисло\] мод колебаний.
Ссылки
- Харрис, Дэниел С. и Майкл Д. Бертолуччи. Симметрия и спектроскопия: введение в колебательную и электронную спектроскопию . Нью-Йорк: Dover Publications, 19.89. Печать.
- Хаускрофт, Кэтрин Э. и Алан Г. Шарп. Неорганическая химия . Харлоу: Pearson Education, 2008. Печать.
Симметрия и спектроскопия: введение в колебательную и электронную спектроскопию . Нью-Йорк: Dover Publications, 19.89. Печать.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- № на стр.
- Теги
Нормальные режимы вибрации | CH 431 Неорганическая химия
Для чего нужны таблицы символов?
Здесь возникает хороший вопрос: какой смысл изучать таблицы символов? Простой ответ заключается в том, что симметрия и соответствующая таблица характеристик молекулы могут использоваться для интерпретации и предсказания многих аспектов химически значимой спектроскопии, а также связи. Далее мы проиллюстрируем это, сосредоточившись на колебательных модах молекулы.
В лаборатории мы можем собирать полезные экспериментальные данные, используя инфракрасную (ИК) и рамановскую спектроскопию. Эти данные можно сравнить с количеством активных полос ИК и/или Рамана, предсказанным на основе применения теории групп и правильной таблицы характеристик. Математика (теория групп и матричная алгебра), лежащая в основе этой обработки, служит прочной теоретической основой.
Описанные ниже манипуляции работают, потому что все операции симметрии молекулы составляют математическую группу и подчиняются правилам группы. Как отмечалось ранее, нам не нужно осваивать эту область математики, чтобы эффективно использовать таблицы символов.
Степени свободы и колебания в молекулах
Здесь мы сначала обсудим степени свободы для простой молекулы (воды). Мы очень быстро увидим, почему использование симметрии очень выгодно при исследовании более крупных молекул.
Для молекулы с “N” атомами существует 3N степеней свободы (помните, что мы живем в трехмерном мире с координатами x, y, z). Для нелинейной молекулы к поступательным движениям можно отнести 3 степени свободы – движение тела как целого (Т x , T y , T z ) и 3 оборота (R x , R y , R z ). Остальные движения атомов — это смещения атомов из их средних положений — центр тяжести не меняется. Эти фундаментальные колебания называются «нормальными модами».
Таким образом, нелинейная молекула имеет 3N-6 нормальных мод. Для воды число нормальных режимов равно 3 (3 х 3 – 6 = 3). Для линейных молекул имеется 3N-5 нормальных мод.
Для воды, которая, конечно же, интенсивно изучалась, мы знаем, что 3 вибрации следующие.
Символы, используемые для описания этих режимов (A 1 , B 1 ), — это те же символы Малликена, с которыми мы столкнулись при обсуждении таблиц символов. Другими словами, колебания, которые являются молекулярными свойствами, могут быть описаны видами симметрии или неприводимыми представлениями. На самом деле большая часть литературы, посвященной колебательной спектроскопии, использует эти символы как сокращенный способ передачи информации.
Должно быть совершенно очевидно, что число колебаний быстро увеличивается даже при небольшом увеличении числа атомов в молекуле. Определить виды колебаний путем осмотра (как мы это делали для воды) теперь становится гораздо труднее. Например, рассмотрим следующие соединения:
H 2 O 3 atoms 3 vibrations
PH 3 4 atoms 6 vibrations
CO 2 2- 4 atoms 6 vibrations
XeF 4 5 atoms 9 vibrations
B 2 H 6 8 атомов 18 колебаний
Для диборана (B 2 H 6 ), который имеет симметрию D 2h , было бы непростой задачей выяснить природу и симметрию колебаний всех 18 видов.
Однако вооружившись таблицей символов для D 2h и знание свойств симметрии задача определения видов симметрии всех вибраций проста.
Для воды мы могли бы представить таблицу символов (C 2v ) с 3 колебаниями (ν1, v2, v3), перечисленными в столбце молекулярных свойств, как показано ниже. (ν = греческий символ «ню»)
Однако в целом такой подход непрактичен. Возьмем, к примеру, пиридин (C 5 H 5 N). Точечная группа также C 2v но в молекуле 11 атомов. Число основных форм вибрации равно 27 (3 х 11 – 6 = 27).
В этом случае мы должны были бы составить таблицу символов C 2v , показывающую симметрии всех 27 вибраций. По этой причине вибрации обычно не включаются в таблицы символов. Вместо этого пользователь (вас) должен определить количество и тип колебаний (в соответствии с их видами симметрии) для любых встречающихся молекул. Как мы это делаем, описано ниже.
Приводимые представления
Как отмечалось ранее, одним из важных свойств таблиц символов является то, что операции симметрии являются членами математической группы и между ними существуют важные отношения.
В целом то же самое можно сказать о видах симметрии или неприводимых представлениях молекулярных свойств. Произведения комбинирования символов неприводимых представлений путем умножения или сложения/вычитания также подчиняются правилам группы. Новые представления больше не являются самыми простыми из возможных и называются «приводимыми представлениями», поскольку их можно «свести» к составным частям.
Например, для воды симметрии переводов (T x , T y , T z ) можно получить непосредственно из таблицы символов C 2v . Это A 1 , B 1 и B 2 . Мы можем представить все три из этих степеней свободы представлением Γ T и написать выражение ниже. ( Γ = заглавная греческая буква «гамма»).
Г Т = A 1 + B 1 + B 2
Мы знаем, что A 1 , B 1 и B 2 являются просто краткими представлениями симметрии (редуктивные виды симметрии не являются редуктивными представлениями).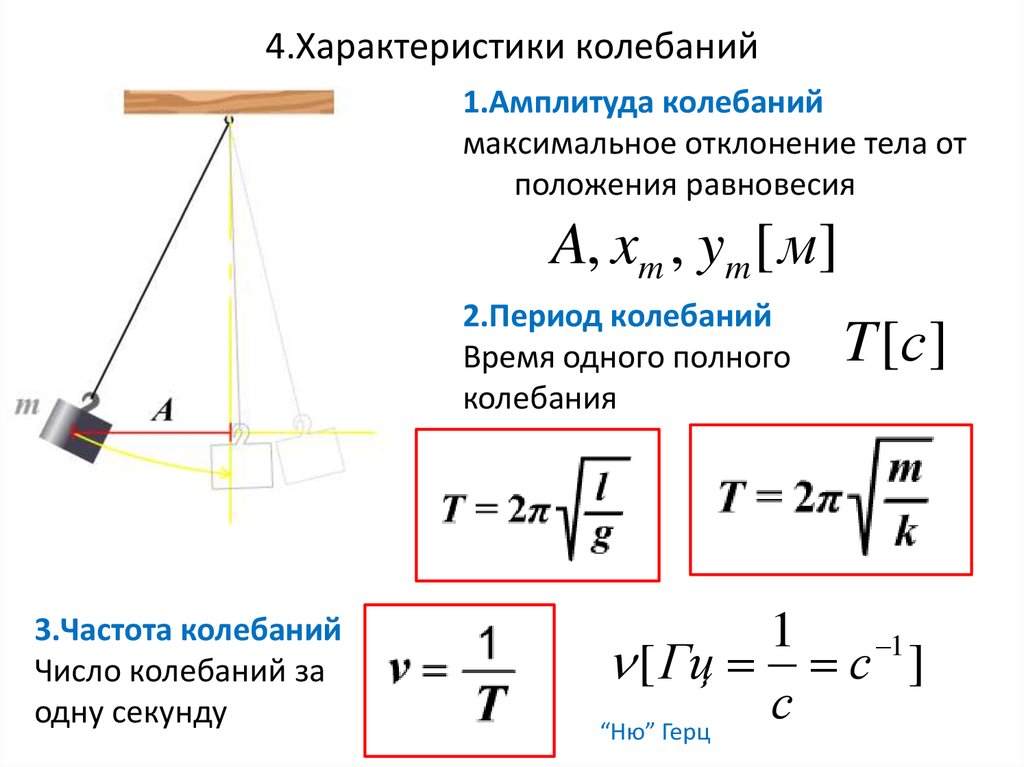
Таким образом, мы можем просто записать символы Γ T , добавив отдельные символы для A 1 , B 1 и B 2 из таблицы символов C 2v .
Итак, Γ T = 3 -1 1 1.
Это допустимое приводимое представление и член группы C 2v .
Аналогичным образом мы можем записать приводимое представление для всех трех вращений и всех колебаний.
The representation for ALL the degrees of freedom for the molecule (3N) can be written as
Γ 3N = Γ T + Γ R + Γ VIB
и приводимое представление для него получается простым суммированием символов для Γ T , Γ R и Γ 5
4 .Γ 3N = 9 -1 3 1
Запишите это – оно появится позже!
Хотя набор символов 9 -1 3 1 является действительным членом группы C 2v , он не особенно полезен при обсуждении молекулярных свойств.
Что действительно требуется, так это язык сокращенных видов симметрии (символы Малликена, A 1 , B 1 и т. д.). Другими словами, мы хотим выразить Γ 3N через A 1 , B 1 и т. д. Из вышеприведенной информации можно легко показать путем проверки, что:
Γ 5 9023 3A 1 +A 2 + 3B 1 +2B 2
Хорошая новость заключается в том, что для других более сложных молекул нам не нужно выполнять эту задачу путем проверки, потому что:
1. Мы можем легко сгенерировать Γ 3N как приводимое представление для молекулы (если мы знаем ее точечную групповую симметрию).
2. Мы можем легко преобразовать приводимое представление Γ 3N в сумму его разновидностей симметрии (символов Малликена), используя «простую» формулу, известную как формула приведения.
Общий метод получения Γ 3N
Шаг 1
Возьмите таблицу символов для молекулы и добавьте строку внизу.
В этой строке сгенерируйте приводимое представление для Γ T (или Γ xyz ), как мы делали выше, просто добавляя символы для каждой операции, которые соответствуют молекулярным свойствам для x, y и z. Для C 2v мы уже показали, что это символы, соответствующие A 1 , B 1 и B 2 .
Шаг 2
Добавьте еще одну строку ниже Γ T и запишите количество атомов, которые НЕ МЕНЯЮТ их расположение во время каждой операции симметрии. Здесь вы понимаете, насколько полезен набор реальных молекулярных моделей. Для этого вам также необходимо знать, где находятся элементы симметрии и как операции симметрии влияют на молекулу. Конечно, вы уже знаете, как это сделать, потому что изучили обозначения Шёнфлиса и знаете, как присвоить точечную группу молекуле. Таблица символов также содержит все операции симметрии, перечисленные по классам в верхней строке.
Таким образом, для воды (3 атома) под E 3 неподвижных атома, а для C 2 оба атома H движутся, но, поскольку атом O находится на оси C 2 , он не меняет своего положения, поэтому мы записываем 1 в столбце C 2 . Новый набор чисел, сгенерированный на шаге 2 (3 1 3 1), также является приводимым представлением в C 2v и подчиняется правилам группы.
Шаг 3
На этом шаге мы просто перемножаем символы, которые были сгенерированы на шагах 1 и 2. Результат (третья строка) является приводимым представлением для Γ 3N (или Γ TOT ). Это так просто.
Обратите внимание, что новое приводимое представление (9 -1 1 3) идентично представлению для Γ 3N , которое мы получили ранее путем проверки.
Редукция приводимого представления
Чтобы преобразовать ЛЮБОЕ приводимое представление в сумму его неприводимых представлений (видов симметрии или символов Малликена), мы используем формулу приведения:
Эту информацию легко найти в таблице символов:
Вернемся к нашему примеру для воды: Группа точек C 2v, порядок (g) = 4
Приводимое представление для 5N 5N 3 = 9 -1 3 1
Количество раз, когда A 1 появляется в этом представлении, равно
a A1 = 1/4 { 1.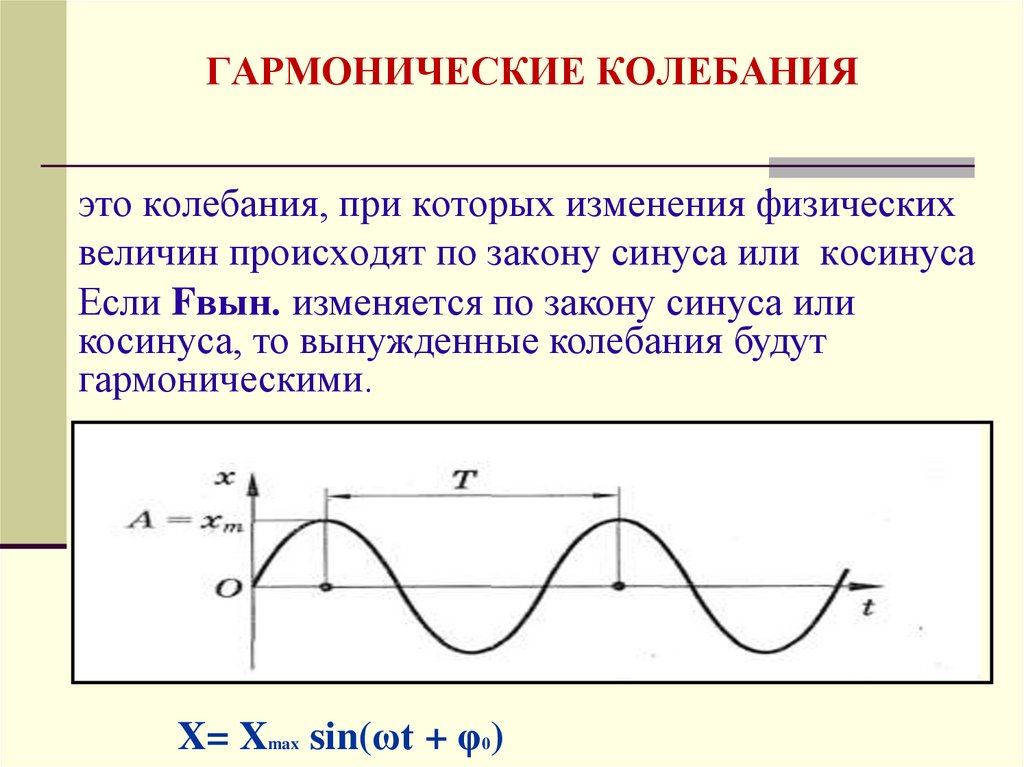
1.9 + 1.1. (-1) + 1.1.3 +1.1.1} = 3
поэтому Γ 3N содержит 3 вида симметрии A 1 . Числа остальных видов симметрии рассчитываются следующим образом:
a A2 = 1/4 { 1.1.9 + 1.1.(-1) + 1.(-1.3) + 1.(-1). 1 } = 1 один A 2 присутствует
a B1 = 1/4 { 1.1.9 + 1.(-1).(-1) + 1.1.3 + 1.(-1).1} = 3 3 B 1 присутствует
a B2 = 1/4 {1.1.9 + 1.(-1)(-1) + 1.(-1).3 + 1.1.1} = 2 2 B 2 присутствует
Теперь мы можем написать Γ 3N = 3A 1 + A 2 + 3B 1 + 2B 2 (именно то, что мы получили при «проверке» выше. это даст нам число и виды симметрии основных мод колебаний. 1 + A 2 + 3B 1 + 2B 2
Γ T = A 1 + B 1 + B 2
Γ R = A 2 + B 1 + B 2
Γ VIB = Γ 3N – Γ T – Γ R = 2A 1 +B 1
Итак, три нормальные моды вибрации воды имеют симметрии A 1 , А 1 и В 1 .