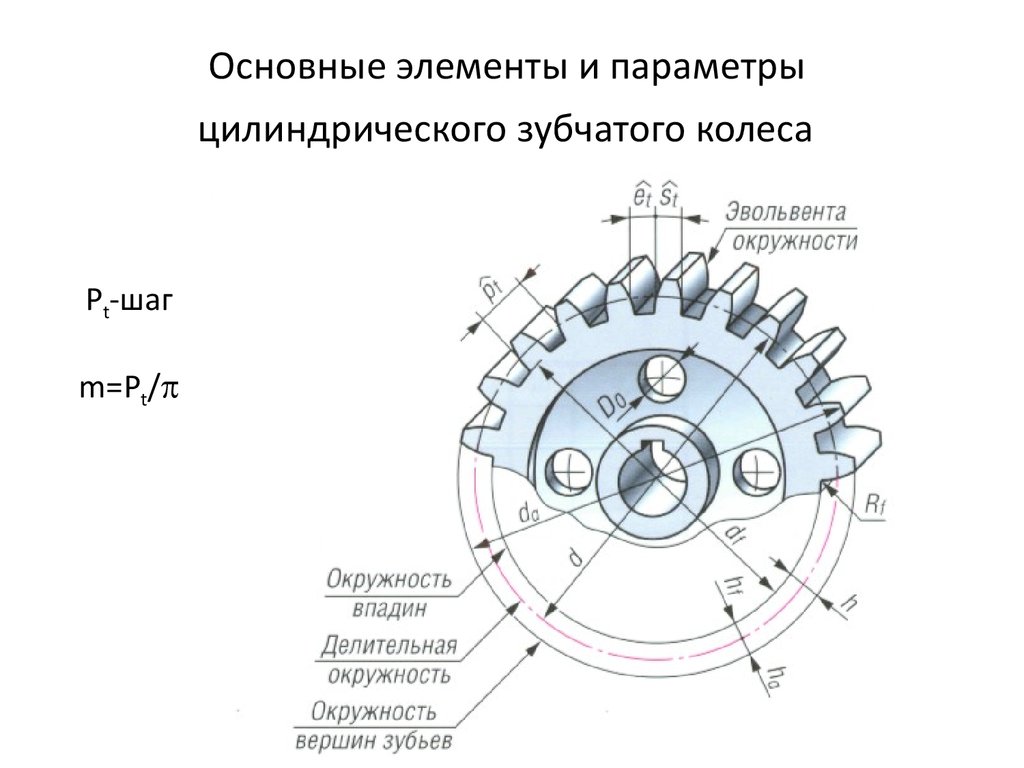
Нормальный модуль зубчатого колеса: Стандартные модули зубчатых колес
alexxlab | 22.06.2023 | 0 | Разное
Цилиндрические зубчатые передачи,основные термины и обозначения
Термины и обозначения приведены в табл. 1, определения терминов см. ГОСТ 16530—83 и 16531-83.
[gview file=»https://www.cb-online.ru/wp-content/uploads/2014/05/GOST-16530—83.pdf»]
[gview file=»https://www.cb-online.ru/wp-content/uploads/2014/05/GOST-16531—83.pdf»]
1. Термины и обозначения цилиндрических зубчатых передач
Делительное межосевое расстояние — a
Межосевое расстояние — aw
Ширина венца цилиндрического зубчатого колеса — b
Рабочая ширина венца зубчатой передачи — bw
Радиальный зазор пары исходных контуров — c
Коэффициент радиального зазора нормального исходного контура – c*
Высота зуба цилиндрического зубчатого колеса — h
Высота делительной головки зуба цилиндрического зубчатого колеса — h
Коэффициент высоты головки исходного контура – ha*
Высота до хорды зуба колеса —
Высота до постоянной хорды зуба —
Высота до хорды дуги окружности —
Глубина захода зубьев колеса, а также глубина захода зубьев исходных реек —
Высота делительной ножки зуба колеса — hf
Граничная высота зуба колеса — hl
Делительный диаметр зубчатого колеса — d
Диаметр вершин зубьев колеса — da
Основной диаметр зубчатого колеса — db
Диаметр впадин зубчатого колеса — df
Диаметр окружности граничных точек зубчатого колеса — dl
Начальный диаметр зубчатого колеса — dw
Радиус зубчатого колеса — r
Расчетный модуль цилиндрического зубчатого колеса — m
Нормальный модуль зубьев — mn
Окружной модуль зубьев (торцовый) — mt
Шаг эвольвентного зацепления — pb
Нормальный шаг зубьев рейки — pn
Торцовый шаг зубьев рейки — pt
Осевой шаг зубьев рейки — px
Основной нормальный шаг зубьев — pbn
Основной окружной шаг зубьев — pbt
Основная нормальная толщина зуба — sbn
Постоянная хорда зуба —
Нормальная толщина зуба рейки — sn
Осевая толщина зуба рейки — sx
Торцовая толщина зуба рейки — st
Толщина по хорде зуба —
Окружная толщина на заданном диаметре d
Толщина по хорде —
Длина обшей нормали зубчатого колеса — W
Коэффициент смещения исходного контура — x
Коэффициент наименьшего смещения исходного контура — xmin
Коэффициент суммы смещений хΣ
Коэффициент воспринимаемого смещения — у
Коэффициент уравнительного смещения — Δу
Число зубьев зубчатого колеса (число зубьев секторно-зубчатого колеса) — z
Наименьшее число зубьев, свободное от подрезания — zmin
Число зубьев в длине обшей нормали — zw
Нормальный боковой зазор эвольвентной цилиндрической зубчатой передачи — jn
Эвольвентный угол профиля зуба – inv a
Эвольвентный угол, соответствующий точке профиля на окружности d y– inv ay
Частота вращения зубчатого колеса в минуту — n
Передаточное число зубчатой передачи (z2/z1; d2/d1; n1/n2) — u
Угол профиля зуба исходного контура в нормальном сечении — a
Угол профиля зуба в торцовом сечении — at
Угол зацепления — atw
Угол профиля в точке на концентрической окружности заданного диаметра dy — ay
Угол наклона линии зуба соосной цилиндрической поверхности диаметраdy— βy
Угол наклона линии зуба — β
Основной угол наклона линии зуба (косозубого колеса на его основном цилиндре) — βb
Угол развернутости эвольвенты зуба — v
Половина угловой толщины зуба — ψ
Половина угловой толщины зуба эквивалентного зубчатого колеса, соответствующая концентрической окружности диаметра dy/cos2βy — ψyv
Угловая скорость — ω
Шестерня — зубчатое колесо передачи с меньшим числом зубьев, колесо — с большим числом зубьев.
При одинаковом числе зубьев зубчатых колес передачи шестерней называют ведущее зубчатое колесо, а колесом — ведомое. Индекс 1 — для величин, относящихся к шестерне, индекс 2 — относящихся к колесу.
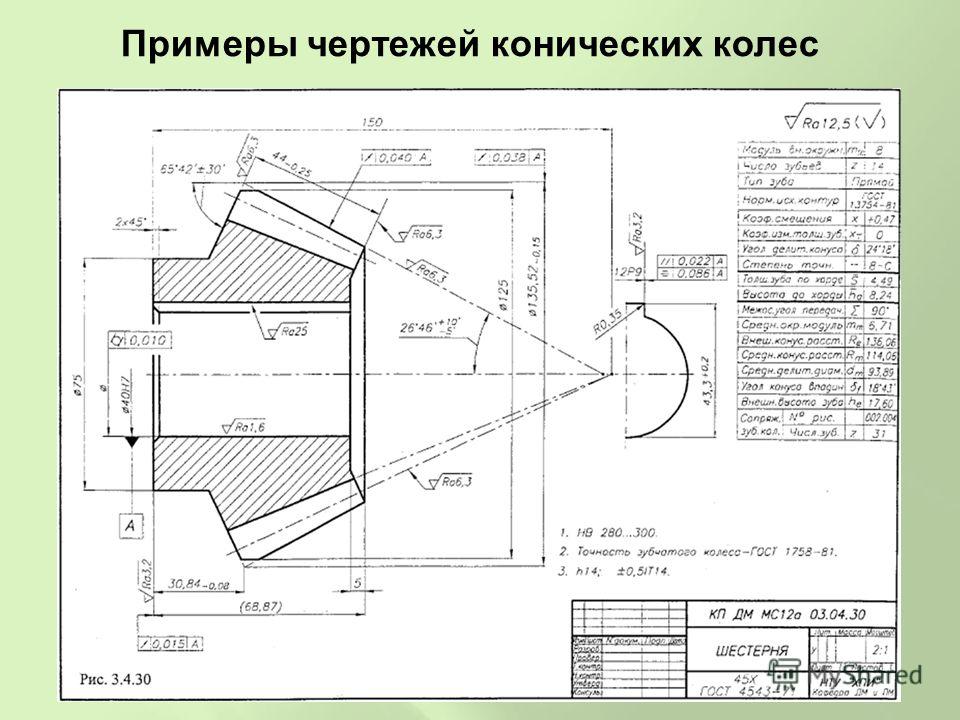
Рис. 1. Исходный контур зубчатых цилиндрических колес эвольвентного зацепления по ГОСТ 13755—81 и конических колес с прямыми зубьями по ГОСТ 13754— 81
Индекс n — для величин, относящихся к нормальному сечению, t — к окружному (торцовому) сечению. В тех случаях, когда не может быть разночтения и неясности, индексы n и t можно исключить.
Термины параметров нормального исходного контура и нормального исходного производящего контура, выраженных в долях модуля нормального исходного контура, образуют добавлением слова «коэффициент» перед термином соответствующего параметра.
Обозначения коэффициентов соответствуют обозначениям параметров с добавлением знака «*», например коэффициент радиального зазора пары исходных контуров с*.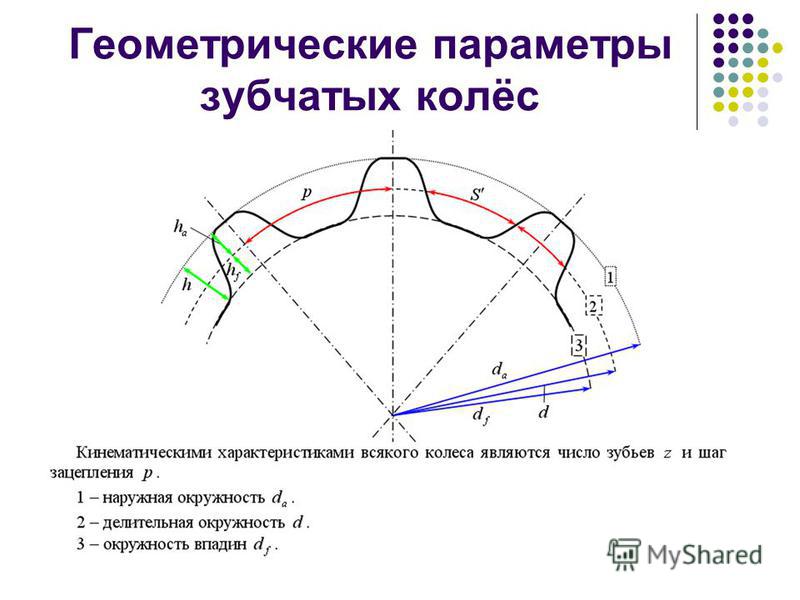
Модули (по ГОСТ9563—60). Стандарт распространяется на эвольвентные цилиндрические зубчатые колеса и конические зубчатые колеса с прямыми зубьями и устанавливает:
для цилиндрических колес — значения нормальных модулей;
для конических колес — значения внешних окружных делительных модулей.
Числовые значения модулей:
Ряд 1 | Ряд 2 | Ряд 1 | Ряд 2 | Ряд 1 | Ряд 2 | Ряд 1 | Ряд 2 |
1 | 1,125 | — | — | 5 | 5,5 | 12 | 14 |
1,25 | 1,375 | 2,5 | 2,75 | 6 | 7 | 16 | 18 |
1. | 1..75 | 3 | 3,5 | 8 | 9 | 20 | 22 |
2 | 2,25 | 4 | 4,5 | 10 | 11 | 25 | 28 |
32 | 36 | ||||||
5Примечания:
1. При выборе модулей ряд 1 следует предпочитать ряду 2.
2. Для цилиндрических зубчатых колес допускается:
а) в тракторной промышленности применение модулей 3,75; 4,25 и 6,5мм;
б) в автомобильной промышленности применение модулей, отличающихся от установленных в настоящем стандарте;
в) в редукторостроении применение модулей 1,6; 3,15; 6,3; 12,5м.
3. Для конических зубчатых колес допускается:
а) определять модуль на среднем конусном расстоянии;
б) в технически обоснованных случаях применение модулей, отличающихся от указанных в таблице.
4. Стандарт предусматривает применение модулей в диапазоне значений от 0,05 до 100мм.
Исходный контур цилиндрических зубчатых колес. Под исходным контуром колес (рис. 1) подразумевают контур зубьев рейки в нормальном к направлению зубьев сечении. Радиальный зазор с = 0,25m, радиус кривизны переходной кривой зуба p f = 0.4m. Допускается увеличение радиуса рfесли это не нарушает правильности зацепления, и увеличение с до 0,35m при обработке колес долбяками и шеверами и до 0,4m при шлифовании зубьев.
Для цилиндрических колес внешнего зацепления при окружной скорости более указанной в табл. 2 применяют исходный контур с модификацией профиля головки зуба (рис.
2). При этом линия модификации — прямая, коэффициент модификации hg* должен быть не более 0,45, а коэффициент глубины модификации Δ* — не более 0,02.
Рекомендуемые значения коэффициента Δ* приведены в табл. 3.
Основные элементы зубчатого зацепления указаны на рис. 3 и 4 в соответствии с обозначением по табл. 1.
Смещение колес зубчатых передач с внешним зацеплением.
Рис. 2. Исходный контур с профильной модификацией
2. Окружная скорость колес в зависимости от их точности
Тип колес | Окружная скорость в м/спри степени точности колеса по ГОСТ 1643-81 | ||
6 | 7 | 8 | |
Прямозубые | 10 | 6 | 4 |
Косозубые | 16 | 10 | 6 |
3.
Коэффициент глубины модификации Δ* в зависимости от модуля и степени точности
Модуль m,мм | Степень точности по нормам плавности работы по ГОСТ 1643-81 | ||
6 | 7 | 8 | |
До 2 | 0,010 | 0,015 | 0,020 |
Св. 2 до 3,5 | 0,009 | 0,012 | 0,018 |
» 3,5 » 6,3 | 0,008 | 0,010 | 0,035 |
» 6,3 » 10 | 0,006 | 0,008 | 0,012 |
» 10 » 16 | 0,005 | 0,007 | 0,010 |
» 16 » 25 | — | 0,006 | 0,009 |
» 25 » 40 | — | — | 0,008 |
1) при смещении передач, у которых шестерня имеет малое число зубьев (z1 < 17), так как при этом устраняется подрез у корня зуба;
2) при больших передаточных числах, так как в этом случае значительно снижается относительное скольжение профилей.
Рис. 3
Рис. 4
Положение исходного производящего контура относительно нарезаемого колеса, при котором делительная прямая рейка касается делительной окружности колеса, называют номинальным положением (рис. 5, а). Колесо, зубья которого образованы при номинальном положении исходной производящей рейки, называют колесом, нарезанным без смешения исходного контура (по старой терминологии — некорригированное колесо).
Положение производящего реечного контура относительно заготовкиРис. 5. Положение производящего реечного контура относительно заготовки:
а — номинальное; б — с отрицательным смещением; в — с положительным смещением
График для определения нижнего предельного значения z1 в зависимости от z2 при которыхРис. 6. График для определения нижнего предельного значения z1 в зависимости от z2 при которых
εа = 1,2 (x1= х2 = 0,5)
График для определения хmin в зависимости от z и β или zmin — х и βРис.
7. График для определения хmin в зависимости от z и β или zmin — х и β
(округляется до ближайшего большего целого числа)
Примеры.
1. Дано: z = 15; β = 0. По графику определяем хmin = 0,12 (см. штриховую линию).
2. Дано: х = 0; β = 30°. По графику определяем наименьшее число зубьев = 12 (cм. штриховую линию)
Влияние смещения исходного контура на геометрию зубьевРис. 8. Влияние смещения исходного контура на геометрию зубьев
Если исходная производящая рейка в станочном зацеплении смещена из номинального положения и установлена так, что ее делительная прямая не касается делительной окружности нарезаемого колеса, то в результате обработки получится колесо, нарезанное со смещением исходного контура (по старой терминологии — корригированное колесо).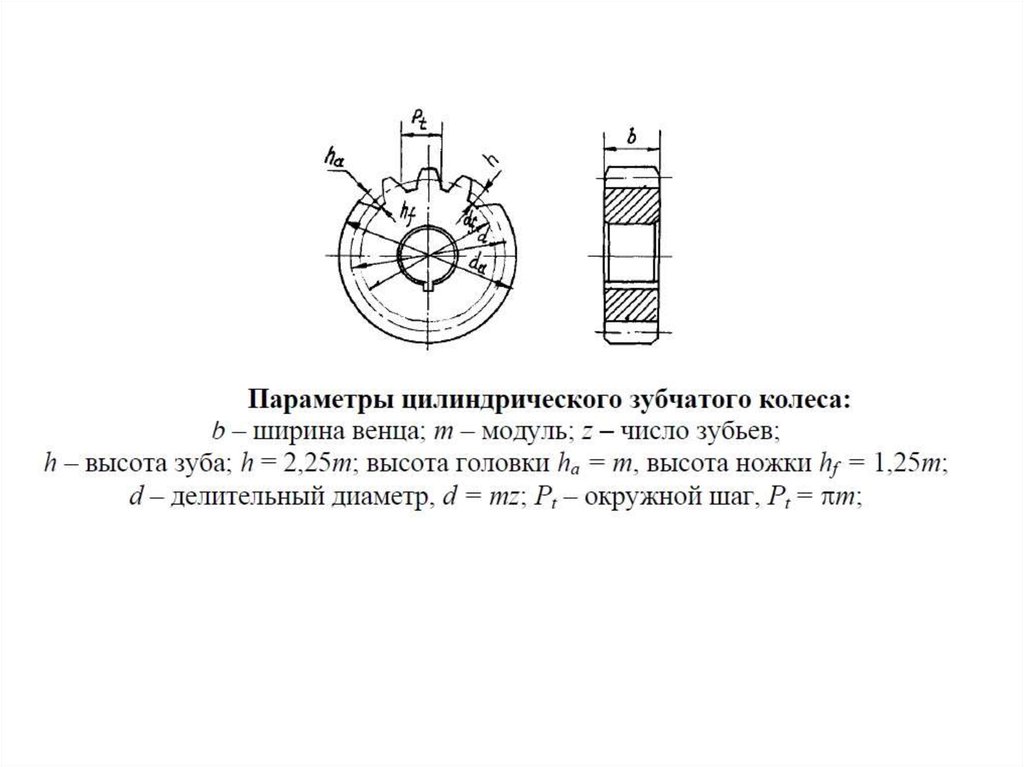
Рис. 9. Зацепление (в сечении, параллельном торцовому) зубчатого колеса со смещением с исходной производящей рейкой
4. Коэффициенты смещения у зубчатых колес прямозубой передачи
Коэффициент смещения | Область применения | |||
у шестерни х1 | у колеса х2 | |||
0 | 0 | Межосевое расстояние aw задано равным 0,5(z1 + z2)m или не задано | Кинематические передачи | z1 ≥ 17 |
0,3 | -0,3 | 12 ≤ z1 < 16 и z2 ≥ 22 | ||
0 | 0 | Межосевое расстояние aw задано равным 0,5(z1 + z2)m | Силовыепередачи | z1 ≥ 21 |
0,3 | -0,3 | 14 ≤ z1 ≤ 20 и u ≥ 3,5 | ||
0 | 0 | Межосевое расстояние aw не задано | z1> 30 | |
0,5 | 0,5 | 10 ≤ z1 ≤ 30. | ||
В пределах 10 ≤ z1 ≤ 16 нижнее предельное значение z1 определяется по графику (рис.6)5. Коэффициент смещения у зубчатых колес косозубой и шевронной передач
Коэффициент смещения | Область применения | |||
у шестерни х1 | у колеса х2 | |||
0 | 0 | Межосевое расстояние aw задано равным (z1+z2)m/(2cosβ) или не задано | Кинематическиепередачи | |
0,3 | -0,3 | |||
0 | 0 | Силовыепередачи | ||
0,3 | -0,3 | |||
Рис.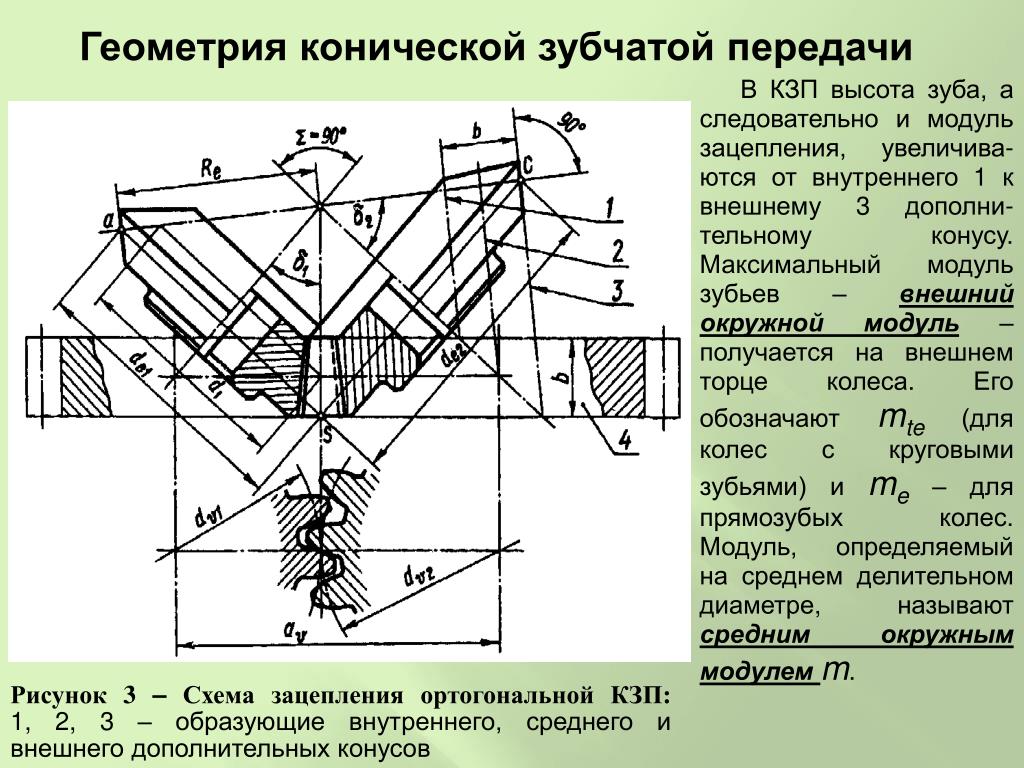
10. Толщина зуба по постоянной хорде и высота до постоянной хорды в нормальном сечении
Расстояние от делительной прямой исходной производящей рейки (или исходного контура) до делительной окружности колеса является величиной смещения.
Отношение смещения исходного контура к расчетному модулю называют коэффициентом смещения (х).
Если делительная прямая исходного контура пересекает делительную окружность зубчатого колеса (рис. 5, б), смещение называют отрицательным (х < 0), если не пересекает и не соприкасается (рис. 5, в) — положительным (х > 0). При номинальном положении исходного контура смещение равно нулю (х = 0).
Коэффициент смещения х обеспечивается установкой инструмента относительно заготовки зубчатого колеса в станочном зацеплении.
Коэффициенты смещения у зубчатых колес рекомендуется выбирать по табл. 4 для прямозубой передачи и по табл. 5 — для косозубой и шевронной передач.
Основные элементы зубчатого зацепления со смещением указаны на рис. 8, 9, 10.
6. Разбивка коэффициента суммы смещения xΣ у прямозубой передачи на составляющие х1 и х2
Коэффициент суммы смещения хΣ | Коэффициент смещения | Область применения | ||
у шестерни х1 | у колеса x2 | |||
0 < xΣ ≤ 0,5 | xΣ | 0 | Кинематические передачи | |
Силовые передачи | ||||
0,5 < хΣ ≤ 1 | 0,5 | хΣ — 0,5 | Кинематические передачи | |
Силовые передачи | ||||
Примечания:
1.
При заданном межосевом расстоянии aw требуемое значение коэффициента суммы смещений хΣ можно получить за счет изменения числа зубьев z1 или z2, если это изменение допускается.
2. При 0.3 < хΣ < 0,7 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.
3. При u = 1 рекомендуется x1 = x2 = 0,5хΣ.
7. Разбивка коэффициента суммы смещения xΣ у косозубой или шевронной передачи на составляющие х1 и x2
Коэффициент суммы смещения хΣ | Коэффициент смещения | Область применения | ||
у шестерни х1 | у колеса x2 | |||
0 < xΣ ≤ 0,5 | xΣ | 0 | Кинематическиепередачи | |
0 < xΣ ≤ 0,5 | xΣ | 0 | Силовыепередачи | |
Примечания:
1.
При заданном межосевом расстоянии aw требуемое значение коэффициента суммы смещений хΣ можно получить за счет изменения числа зубьев z1 или z2, угла наклона β, если эти изменения допускаются.
2. При хΣ > 0,3 и u < 2 наибольшая скорость скольжения в зацеплении будет большей, чем в передаче без смещения.
3. При u = 1 рекомендуется х1 = х2 = 0,5xΣ.
8. Значения наименьшего числа зубьев zmin зубчатого колеса с коэффициентом смещения х = 0 при станочном зацеплении с исходной производящей рейкой
βº | zmin | βº | zmin | βº | zmin |
До 12 | 17 | Св. | 14 | Св. 31 до 34 | 11 |
Св. 12 » 17 | 16 | » 24 » 28 | 13 | » 34 | 10 |
» 17 » 21 | 15 | » 28 » 31 | 12 | ||
21до 24[Цилиндрические зубчатые передачи] Далее »
УПРОЧНЕНИЕ ЗУБЧАТЫХ КОЛЕС
Автор:
А. С. Калашников, д. т.н., профессор, Московский политехнический университет, e‑mail: [email protected]
ГАЗОВАЯ ВАКУУМНАЯ ЦЕМЕНТАЦИЯ С ЗАКАЛКОЙ ГАЗОМ ПОД ДАВЛЕНИЕМ ОБЕСПЕЧИВАЕТ ЗУБЧАТЫМ КОЛЕСАМ ИЗ ЛЕГИРОВАННЫХ СТАЛЕЙ ВЫСОКИЕ ПОКАЗАТЕЛИ ТВЕРДОСТИ ПОВЕРХНОСТИ, КОНТАКТНОЙ И ИЗГИБНОЙ ВЫНОСЛИВОСТИ ЗУБЬЕВ.
Зубчатые передачи относятся к деталям приводной техники, подвергаемым значительным циклическим нагрузкам. В условиях высоких окружных скоростей и передаваемых мощностей зубчатые передачи должны обладать соответствующими прочностными свойствами. Объективным критерием оценки прочности является изгибная и контактная выносливость зубьев.
Для обеспечения высоких эксплуатационных свойств зубчатые колеса подвергают химико-термической обработке (ХТО). Химико-термическая обработка представляет собой совокупность процессов теплового и химического воздействий, направленных на изменение химического состава и структуры поверхностного слоя зубчатых колес. Она характеризуется введением в поверхностный слой металла благодаря химической реакции различных элементов из внешней среды: углерода, азота, кислорода, кремния и др. При этом на поверхности зубчатых колес образуется твердый диффузионный слой, который по мере углубления характеризуется падением концентрации диффундирующих элементов и микротвердости.
Для эффективного упрочнения поверхности зубчатых колес часто применяют цементацию и нитроцементацию, реже азотирование [1].
Контактная выносливость зубьев характеризуется сопротивлением типовым отказам рабочих поверхностей зубьев — питингу (выкрашиванию поверхностей зубьев в виде ямок) и микротрещинам, а также износу под действием контактных напряжений. При этом большое значение имеет равномерный износ по всей поверхности зуба, который достигается за счет модификаций по профилю и длине зуба. Так называемое «пятно контакта» — площадь контакта на поверхности зубьев при зацеплении должно занимать максимальную площадь, но не выходить на кромки зубьев даже при максимальных нагрузках.
Повышению сопротивления поверхностей зубьев износу под действием контактных напряжений способствует также наличие в поверхностных слоях зубьев остаточных внутренних напряжений сжатия глубиной до 0,02 мм.
Область применения различных материалов и химико-термических процессов при изготовлении зубчатых колес, а также достигаемая контактная выносливость зубьев в соответствии со стандартом ISO 6336 приведены на рис.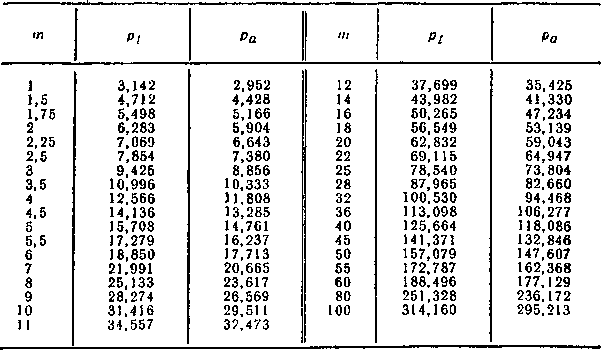
1.
Рис. 1. Контактная выносливость и твердость поверхности зубьев колес при различных методах ХТО
При этом указаны не конкретные марки, а широкий спектр сталей, входящих в группу, например, легированных, улучшаемых, азотируемых и других. Каждая группа охватывает большое число марок сталей, которые по составу и свойствам значительно отличаются друг от друга. Безусловно, при определении марки стали и химико-термической обработки должны быть учтены конструктивные особенности зацепления зубчатых передач и условия их эксплуатации.
Следует отметить, что для зубчатых колес, работающих при высоких нагрузках и окружных скоростях и имеющих значительные контактные напряжения, наиболее часто применяют легированные стали после цементации (нитроцментации) и закалки, характеризующиеся пределом контактной выносливости боковых поверхностей 1300 –1650 Н/мм2 [1, 2].
Наряду с высокой контактной прочностью зубчатые колеса из легированных сталей после цементации (нитроцементации) и закалки имеют также высокие показатели по изгибной выносливости в пределах 320–540 Н/мм2 (рис.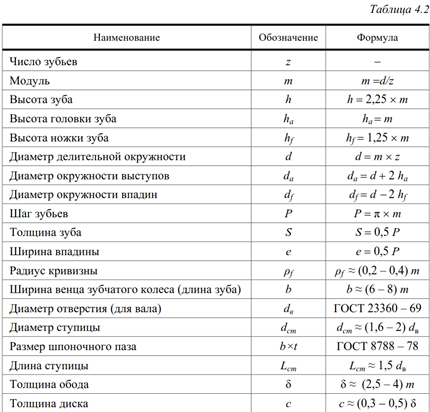
2).
Рис. 2. Изгибная выносливость и твердость поверхности зубьев колес при различных методах ХТО
Изгибная выносливость зубьев характеризуется сопротивлением зубчатого зацепления усталостным поломкам, возникающим в основании зуба. Сила Fn, которая достигает максимального значения при зацеплении в области делительной линии зуба и действует перпендикулярно его поверхности, а также плечо изгиба hf определяют напряжения в основании зуба (рис. 3). При этом решающее значение для достижения высокой прочности на изгиб под действием силы Fn имеет максимально возможный радиус закругления rf в основании зуба и толщина ножки зуба по хорде Sf.
Рис. 3. Схема определения изгибной выносливости в основании зуба
Большое влияние на изгибную выносливость зубьев оказывает также технологический процесс изготовления зубчатых колес. Плавное сопряжение боковых поверхностей зубьев с их основанием при максимальном радиусе закругления rf, который получают, например, при одновременном шлифовании боковых поверхностей и дна впадины зубьев позволяет существенно повысить прочность зубьев, на изгиб.
Как правило, зубчатые колеса после цементации имеют более высокие показатели по изгибной выносливости по сравнению с зубчатыми колесами после азотирования, при этом шлифование боковых поверхностей зубьев и дна впадины позволяет повысить изгибную выносливость как цементованных, так и азотированных зубчатых колес.
Проведенные исследования позволили установить основные преимущества процессов цементации и нитроцементации по сравнению с азотированием:
1. Широкий диапазон регулирования толщины упрочненного слоя.
2. Возможность проведения ХТО зубчатых колес из экономно легированных сталей (низко- и среднелегированных).
3. Высокая производительность ХТО зубчатых колес с возможностью проведения закалки после подстуживания или непосредственно с температуры диффузионного насыщения.
4. Высокие показатели изгибной и контактной выносливости зубьев.
Зубчатые колеса из низко- и среднелегированных сталей после цементации и закалки получают твердость поверхности HRC 55…63 при концентрации углерода 0,8…1,1%, а сердцевина сохраняет вязкую структуру c твердостью HRC 33…45, устойчивую к ударным нагрузкам.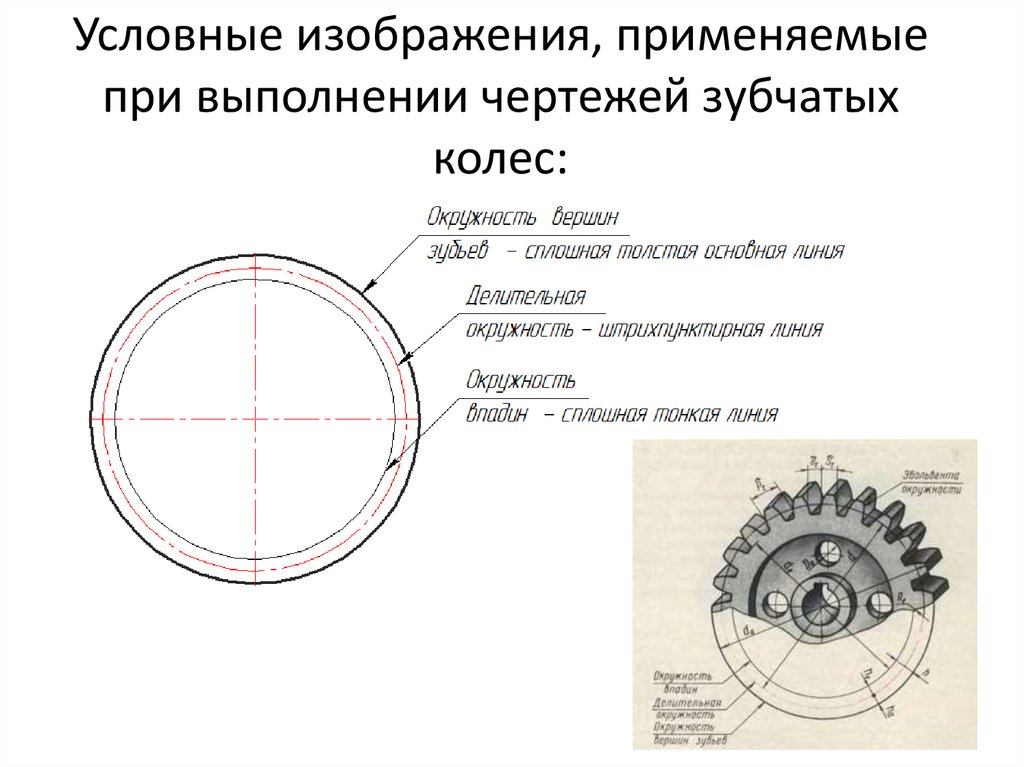
Для колес, работающих при высоких контактных нагрузках, концентрацию углерода в поверхностных слоях зубьев увеличивают до 1,1…1,4% без повышения твердости. Толщина цементованного слоя 1 (расстояние 2 от боковой поверхности зуба до слоев металла с твердостью HRC ≤ 51) зависит главным образом от модуля зубчатого колеса и в среднем составляет 0,2 mn (0,1…2,0 мм и более) (рис. 4). При необходимости, например, в целях повышения прочностных свойств зубчатых колес или увеличения припуска на чистовую обработку после ХТО, толщина цементованного слоя может быть увеличена.
Рис. 4. Твердость зуба по HRC в поперечном сечении после цементации и закалки
Для получения необходимых прочностных свойств у стальных зубчатых колес цилиндрических и конических передач преимущественно применяют методы газовой цементации (нитроцементации) в контролируемых эндотермических атмосферах с последующей закалкой в масло [3]. При этом процесс ХТО выполняют в автоматизированных проходных и камерных агрегатах, обладающих высокой производительностью и обеспечивающих полный цикл обработки от нагрева до закалки.
Однако практика показала, что применение такой технологии имеет ряд существенных недостатков:
— большой расход атмосферы процесса и высокие затраты на ее изготовление;
— постоянный выброс СО2 и СО в окружающую среду из-за неполного сгорания атмосферы после завершения процесса.
— окисление рабочих поверхностей зубьев колес, которое снижает твердость поверхности зубьев и их контактную прочность;
— большие энергетические расходы и трудоемкость обслуживания оборудования.
Наряду с необходимым упрочнением цилиндрические и конические зубчатые колеса при ХТО получают значительную объемную деформацию, точность зубьев снижается на 1–2 степени соответственно по ГОСТ 1643–81 и ГОСТ 1758–81. Деформируются также базовые и другие ответственные поверхности заготовок зубчатых колес: отверстия, цилиндрические поверхности валов, торцы, боковые поверхности зубьев и шлиц [2, 3].
Известно, что на деформацию зубчатых колес при ХТО оказывает влияние большое число факторов, среди которых: конструкция заготовки, свойства применяемой стали, методы получения поковок, предварительная термическая обработка, условия выполнения механической обработки и др.
Решающее влияние на деформацию оказывает неодинаковая интенсивность охлаждения различных поверхностей заготовок при закалке [1, 2, 4].
При закалке в масло нагретая в процессе цементации заготовка находится в трех различных зонах: конвекции, пузырькового и пленочного кипения. Это вызывает большие перепады температуры у заготовок типа вала по длине, а также внутри заготовки и на ее поверхности. Различная интенсивность охлаждения отдельных частей и поверхностей заготовки при закалке в масло является причиной возникновения значительных деформаций [5].
В связи с этим в последнее время все более широкое применение получает газовая вакуумная цементация. При этом наилучшие результаты были достигнуты при применении вакуумной цементации в комбинации с последующей закалкой газом (гелий, азот) под высоким давлением.
Большим преимуществом газового науглероживания при низком давлении является возможность значительного повышения производительности процесса цементации и сокращения затрат энергии и цикла изготовления зубчатых колес.
Приведенная в таблице 1 ХТО цилиндрического косозубого зубчатого колеса коробки передач (mn = 4,0 мм, z = 37, β = 23°) с достижением толщины цементационного слоя 0,8 мм (0,35% С) показало, что метод вакуумной цементации с последующей закалкой производительней газовой на ≈18%.
| Этапы процесса | Вакуумная установка | Газовая установка |
|---|---|---|
| Загрузка | 15 мин | 5 мин |
| Нагрев до 980°С | 90 мин | 90 мин |
| Цементация и диффузия | 120 мин | 180 мин |
| Уменьшение температуры | 45 мин | 60 мин |
| Закалка | 20 мин | 20 мин |
| Выгрузка | 5 мин | 5 мин |
| Общее время | 295 мин | 360 мин |
В целях снижения деформации криволинейных зубьев ведущей гипоидной шестерни было принято решение производить химико-термическую обработку, используя комбинацию процессов вакуумной цементации и закалки газом под давлением [6].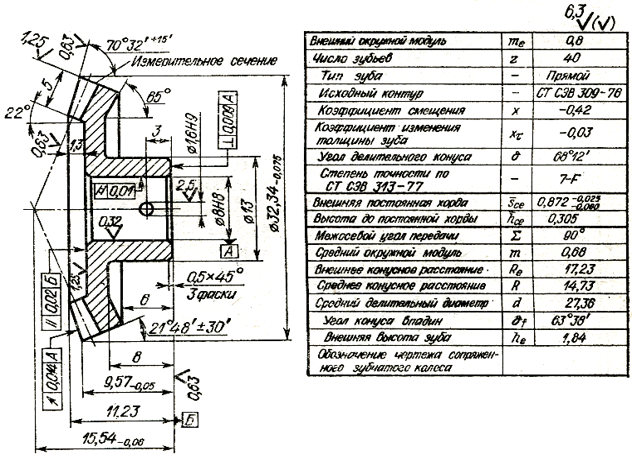
Ведущая гипоидная шестерня типа вала из низкоуглеродистой стали 25ХГТ имела следующие параметры: число зубьев z = 11, внешний окружной модуль mte = 7,37 мм, внешняя высота зуба he = 16 мм, средний угол наклона на поверхности впадин β = 45° 23′, гипоидное смещение а = 36 мм, нормальный угол давления: на рабочей стороне (вогнутой) зуба αр = 20° 15′; на обратной стороне (выпуклой) зуба αо = 24° 45′ (рис. 5).
Рис. 5. Ведущая гипоидная шестерня-вал
Вакуумный процесс науглероживания начинался с создания вакуума в печи нагрева заготовки до высокой температуры 980°С (возможно до 1050°С) в атмосфере без кислорода, в среде азота, что препятствовало образованию вредного окисления (рис. 6).
Рис. 6. Схема вакуумной цементации и закалки газом под давлением
Вакуумную цементацию производили при низком давлении в среде ацетилена (содержание углерода С ≈ 92%), который при высокой температуре обладает значительной скоростью диссоциации.
Высокая скорость передачи углерода поверхности заготовки ведущей гипоидной шестерни позволила значительно снизить время по сравнению с атмосферным науглероживанием и повысить производительность процесса цементации. Чтобы избежать образования карбидов в области головки зуба, вакуумную цементацию проводили импульсами путем чередования коротких фаз насыщения углеродом и продолжительных фаз диффузии углерода в поверхностный слой заготовки [6, 7].
Непосредственно после цементации гипоидные шестерни поступали в закалочную камеру, обеспечивающую высокое давление (до 2 МПа) охлаждающего газа (гелия) с возможностью регулирования скорости подачи (до 25 м/с) и реверсирования потока газа. Решающим преимуществом закалки газом под давлением по сравнению с охлаждением в масло является снижение погрешностей зубчатых колес, возникающих при фазовом переходе. Теплообмен осуществляется гомогенно, поэтому возникают условия для минимизации погрешности размеров и формы зубьев, а также базовых и вспомогательных поверхностей.
В существующих производствах у гипоидных шестерен типа вала с криволинейными зубьями после цементации (нитроцементации) и закалки в масло зачищают центровые отверстия от следов сажи и пригара, контролируют радиальное биение базовых шеек и правят при установке в центрах.
Так как при ХТО возникают большие деформации вала, характеризуемые радиальным биением шейки (рис. 7), при правке могут образовываться микротрещины и глубокие риски, которые являются причиной возникновения бракованных заготовок.
Исследования показали, что при охлаждении газом (гелием) под давлением максимальные значения радиального биения шеек и их разброс (кривая 1) значительно снижаются по сравнению с закалкой в масло (кривая 2). Это позволяет избежать операций зачистки центров и правки. Очень важно, что при снижении деформации вала уменьшается колебание припуска под последующую чистовую обработку зубьев.
Рис. 7. Схема контроля радиального биения шеек у шестерни-вала
Проведенные измерения показателя нормы кинематической точности радиального биения зубчатого венца Fr, наибольшей разности расстояний от рабочей оси зубчатого колеса до элемента нормального исходного контура показали, что точность зубчатого венца после газовой вакуумной цементации и закалки газом под давлением приблизительно на одну степень по ГОСТ 1758–81 выше по сравнению с цементацией в эндотермических атмосферах и закалкой в масло.
При этом показатель нормы плавности работы — отклонение шага fpt = ± (15–33) мкм также был в пределах 8‑й степени точности по ГОСТ 1758–81.
Рис. 8. Радиальное биение шеек гипоидных шестерен после ХТО
Величина максимального припуска в значительной степени зависит от погрешностей зубьев, полученных на предшествующей операции [2, 4]. Так как газовая вакуумная цементация с последующей непосредственной закалкой газом под высоким давлением позволила снизить погрешности норм кинематической точности, плавности работы, контакта зубьев и бокового зазора в среднем на 20–25% по сравнению атмосферной цементацией и закалкой в масло,то величина припуска на сторону зуба снизилась на 10–15%. Это позволило увеличить производительность чистовой обработки зубошлифованием и снизить влияние «технологической наследственности» на точность изготовления (рис. 9). Режимы резания при шлифовании зубьев высокопористыми кругами марки 2516 СМ112 К5: число рабочих ходов 4; скорость резания V = 33 м/c; время обработки одного зуба t = 30 с.
Рис. 9. Схема шлифования зубьев гипоидной шестерни-вала
В массовом, крупно- и реже среднесерийном производстве, как правило, применяют поточную организацию предварительной и окончательной механической обработки, которая характеризуется расположением производственного оборудования в последовательности выполнения операций технологического процесса. Движение заготовки от операции к операции производят с определенным тактом. Для выполнения ХТО поточное производство прерывают, заготовки укладывают в специальную тару и транспортируют в термический цех с использованием промежуточных складов. Даже на предприятиях с высокой организацией технологического процесса операцию ХТО выполняют за несколько рабочих дней.
Рис. 10. Схема установки для вакуумной цементации и закалки газом под давлением
Разработанные компанией ALD Vacuum Technologies установки для газовой вакуумной цементации с последующей закалкой газом под давлением можно с успехомвстроить в поточную линию, не прерывая предварительную и окончательную механическую обработку (рис.
10). Камера 2 предназначена для вакуумного науглероживания заготовок. С помощью электронагрева 3 и вентилятора 1 обеспечивается постоянный и равномерный нагрев камеры. Поддоны 4 с заготовками устанавливаются на стол 9. Для охлаждения газом под высоким давлением служит закалочная камера 6. Благодаря теплоизоляции по всему контуру внешняя оболочка камеры остается «холодной» (температура 20–25°C), что не вызывает трудностей при установке ее на участке механической обработки. Перемещение поддонов с заготовками из камеры в камеру производится транспортным модулем 8. Загрузка поддонов в установку осуществляется с помощью герметичных дверей 5 и 7.
Конструкция установки ALD Dual Therm (пропускная способность 100–200 кг/час) позволяет интегрировать ее в поточную механообрабатывающую линию для ХТО заготовок зубчатых колес с массой 2–5 кг, значительно снизить цикл обработки и избежать затрат на транспортирование и хранение заготовок на складе (рис.
11).
Рис. 11. Установка для вакуумной цементации и закалки газом под давлением
Большое значение для равномерности процесса охлаждения заготовок зубчатых колес имеет циркуляция потока газа в закалочной камере. Внутренняя система потока газа равномерно проходит через поддон (1) с заготовками (рис. 12). Камера может быть оснащена устройством для реверсирования потоков, которое позволяет периодически изменять направления газа для охлаждения заготовок сверху вниз (2) или снизу вверх.
Рис. 12. Схема потоков охлаждающего газа в закалочной камере
Высокая гибкость процесса вакуумной цементации и закалки газом под давлением позволяет производить ХТО заготовок зубчатых колес различной конструкции с маленькой, средней или большой толщиной цементационного слоя. Для зубчатых колес, работающих при значительных изгибных нагрузках, необходима высокая твердость сердцевины HRC ≥ 35 в основании зуба, поэтому закалка таких колес производится с интенсивным охлаждением при реверсировании потоков газа, а также высоких значениях давления и скорости его подачи [6, 7].
Газовая вакуумная цементация в комбинации с закалкой газом под высоким давлением представляет собой современную химико-термическую технологию. Она обеспечивает зубчатым колесам из легированных сталей высокие показатели твердости поверхности HRC 58–63, контактной (300–1650 Н/мм2) и изгибной (320–540 Н/мм2) выносливости зубьев. Проведенные исследования при изготовлении гипоидных конических шестерен показали следующие основные преимущества этой технологии:
1. Снижение деформаций зубьев гипоидной шестерни, что позволяет на 10–15% снизить величину припусков на зубьях, повысить производительность зубошлифования после ХТО и уменьшить влияние «технологической наследственности» на точность изготовления шестерни.
2. Уменьшение деформации вала и отсутствие загрязнений (следы сажи и пригара) после ХТО, характерных для цементации в атмосферных печах и закалки в масло, позволяет исключить из технологического процесса операции правки и мойки заготовок.
3.
Производительность установок газовой вакуумной цементации и закалки газом под высоким давлением и низкий такт выпуска одной заготовки позволяет встраивать их в поточные линии механической обработки.
Литература
1. Зинченко В. М. Инженерия поверхности зубчатых колес методами химико-термической обработки. М.: Изд-во МГТУ им. Н. Э. Баумана, 2001. 302 с.
2. Козловский И. С. Химико-термическая обработка шестерен. М.: Машиностроение, 1970. 232 с.
3. Bausch Tomas. Innovative Zahnradfertidung. Expert verlag GmbH, D‑71262, Reningen, Germany, 2006, 778 s.
4. Калашников А. С., Моргунов Ю. А., Калашников П. А. Современные методы обработки зубчатых колес. М.: Издательский дом «Спектр», 2012. 238 с.
5. Саушкин Б. П., Шандров Б. В., Моргунов Ю. А. Перспективы развития и применения физико-химических методов и технологий в производстве двигателей. «Известия МГМУ «МАМИ». 2012. № 2 (14).Т. 2. С. 242–248.
6. Loser K. Innovative Warmebehandlungsprozesse und-anlagen in der Getriebeproduktion.
Доклад на конгрессе «GETRO», Германия, Вюрцбург. Март 2007. 15 с.
7. Калашников А. С., Моргунов Ю. А., Калашников П. А. Химико-термическая обработка зубчатых колес с использованием газовой вакуумной цементации. Справочник. Инженерный журнал. 2013. № 10. С. 12–16.
Источник журнал “РИТМ машиностроения” № 3-2019
Поперечный модуль косозубого зубчатого колеса, заданный Калькулятором нормального модуля
✖Нормальный модуль косозубого зубчатого колеса определяется как единица размера, указывающая, насколько велика или мала косозубая шестерня.ⓘ Нормальный модуль косозубого зубчатого колеса [m n ] | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical Lea gue UKМорская миля (Международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростникТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Угол винтовой передачи — это угол между любой косозубой шестерней и осевой линией справа, круговым цилиндром или конусом. | CircleCycleDegreeGonGradianMilMilliradianMinuteMinutes of ArcPointQuadrantQuartercircleRadianRevolutionRight AngleSecondSemicircleSextantSignTurn | +10% -10% |
ⓘ Угол наклона винтовой передачи. Gear [ψ]✖Поперечный модуль косозубого зубчатого колеса — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения.ⓘ Поперечный модуль косозубого зубчатого колеса с учетом нормального модуля [м] | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Поперечный модуль косозубого колеса с заданным нормальным модульным решением
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Нормальный модуль косозубого зубчатого колеса: 3 миллиметра –> 0,003 метра (проверьте преобразование здесь)
Угол подъема косозубого зубчатого колеса: 25 Degree –> 0.
4363323129985 Radian (Check conversion here)
STEP 2: Evaluate Formula
STEP 3: Convert Result to Output’s Unit
0.00331013375688735 Meter –>3.31013375688735 Millimeter (Check conversion here)
< 16 основных формул калькуляторов винтовых зубчатых колесРасстояние от центра до центра между двумя шестернями
Идти Межцентровое расстояние косозубых шестерен = Нормальный модуль косозубой шестерни*(Количество зубьев 1-й косозубой шестерни+Количество зубьев 2-й косозубой шестерни)/(2*cos(Угол винтовой шестерни))
Угол поперечного давления косозубого колеса при заданном угле подъема
Идти Угол поперечного давления косозубой шестерни = atan(tan(нормальный угол наклона косозубой шестерни)/cos(угол наклона косозубой шестерни))
Нормальный угол давления косозубого колеса при заданном угле подъема
Идти Нормальный угол давления косозубой шестерни = atan(tan(поперечный угол наклона косозубой шестерни)*cos(угол наклона косозубой шестерни))
Нормальный круговой шаг косозубого колеса с учетом виртуального числа зубьев
Идти Нормальный окружной шаг винтовой шестерни = 2*pi*Виртуальный радиус окружности делительной окружности для косозубой шестерни/виртуальное количество зубьев на косозубой шестерне
Большая полуось эллиптического профиля, заданная радиусом кривизны в точке
Идти Большая полуось зубьев косозубой шестерни = sqrt (радиус кривизны косозубой шестерни * малая полуось зубьев косозубой шестерни)
Поперечный модуль косозубого колеса с заданным нормальным модулем
Идти Поперечный модуль косозубого зубчатого колеса = нормальный модуль косозубого зубчатого колеса/cos(угол винтового зубчатого колеса)
Шаг винтовой передачи с нормальным круговым шагом
Идти Шаг косозубой шестерни = нормальный круговой шаг косозубой шестерни/cos(угол винтовой шестерни)
Нормальный круговой шаг винтовой передачи
Идти Нормальный круговой шаг косозубой шестерни = Шаг косозубой шестерни * cos (угол наклона косозубой шестерни)
Малая полуось эллиптического профиля с заданным радиусом кривизны в точке 92/Радиус кривизны винтовой передачи
Осевой шаг винтовой шестерни при заданном угле наклона
Идти Осевой шаг косозубой шестерни = шаг косозубой шестерни/тангенс (угол наклона косозубой шестерни)
Шаг винтовой передачи с учетом осевого шага
Идти Шаг косозубого колеса = осевой шаг косозубого зубчатого колеса * tan (угол наклона косозубого зубчатого колеса)
Угловая скорость шестерни при заданном коэффициенте скорости
Идти Скорость косозубой шестерни = Коэффициент скорости косозубой шестерни * Скорость косозубой шестерни
Угловая скорость зубчатого колеса с учетом передаточного отношения
Идти Скорость косозубой шестерни = скорость косозубой шестерни к соотношению скоростей косозубой шестерни
Отношение скоростей для винтовых зубчатых колес
Идти Отношение скоростей косозубой шестерни = скорость косозубой шестерни/скорость косозубой шестерни
Поперечный диаметральный шаг косозубого колеса с учетом поперечного модуля
Идти Поперечный диаметральный шаг косозубой шестерни = 1/поперечный модуль косозубой шестерни
Поперечный модуль косозубого колеса с заданным поперечным диаметральным шагом
Идти Поперечный модуль косозубой шестерни = 1/поперечный диаметральный шаг косозубой шестерни
Поперечный модуль косозубого колеса с заданной формулой нормального модуля
Поперечный модуль косозубого зубчатого колеса = нормальный модуль косозубого зубчатого колеса/cos(угол винтового зубчатого колеса)
m = m n /cos(ψ)
Дайте определение косозубым зубчатым колесам?
Косозубая шестерня имеет цилиндрическую делительную поверхность и зубья, которые следуют по спирали на делительном цилиндре.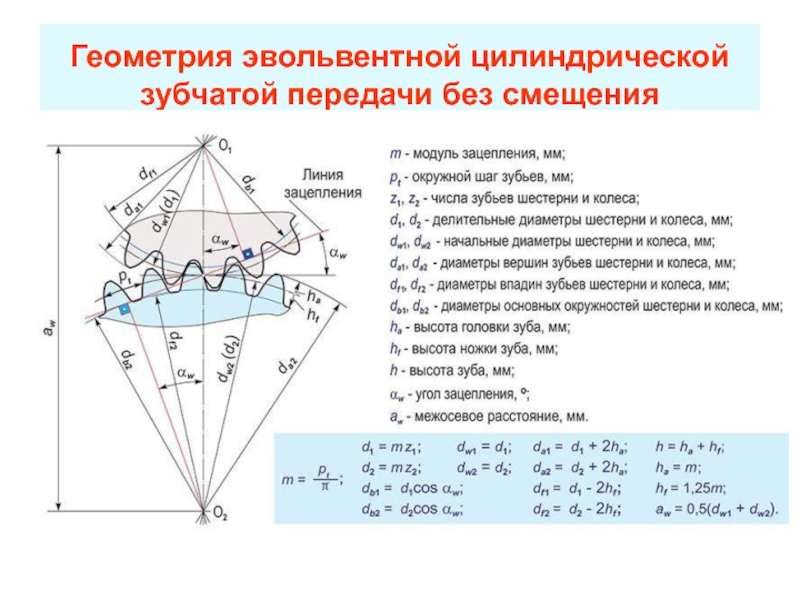
У наружных косозубых шестерен зубья выступают наружу, а у внутренних косозубых шестерен зубья выступают внутрь.
Как рассчитать поперечный модуль косозубого колеса с учетом нормального модуля?
Поперечный модуль косозубой шестерни с учетом нормального модуля Калькулятор использует Поперечный модуль косозубой шестерни = нормальный модуль косозубой шестерни/cos(угол винтовой шестерни) для расчета поперечного модуля косозубой шестерни, поперечный модуль косозубой шестерни с учетом нормального модуля равен модуль косозубого колеса, измеренный в плоскости вращения. Это то же самое, что и в случае цилиндрического зубчатого колеса. Поперечный модуль косозубого колеса обозначен символом м .
Как рассчитать поперечный модуль косозубого колеса с учетом нормального модуля с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для поперечного модуля косозубой шестерни с учетом нормального модуля, введите Нормальный модуль косозубой шестерни (m n ) и угол подъема винтовой шестерни (ψ) и нажмите кнопку расчета.
Вот как можно объяснить поперечный модуль косозубого колеса с учетом расчета нормального модуля с заданными входными значениями -> 3,310134 = 0,003 / cos (0,4363323129)985) .
Часто задаваемые вопросы
Что такое поперечный модуль косозубого колеса с учетом нормального модуля?
Поперечный модуль косозубого зубчатого колеса, заданный Нормальный модуль — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения. Он такой же, как и в случае цилиндрического зубчатого колеса, и представлен как m = m n /cos(ψ) или Поперечный модуль косозубого зубчатого колеса = нормальный модуль косозубого зубчатого колеса/cos(угол винтового зубчатого колеса) . Нормальный модуль косозубой шестерни определяется как единица размера, которая указывает, насколько велика или мала косозубая шестерня, а угол наклона косозубой шестерни – это угол между любой косозубой шестерней и осевой линией справа от нее, круглым цилиндром или конусом.
Как рассчитать поперечный модуль косозубого колеса с учетом нормального модуля?
Поперечный модуль косозубого зубчатого колеса, заданный Нормальный модуль — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения. Он такой же, как и в случае цилиндрического зубчатого колеса, рассчитывается с использованием Поперечный модуль косозубого зубчатого колеса = Нормальный модуль косозубого зубчатого колеса/cos(Угол винтового зубчатого колеса) . Чтобы рассчитать поперечный модуль косозубого колеса с учетом нормального модуля, вам потребуется Нормальный модуль косозубого зубчатого колеса (m n ) и угол наклона косозубого зубчатого колеса (ψ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для нормального модуля винтовой шестерни и угла наклона винтовой шестерни и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов расчета поперечного модуля винтовой передачи?
В этой формуле поперечный модуль косозубого зубчатого колеса использует нормальный модуль косозубого зубчатого колеса и угол наклона косозубого зубчатого колеса.
Мы можем использовать 1 другой способ (способы) для расчета того же самого, который выглядит следующим образом:
- Поперечный модуль косозубого зубчатого колеса = 1/поперечный диаметральный шаг косозубого зубчатого колеса
Доля
Скопировано!
Обычный модуль калькулятора винтовых зубчатых колес
✖Поперечный модуль косозубого зубчатого колеса — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения.ⓘ Поперечный модуль косозубого зубчатого колеса [м] | )Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsec MeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (ткань)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck L engthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | +10% -10% | |
✖Угол винтовой передачи — это угол между любой косозубой шестерней и осевой линией справа, круговым цилиндром или конусом. | CircleCycleDegreeGonGradianMilMilliradianMinuteMinutes of ArcPointQuadrantQuartercircleRadianRevolutionRight AngleSecondSemicircleSextantSignTurn | +10% -10% |
ⓘ Угол наклона винтовой передачи. Gear [ψ]✖Нормальный модуль косозубого зубчатого колеса определяется как единица размера, указывающая, насколько большим или маленьким является косозубое зубчатое колесо.ⓘ Нормальный модуль косозубого зубчатого колеса [m n ] | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Нормальный модуль винтового зубчатого колеса
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Поперечный модуль косозубого колеса: 3,4 миллиметра –> 0,0034 метра (проверьте преобразование здесь)
Угол наклона косозубого зубчатого колеса: 25 Градус –> 0,4363323129985 Радиан (Проверьте преобразование здесь)
ШАГ 2: Вычислите формулу
ШАГ 3: Преобразуйте результат в единицу измерения
0,00308144647592473 Метр –> 3,08144463759 метр (проверьте преобразование
24463759 метр) здесь< 14 Калькулятор соотношения зубовНормальный модуль винтовой шестерни с заданным межосевым расстоянием между двумя шестернями
Идти Нормальный модуль косозубой шестерни = Расстояние от центра до центра косозубой шестерни * (2 * cos (угол наклона косозубой шестерни)) / (количество зубьев на 1-й косозубой шестерне + количество зубьев 2-й косозубой шестерни) 92)
Угол подъема винтовой шестерни с учетом диаметра окружности приложения
Идти Угол наклона косозубой шестерни = acos(Количество зубьев косозубой шестерни/((Дополнение Диаметр окружности косозубой шестерни/Нормальный модуль косозубой шестерни)-2))
Нормальный модуль косозубого зубчатого колеса с учетом диаметра окружности приложения
Идти Нормальный модуль косозубого зубчатого колеса = Дополнение Диаметр окружности косозубого зубчатого колеса/((Число зубьев на косозубом зубчатом колесе/cos(Угол наклона косозубого зубчатого колеса))+2)
Количество зубьев на шестерне с учетом диаметра окружности приложения
Идти Количество зубьев на косозубой шестерне = ((дополнительный диаметр окружности косозубой шестерни/нормальный модуль косозубой шестерни)-2)*cos(угол наклона косозубой шестерни)
Приложение Диаметр окружности шестерни
Идти Дополнение Диаметр окружности косозубой шестерни = Нормальный модуль косозубой шестерни*((Число зубьев косозубой шестерни/cos(Угол винтовой шестерни))+2)
Нормальный модуль косозубого колеса с заданным диаметром делительной окружности
Идти
Нормальный модуль косозубой шестерни = диаметр делительной окружности косозубой шестерни * cos (угол наклона косозубой шестерни) / количество зубьев косозубой шестерни.
Виртуальное количество зубьев на винтовой передаче
Идти Виртуальное количество зубьев на косозубом колесе = 2*pi*Виртуальный радиус делительной окружности для косозубого зубчатого колеса/нормальный круговой шаг косозубого зубчатого колеса 9(3))*Виртуальное количество зубьев на косозубом колесе
Виртуальное количество зубьев на косозубом колесе задано Фактическое количество зубьев
Идти Виртуальное количество зубьев на косозубой шестерне = количество зубьев на косозубой шестерне/(cos(угол винтовой шестерни))^3
Обычный модуль винтовой передачи
Идти Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса)
Приложение о шестернях с учетом диаметра окружности приложения
Идти Дополнение по косозубому зубчатому колесу = (дополнение диаметр окружности косозубого зубчатого колеса-диаметр делительной окружности косозубого зубчатого колеса)/2
Приложение Диаметр окружности зубчатого колеса с учетом диаметра делительной окружности
Идти Дополнение Диаметр окружности косозубой шестерни = 2*Дополнение косозубой шестерни+Диаметр делительной окружности косозубой шестерни
Дедендум Диаметр окружности зубчатого колеса с учетом диаметра делительной окружности
Идти Диаметр делительной окружности косозубой шестерни = Диаметр делительной окружности косозубой шестерни-2 * Дедендум косозубой шестерни
Нормальный модуль формулы винтовой передачи
Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса)
m n = m*cos(ψ)
Дайте определение косозубым зубчатым колесам?
Косозубая шестерня имеет цилиндрическую делительную поверхность и зубья, которые следуют по спирали на делительном цилиндре.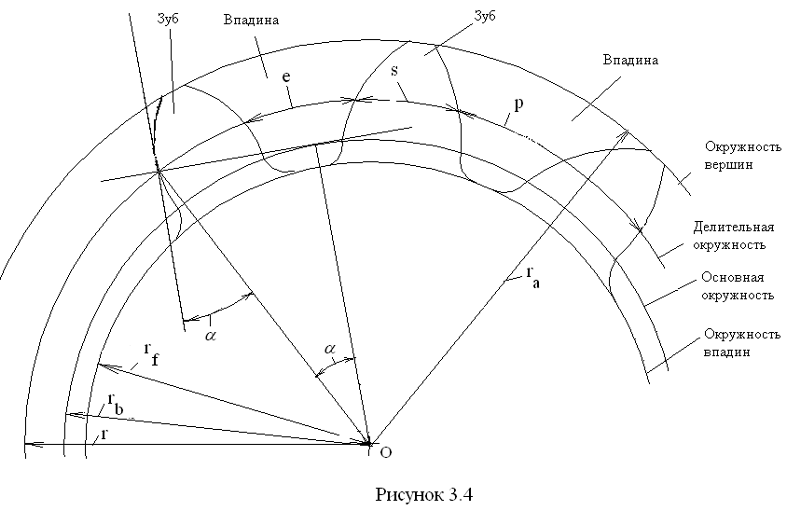
У наружных косозубых шестерен зубья выступают наружу, а у внутренних косозубых шестерен зубья выступают внутрь.
Как рассчитать нормальный модуль винтовой передачи?
Калькулятор нормального модуля косозубого зубчатого колеса использует Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса * cos (угол винтового зубчатого колеса) для расчета нормального модуля косозубого зубчатого колеса, формула нормального модуля косозубого зубчатого колеса определяется как модуль опорная точка зуба ортогональна спирали резьбы. Нормальный модуль косозубого колеса обозначается м n символ.
Как рассчитать нормальный модуль винтовой передачи с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для нормального модуля косозубой шестерни, введите поперечный модуль косозубой шестерни (м) и угол наклона косозубой шестерни (ψ) и нажмите кнопку расчета.
Вот как можно объяснить расчет нормального модуля винтовой передачи с заданными входными значениями -> 3,081446 = 0,0034*cos(0,4363323129985) .
Часто задаваемые вопросы
Что такое обычный модуль винтовой передачи?
Формула нормального модуля косозубого зубчатого колеса определяется как модуль базы зуба, ортогональной спирали резьбы, и представляется как м n = m*cos(ψ) или Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого колеса Шестерня*cos(Угол винтовой шестерни) . Поперечный модуль косозубого зубчатого колеса — это модуль косозубого зубчатого колеса, измеренный в плоскости вращения, а угол наклона косозубого зубчатого колеса — это угол между любым косозубым зубчатым колесом и осевой линией на его правом круговом цилиндре или конусе.
Как рассчитать нормальный модуль винтовой передачи?
Формула нормального модуля косозубого зубчатого колеса определяется как модуль базовой точки зуба, ортогональный спирали резьбы, который рассчитывается с использованием Нормальный модуль косозубого зубчатого колеса = поперечный модуль косозубого зубчатого колеса*cos(угол наклона косозубого зубчатого колеса) .