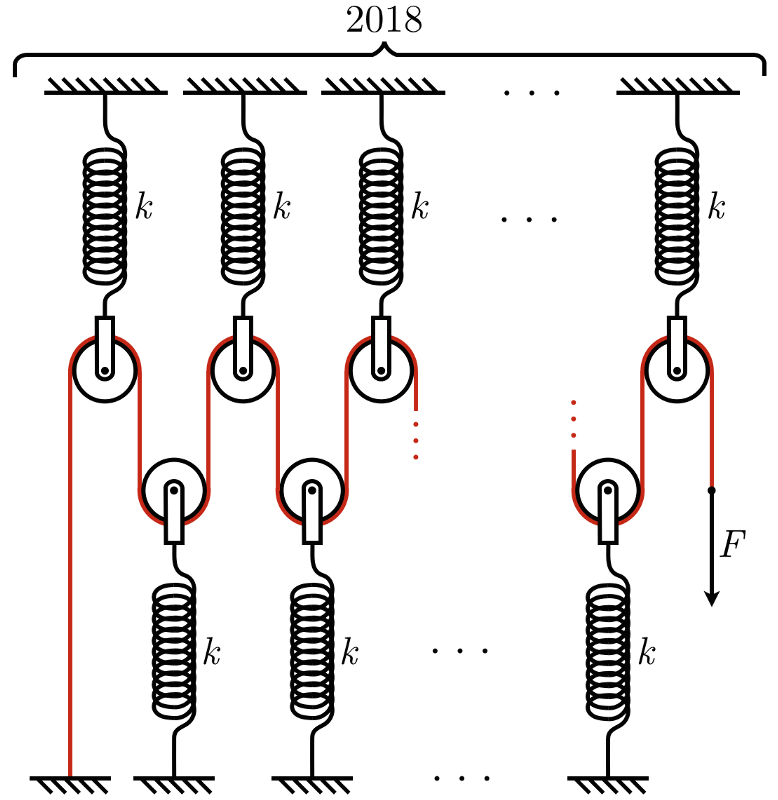
Параллельное и последовательное соединение пружин: Физика и математика для школьников
alexxlab | 09.08.1984 | 0 | Разное
Параллельное соединение пружин
При параллельном соединении двух пружин, имеющих коэффициенты жесткости с1, с2 (рис. 2.5), смещение тела равно деформации каждой из пружин:
. (2.9)
Рис. 2.5 Параллельное соединение пружин
Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна сумме сил упругости двух установленных пружин, откуда с учетом (2.9) получаем
,
окончательно
. (2.10)
При последовательном соединении двух пружин, имеющих коэффициенты жесткости с1, с2 (рис. 2.6), смещение тела равно сумме деформаций пружин:
. (2.11)
Рис. 3.6 Последовательное соединение пружин
Сила упругости эквивалентной пружины с коэффициентом жесткости с* будет равна каждой из сил упругости установленных пружин, откуда
,
,
откуда
Окончательно с учетом (2. 11) получаем
11) получаем
. (2.12)
Влияние сопротивления на свободные колебания
Пусть на точку массы m, совершающую прямолинейное движение, действуют две силы (рис. 2.7):
Восстанавливающая сила (сила упругости пружины): .
Сила сопротивления, пропорциональная скорости движения точки (сила сопротивления демпфера): .
Рис. 2.7 Движение массы с демпфированием
Дифференциальное уравнение движения точки запишется как
;
,
обозначая
, , (2.13)
получаем линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:
. (2.14)
Характеристическое уравнение имеет вид
, (2. 15)
15)
его корни равны
, (2.16)
где – дискриминант.
Как известно из курса высшей математики, общее решение дифференциального уравнения (2.14) существенно зависит от знака дискриминанта , т.е. от соотношения между b и k.
1-й случай (малое сопротивление): b k , D 0.
Обозначим , причем k* k. Тогда корни (2.16) характеристического уравнения будут комплексно сопряженными:
,
Общее решение дифференциального уравнения (2.14) в данном случае имеет вид
, (2.17)
это затухающие колебания с частотой k* и периодом (рис.3.8).
Амплитуда колебаний убывает со временем. Отношение последующей амплитуды к предыдущей называется декрементом затухания:
< 1 (2. 18)
18)
Рис. 2.8 Затухающие колебания
Часто используется также логарифмический декремент .
Таким образом, амплитуды образуют геометрическую прогрессию с показателем q, меньшим единицы.
Видим также, что наличие сопротивления приводит к уменьшению частоты колебаний (k * k) и к увеличению их периода (Т* > Т).
2-й случай (граничный): b = k , D = 0.
Корни (2.16) характеристического уравнения получаются кратные, , и решение дифференциального уравнения (2.14) приобретает вид
. (2.19)
Поскольку
экспонента убывает быстрее, чем растёт
линейная функция времени, в зависимости
от начальных условий движения получим
ту или иную картину затухающего
апериодического (т. е. не колебательного)
движения (рис.2.9).
е. не колебательного)
движения (рис.2.9).
3-й случай (большое сопротивление): b > k, D > 0.
В этом случае обозначим >0, и оба корня (2.16) характеристического уравнения будут действительными и отрицательными:
< 0, < 0,
общее решение
. (2.20)
Рис. 2.9 График затухающего апериодического движения
Здесь также получаем затухающие апериодическое движение, графики будут такие же, как и в случае b= k.
Изучение гармонических колебаний спиральных пружин при параллельном и последовательном соединениях
Nach oben
Информация
- Контактное лицо
- Условия сотрудничества
- Декларация о конфиденциальности
- Вводные данные
Обслуживание
- Краткий обзор услуг
- Скачать
- Каталоги
- Вебинары и Видео
- Связаться со службой поддержки клиентов
Компания
- О нас
- Безопасность в классе
Please note
* Prices subject to VAT.
We only supply companies, institutions and educational facilities. No sales to private individuals.
Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.
Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина.
Сохраненные корзины вы можете найти в разделе My Account.
Название корзины
Помогите решить / разобраться (Ф)
| sasha_vertreter |
| ||
27/04/09 |
| ||
| |||
| meduza |
| |||
03/06/09 |
| |||
| ||||
| sasha_vertreter |
| ||
27/04/09 |
| ||
| |||
| meduza |
| |||
03/06/09 |
| |||
| ||||
| sasha_vertreter |
| ||
27/04/09 |
| ||
| |||
| spaar |
| ||
08/04/10 |
| ||
| |||
| meduza |
| |||
03/06/09 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| meduza |
| |||
03/06/09 |
| |||
| ||||
| sasha_vertreter |
| ||
27/04/09 |
| ||
| |||
| spaar |
| ||
08/04/10 |
| ||
| |||
| sasha_vertreter |
| ||
27/04/09 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Eule_A, Pphantom, photon, Aer, whiterussian, Jnrty, profrotter, Парджеттер, Супермодераторы
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.
 1 Кинематика
1 Кинематика - 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 2.
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.
 3 Магнетизм
3 Магнетизм - 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика.
 Квантовая теория
Квантовая теория - 6.2 Ядерная физика
- 6.1 Атомная физика.
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Лабораторная работа Измерение ж сткости пружины
Сила упругости и закон Гука
Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.
Примеры упругой деформации:
- Сжатый воздушный шарик распрямляется после того, как его отпустят.
- Если согнуть ластик, а затем отпустить, он распрямится.
- Мостик из доски, перекинутой через ручей, прогибается под пешеходом. Но когда пешеход ступает на землю, доска распрямляется.
Примеры пластической деформации:
- Скомканная бумага остается скомканной и после того, как ее отпустили.
- Пластилин сохраняет форму вылепленной из него фигуры.
- Согнутая металлическая пластина остается согнутой.
Закон Гука
При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.
Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.
x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.
Абсолютное удлинение определяется формулой:
l0 — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.
Источник
Сила упругости
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
- Деформация растяжения
- Деформация сжатия
- Деформация сдвига
- Деформация при кручении
- Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно упругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Никакой жесткости в онлайн-школе Skysmart. Только дружелюбная атмосфера, контакт с учеником и интерактивные задания на уроках по физике, которые хочется решать еще и еще.
Источник
Урок 9. Закон Гука
Одно из проявлений взаимодействия тел – их деформация.
Деформация – это изменение формы и размеров тела, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.
Почему у различных тел деформации неодинаковы?
Вспомнили строение вещества, силы взаимодействия.
Силы упругости – это силы, возникающие при деформации любых твёрдых тел, а также при сжатии жидкостей и газов.
Главная особенность силы упругости в том, что она препятствует изменению размеров и формы тела.
Следует помнить, что сила упругости всегда перпендикулярна поверхности соприкосновения взаимодействующих тел.
Если взаимодействуют пружины или нити, то силы упругости направлены вдоль их осей.
Виды деформации: растяжение, сжатие, изгиб, кручение, сгиб. Упругие и пластичные деформации.
Закон Гука. Закон, который позволяет рассчитать величину этих деформаций: $F = -k \Delta l = -k(l — l_0)$.
Лабораторная работа «Измерение жёсткости пружины»
Сила упругости
Силы в природе делятся на четыре фундаментальных взаимодействия: 1 – гравитационные (сила тяжести), 2 – электромагнитные (сила упругости и сила трения), 3 – сильные (ядерные силы), 4 – слабые (превращения элементарных частиц). Первые два из них относятся к макроскопическому миру, а следующие два взаимодействия относятся к микроскопическому миру.
Под воздействием внешних сил тела в разной степени деформируются т. е. изменяют свою форму и объём. При деформации молекулы тела смещаются, и тело выводится из состояния равновесия. При этом, вследствие взаимодействия молекул, в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы действуют на каждый элемент поверхности произвольного объёма, выделенного в теле, со стороны окружающих его частей. Любое тело состоит из частиц (молекул, атомов, ионов, элементарных частиц). Между заряженными частицами существуют силы электромагнитного притяжения и отталкивания. Если частицы находятся в состоянии равновесия, то силы притяжения и отталкивания уравновешивают друг друга. В случае деформации тела происходят изменения во взаимном расположении частиц. Если расстояние между частицами увеличивается, то электромагнитные силы притяжения превышают силы отталкивания. Если же частицы сближаются, то преобладают силы отталкивания. Силы, возникающие в результате изменения расположения частиц очень малы. Но вследствие деформации изменяется расположение очень большого количества частиц, поэтому равнодействующая всех сил уже является значительной.
е. изменяют свою форму и объём. При деформации молекулы тела смещаются, и тело выводится из состояния равновесия. При этом, вследствие взаимодействия молекул, в теле возникают силы, стремящиеся вернуть его в состояние равновесия. Эти силы действуют на каждый элемент поверхности произвольного объёма, выделенного в теле, со стороны окружающих его частей. Любое тело состоит из частиц (молекул, атомов, ионов, элементарных частиц). Между заряженными частицами существуют силы электромагнитного притяжения и отталкивания. Если частицы находятся в состоянии равновесия, то силы притяжения и отталкивания уравновешивают друг друга. В случае деформации тела происходят изменения во взаимном расположении частиц. Если расстояние между частицами увеличивается, то электромагнитные силы притяжения превышают силы отталкивания. Если же частицы сближаются, то преобладают силы отталкивания. Силы, возникающие в результате изменения расположения частиц очень малы. Но вследствие деформации изменяется расположение очень большого количества частиц, поэтому равнодействующая всех сил уже является значительной. Это и есть сила упругости. Следовательно, сила упругости по своему происхождению – электромагнитная сила. Чтобы не рассматривать сложные электромагнитные взаимодействия в механике для характеристики этих явлений вводят силу упругости.
Это и есть сила упругости. Следовательно, сила упругости по своему происхождению – электромагнитная сила. Чтобы не рассматривать сложные электромагнитные взаимодействия в механике для характеристики этих явлений вводят силу упругости.
НАШИ ПАРТНЁРЫ
© Государственная образовательная платформа «Российская электронная школа»
Источник
Сила упругости. Закон Гука
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x ≪ l справедлив закон Гука.
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε = x l . Напряжением в теле называется отношение σ = — F у п р S . Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E ≈ 2 · 10 11 Н м 2 , а для резины E ≈ 2 · 10 6 Н м 2
Закон Гука можно обобщить для случая сложных деформаций.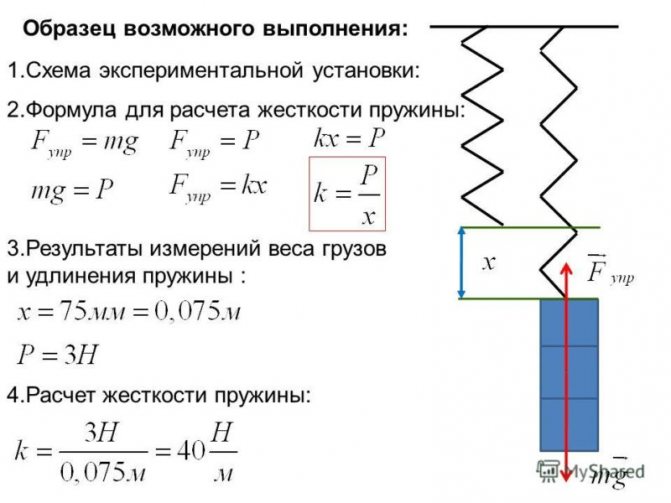 Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
Концы стержня лежат на двух опорах, которые действуют на тело с силой N → , называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k ).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
Анатомия автомата “Репка”
Анатомия автомата “Репка”.
СТАТЬЯ
Как связан советский силомер и Закон Гука? Как устройство понимает, какую силу приложил игрок? И где еще в повседневной жизни встречаются пружины?
Исторически первыми упругими элементами, применяемыми человеком, считаются различные бытовые пинцеты и прищепки-зажимы, луки и удочки. Еще в пятом тысячелетии до нашей эры в Месопотамии применялись весы, использовавшие принцип рычага для достижения равновесия, а позже, в Греции, был изобретен безмен, позволивший изменять плечо приложения силы, что сделало использование весов более удобным.
Давайте посмотрим на автомат Репка и подумаем, каким же образом он определяет вашу силу. Дело в том, что в ручке автомата установлена пружина — упругий элемент машин и различных механизмов, накапливающий и отдающий, или поглощающий механическую энергию.
Удлинение пружины описывается законом Гука (1660 год, Р. Гук), который гласит, что растяжение эластичного стержня пропорционально приложенной к нему силе, направленной вдоль его оси. В реальности этот закон выполняется не точно, а только при малых растяжениях и сжатиях.
С точки зрения классической физики, пружину можно рассматривать как устройство, накапливающее потенциальную энергию путём изменения расстояния между атомами эластичного материала.
Основой автомата «Репка» можно с уверенностью назвать систему из нескольких пружин и рукоятку, за которую нужно тянуть при игре. Приведём схематичный и весьма упрощенный рисунок этой части автомата для упрощения рассказа:
СОСТАВЛЯЮЩИЕ ЧАСТИ:
- Основная пружина (1)
- Пружина для поддержки ручки (2)
- Малая пружина для натяжения измерительного троса (3)
- Ручка (4)
- Защитный кожух (5)
- Внутренняя защитная оболочка (6)
- Измерительный трос (7)
- Платформа (8)
- Датчик поворота (9)
- Электротехническая магия (10)
ОСНОВНАЯ ПРУЖИНА
Эта пружина принимает основное участие в «игре», создаёт силу, противодействующую игроку.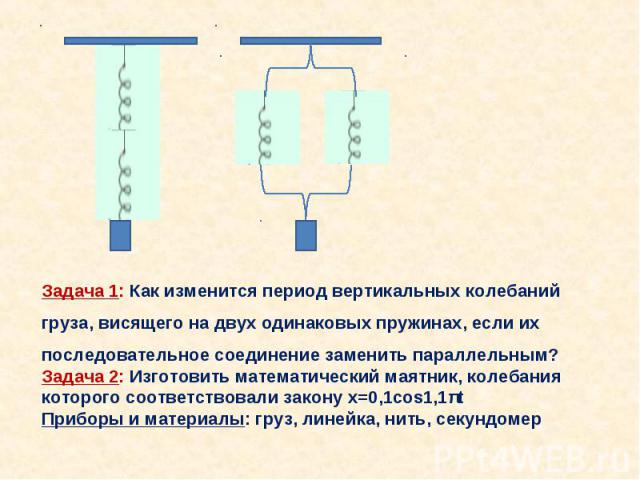
ПРУЖИНА ДЛЯ ПОДДЕРЖАНИЯ РУЧКИ
Несмотря на приличные размеры, этот элемент автомата участия в игре не принимает и необходим для удерживания ручки на весу, когда ее не держит игрок.
МАЛАЯ ПРУЖИНА
Служит для натяжения измерительного троса – натягивает измерительный трос, а также позволяет ему изменять свою длину
Ручка – за неё держится игрок. Сделана из жесткого советского пластика.
ЗАЩИТНЫЙ КОЖУХ
Защищает пружину для поддержания ручки (2) от внешнего воздействия: пыли, жидкостей и любознательных индивидуумов.
ВНЕШНЯЯ ЗАЩИТНАЯ ОБОЛОЧКА
Находится снаружи корпуса автомата. Защищает от механических повреждений и прочих воздействий.
ВНУТРЕННЯЯ ЗАЩИТНАЯ ОБОЛОЧКА
Находится внутри корпуса автомата и носит несколько функций: защищает от внешних воздействий пружину (1), направляет движение платформы (8) и является опорой для крепежа малой пружины (3).
ИЗМЕРИТЕЛЬНЫЙ ТРОС
Соединён своими концами с пружиной (3) и платформой (8). Средняя часть троса обмотана вокруг датчика поворота (9).
ПЛАТФОРМА
Платформа – соединена с ручкой (4) при помощи стального стержня. Необходима для создания упора пружины (1).
ДАТЧИК ПОВОРОТА
Способен менять электрический сигнал в зависимости от угла поворота его цилиндрической части. Работает по принципу реостата – изменяет своё сопротивление.
ЭЛЕКТРОТЕХНИЧЕСКАЯ МАГИЯ
Итогом ее работы является преобразование сигнала датчика (9) в значение усилия, которое создал игрок. Ну и зажигать лампочку напротив персонажей сказки.
ПРИНЦИП РАБОТЫ АВТОМАТА
Изначально игрок становится рядом с автоматом и тянет за ручку (4). Ручка при помощи стального стержня жестко связана с пластиной (8). Таким образом, пытаясь вытянуть на себя ручку, игрок на самом деле пытается переместить в свою сторону пластину (8), что приводит к сжатию основной пружины (1).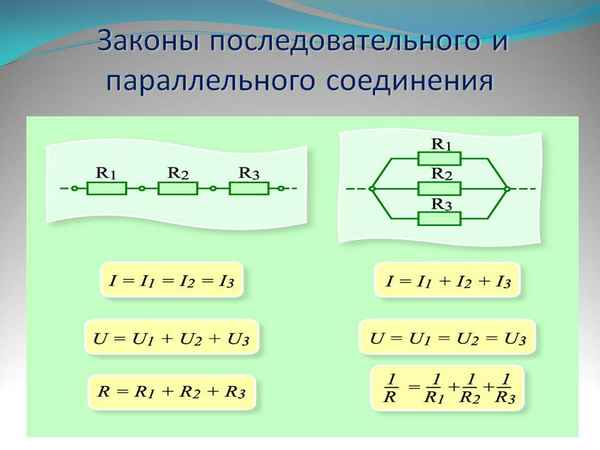 Жесткость этой пружины достаточно велика, чтобы оказывать серьезное сопротивление такому сжатию! Например, чтобы добраться хотя бы до уровня «Внучка», необходимо приложить силу около 1400 Н – что равносильно удерживанию (пусть и на долю секунды) тела массой почти 140 кг…
Жесткость этой пружины достаточно велика, чтобы оказывать серьезное сопротивление такому сжатию! Например, чтобы добраться хотя бы до уровня «Внучка», необходимо приложить силу около 1400 Н – что равносильно удерживанию (пусть и на долю секунды) тела массой почти 140 кг…
Но как же устройство понимает, какую силу приложил игрок?
Когда пластина двигается (пусть и на очень малое расстояние), прикреплённый к ней трос также вытягивается в сторону ручки. Такое движение заставляет трос натягиваться, ведь расстояние между его концами увеличивается. Обычный стальной трос быстро порвётся от таких нагрузок, но в данном случае на помощь приходит пружина (3) – она достаточно мягкая и легко растягивается. Тем самым она позволяет тросу «увеличить свою длину» и повернуть чувствительный элемент датчика (9) вокруг его оси.
Поворот чувствительного элемента приводит к изменению сигнала и работе электросхемы внутри автомата.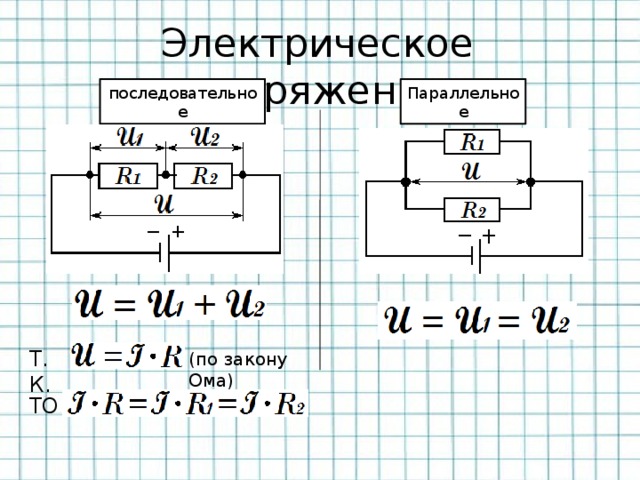 Конкретный механизм обработки сигнала сложен и мы его рассматривать не будем. А вот принцип влияния на сигнал поворота элемента датчика разберём обязательно, но на примере другого автомата.
Конкретный механизм обработки сигнала сложен и мы его рассматривать не будем. А вот принцип влияния на сигнал поворота элемента датчика разберём обязательно, но на примере другого автомата.
ЗАКОН ГУКА
Закон Роберта Гука (17 в. Н.Э.) возник в результате длительного исследования упругого поведения различных материалов при сжатии, растяжении и более сложных типов деформации. Было обнаружено, что сила , с которой материал сопротивляется деформации (а кто из нас хочет, чтобы его деформировали?) прямо пропорциональна величине этой деформации . Таким образом,
Однако, хотя это и позволяет нам оценивать силу, возникающую в пружине, точное значение мы можем получить только, если будем знать значение специального коэффициента упругости . Эта величина определяется для каждого упругого элемента отдельно и зависит от многих параметров – материал, форма, размер, температура и т.д. Финально получаем закон Гука:
УПРУГИЕ СИСТЕМЫ
Зачастую одной пружины оказывается недостаточно для достижения желаемого результата – слишком маленький коэффициент упругости, слишком большой размер пружины или необходимость удерживать в слишком большое тело. Многие задачи требуют применения нескольких упругих элементов – формировать упругие системы.
Многие задачи требуют применения нескольких упругих элементов – формировать упругие системы.
Здесь мы посмотрим на две самые простые схемы – последовательное и параллельное соединения пружин.
Последовательное соединение – позволяет комбинировать пружины, подсоединяя их концами друг к другу. В таком случае, коэффициент упругости системы определяется по следующей схеме:
Как видно, такое соединение позволяет уменьшить упругость системы и достигать более «тонкой» настройки устройства.
Параллельное соединение, напротив, позволяется значительно увеличить упругость и добиться гораздо большей жесткости. В данном случае используется правило:
Использование же нескольких таких соединений в одном устройстве позволяет добиться почти любых желаемых упругих характеристик системы.
ПРУЖИНЫ В НАШЕЙ ПОВСЕДНЕВНОЙ ЖИЗНИ
В мире существует большое разнообразие аппаратов для взвешивания объектов – начиная от простейших чашечных весов (какие использовала, например, греческая богиня закона Фемида) и заканчивая ультрасовременными системами, которые помимо веса оценивают многие параметры организма человека. Однако, самыми популярными и ходовыми можно назвать Пружинные весы.
Однако, самыми популярными и ходовыми можно назвать Пружинные весы.
Суть их работы заключает в растяжении тяжелыми (или не очень) грузом специально подобранной пружины. И на основании этого силы этого растяжения сделать вывод о весе тела.
Другим примером может служить система амортизации у автомобиля. Самые простые системы включают в себя одну или несколько пружин, обеспечивающих мягкость поездки.
Ещё одним, но более сложным, примером для нас может послужить обычная дверная ручка. Внутри каждого замка существует пружина (спиральная), которая удерживает ручку в горизонтальном положении и не даёт замку самопроизвольно открываться. Кстати, такие же пружины (только маленькие) используются и в заводных механизмах разнообразных игрушек, наручных и настенных часов.
Лучший университет Индии
Объявленный результат — июль 2022 г. (новый) | Прием открыт 2022-23 | Уведомление об экзамене курсовой работы Ph. D
|
Прием открыт БАМС и БУМС
|
Онлайн-викторина
|
Всемирный день аптеки 2021 г. Запросить обратный звонок
D
|
Прием открыт БАМС и БУМС
|
Онлайн-викторина
|
Всемирный день аптеки 2021 г. Запросить обратный звонокЗдесь вы можете оставить заявку на обратный звонок
Выберите курсB.PharmacyD.PharmacyB.Sc. Медицинская лаборатория технологийB.Sc. Биотехнология**B.Sc. Бакалавр микробиологии. Сельское хозяйство**B.Sc. Лесное хозяйствоBBAB.COMMBABBA LLBBA LLBLLBБакалавр образования**B.Sc MathematicsBCAMCAB.Tech Civil Engineering**B.Tech Petroleum EngineeringB.Tech CSEB.Tech Machine Engineering**B.Tech ECEM.Tech CSE**Диплом гражданского строительства**Диплом in Нефтяная инженерия**Диплом CSE**Диплом ME**Диплом электроники и связиBUMSBAMSANMGNMM. Sc. Доктор биотехнологий CSE**Диплом по электротехнике**Магистр зоологииМагистр микробиологииДоктор философии по зоологииM.Tech в области теплотехники**MBBSPHD в области фармацевтики**B.B.A. в области спортивного менеджмента**бакалавр журналистики и массовых коммуникацийB.Com (с отличием)B.Tech. (с отличием) Машиностроение**B.Tech. в области электротехники **B.Sc (с отличием). Биотехнология**B.Sc (с отличием) в области микробиологии**Диплом в области автомобилестроения**BSc (с отличием)Медицинская микробиология**B.Tech. Бакалавр горного дела** Бакалавр наук о нефти** Диплом бакалавра химии Диплом специалиста по МРТ** Диплом оптометрии** Бакалавр наук (с отличием) в области медицинских лабораторных технологий** Бакалавр наук в области технологии OT**B Бакалавр наук в области ботаники** Бакалавр наук в области перфузионных технологий Бакалавр наук в области банковского дела и страхования Коммерция**Диплом специалиста по диализуДиплом специалиста по технологии операционных заловДип. Я не. ТехникДиплом в области КТ-сканирования.
Sc. Доктор биотехнологий CSE**Диплом по электротехнике**Магистр зоологииМагистр микробиологииДоктор философии по зоологииM.Tech в области теплотехники**MBBSPHD в области фармацевтики**B.B.A. в области спортивного менеджмента**бакалавр журналистики и массовых коммуникацийB.Com (с отличием)B.Tech. (с отличием) Машиностроение**B.Tech. в области электротехники **B.Sc (с отличием). Биотехнология**B.Sc (с отличием) в области микробиологии**Диплом в области автомобилестроения**BSc (с отличием)Медицинская микробиология**B.Tech. Бакалавр горного дела** Бакалавр наук о нефти** Диплом бакалавра химии Диплом специалиста по МРТ** Диплом оптометрии** Бакалавр наук (с отличием) в области медицинских лабораторных технологий** Бакалавр наук в области технологии OT**B Бакалавр наук в области ботаники** Бакалавр наук в области перфузионных технологий Бакалавр наук в области банковского дела и страхования Коммерция**Диплом специалиста по диализуДиплом специалиста по технологии операционных заловДип. Я не. ТехникДиплом в области КТ-сканирования. Бакалавр радиологических методов визуализации. in MLT**Phd In Bio Chemistry**M.Phil in Chemistry**PhD_Micro**PhD in English**PhD in BotanyPhD Education**Ph.D. Науки об окружающей среде**PhD PhysiologyPhD Biotech Agri**B.Sc. в сестринском делеPh.D. МенеджментPh.D. Сельское хозяйствоPHD PharmacyPh.D. Коммерция**Ph.D. кандидат политических наук**Ph.D. Electronics Communication**M.Phil в зоологииPhD. Кандидат юридических наук**Магистр математики**Магистр философии по биотехнологии**Магистр философии по компьютерным наукам**Магистр философии по английскому языку**Магистр философии. в социологии ** Магистр наук. В области агрономии**Магистр философии в области физики**Магистр философии в области образования**Магистр философии в области политических наук**Магистр философии в области экономики**Магистр философии в области ботаники**Доктор философии. Кандидат экономических наук * BBA в области управления цепями поставок ** MBA в области управления логистикой ** MBA в области управления безопасностью ** BSC в области охраны здоровья и окружающей среды ** BSC в области пожарной и промышленной безопасности ** Кандидат наук в области агрономии ** Кандидат математических наук ** Кандидат наук.
Бакалавр радиологических методов визуализации. in MLT**Phd In Bio Chemistry**M.Phil in Chemistry**PhD_Micro**PhD in English**PhD in BotanyPhD Education**Ph.D. Науки об окружающей среде**PhD PhysiologyPhD Biotech Agri**B.Sc. в сестринском делеPh.D. МенеджментPh.D. Сельское хозяйствоPHD PharmacyPh.D. Коммерция**Ph.D. кандидат политических наук**Ph.D. Electronics Communication**M.Phil в зоологииPhD. Кандидат юридических наук**Магистр математики**Магистр философии по биотехнологии**Магистр философии по компьютерным наукам**Магистр философии по английскому языку**Магистр философии. в социологии ** Магистр наук. В области агрономии**Магистр философии в области физики**Магистр философии в области образования**Магистр философии в области политических наук**Магистр философии в области экономики**Магистр философии в области ботаники**Доктор философии. Кандидат экономических наук * BBA в области управления цепями поставок ** MBA в области управления логистикой ** MBA в области управления безопасностью ** BSC в области охраны здоровья и окружающей среды ** BSC в области пожарной и промышленной безопасности ** Кандидат наук в области агрономии ** Кандидат математических наук ** Кандидат наук. Магистр энтомологии**Магистр наук об окружающей среде**Магистр истории**Магистр философии по менеджменту**Доктор философии. Лесное хозяйство** Магистр наук Медицинская лаборатория технологий**Диплом в области сельского хозяйстваM.Tech Civil Engineering**M.Phill в области государственного управления**PhD. в области химииМагистр технологий в области проектирования конструкцийМагистр технологий в области производства и промышленной инженерии**Магистр технологий в области инженерии окружающей средыLLMM.Pharm (фармакология)M.Pharm (фармацевтика)**B.Sc. Оптометрия
Магистр энтомологии**Магистр наук об окружающей среде**Магистр истории**Магистр философии по менеджменту**Доктор философии. Лесное хозяйство** Магистр наук Медицинская лаборатория технологий**Диплом в области сельского хозяйстваM.Tech Civil Engineering**M.Phill в области государственного управления**PhD. в области химииМагистр технологий в области проектирования конструкцийМагистр технологий в области производства и промышленной инженерии**Магистр технологий в области инженерии окружающей средыLLMM.Pharm (фармакология)M.Pharm (фармацевтика)**B.Sc. Оптометрия
О ГЛОКАЛЬНОМ
200
+
Опытный
Факультет
55
+
UG и PG
Программы
350
+
Акров
Кампус
15
+
Страна
Студенты
НАГРАДЫ И ДОСТИЖЕНИЯ
Glocal University, Glocal пользуется высоким авторитетом среди многих национальных рейтинговых служб, которые оценивают
качество образования, исследовательская деятельность, доступность и спортивные достижения.
ОТЛИЧНЫЙ КАМПУС ГОДА
Самый инновационный университет с отличным кампусом года
ЛУЧШИЙ УНИВЕРСИТЕТ СЕВЕРНОЙ ИНДИИ
Награжден как лучший Университет
в СЕВЕРНОЙ ИНДИИ от jagranjosh.com
ЛУЧШАЯ развивающаяся бизнес-школа
Деванг Мехта Национальная награда
за лучшую развивающуюся бизнес-школу
150+
Посещенные компании
18+
Самый высокий пакет Lacs
4.5+
Средний пакет
4,5+
Студент занял 9 место0082
НАШИ УВАЖАЕМЫЕ РЕКРУТЕРЫ
События
Новости
Конкурс по чтению книг
08 сентября 2022 года для всех учащихся
Glocal University Департаментом социального обеспечения студентов.
Новости
Документальные фильмы Шоу Празднование Дня учителя
Учитель Быть одним — высшая привилегия, иметь его — лучшее благословение. День учителя в Индия отмечается 5 сентября в ознаменование т
Новости
Празднование Дня учителя
Празднование Дня учителя в Glocal University
5 сентября 2022 г.
ОТЧЕТ О СОБЫТИИ
Если страна с
Новости
Празднование Дня Независимости
Празднование 76-го Дня Независимости
Подробнее…
Полученные результаты
Результаты
Академический календарь
Академический календарь
Свяжитесь с нами
Свяжитесь с нами
Места размещения
Размещение
ОТЗЫВЫ СТУДЕНТОВ
Целью данного исследования является изучение влияния на жесткость пружины параллельного и последовательного соединения двух идентичных пружин и того, как результирующие жесткости параллельного и последовательного комплектов пружин сравнивать.
 – Наука уровня A
– Наука уровня A- Поиск
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Выдержки из этого документа…
Постоянная жесткости последовательно и параллельно соединенных пружин
Курсовая работа AS Physics
Автор Malcolm Davis
Планирование
одинаковые пружины в параллельном и последовательном сочетании, и как результирующие жесткости параллельного и последовательного комплектов пружин сравниваются с параметрами одиночной пружины с одинаковой жесткостью пружины.
Гипотеза
Закон Гука гласит, что «Величина жесткости пружины (k) равна приложенной силе растяжения (F), деленной на результирующее удлинение (x)», должна быть возможность определить жесткость пружины для каждого весенний комплект.
Исходя из существующих знаний о пружинах, я предлагаю, чтобы набор последовательных пружин имел меньшую жесткость пружины (и, следовательно, в соответствии с законом Гука демонстрировал большее растяжение), чем набор параллельных пружин. Кроме того, поскольку закон Гука является линейной функцией, жесткость последовательного набора пружин должна быть ровно вдвое меньше, чем у одинарной пружины, тогда как жесткость параллельного набора должна быть ровно вдвое больше, чем у одинарной пружины. Это также означает, что если результирующее удлинение или длина пружины наборов пружин графически отобразить по оси y, а возрастающую силу отобразить по оси x (чтобы результаты можно было отобразить в традиционном научном графическом виде), градиент будет равен обратная жесткость пружины.
Кроме того, поскольку закон Гука является линейной функцией, жесткость последовательного набора пружин должна быть ровно вдвое меньше, чем у одинарной пружины, тогда как жесткость параллельного набора должна быть ровно вдвое больше, чем у одинарной пружины. Это также означает, что если результирующее удлинение или длина пружины наборов пружин графически отобразить по оси y, а возрастающую силу отобразить по оси x (чтобы результаты можно было отобразить в традиционном научном графическом виде), градиент будет равен обратная жесткость пружины.
Эта гипотеза подтверждается многими источниками, одним из таких источников является «Физика» Кена Добсона, Дэвида Грейса и Дэвида Ловетта, в котором в издании 2000 года на странице 90 говорится, что жесткость двух последовательно соединенных пружин равна k = k/2. а для двух параллельных пружин k = 2k
Однако эта гипотеза, вероятно, будет верна только тогда, когда пружина растягивается прямо пропорционально увеличению силы, действующей на пружину.
…читать дальше.
9
382
385,5
384
383.83
10
401
423
410
411.33
Series | ||||||||||
Mass / 100g | Length 1 /mm | Length 2 /mm | Length 3 /mm | Average /mm | ||||||
1 | 129. | 134.3 | 136.1 | 133.30 | ||||||
2 | 206 | 210.5 | 224 | 213.50 | ||||||
3 | 283 | 283 | 307,5 | 91,17979 | 99999999999999999999999999999999999999999999999999999999999999999999999999999999999н0255 | 4 | 358.5 | 358 | 386 | 367. |
5 | 433 | 434 | 466 | 444.33 | ||||||
6 | 511 | 507 | 546 | 521.33 | ||||||
7 | 591 | 580.5 | 627.5 | 599.67 | ||||||
8 | 663 | 654 | 704 | 673. | ||||||
9 | 746 | 728 | 786 | 753.33 | ||||||
10 | 826 | 795 | 864 | 828.33 |
Parallel | ||||
Mass / 100 г | Длина 1 /мм | Длина 2 /мм | Длина 3 /мм | 0 Среднее значение /мм |
1 | 37. | 37 | 36 | 36.83 |
2 | 58 | 57 | 58 | 57.67 |
3 | 79 | 78 | 77.8 | 77.93 |
4 | 99 | 97.9 | 99.4 | 98.77 |
5 | 118. | 117 | 116,8 | 117,43 |
6 | 138 | 1400007 99999999999999999999999999999999999999999999999999999999999999999999999999999999ня | 999999999999999999999999999999999999999999999999999999999999999999999999999н0002 139139.00 | |
7 | 159 | 158 | 160.2 | 159.07 |
8 | 178 | 178 | 179 | 178. |
9 | 197.2 | 198 | 198.4 | 197.87 |
10 | 219 | 218 | 220.2 | 219.07 |
Analysis of Results
As mentioned in the план, приведенные выше результаты не показывают фактическое растяжение пружин (что следует учитывать при анализе), однако они показывают общую длину пружины (пружин), включая исходную длину пружины.
Для этого я заполнил приведенные ниже таблицы фактического удлинения пружины в каждом случае. Эти значения растяжения были найдены путем вычитания исходной длины пружины (найденной перед проведением каждого эксперимента) из общей длины, указанной в приведенных выше таблицах. Поскольку в анализе используются только средние результаты 3 прогонов для каждой пружины
Поскольку в анализе используются только средние результаты 3 прогонов для каждой пружины
…читать дальше.
Все эти ограничения могли отрицательно сказаться на результатах, и в будущих экспериментах было бы целесообразно внести изменения, чтобы свести их к минимуму. Некоторыми возможными решениями для преодоления вышеупомянутых проблем могут быть соответственно:
- Радиолокационное устройство для измерения расстояния можно разместить под комплектом пружин и грузами, чтобы более точно оценить растяжение пружин:
- В качестве пружин можно использовать более жесткие пружины (т. колебания будут затухать намного быстрее, а также, если пружины растянуть до предполагаемого нового положения перед тем, как их отпустить, потенциал вертикальных колебаний уменьшится. Также полезно, чтобы эксперименты проводились в среде, свободной от движения воздуха (т. е. в вакууме), чтобы не возникало дальнейших колебаний.
- Поскольку это ограничение также возникло из-за использования линейки, расположенной в паре сантиметров от пружины, ограничение было бы устранено, если бы использовалось то же устройство, которое использовалось для устранения ограничения 1.

- Эта проблема может быть решена путем использования более симметричного или специализированного оборудования, с помощью которого лучше обеспечивается равномерное распределение нагрузки на 2 пружины, такое оборудование может включать что-то вроде:
Резюме
В заключение, это исследование позволило экспериментально доказать влияние последовательного и параллельного размещения пружин на их общую жесткость. Он убедительно показал, что жесткость пружины уменьшается вдвое, когда 2 пружины этого типа расположены последовательно, и удваивается, когда 2 пружины этого типа расположены параллельно.
Эксперименты, использованные в этом исследовании, можно было бы улучшить, используя указанные выше модификации, однако в целом использованные эксперименты оказались удовлетворительными для получения результатов, которые были достаточно точными, чтобы выявить описанную взаимосвязь.
…читать дальше.
Эта письменная работа студента — одна из многих, которые можно найти в разделе AS и A Level Waves & Cosmology.
Нашли то, что искали?
Не тот? Найдите название своего сочинения…
- Присоединяйтесь к более чем 1,2 миллионам студентов каждый месяц
- Ускорьте свое обучение на 29%
- Неограниченный доступ всего от 6,99 фунтов стерлингов в месяц
Посмотреть связанные эссе
Мне удалось показать, что закон Гука верен, что сила, приложенная к упругому телу, пропорциональна тому, насколько оно растягивается. Мои измерения были достаточно точными, но эксперимент мог быть ошибочным из-за нескольких факторов: * Пружина могла быть деформирована вне визуального обнаружения, поэтому результаты не были пропорциональны.
0,401 k = 4×2 = 30,627 1,289 График 3 Последний график, который я нарисую, позволит мне оценить гравитацию. Надеюсь, это значение будет примерно 90,81 Н/м2, так как это значение силы тяжести, и это будет означать, что данные, которые я собрал, точны.

Правило метра. (iv) 2 зажима и стойки. (v) 2 коробки веса. (vi) Световой указатель пружины. (vii) Секундомер. (c) Метод: (i) Подвесьте световую пружину к зажиму и прикрепите световую указку к пружине. (ii) Установите фиксированную вертикальную линейку рядом с пружиной, используя зажим и подставку.
дешевые весы с верхней тарелкой с низкой точностью могут иметь ошибку при считывании их значений. Если оборудование точное и систематическая ошибка мала, мы говорим, что измерения точны. Случайная ошибка – это ошибка, допущенная во время измерений, например.
выполните 10 измерений растяжения, начиная с 1 Н до 10 Н силы на пружине. Таблица результатов Усилие в Н Тест 1 Тест 2 Тест 3 Среднее 1 33 31 35 33 2 71 75 70 72 3 114 112 115 113 4 150 148 146 148 5 185 183
по мере удаления гири проводится измерение) * Гири снова добавляются и производятся записи, чтобы можно было взять среднее значение из трех наборов показаний и определить значение K.
 РЕЗУЛЬТАТЫ: 1 2 3 Вес (кг) (x10-3) Длина (м) (x10-3) Расчетное удлинение (м) (x10-3)
РЕЗУЛЬТАТЫ: 1 2 3 Вес (кг) (x10-3) Длина (м) (x10-3) Расчетное удлинение (м) (x10-3)
Я также должен убедиться, что во время моих измерений они читаются на уровне глаз, чтобы избежать ошибки параллакса. Я также измерю диаметр конфеты в двух разных точках и возьму среднее из двух, так как диаметр по длине эластичной конфеты неодинаков.
Измерьте длину пружины 3 раза и запишите длину в ненагруженном состоянии в таблице пружин 4. Зацепите пружину за край зажимной стойки, как показано на рисунке, и закрепите эластичной лентой 5. Наденьте защитные очки 6.
- Более 160 000 штук
письменных работ студентов - Аннотировано
опытными учителями - Идеи и отзывы для
улучшения вашей работы
Аналитические подходы к генераторам с нелинейными пружинами при параллельном и последовательном соединении
ScienceDirect Корпоративный входВход/регистрация0002 Том 93, ноябрь 2015 г. , стр. 39-52
, стр. 39-52
https://doi.org/10.1016/j.mechmachtheory.2015.06.007Get rights and content
Мы разрабатываем аналитические подходы и анализируем область их применимости к генераторам с двумя нелинейными пружины в параллельном и последовательном соединении. В частности, мы фокусируем наше исследование на системах с упрочняющими пружинами и кубическими нелинейностями. В обоих случаях осциллятор управляется тремя безразмерными параметрами, а именно λ = k 2 / 9. Здесь k 1,2 и ε 1,2 — линейная жесткость и коэффициент нелинейности обеих пружин соответственно, а A — амплитуда положения массы, в параллели случае или отклонение пружины, соединенной с массой ( k 2 , ε 2 ), в последовательном случае. Установлено, что в параллельной конфигурации при λ > 0 и 0 < ϵ 1,2 ≤ 1 аналитическое решение дает превосходный подход к точному решению, найденному численно. Однако при последовательном соединении численное моделирование показывает, что решение осциллятора становится значительно сложнее, чем при параллельном соединении, и аналитические подходы прекрасно работают в диапазонах 0 < λ ≤ 1, 0 < ϵ 1,2 ≤ 0,1, и, 0 < λ ≤ 0,1, 0 < ϵ 1,2 ≤ 1,
Однако при последовательном соединении численное моделирование показывает, что решение осциллятора становится значительно сложнее, чем при параллельном соединении, и аналитические подходы прекрасно работают в диапазонах 0 < λ ≤ 1, 0 < ϵ 1,2 ≤ 0,1, и, 0 < λ ≤ 0,1, 0 < ϵ 1,2 ≤ 1,
Проблема нелинейных осцилляторов возникает во многих реальных системах от макро до нано масштабов длины. Поэтому нелинейные осцилляторы появляются во многих областях науки, таких как математика, физика, механика, электроника, химия, биология, астрономия и т. д. Обычно математическая модель нелинейного осциллятора представляет собой сильное нелинейное дифференциальное уравнение второго порядка. Такое нелинейное уравнение очень трудно решить, особенно аналитическими методами [1], [2], [3], [4], [5].
Было предложено много эффективных аналитических методов для решения основных осцилляторов с одной нелинейной пружиной, таких как вариационный метод [6], [7], [8], метод гомотопических возмущений [9], [10], [11], [12], [13], метод разложения по параметрам [14], [15], метод баланса энергии [16], [17], [18], [19], метод гармонического баланса [20], [21], [ 22] или метод Гамильтона, разработанный Хе [23], [24], [25], [26] среди прочих. Что касается комбинированных осцилляторов с последовательной линейной и нелинейной жесткостью, Телли и Копмаз [27] показали, что последовательное движение массы, заземленной с помощью линейных и нелинейных пружин, приводит к системе дифференциальных алгебраических уравнений. Они показали, что, вводя подходящую переменную, представляющую прогиб нелинейной пружины, можно получить нелинейное обыкновенное дифференциальное уравнение, которое можно решить с помощью метода Линдстедта [28], [29].] и метод гармонического баланса. Лай и Лим [30] расширили методы теории возмущений и гармоник для нелинейной системы, объединяющей последовательно линейные и нелинейные пружины. Основное уравнение было линеаризовано и связано с методом гармонического баланса для получения новых и точных аналитических приближенных решений более высокого порядка. Используя метод гомотопического анализа и гомотопический метод Паде для ускорения скорости сходимости решения ряда, Hoseini et al. В работе [31] проанализированы нелинейные свободные колебания консервативных осцилляторов с кубической нелинейностью инерционного и статического типа.
Что касается комбинированных осцилляторов с последовательной линейной и нелинейной жесткостью, Телли и Копмаз [27] показали, что последовательное движение массы, заземленной с помощью линейных и нелинейных пружин, приводит к системе дифференциальных алгебраических уравнений. Они показали, что, вводя подходящую переменную, представляющую прогиб нелинейной пружины, можно получить нелинейное обыкновенное дифференциальное уравнение, которое можно решить с помощью метода Линдстедта [28], [29].] и метод гармонического баланса. Лай и Лим [30] расширили методы теории возмущений и гармоник для нелинейной системы, объединяющей последовательно линейные и нелинейные пружины. Основное уравнение было линеаризовано и связано с методом гармонического баланса для получения новых и точных аналитических приближенных решений более высокого порядка. Используя метод гомотопического анализа и гомотопический метод Паде для ускорения скорости сходимости решения ряда, Hoseini et al. В работе [31] проанализированы нелинейные свободные колебания консервативных осцилляторов с кубической нелинейностью инерционного и статического типа. Барфоруши и др. В [32] применялся также метод гомотопических возмущений для решения нелинейных свободных колебаний систем с последовательной линейной и нелинейной жесткостями. Они обнаружили, что этот метод подходит для такого рода генераторов, хотя и показали ограничения такого метода для систем с более высокой степенью свободы. Недавно приблизительное значение эквивалентной жесткости для последовательно соединенных линейных и нелинейных пружин было получено Bayat et al. [33], применяя процедуру усреднения [34]. Более того, они показали, что приближенное значение эквивалентной частоты колебаний осциллятора соответствует значению, которое получается при гамильтоновом подходе.
Барфоруши и др. В [32] применялся также метод гомотопических возмущений для решения нелинейных свободных колебаний систем с последовательной линейной и нелинейной жесткостями. Они обнаружили, что этот метод подходит для такого рода генераторов, хотя и показали ограничения такого метода для систем с более высокой степенью свободы. Недавно приблизительное значение эквивалентной жесткости для последовательно соединенных линейных и нелинейных пружин было получено Bayat et al. [33], применяя процедуру усреднения [34]. Более того, они показали, что приближенное значение эквивалентной частоты колебаний осциллятора соответствует значению, которое получается при гамильтоновом подходе.
Для проверки прокомментированных выше аналитических подходов также необходимы численные решения нелинейных осцилляторов. Одним из наиболее эффективных методов интегрирования численно сильных нелинейных дифференциальных уравнений второго порядка является метод Рунге–Кутты четвертого порядка [19], [35], [36], [37]. Однако существуют альтернативные методы, еще более точные для численного решения таких уравнений. Раззаги и Эльнагар [38] использовали псевдоспектральный метод для нахождения численного решения осциллятора Дуффинга. Арикоглу и Озкол [39] решали численно различные нелинейные интегро-дифференциальные уравнения с использованием метода дифференциального преобразования (DTM). Они показали, что метод DTM является очень быстрой сходимостью, точным и экономичным инструментом для решения этих нелинейных уравнений. Используя преобразование Лапласа и аппроксимацию Паде, Момани и Эртюрк [40] предложили новый метод точного захвата частоты отклика нелинейных осцилляторов.
Однако существуют альтернативные методы, еще более точные для численного решения таких уравнений. Раззаги и Эльнагар [38] использовали псевдоспектральный метод для нахождения численного решения осциллятора Дуффинга. Арикоглу и Озкол [39] решали численно различные нелинейные интегро-дифференциальные уравнения с использованием метода дифференциального преобразования (DTM). Они показали, что метод DTM является очень быстрой сходимостью, точным и экономичным инструментом для решения этих нелинейных уравнений. Используя преобразование Лапласа и аппроксимацию Паде, Момани и Эртюрк [40] предложили новый метод точного захвата частоты отклика нелинейных осцилляторов.
Хотя численные методы могут быть очень точными инструментами для поиска нелинейных решений, у них есть недостаток, заключающийся в том, что они применимы только для определенных численных параметров. Таким образом, численные результаты применимы для решения различных технических задач количественно, хотя их недостаточно для глубокого качественного анализа задачи. Из-за этого ограничения нам нужен аналитический подход к решению нелинейной задачи, который должен быть пригоден для обсуждения.
Из-за этого ограничения нам нужен аналитический подход к решению нелинейной задачи, который должен быть пригоден для обсуждения.
Таким образом, основной целью настоящей работы является расширение применения процедуры усреднения, основанной на эквивалентной жесткости, для поиска аналитических подходов к генераторам с двумя нелинейными пружинами как в параллельном, так и в последовательном соединении. Кроме того, также предлагается подходящий безразмерный анализ, чтобы легко определить диапазоны применения найденных аналитических подходов. Эта статья начинается с вывода аналитических подходов к осцилляторам с нелинейными пружинами в параллельном и последовательном соединении, которые развиты в 2. Аналитический подход к осциллятору с нелинейными пружинами в параллельной конфигурации, 3. Аналитический подход к осциллятору с нелинейными пружинами в последовательном соединении. конфигурации соответственно. Сравнение аналитических подходов с численными решениями, а также диапазоны их применимости приведены в Разделе 3. Основные выводы и предложения для будущей работы изложены в Разделе 4, а численные аспекты подробно описаны в Приложении A.
Основные выводы и предложения для будущей работы изложены в Разделе 4, а численные аспекты подробно описаны в Приложении A.
Фрагменты сечений
Нелинейная пружина имеет нелинейную зависимость между силой и смещением. В настоящей работе рассматриваются упрочняющие пружины с нелинейной жесткостью sky=k01+εy2, где y — чистый прогиб нелинейной пружины, k 0 — постоянная жесткость, а ε — коэффициент нелинейности. . Такого рода нелинейные пружины появляются в так называемом уравнении Дюффинга, которое широко изучается [23], [41]. Дело ε > 0 соответствует упрочняющей пружине, а ε < 0 указывает на размягчающуюся, см.
. Рассмотрим систему, показанную на рис. 3, и выведем соответствующее дифференциальное уравнение движения. Система полностью описывается двумя координатами x 1 ( t ) и x 2 ( t ), которые дают положение точки соединения между пружинами и массой m , . соответственно, для любого произвольного времени.
соответственно, для любого произвольного времени.
Чтобы получить дифференциальное уравнение, мы применяем третий закон Ньютона к точке соединения и принцип Даламбера к массе m . Поэтому, суммируя силы в горизонтальном направлении, мы можем написать
. В этом разделе мы сравниваем аналитические подходы к нелинейным осцилляторам, определенные в предыдущих разделах, с их точными решениями, рассчитанными численно в Matlab ® (The MathWorks, Inc., Натик, Массачусетс, США) с использованием метода переменного состояния и численного алгоритма Рунге-Кутты.
Используя метод эквивалентной жесткости, мы нашли аналитические подходы первого порядка к генераторам с двумя нелинейными пружинами при параллельном и последовательном соединении. Мы сосредоточили наше исследование на системах с упрочняющими пружинами и кубическими нелинейностями. Точные решения рассчитаны численно в пакете Matlab ® с использованием метода состояний и алгоритма Рунге-Кутты. В случае параллельной конфигурации погрешности частоты и формы сигнала не зависят от коэффициента линейной жесткости λ, и
В случае параллельной конфигурации погрешности частоты и формы сигнала не зависят от коэффициента линейной жесткости λ, и
Эта работа была поддержана Universidad de Jaén (Испания) и Universidad de Córdoba (Испания) .
Каталожные номера (42)
- Z.F. Рен и др.
Простой подход к нелинейным генераторам
Физ. лат. A
(2009)
- С. Момани и др.
Решения нелинейных осцилляторов методом модифицированного дифференциального преобразования
Вычисл. Мат. заявл.
(2008)
- А. Арикоглу и др.
Решение краевых задач для интегро-дифференциальных уравнений методом дифференциального преобразования
Прил. Мат. вычисл.
(2005)
- М. Раззаги и др.
Численное решение управляемого осциллятора Дуффинга псевдоспектральным методом
J. Comput. заявл. Мат.
(1994)
- С.
 Момани и др.
Момани и др. Модифицированный метод гомотопических возмущений для решения сильно нелинейных осцилляторов
Вычисл. Мат. заявл.
(2009)
- Х. Хейн и др.
Отклик нелинейных генераторов со случайной частотой возбуждения, пересмотренный
J. Sound Vib.
(2007)
- М. Баят и др.
Нелинейные свободные колебания систем с кубической нелинейностью инерционного и статического типа: аналитический подход
Мех. Мах. Теория
(2014)
- С.Х. Хосейни и др.
Нелинейные свободные колебания консервативных осцилляторов с кубической нелинейностью инерционного и статического типа методом гомотопического анализа
J. Sound Vib.
(2008)
- С.К. Лай и др.
Точные приближенные аналитические решения для нелинейных свободных колебаний систем с последовательной линейной и нелинейной жесткостью
Дж.
 Саунд Виб.
Саунд Виб.(2007)
- Т. Озис и др.
Определение периодического решения для силы
u 1/3 модифицированным методом Линдштедта-Пуанкаре ХэJ. Sound Vib.
(2007)
Модифицированные методы Линдстедта-Пуанкаре для некоторых сильно нелинейных колебаний, часть I: разложение константы
Int. J. Нелинейный мех.
(2002)
Свободные колебания массы, заземленной последовательно линейными и нелинейными пружинами
J. Sound Vib.
(2006)
Гамильтонов подход к нелинейным осцилляторам
Phys. лат. A
(2010)
Применение модифицированного метода рационального гармонического баланса для класса сильно нелинейных осцилляторов
Физ. лат. A
(2008)
 Hu
HuРешение нелинейного осциллятора со смешанной четностью: гармонический баланс
J. Sound Vib.
(2007)
Численный метод обобщенного гармонического баланса для определения аналитических аппроксимаций периодических решений потенциала
x 4/3J. Sound Vib.
(2002)
Применение метода вариационных итераций для нелинейных свободных колебаний консервативных осцилляторов
Науч. Иран. B
(2012)
Применение модифицированного метода гомотопических возмущений Хе для получения высших приближений силового нелинейного осциллятора
Физ. лат. А
(2007)
Неодновременный вариационный подход для генераторов с нелинейностью мощности дробного порядка
Прил. Мат. вычисл.

(2010)
Вариационный подход для нелинейных осцилляторов
Хаос, солитоны Фракталы
(2007)
Метод вариационных итераций — разновидность нелинейного аналитического метода: некоторые примеры
Int. J. Нелинейный мех.
(1999)
Нелинейный анализ системы с двумя степенями свободы с нелинейными пружинами (2DOF). Вибрация двухмассовой системы математически моделируется двумя связанными уравнениями второго порядка. Предполагается, что система является сильно нелинейной, и для ее решения разработан метод гомотопических возмущений (HPM) высокого порядка. Частота вибрации получена во втором приближении. Для валидации метода рассматриваются два примера. Решения HPM сравниваются с решениями гармонического баланса Ньютона (NHB) и численными подходами. Было продемонстрировано, что HPM приводит к высокоточному решению даже при первой итерации решения и действителен для широкого диапазона амплитуд колебаний, показывая перспективность в качестве средства для обеспечения точного или замкнутого решения нелинейных динамических систем.
 как показано в следующих примерах.
как показано в следующих примерах.Модифицированный ньютоновско-гармонический балансовый подход к сильно нечетным нелинейным осцилляторам
2020, Журнал вибрационной техники и технологий
Приближенное периодическое решение и качественный анализ неестественных осцилляторов на основе восстанавливающей силы
2,2,2,2,2 ExpressМногокомпонентная коническая пружинная модель мягких тканей в виртуальной хирургии
2020, IEEE Access
Геометрически нелинейная переходная реакция ламинированных пластин с нелинейными упругими ограничениями
2017, шок и вибрация
Упрощенные вариационные итерационные методы. со ссылками на статьи в Scopus
Научная статья
Нелинейные плоские волны в материалах с гексагональной внутренней структурой
Международный журнал нелинейной механики, том 67, 2014, стр. 27-33
Получены три различных континуальных предела для моделирования нелинейных плоских волн в двумерной гексагональной решетке.
 Получены новые связанные уравнения нелинейной сплошной среды для исследования взаимодействия волны макродеформации и волн, вызванных изменениями внутренней структуры. Получены новые аналитические решения для описания локализованных волн нелинейной деформации. Показано, что решения отличаются от решений одномерной решеточной модели за счет учета в решетке несмежных взаимодействий.
Получены новые связанные уравнения нелинейной сплошной среды для исследования взаимодействия волны макродеформации и волн, вызванных изменениями внутренней структуры. Получены новые аналитические решения для описания локализованных волн нелинейной деформации. Показано, что решения отличаются от решений одномерной решеточной модели за счет учета в решетке несмежных взаимодействий.Научная статья
Усовершенствованная модель балки для тонких призматических тел, находящихся в контакте с жестким основанием
Международный журнал механических наук, том 93, 2015 г., стр. 181-190 для полубесконечного призматического тела, контактирующего с твердой опорой без трения. Чтобы обойти решение плоской задачи упругости, мы предлагаем расширение усовершенствованной балочной теории Baluch et al. (1985) [6], в котором учитываются контактные взаимодействия с твердым основанием без трения. Мы определенным образом комбинируем двумерную упругость (плоское напряжение) и классическую инженерную теорию балки с целью получения уточненной модели балки, учитывающей влияние поперечной нормальной деформации, а также условия контакта.
 Результаты, полученные с помощью предложенной аналитической модели, сравниваются с полуаналитическими решениями для задач с отступающими контактами и с уточненным анализом FE. Показано, что предложенная модель дает точные результаты и является эффективным инструментом для решения задач с полубесконечными балками, находящимися в одностороннем контакте без трения с жестким основанием.
Результаты, полученные с помощью предложенной аналитической модели, сравниваются с полуаналитическими решениями для задач с отступающими контактами и с уточненным анализом FE. Показано, что предложенная модель дает точные результаты и является эффективным инструментом для решения задач с полубесконечными балками, находящимися в одностороннем контакте без трения с жестким основанием.Исследовательская статья
Моделирование систем перекрытий для расчета обрушения
Инженерные конструкции, Том 127, 2016, стр. 278-286 опасности в значительной степени зависят от реакции пола. В статье исследуется влияние моделирования системы перекрытий на сопротивление обрушению поврежденных конструкций. В частности, оцениваются и характеризуются осевые и изгибные ограничения, налагаемые плитой перекрытия на балки и балки железобетонных конструкций. Осевое ограничение, создаваемое плитой, приводит к дополнительной сжимающей силе, повышая реакцию на изгиб и, в свою очередь, несущую способность балок и балок.
 Ограничение на изгиб может быть зафиксировано правильными подходами к моделированию и может помочь улучшить реакцию балок и балок перекрытий. Показано, что метод моделирования системы перекрытий оказывает значительное влияние на реакцию перекрытий после потери несущих элементов. Влияние методов моделирования на реакцию конструкции также оценивается с энергетической точки зрения. Оценены и охарактеризованы эффекты изгибно-осевого, а также крутильного растрескивания плиты перекрытия.
Ограничение на изгиб может быть зафиксировано правильными подходами к моделированию и может помочь улучшить реакцию балок и балок перекрытий. Показано, что метод моделирования системы перекрытий оказывает значительное влияние на реакцию перекрытий после потери несущих элементов. Влияние методов моделирования на реакцию конструкции также оценивается с энергетической точки зрения. Оценены и охарактеризованы эффекты изгибно-осевого, а также крутильного растрескивания плиты перекрытия.Исследовательская статья
Устойчивость анизотропных и ауксетических балок на основе сплошной среды
Mechanics Research Communications, Volume 69, 2015, pp. 114-120 уравнения трехмерной упругости, а не типичные балочные теории. На эти нагрузки влияет как характер предполагаемого поля перемещений по поперечному сечению балки, так и включение членов полного определяющего тензора. Особый интерес представляют пучки, которые являются либо анизотропными, либо ауксетичными. Для анизотропных балок повышенное отношение продольного модуля к модулю сдвига для консольных балок увеличивает возникновение потери устойчивости при сдвиге, а не при изгибе.
 Для изотропных ауксетичных балок обсуждаются значения коэффициента Пуассона, которые определяют предел между нагрузками на изгиб, которые приближаются к классической нагрузке на изгиб сверху или снизу.
Для изотропных ауксетичных балок обсуждаются значения коэффициента Пуассона, которые определяют предел между нагрузками на изгиб, которые приближаются к классической нагрузке на изгиб сверху или снизу.Исследовательская статья
Новый метод активного определения положения для бесканатного лифта
Мехатроника, том 23, выпуск 2, 2013 г., стр. 182-189 кабеля ограничивает полезную нагрузку, а его эластичность снижает эффективность управления. Кроме того, механически невозможно включить несколько кабин лифта в одну и ту же шахту из-за троса. Однако такие системы лифтов с несколькими кабинами желательны, поскольку они сокращают время ожидания пассажиров и уменьшают требования к площади лифтовой системы. Многообещающим решением является использование линейных двигателей с длинным якорем, охватывающих шахту, для непосредственного привода кабин лифта. В таких приложениях метод определения положения двигателя должен быть явно рассмотрен, поскольку для большинства активных методов определения положения требуются движущиеся тросы, которые также являются препятствием для систем лифтов с несколькими кабинами.

В этой статье формально представлен метод измерения активного положения линейного двигателя, а также представлены принцип работы, конструкция и методы работы в реальном времени. Предлагаемый метод используется для измерения положения движителя линейного синхронного двигателя с постоянными магнитами с длинным якорем, не требующего активных компонентов на движителе, таким образом исключаются движущиеся кабели. Принцип работы основан на линейном регулируемом дифференциальном трансформаторе: магнитный шунт, расположенный на фиксированном расстоянии перед двигателем, деформирует магнитное поле, создаваемое одной из катушек якоря. Деформацию можно определить, измерив индуцированные напряжения на соседних катушках, и можно рассчитать положение шунта и, следовательно, движителя.
Представлен метод проектирования оптимальных размеров шунта для данного якоря, обеспечивающий большой диапазон измерения и малую максимальную ошибку положения, сопровождаемый алгоритмом измерения в реальном времени, который позволит управлять двигателем с использованием этого метода.
 Наконец, метод проверяется моделированием и экспериментальными результатами, проведенными на полномасштабном прототипе лифта с линейным двигателем, который был построен в лаборатории.
Наконец, метод проверяется моделированием и экспериментальными результатами, проведенными на полномасштабном прототипе лифта с линейным двигателем, который был построен в лаборатории.Исследовательская статья
Осуществимость законов движения для плоских рычажных механизмов с одной степенью свободы в конфигурациях с мертвой точкой
Механические системы и обработка сигналов, Том 98, 2018, стр. 834-851
В этой статье предлагается аналитическое решение задачи обратной кинематики (IK) в конфигурациях мертвой точки для любого плоского рычажного механизма с одной степенью свободы с учетом непрерывности Cn закона движения. Анализируются системы, элементы которых связаны с нижними парами и не содержат избыточности. Исследование направлено на то, чтобы предоставить пользователю некоторые правила, облегчающие проектирование возможных профилей движения, которые будут воспроизводиться обычными электрическими приводами в этих конфигурациях. В течение последних десятилетий было разработано несколько методов и приемов для изучения этой конкретной конфигурации.
 Однако эти методы в основном ориентированы на численное решение неопределенности IK, а не на анализ законов движения, которые механизмы могут выполнять в этих конкретных конфигурациях. Анализ, представленный в данной статье, выполнен путем дифференцирования и применения правила Лопиталя к системе уравнений связи ϕ(q) механизма. В исследовании также рассматривается возможность воспроизведения профилей во временной области с помощью обычных электрических приводов (например, двигателей переменного/постоянного тока, линейных приводов и т. д.). Чтобы показать полезность и эффективность метода, разработка включает аналитическое приложение и численное моделирование для двух распространенных систем с одной степенью свободы: ползунково-кривошипного механизма и четырехрычажного механизма. Наконец, экспериментальные результаты представлены на испытательном стенде с четырьмя рычажными механизмами.
Однако эти методы в основном ориентированы на численное решение неопределенности IK, а не на анализ законов движения, которые механизмы могут выполнять в этих конкретных конфигурациях. Анализ, представленный в данной статье, выполнен путем дифференцирования и применения правила Лопиталя к системе уравнений связи ϕ(q) механизма. В исследовании также рассматривается возможность воспроизведения профилей во временной области с помощью обычных электрических приводов (например, двигателей переменного/постоянного тока, линейных приводов и т. д.). Чтобы показать полезность и эффективность метода, разработка включает аналитическое приложение и численное моделирование для двух распространенных систем с одной степенью свободы: ползунково-кривошипного механизма и четырехрычажного механизма. Наконец, экспериментальные результаты представлены на испытательном стенде с четырьмя рычажными механизмами.
Copyright © 2015 Elsevier Ltd. Все права защищены.
183_notes:model_of_a_wire [Проекты и практики по физике]
Разделы 4.
 4 и 4.5 в Материи и взаимодействиях (4-е издание)
4 и 4.5 в Материи и взаимодействиях (4-е издание)Моделирование сплошной проволоки с пружинами
Чтобы понять, как твердые тела проявляют различные силы, вы должны узнать, как микроскопическая модель шара и пружины соотносится с более макроскопическими показателями, такими как удлинение/сжатие и сила. Для этого нам потребуется смоделировать межатомную связь между двумя атомами в кубической решетке пружиной. В этих заметках вы прочтете о взаимосвязи между микроскопическими и макроскопическими физическими величинами, поскольку они относятся к растяжению или сжатию твердых материалов.
Видео-лекция
Моделирование межатомной связи пружиной
Модель кубической решетки твердого тела с межатомным расстоянием $d$.
Чтобы смоделировать межатомную связь как пружину, нам нужно сначала определить, насколько «длинной» является связь. Возьмем конкретный пример платины (Pt). Один моль Pt содержит $6,02\times10^{23}$ атомов и имеет атомную массу $19.
 {-10}м$$
{-10}м$$Это примерно расстояние между атомами в твердом куске Pt. Мы думаем об этом как о «длине межатомной связи». Для большинства металлов это составляет от 0,1 до 0,2 нм, как вы подсчитали выше.
Модель из проволоки, в которой используются параллельные цепочки пружин.
Самая простая модель, которую мы можем использовать для проволоки (помимо одной цепочки атомов), состоит в том, чтобы смоделировать ее как множество длинных параллельных цепей, соединенных пружинами. Чтобы понять эту модель, вам нужно понять, как смоделировать две пружины, соединенные встык (последовательно), и две пружины, соединенные бок о бок (параллельно).
Две пружины, соединенные встык (последовательно)
Две пружины, соединенные встык.
Давайте рассмотрим присоединение шарика 100 Н к одной пружине 100 Н/м. Если мы позволим грузу просто висеть неподвижно (импульс не изменится), мы знаем из принципа импульса, что результирующая сила, действующая на мяч, равна нулю.
 Следовательно,
Следовательно,$$\Delta \vec{p} = 0\:\:\:\mathrm{подразумевает}\:\:\:\vec{F}_{net} = \vec{F}_{grav} + \vec {F}_{весна} = 0$$ $$\vec{F}_{grav} + \vec{F}_{spring} = \langle 0, -mg \rangle + \langle 0, k_s s\rangle = 0$$ $$s = \dfrac{мг}{k} = \dfrac{100N}{100N/м} = 1m$$
Следовательно, одна пружина с усилием 100 Н/м растянется ровно на 1 м, если на ней будет подвешен мяч с усилием 100 Н.
Когда мы прикрепим вторую пружину 100 Н/м к концу первой, а затем прикрепим груз, обе пружины растянутся на 1 м. То есть общее растяжение системы пружин-масс составляет 2м.
В последовательном порядке каждая пружина растягивается, как если бы масса была прикреплена только к этой пружине , и сумма всех этих растяжений дает общее растяжение.
Моделирование двух сквозных пружин как одной пружины (эффективная жесткость пружины)
Вам часто будет полезно рассматривать всю цепочку пружин как одну пружину. То есть вы можете смоделировать пружины, соединенные встык, как одну гипотетическую пружину, которая растягивается на ту же величину при той же нагрузке, что и цепочка пружин.
 Это называется использованием эффективной жесткости пружины. Это эффективное в том смысле, что оно моделирует эффект наличия этой цепочки пружин, а не в каком-то смысле более эффективный. В приведенном выше примере вы можете найти единственную пружину, которая растягивается на 2 м, когда к ней прикреплен шар 100 Н.
Это называется использованием эффективной жесткости пружины. Это эффективное в том смысле, что оно моделирует эффект наличия этой цепочки пружин, а не в каком-то смысле более эффективный. В приведенном выше примере вы можете найти единственную пружину, которая растягивается на 2 м, когда к ней прикреплен шар 100 Н.$$\Delta \vec{p} = 0\:\:\:\mathrm{подразумевает}\:\:\:\vec{F}_{net} = \vec{F}_{grav} + \vec {F}_{эфф,пружина} = 0$$ $$\vec{F}_{grav} + \vec{F}_{eff,spring} = \langle 0, -mg \rangle + \langle 0, k_{s,eff} s\rangle = 0$$ $$k_{s,eff} = \dfrac{mg}{s} = \dfrac{100N}{2m} = 50N/м$$
Очевидно, две последовательные пружины с одинаковой жесткостью можно смоделировать одной (более гибкой) пружиной с половинной жесткостью каждой из двух пружин. Мы можем сложить пружины последовательно, чтобы найти эффективную постоянную пружины, используя эту формулу обратной связи, где обратная величина каждой жесткой постоянной для каждой пружины в цепи складывается вместе (а затем инвертируется).

$$\dfrac{1}{k_{s,eff}} = \sum_i \dfrac{1}{k_i} = \dfrac{1}{k_1} + \dfrac{1}{k_2} + \dfrac{1} {k_3} + \dots$$
Например, в нашем случае
$$\dfrac{1}{k_{s,eff}} = \sum_i \dfrac{1}{k_i} = \dfrac{1}{100 Н/м} + \dfrac{1}{100 Н/м} = \dfrac{2}{100 Н/м} = \dfrac{1}{50 Н/м}$$
$$k_{s,eff} = 50 Н/м$$
Две пружины рядом (параллельно)
Давайте рассмотрим присоединение мяча 100 Н к двум пружинам 100 Н/м, где каждая пружина соединена с мячом, а не друг с другом. При этом обе пружины должны растянуться на одинаковую величину. Если мяч висит неподвижно (импульс не меняется), мы можем использовать принцип количества движения, чтобы определить, насколько растягиваются эти пружины.
Две пружины, соединенные бок о бок.
$$\Delta \vec{p} = 0\:\:\:\mathrm{подразумевает}\:\:\:\vec{F}_{net} = \vec{F}_{grav} + \vec {F}_{пружина,1} + \vec{F}_{пружина,2} = 0$$ $$\vec{F}_{grav} + \vec{F}_{spring,1} + \vec{F}_{spring,2} = \langle 0, -mg \rangle + \langle 0, k_s s\rangle + \langle 0, k_s s\rangle = \langle 0, -mg \rangle + 2\langle 0, k_s s\rangle = 0$$ $$s = \dfrac{мг}{2k} = \dfrac{100N}{200N/м} = 0,5 м$$
Когда мы присоединяем к шару вторую пружину 100 Н/м, обе пружины растягиваются на 0,5 м.
 То есть общее растяжение системы пружина-масса вдвое меньше, чем с одной пружиной.
То есть общее растяжение системы пружина-масса вдвое меньше, чем с одной пружиной.Параллельно каждая пружина растягивается на одинаковую величину .
Моделирование двух расположенных рядом пружин как одной пружины (эффективная жесткость пружины)
Вам часто будет полезно рассматривать несколько расположенных рядом пружин как одну пружину. Подобно тому, как это делалось с последовательными пружинами, вы можете моделировать расположенные рядом пружины как одну гипотетическую пружину, которая растягивается на ту же величину при той же нагрузке, что и расположенные рядом пружины. В приведенном выше примере вы можете найти единственную пружину, которая растягивается на 0,5 м, когда к ней прикреплен шарик 100 Н.
$$\Delta \vec{p} = 0\:\:\:\mathrm{подразумевает}\:\:\:\vec{F}_{net} = \vec{F}_{grav} + \vec {F}_{эфф,пружина} = 0$$ $$\vec{F}_{grav} + \vec{F}_{eff,spring} = \langle 0, -mg \rangle + \langle 0, k_{s,eff} s\rangle = 0$$ $$k_{s,eff} = \dfrac{mg}{s} = \dfrac{100N}{0,5 м} = 200N/м$$
Очевидно, две параллельные пружины с одинаковой жесткостью можно смоделировать одной (более жесткой) пружиной с удвоенной жесткостью каждой из двух пружин.
 Мы можем добавить пружины параллельно, чтобы найти эффективную жесткость пружины, используя эту формулу.
Мы можем добавить пружины параллельно, чтобы найти эффективную жесткость пружины, используя эту формулу.$${k_{s,eff}} = \sum_i {k_i} = {k_1} + {k_2} + {k_3} + \dots$$
Например, в нашем случае
$${k_{s,eff}} = \sum_i {k_i} = {100 Н/м} + {100 Н/м} = {200 Н/м}$$
Этот способ моделирования сквозных и параллельных пружин будет очень полезен для моделирования сжатия и растяжения реальных материалов.
1)
Это количество Pt будет стоить около 700 000 000 долларов.
Серийное и параллельное расположение пружин MCQ [Бесплатный PDF] – Ответ на объективный вопрос для последовательного и параллельного расположения пружин Викторина
Последний ряд и параллельное расположение пружин MCQ Целевые вопросы
Серийное и параллельное расположение пружин MCQ Вопрос 1:
Две пружины с жесткостью «K» соединены последовательно. Эквивалентная жесткость будет
- \(\frac{K}{4}\)
- \(\frac{K}{2}\)
- K
- 2K
Ответ (подробное решение ниже)
Вариант 2 : \(\frac{K}{2}\)
Концепция :
Когда две пружины с жесткостью k1 и k2 соединены последовательно, эквивалентная жесткость определяется выражением –
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1 }}} + \frac{1}{{{k_2}}}\)
Когда две пружины с жесткостью k1 и k2 соединены параллельно, эквивалентная жесткость определяется выражением:
keq = k1 + k2
Расчет :
Дано :
k 1 = k 2 = K
При последовательном соединении:
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}}\)
\ (\frac{1}{{{k_{eq}}}} = \frac{1}{{{K}}} + \frac{1}{{{K}}}=\frac{2}{K }\)
∴ k экв = \(\frac{K}{2}\).

Рядное и параллельное расположение пружин MCQ Вопрос 2:
Масса подвешена к основанию двух последовательных пружин жесткостью 10 Н/мм и 5 Н/мм. Эквивалентная жесткость двух пружин составляет почти
- 0,3 Н/мм
- 3,3 Н/мм
- 5 Н/мм
- 15 Н/мм
Ответ (подробное решение ниже)
Вариант 2: 3,3 Н/мм когда они соединены встык, и параллельно, когда они соединены бок о бок.
Эквивалентная жесткость пружины
Последовательное соединение:
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\)
\({k_{eq}} = \frac{{{k_1} \times {k_2}}}{{{k_1} + {k_2}}}\)
Параллельное соединение:
\( {k_{eq}} = {k_1} + {k_2}\)
Расчет:
Дано:
k1 = 10 0 Н/мм, k2 = 0 0 0 5 0 Н/мм эквивалент константа пружины:
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\ )
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{10}}} + \frac{1}{{{5}}}\)
\(\frac{1}{{{k_{eq}}}} = \frac{1+2}{10}\)
\(k_{eq}= \frac{10}{3}= 3,33~ Н/мм\)
Серийное и параллельное расположение пружин MCQ Вопрос 3:
Рассчитайте эффективную жесткость следующего: (Предположим, что упругое тело представляет собой пружину с жесткостью 2k)
- k
- k/2
- k/4
- 2k
Ответ (подробное решение ниже)
Вариант 2: k/2
Концепция:
Пружины параллельные, k = ∑ k i
\({\rm{Пружины последовательно}},\frac{1}{k} = \sum {\left( {\frac{1 }{k}} \right)_i}\)
Упругое тело можно заменить пружиной.

Расчет:
\(\следовательно \frac{1}{k} = \frac{4}{{2k}} = \frac{2}{k}\)
∴ k = k/2
Рядное и параллельное расположение пружин MCQ Вопрос 4:
Для пружинной системы, приведенной на рисунке, эквивалентная жесткость составляет
- 0,4 K
- 4 K
- 2,5 K
- K
Ответ (подробный раствор ниже)
Вариант 1: 4000777777777777.
Концепция:
Пружины в серии:
\(\frac{1}{{{k_e}}} = \frac{1}{{{k_1}}} + \frac{1}{{ {k_2}}}\)
Пружины параллельно:
ke = k1 + k2
Расчет:
Дано:
Пружины с жесткостью k и k соединены параллельно,
Пусть их эквивалентная жесткость пружины равна k1
k1 = k + k
Теперь k1 = 2k 90 07 90 k и k соединены последовательно, пусть их эквивалентная жесткость пружины равна keq
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{k_e}} + \frac{1 }{{k}} + \frac{1}{{k}} \)
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{2k}} + \frac{1}{{k}} + \frac{1}{{k}} \)
\(\frac{1}{k_{eq}}=\frac{1+2+2}{2k}\)
\(\frac{1}{k_{eq}}=\frac{5 }{2k}\)
\(k_{eq}=\frac{2k}{5}\)
k eq = 0,4 k
Последовательное и параллельное расположение пружин MCQ Вопрос 5:
Винтовая спиральная пружина жесткости k разрезана на две равные половины, которые затем соединены параллельно, чтобы поддерживать вибрирующую массу m.
 Угловая частота вибрации, ω n равна
Угловая частота вибрации, ω n равна- \(\sqrt {\frac{k}{m}} \)
- \(\ sqrt {\ frac {2k} {m}} \)
- \ (\ sqrt {\ frac {4k} {m}} \)
- \ (\ sqrt {\ frac {k} {4m }} \)
Ответ (подробное решение ниже)
Вариант 3 : \(\sqrt {\frac{4k}{m}} \)
Понятие:
Когда пружина постоянного ко и длины Lo разрезается на куски длины, скажем, l1, l2, l3, ……. Ln, их соответствующие коэффициенты упругости можно рассчитать как
k1l1 = k2l2 = k3l3 = ……. = knln = kolo
Здесь пружина разрезана на две равные части: l1 = l2 = L/2
k1l1 = k2l2 = KL
\({k_1}\frac{L}{2} = {k_2}\frac{L}{2} = KL\)
k1 = k2 = 2K
При расположении в параллельно, эквивалентная жесткость будет 4K
Следовательно, угловая частота будет
\(\omega_{n}=\sqrt {\frac{k_{eq}}{m}}= \sqrt {\frac {4k}{m}} \)
Верхний ряд и параллельное расположение пружин Целевые вопросы MCQ
Винтовая спиральная пружина жесткости k разрезается на две равные половины, которые затем соединяются параллельно, чтобы поддерживать вибрирующую массу m.
 Угловая частота вибрации, ω n равно
Угловая частота вибрации, ω n равно- \(\ sqrt {\ frac {k} {m}} \)
- \ (\ sqrt {\ frac {2k} {m}} \)
- \ (\ sqrt {\ frac {4k}{m}} \)
- \(\sqrt {\frac{k}{4m}} \)
Ответ (подробное решение ниже)
Вариант 3: \(\sqrt {\frac{4k }{m}} \)
Понятие:
Когда пружину постоянного ko и длины Lo разрезают на куски длины, скажем, l1, l2, l3, ……. Ln, их соответствующие коэффициенты упругости можно рассчитать как
k1l1 = k2l2 = k3l3 = ……. = knln = коло
Здесь пружина разрезана на две равные части: l1 = l2 = L/2
k1l1 = k2l2 = KL
\({k_1}\frac{L}{2} = {k_2}\frac{L} {2} = KL\)
k1 = k2 = 2K
При параллельном расположении эквивалентная жесткость будет 4K
Следовательно, угловая частота будет
\(\omega_{n}=\sqrt {\ frac {k_ {eq}} {m}} = \ sqrt {\ frac {4k} {m}} \)
Скачать решение PDFПоделиться в WhatsApp
Для пружинной системы, представленной на рисунке, эквивалентная жесткость равна
- 0.
 4 k
4 k - 4 k
- 2.5 k
- k
Answer (Detailed Solution Below)
Option 1 : 0.4 k
Concept:
Springs in series:
\(\frac{1}{{{k_e}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\)
Параллельные пружины:
ke = k1 + k2
Расчет:
Дано:
Пружины с жесткостью k и k соединены параллельно,
Пусть их эквивалентная жесткость пружины равна k1
k1 = k + k
k1 = 2k
Теперь k1, k и k соединены последовательно, пусть их эквивалентная жесткость пружины равна keq
\(\frac{1} {{{k_{eq}}}} = \frac{1}{{k_e}} + \frac{1}{{k}} + \frac{1}{{k}} \)
\(\ frac{1}{{{k_{eq}}}} = \frac{1}{{2k}} + \frac{1}{{k}} + \frac{1}{{k}} \)
\(\frac{1}{k_{eq}}=\frac{1+2+2}{2k}\)
\(\frac{1}{k_{eq}}=\frac{5} {2k}\)
\(k_{eq}=\frac{2k}{5}\)
к экв. = 0,4 к
Скачать решение PDFПоделиться в WhatsApp
Спиральная пружина жесткости k разрезается точно посередине, и две полученные таким образом пружины располагаются параллельно, чтобы вместе воспринимать сжимающую нагрузку.
 Эквивалентная жесткость двух пружин составляет
Эквивалентная жесткость двух пружин составляет- 0,25k
- 0,5k
- 2k
- 4k
Ответ (подробное решение ниже)
907 907Вариант 4 : 0 43}n}}\)
G = модуль жесткости, D = средний диаметр витка, R = средний радиус, d = диаметр проволоки, n = количество витков
Жесткость обратно пропорциональна количеству витков
При ‘n ‘ пружины соединены последовательно
Эквивалентная жесткость определяется выражением,
\(\frac{1}{{k\left( {eq} \right)}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}} + \ldots + \frac{1}{{{k_n}}}\)
Когда n пружин соединены параллельно
k eq = k 1 + k 2 + k 3 + ….. + k n
Расчет:
При разрезании пружины на две равные части.
Жесткость каждой части увеличивается в 2 раза, так как n становится n/2
Пусть исходная жесткость равна k
Новая жесткость = 2k каждой
Параллельное соединение = 2k + 2k = 4k
пружина разделена на n равных частей, и эти части соединены параллельно.

Новая жесткость = n 2 k
Детали, соединенные последовательно
Новая жесткость = k (напоминает оригинальную пружину)
Скачать решение PDFПоделиться в WhatsApp
Винтовая пружина номиналом 10 Н/мм установлена поверх другой винтовой пружины номиналом 8 Н/мм. Усилие, необходимое для полного комбинированного отклонения на 45 мм от двух пружин, составляет
- 100 Н
- 150 Н
- 200 Н
- 250 Н
Ответ (подробное решение ниже)
Вариант 3 : 200 Н
Концепция:
Пружины друг над другом = Пружины последовательно
При последовательном соединении пружин равной жесткости
2 определяется как:
\(\frac{1}{{{k_{\left( {eq} \right)}}}} = \frac{1}{{{k_1}}} + \frac{1}{ {{k_2}}} + \ldots + \frac{1}{{{K_n}}}\)
Расчет:
Дано :
k 1 = 10 Н/мм, k 2 = 8 Н/мм и δ = 45 мм
Эквивалентная жесткость \({k_{eq}} = \frac{{{k_1}\;{ k_2}}}{{{k_1}\; + \;{k_2}}}\)
Эквивалентная жесткость \({k_{eq}} = \left(\frac{{10\; \times \;8} }{{10\; + \;8}}\right) = \frac{{80}}{{18}} = \frac{{40}}{9}\;Н/мм\)
\( Жесткость = \frac{{Нагрузка}}{{Прогиб}}\)
Нагрузка = Жесткость × Прогиб
\(\следовательно, F=\frac{{40}}{9} \times 45 = 200\;N\ )
Скачать решение PDFПоделиться в WhatsApp
Груз подвешен к основанию двух последовательно соединенных пружин жесткостью 10 Н/мм и 5 Н/мм.
 Эквивалентная жесткость двух пружин составляет почти
Эквивалентная жесткость двух пружин составляет почти- 0,3 Н/мм
- 3,3 Н/мм
- 5 Н/мм
- 15 Н/мм
Ответ (подробное решение ниже)
9003 Н/ммПонятие:
Две или более пружины называются последовательными, если они соединены встык, и параллельными, если они соединены бок о бок.
Эквивалентная жесткость пружины
Последовательное соединение:
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\)
\({k_{eq}} = \frac{{{k_1} \times {k_2}}}{{{k_1} + {k_2}}} \)
В параллельном соединении:
\ ({k_ {eq}} = {K_1} + {K_2} \)
Расчет:
:
:
:
. 10 Н/мм, k2 = 5 Н/мм
эквивалентная жесткость пружины:
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2} }}\)
\(\frac{1}{{{k_{eq}}}} = \frac{1}{{{10}}} + \frac{1}{{{5}}}\ )
\(\frac{1}{{{k_{eq}}}} = \frac{1+2}{10}\)
\(k_{eq}= \frac{10}{3} =3,33~ Н/мм\)
Скачать решение PDFПоделиться в WhatsApp
Машина, смонтированная на одной винтовой пружине, имеет период свободных колебаний Т.
 Если пружину разрезать на четыре равные части и поставить параллельно, а машину смонтировать из них, то период свободных колебаний новой системы составит быть:
Если пружину разрезать на четыре равные части и поставить параллельно, а машину смонтировать из них, то период свободных колебаний новой системы составит быть:- 16T
- T/4
- 4T
- T/16
ОТВЕТ (подробное решение ниже)
Вариант 2: T/4
Концепция:
2 . ) свободных колебаний определяется выражением:\(T =\frac{2\pi}{ω_n}\)
, где ω n = собственная частота системы и определяется как ⇒ \ (\ omega_n = \ sqrt {\ frac {k_ {eq}} {m}} \)
, где k 9093N}\)
где G = модуль жесткости, d = диаметр проволоки пружины, D = диаметр витка пружины и N = №. витков
При последовательном соединении пружины :
\(\frac{1}{k_{eq}}=\frac{1}{k_1}+\frac{1}{k_2}+.. ….+\frac{1}{k_n}\)
При параллельном соединении пружины :
k eq = k 1 + k 2 + .
 ….. .+ k n
….. .+ k n Расчет: 93N}\)
\(∴\;k\propto\frac{1}{N}\)
\(\frac{k_2}{k_1}=\frac{N_1}{N_2}\;\;\ ;(если\;другие\;параметры\;остаются\;постоянными)\)
∴ k 2 = 4k 1 ⇒ 4k.
т.е. жесткость каждой из четырех пружин 4к.
∵ новая система подключена параллельно
∴ k eq = 4k + 4k + 4k + 4k ⇒ 16k.
Период времени исходной системы:
\(T=2\pi\sqrt{\frac{m}{k}}\)
\(\следовательно \;T\propto\frac{1}{ \sqrt{k}}\)
Пусть T 2 будет периодом времени новой системы:
\(\frac{T_2}{T_1}=\sqrt{\frac{k_1}{k_2}} \)
\(\frac{ T_2}{T_1}=\sqrt{\frac{k}{16k}}\Rightarrow\frac{1}{4}\)
\(\следовательно, T_2=\frac{T_1}{4}\)
Скачать решение PDFПоделиться в WhatsApp
Две концентрические пружины, имеющие одинаковое число витков и длину в свободной оси, изготовлены из одного и того же материала.
 Одна пружина имеет средний диаметр витка 12 см и диаметр проволоки 1,0 см. Другой имеет средний диаметр катушки 8 см и диаметр проволоки 0,6 см. Если набор пружин сжать под действием осевой нагрузки 2000 Н, нагрузки, разделяемые пружинами, составят 94}}}\)
Одна пружина имеет средний диаметр витка 12 см и диаметр проволоки 1,0 см. Другой имеет средний диаметр катушки 8 см и диаметр проволоки 0,6 см. Если набор пружин сжать под действием осевой нагрузки 2000 Н, нагрузки, разделяемые пружинами, составят 94}}}\)где, P = нагрузка, D = диаметр катушки, d = диаметр проволоки, n = номер. витков, G = модуль жесткости
Здесь сосредоточенная пружина сжимается под нагрузкой W, поэтому прогиб обеих пружин одинаков. т.е. Δ 1 = Δ 2
Расчет:
Дано:
D 1 = 12 см, D 2 = 8 CM, D = = = = = = = = = = = = . 2 = 0,6 см, Ш = Ш1 + Ш2 = 2000, № 94} \) = 2,286
∴ W 1 = 2,286W 2
⇒ 2,286W 2 + W 2 = 2000
∴ W 2 = 40904 = 6904 = 6904 = 6904 = 40904 = 6904 = 6904 = 40904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 6904 = 40904 w 2 = 2000
∴ W 2 = 2000
∴ W 2 909.
Скачать решение PDF 1391.357 N
1391.357 NПоделиться в WhatsApp
Винтовая пружина сжатия жесткости K разрезана на две части, каждая из которых имеет одинаковое число витков и сжата рядом друг с другом. Эквивалентная жесткость пружины этой новой компоновки равна:
- 4K
- 2K
- K
- 0,5K
Ответ (Подробное решение ниже)
Вариант 1: 4K
и параллельное расположение Springs McQ Вопрос 14:
A Shelical Series и Spresmness Springs of Springs McQ. разрезать на две равные половины, а затем соединить их параллельно, чтобы поддерживать вибрирующую массу m. Угловая частота вибрации, ω n равна
- \(\sqrt {\frac{k}{m}} \)
- \(\sqrt {\frac{2k}{m}} \)
- \(\sqrt {\frac{4k}{m}} \)
- \(\sqrt {\frac{k}{4m}} \)
Ответ (подробное решение ниже)
Вариант 3: \(\sqrt {\frac{4k}{m}} \)
Понятие:
Когда пружину постоянного ko и длины Lo разрезают на куски длины, скажем, l1, l2, l3, …….
 Ln, их соответствующие коэффициенты упругости можно рассчитать как
Ln, их соответствующие коэффициенты упругости можно рассчитать какk1l1 = k2l2 = k3l3 = ……. = knln = kolo
Здесь пружина разрезана на две равные части: l1 = l2 = L/2
k1l1 = k2l2 = KL
\({k_1}\frac{L}{2} = {k_2}\frac{L}{2} = KL\)
k1 = k2 = 2K
При расположении в параллельно, эквивалентная жесткость будет 4K
Следовательно, угловая частота будет
\(\omega_{n}=\sqrt {\frac{k_{eq}}{m}}= \sqrt {\frac {4k}{м}} \)
Рядное и параллельное расположение пружин MCQ Вопрос 15:
Для пружинной системы, представленной на рисунке, эквивалентная жесткость равна
- 0.4 k
- 4 k
- 2.5 k
- k
Answer (Detailed Solution Below)
Option 1 : 0.4 k
Concept:
Springs in series:
\( \frac{1}{{{k_e}}} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}}\)
Параллельные пружины:
ke = k1 + k2
Расчет:
Дано:
Пружины с жесткостью k и k соединены параллельно,
Пусть их эквивалентная жесткость пружины равна k1
k1 = k + k
k1 = 2k
Теперь k1, k и k соединены последовательно, пусть их эквивалентная жесткость пружины равна keq
\(\frac{1} {{{k_{eq}}}} = \frac{1}{{k_e}} + \frac{1}{{k}} + \frac{1}{{k}} \)
\(\ frac{1}{{{k_{eq}}}} = \frac{1}{{2k}} + \frac{1}{{k}} + \frac{1}{{k}} \)
\(\frac{1}{k_{eq}}=\frac{1+2+2}{2k}\)
\(\frac{1}{k_{eq}}=\frac{5} {2k}\)
\(k_{eq}=\frac{2k}{5}\)
k eq = 0,4 k
Последовательные и параллельные цепи: примеры и правила
Мы используем электрические устройства каждый день и постоянно слышим об электрических цепях.
 Но знаете ли вы, что на самом деле существует два основных типа схем, и что у них обоих разные правила и приложения? Это объяснение погрузится прямо в эти два типа схем, известные как последовательные и параллельные схемы, и чем именно они отличаются, и где мы применяем каждый тип!
Но знаете ли вы, что на самом деле существует два основных типа схем, и что у них обоих разные правила и приложения? Это объяснение погрузится прямо в эти два типа схем, известные как последовательные и параллельные схемы, и чем именно они отличаются, и где мы применяем каждый тип!Определение параллельной и последовательной цепи
Если мы хотим соединить два компонента цепи вместе в цепи, то у нас есть два способа сделать это последовательно и параллельно.
Цепь серии состоит из компонентов, которые соединены последовательно , т.е. они соединены один за другим в своего рода «цепочку» компонентов.
Параллельная цепь состоит из компонентов, соединенных параллельно . Для этого мы разделяем схему на две части и размещаем компоненты рядом на нескольких разных ветвях, после чего снова объединяем ветви.
Так в чем именно разница между этими двумя типами схем и как мы видим ее на принципиальных схемах?
Разница между последовательными и параллельными цепями
На изображении ниже мы можем очень четко увидеть разницу между электрическими компонентами, которые соединены последовательно или параллельно.

Три лампы соединены слева параллельно, а справа последовательно, Wikimedia Commons CC BY-SA 4.0.
Разница между последовательной и параллельной схемой заключается в том, в какой конфигурации компоненты соединены друг с другом.
Формулы и правила для последовательных и параллельных цепей
Тремя основными величинами, соответствующими цепям, являются напряжение, ток и сопротивление. В общем, напряжение можно рассматривать как «силу», толкающую заряженные частицы через цепь, ток можно рассматривать как количество заряженных частиц, которые могут пройти через цепь, а сопротивление можно рассматривать как сужение дороги или маленькая дверь: чем больше сопротивление, тем меньше дверь, через которую должны пройти заряженные частицы.
С помощью этих сравнений мы можем понять закон Ома, если сформулируем его следующим образом:
Если мы увеличим толчок (увеличим напряжение) или сделаем дорогу шире (уменьшим сопротивление), больше частиц сможет пройти (ток увеличится).

Правила последовательной цепи
Для последовательной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены последовательно по напряжению.
Серийная схема A, Wikimedia Commons CC BY-SA 4.0.
Правила для последовательных цепей:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов. Таким образом, полное сопротивление в цепи выше равно.
- Ток одинаков через все резисторы. Зная это, мы можем теперь рассчитать этот ток, используя закон Ома, чтобы быть.
- В результате предыдущего пункта мы можем рассчитать напряжение на отдельных резисторах (и) и получить . Таким образом, напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений равна общему напряжению.
Запомните эти правила, разбираясь в них! Вот способ взглянуть на правила и формулы для последовательных цепей.
- Если вы заряженная частица, вы должны пройти через оба барьера.
 Общий барьер, с которым вы сталкиваетесь, представляет собой сумму двух отдельных барьеров, потому что вы дважды замедляетесь на своем пути.
Общий барьер, с которым вы сталкиваетесь, представляет собой сумму двух отдельных барьеров, потому что вы дважды замедляетесь на своем пути. - Если ток не везде одинаков, то где-то будет нарастание или потеря заряда, что невозможно в идеальной цепи. Одна партия заряженных частиц не может обогнать другую, потому что ветвь только одна. Добавление большего количества резисторов увеличит общий барьер, поэтому ток будет меньше.
- Это правило следует закону Ома.
Предположим, что два резистора на самом деле являются двумя лампами. Мощность компонента в электрической цепи можно рассчитать по формуле, поэтому мощность лампы 1 равна:
и мы можем сделать аналогичный расчет для лампы 2. Мы видим, что лампа с большим сопротивлением потребляет больше мощности от последовательной цепи.
Правила параллельной цепи
Для параллельной цепи мы находимся в ситуации, показанной на рисунке ниже, в которой два (или более) резистора с сопротивлением и соединены параллельно по напряжению.

Параллельная цепь, Wikimedia Commons CC BY-SA 4.0.
Правила параллельных цепей:
- Напряжение на всех ветвях одинаковое, а именно полное напряжение, а ток через отдельные резисторы можно рассчитать по закону Ома.
- Общий ток представляет собой сумму токов отдельных резисторов. Следовательно, общее сопротивление меньше, чем сопротивление отдельных резисторов.
Вот способ разобраться в этих правилах и формулах для параллельных цепей.
- Оба резистора напрямую подключены к электрической ячейке с обоих концов, поэтому напряжение на них должно быть напряжением ячейки.
- Теперь у заряженных частиц есть несколько способов добраться до другого конца клетки: есть две двери из стороны в сторону, и частицы могут выбирать, к какой из них они хотят встать в очередь. Таким образом, через двери можно пропустить больше заряженных частиц.
- Ток — это то, сколько заряженных частиц проходит контрольную точку в секунду. Эта величина везде одинакова, поэтому сумма отдельных токов должна составлять общий ток.
 Как будто два потока бегунов сливаются воедино на одной большой улице.
Как будто два потока бегунов сливаются воедино на одной большой улице.
Предположим, что два резистора на самом деле являются двумя лампами. Тогда мощность над лампой равна , и мы можем сделать аналогичный расчет для лампы. Мы видим, что лампа с меньшим сопротивлением получает большую мощность от параллельной цепи.
Мы можем рассчитать общее сопротивление параллельной цепи. Рассчитываем:
.
Проще говоря, мы можем сказать, что общее сопротивление параллельной цепи равно обратной сумме обратных величин отдельных сопротивлений. Мы видим, что действительно общее сопротивление меньше, чем сопротивление отдельных резисторов. Это приводит к большему общему току, чем если бы была только одна ветвь. Это означает, что создание параллельных ветвей в цепи уменьшит сопротивление и увеличит ток в цепи. Это имеет смысл в рамках нашей аналогии с дверьми.
Пример последовательной и параллельной цепей и расчеты
Давайте рассмотрим сложный пример, сочетающий последовательную и параллельную цепи.
 См. рисунок ниже для настройки. В большинстве практических ситуаций вы можете определить напряжение В 1 самостоятельно и выбрать резисторы, которые вы используете, и ваша задача — найти другие величины. Это то, что мы будем делать.
См. рисунок ниже для настройки. В большинстве практических ситуаций вы можете определить напряжение В 1 самостоятельно и выбрать резисторы, которые вы используете, и ваша задача — найти другие величины. Это то, что мы будем делать.Цепь, содержащая последовательные и параллельные соединения, с сопротивлениями R i , амперметры A i и вольтметры V i , Wikimedia Commons CC BY-SA 4.0.
Обратите внимание, как напряжения на сопротивлениях измеряются прибором, подключенным параллельно сопротивлениям. Это связано с тем, что напряжение на параллельной цепи одинаково на всех ветвях, поэтому напряжение, которое измеряет вольтметр, совпадает с напряжением на сопротивлении, к которому он подключен параллельно!
Предположим, мы подключили вольтметр последовательно к сопротивлению, на котором мы хотим измерить напряжение. Тогда напряжение будет разделено между вольтметром и сопротивлением, и вольтметр будет измерять только напряжение на себе, что будет близко к общему напряжению, выдаваемому батареей, потому что вольтметры имеют чрезвычайно высокое сопротивление.

Обратите также внимание на то, как ток в цепи измеряется прибором, подключенным последовательно к сопротивлениям, через которые мы хотим измерить ток. Это связано с тем, что ток через последовательную цепь везде одинаков, поэтому ток, который измеряет амперметр, такой же, как ток через сопротивления, к которым он подключен последовательно!
Предположим, мы подключили амперметр параллельно сопротивлению, через которое мы хотим измерить ток. Тогда ток будет разделен между амперметром и сопротивлением, и амперметр будет измерять ток только через свою собственную ветвь, а не через ветвь интересующего сопротивления вообще! Этот ток будет очень высоким, потому что амперметры имеют чрезвычайно низкое сопротивление.
Вопрос дает значения , и.
Видим, что у нас параллельная цепь, но одна из ветвей параллельной цепи содержит два резистора, которые соединены последовательно. Приведем общее сопротивление резисторов и название, а общее напряжение над названием.

Из правил параллельных цепей мы знаем, что и. Мы также знаем, что сумма отдельных токов есть общий ток, т.е.
По правилам последовательного соединения мы знаем то и это. Все идет нормально.
Теперь мы можем использовать закон Ома, чтобы заключить, что
И
Тогда общий ток равен
Мы снова используем закон Ома, чтобы узнать, какие напряжения
И
Теперь мы успешно выразили неизвестные величины через известные величины, так что мы закончили! В процессе мы использовали правила как для последовательных, так и для параллельных схем, потому что эта схема представляет собой комбинацию этих двух.
Идентификация последовательных и параллельных цепей
Определить последовательную цепь довольно легко, потому что последовательные цепи имеют только один провод, по которому может проходить ток: в последовательных цепях нет дополнительных ответвлений. С другой стороны, параллельная цепь — это цепь, в которой все компоненты напрямую подключены к обеим сторонам источника напряжения.
 Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.
Трудности возникают, когда нам нужно идентифицировать компоненты в комбинированной схеме. Короче говоря, компоненты, соединенные последовательно, расположены встречно, а компоненты, соединенные параллельно, расположены бок о бок.Мы можем рассматривать непрерывный кусок провода как узел : различные узлы разделены компонентами внутри цепи. Два компонента соединены параллельно, если (и только если) они имеют два общих узла, т. е. они соединены с одними и теми же двумя узлами.
Два компонента соединены последовательно, если (и только если) они имеют ровно один общий узел, который не разветвляется между двумя компонентами. Это хорошее упражнение — попытаться идентифицировать узлы на всех рисунках в этой статье. Вы можете сделать это, дав им имена или цвета. Тогда посмотрите, пришли ли вы к правильным выводам о том, как все компоненты связаны на основе этого метода! См. приведенный ниже пример реализации этого метода.
Оба резистора имеют общий синий и красный узел, поэтому они соединены параллельно, адаптировано из Paulgwilliamson, Wikimedia Commons CC BY-SA 4.
 0.
0.Использование последовательных и параллельных цепей
В общем, выбор между последовательными и параллельными цепями прост. Мы подключаем выключатель последовательно с лампой так, чтобы отключение тока в выключателе путем его щелчка также отключало ток через лампу. Мы также подключаем резистор последовательно с диодами, чтобы ток через диоды не был слишком большим, предотвращая перегрев диодов.
С другой стороны, мы подключаем фары в автомобилях параллельно, так что, если одна из ветвей цепи выходит из строя, другая ветвь все еще проводит ток. Таким образом, у вас все еще будет одна рабочая фара, если другая выйдет из строя: параллельное подключение добавляет фактор безопасности. Бытовые приборы тоже подключаем параллельно, чтобы они все были под одним напряжением. Имея выключатели, соединенные последовательно с отдельными приборами, мы можем управлять током через отдельные приборы. Если бы все приборы были соединены последовательно, нам пришлось бы выбирать между всем включенным и всем выключенным!
Последовательные и параллельные цепи — основные выводы
- Последовательное соединение состоит из компонентов, расположенных один за другим.

- Параллельное соединение имеет компоненты, параллельные друг другу.
- Правила последовательного соединения:
- Общее сопротивление всех резисторов равно сумме сопротивлений отдельных резисторов.
- Ток одинаков через все резисторы.
- Напряжение на резисторах пропорционально их сопротивлениям, а сумма отдельных напряжений составляет общее напряжение.
- Правила параллельного соединения:
- Общее сопротивление всех резисторов меньше, чем сопротивление отдельных резисторов, и определяется по формуле.
- Общий ток представляет собой сумму токов отдельных резисторов.
- Напряжение на всех резисторах одинаковое, а именно общее напряжение.
- Для выявления последовательных и параллельных соединений можно использовать метод узлов.
- Всякий раз, когда ситуация требует фактора безопасности, вы обычно видите параллельные соединения, как в бытовых приборах. Последовательные соединения используются для переключения и предотвращения перегрева компонентов.




 )
) )
) )
)
 жесткость, как конденсатор – не удлинение.Спасибо!
жесткость, как конденсатор – не удлинение.Спасибо!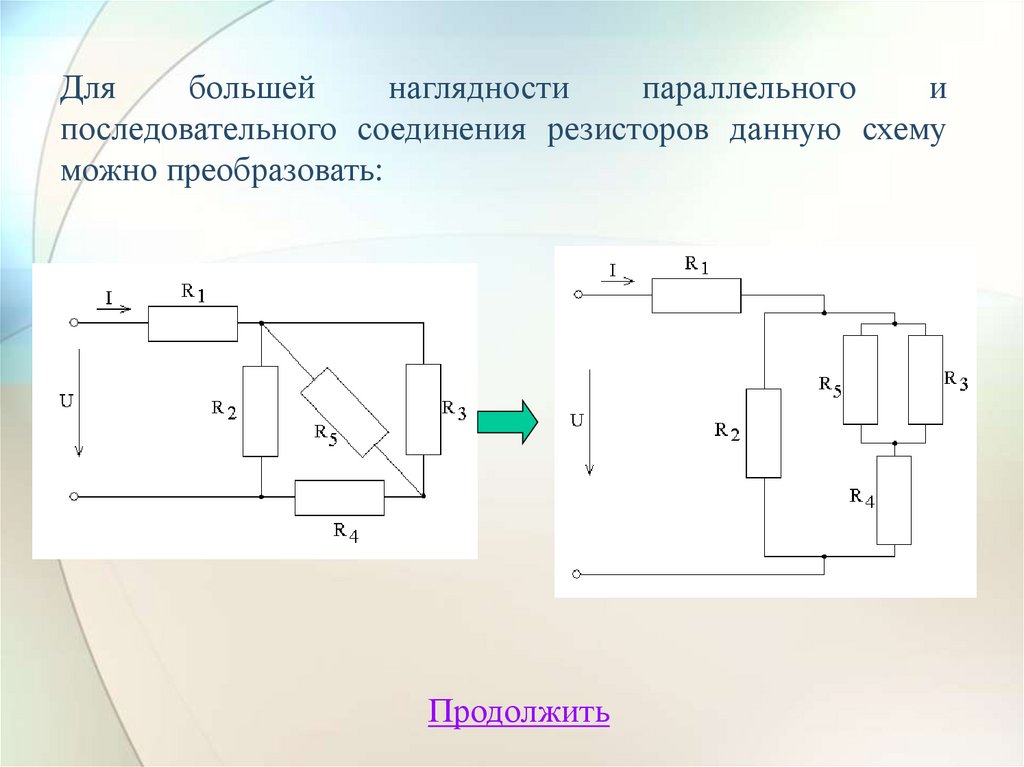 5 (верно?)
5 (верно?)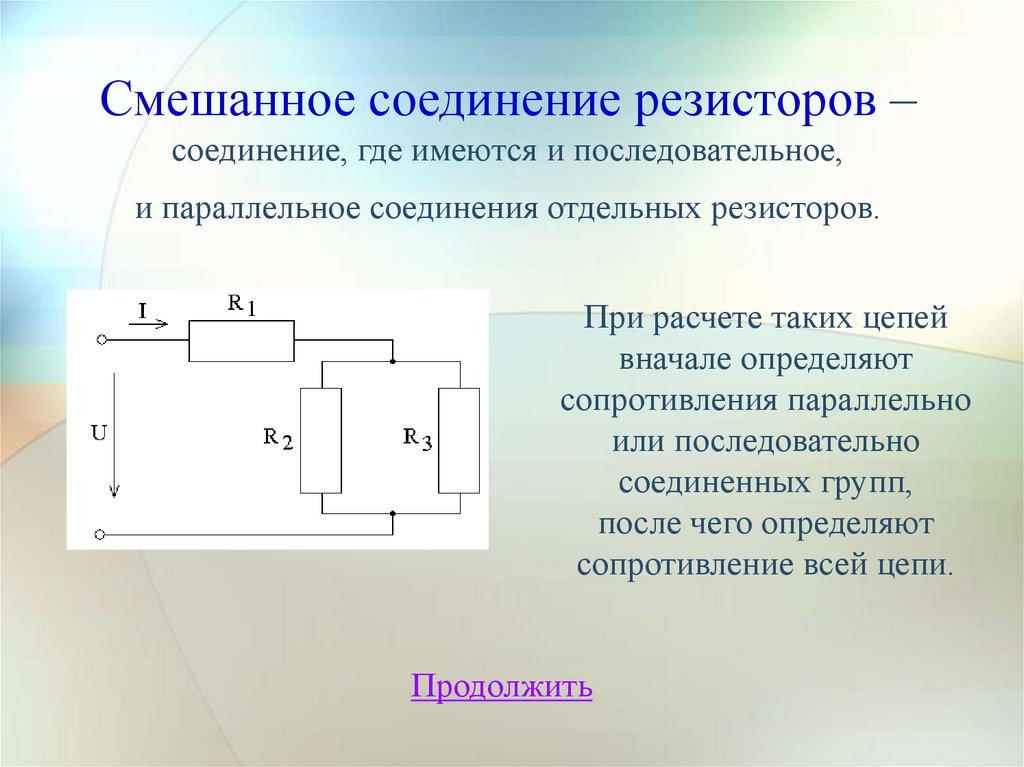 Каждая из пружин растянется на (т. к. жёсткость двух параллельных пружинок вдвое больше, чем одной), но в сумме будет . По-моему, всё же имелось в виду растяжение каждой пружинки, ибо это интересней.
Каждая из пружин растянется на (т. к. жёсткость двух параллельных пружинок вдвое больше, чем одной), но в сумме будет . По-моему, всё же имелось в виду растяжение каждой пружинки, ибо это интересней.
 (Правило с конденсаторами лишь для запоминания.)
(Правило с конденсаторами лишь для запоминания.)
 Каждая из пружин растянется на (т. к. жёсткость двух параллельных пружинок вдвое больше, чем одной), но в сумме будет . По-моему, всё же имелось в виду растяжение каждой пружинки, ибо это интересней.
Каждая из пружин растянется на (т. к. жёсткость двух параллельных пружинок вдвое больше, чем одной), но в сумме будет . По-моему, всё же имелось в виду растяжение каждой пружинки, ибо это интересней.