Параметры зубьев шестерни: Что такое модуль шестерни? Как вычислить модуль зубчатого колеса

alexxlab | 16.01.2023 | 0 | Разное

Модуль зуба шестерни. Определение, расчет, применение

Зубчатая передача представляет собой способ передачи энергии от одной детали к другой. Осуществляется данное взаимодействие с помощью таких изделий, как шестерни. Такая деталь представляет собой колесо, на поверхности которого имеются зубья. Всё разнообразие шестерней, производимых для различных механизмов или оборудования, изготавливаются с конкретным количеством зубьев, которые имеют определенные параметры модуля и шага. Модуль зуба шестерни является одним из наиболее важных параметров и используется при необходимости выбора парных шестерней, так как модуль в ведущей и ведомой шестерне должен быть одинаковым. По своей сути модуль представляет собой форму зуба шестерни, его размер и иные показатели. Для бесперебойной работы механизма значение модуля в обязательном порядке должно быть одинаковым у деталей, которые работают в зацеплении друг с другом. Параметры же диаметра или количество зубьев подбираются в зависимости от необходимой мощности.

Модуль зуба шестерни является универсальным параметром, позволяющим определить прочие необходимые показатели шестерни. Он показывает величину дуги, которая приходится на один зуб колеса. Данная величина измеряется в миллиметрах. Стандартные параметры данного показателя определяются в соответствии с нормативными актами, такими как госты. При изготовлении шестерен отталкиваются именно от параметров модуля, исходя из которых происходит расчет других величин, необходимых для производства. Величина модуля подбирается в зависимости от необходимых параметров прочности изделия, которые также зависят от требуемой мощности детали при работ механизма. После выбора нужной величины модуля и количества зубьев, необходимых для каждого конкретного случая, производятся вычисления прочих параметров, таких как диаметр впадин и вершин, длина окружного шага, толщину зубьев, а также расстояние между зубьями.

Как правило, в большинстве случае расчеты производятся для всех шестерней, входящих в состав механизма, однако, бывают случаи, требующие индивидуального расчета.

В первую очередь определяется необходимое количество зубьев и параметры модуля.

• Для определения модуля требуется произвести расчеты на прочность. Они проводятся в зависимости от срока службы изделия, а также используемого материала. Также на этом этапе происходит определение расстояния между осями колес.
• По результатам полученных расчетов необходимой выносливости детали, определяют наиболее подходящую величину модуля зуба шестерни. Для этого используются данные, содержащиеся в нормативной литературе, устанавливающей минимально необходимые значения модулей для конкретных параметров выносливости.
• В зависимости от требуемых показателей мощности подбирается необходимое число зубьев будущей детали.
• На основании полученных данных относительно количества зубьев и их числа, производится расчет прочих параметров, необходимых для производства изделия.

В результате всех произведенных вычислений происходит проверка изделий на прочность. При успешной проверке рассчитанные параметры используют для производства остальных деталей механизма.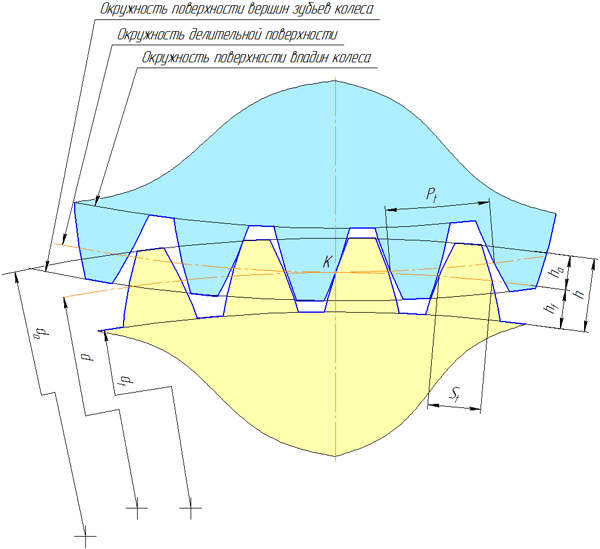

Определение параметров зубчатых колес с использованием обмеров

Лабораторная работа № 4

1. Цель работы

Привитие студентам навыков в определении основных геометрических параметров зубчатых колес с эвольвентным боковым профилем зуба, используя обмеры.

1. Основные положения

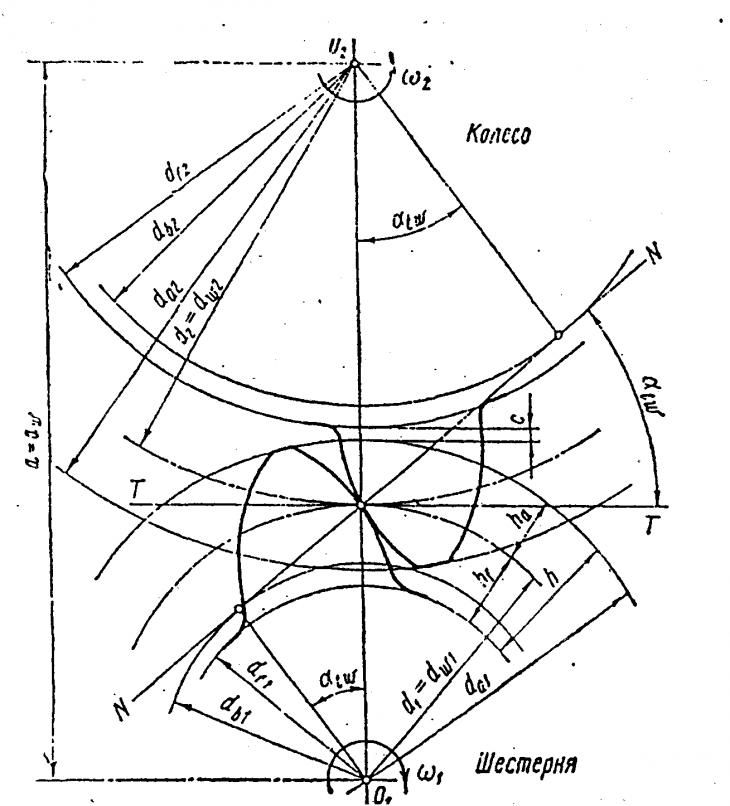
Основными параметрами любого зубчатого колеса с эвольвентным боковым профилем зуба являются модуль m, число зубьев z и угол профиля производящей рейки _р .Все остальные величины зубчатых колес могут быть выражены через указанные основные параметры. Некоторые вели­чины (например, число зубьев, диаметры окружностей выступов и впадин) могут быть определены или измерены непосредственно, большинство же величин определяется путем измерений и после­дующих вычислений.

3. Порядок выполнения работы

Начинается работа с определения числа зубьев колеса. Затем определяется модуль зацепления, для чего используется свойство эвольвенты – нормаль в любой точке эвольвенты является каса­тельной к основной окружности.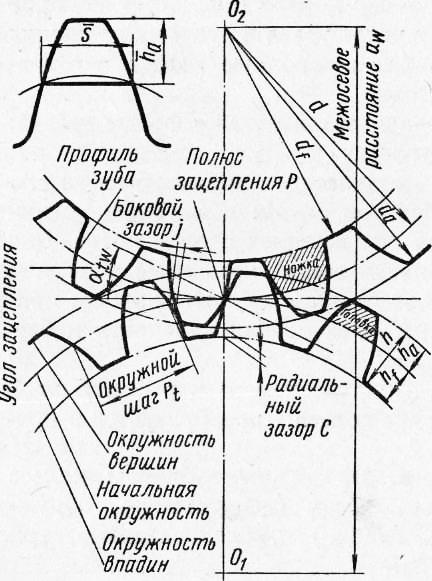 Кроме того, известно, что два (в общем случае криволинейных) профиля в точке контакта их имеют общую нормаль. Отсюда следует вывод, что если охватить несколь­ко зубьев колеса губками штангенциркуля (размер АВ, рис. 1), то линия АВ будет касательной к основной окружности, так как она нормальна в точках А и В к рабочим плоскостям губок штан­генциркуля и, следовательно, нормальна профилям зубьев в этих точках. Отметим также, что если отрезок АВ

катить по ос­новной окружности (по часовой и против часовой стрелки), то, по свойству эвольвенты, точка А придет в точку А₀ точка D в точку D₀ и точка В в точку В₀. Из чертежа (рис. 1) видно, что:

DB = D₀ S₀ = t₀ .

Таким образом, если измерить вначале размер С_п ,соответствую­щий п – зубьям, а затем измерить размер С_п+1 , охватив губками штангенциркуля на один зуб больше, то шаг по основной окруж­ности определится, как разность этих двух измерений:

t₀ = С_п+1 – С_n . (1)

С_п+1

С_п

D

B

B₀

A

A₀

D₀

t₀

t₀

S₀

A₀

A

Рис. 1. Измерение расстояния между боковыми профилями с помощью штангенциркуля

Последнее выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профи­ля зуба.

Модуль зацепления определится по формуле:

. (2)

Так как размеры С_п+1 и С_п определяются с некоторыми погрешностями (ошибки при изготовлении колеса и измерениях), то полученное значение модуля будет приближённым и его необходимо сопоставить со стандартными значениями модулей характеризующимися следующими цифрами:

0,3 –0,8 мм через 0,1 мм

1,0 – 4,5 » » 0,25 »

4,5 –7,0 » » 0,5 »

7,0 – 16,0 » » 1,0 »

16,0 – 30,0 » » 2,0 »

30,0 – 45,0 » » 3,0 »

более 45,0 » » 5 »

За истинный модуль следует принять ближайший по величине из стандартного ряда. По уточненному значению модуля рассчиты­ваются шаги зацепления по делительной и основной окружности, диаметры делительной и основной окружности.

После того как основные параметры определены, необходимо выяснить вопрос, с каким зубчатым колесом мы имеем дело – нуле­вым или корригированным, и вычислить коэффициент коррекции (относительный сдвиг)

. Это можно сделать, если измерить толщи­ну зуба по основной окружности и сопоставить результат измере­ния с расчетным значением толщины зуба по основной окружности для нулевого колеса. Для определения фактической толщины зуба по основной окружности можно воспользоваться измеренным выше размером АВ=С_п+1.

Действительно из рис. 1 следует, что С_п+1= пt₀ +s₀ и, следовательно:

s₀=С_п+1 – пt₀. (3)

Для определения расчетной толщины зуба по основной окруж­ности воспользуемся формулой:

.

Здесь для нулевого колеса , для корригированного колеса

.

Составим разность толщины зубьев по основной окружности корригированного колеса и нулевого, обозначив их соответственно и , очевидно:

.

Подставив сюда значения s¹ и s и замечая, что

,

получим:

,

. (4)

Вычислив величину s₀ по формуле (3) и вычислив обычным пу­тем толщину зуба s₀ по основной окружности нулевого колеса, по формуле (4) определяем коэффициент коррекции (относитель­ный сдвиг) .

Для дополнительного контроля сопоставляется теоретически рассчитанная измеренная штангензубомером толщина зуба s_x по хорде на делительной окружности (для нулевого колеса).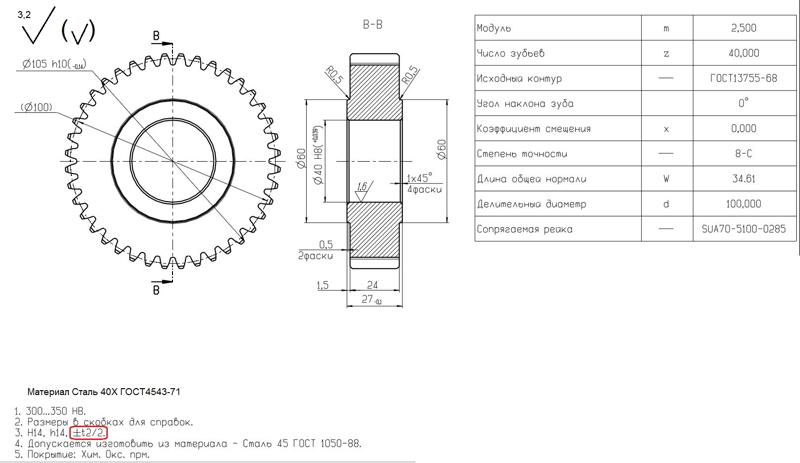

Из рис. 2 следует:

s_x = 2r_д sin,

так как

,

то

.

Если обозначить , тогда s_x = m P₁.

S_x



r_д

Рис. 2. Боковой профиль зуба

Определим расстояние от хорды по делительной окружности до окружности выступов:

H = h’ + h.

h’ = т – при нормальной высоте головки зуба.

.

Следовательно:

.

Если обозначить

,

то

H = m H₁.

Величины Р₁ и H_l , вхо­дящие в формулы (5) и (6), являются функциями от числа зубьев z, вычис­ленные значения их приведены в таблице 1.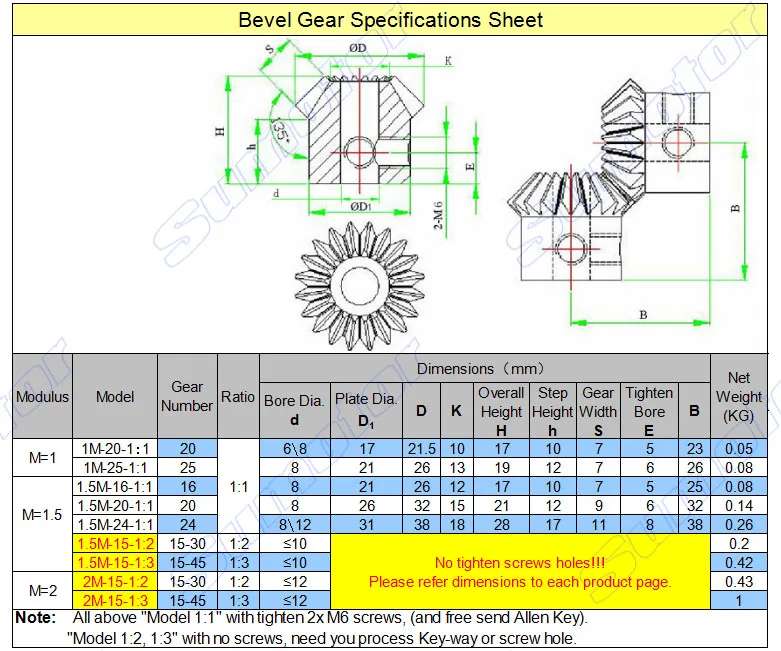

Таблица 1. Значения величин Н₁ и Р₁в зависимости от числа зубьев колеса.

z	Коэффициенты		z	Коэффициенты		z	Коэффициенты
	H1	P1		H1	P1		H1	P1
10	1,0615	1,5643	21	1,0293	1,5693	34	1,0183	1,5702
11	1,0559	1,5654	22	1,0280	1,5694	35	1,0176	1,5702
12	1,0153	1,5663	23	1 , 0268	1,5695	38	1,0162	1,5703
13	1,0473	1,5669	24	1,0256	1,5696	40	1,0154	1,5703
14	1,0440	1,5675	25	1,0245	1,5697	42	1,0146	1,5704
15	,0410	1,5679	26	1,0237	1,5693	45	1,0137	1,5704
16	,0385	1,5682	27	1 , 0228	1,5699	48	1,0128	1,5705
17	,0362	1,5635	28	1,0220	1,5699	50	1,0123	1,5705
18	,0342	1,5688	29	1,0212	1,5700	55	1,0112	1,5705
19	,0324	1,5690	30	1,0206	1,5700	80	1,0077	1,5706
20	,0308	1,5691	32	1,0192	1,5701	135	1,0045	1,5707

Теоретическое значение s_x вычисляется по формуле (5), фактическая величина f_x измеряется штангензубомером, устройство которого ясно из чертежа (рис.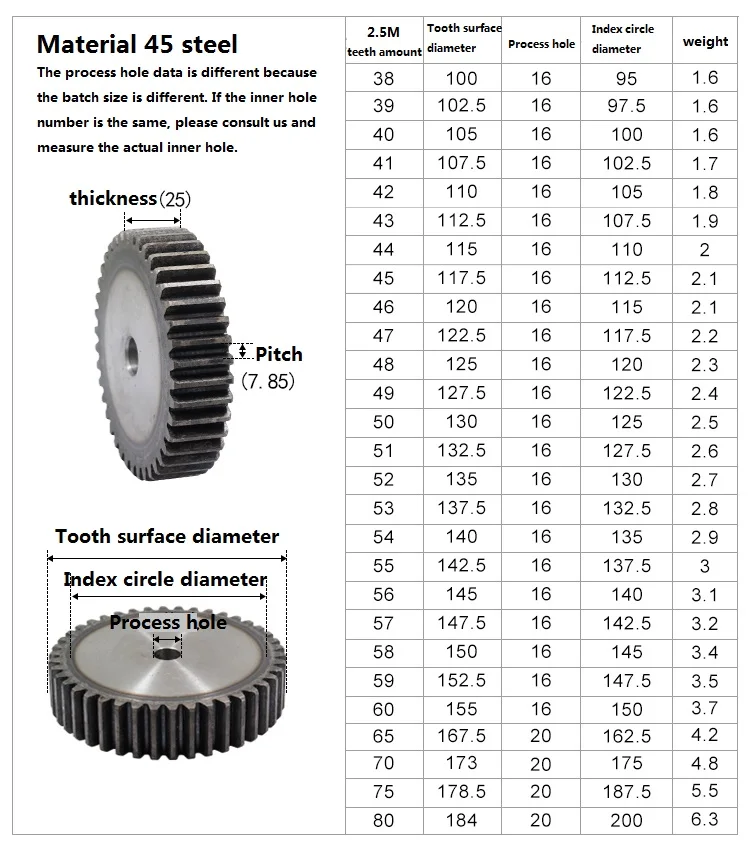 3). На этом же чертеже показана схема измерения хорды. Разность s_x1 – s_x может быть использова­на для определения класса точности колеса.

При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов и впадин. Если число зубьев шестерни четное, то оба эти диаметра могут быть непосред­ственно измерены штангенциркулем. При нечетном числе зубьев измерения проводятся по схеме, изображенной на рис. 4. Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни (d_отв.) и размер L₁. Тогда диаметр окружно­сти выступов будет равен D_e = d_отв +2L₁.

S_x

l₂

l₁

d_отв

Рис. 3. Штангензубомер Рис. 4. Измерение диаметров шестерни

с нечетным числом зубьев

Совершенно аналогично измеряется диаметр окружности впа­дин

D_l = d_отв +2L₂.

Имея диаметр окружности выступов, можно определить коэф­фициент высоты головки зуба нулевого колеса. Действительно:

D_e = m z + 2fm.

Решая это выражение относительно f, получим:

.

Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измери­тельный инструмент – штангенциркуль и штангензубомер (от­счет по обоим нониусам с точностью до 0,02 мм). Запись результа­тов измерений и вычислений ведется, следуя форме бланка отчета о проведенной работе.

Влияние параметров конструкции зубчатого колеса на чувствительность обнаружения повреждений зубьев зубчатого колеса | Дж.

Мех. Дес.

Пропустить пункт назначения навигации

Технические документы

Линь Лю, старший научный сотрудник,

Дэррил Дж. Пайнс, адъюнкт-профессор, адъюнкт-стипендиат AIAA, AHS, ASME, IOP.

Информация об авторе и статье

Предоставлено Комитетом по силовым передачам и зубчатым передачам для публикации в ЖУРНАЛЕ МЕХАНИЧЕСКОГО ПРОЕКТИРОВАНИЯ. Рукопись получена в июне 2001 г. Заместитель редактора: Р. Ф. Хандшу.

J. Mech. Дез . Декабрь 2002 г., 124(4): 794-804 (11 страниц)

https://doi.org/10.1115/1.1519275

Опубликовано в Интернете: 26 ноября 2002 г.

История статьи

Получено:

1 июня 2001 г.

Онлайн:

26 ноября 2002 г.

• Просмотры
  • Содержание статьи
  • Рисунки и таблицы
  • Видео
  • Аудио
  • Дополнительные данные
  • Экспертная оценка
• Делиться
  • Facebook
  • Твиттер
  • LinkedIn
  • MailTo

• Иконка Цитировать Цитировать

• Разрешения

• Поиск по сайту

Citation

Лю Л. и Пайнс Д. Дж. (26 ноября 2002 г.). «Влияние параметров конструкции шестерни на чувствительность обнаружения повреждения зубьев шестерни». КАК Я. Дж. Мех. Дез . декабрь 2002 г.; 124(4): 794–804. https://doi.org/10.1115/1.1519275

Скачать файл цитаты:

• Рис (Зотеро)
• Менеджер ссылок
• EasyBib
• Подставки для книг
• Менделей
• Бумаги
• КонецПримечание
• РефВоркс
• Бибтекс
• Процит
• Медларс

панель инструментов поиска

Расширенный поиск

В этой статье разработана аналитическая модель для моделирования контакта зубчатого зацепления для пары цилиндрических зубчатых колес с повреждением зубьев и без них. Моделируются три распространенные неисправности зубьев шестерен, включая точечную коррозию, износ и корневые трещины. Исследовано влияние ширины передней поверхности зуба на чувствительность обнаружения питтинга и влияние ширины трещины на чувствительность обнаружения трещины. Используя статические показатели производительности, такие как ошибка передачи, результаты показывают, что основные параметры конструкции зубчатого колеса, такие как диаметральный шаг, угол давления и количество зубьев, могут оказывать значительное влияние на чувствительность обнаружения повреждений. Похоже, что уменьшение диаметрального шага повысит чувствительность обнаружения повреждений для всех трех типов повреждений. Увеличение угла давления или количества зубьев повысит чувствительность обнаружения точечной коррозии, но имеет тенденцию снижать чувствительность к трещинам или повреждениям из-за износа.

Раздел выпуска:

Технические документы

Ключевые слова:

машиностроение, диагностика неисправностей, обнаружение трещин, моделирование, анализ чувствительности

Темы:

Ущерб, Дизайн, Излом (Материалы), Зубья шестерни, Шестерни, Давление, Носить, Моделирование, Ошибки, Отказ, Стресс

1.

Learmount

,

D.

,

2000

, «

Rotary.

,

157

, стр.

34

–

44

.

2.

Чемберлен, М., 1994, «U.S. Военно-морской флот проводит исследования в области диагностики летательных аппаратов», Vertiflite, март/апрель.

3.

Stewart, R. M., 1977, Некоторые полезные методы анализа данных для диагностики коробок передач г., Отчет MHM/R/10/77, Группа мониторинга состояния машин, Институт исследований звука и вибрации, Саутгемптонский университет, июль.

4.

Закрайсек, Дж. Дж., Таунсенд, Д. П., и Декер, Х. Дж., 1993, Анализ методов обнаружения отказов зубчатых колес применительно к данным об отказах от точечной усталости , NASA TM-105950, AVSCOM TR-92-C- 035.

5.

Закрайсек, Дж. Дж., 1994, Обзор исследований диагностики трансмиссии в Исследовательском центре Льюиса НАСА , НАСА TM-106746, ARL-TR-599.

6.

Forrester, B.D., 1990, «Анализ вибрации зубчатых колес в частотно-временной области», 44-е совещание Группы по предотвращению механических отказов , февраль.

7.

Wang

,

W. J.

и

McFadden

,

P. D.

,

1995

, «

Применение Orthogonal WaveLets wavelets to

Мех. Сист. Сигнальный процесс.

,

9

(

5

), стр.

497

–

507

900 сентября.

8.

Samuel

,

P. D.

,

Pines

,

D. J.

, and

Lewicki

,

D. G.

,

2000

, “

Сравнение стационарной и нестационарной трансмиссии для раннего обнаружения неисправностей в главной трансмиссии OH-58A

»,

J. Am. Вертолет Соц.

,

45

(

2

), стр.

125

–

136

3 90.

9.

Randall

,

R.

,

1982

, «

Новый метод моделирования разломов передачи

»,

Asme J.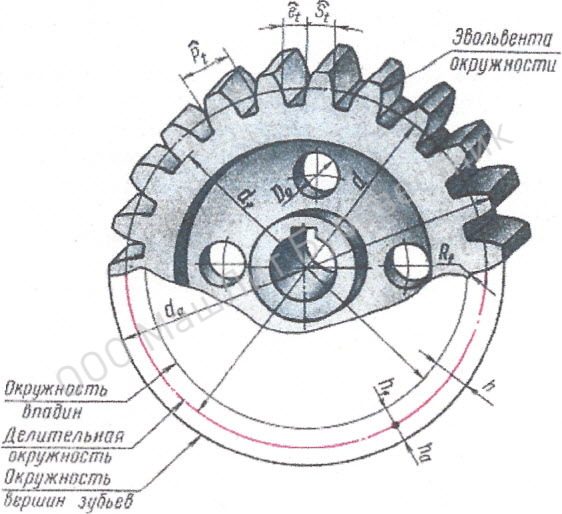 Mech., Trancer., Autom. Дес.

,

104

, стр.

259

–

267

.

10.

Badaoui, M., Cahouet, V., Guillet, F., Daniere J., and Velex, P., 1999, «Моделирование и обнаружение локализованных дефектов зубьев в зубчатых передачах», Proceedings of the 1999 ASME Design Engineering Technical Conferences , 12–15 сентября, Лас-Вегас, Невада.

11.

Куанг, Дж. Х., и Лин, А. Д., 1999 г., «Влияние износа зубьев на спектр вибрации пары цилиндрических зубчатых колес», Труды 19-й99 ASME Design Engineering Technical Conferences , 12–15 сентября, Лас-Вегас, Невада.

12.

Берри, С., и Клоснер, Дж., 2000, «Динамика системы трансмиссии, имеющей треснувший зубчатый венец», Материалы технических конференций ASME Design Engineering Technical Conferences 2000 , 10–13 сентября, Балтимор, Мэриленд.

13.

Дикарь

,

М.

,

Кой

,

Дж.0003

,

D. P.

,

1982

, «

Оптимальное количество зубьев для компактных стандартных цилиндрических зубчатых колес

»,

ASME

. Дес.

,

104

(

3

), окт., стр.

749

–

758

2.

14.

Кэрролл

,

Р. К.

,

Джонсон

,

Г. Э.

,

1984

, «

Оптимальный дизайн компактных наборов цилиндрических зубчатых колес

»,

ASME J. Mech., Transm., Autom. Дес.

,

106

, стр.

95

–

101

.

15.

Левицки, Д. Г., 2001, Исследования пути распространения трещины в зубчатых колесах – Руководство по сверхбезопасному проектированию , NASA/TM-2001-211073, ARL-TR-2468, июль.

16.

Линь

,

J.

и

Parker

,

R. G.

,

2002

, «

. ВИДЕНИЯ ПРЕДОСТАВЛЕНИЯ МЕШЕ В ДВУГОДНЫХ ШЕГОВОДОМ

,

ASME J. Вибр. акуст.

,

124

, стр.

68

–

76

.

17.

Август Р. и Касуба Р., 1984, Dynamics of Planetary Gear Trains , NASA CR Report 3793 июня.

18.

Smith, JD, 1983, Шестерни и их вибрация , Marcel Dekker, Inc. ISBN 0-8247-1759-7.

19.

Корома, А. М., 1995, «Мониторинг задиров и абразивного износа в цилиндрических зубчатых колесах с использованием простых методов на основе вибрации», Вторая международная конференция по шуму, вибрации и диагностике редукторов, IMechE Conference Transaction , 16 ноября. –17.

20.

Корнелл

,

Р. В.

,

1981

, «

Податливость и чувствительность к напряжению зубьев цилиндрического зубчатого колеса

»,

ASME J. Mech. Дес.

,

103

, стр.

447

–

459

.

21.

Weber, C., 1949, Деформации нагруженных зубчатых колес и влияние на их несущую способность , Спонсируемые исследования (Германия), Британский департамент научных и промышленных исследований, Отчет № 3.

22.

Welbourn, D.B., 1979, «Фундаментальные знания о шуме шестерен — обзор», Proceedings of Noise and Vibration of Eng. и транс. I. Мех. E. , Крэнфилд, Великобритания, июль, стр. 9–14.

23.

Gregory

,

R. W.

,

Harris

,

S. L.

, and

Munro

,

R. G.

,

1963

, “

Метод измерения погрешности передачи в цилиндрических зубчатых передачах с передаточным числом 1:1

»,

J. Sci. Инструм.

,

40

, январь, стр.

5

–

9

.

24.

Манро Р. Г. и Йилдирим Н., 1994 г., «Некоторые измерения статических и динамических погрешностей передачи прямозубых зубчатых колес», Труды Международной конференции по зубчатым передачам 1994 г. , сентябрь, Университет Ньюкасл-апон-Тайн , Великобритания, стр. 371–376.

25.

Корнелл, Р. В., 1994 г., «Измерения динамических ошибок передачи во временной области в высокоскоростных передачах», Материалы Международной конференции по зубчатым передачам 1994 г. , сентябрь, Университет Ньюкасл-апон-Тайн, Великобритания, стр. 363–370.

26.

Dudley, D.W., 1984, Справочник по практическому проектированию зубчатых колес , McGraw-Hill Book Company, Inc.

В настоящее время у вас нет доступа к этому содержимому.

25,00 $

Покупка

Товар добавлен в корзину.

Проверить Продолжить просмотр Закрыть модальный

Характеристики и основные параметры зубчатой ​​рейки – Отраслевые знания

Характеристики и основные параметры зубчатой ​​рейки

Рейка представляет собой специальную шестерню с распределенными на стержне зубьями. Рейки также делятся на прямые и косозубые, которые работают в паре с прямыми и цилиндрическими зубчатыми колесами соответственно; профиль зуба рейки представляет собой прямую линию, а не эвольвенту (плоская поверхность для поверхности зуба), эквивалентную цилиндрической шестерне с бесконечным радиусом окружности.

Concept

Рейка представляет собой стержневую деталь, соответствующую шестерне. Он равен участку окружности шестерни бесконечного диаметра. С одной стороны равномерно распределено множество зубьев, которые входят в зацепление с шестернями, превращая вращение в движение или превращая движение во вращение. Рейка длинная и имеет зубья с одной стороны. Его можно рассматривать как сечение шестерни бесконечного диаметра.

Основная особенность

(1) Поскольку профиль зуба рейки представляет собой прямую линию, все точки на профиле зуба имеют одинаковый угол давления и равны углу наклона профиля зуба. Этот угол называется углом профиля зуба, и его стандартное значение равно 20°.

(2) Любая прямая, параллельная линии дополнения, имеет одинаковый шаг и модуль.

(3) Прямая линия, параллельная верхней линии зуба и имеющая толщину зуба, равную ширине паза зуба, называется разделительной линией (осевой линией), которая является базовой линией для расчета размера рейки.

Основные параметры

Основными параметрами рейки являются: ширина зуба,добавка зуба,выступ зуба,высота зуба, толщина зуба, радиус корня зуба и др.

Альвеолярный

Канавка зуба представляет собой вогнутую часть между зубьями шестерни.

Пространство между двумя соседними зубьями на шестерне называется зубчатым или межзубным. Размер канавки зуба выражается шириной канавки, а ширину канавки зуба можно разделить на два типа: ширину канавки торца и ширину нормальной канавки.

(1) Ширина торцевой канавки (ширина канавки) – на торцевой плоскости длина разделительной дуги между профилями зубьев по обеим сторонам канавки зуба обозначается буквой е. Ширина паза на любой окружности обозначается буквой ei.

(2) Нормальная ширина паза (нормальная ширина паза) – в пазу косозубого колеса нормальная спираль линии зуба по обеим сторонам винтовой линии расположена в шлице на длине паза, называемом нормальным пазом ширина.

Приложение

Часть между разделительной окружностью и окружностью добавления называется дополнением шестерни. Радиальное расстояние называется высотой вершины зуба и обозначается буквой ha. Высота вершины зуба цилиндрической шестерни рассчитывается по следующей формуле:

В формуле: ha — коэффициент высоты вершины зуба цилиндрической шестерни, ha=1 для нормальных зубьев, ha=0,8 для коротких зубьев;

м-модуль зубчатого зацепления.

Корень зуба

Часть между разделительной окружностью и окружностью корня зуба называется корнем зуба. Радиальное расстояние называется высотой корня и обозначается буквой hf. Высота основания цилиндрической шестерни рассчитывается следующим образом:

В формуле ha — коэффициент высоты вершины зуба цилиндрической шестерни, ha=1 для нормальных зубьев и ha=0,8 для коротких зубьев;

C——Коэффициент верхнего зазора цилиндрической шестерни, C=0,25 для нормальных зубьев, C=0,3 для коротких зубьев;

m——модуль зубчатого колеса.

Предпочтения

(1) Квалифицированы ли биение шестерни, полная глубина зуба, общая нормаль, направление зуба, разница в шаге одного зуба и выходит ли погрешность кольцевого соединения за пределы допуска.