Передаточное число формула: Передаточное число: расчет, формула, определение
alexxlab | 01.04.1993 | 0 | Разное
Передаточное число: расчет, формула, определение
Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.
Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.
Содержание
Общее определение
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:
- ременная;
- цепная;
- зубчатая.
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.
Переходной конструкцией является ременная зубчатая передача.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.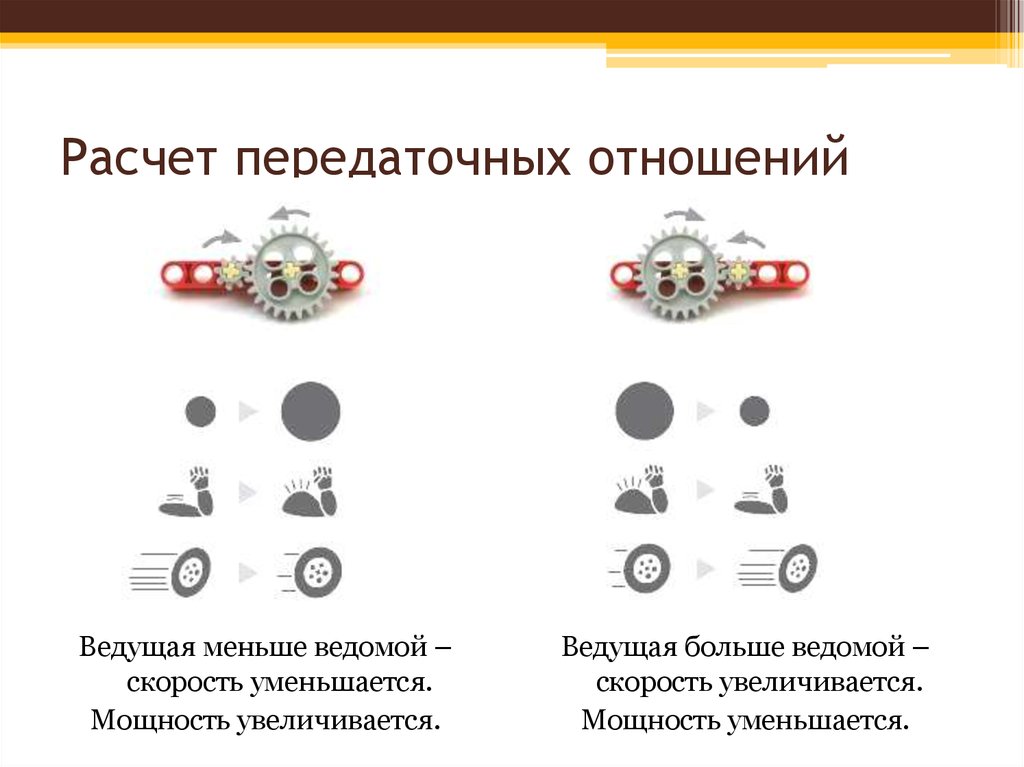
Модуль – размер между одинаковыми точками двух соседних зубьев.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.
Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает.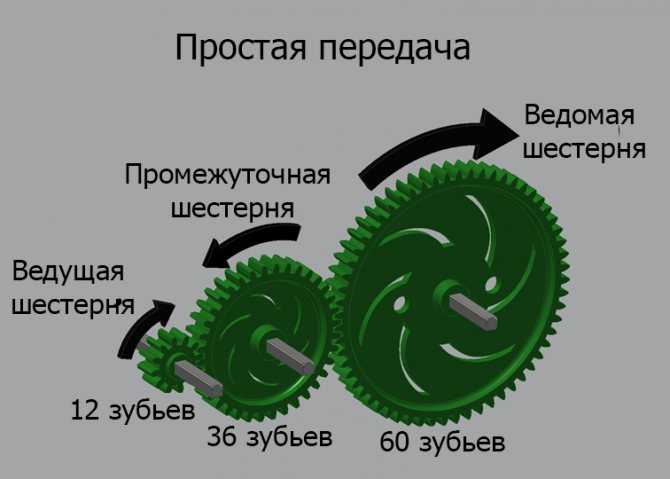 Такие передачи называют понижающими.
Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.
Виды зубчатых соединений
Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:
- прямозубая;
- косозубая;
- шевронная;
- коническая;
- винтовая;
- червячная.

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.
Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.
Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.
Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.
Оно ставится только на механизмах с очень большой нагрузкой.
В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.
Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях.
У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.
Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.
Многоступенчатые редукторы
Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.
Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.
Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.
Uр = U1×U2 × … ×Un;
Где:
Uр – передаточное число редуктора;
U1,2,n – каждой из пар.
Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.
В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.
Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.
Редуктор и коробка скоростей
Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.
Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.
Трансмиссия автомобиля
В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.
В состав трансмиссии входит несколько редукторов. Это, прежде всего:
Это, прежде всего:
- коробка передач – скоростей;
- дифференциал.
Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.
Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.
Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
youtube.com/embed/S3XcGCWR-RI?feature=oembed” frameborder=”0″ allow=”accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture” allowfullscreen=””>Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Передаточное отношение зубчатой передачи
Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.
Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.
При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.
Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.
Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.
Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.
Цифровое значение совпадает с переданным числом оборотов.
Передаточное отношение редуктора вычисляется по формуле:
U12 = ±ω1/ω2=±n1/n2
где U12 – передаточное отношение шестерни относительно колеса;
ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения;
n1 и n2 – частота вращения.
Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.
Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.
2.3 Определение передаточного числа главной передачи
Передаточное число главной передачи влияет на тягово-динамические и экономические показатели автомобиля. Его определяют, пользуясь выражением:
2. 9
9
Передаточное число главной передачи, полученное расчетом соответствует табличному.
2.4 Определение передаточных чисел в коробке передач
Передаточные числа в коробке передач определяют из условия обеспечения наибольшей интенсивности разгона и плавности переключения шестерен при последовательном переходе с одной передачи на другую, а также для обеспечения движения на первой передаче без буксования по заданной дороге.
Знаменатель геометрической прогрессии ряда, образуемого передаточными числами коробки передач, находят по формуле
2.10
где т — число передач в коробке.
Передаточное число в коробке при работе на первой передаче определяют из условия преодоления заданного сопротивления движению по формуле
2.11
где Мmах— максимальный крутящий момент двигателя, Н*м;
ψ1mах — суммарный коэффициент дорожного
сопротивления (берем из задания на
проектирование автомобиля).
Проверяем условие движения автомобиля без буксования по заданной дороге. Должно быть удовлетворено условие
2.12
где — коэффициент сцепления движителей с дорогой;
λк – коэффициент нагрузки на ведущие колеса;
λк = 1 – для машин повышенной и высокой проходимости;
λк = 0,5—0,55 – для легковых автомобилей 4×2;λк = 0,65—0,75 – для грузовых автомобилей 4×2.
Для нашего расчета принимаем λк =
Вывод – передаточное число удовлетворяет условию
Тогда:
iкп 1 = 6,046
iкп 2 = 3,4
iкп 3 = 1,91
iкп 4 = 1,075
2.
 5 Определение скоростей движения автомобиля на различных передачах
5 Определение скоростей движения автомобиля на различных передачахМаксимальная скорость движения на прямой передаче задана. Скорости движения на промежуточных передачах определим из соотношений:
V1 = 4,69м/с
V2 = 8,34м/с
V3 = 14,84м/с
V4 = 26,39м/с
3. ДИНАМИЧЕСКИЙ РАСЧЕТ АВТОМОБИЛЯ
В процессе динамического расчета выполняют построение динамической характеристики автомобиля.
Динамический
фактор D
предложен Е.А.
Чудаковым. Используют его для сравнительной
оценки динамических качеств различных
автомобилей в различных условиях их
движения (качество дороги, нагрузка
автомобиля). Так как в условиях
установившегося движения численные
значения динамического фактора и
суммарного коэффициента дорожного
сопротивления равны, т.е. ψ
= D.
Зная динамический
фактор автомобиля, можно определить,
какое дорожное сопротивление он будет
преодолевать.
Динамический фактор есть отношение избыточной силы тяги, к полному весу автомобиля:
3.1
Так как касательная сила тяги Рк и сила сопротивления воздуха Рw изменяются с изменением скоростного и нагрузочного режимов работы автомобиля, то и динамический фактор в условиях эксплуатации не остается постоянным. Его оценивают с помощью динамической характеристики, которая представляет собой D = ƒ(V).
Основой для построения динамической характеристики (рис. 2) является внешняя скоростная характеристика карбюраторного двигателя или регуляторная характеристика дизеля, а также данные тягового расчета и ряд параметров автомобиля-прототипа
а) Построение динамической характеристики автомобиля. Наметим не менее пяти точек скоростных режимов автомобиля на каждой передаче. Скорости движения автомобиля при движении на различных передачах и при различных значениях частот вращения вала двигателя определяют по формуле
3. 2
2
Значение частоты | 1-ая передача | 2-ая передача | 3-ья передача | 4-ая передача |
б) Для этих скоростных режимов находим значения крутящих моментов двигателя и определяют касательные силы тяги на каждой передаче по формуле:
3.3
Значение Мк | 1-ая передача | 2-ая передача | 3-ая передача | 4-ая передача |
Для определения
силы сопротивления воздуха используют
зависимость.
1-ая передача
2-ая передача
3-ья передача
Значения коэффициента сопротивления воздуха kw и площади поперечного сечения автомобиля Fа принимают из тягового расчета.
в) Значения динамического фактора для каждой передачи подсчитывают
по формуле:
Используя
полученные значения динамического
фактора, строят характеристику D
= ƒ(V).
1-ая передача | 2-ая передача | 3-я передача | 4-ая передача | |
Рис. 2. Динамическая характеристика автомобиля
Библиографический список
Чудаков Е.Д. Теория автомобиля. М.: Машгиз, 1940.

Скотников В.А., Мащенский А.Н., Солонский А.С. Основы теории и расчета трактора и автомобиля. М.: Агропромиздат, 1986.
Колчин А.И., Демидов В.П. Расчет автомобильных и тракторных двигателей. М.: Высшая школа, 1980.
Чернышев В.А. Тягово-динамический расчет автомобиля: Учебное пособие. М: МГАУ им. В.П. Горячкина, 1994.
Чернышев В.А. Тяговый расчет трактора: Методические рекомендации. М.:-ГОСНИТИ, 1982.
Как рассчитать передаточное число – x-engineer.org
Шестерни являются жизненно важными компонентами машин, робототехники, транспортных средств, аэрокосмической продукции и так далее. Наверное, все, что движется, в каждой машине есть хотя бы одна передача.
Самое простое применение – редуктор . Это машина, оборудование, которое преобразует входную скорость и крутящий момент в выходную скорость и крутящий момент. Под трансформацией мы подразумеваем усиление или уменьшение . Уровень трансформации определяется цифрой 9.0005 передаточное число .
Под трансформацией мы подразумеваем усиление или уменьшение . Уровень трансформации определяется цифрой 9.0005 передаточное число .
Редуктор представляет собой коробку передач, имеющую только одну передачу. Передаточное число получается путем зацепления двух цилиндрических шестерен .
Изображение: анимация зубчатого редуктора (нажмите на изображение, чтобы увидеть анимацию)
Зубчатый редуктор обычно используется в качестве усилителя крутящего момента . Например, вам нужно привести в действие гидравлический насос, которому требуется большой крутящий момент. Ваш источник энергии, скажем, электродвигатель. Между мотором и насосом укладываем шестеренчатый редуктор.
Как рассчитать передаточное число?
Если вам необходимо увеличить крутящий момент двигателя в 3 раза, вам понадобится редуктор с передаточным числом 3,0 . Чтобы рассчитать передаточное отношение двух зацепленных шестерен, нам нужно знать:
- количество зубьев обеих входных и выходных шестерен
- базовый диаметр или радиус обеих входных и выходных шестерен
Изображение: Схема сил зубчатого зацепления
В таблице ниже приведены все физические значения, которые мы собираемся использовать в наших расчетах. Со знаком вопроса (?) у нас есть все переменные, которые нам нужно вычислить.
Со знаком вопроса (?) у нас есть все переменные, которые нам нужно вычислить.
| Переменная | Описание | Значение | Блок | ||||||
| \ [Z_ {in \] | Number of Toots ofots ofots ofots ofots of toot | ||||||||
| \[z_{OUT}\] | number of teeth of the output gear | 24 | – | ||||||
| \[r_{IN}\] | base radius of the input gear | 80 | mm | ||||||
| \[r_{OUT} \] | базовый радиус выходной шестерни | 120 | мм | ||||||
| \[i\] | передаточное отношение | ? | – | ||||||
| \[Tq_{IN}\] | входной крутящий момент | 250 | Нм | ||||||
| \[Tq_{OUT}\] | выходной крутящий момент | ? | NM | ||||||
| \ [\ omega_ {in} \] | Вход (вращение) Скорость | 1500 | об / мин | ||||||
| \ [\ omega_ {Out} \] | |||||||||
| \ [\ omega_ {Out} \] | \ [\ omega_ {Out} \] | \ [\ omega_ {Out} \] | 7 | \ [\ omega_ {out} \] | 77 70047. | ? | об/мин | ||
| \[F_{t}\] | контактное (касательное) усилие | (не требуется) | Н | ||||||
| \[ | \[9005\] | скорость контакта (тангенса) | (не нужно) | м/с |
Под входом мы понимаем источник питания, в нашем случае это может быть электродвигатель. Под выходом мы подразумеваем, куда подается мощность (например, гидравлический насос).
Передаточное число i можно рассчитать двумя способами:
- как отношение числа зубьев выходной шестерни к числу зубьев входной шестерни
\[i=\frac{z_ {OUT}}{z_{IN}}\]
- как отношение базового радиуса выходной шестерни к базовому радиусу входной шестерни
\[i=\frac{r_{OUT}}{r_{IN}}\]
Базовый радиус измеряется от центра вращения шестерни до точки касания зубьев. Тот же результат получается при использовании внешнего радиуса, который находится от центра шестерни до вершины зубьев.
Заменив математические выражения реальным количеством зубьев и радиусом, получим передаточное число i :
\[ \begin{equation*} \begin{split}
i &= \frac{z_{OUT}}{z_{IN}} &= \frac{24}{16 } &= 1,5\\
i &= \frac{r_{OUT}}{r_{IN}} &= \frac{120}{80} &= 1,5
\end{split} \end{equation*} \ ]
Связь между выходным крутящим моментом и входным крутящим моментом следующая:
\[ \begin{equation*} \begin{split}
Tq_{OUT} = i \cdot Tq_{IN}
\end{split } \end{equation*} \]
Редуктор будет увеличивать входной крутящий момент в число раз, равное передаточному числу:
\[ \begin{equation*} \begin{split}
Tq_{OUT} = 1,5 \cdot 250 = 375 \text{ Нм}
\end{split} \end{equation*} \]
Связь между выходной скоростью и входной скоростью следующее:
\[ \begin{equation*} \begin{split}
\omega_{OUT} = \frac{\omega_{IN}}{i}
\end{ split} \end{equation*} \]
Редуктор уменьшит входную скорость в число раз, равное передаточному числу:
\[ \begin{equation*} \begin{split}
\omega_{OUT} = \frac{1500}{1. 5} = 1000 \text{ об/мин}
5} = 1000 \text{ об/мин}
\end{split} \end{equation*} \]
Теперь мы продемонстрируем, почему выходное значение крутящий момент – это входной крутящий момент, умноженный на передаточное число. Кто придумал эту формулу?
В месте контакта между зубьями шестерен действует тангенциальная сила. Эта тангенциальная сила может быть рассчитана функцией входной шестерни и функцией выходной шестерни.
Мы знаем, что крутящий момент – это произведение приложенной силы на длину плеча рычага. В нашем случае сила — это тангенциальная сила между зубьями, а плечо рычага — радиус шестерни.
\[ \begin{equation*} \begin{split}
Tq_{in} = r_{IN} \cdot F_{t}\\
\end{split} \end{equation*} \]
From это мы извлекаем тангенциальную силу:
\[ \begin{equation*} \begin{split}
F_{t} = \frac{Tq_{IN}}{r_{IN}}
\end{split} \end {equation*} \]
Та же сила приложена к выходной шестерне:
\[ \begin{equation*} \begin{split}
F_{t} = \frac{Tq_{OUT}}{r_{ OUT}}
\end{split} \end{equation*} \]
Объединяя два математических выражения касательной силы, получаем:
\[ \begin{equation*} \begin{split}
\frac{Tq_{OUT}}{r_{OUT}} &= \frac{Tq_{IN}}{r_{IN}}\\
Tq_ {OUT} &= \frac{r_{OUT}}{r_{IN}} \cdot Tq_{IN}\\
Tq_{OUT} &= i \cdot Tq_{IN}
\end{split} \end{ уравнение*} \]
Теперь давайте продемонстрируем влияние передаточного числа на выходную скорость. Мы используем то же изображение, что и выше, но с обозначениями скорости вместо сил.
Мы используем то же изображение, что и выше, но с обозначениями скорости вместо сил.
Изображения: Схема скоростей зацепления зубчатых колес
Тангенциальная скорость одинакова в точке контакта двух зубчатых колес. В качестве тангенциальной силы мы можем записать функцию тангенциальной скорости входной и выходной шестерни:
Мы знаем, что тангенциальная скорость — это произведение радиуса на скорость вращения.
\[ \begin{equation*} \begin{split}
v_{t} = \omega_{IN} \cdot r_{IN}
\end{split} \end{equation*} \]
То же скорость применяется к выходной шестерне:
\[ \begin{equation*} \begin{split}
v_{t} = \omega_{OUT} \cdot r_{OUT}
\end{split} \end{equation *} \]
Сложив два математических выражения тангенциальной скорости, получим:
\[ \begin{equation*} \begin{split}
\omega_{OUT} \cdot r_{OUT} &=\omega_{IN} \cdot r_{IN}\\
\omega_{OUT} &= \frac{r_{IN}}{r_{OUT}} \cdot \omega_{IN}\\
\omega_{OUT} &= \frac{\omega_{IN}}{i}
\end{split} \ end{equation*} \]
К концу этого урока вы должны знать, как рассчитать функцию передаточного числа шестерен, а также влияние передаточного отношения на крутящий момент и скорость.
Если у вас есть какие-либо вопросы или замечания относительно этого урока, пожалуйста, используйте форму комментариев ниже.
Не забудьте поставить лайк, поделиться и подписаться!
Зубчатая передача: расчет передаточного числа, крутящего момента и скорости
Зубчатая передача состоит из двух или более шестерен, соединенных последовательно. Он используется для увеличения или уменьшения скорости или крутящего момента выходного вала. Термин передаточное число используется для расчета скорости и крутящего момента выходной шестерни, когда крутящий момент прикладывается к входной шестерне.
Цилиндрическая шестерня в движении Например, коробка передач — это тип зубчатой передачи, который используется для увеличения крутящего момента двигателя и снижения скорости колес автомобиля. Увеличение крутящего момента зависит от того, на какой передаче вы едете на своем автомобиле. В этой статье мы обсудим, как рассчитать передаточное число, скорость и крутящий момент для различных зубчатых передач.
Чтобы понять передаточное отношение, мы предлагаем вам сначала прочитать эту статью о Терминологии передач (различные термины, используемые в передачах) и различных типах передач.
СОДЕРЖАНИЕ
- Закон передачи
- передаточный численность
- Скорость и скорость передачи
- . что отношение угловых скоростей между сопрягаемыми шестернями всегда остается постоянным. Для достижения условия постоянной угловой скорости общие нормаль в точке контакта сопряженных зубьев шестерни всегда проходят через точку тангажа. Где Точка шага — это точка контакта между окружностями шага сопрягаемой шестерни.
Если угловая скорость сопрягаемой шестерни постоянна, мы можем заключить следующее соотношение:
Где ω1 и ω2: Угловая скорость в радианах/с для ведущей и ведомой шестерен соответственно.
n1 и n2 = Скорость передачи в об/мин для ведущей и ведомой шестерен соответственно.
d1 и d2 = диаметр ведущей и ведомой шестерен соответственно.

T1 и T2 = Количество зубьев на ведущей и ведомой шестернях соответственно.
Передаточное число
Передаточное число — это отношение числа зубьев ведомой и ведущей шестерен. Он используется для расчета скорости и крутящего момента выходного вала, когда входной и выходной валы соединены зубчатой передачей.
Входная шестерня, к которой прикладывается крутящий момент, известна как привод . В то время как выходная шестерня известна как ведомая шестерня . А шестерни, используемые между ведущей и ведомой шестернями, известны как промежуточные шестерни .
Передаточное отношение и скорость
Передача мощности через зубчатую передачу влияет на скорость вращения выходного вала.
Следовательно:
Скорость вторичного вала = Скорость входного вала / Передаточное число
Передаточное отношениеКак показано выше, если число шестерен на выходном валу больше, чем шестерен на входном валу.
Цилиндрическое зубчатое колесо для увеличения скорости Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом.
Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом.Принимая во внимание, что когда мы реверсируем расположение. Другими словами, если количество шестерен на вторичном валу меньше, чем шестерен на входном валу. Скорость выходного вала будет иметь большую скорость по сравнению с входным валом.
Передаточное число и крутящий момент
По закону передаточных чисел. В зубчатой передаче отношение выходного крутящего момента к входному крутящему моменту также постоянно и равно передаточному числу. Следовательно, если входной крутящий момент известен. Выходной крутящий момент можно рассчитать, умножив входной крутящий момент на передаточное число.
Типы зубчатых передач и их расчет
Зубчатая передача состоит из ряда шестерен для передачи мощности с одного вала на другой.
 Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой передачи.
Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой передачи.- Простая зубчатая передача
- Составная зубчатая передача
- Реверсивная зубчатая передача
- Планетарная зубчатая передача
1) Расчет передаточного числа для простой зубчатой передачи
Простая зубчатая передача может быть двухступенчатой или многоступенчатой.
1.1) Двухступенчатая передача
Двухступенчатая передача — это тип простой зубчатой передачи. Он состоит из двух соединенных шестерен. Например, как показано ниже в двухступенчатом поезде. Gear-1 является ведущей, а Gear-2 — ведомой. Когда ведущая шестерня вращается по часовой стрелке, ведомая шестерня будет вращаться против часовой стрелки.
Вопрос:
Рассчитайте скорость и крутящий момент выходного вала для простой зубчатой передачи. Где количество зубьев на ведущей и ведомой шестернях 40 и 20 соответственно. Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.
Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.Количество зубьев ведущей шестерни (T1) = 40
Количество зубьев ведомой шестерни (T2) = 20
Скорость ведущей шестерни (n1) = 100 об/мин Двухступенчатая передача
Расчет передаточного числа
GR = T2 / T1 = 20/40 = 0,5
Расчет скорости выходного вала
Скорость выходного вала/GR = 5,0. = 200 об/мин
Расчет крутящего момента выходного вала/шестерни
Крутящий момент, создаваемый ведомой шестерней = GR × Крутящий момент, создаваемый водителем
= 0,5 × 10 = 5 Н·м передача движения с одного вала на другой. Результирующее передаточное число может быть рассчитано путем умножения отдельных передаточных чисел.
Вопрос: Рассчитайте передаточное число для многоступенчатых поездов. Где количество зубьев на ведущей, промежуточной и ведомой шестернях составляет 40, 20 и 10 соответственно.
Многозубчатая передача
Заданное количество зубьев
T1 = 40, T2 = 20, T2 = 10 между Gear-1 и Gear-2 (водитель и натяжитель).
GR(1-2) = 20/40 = 0,5
Шаг 2: Рассчитайте GR между шестерней-2 и шестерней-3 (промежуточная и ведомая шестерни).
GR(2-3) = 10/20 = 0,5
Шаг 3: Умножая передаточное число от 1 до 2 и от 2 до 3. Мы получим результирующий GR между ведущей и ведомой шестернями.
Результирующая многоступенчатая передача GR = 0,5 × 0,5 = 0,25
Из вышеприведенного расчетного передаточного числа мы можем рассчитать скорость и крутящий момент на выходной передаче.
2) Расчет передаточного числа для составной зубчатой передачи
Составные шестерни состоят из более чем одной шестерни на одной оси. Поэтому шестерни на одном валу вращаются с одинаковой скоростью и крутящим моментом.
Вопрос: Рассчитайте передаточное число составной зубчатой передачи.
Составная зубчатая передача Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.
Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.Заданное количество зубьев
T1 = 40, T2 = 30, T3 = 20, T4 = 10
Расчет передаточного числа для составной шестерни
-3 находятся на одном валу.
Шаг-1: Рассчитать передаточное отношение между Шестерня-1 и Шестерня-2
GR(1-2) = 30/40 = 0,75 4.
ГР(3-4) = 10/20 = 0,5
Шаг 3: Умножить GR(1-2) и GR(3-4)
Полученная составная шестерня GR = 0,375
3) Перевернутая зубчатая передача.
Реверсивная зубчатая передачаРеверсивная зубчатая передача представляет собой тип составной зубчатой передачи, в которой входной и выходной валы находятся на одной оси.





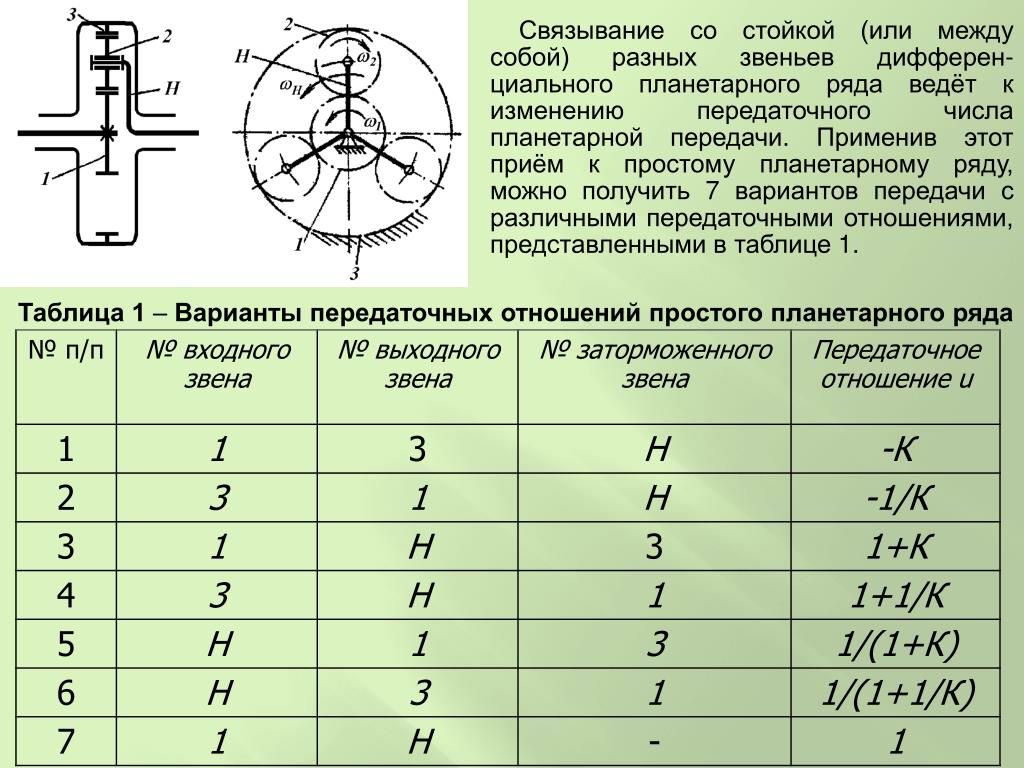


 Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом.
Эта компоновка также известна как редуктор . При таком расположении выходной вал будет иметь более низкую скорость по сравнению с входным валом. Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой передачи.
Например, мощность от двигателя передается на колеса через коробку передач. Вот четыре различных типа зубчатой передачи.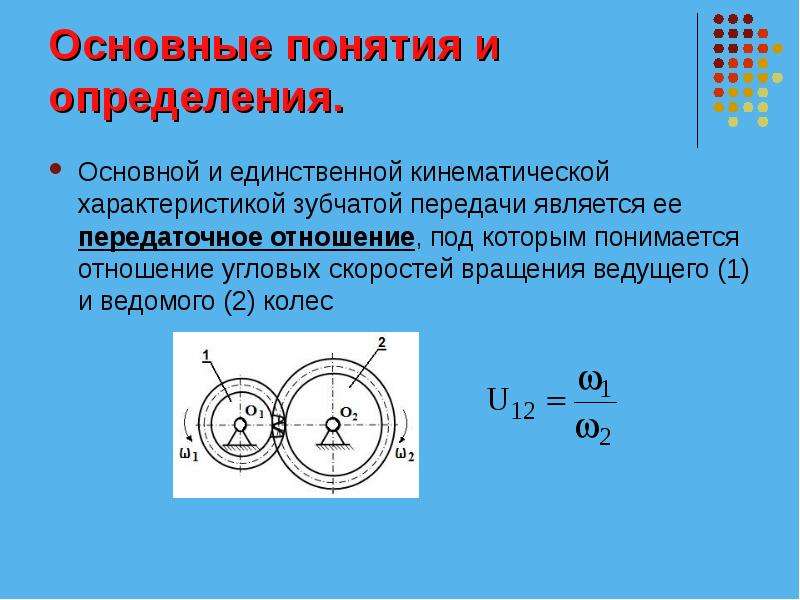 Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.
Шестерня привода вращается со скоростью 100 об/мин и крутящим моментом 10 Нм.
 Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.
Где количество зубьев на ведущей и ведомой шестернях 40 и 10 соответственно с одной составной шестерней. Составная шестерня имеет одну шестерню, соединенную с ведущей шестерней с 30 зубьями, и другую шестерню, соединенную с ведомой шестерней с 20 зубьями.