Передаточное число зубчатой передачи: Зубчатые передачи

alexxlab | 21.05.2023 | 0 | Разное

Передаточное число редуктора

Передаточное отношение – это соотношение угловых скоростей или крутящих моментов валов (в зависимости от строения механизма).
Передачи применяются для того, чтобы передать вращающий момент от электродвигателя к исполнительному устройству. Почему это необходимо? Дело в том, что сам мотор обычно не может передать требуемый вращающий момент, кроме того, частота вращения вала электродвигателя оказывается слишком велика, поэтому её надо понизить. Для этого и сконструированы понижающие передачи, редукторы. Таким образом удаётся изменить сразу и частоту вращения вала, и крутящий момент.

Передачи с крутящим моментом

Механизм передачи крутящего момента — редуктор — имеет входной и выходной валы.
Существует два способа передачи вращающего момента: жёсткий (момент передается жесткими звеньями, например, шестернями) и фрикционный (момент передается силами трения, работающих на поверхностях вала, например, ременная передача). Также есть возможность совмещать эти способы передачи.
Характеристика зубчатой передачи редуктора
Зубчатая передача редуктора – это механизм, состоящих из отдельных звеньев для передачи мощности через вращение зубчатых колёс. Такую зубчатую передачу используют в механических редукторах для преобразования движения.
Зубчатые редукторы очень часто задействуют в машиностроении. Именно их выбирают благодаря большому количеству преимуществ: высокому КПД, долгому сроку службы механизма, маленьким габаритам, постоянству передаточного отношения, простой и надёжной конструкции.
Также у этих редукторов есть и недостатки. К ним относят шум при больших скоростях и большие размеры редукторов, если передаточные отношения велики. Тем не менее, плюсов их использования гораздо больше, чем минусов, что и определяет итоговую востребованность.

Многоступенчатые редукторы

Как известно, современные электродвигатели выдают частоту ведущего вала примерно в районе полутора тысячи (1500) оборотов в минуту. А конечным потребителям в цепочке передачи движения обычно требуется куда меньшая частота. Стоит рассмотреть для лучшего понимания на конкретном примере. Возьмём, скажем, ленту транспортёра. Она движется медленно. Как же сделать так, чтобы надежно передать вращающий момент от электродвигателя к конечному устройству?
Здесь на помощь как раз и придут многоступенчатые редукторы. Наличие нескольких ступеней позволяет сделать компактное устройство, значительно снижающее частоту вращения вала.

Как правильно рассчитать передаточное число

Передаточное число многоступенчатого редуктора вычисляется как произведение передаточных чисел каждой ступени. Пример. В редукторе четыре зубчатые пары, передаточные отношения каждой из которых тоже равны 4. Общее передаточное число тогда будет равно 4х4х4х4 = 256.
В общем случае общее передаточное отношение редуктора равно отношению частоты вращения входного (ведущего) вала и частоты вращения ведомого (выходного) вала. Отсюда следует, что если выходной вал вращается медленнее входного, то передаточное отношение будет больше единицы. Такие передачи называют понижающими. Если же скорость выходного вала будет выше скорости входного вала, то передаточное число будет меньше единицы. В этом случае говорят о повышающей передаче или мультипликаторе.
При передаче движения всегда соответственно меняется и крутящий момент: если передача понижающая, то момент увеличивается, если повышающая, то уменьшается. Поэтому передаточное число можно представить как отношение крутящего момента на выходе к крутящему моменту на входе в редуктор.

Расчёт без учета сопротивления

Любой редуктор состоит из зубчатых пар. Чтобы рассчитать передаточное число каждой пары, надо разделить количество зубьев ведущего колеса на количество зубьев ведомого колеса.

Важно! При этом надо смотреть, меняется ли направление вращения шестеренки. Если меняется, то передаточное отношение принимается со знаком минус, если не меняется, то плюс. Направление вращения не меняется, если у колеса нарезка зубьев сделана внутри колеса.

Если в передаче участвует так называемая паразитка, то она в расчете передаточного отношения не участвует, так как ее задача лишь менять направление движения.
Также при расчете передаточных отношений можно использовать наружный диаметр шестерни. Иногда это удобно, если посчитать число зубьев затруднительно. Важно: зубчатая передача жесткая, здесь нет проскальзывания, как в ременной передаче, поэтому передаточное число всегда можно рассчитать с абсолютной точностью.
Если в редукторе применен червячный редуктор, то его передаточное отношение определяется как отношение числа зубьев ведущего колеса к числу заходов (витков) червяка. Чаще всего у червяка один заход, поэтому ясно: передаточное отношение червячной пары огромно, а вращающий момент может повышаться в десятки раз.

КПД зубчатой передачи

Преимуществами данной передачи считаются:

1. Большая и неограниченная мощность.
2. Небольшая масса и габариты.
3. Большой коэффициент полезного действия (приблизительно 0,95-0,99).
4. Надёжны, но нуждаются в большой точности изготовления.

КПД определяется как отношение реально полученной энергии к потребленной. Чем выше КПД механизма, тем больше энергии преобразовывается на полезные цели, тем меньше потери, тем эффективнее механизм.
Учёные всего мира постоянно ведут борьбу именно за сокращение непроизводительных потерь. Чтобы обеспечить хорошую работу машины с большим КПД, можно использовать масла с различными свойствами при больших изменениях температуры среды. При экспериментах с различными видами масла совместно с допустимой нагрузочной способности зубчатых передач на рабочих поверхностях зубьев не обнаружили развитие процесса разрушения, что обеспечивает отличные технико-экономические показатели машины.

Важно! КПД зубчатой передачи сильно зависит от точности изготовления зубчатых колес. В случае грубых нарушений геометрии в редукторе будут большие расходы энергии, он будет нагреваться, его КПД значительно упадёт. Поэтому редукторы следует приобретать только у проверенных производителей.

Постоянное и переменное передаточное отношение редуктора

Передаточное отношение может быть как постоянным, так и переменным. При переменном случае оно может меняться бесступенчато или ступенчато. В промышленности нашли применение обе эти схемы. Если передаточное число меняется плавно, то такое устройство называют вариатором. Эти устройства дороги и требуют точной сборки и квалифицированного обслуживания. Но всё это оправдывается конечным результатом – их полезность уже проверена временем.

Передаточное число составной зубчатой передачи Калькулятор

✖Произведение количества зубьев на ведомых колесах – это величина, полученная путем умножения количества зубьев на ведомых колесах.ⓘ Произведение количества зубьев на ведомом [Pdriven]			+10% -10%
✖Произведение количества зубьев на приводе – это значение, полученное путем умножения количества зубьев на приводе.ⓘ Произведение количества зубьев на драйверах [Pdriver ]			+10% -10%

✖Отношение скоростей – это расстояние, на которое перемещается какая-либо часть машины, к той, на которую за то же время перемещается движущая часть. ⓘ Передаточное число составной зубчатой передачи [i]

⎘ копия

👎

Формула

сбросить

👍

Передаточное число составной зубчатой передачи Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Произведение количества зубьев на ведомом: 16 –> Конверсия не требуется
Произведение количества зубьев на драйверах: 27 –> Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

0. 592592592592593 –> Конверсия не требуется

< 13 Поезда передач Калькуляторы

Выходной крутящий момент на ведомом элементе с учетом угловой скорости ведомого и приводного элемента

Идти Выходной крутящий момент или крутящий момент нагрузки на ведомом элементе = (Входной крутящий момент на ведущем элементе)*(Угловая скорость приводного элемента в об/мин/Угловая скорость ведомого элемента в об/мин)

Выходной крутящий момент или момент сопротивления или нагрузки на ведомом элементе

Идти Выходной крутящий момент или крутящий момент нагрузки на ведомом элементе = -(Входной крутящий момент на ведущем элементе)*(Угловая скорость ведущего звена/Угловая скорость ведомого элемента)

Удерживающий, тормозной или фиксирующий момент на неподвижном элементе

Идти Общий крутящий момент = Входной крутящий момент на ведущем элементе*((Угловая скорость приводного элемента в об/мин/Угловая скорость ведомого элемента в об/мин)-1)

Торможение или удержание крутящего момента на фиксированном стержне при заданном входном крутящем моменте

Идти Общий крутящий момент = Входной крутящий момент на ведущем элементе*((Угловая скорость ведущего звена/Угловая скорость ведомого элемента)-1)

Удержание, торможение или фиксация крутящего момента на фиксированном стержне при заданном входном и выходном крутящем моменте

Идти Общий крутящий момент = -(Входной крутящий момент на ведущем элементе+Выходной крутящий момент или крутящий момент нагрузки на ведомом элементе)

Передаточное число составной зубчатой передачи

Идти Коэффициент скорости = Произведение количества зубьев на ведомом/Произведение количества зубьев на драйверах

Значение поезда составной зубчатой передачи с учетом произведения зубьев на ведомой и ведущей шестернях

Идти Стоимость поезда = Произведение количества зубьев на драйверах/Произведение количества зубьев на ведомом

Отношение скоростей составного ременного привода, заданное произведением диаметра ведомого

Идти Коэффициент скорости = Произведение диаметров драйверов/Произведение диаметров приводов

Соотношение скоростей составного ременного привода

Идти Коэффициент скорости = Скорость последнего ведомого шкива/Скорость первого водителя

Значение поезда составной зубчатой передачи с учетом скорости ведомой и ведущей шестерни

Идти Стоимость поезда = Скорость последнего ведомого шкива/Скорость первого водителя

Соотношение скоростей

Идти Коэффициент скорости = Количество зубьев на ведомом/Кол-во зубьев на драйвере

Значение поезда с заданным количеством зубьев

Идти Стоимость поезда = Кол-во зубьев на драйвере/Количество зубьев на ведомом

Значение поезда с учетом скорости ведомого и водителя

Идти Стоимость поезда = Скорость последователя/Скорость водителя

Передаточное число составной зубчатой передачи формула

Коэффициент скорости = Произведение количества зубьев на ведомом/Произведение количества зубьев на драйверах
i = P_driven/P_driver

Что такое передаточное число?

Передаточное число (или отношение скоростей) зубчатой передачи – это отношение скорости водителя к скорости ведомого или ведомого (или) отношение скоростей любой пары шестерен в зацеплении является обратным их количеству. зубы.

Share

Copied!

Выбор правильного передаточного числа рыболовной катушки

Покупка новых рыболовных катушек ошеломляет многих рыболовов, так как обилие вариантов может замутить воду. Одним из важных решений является выбор катушки с правильным передаточным числом. Понимание передаточных чисел в рыболовных катушках повысит вашу эффективность на воде и снизит уровень стресса, когда вы сталкиваетесь с важным решением о покупке.

Передаточное отношение катушки измеряется количеством оборотов шпули при каждом отдельном обороте рукоятки. Например, если передаточное число катушки составляет 6,4:1, каждый раз, когда вы поворачиваете ручку, шпуля внутри поворачивается ровно 6,4 раза.

В результате катушка с передаточным числом 5,1:1 будет намного медленнее, чем катушка с передаточным числом 7,1:1 — шпуля катушки с передаточным числом 5,1:1 будет вращаться 5,1 раза при каждом повороте рукоятки. , в то время как шпуля 7,1:1 будет поворачиваться 7,1 раза при каждом повороте рукоятки.

Также полезно знать IPT катушки или количество дюймов на оборот. Это мера того, сколько лески втягивается в катушку за один поворот ручки. Это также может означать, что катушка с передаточным числом, которая претендует на звание самой быстрой, на самом деле может быть такой же, как и другие высокоскоростные катушки. Это не обязательно означает, что за один оборот она наматывает больше лески, чем катушка 7,1:1 — это также зависит от катушки и размера лески.

( 1 из 4)

Катушка с низким передаточным числом | от 5,1:1 до 5,4:1

Катушка с более низким передаточным числом идеально подходит для больших наживок, которые сильно тянут, таких как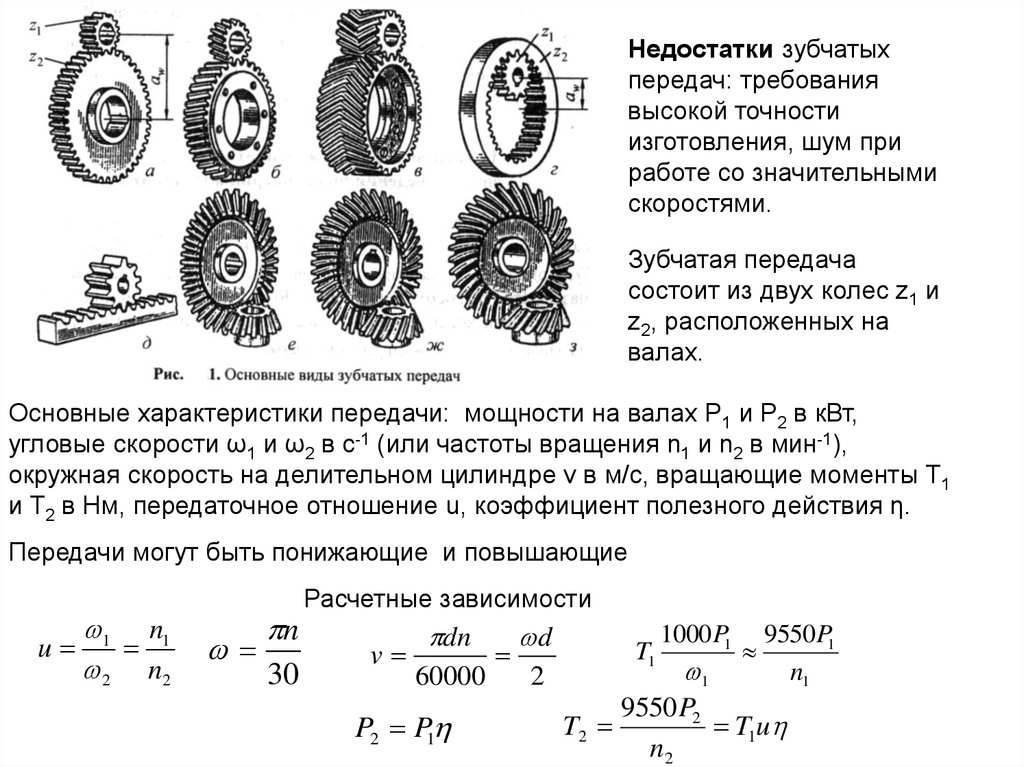

Deep Crankbaits . Эти катушки имеют самый высокий крутящий момент, что позволяет вам прилагать меньше усилий для извлечения наживки и больше энергии для поиска рыбы.

Эти катушки также отлично подходят для медленного проката больших и тяжелых приманок, таких как спиннербейты и свимбейты . В холодной воде , когда басы особенно осторожны, низкое передаточное число идеально подходит для этих более медленных, не угрожающих презентаций. Медленная катушка также помогает дольше удерживать эти приманки в зоне удара, что может оказаться неоценимым при ловле на подвижные приманки в глубокой воде.

• Глубокие воблеры
• Большие приманки
• Глубоководные блесны

 

( 2 из 4)

Катушка со средним передаточным числом | от 6,1:1 до 6,4:1

Эти катушки для ловли окуня отлично подходят для различных техник и презентаций, что делает их очень популярными среди рыболовов. Пробираетесь ли вы через отвратительное укрытие с квадратным клювом во время перед нерестом или бомбите спиннербейтами на мелководье осенью подойдет катушка со средним передаточным числом.

Я предпочитаю барабан 6,4:1 всякий раз, когда использую что-либо, вызывающее ответный удар. Дополнительная скорость позволяет мне быстро ловить наживку, заставляя реагировать самую агрессивную рыбу. И наоборот, я выберу катушку 6,1: 1 при ловле на воблеров, которые работают в диапазоне от 8 до 14 футов. Небольшое снижение скорости помогает дольше удерживать их в зоне удара, сохраняя при этом достаточную скорость, чтобы вызвать ответный удар, и дает мне дополнительный крутящий момент

• Воблеры Squarebill
• Воблеры средней глубины
• Мелкие блесны
• Неглубокие складные зонты

Катушка На фото: Катушка Abu Garcia REVO X Gen 4

( 3 из 4)

wired2fish.com/fishing-tips/choosing-the-right-gear-ratio-fishing-reel/#slide_2″ data-url-slide=”https://www.wired2fish.com/fishing-tips/choosing-the-right-gear-ratio-fishing-reel/#slide_3″ data-layer-triggered=”0″> Катушка с высоким передаточным числом | от 7,1:1 до 8,1:1

Если вы ловите любую приманку для ловли окуня, которая в основном работает с вашей удочкой, вам подойдет катушка с высоким передаточным числом. Вы часто подтягиваете наживку кончиком удилища , но вам нужно иметь возможность быстро подтягиваться при поклевке. Быстрая катушка также помогает при борьбе с большим окунем — вам нужна вся скорость, которую вы можете получить, чтобы быстро увести его от любых опасностей, связанных с изнашиванием лески.

Topwaters, джеркбейты, джиг , пластик и даже лучшие безгубые воблеры гарантирует использование высокоскоростной катушки. Эти приемы сильно провисают в вашей леске, и если вы получаете поводок в 30 ярдах от лодки, вам пригодится высокое передаточное число, чтобы получить надежный крючок.

• Джиги и большие червяки
• Трясущиеся головки
• Техасские буровые установки
• Буровые установки Каролина
• Топуотерс
• Джеркбейты
• Безгубые воблеры

Катушка На фото: Катушка Daiwa Tatula 100 Casting

( 4 из 4)

Заключительные мысли

Выбор правильной катушки для ловли окуня может быть немного запутанным, но с некоторым базовым пониманием того, что на самом деле означают цифры, это становится намного проще понять. Покупая следующую катушку, постарайтесь не усложнять задачу, запомнив это простое руководство по передаточному числу.

Как работают передаточные числа?

Передаточные числа — это основная наука, стоящая почти за каждой машиной в современную эпоху. Они могут максимизировать мощность и эффективность и основаны на простой математике. Итак, как они работают?

Если вы работаете с передаточными числами каждый божий день, этот пост, вероятно, не для вас. Но если вы хотите улучшить свое понимание этого важного элемента конструкции машины, продолжайте читать.

Передаточные отношения просты, если вы понимаете некоторые математические операции, лежащие в основе кругов. Я избавлю вас от школьной математики, но важно знать, что длина окружности связана с диаметром окружности. Эта математика важна при расчете передаточного числа.

Основы расчета передаточных чисел и передаточного отношения

Чтобы понять передаточные числа, проще всего начать с удаления зубьев с шестерен. Представьте себе два круга, катящихся друг против друга и не допускающих проскальзывания, как в школе физики 1. Задайте диаметр первого круга 2,54 дюйма . Умножив это на число пи, мы получим длину окружности 8 дюймов или, другими словами, один полный оборот окружности даст 8 дюймов смещения.

Задайте диаметр второй окружности .3175 дюймов , что даст нам длину окружности 1 дюйм . Если эти два круга катятся вместе, они будут иметь передаточное число 8:1, так как первый круг имеет длину окружности 8 раз большую, чем второй круг. Передаточное отношение 8:1 означает, что второй круг совершает 8 оборотов по за каждый один оборот первого круга. Не засыпай еще на мне; мы будем становиться все более и более сложными.

Шестерни не круги, потому что, как вы знаете, у них есть зубья. Шестерни должны иметь зубья, потому что в реальном мире нет бесконечного трения между двумя катящимися кругами. Зубья также облегчают достижение точных передаточных чисел.

Вместо того, чтобы иметь дело с диаметрами шестерен, вы можете использовать количество зубьев на шестерне для достижения очень точных передаточных чисел. Передаточные числа никогда не являются произвольными значениями, они сильно зависят от необходимого крутящего момента и выходной мощности, а также от прочности шестерни и материала. Например, если вам нужно передаточное число 3,57:1 , можно было бы разработать две совместимые шестерни , одну с 75 зубьями , а другую с 21 .

СВЯЗАННЫЕ: ЭТОТ ТУРБОВЕНТИЛЯТОР С РЕДУКТОРОМ НА 15 ПРОЦЕНТОВ ЭФФЕКТИВНЕЕ, ЧЕМ ДРУГИЕ САМОЛЕТНЫЕ ДВИГАТЕЛИ

Другим важным аспектом, влияющим на использование зубьев в шестернях, являются производственные допуски. Большинство шестерен могут быть изготовлены с довольно широкими допусками, и мы знаем, что чем уже становится допуск, тем дороже их производство. Зубья позволяют несколько варьировать изготовление шестерен с заданными диаметрами, что означает более дешевое производство. По сути, зубья становятся буфером, который допускает дефекты в производстве зубчатых колес.

Расчет передаточных чисел при проектировании машин

Хотя базовое передаточное число довольно просто понять, оно может оказаться намного сложнее. Большие промежутки зубчатых колес, называемые зубчатыми передачами, часто необходимы в конструкции машин. Они состоят из множества шестерен, которые часто укладываются друг на друга или укладываются друг за другом. Зубчатые передачи необходимы для достижения более надежных передаточных чисел, а также для влияния на направление вращения. Поскольку две соединенные шестерни будут вращаться в противоположных направлениях, зубчатые передачи часто необходимы для передачи мощности через определенные отношения, не влияя на вращение.

Например, использование трехступенчатой ​​зубчатой ​​передачи , с передаточным числом 1:5, даст 2500% увеличение скорости вращения, сохраняя при этом выходное направление в том же направлении, что и входное. Чтобы привести более конкретный пример, двигатель, который подал 100 об/мин на начальный конец этой зубчатой ​​передачи, выдаст 2500 об/мин на другом конце в том же направлении. Вы также можете изменить направление подачи питания и уменьшить 2500 об / мин 9.0012 на мощность 100 об/мин . Эти изменения позволяют регулировать как крутящий момент, так и скорость.

Самые популярные

ОПЕРЕДАЙТЕ СВОИХ КОЛЛЕКТИВОВ С BLUEPRINT

Подписываясь, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности.

СВЯЗАННЫЕ С: ФУТУРИСТИЧЕСКАЯ РОССИЙСКАЯ ПЕХОТНАЯ СНАРЯЖЕНИЕ ПОЛУЧАЕТ АТОМНО-УСТОЙЧИВЫЙ ОБНОВЛЕНИЕ

Более сложные комбинации шестерен и передаточных чисел дают некоторые интересные конструкции машин. Теоретически передаточные числа просты, но как инженер вы можете оказаться вовлеченным в сложные конструкции зубчатых передач, которые кажутся немного сложными. Как и в случае с другими инженерными навыками, для полного развития навыков проектирования передаточных чисел требуется время.

Трансмиссии – практическое применение передаточных чисел

Трансмиссии являются одними из лучших примеров практического применения передаточных чисел. Любой, кто ездил на автомобиле или другом моторизованном транспортном средстве, в той или иной форме извлек пользу из трансмиссии. И каждая трансмиссия — это, по сути, просто набор шестерен и передаточных чисел, тесно связанных друг с другом. Посмотрите невероятно полезное видео от Learn Engineering ниже, чтобы узнать больше о том, как работают механические коробки передач.

Важно отметить, что, хотя механические коробки передач теряют популярность у автопроизводителей, поскольку их нелегко интегрировать в гибридные или электрические автомобили, они работают почти так же, как и автоматические коробки передач, в том, что касается передачи.