Период гармонических колебаний пружинного маятника: Период колебаний пружинного маятника – формула для свободных и незатухающих колебаний

alexxlab | 08.07.2023 | 0 | Разное

Период колебаний пружинного маятника – формула для свободных и незатухающих колебаний

4.7

Средняя оценка: 4.7

Всего получено оценок: 86.

4.7

Средняя оценка: 4.7

Всего получено оценок: 86.

Одной из простейших колебательных систем, удобных для изучения, является пружинный маятник. Рассмотрим его подробнее, получим формулу периода колебаний.

Пружинный маятник

Идеальный пружинный маятник представляет собой некоторую точечную массу $m$, которая закреплена на одном конце пружины с постоянной жесткостью $k$, а другой конец пружины – закреплен к неподвижной опоре. Больше никакие силы на пружинный маятник не действуют, и он способен к совершению свободных незатухающих колебаний.

Рис. 1. Горизонтальный пружинный маятник.

Уравнение движения пружинного маятника

Пусть начало координат находится в точке покоя маятника. Тогда, если маятник выведен из состояния равновесия на расстояние $x$, со стороны пружины на него начинает действовать сила $F=-kx$.

Знак «минус» означает, что направление действия этой силы противоположно смещению маятника.

Согласно второму закону Ньютона, если на тело действует сила, то оно приобретает ускорение:

$$a=-{kx\over m}$$

Скорость – это производная координаты. А ускорение – производная скорости. Следовательно, ускорение – это вторая производная координаты. Получим уравнение:

$$x”=-{k\over m}x$$

То есть, вторая производная координаты пропорциональна самой координате, взятой с противоположным знаком. Это дифференциальное уравнение, и в высшей математике доказывается, что единственная функция, являющаяся его решением – это круговая функця (синус или косинус).

Полное же решение данного уравнения выглядит следующим образом:

$$x(t)=A cos \sqrt{k\over m}t$$

Если взять вторую производную этой функции, то можно убедиться, что она равна самой себе, с противоположным знаком и необходимым коэффициентом.

Период колебаний маятника

Сравним полученное уравнение с уравнением гармонических колебаний:

$$x(t)=A cos( \omega t+\varphi)$$

Можно видеть, что фаза $\varphi$ в уравнении координаты движения маятника равна нулю, а коэффициент $\sqrt {k\over m}$ представляет собой круговую частоту.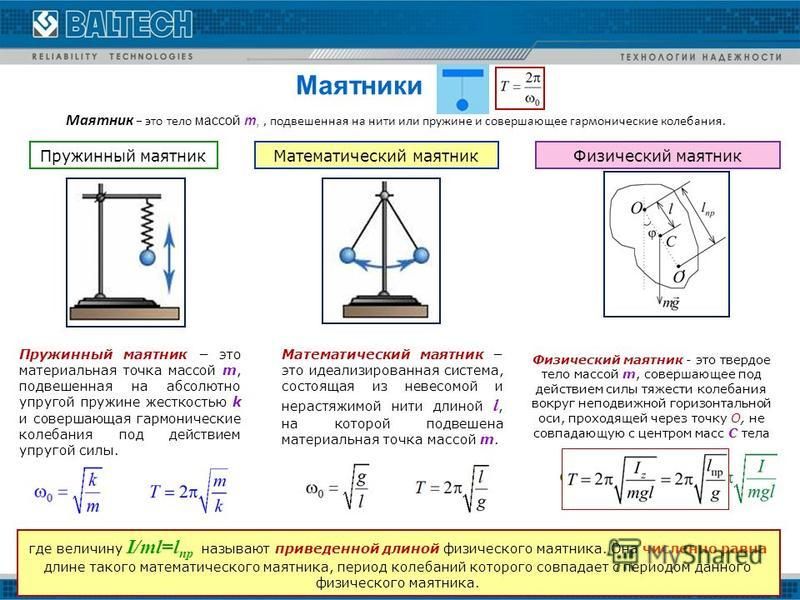 Учитывая формулу, связывающей круговую частоту и период, получим формулу периода колебаний пружинного маятника:

$$T={2\pi \over \omega}=2\pi\sqrt {m\over k}$$

Действительно, чем больше масса пружинного маятника, тем дольше будут совершаться колебания. А чем больше жесткость пружины, тем период колебаний будет меньше. Но величины эти связаны с периодом не прямо, а через коренную зависимость, то есть, для увеличения периода маятника вдвое, надо либо увеличить массу маятника вчетверо, либо во столько же раз уменьшить жесткость пружины.

Рис. 2. Период колебаний пружинного маятника.

В реальности на маятник всегда действует сила тяжести, кроме того, в нем происходят потери, связанные с трением и нагревом пружины. Поэтому, его колебания будут затухающими, а их период будет немного отличаться от расчетного. Наиболее близким к идеальному пружинному маятнику является механизм часового балансира.

Рис. 3. Часовой балансир.

Что мы узнали?

Пружинный маятник – это точечная масса, двигающая под воздействием пружины постоянной жесткости. Период колебаний пружинного маятника пропорционален корню из отношения его массы к жесткости пружины.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 86.

---

А какая ваша оценка?

Белорусский государственный университет транспорта – БелГУТ (БИИЖТ)

Регистрация на конференцию «Феноменология транспорта
в литературе и искусстве: прошлое, настоящее, будущее»

Как поступить в БелГУТ

Как получить место

в общежитии БелГУТа

ГОРЯЧАЯ ЛИНИЯ 
по вопросам приемной кампании

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
					1	2
3	4	5	6 Дата : 2023-04-06	7 Дата : 2023-04-07	8	9
10 Дата : 2023-04-10	11	12	13 Дата : 2023-04-13	14	15	16
17 Дата : 2023-04-17	18	19 Дата : 2023-04-19	20 Дата : 2023-04-20	21 Дата : 2023-04-21	22	23
24	25	26 Дата : 2023-04-26	27 Дата : 2023-04-27	28	29	30

Все анонсы

• Вопросы к собеседованию для прошедших обучение в Н. ..
• Дни доноров 26 и 27 апреля 2023
• Смотр-кастинг конкурса «Мисс и Мистер БелГУТа»…
• ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …
• Билеты на концерт Дианы Анкудиновой…
• Музыкальный квартирник
• Программа. V Международная научно-практическая кон…
• Программа. I Международная научно-практическая кон…
• ЕДИ «Ключевые аспекты послания Президента Республ…
• Игра между сборными командами БелГУТа и БГЭУ…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Вопросы к собеседованию для прошедших обучение в Н…

Дни доноров 26 и 27 апреля 2023

Смотр-кастинг конкурса «Мисс и Мистер БелГУТа»…

ФИНАЛ весенней серии игр «ЧТО? ГДЕ? КОГДА?» среди …

Новости

Университет

Международные связи

Спорт

ИВР

Жизнь студентов

Новости подразделений



• Воспитательная работа

IX Международная научно-практическая конференция «Инновационный опыт и.

..
26 апреля 2023

• Воспитательная работа

VI Пленум Гомельского городского комитета БРСМ…
26 апреля 2023

• Университет

Профориентационная работа в Новозыбкове и Клинцах…
25 апреля 2023

• Воспитательная работа

26 апреля 1986…
25 апреля 2023

• Спорт

Открытие велосипедного сезона
24 апреля 2023

• Воспитательная работа

Сделаем чище свой Дом!
23 апреля 2023

• Университет

Повышение квалификации бухгалтеров Белорусской железной дороги. ..
21 апреля 2023

• Университет

Лекторский потенциал – достояние университета!…
21 апреля 2023

• Воспитательная работа

Послание Президента обсудили с молодежью Жлобинщины…
21 апреля 2023

Другие новости

• На форуме ТИБО-2023 «Цифровое развитие Беларуси»…
• Спартакиада вузов по гиревому спорту
• Дорогами мира и созидания. Мемориал в д. Бацунь…
• Встреча с председателем ЦИК Беларуси
• С юбилеем! Борис Валерьевич Рябцев
• Образование на всю жизнь
• Неделя леса – БелГУТ посадил дубовую рощу…
• «Праздник Светлой Пасхи» в БелГУТе
• Эстафета «Живая память благодарных поколений» передана дальше…
• Победа БелГУТа в матче Республиканской студенческий футбольной лиги. ..
• Диалоговая площадка, посвященная обсуждению послания президента Респуб…

БелГУТ на Доске почета

Достижения университета

КУДА ПОСТУПАТЬ

Все факультеты

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

ньютоновская механика – Пружинный маятник – почему можно использовать это уравнение?

спросил 6 лет, 11 месяцев назад

Изменено 6 лет, 11 месяцев назад

Просмотрено 2к раз

$\begingroup$

Известно, что при описании пружинного маятника мы обязаны пользоваться формулой $T = 2\pi \sqrt{m/k}$, однако можно пойти дальше и положить

$\omega = \frac{2\pi}{T}$
Я размышляю, почему эта замена законна, ведь в этом маятнике нет углового движения!

• ньютоновская механика
• гармонический осциллятор
• частота
• пружина

$\endgroup$

2

$\begingroup$

В этом уравнении $\omega$ относится не к скорости углового движения, а к частоте колебаний, измеренной в угловых единицах (обычно в радианах/сек, но может быть и в градусах/сек). Частота обычно измеряется в циклах в секунду (Герцах), но иногда ее удобнее измерять в угловых единицах, когда ее называют угловой частотой.

Угол, который здесь измеряется, является фазовым углом, который описывает, как далеко за цикл прошло колебание, как если бы колебание двигалось по кругу с постоянной угловой скоростью $\omega$.

Вы можете быть сбиты с толку, потому что не видите никакого углового движения в «пружинном» маятнике. Но это еще более запутанно, когда имеешь дело со «струнным» маятником, потому что здесь смещение измеряется углом $\theta$, но этот угол не совпадает с фазовым углом (который обычно называют $\phi$, т.е. греческое фи для фазы). Угловая скорость равна $\large{\frac{d\theta}{dt}}$, что обычно называют $\omega$, но это $\omega=\large{\frac{d\theta}{dt}} $ не совпадает с угловой частотой $\omega=\large{\frac{d\phi}{dt}=\frac{2\pi}{T}}$. Угловая скорость во время колебаний изменяется от $0$ в крайних точках до максимальной при прохождении через вертикаль. Но угловая частота при колебании не меняется, она является постоянной величиной для идеальных струнных или пружинных маятников, зависящей от $\large{\frac Lg}$ или $\large{\frac km}$.

$\endgroup$

$\begingroup$

Представьте себе точку $P$, движущуюся по окружности радиуса $R$ с угловой скоростью $\omega$.

Проекция $P$ на ось $y$:

$$y=R\sin \theta=R\sin \omega t$$

Точка $P’$ находится в простых гармонических колебаниях (ШО).

Для системы пружинных масс так получилось, что:

$$x=A\sin \omega t$$ где: $$\omega=\sqrt{\frac{k}{m}}$$

Итак, хотя в пружинной массе SHO нет углового движения, по аналогии с SHO точки $P’$ мы все же называем его угловой скоростью.

$\endgroup$

$\begingroup$

Уравнение для периода $T$ получено путем использования второго закона Ньютона $F=ma$ для получения уравнения движения системы пружина-масса

$$-kx =ma \Rightarrow a=-\frac k m$ $

, где $x$ — смещение от фиксированной точки, а $a$ — ускорение. 92 x$, где $\omega$ — константа простого гармонического движения.

Можно показать, что для простого гармонического движения $ T = \frac{2 \pi}{\omega}$, что дает $T=2\pi \sqrt{\frac{m}{k}}$.

Возможным уравнением для смещения массы как функции времени $t$ является $x= \sin \omega t$.

Так как углы обычно измеряются в радианах, а время в секундах, единицей постоянной $\omega$ является радиан в секунду.

Таким образом, в этом случае движение массы является линейным, и причина, по которой появляется единица измерения угла, радиан, заключается в том, что функция синуса является частью уравнения для смещения.

Ваша путаница, вероятно, связана с тем, что вы встретили тот же символ $\omega$, что и угловая скорость, которая также имеет единицу радиан в секунду и то же уравнение $T=\frac{2\pi}{\omega }$ при круговом движении.

$\endgroup$

ньютоновская механика – Почему период времени маятника с пружиной постоянной силы $k$ и грузом значительной массы $m$ на Луне такой же, как и на Земле?

Задавать вопрос

спросил 2 года 5 месяцев назад

Изменено 2 года, 4 месяца назад

Просмотрено 433 раза

$\begingroup$

Вопрос, с которым я столкнулся сегодня в классе:

Как изменится период времени нагруженной пружины, когда ее доставят на Луну? 9\frac{1}{2}$$

$T$ в этом выражении не зависит от $g$. Таким образом, период времени нагруженной пружины на Луне будет таким же, как и на Земле.

Мои мысли

Я думаю, что значение $k$ для пружины, подвешенной вверх ногами, зависит от гравитационного притяжения. Из закона Гука получаем, что возвращающая сила пружины линейно зависит от смещения.

$$ F(x) = -k(x) \\ k = \frac{-F(x)}{x} $$

Когда масса подвешена вертикально, $x$ зависит от гравитационного притяжения $g $. 9\frac{1}{4} $$

Таким образом, период времени на Луне будет немного больше, чем на Земле. Может ли кто-нибудь сказать мне, правильно ли я это сделал?

• ньютоновская механика
• ньютоновская гравитация
• гармонический осциллятор
• пружина
• осцилляторы

$\endgroup$

$\begingroup$

Обратите внимание, что масса $m$ и жесткость пружины $k$ на Земле такие же, как и на Луне. Следовательно, период времени пружины не зависит от разницы, вызванной ускорением силы тяжести. Следовательно, он не изменится, когда его доставят на Луну.

Я думаю, что значение 𝑘 для пружины, подвешенной вверх ногами, зависит от гравитационного притяжения

Нет. Это константа. Приведенный вами математический аргумент содержит много ошибок, но достаточно сказать, что период нагруженной пружины не будет отличаться.

Единственное, что будет отличаться, это положение равновесия массы, в этом случае на Луне она будет выше.

$\endgroup$

$\begingroup$

Чтобы проиллюстрировать независимость величины гравитационного поля, можно установить систему пружинных масс на горизонтальном столе, и при отсутствии трения период колебаний все равно будет $2\pi \sqrt{\frac mk}$ при условии, что пружина может подвергаться как сжатию, так и растяжению.

Причина такой независимости в том, что восстанавливающая сила, $F$, зависит от смещения массы из положения равновесия, на нее не действует результирующая сила, которая не является функцией гравитационного поля и массы $m$ , также не зависит от гравитационного поля, поэтому ускорение массы $a=\frac Fm$ не зависит от гравитационного поля.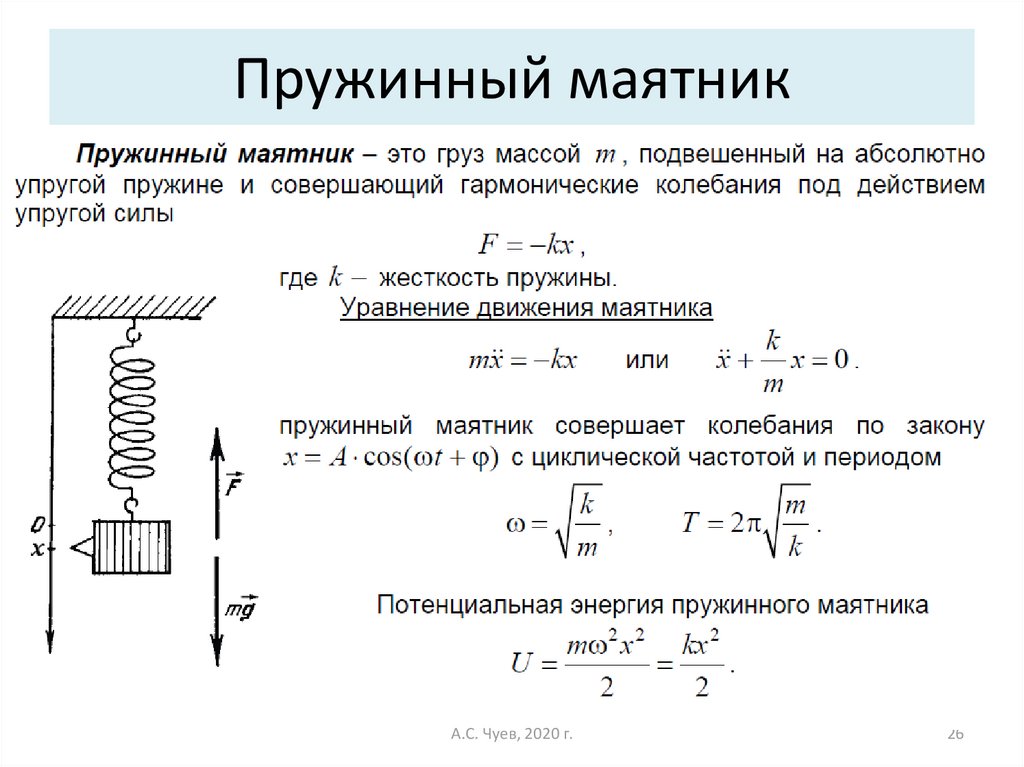

Соотношение $l$ и $g$, которое, по-видимому, показывает зависимость периода от силы гравитационного поля, не показывает этого, потому что $l$ и $g$ не независимы друг от друга и подобны уравнению $kl =mg$, так что $g$ увеличивается вместе с $l$ в той же пропорции.

$\endgroup$

$\begingroup$

… имеем, что возвращающая сила в пружине линейно зависит от смещения. $$F(x) = -k(x) \\ k = \frac{-F(x)}{x}$$

Этот расчет силы неверен.

Собственно сила ($F$) состоит из двух частей:

• Возвращающая сила пружины ($-kx$) который пропорционален текущему смещению ($x$). И константа пружины $k$ по-прежнему остается постоянной.
• Сила гравитации ($mg$) которое не зависит от текущего смещения ($x$)

Итак, у нас есть общая сила $$F=-kx+мг. \tag{1}$$

Согласно второму закону Ньютона ($m\ddot{x}=F$) получаем уравнение движения $$m\ddot{x}=-kx+mg.