Период колебаний физического маятника формула: Ничего не найдено для %25D0%25Ba%25D0%25Be%25D0%25Bb%25D0%25B5%25D0%25B1%25D0%25B0%25D0%25Bd%25D0%25B8%25D1%258F %25D0%25B8 %25D0%25B2%25D0%25Be%25D0%25Bb%25D0%25Bd%25D1%258B %25D0%25Bf%25D0%25B5%25D1%2580%25D0%25B8%25D0%25Be%25D0%25B4 %25D1%2584%25D0%25B8%25D0%25B7%25D0%25B8%25D1%2587%25D0%25B5%25D1%2581%25D0%25Ba%25D0%25Be%25D0%25B3%25D0%25Be %25D0%25Bc%25D0%25B0%25D1%258F%25D1%2582%25D0%25Bd%25D0%25B8%25D0%25Ba%25D0%25B0
alexxlab | 18.03.1987 | 0 | Разное
Лабораторная работа 112
Лабораторная работа № 112
Физический маятник
Цель работы: Экспериментальное определение ускорения свободного падения методом колебания физического маятника. Определение момента инерции физического маятника.
Приборы и принадлежности: универсальный маятник ФП-1, секундомер, линейка.
Теоретическое введение
В теории колебаний физическим маятником называется твердое тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр масс и способное совершать колебания относительно этой оси (рис.1).
Можно показать, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания.

Обозначим через J момент инерции маятника относительно оси О. Пусть точка С является центром масс. Силу тяжести можно разложить на две составляющие, одна из которых уравновешивается реакцией оси. Маятник приходит в движение под действием другой составляющей , величина, которой:
Для малых углов sina » a и выражение (1) запишем:
Знак минус означает, что сила направлена в сторону, противоположную отклонению маятника от положения равновесия.
Основное уравнение динамики вращательного движения для физического маятника запишется:
Момент силы относительно оси О с учетом (2):
где l
– расстояние от центра масс С до оси О.
Угловое ускорение маятника:
Поставив (4) и (5) в уравнение (3), получим:
откуда
Обозначив
получим:
По структуре уравнение (6) является дифференциальным уравнением гармонических колебаний с циклической частотой
Отсюда момент инерции физического маятника:
Величина
называется приведенной длиной физического
маятника, равной длине математического маятника, имеющего тот же период
колебаний, что и физический, т. е.
е.
Точка О1, лежащая на прямой, проведенной через точку подвеса О и центр масс С, на расстоянии приведенной длины l0 от оси вращения, называется центром качания маятника (рис.1). Центр качания лежит всегда ниже центра масс. Точка подвеса О и центр качания О1 сопряжены друг с другом, т.е. перенос точки подвеса в центр качания не меняет периода колебания маятника. Точка подвеса и центр качания обратимы, а расстояние между этими точками представляет собой приведенную длину l0 одного из типов физического маятника, так называемого оборотного маятника.
Обозначим через J0 момент инерции маятника относительно оси, проходящей через его центр масс. На основании теоремы Штейнера момент инерции J относительно любой оси, параллельной первой:
где m
– масса маятника, l
– расстояние между осями.
Тогда при подвешивании маятника за точку подвеса О период колебаний:
а при подвешивании за центр качания О1, когда маятник находится в перевернутом положении, период:
где l2 и l1 – расстояние между центром масс и соответствующими осями колебаний.
Из уравнений (9) и (10):
откуда:
Формула (11) остается
справедливой при колебаниях маятника относительно двух произвольных осей О и О /, не обязательно сопряженных, но
расположенных по разные стороны от центра масс маятника.
Описание рабочей установки и метода измерений.
Для определения ускорения свободного падения применяется прибор ФП-1 (рис.2),
состоящий из
настенного кронштейна 1, на котором смонтированы подушки 2 опорных призм и
физического маятника представляющего собой однородный металлический стержень
11, на котором крепятся чечевицы 5 и 9. Чечевица 9 закреплена жестко и является
неподвижной. Чечевица 5, находящаяся на конце стержня, может перемещаться по
шкале 3 с нониусом 4 и фиксируется в нужном положении винтом 6. Маятник можно
подвешивать на опорные призмы 7 и 10. В комплект прибора входит специальная
подставка для определения положения центра масс маятника. Перемещением
чечевицы 5 можно добиться равенства периодов колебаний маятника при подвесе
его на опорные призмы 7 и 10, и тогда оси колебаний становятся сопряженными,
расстояние между опорными призмами становится равным приведенной длине
физического маятника.
Величина ускорения свободного падения определяется на основе формулы (11). Эксперимент сводится к измерению величин Т1, Т2, l1, l2. Формула (8) является исходной для определения момента инерции физического маятника.
Ход работы
1) Определение ускорения свободного падения.
1. Подвесить маятник на опорную призму 7, отклоняют на небольшой угол и измеряют секундомером время t1 30-50 полных колебаний. Опыт повторяют не менее 5 раз и находят среднее значение времени <t1> выбранного числа колебаний.
2. Определяют период колебания:
где n – число колебаний.
3. Для нахождения положения
центра масс маятника снять его с подушек опорных призм и балансировать на
горизонтальном ребре призмы, укрепленном на столе до тех пор, пока моменты сил тяжести, действующие на правую и левую часть маятника
окажутся равными. В случае равновесия центр масс маятника будет расположен
в стержне против точки опоры. Не снимая маятник с ребра призмы, линейкой
измеряют расстояние l1
В случае равновесия центр масс маятника будет расположен
в стержне против точки опоры. Не снимая маятник с ребра призмы, линейкой
измеряют расстояние l1
4. Перевернув маятник, подвешивают его на опорную призму 10. Выбрать то же число колебаний n и, повторить опыт не менее 5 раз, находят период колебания:
При этом измеренные значения периодов Т1 и Т2 должны отличаться не более чем на 5%
5. Найти расстояние l2 между ребром опорной призмы 10 и центром масс: l2 = l0 – l1, где l0 – расстояние между ребрами опорных призм 7 и 10 (для данного маятника l0=0,730м).
6. Вычисляют среднее значение <g> по формуле (11)
7. Оценивают абсолютную
погрешность результата, исходя из табличного значения искомой величины gтабл для широты г. Братска.
Найти относительную погрешность.
Оценивают абсолютную
погрешность результата, исходя из табличного значения искомой величины gтабл для широты г. Братска.
Найти относительную погрешность.
8. Результаты измерений и вычислений заносят в таблицу 1.
Таблица 1
|
№ |
п |
t1 |
<t1> |
T1 |
t2 |
<t2> |
T2 |
l1 |
l2 |
g |
Dg |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Определение
момента инерции физического маятника.
1. Найти среднее значение момента инерции физического маятника J относительно оси колебаний по формуле (8). Для колебаний маятника, подвешенного на опору 10, Т =Т2 и l = l2. Масса маятника m = 10,65кг.
2. Методом расчета погрешностей косвенных измерений найти абсолютную погрешность результата DJ.
3. Данные результатов измерений и вычислений заносят в таблицу 2.
Таблица 2
|
№ |
т |
l |
T |
J |
DJ |
E |
|
|
|
|
|
|
|
|
Вопросы для допуска к работе
1. Какова цель работы?
Какова цель работы?
2. Что называется физическим маятником? Какой маятник называется оборотным?
3. Запишите формулу периода колебаний физического маятника и поясните физический смысл величин, входящих в нее. При каких условиях справедлива эта формула?
4. Опишите рабочую установку и ход эксперимента.
5. Оцените погрешность метода измерения момента инерции физического маятника.
Вопросы для защиты работы
1. Выведите формулу для периода колебаний физического маятника.
2. Получите дифференциальное уравнение гармонических колебаний физического маятника, приведите его решение.
3. Что называется приведенной длиной физического маятника?
4.
Сформулируйте теорему Штейнера.
5. Выведите рабочую формулу:
для определения ускорения свободного падения;
для определения момента инерции физического маятника.
6. Получите дифференциальным методом формулу для расчета относительной погрешности DJ/J и укажите пути повышения точности результата эксперимента.
Формула периода колебаний математического маятника
Формула периода колебаний математического маятникаМатематический маятник
Определение
Математический маятник – это частный случай физического маятника, масса которого находится в одной точке.
Обычно математическим маятником считают маленький шарик (материальную точку), имеющий большую массу, подвешенный на длинной нерастяжимой нити (подвесе). Это идеализированная система, которая совершает колебания под воздействием силы тяжести. Только для углов порядка 50-100 математический маятник является гармоническим осциллятором, то есть совершает гармонические колебания.
Изучая качание паникадила на длинной цепи Галилей изучал свойства математического маятника. Он понял, что период колебаний данной системы не зависит от амплитуды при малых углах отклонения.
Формула для периода колебаний математического маятника
Пусть точка подвеса маятника неподвижна. Груз, подвешенный к нити маятника, движется по дуге окружности (рис.1(a)) с ускорением, на него действует некоторая возвращающая сила ($\overline{F}$). Данная сила изменяется при движении груза. В результате чего расчет движения становится сложным. Введем некоторые упрощения. Пусть маятник совершает колебания не в плоскости, а описывает конус (рис.1 (b)). Груз в этом случае перемещается по окружности. Период интересующих нас колебаний будет совпадать с периодом конического движения груза. Период обращения конического маятника по окружности равен времени, которое тратит груз на один виток по окружности:
\[T=\frac{L}{v}=\frac{2\pi R}{v}\left(1\right),\]
где $L$ – длина окружности; $v$ – скорость движения груза. 2}{R}=mg\frac{R}{l}\ \to v=R\sqrt{\frac{g}{l}}\left(4\right).\]
2}{R}=mg\frac{R}{l}\ \to v=R\sqrt{\frac{g}{l}}\left(4\right).\]
Полученную скорость подставим в формулу (1), имеем:
\[T=\frac{2\pi R}{R\sqrt{\frac{g}{l}}}\to \] \[T=2\pi \sqrt{\frac{l}{g}}\left(5\right).\]
Из формулы (5) мы видим, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения. Формулу (5) для периода математического маятника называют формулой Гюйгенса, она выполняется, когда точка подвеса маятника не движется.
Используя зависимость периода колебаний математического маятника от ускорения свободного падения, определяют величину данного ускорения. Для этого измеряют длину маятника, рассматривая большое количество колебаний, находят период $T$, затем вычисляют ускорение свободного падения.
Примеры задач с решением
Пример 1
Задание. Как известно, величина ускорения свободного падения зависит от широты. 2}$
2}$
Пример 2
Задание. Каким будет период колебаний математического маятника, если точка его подвеса движется вертикально вниз 1) с постоянной скоростью? 2) с ускорением $a$? Длина нити этого маятника равна $l.$
Решение. Сделаем рисунок.
1) Период математического маятника, точка подвеса которого движется равномерно, равен периоду маятника с неподвижной точкой подвеса:
\[T_1=2\pi \sqrt{\frac{l}{g}}\left(2.1\right).\]
2) Ускорение точки подвеса маятника можно рассматривать как появление дополнительной силы, равной $F=ma$, которая направлена против ускорения. То есть, если ускорение направлено вверх, то дополнительная сила направлена вниз, значит, она складывается с силой тяжести ($mg$). Если точка подвеса движется с ускорением, направленным вниз, то дополнительная сила вычитается из силы тяжести.
Период математического маятника, который совершает колебания и у которого точка подвеса движется с ускорением, найдем как:
\[T_2=2\pi \sqrt{\frac{l}{a_p}}\left(2. 2\right),\]
2\right),\]
где:
\[a_p=g-a\ \left(2.3\right),\]
тогда:
\[T_1=2\pi \sqrt{\frac{l}{g-a}}.\]
Ответ. 1) $T_1=2\pi \sqrt{\frac{l}{g}}$; 2) $T_1=2\pi \sqrt{\frac{l}{g-a}}$
Читать дальше: формула периода колебаний пружинного маятника.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
формула расчета, как найти для физического маятника
Содержание:
- Что такое колебательный процесс
-
Определение периода колебаний, формула
- Как найти период для физического маятника
- Примеры решений
Содержание
- Что такое колебательный процесс
-
Определение периода колебаний, формула
- Как найти период для физического маятника
- Примеры решений
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.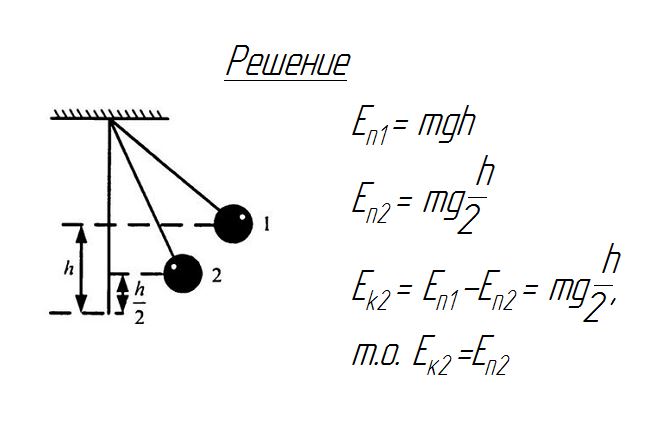
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
\(F=F_{0}\cos \cot\)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
\(x(t)=A\times \cos \left(\omega _{0}t+\phi _{0} \right)\)
Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
\(\omega _{0}\) равно циклической или круговой частоте колебаний;
\(\phi _{0}\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
\(cp(t)=(co_{0}t+cp_{0})\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)
то х остается без изменений при фазе колебаний, получающей приращение в $$2\pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на \(2\pi:\)
\(\omega _{0}(t+T)+\phi _{0}=\left(\omega _{0}t+\phi _{0} \right)+2\pi\)
Из данного равенства можно вычислить период колебаний:
\(T=\frac{2\pi }{\omega _{0}}\)
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
\(v=\frac{\omega _{0}}{2\pi}\)
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t. {2}x(t)=0\)
{2}x(t)=0\)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
\(\omega =\sqrt{\frac{mgl}{J}}\)
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
\(T =\frac{2\pi }{\omega }=2\pi \sqrt{\frac{J}{mgl}}\)
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника \(T =2\pi \sqrt{\frac{m}{k}}\)
- Период математического маятника \(T =2\pi \sqrt{\frac{L}{g}}\)
- Период крутильного маятника \(T =2\pi \sqrt{\frac{I}{K}}\)
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Задача № 1
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Необходимо определить, каковы период и частота колебаний шарика.
Решение
\(T =\frac{t}{N}=\frac{120}{60}=2\)
\(V=\frac{1}{T}=\frac{1}{2}=0.5\)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
Задача № 2
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
\(V=\frac{1}{T}=\frac{1}{0,8}=1,25\)
\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)
Задача № 3
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. {2}}\approx 0.16\)
{2}}\approx 0.16\)
Ответ: длина математического маятника примерно составляет 0,16 метра.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Выведите формулу для периода колебаний физического маятника
43. Дайте определение и выведите формулу периода колебаний физического маятника.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:
При отклонении от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:
,
где m – масса маятника, l – расстояние между точкой подвеса О и центром инерции C маятника. Знак “ – ” имеет тоже значение, что и в случае квазиупругой силы . Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать основной закон динамики:
В случае малых колебаний это уравнение переходит в уже известное нам уравнение незатухающих гармонических колебаний:
,
где через обозначена в данном случае следующая величина:
Из этого уравнения следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. При этом период колебаний физического маятника определяется выражением:
Проведенное выше рассмотрение имеет место и для математического маятника. В этом случае маятник представляет собой материальную точку, момент инерции которой относительно оси, проходящей через точку подвеса, равен .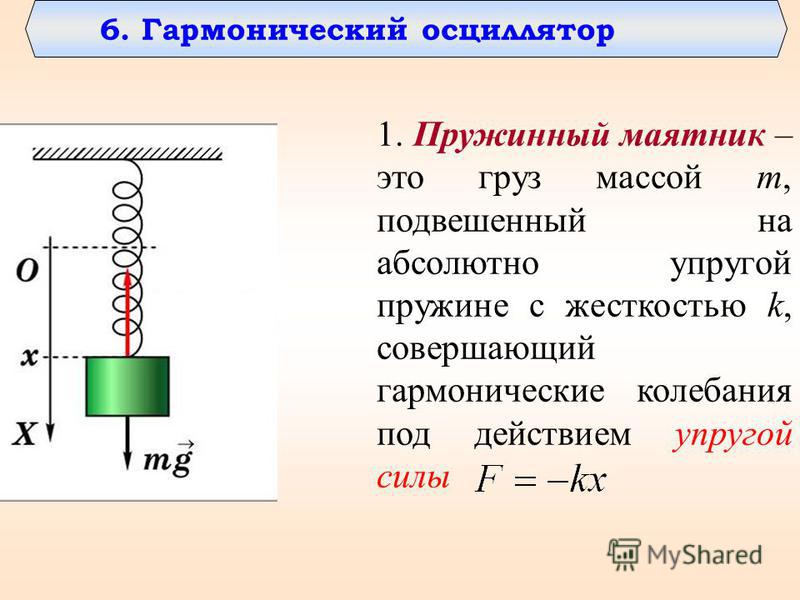 С учетом этого, получаем формулу для периода колебаний математического маятника:
С учетом этого, получаем формулу для периода колебаний математического маятника:
Для физического маятника вводится понятие приведенной длины . Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника, т.е. .
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку на рисунке). Можно показать, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания точка подвеса становится новым центром качания.
Получите дифференциальное уравнение затухающих гармонических колебаний.
45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
43. Дайте определение и выведите формулу периода колебаний физического маятника.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. При отклонении от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:
Этот момент равен:
,
где m – масса маятника, l – расстояние между точкой подвеса О и центром инерции C маятника. Знак “ – ” имеет тоже значение, что и в случае квазиупругой силы . Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать основной закон динамики:
В случае малых колебаний это уравнение переходит в уже известное нам уравнение незатухающих гармонических колебаний:
,
где через обозначена в данном случае следующая величина:
Из этого уравнения следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. При этом период колебаний физического маятника определяется выражением:
Проведенное выше рассмотрение имеет место и для математического маятника. В этом случае маятник представляет собой материальную точку, момент инерции которой относительно оси, проходящей через точку подвеса, равен . С учетом этого, получаем формулу для периода колебаний математического маятника:
С учетом этого, получаем формулу для периода колебаний математического маятника:
Для физического маятника вводится понятие приведенной длины . Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника, т.е. .
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку на рисунке). Можно показать, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания точка подвеса становится новым центром качания.
Получите дифференциальное уравнение затухающих гармонических колебаний.
45. По какому закону изменяется колеблющаяся величина при затухающих гармонических колебаниях? Приведите график зависимости
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Давай те выведем формулу для периода физического маятника.
При небольших углах отклонения
физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла
Так как угол маленький, у нас получается, что F равно:
Для вывода закона движения физического маятников используем основное уравнение динамики вращательного движения:
Так как момент силы определить в явном виде нельзя. Надо записать дифференциальное уравнение колебаний физического маятника:
Надо записать дифференциальное уравнение колебаний физического маятника:
Сравнивая полученное выражение с уравнением гармонических колебаний:
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
Тогда период колебаний математического маятника будет равен:
Период пружинного маятника
Период математического маятника
Период крутильного маятника
В Формуле мы использовали :
T — Период физического маятника
J — Момент силы маятника относительно оси вращения
l — Расстояние от оси вращения до центра масс
Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую и правую часть этого уравнения на . Тогда:
.
Интегрируя это уравнение, получаем.
,
где
произвольная
постоянная. Её можно найти из граничного
условия, что в моменты
.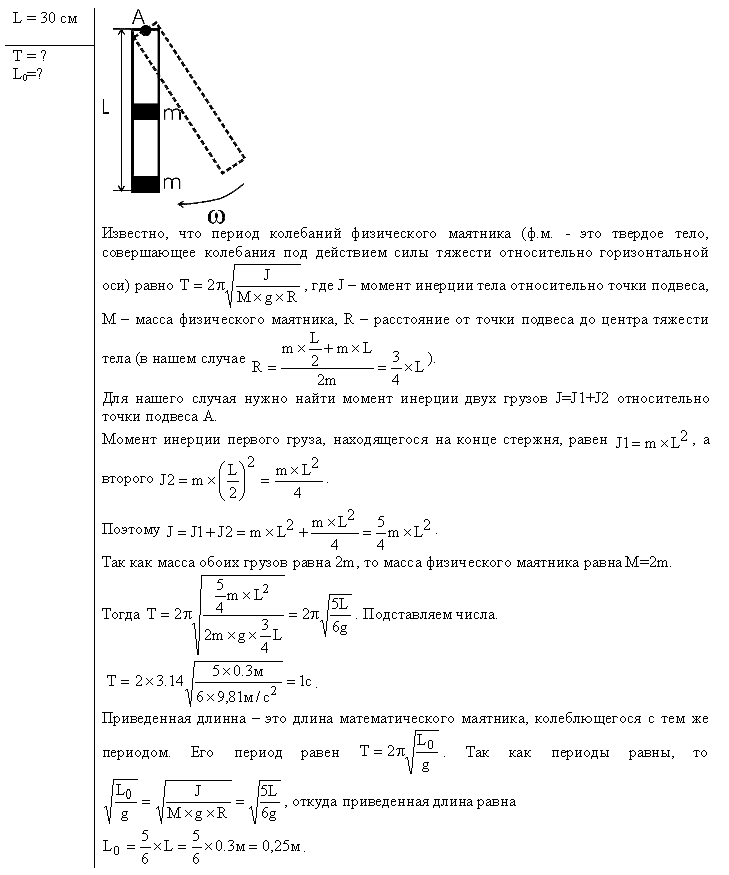 Получаем:
.
Подставляем и преобразовываем получившееся
уравнение:
Получаем:
.
Подставляем и преобразовываем получившееся
уравнение:
.
Отделяем переменные и интегрируем это уравнение:
.
Удобно сделать замену переменной, полагая . Тогда искомое уравнение принимает вид:
.
Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
.
Здесь — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:
.
[Править]Период малых колебаний физического маятника
Если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:
.
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°)
.
Вопрос 4. Энергия гармонических колебаний
При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:
(Скорость тела v = ds/dt)
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:
где U – потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:
| для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы: |
1. Полная механическая энергия тела не
изменяется при колебаниях:
2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.
3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на (на
полпериода). Когда кинетическая энергия
достигает максимума, потенциальная –
минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.
Полная механическая энергия тела не
изменяется при колебаниях:
2.
Частота колебаний кинетической и
потенциальной энергии в 2 раза больше
частоты колебаний маятника.
3.
Колебания кинетической и потенциальной
энергии сдвинуты друг относительно
друга по фазе на (на
полпериода). Когда кинетическая энергия
достигает максимума, потенциальная –
минимума (нуля) и наоборот. Энергия при
колебаниях постоянно перекачивается
из потенциальной в кинетическую и
обратно.
Вопрос 5.
Ускоре́ние свобо́дного паде́ния g (оно же ускорение силы тяжести), — ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационногопритяжения планеты (или другого астрономического тела) и сил инерции, вызванных её вращением, за исключением кориолисовых сил инерции[1]. В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Значение
ускорения свободного падения на
поверхности Земли обычно
принимают равным 9,8 или 10 м/с². Стандартное («нормальное») значение,
принятое при построении систем единиц, g =
9,80665 м/с²[2],
а в технических расчётах обычно
принимают g =
9,81 м/с².
Стандартное («нормальное») значение,
принятое при построении систем единиц, g =
9,80665 м/с²[2],
а в технических расчётах обычно
принимают g =
9,81 м/с².
Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте45,5° на уровне моря.
Реальное ускорение свободного падения на поверхности Земли зависит от широты, времени суток и других факторов. Оно варьируется от 9,780 м/с² на экваторе до 9,832 м/с² наполюсах[3]. Оно может быть вычислено (в м/с²) по эмпирической формуле:
где — широта рассматриваемого места, — высота над уровнем моря в метрах.[4] Эта формула применима лишь в ограниченном диапазоне высот от 0 до нескольких десятков км, где убывание ускорения свободного падения с высотой можно считать линейным (на самом же деле оно убывает квадратично).
Как в лабораторке измеряли я хз ибо проебал^^
Запишите формулу периода колебаний физического маятника
Содержание
- Основные формулы
- Кинематика колебаний маятника
- Вопросы для самопроверки
- Упражнения
Основные формулы
Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной оси. Рассмотрим малые колебания маятника. Положение тела в любой момент времени можно характеризовать углом отклонения его из положения равновесия (рис. 2.1).
Рассмотрим малые колебания маятника. Положение тела в любой момент времени можно характеризовать углом отклонения его из положения равновесия (рис. 2.1).
Запишем уравнение моментов относительно оси вращения OZ (ось OZ проходит через точку подвеса О перпендикулярно плоскости рисунка “от нас”), пренебрегая моментом сил трения, если известен момент инерции тела
Здесь – момент инерции маятника относительно оси OZ,
– угловая скорость вращения маятника,
Mz=- – момент силы тяжести относительно оси OZ,
a – расстояние от центра тяжести тела С до оси вращения.
Если считать, что при вращении, например, против часовой стрелки угол увеличивается, то момент силы тяжести вызывает уменьшение этого угла и, следовательно, при момент Mz
Сравнивая формулы (3) и (4), заключаем, что период колебаний физического маятника равен периоду колебаний математического маятника с длиной l, называемой приведенной длиной физического маятника:
Период колебаний физического маятника (а, следовательно, и его приведенная длина ) немонотонно зависит от расстояния . Это легко заметить, если в соответствии с теоремой Гюйгенса-Штейнера момент инерции выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс: Тогда период колебаний будет равен:
Это легко заметить, если в соответствии с теоремой Гюйгенса-Штейнера момент инерции выразить через момент инерции относительно параллельной горизонтальной оси, проходящей через центр масс: Тогда период колебаний будет равен:
Изменение периода колебаний при удалении оси вращения от центра масс O в обе стороны на расстояние а показано на рис. 2.2.
Кинематика колебаний маятника
Маятником является всякое тело, подвешенное так, что его центр тяжести находится ниже точки подвеса. Молоток, висящий на гвозде, весы, груз на веревке — все это колебательные системы, подобные маятнику стенных часов (рис. 2.3).
У всякой системы, способной совершать свободные колебания, имеется устойчивое положение равновесия. У маятника — это то положение, при котором центр тяжести находится на вертикали под точкой подвеса. Если мы выведем маятник из этого положения или толкнем его, то он начнет колебаться, отклоняясь то в одну, то в другую сторону от положения равновесия. Наибольшее отклонение от положения равновесия, до которого доходит маятник, называется амплитудой колебаний. Амплитуда определяется тем первоначальным отклонением или толчком, которым маятник был приведен в движение. Это свойство — зависимость амплитуды от условий в начале движения — характерно не только для свободных колебаний маятника, но и вообще для свободных колебаний очень многих колебательных систем.
Наибольшее отклонение от положения равновесия, до которого доходит маятник, называется амплитудой колебаний. Амплитуда определяется тем первоначальным отклонением или толчком, которым маятник был приведен в движение. Это свойство — зависимость амплитуды от условий в начале движения — характерно не только для свободных колебаний маятника, но и вообще для свободных колебаний очень многих колебательных систем.
Если прикрепить к маятнику волосок — кусочек тонкой проволочки или упругой нейлоновой нити — и будем двигать под этим волоском закопченную стеклянную пластинку, как показано на рис. 2.3. Если двигать пластинку с постоянной скоростью в направлении, перпендикулярном к плоскости колебаний, то волосок прочертит на пластинке волнистую линию (рис. 2.4). Мы имеем в этом опыте простейший осциллограф — так называются приборы для записи колебаний. Кривые, которые записывает осциллограф, называются осциллограммами. Таким образом, рис. 2.2.3. представляет собой осциллограмму колебаний маятника. Амплитуда колебаний изображается на этой осциллограмме отрезком АВ, дающим наибольшее отклонение волнистой кривой от прямой линии ab, которую волосок прочертил бы на пластинке при неподвижном маятнике (покоящемся в положении равновесия). Период изображается отрезком CD, равным расстоянию, на которое передвигается пластинка за период маятника.
Амплитуда колебаний изображается на этой осциллограмме отрезком АВ, дающим наибольшее отклонение волнистой кривой от прямой линии ab, которую волосок прочертил бы на пластинке при неподвижном маятнике (покоящемся в положении равновесия). Период изображается отрезком CD, равным расстоянию, на которое передвигается пластинка за период маятника.
Запись колебаний маятника на закопченной пластинке
Осциллограмма колебаний маятника: АВ — амплитуда, CD — период
Так как мы двигаем закопченную пластинку равномерно, то всякое ее перемещение пропорционально времени, в течение которого оно совершалось. Мы можем сказать поэтому, что вдоль прямой аb в определенном масштабе (зависящем от скорости движения пластинки) отложено время. С другой стороны, в направлении, перпендикулярном к аb, волосок отмечает на пластинке расстояния конца маятника от его положения равновесия, т.е. путь, пройденный концом маятника от этого положения. Таким образом, осциллограмма есть не что иное, как график движения — график зависимости пути от времени.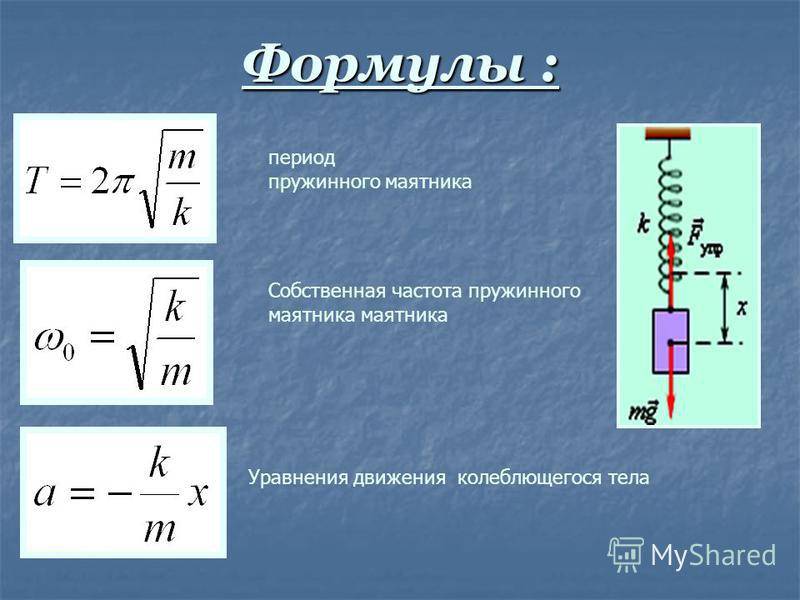
Как мы знаем, наклон линии на таком графике изображает скорость движения. Через положение равновесия маятник проходит с наибольшей скоростью. Соответственно этому и наклон волнистой линии на рис. 2.2.3. наибольший в тех точках, где она пересекает прямую ab. Наоборот, в моменты наибольших отклонений скорость маятника равна нулю. Соответственно этому и волнистая линия на рис. 4 в тех точках, где она наиболее удалена от ab, имеет касательную, параллельную ab, т. е. наклон, равный нулю.
Физическим маятником называется твердое тело, находящееся в поле силы тяжести и имеющее горизонтальную ось вращения, не проходящую через центр тяжести тела.
Пусть — масса тела, J — его момент инерции относительно оси вращения — расстояние от центра тяжести до оси вращения (рис. 36). Выведенное из положения равновесия, тело будет вращаться либо совершать колебательное движение. В обоих случаях дифференциальное уравнение движения имеет один и тот же вид (силами трения пренебрегаем):
Пусть начальные условия таковы, что угол все время остается малым (максимальное отклонение от вертикали не превышает ). Тогда можно приближенно принять (в радианах) и рассматривать более простое уравнение:
Тогда можно приближенно принять (в радианах) и рассматривать более простое уравнение:
или, что то же, уравнение
Это уравнение называется дифференциальным уравнением малых колебаний физического маятника. Из него следует, что малые колебания физического маятника являются гармоническими колебаниями частоты
Амплитуда и фаза колебаний будут определяться начальным отклонением и начальной угловой скоростью физического маятника.
Вопросы для самопроверки
1. Что называется моментом количества движения материальной точки?
2. Что называется кинетическим моментом механической системы относительно данного центра, данной оси?
3. Приведите общие формулы для определения кинетического момента механической системы (относительно данного центра, данной оси).
4. Приведите математическую запись теоремы об изменении кинетического момента. Дайте словесную формулировку теоремы.
5. В каких случаях кинетический момент системы или его проекция на ось остаются постоянными при движении системы?
6. Какие координатные оси называются осями Кенига?
Какие координатные оси называются осями Кенига?
7. Приведите общую формулу для определения кинетического момента твердого тела относительно данного неподвижного центра?
8. Как вычисляется кинетический момент тела при его поступательном и вращательном движениях?
9. Как составляются дифференциальные уравнения движения тела при его поступательном движении? При вращении вокруг неподвижной оси? При плоскопараллельном движении?
10. Что называется физическим маятником? Как определяется период его малых колебаний?
Упражнения
1. Материальная точка М массы движется по окружности радиуса R согласно уравнению (рис. 37). Вычислить и построить количество движения и момент количества движения точки при .
2. Сплошной однородный диск массы и радиуса R вращается вокруг своей оси согласно уравнению . Найти кинетический момент диска относительно оси вращения.
3. Решить в указанном порядке следующие задачи из сборника И.В. Мещерского 1981 г. издания: 28. 4; 37.1; 37.56; 37.43; 37.5; 37.6; 37.16.
4; 37.1; 37.56; 37.43; 37.5; 37.6; 37.16.
6.11. Физический маятник
Твердое тело произвольной формы, свободно совершающее колебания вокруг неподвижной горизонтальной оси, не проходящей через его центр масс, называют физическим маятником .
Согласно определению, физический маятник при колебаниях имеет одну степень свободы, т.е. действительно является одномерным гармоническим классическим осциллятором (рис. 6.14, где точка 0 называется осью качаний, а точка 0 * – центром качания физического маятника, точка C – центр масс).
При гармонических колебаниях угол отклонения от положения равновесия q мал и составляет не более трех-пяти градусов, что позволяет в некоторых случаях полагать sin q » q (если угол q брать в радианах, а не в градусах), а сами колебания считать гармоническими и изохронными , т.е. их период или частота не зависят от амплитуды колебания.
Сначала напишем дифференциальное уравнение колебаний физического маятника. Для этого рассмотрим, какие на него действуют силы. = mg · sin q и G | | = mg · cos q (рис. 6.14). Тогда силы нормальной реакции опоры и параллельная составляющая силы тяжести взаимно компенсируют друг друга (третий закон Ньютона). Поэтому силой, заставляющей физический маятник продолжать совершать гармонические колебания, остается перпендикулярная составляющая силы тяжести, которую часто называют возвращающей силой.
= mg · sin q и G | | = mg · cos q (рис. 6.14). Тогда силы нормальной реакции опоры и параллельная составляющая силы тяжести взаимно компенсируют друг друга (третий закон Ньютона). Поэтому силой, заставляющей физический маятник продолжать совершать гармонические колебания, остается перпендикулярная составляющая силы тяжести, которую часто называют возвращающей силой.
Такой же результат можно получить, если сложить вектор силы тяжести и вектор силы нормальной реакции опоры по правилу параллелограмма. (Представляем читателю выполнить эту операцию самостоятельно).
Из динамики вращательного движения ( 5.17 ) следует , что в этом случае на физический маятник (как любое твердое тело) действует момент силы М относительно оси Z, равный произведению момента инерции тела I на угловое ускорение e относительно этой же оси:
| M = I ×e , |
| . |
5 фактов, которые вы должны знать — Lambda Geeks
Автор: Кирти Муртиин Science
В классической механике маятник — одна из интересных концепций для изучения движения объекта.
Когда предполагается, что тело подвешено к фиксированной точке, которая может свободно двигаться вперед и назад, это называется маятником. Простой и физический маятники очень похожи, но некоторые свойства могут различаться. Давайте изучим разницу между простым и физическим маятником в этом посте.
Простой маятник:
Возможно, вы видели простой маятник в лаборатории.
Груз определенной массы «m» подвешен к фиксированной точке с помощью нерастяжимого троса, который должен раскачиваться взад и вперед и называется простым маятником.
Изображение предоставлено: изображение Герда Альтманна из PixabayФизический маятник:
Вы когда-нибудь видели какой-либо объект, висящий в фиксированной точке вокруг вас? Если да, то это не что иное, как физический маятник.
Любой объект, свободно висящий и совершающий возвратно-поступательное движение, подобен простому маятнику, но он не должен висеть на веревке или тросе и называется физическим маятником.
Несмотря на то, что простой маятник и физический маятник звучат похоже, между ними есть некоторые различия, которые перечислены в таблице ниже.
| Простой маятник | Физический маятник | |
| Модель | Простая маячка считается идеальной моделью, потому что это трудно достигать в реальности. | Физический маятник — реалистичная модель маятника; оно имеет конечное тело и форму. |
| Подвеска | Простому маятнику требуется гусеница или веревка для подвешивания к жесткой опоре. | Физическому маятнику не нужна веревка для подвески. |
| Натяжение | На струну действует сила натяжения, которая помогает предмету подвешиваться. | Так как физический маятник не нуждается в веревке для подвешивания, натяжения не будет. |
| Период времени | Период времени зависит от квадратного корня из отношения длины маятника к ускорению свободного падения. | Время зависит от отношения квадратного корня из 2/3 длины и ускорения свободного падения. |
| Механическая энергия | Механическая энергия сохраняется при каждом колебании. | Здесь также сохраняется механическая энергия при каждом колебании. |
| Колебания | Простой маятник колеблется под большим углом за короткий промежуток времени. | Угол колебания физического маятника мал. |
| Гравитация | Гравитация действует в центре груза маятника. | Гравитация действует на центр масс физического маятника. |
Крутящий момент Когда простой маятник может свободно вращаться, крутящий момент возникает из-за силы тяжести или углового ускорения. | Физический маятник свободно вращается за счет крутящего момента, приложенного к центру масс. |
- Гравитация действует как возвращающая сила как для простого, так и для физического маятника.
- Струна, используемая в случае простого маятника, должна быть нерастяжимой и невесомой.
- В физическом маятнике момент инерции не равен произведению массы на квадрат длины объекта, как в случае простого маятника. Центр масс находится на половине длины, так что момент инерции в центре равен
Момент инерции в точке подвеса равен
Суммарный момент инерции определяется как I = I c + I 0
- Точка колебания может быть изменена, если точка подвеса изменится.
- Наиболее эффективным способом расчета ускорения свободного падения является «физический маятник».
 Это дается как;
Это дается как;
- В простом маятнике повышение температуры может вызвать изменение длины. Изменение длины, заданное
L’ = L (1+α∆θ)
где; α и θ – температурные коэффициенты.
- Если рассматривать физический маятник как простой маятник, то можно считать, что масса сосредоточена только в одной точке, так что период времени обоих маятников будет одинаковым.
Среднее положение маятника — это положение, при котором маятник подвешен вертикально, а груз находится в состоянии покоя, поэтому его можно выбрать в качестве точки отсчета для расчета называется средней позицией.
Амплитуда маятника – это расстояние, пройденное маятником от его среднего положения до одного крайнего положения.
Центр масс маятника – точка на теле, в которой сосредоточена вся масса системы.
На увеличение периода маятника влияет следующий фактор.
- Длина подвесной струны
Движение вперед и назад увеличивается по мере увеличения длины струны, что помогает увеличить период времени.
- Угол
Когда маятник делает больший угол, амплитуда увеличивается, время падения маятника становится меньше, а период времени увеличивается.
Зависят ли колебания маятника от массы?Колебания маятника полностью не зависят от массы.
Хотя масса влияет на инерцию, она не влияет на силу, действующую через маятник. Так что колебания остаются теми же, даже если масса больше или меньше.
Влияет ли сопротивление воздуха на маятник? При отсутствии сопротивления воздуха маятник непрерывно колеблется с постоянной амплитудой.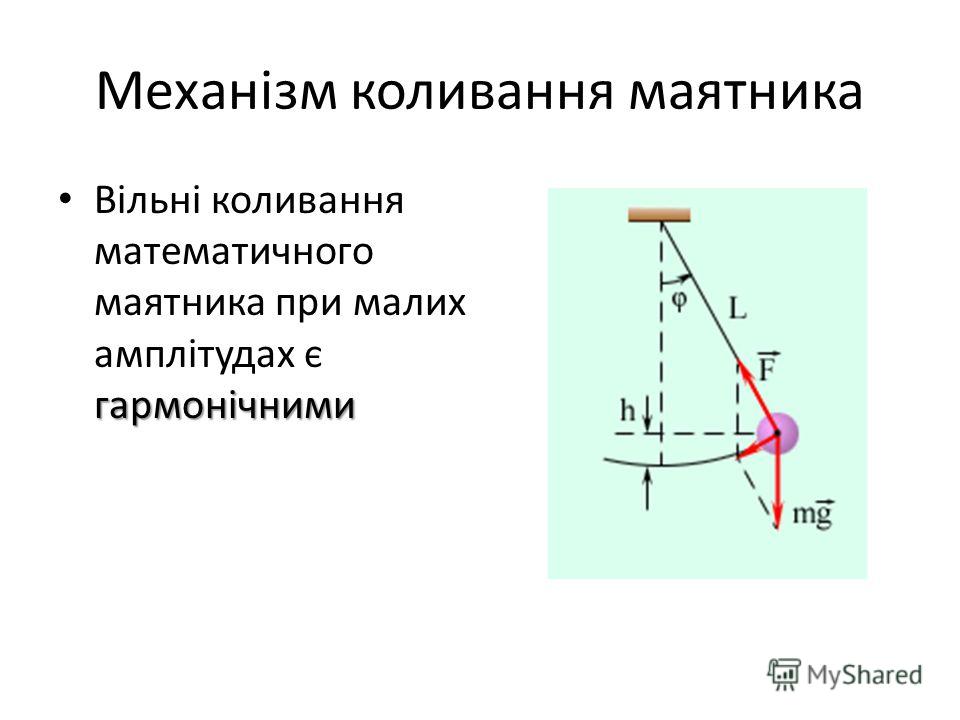
Когда маятник колеблется с определенным периодом времени, сопротивление воздуха препятствует ускорению груза и, следовательно, постепенно сокращает период времени. Уменьшение периода времени заставляет маятник вернуться в исходное положение покоя.
Объясните действие механической энергии маятника.В простом маятнике без трения механическая энергия всегда сохраняется и представляет собой сумму кинетической и гравитационной потенциальной энергии, действующих на маятник.
При качании маятника будет происходить постоянный обмен энергией. Обмен кинетической энергией и гравитационной потенциальной энергией происходит при каждом колебании. Эта механическая энергия, участвующая в движении, помогает поддерживать постоянный период маятника.
Последние сообщения
ссылка на май В пассивном залоге: 5 фактов (когда, как и примеры)Май в пассивном залоге: 5 фактов (когда, как и примеры)
В английском языке глагол «may» попадает под модальные вспомогательные глаголы. Давайте здесь узнаем, как глагол «может» может быть изменен в пассивный залог.
Модальный вспомогательный глагол…
Давайте здесь узнаем, как глагол «может» может быть изменен в пассивный залог.
Модальный вспомогательный глагол…
Продолжить чтение
ссылка на Является ли электрическое поле вектором? 5 фактов, которые вы должны знатьЯвляется ли электрическое поле вектором? 5 фактов, которые вы должны знать
Электрическое поле создается заряженной частицей. В этой статье будет выяснено, является ли электрическое поле скалярной или векторной величиной. Электрическое поле является вектором, поскольку оно имеет…
Продолжить чтение
Физический маятник: определение момента инерции
Введение в физический маятник Установите любое твердое тело так, чтобы оно могло качаться в вертикальной плоскости вокруг оси, проходящей через тело. Вы сконструировали так называемый физический маятник . На видео ниже показан пример такого маятника. В этом видео твердое круглое тело качается вокруг оси, очень близкой к краю круга. Круг был вырезан из куска картона. PocketLab Voyager опирается на кольцевую подставку прямо под точкой вращения маятника. Крошечный магнит был прикреплен к нижней части круга. Вы заметите, что PocketLab дважды в течение каждого периода фиксирует всплеск напряженности магнитного поля, когда магнит находится ближе всего к PocketLab. Анализ этих всплесков за несколько периодов дает точное определение периода колебаний физического маятника.
PocketLab Voyager опирается на кольцевую подставку прямо под точкой вращения маятника. Крошечный магнит был прикреплен к нижней части круга. Вы заметите, что PocketLab дважды в течение каждого периода фиксирует всплеск напряженности магнитного поля, когда магнит находится ближе всего к PocketLab. Анализ этих всплесков за несколько периодов дает точное определение периода колебаний физического маятника.
На рис. 1 показан объект неправильной формы, который вращается вокруг оси без трения, перпендикулярной плоскости фигуры в точке P. Объект смещен от положения равновесия на угол θ . Положение равновесия – это когда центр масс C объекта находится непосредственно под точкой вращения. Расстояние между точкой вращения и центром масс составляет d . С учетом вовлеченной динамики на рисунке показан вывод уравнения для периода T физического маятника. Решая это уравнение для момента инерции I , получаем уравнение в рамке внизу рисунка. Ускорение свободного падения g принимается за известную величину, а T , M и d поддаются измерению. Таким образом, это уравнение позволяет нам определить момент инерции любого объекта через любую конкретную точку вращения на этом объекте! Обратите внимание на предположение, что θ предполагается малым. Если угол поворота сохраняется не более 30⁰, то θ и sin θ будут отличаться не более чем на 4%. Вычисление I немного утомительно, когда его нужно повторять много раз. Поэтому вам может быть удобно составить электронную таблицу для расчета I после ввода значений T, g, M, и d.
Решая это уравнение для момента инерции I , получаем уравнение в рамке внизу рисунка. Ускорение свободного падения g принимается за известную величину, а T , M и d поддаются измерению. Таким образом, это уравнение позволяет нам определить момент инерции любого объекта через любую конкретную точку вращения на этом объекте! Обратите внимание на предположение, что θ предполагается малым. Если угол поворота сохраняется не более 30⁰, то θ и sin θ будут отличаться не более чем на 4%. Вычисление I немного утомительно, когда его нужно повторять много раз. Поэтому вам может быть удобно составить электронную таблицу для расчета I после ввода значений T, g, M, и d.
Использование PocketLab, как описано выше в этом уроке, имеет явное преимущество.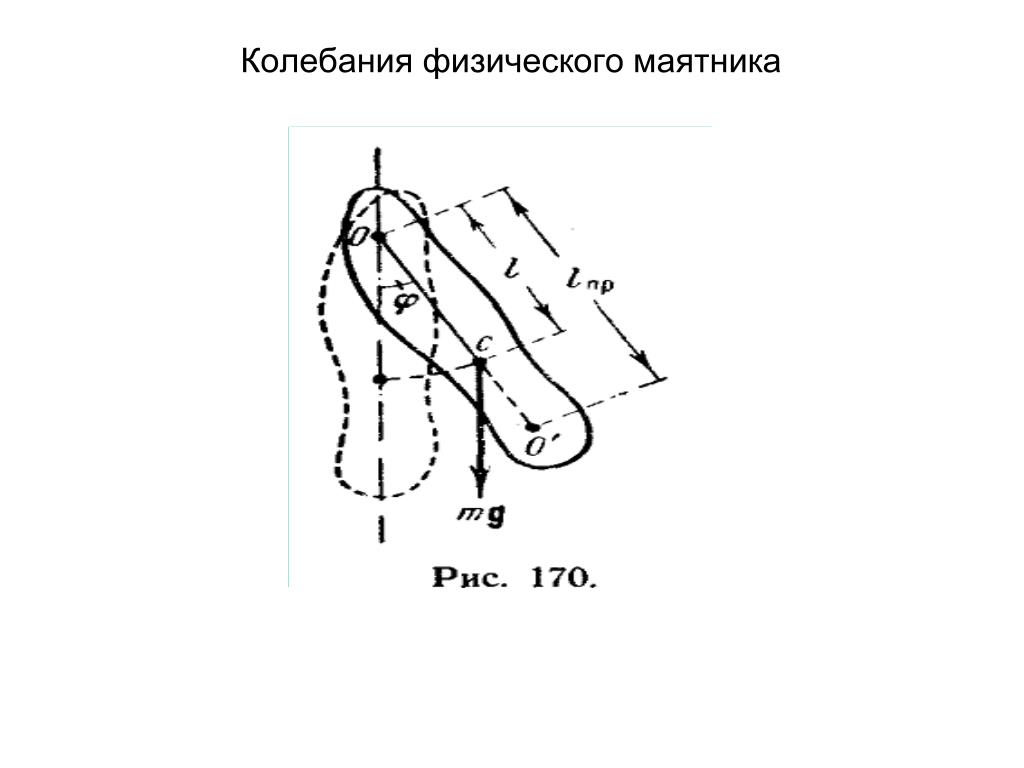 PocketLab позволяет рассчитать период физического маятника гораздо точнее, чем это возможно с помощью секундомера. Использование PocketLab для этой цели исключает ошибки, связанные со временем реакции при запуске и остановке секундомера. PocketLab также должен быть настроен на максимально возможную скорость передачи данных (50 точек в секунду). Успех в этом уроке зависит от точных измерений периода Т физического маятника. Также рекомендуется измерять массу маятника с помощью весов, допускающих погрешность до 0,1 г или даже 0,01 г, если это возможно.
PocketLab позволяет рассчитать период физического маятника гораздо точнее, чем это возможно с помощью секундомера. Использование PocketLab для этой цели исключает ошибки, связанные со временем реакции при запуске и остановке секундомера. PocketLab также должен быть настроен на максимально возможную скорость передачи данных (50 точек в секунду). Успех в этом уроке зависит от точных измерений периода Т физического маятника. Также рекомендуется измерять массу маятника с помощью весов, допускающих погрешность до 0,1 г или даже 0,01 г, если это возможно.
Для наглядности на рис. 2 показан вид устройства под углом. Физический маятник, картонный прямоугольник, подвешен к точке вращения очень близко к короткому краю прямоугольника. Шарнир представляет собой тонкий металлический стержень, закрепленный на кольцевой стойке. Также используется деревянный стержень для дюбеля (или что-то подобное), так как винт зажима не вкручивается достаточно сильно, чтобы прижать металлический стержень к зажиму. Учащиеся должны носить защитные очки, чтобы не допустить попадания в глаза тонкого металлического стержня. PocketLab опирается на нижнюю часть кольцевой подставки. Крошечный магнит был приклеен к центру короткого нижнего края прямоугольника. Магнитометр PocketLab определяет магнитное поле каждый раз, когда магнит проходит мимо PocketLab.
Учащиеся должны носить защитные очки, чтобы не допустить попадания в глаза тонкого металлического стержня. PocketLab опирается на нижнюю часть кольцевой подставки. Крошечный магнит был приклеен к центру короткого нижнего края прямоугольника. Магнитометр PocketLab определяет магнитное поле каждый раз, когда магнит проходит мимо PocketLab.
Момент инерции объекта, вращающегося вокруг определенной оси, в некоторой степени аналогичен обычной массе объекта. Момент инерции можно определить по уравнению
момент инерции – это сумма масс частиц, составляющих объект, умноженная на квадрат их соответствующих расстояний от оси вращения . Для непрерывных жестких объектов уравнение будет аналогичным, но с использованием интегралов вместо суммы. Следует отметить, что по определению момент инерции тела зависит не только от конкретной оси, вокруг которой оно вращается, но и от его формы и от того, как распределена его масса. Вычисление этих интегралов может быть очень утомительным. Поэтому на этом уроке мы воспользуемся таблицей моментов инерции, чтобы мы могли сосредоточиться на физике и не беспокоиться о вычислении часто сложных интегралов.
Вычисление этих интегралов может быть очень утомительным. Поэтому на этом уроке мы воспользуемся таблицей моментов инерции, чтобы мы могли сосредоточиться на физике и не беспокоиться о вычислении часто сложных интегралов.
- На этом уроке вы определите момент инерции для нескольких распространенных геометрических картонных фигур относительно определенной точки вращения каждого объекта. Объекты будут физическими маятниками, которые качаются вокруг заданной оси, перпендикулярной плоскости фигуры. PocketLab будет использоваться для измерения периода каждого маятника.
- Затем вы сравните свои экспериментальные моменты инерции с теоретическими моментами инерции, представленными в статье Википедии «Список моментов инерции». Сравнения будут выражены как процентная разница между вашим экспериментальным результатом и теоретическим моментом инерции, основанная на части теоретического момента инерции. Разница в процентах будет отрицательной, если ваш экспериментальный результат меньше теоретического, и положительной, если экспериментальный результат больше теоретического.
 Формы будут исследоваться в порядке сложности соответствующих физических и математических методов. Эти формы, в порядке их исследования, следующие:
Формы будут исследоваться в порядке сложности соответствующих физических и математических методов. Эти формы, в порядке их исследования, следующие:- Прямоугольник
- Круг
- Квадрат
- Равносторонний треугольник
- Наконец, вы определите момент инерции относительно определенной оси обычного прямоугольника, неправильной криволинейной формы и объекта с “отрицательным пространством”. В таблице Википедии для этих форм не представлены теоретические формулы. Тем не менее, вы все же можете определить эти моменты инерции экспериментально . Основываясь на процентах ошибок, которые вы получили от известных форм в задаче 2, насколько вы уверены в моментах инерции общего прямоугольника, неправильной изогнутой формы и объекта с отрицательным пространством?
Вырежьте из картона прямоугольник, размер и форма которого аналогичны прямоугольнику, показанному на рис. 2. Экспериментально определите его момент инерции относительно оси, показанной на рис. 2.
2. Экспериментально определите его момент инерции относительно оси, показанной на рис. 2.
Прокрутите вниз список моментов инерции в Википедии, пока не увидите запись, показанную на рисунке 3. Эта запись соответствует прямоугольнику, который вы сейчас исследуете. Используя формулу, показанную на рисунке 3, определите теоретический момент инерции вашего прямоугольника относительно оси вращения 90 269 x 90 270 . Вычислите разницу в процентах и запишите результаты в таблицу данных.
Рисунок 3. Прямоугольная пластина (из списка моментов инерции Википедии) Circle InvestigationВырежьте из картона круг, похожий по размеру на тот, который показан во встроенном видео. Экспериментально определите его момент инерции относительно оси, показанной на видео.
Прокрутите вниз список моментов инерции в Википедии, пока не увидите запись, показанную на рисунке 4. Вас интересует момент инерции z . Это дает вам момент инерции окружности, равной 90 269, вращающейся вокруг своего центра масс 90 270 .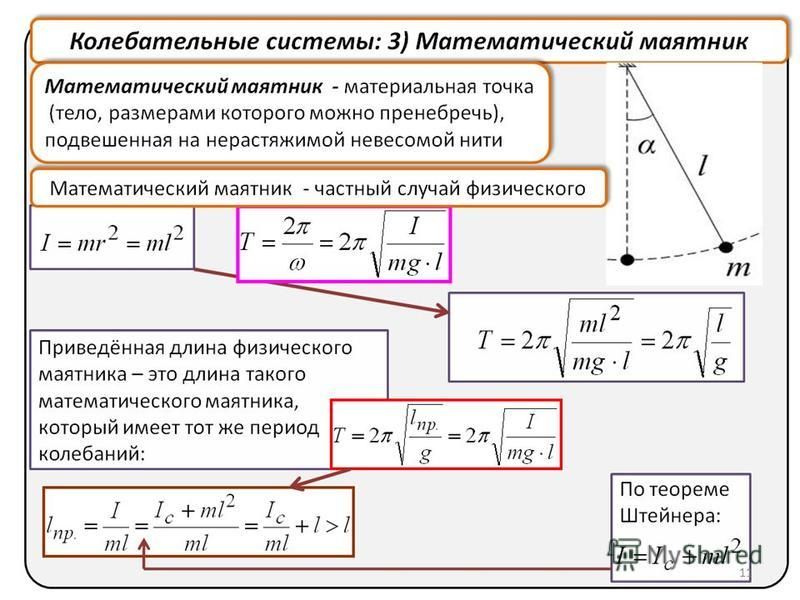 Но ваш круглый картон вращается вокруг точки у края круга! Как упоминалось ранее, момент инерции зависит от конкретной оси вращения . Итак… как мы можем определить момент инерции, когда круг вращается вокруг точки рядом с его краем?
Но ваш круглый картон вращается вокруг точки у края круга! Как упоминалось ранее, момент инерции зависит от конкретной оси вращения . Итак… как мы можем определить момент инерции, когда круг вращается вокруг точки рядом с его краем?
Используйте теорему о параллельной оси и запись z в таблице Википедии, чтобы определить уравнение для момента инерции относительно точки рядом с краем круглой пластины. Уравнение, которое вы получите, должно согласовываться с записью в Википедии, показанной на рис. 5.
Рисунок 5. Равномерный диск (из списка моментов инерции Википедии)
Равномерный диск (из списка моментов инерции Википедии)Рассчитайте теоретическое значение этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите результаты в таблицу данных.
Исследование квадратаВырежьте из картона квадрат, размер которого подобен показанному на рис. 6. Экспериментально определите его момент инерции относительно оси, показанной на этом рисунке, т. е. оси, очень близкой к одной из вершин квадрата.
Рисунок 6. Квадратный физический маятникПрокрутите вниз список моментов инерции в Википедии, пока не увидите запись, показанную на рисунке 7.
- Каково значение n в уравнении, показанном для вашего квадрата?
- Получите формулу момента инерции относительно центра масс (барицентра) через м и R ?
- Переформулируйте уравнение через м и a , где a — длина каждой стороны квадрата.

- Используйте теорему о параллельных осях, чтобы найти уравнение для теоретического момента инерции относительно вершины квадрата через м и a .
- Рассчитайте теоретическое значение этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите результаты в таблицу данных.
Вырежьте из картона равносторонний треугольник, размер которого подобен показанному на рис. 8. Экспериментально определите его момент инерции относительно оси, показанной на этом рисунке, т. е. оси, которая находится очень близко к одной из вершин треугольника. равносторонний треугольник.
Рисунок 8. Физический маятник равностороннего треугольника Теоретическое уравнение для момента инерции равностороннего треугольника относительно его центра масс следует из рисунка 7 для правильного многоугольника.
- Каково значение n в уравнении, показанном для вашего равностороннего треугольника?
- Получите формулу для момента инерции относительно центра масс через м и R ?
- Переформулируйте уравнение в терминах м и a , где a — длина каждой стороны равностороннего треугольника.
- Используйте теорему о параллельных осях, чтобы найти уравнение для теоретического момента инерции относительно вершины равностороннего треугольника через м и .
- Рассчитайте теоретическое значение этого момента инерции и сравните его со значением, полученным экспериментально. Вычислите разницу в процентах и запишите результаты в таблицу данных.
В таблице моментов инерции Википедии нет записей для общего треугольника. Поэтому вы будете только экспериментально определять момент инерции такого треугольника.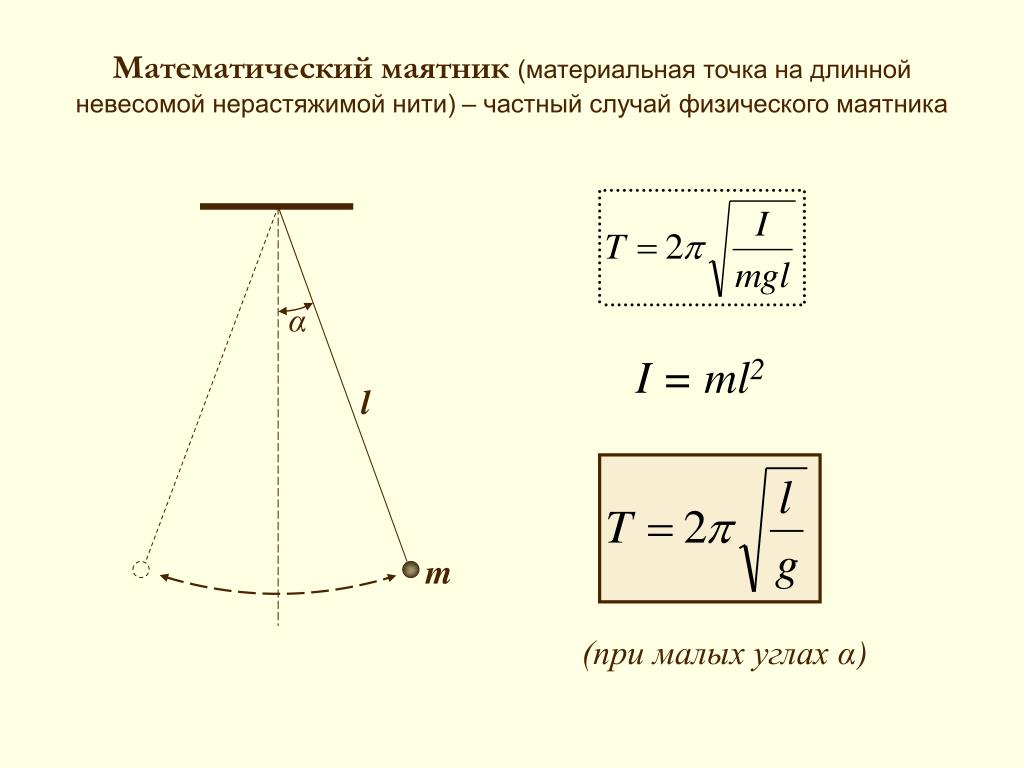 Вырежьте из картона общий треугольник, похожий по форме и размеру на показанный на рис. 9.. Опорную точку следует выбирать рядом с одной из трех вершин.
Вырежьте из картона общий треугольник, похожий по форме и размеру на показанный на рис. 9.. Опорную точку следует выбирать рядом с одной из трех вершин.
Как обычно, чтобы использовать уравнение для момента инерции, показанное на рисунке 1, вам необходимо знать расстояние d между точкой вращения и центром масс. Это означает, что вам нужно знать расположение центра масс. Чтобы найти центр масс, достаточно вспомнить основную теорему из геометрии. Эта теорема утверждает, что три медианы треугольника пересекаются в его центре тяжести (центре масс). Каждая медиана проводится от вершины к центру противоположной, как показано на рисунке 9.. Поэтому вас не должно удивлять, что когда треугольник подвешен к одной из его вершин, медиана лежит вертикально вверх и вниз. Это показано на рис. 9.
Запишите экспериментальный момент инерции в таблицу данных.
Исследование неправильной изогнутой формы Вырежьте из картона неправильную изогнутую форму, похожую по размеру и форме на показанную на рисунке 10. Определите момент этой изогнутой формы. Он вращается вокруг внутренней оси, перпендикулярной форме. Запишите экспериментальный момент инерции в таблицу данных.
Определите момент этой изогнутой формы. Он вращается вокруг внутренней оси, перпендикулярной форме. Запишите экспериментальный момент инерции в таблицу данных.
Рисунок 10. Неправильная изогнутая форма Объект с «негативным пространством» Исследование
Вам может быть интересно, что подразумевается под термином негативное пространство ? Согласно определению художника, негативное пространство можно рассматривать как пространство между объектом и вокруг него. Вырежьте из картона предмет, похожий по размеру и форме на тот, что показан на рисунке 11. Определите момент инерции этой изогнутой формы. Он вращается вокруг оси возле одной из вершин фигуры. Запишите экспериментальный момент инерции в таблицу данных.
Рисунок 11. Объект с «отрицательным пространством»Основываясь на процентах ошибок, полученных вами для известных форм, насколько вы уверены в моментах инерции обычного прямоугольника, неправильной изогнутой формы и объекта с отрицательным пространством?
Таблица данных
Уравнения для простого маятника Рона Куртуса
SfC Home > Physics > Mechanics >
Рон Куртус
Уравнения для простого маятника показывают, как найти частоту и период движения.
Простой маятник состоит из точечной массы, подвешенной на нити или проволоке с незначительной массой. Если груз маятника или груз потянуть на относительно небольшой угол от вертикали и отпустить, он будет качаться вперед и назад с постоянным периодом и частотой. Эти требования позволяют уравнениям быть относительно простыми и называются простое гармоническое движение .
Если грузик больше, проволока имеет массу или угол больше, то маятник называется физическим маятником со сложными уравнениями движения.
Хотя демпфирующие эффекты от сопротивления воздуха и трения являются фактором, им можно пренебречь для основных уравнений, касающихся частоты или периода маятника.
Возможные вопросы:
- Каковы факторы и параметры движения маятника?
- Какие уравнения для частоты и периода?
- Каковы уравнения для длины струны маятника?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц
Факторы и параметры
Основным фактором, включаемым в уравнения для расчета частоты простого маятника, является длина стержня или проволоки при условии, что начальный угол или амплитуда качания малы. Масса или вес боба не влияет на частоту простого маятника, но ускорение под действием силы тяжести является фактором.
Масса или вес боба не влияет на частоту простого маятника, но ускорение под действием силы тяжести является фактором.
Примечание : Это означает, что частота и период будут отличаться на Луне и на Земле.
Зная длину маятника, можно определить его частоту. Или, если вы хотите конкретную частоту, вы можете определить необходимую длину.
Факторы и параметры простого маятника
( См. Демонстрация маятника, чтобы увидеть маятник в движении )
Уравнение периода
Период движения маятника – это время, необходимое для его раскачивания вперед и назад, измеряемое в секундах. Уравнение для периода простого маятника, начинающегося с малого угла α (альфа):
Т = 2π√(л/г)
где
- T – период в секундах (с)
- π — это греческая буква пи и приблизительно равна 3,14
- √ — это квадратный корень из того, что заключено в скобки .
- L длина стержня или проволоки в метрах или футах
- г ускорение свободного падения (9,8 м/с² или 32 фута/с² на Земле)

Таким образом, если L = 2 метра:
T = 2 * 3,14 * √(2/9,8) = 6,28 * √(0,204) = 6,28 * 0,4517
T = 2,837 секунды или немного округлить до Т = 2,8 с.
Частотное уравнение
Частота маятника — это количество колебаний маятника вперед и назад в секунду, измеряемое в герцах.
Частота f является обратной величиной периода T :
f = 1/T
f = 1/[2π√(л/г)]
Уравнение также можно изменить следующим образом:
f = [√(г/л)]/2π
Таким образом, если L = 2 метра,
f = [√(9,8/2)]/2*3,14
f = [√(4,9)]/6,28 = 2,21/6,28 = 0,353 Гц.
Длина провода
Можно найти длину стержня или провода для заданной частоты или периода.
Частота
Решите уравнение для L :
f = [√(г/л)]/2π
2πf = √(г/л)
Возведение в квадрат обеих частей уравнения:
4π 2 f 2 = г/л
Найти L :
L = г/(4π 2 f 2 )
Например, длина маятника с частотой 1 Гц (1 цикл в секунду) составляет около 0,25 метра.
Период
Аналогично длина провода за данный период:
Т = 2π√(л/г)
Квадрат с обеих сторон:
Т 2 = 4π 2 (л/г)
Найти L :
L = gT 2 /4π 2
Резюме
Если вес маятника или груз простого маятника потянуть на относительно небольшой угол и отпустить, он будет качаться вперед и назад с постоянной частотой.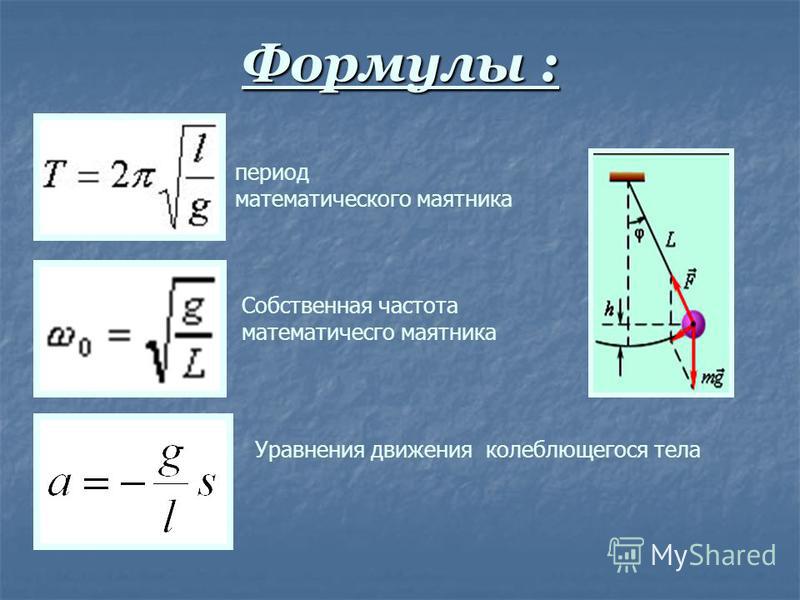 Эти требования позволяют уравнениям быть относительно простыми и называются простое гармоническое движение .
Эти требования позволяют уравнениям быть относительно простыми и называются простое гармоническое движение .
Если демпфирующие эффекты от сопротивления воздуха и трения пренебрежимо малы, можно рассчитать уравнения, касающиеся частоты и периода колебаний маятника, а также длины струны.
Уравнение периода: T = 2π√(л/г)
Частотное уравнение: f = [√(г/л)]/2π
Уравнения длины: L = g/(4π 2 f 2 ) и L = gT 2 /4π 2
Чувствуйте себя хорошо, выполняя свою лучшую
Ресурсы и ссылки
Ron Kurtus ‘Colretins
Веб -сайты
Как Pendulum Whols Works 9052-
Как Pendulum Works 9052–
. Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом на Pendulums
Книги с самым высоким рейтингом по периодическому движению
Книги с самым высоким рейтингом по физике движения
Поделиться этой страницей
Нажмите кнопку, чтобы добавить в закладки или поделиться этой страницей через Twitter, Facebook, или другие услуги:
Студенты и исследователи
Веб-адрес этой страницы:
www. school-for-champions.com/science/
school-for-champions.com/science/
pendulum_equations.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа чемпионов
Темы физики
Уравнения для простого маятника
Pendulums — MCAT Physical
Все физические ресурсы MCAT
8 диагностических тестов 303 практических теста Вопрос дня Карточки Учитесь по концепции
Физическая помощь MCAT » Физика » Ньютоновская механика и движение » Вращательное, круговое и гармоническое движение » Маятники
Какое из следующих изменений увеличило бы частоту колебаний маятника?
Возможные ответы:
Увеличить угол смещения
Увеличить массу на конце маятника
Уменьшить угол смещения
Уменьшить длину нити маятника
Увеличение длины нити маятника
Правильный ответ:
Уменьшение длины нити маятника
Пояснение:
Единственными двумя факторами, влияющими на частоту маятника, являются ускорение свободного падения (g) и длина нити маятника (L). Это можно увидеть в следующей формуле: .
Это можно увидеть в следующей формуле: .
Сообщить об ошибке
Какие факторы увеличивают максимальную скорость маятника?
Возможные ответы:
Уменьшение длины нити маятника и увеличение угла смещения
Уменьшение длины нити маятника и угла смещения
Увеличение длины нити маятника и уменьшение угла смещения
Увеличение как длины нити маятника, так и угла смещения
Правильный ответ:
Увеличение как длины нити маятника, так и угла смещения
Пояснение:
На максимальную скорость маятника влияют как длина нити маятника, так и угол смещения. Увеличение длины нити маятника и увеличение угла смещения увеличивают расстояние, которое маятник должен пройти за один период, увеличивая его потенциальную энергию на максимальной высоте и, следовательно, максимальную скорость в самой низкой точке.
Сообщить об ошибке
Каков период маятника с длиной нити 90,8 м?
Возможные ответы:
Правильный ответ:
Объяснение:
Ключ к ответу на этот вопрос — вспомнить следующую важную формулу для простого маятника: .
Сообщить об ошибке
Какое из следующих изменений маятника повлияет на угловую скорость?
Возможные ответы:
Поднятие высоты, с которой высвобождается масса
Увеличение груза на конце нити
Уменьшение длины нити
Уменьшение высоты, с которой сбрасывается груз
Правильный ответ:
Уменьшение длины нити
Объяснение:
Для маятника угловая скорость определяется уравнением , где – ускорение свободного падения, – длина маятника. Из доступных вариантов ответа только изменение длины струны повлияет на угловую скорость. не зависит ни от массы, ни от точки отпускания маятника.
Из доступных вариантов ответа только изменение длины струны повлияет на угловую скорость. не зависит ни от массы, ни от точки отпускания маятника.
Сообщить об ошибке
Частота колебаний маятника на Земле равна . Какова будет приблизительная частота того же маятника на Луне?
Приблизительная гравитация на Луне .
Возможные ответы:
Правильный ответ:
Объяснение:
Частота маятника определяется соотношением .
Поскольку сила тяжести на Луне составляет одну шестую силы тяжести на Земле, частота на Луне будет такой же, как и на Земле.
Если частота на Земле равна , то частота этого маятника на Луне равна .
Сообщить об ошибке
Период определенного маятника . Каков период после удвоения массы на конце маятника?
Возможные ответы:
Правильный ответ:
Пояснение:
Период маятника находится по формуле:
– это длина плеча маятника или нити, а – ускорение свободного падения. Гравитация постоянна, что говорит о том, что единственный способ управлять периодом маятника — это регулировать длину струны. Следовательно, удвоение длины плеча маятника приведет к увеличению периода. Поскольку масса не фигурирует в уравнении, она не влияет на период маятника.
Гравитация постоянна, что говорит о том, что единственный способ управлять периодом маятника — это регулировать длину струны. Следовательно, удвоение длины плеча маятника приведет к увеличению периода. Поскольку масса не фигурирует в уравнении, она не влияет на период маятника.
Сообщить об ошибке
Маятник пришел в движение. Какое из этих утверждений правильно характеризует механическую энергию в системе?
Возможные ответы:
Механическая энергия в системе изменяется от максимума в точке выброса до половины значения максимума в середине дуги
Ни одно из этих утверждений не верно
механическая энергия изменяется от нуля в середине дуги до максимума в точке срабатывания
Без учета трения механическая энергия постоянна
Механическая энергия изменяется от нуля в точке срабатывания до максимума в середина дуги
Правильный ответ:
Пренебрегая трением, механическая энергия постоянна
Пояснение:
Механическая энергия представляет собой сумму потенциальной энергии и кинетической энергии. Механическая энергия сохраняется, если не вмешивается неконсервативная сила (например, трение).
Механическая энергия сохраняется, если не вмешивается неконсервативная сила (например, трение).
Полная энергия в системе определяется тем, насколько высоко маятник поднят до отпускания, исходя из начальной потенциальной энергии.
Вся потенциальная энергия преобразуется в кинетическую энергию, когда маятник качается через нижнюю или среднюю точку своего движения.
Когда маятник приходит в движение, механическая энергия в системе без трения постоянна.
Сообщить об ошибке
Для маятника, совершающего простое гармоническое движение, отношение веса маятника к смещению маятника из самой нижней точки на его пути всегда равно __________.
Возможные ответы:
Натяжение в строке
Сумма кинетической и потенциальной энергии объекта
Гравитационная постоянная
Пружина Константа
Правильный ответ:
Постоянная пружина
Пояснение: Закон Гука, применимый к простому гармоническому движению, устанавливает связь между силой (F) и перемещением (d). k равно жесткости пружины. Отношение F (силы) к x (смещению) будет равно величине k. В нашей схеме сила равна весу маятника, поэтому отношение веса к смещению равно жесткости пружины. Это справедливо для всех маятников и определяется уравнением . Сообщить об ошибке Маятник имеет длину 2 метра с массой 5 кг на конце. Он имеет максимальный угол 60 градусов от вертикали и свисает с потолка лифта. Когда маятник находится в высшей точке, лифт начинает ускоряться со скоростью . Какова новая максимальная скорость маятника (без учета вертикальной скорости лифта)? Возможные ответы: Правильный ответ: Пояснение: Эта задача охватывает сохранение энергии в форме маятника: Если начальное состояние — когда маятник находится в высшей точке, а конечное состояние — когда маятник находится в низшей точке, мы можно переписать: Подставляя в наши выражения: Переставляя конечную скорость: Мы можем рассчитать высоту, используя максимальный угол, который маятник образует с вертикалью. Следовательно, высота над самой низкой точкой равна: Теперь нам просто нужно выяснить, каково чистое ускорение вниз. Обычно гравитация равна 10, но лифт ускоряется вверх со скоростью . Следовательно, воспринимаемое гравитационное ускорение равно . Подставляем все наши значения: Сообщить об ошибке Уведомление об авторских правах 8 Диагностические тесты
303 практических теста
Вопрос дня
Карточки
Learn by Concept Колебательное движение является основной темой курса физики на всех уровнях бакалавриата. В данной работе мы изучаем демпфирование стержня, действующего как физический маятник, находящегося под действием сопротивления воздуха. View on IOP Publishing Physics, Education Papers in Physics Этот классический эксперимент может привести к интересному и недорогому эксперименту по механике и использованию акселерометра. как радиальные, так и орбитальные ускорения маятника в различных положениях вдоль его оси дают возможность выполнить более сложный анализ. Физика, образование Мы использовали два составных маятниковых датчика для анализа с использованием Arduino и родственного маятника. оценивающий гаджет. Мы указали, что использование акселерометра для измерения… Образование, Физика Измерить колебания простого маятника, вероятно, было первой идеей, пришедшей в голову после появления смартфонов с маленькими, но мощными датчиками ускорения~: Просто подключите телефон к… Физика, образование Physics Education В данной статье демонстрируется использование датчиков смартфона для записи экспериментальных данных для исследования большого угла физического маятника. Физика Physics Education . в смартфонах позволяют точно измерять угловую скорость маятников при больших углах, а фазовые графики зависимости углового ускорения от углового смещения… Физика, образование Обучение физике
 В этой точке маятник проходит расстояние по вертикали:
В этой точке маятник проходит расстояние по вертикали: Все физические ресурсы MCAT
Исследование большеугловых ангармонических колебаний физического маятника с помощью датчика ускорения
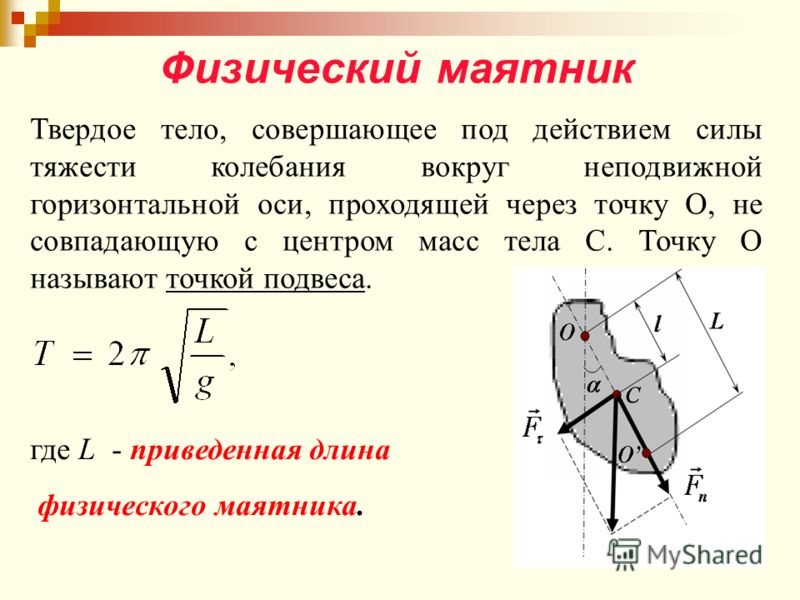 В. Н. Гонсалвес и А. Феррас},
journal={Европейский журнал физики},
год = {2017},
объем = {38}
}
В. Н. Гонсалвес и А. Феррас},
journal={Европейский журнал физики},
год = {2017},
объем = {38}
} Повторное исследование эксперимента с физическим маятником с использованием датчика акселерометра

Датчик акселерометра для физического маятника полная формулировка
Новые измерения простого маятника с использованием датчиков ускорения.
Исследование большой угол физического маятника с использованием датчиков смартфона
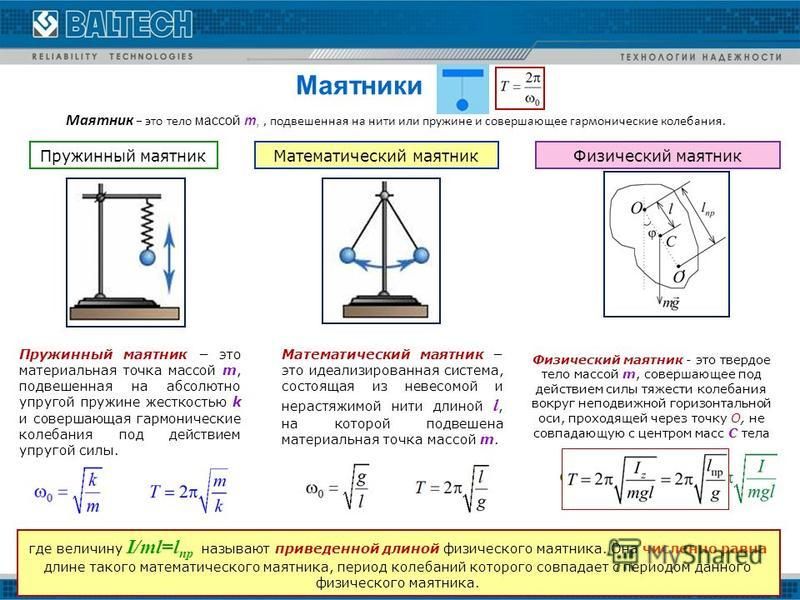 Смартфон (iPhone 5S) был прикреплен к луче к…
Смартфон (iPhone 5S) был прикреплен к луче к… Угловое ускорение нелинейного маятника
Изучение простого маятника с помощью недорогой беспроводной платы сбора данных
Обзор приближенных уравнений для периода маятника
Прецизионные измерения периода маятника как функции амплитуды теперь могут быть выполнены с помощью различных инструментов, включая гироскопы/акселерометры MEM, и, таким образом, теоретические выражения… Pendrill, Conny Modig
Физика, образование
Физика, образование
поездки. Традиционный…
Традиционный…
Колебания пластины из листов бумаги формата А4
- В. Оливейра
Физика, инженерия
European Journal of Physics
- 2019
2 Прямоугольная пластина из недорогих листов бумаги колебаться вокруг оси, перпендикулярной своей плоскости или параллельной малой стороне. Пластина связана с вращательным движением…
Искусство подгонки моделей обыкновенных дифференциальных уравнений к экспериментальным результатам
Усовершенствованная подгонка моделей обыкновенных дифференциальных уравнений к экспериментальным результатам представлена в контексте различных академических уровней студентов и различных областей исследований. Во многих областях…
ПОКАЗАНЫ 1-10 ИЗ 21 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные статьиНедавность
Точная формула для периода колебаний простого маятника за пределами режима малых углов
- Ф. Лима, П. 0 9014 Арун
Физика, образование
- 2005
Получено простое приближенное выражение для зависимости периода простого маятника от амплитуды. Аппроксимация более точна, чем другие простые соотношения. Хорошее согласие с…
Аппроксимация более точна, чем другие простые соотношения. Хорошее согласие с…
Маятник — Богатая физика из простой системы
- Р. Нельсон, М. Олссон
Физика, образование
- 1986
Мы предоставляем всестороннее обсуждение поправок, необходимых для точного обсуждения поправок ускорение силы тяжести с помощью плоского маятника. Описан простой лабораторный эксперимент, в котором g было…
Приближенное выражение для периода большого угла простого маятника
- Р. Парвани
Физика, образование
- 2004
Эвристический, но педагогический период, который точно воспроизводит формулу вывода простой маятник даже для больших амплитуд. Формула сравнивается с другими в…
Новый взгляд на простой маятник
- Н. Аггарвал, Нитин Верма, П. Арун
Физика, образование
- 2005
Мы описываем интерфейс микропроцессора 8085, разработанный для надежных измерений периода времени. С помощью этого интерфейса измерялся период времени каждого колебания простого маятника.
С помощью этого интерфейса измерялся период времени каждого колебания простого маятника.
Колебания квадратично затухающего маятника
- C. Mungan, T. Lipscombe
Физика
- 2013
датчик вращательного движения с низким коэффициентом трения, так что его угловое положение и скорость могут быть точно определены…
Аппроксимация для периода простого маятника с большими углами анализируются и обсуждаются колебания простого маятника. Аналитическая приближенная формула для периода та же самая, что и…0140
Физика
Мы исследуем ангармонизм маятника с большой амплитудой и разрабатываем новый метод обнаружения высоких компонентов Фурье как функции амплитуды для больших амплитуд, близких к 180°.…
Применение уравнение Матье
- Л. Руби
Физика
- 1996
Рассмотрены свойства уравнения Матье с целью обсуждения некоторых приложений, появившихся в последние годы. Упоминаются: колебания в эллиптическом барабане, перевернутый…
Упоминаются: колебания в эллиптическом барабане, перевернутый…
Комментарий к «Приближению периода простого маятника с большими углами» Phys. 30 L25–8) предложил альтернативу аппроксимации периода простого маятника, предложенную ранее Hite (2005 Phys. Teach. 43 290–2)…
Аналитическое решение уравнения движения затухающего нелинейного маятника
- Ким Йоханнессен
Физика
- 2014
Представлено аналитическое приближение решения дифференциального уравнения, описывающего колебания затухающего нелинейного маятника на больших углах. Решение выражается в терминах…
Разница между простым маятником и составным маятником
Прежде чем узнать разницу между простым маятником и составным маятником, мы должны четко знать о простом маятнике и сложном маятнике по отдельности. Маятник — это груз или тело, подвешенное к фиксированной точке так, что оно будет раскачиваться вперед и назад. Есть много разных типов маятников. Простой маятник и составной маятник – это два типа среди множества различных типов маятника.
Простой маятник и составной маятник – это два типа среди множества различных типов маятника.
Что такое простой маятник?
В часах используется простой маятник. Простой маятник просто имеет некоторый вес, называемый бобом, при подвешивании боба к пружине он будет качаться, потому что гравитация тянет вниз.
Чтобы найти период простого маятника, мы должны предположить, что на идеальной плоскости маятник будет качаться, сила тяжести остается постоянной, трение между воздухом и системой остается постоянным, плечо маятника не изгибается и не сжимается, а также должно быть безмассовым только тогда мы сможем найти период простого маятника.
Период времени простого маятника = Общее время/количество колебаний
или
T =2 π √(л/г)
, где T – период времени,
3 903, 903
L — длина маятника, а g — сила тяжести Земли (g = 9,8 м/с 2 ).
Примеры простого маятника: Люлька, Часы, Банджи-джампинг и т. д.
д.
Схема простого маятника показана ниже.
Simple Pendulum
Преимущества Simple Pendulum:
- Простота использования и низкая стоимость установки.
- Операции по обеспечению безопасности выполняются с помощью этого простого маятника.
Недостатки простого маятника:
- Вес простого маятникового поплавка не меньше, чем у тяжелого точечного поплавка.
- Движение боба нелинейно.
- Сопротивление и плавучесть незначительны.
- На трамплинах используется простой маятник.
- В сейсмостойком здании используется простой маятник.
- В банджи-джампинге используется простой маятник.
- В музыкальных инструментах используется простой маятник.
Штанга составного маятника, которая находится в режиме качания и свободно колеблется вокруг горизонтального прохода. Период времени составного маятника измеряется от центра колебаний до уровня поворота. Составной маятник также известен как физический маятник.
Период времени составного маятника измеряется от центра колебаний до уровня поворота. Составной маятник также известен как физический маятник.
Радиус колебания составного маятника = I/(m × R)
где
- I — инерция,
- m — масса, а
- R — расстояние между центром масс и точкой поворота. .
Период времени сложного маятника = 2 × π(√(I/mgR))
, где
- g — ускорение свободного падения.
Примеры составных маятников: машины для распределения веса, парусные лодки, сельскохозяйственные тракторы и т. д.
Общая схема составного маятника представлена ниже.
Составной маятник
Преимущества составного маятника:
- Время можно точно рассчитать с помощью составного маятника.
- Составной маятник обладает большей энергией.
Недостатки составного маятника:
- Составной маятник меняет свое поведение при движении вокруг Земли.

- При изменении температуры период колебания также меняется.
- В сельскохозяйственных тракторах используется составной маятник.
- В парусных судах используется составной маятник.
- В хоккейных клюшках используется составной маятник.
- В гольфе используется составной маятник.

Примеры вопросов
Вопрос 1. Если период времени простого маятника равен 2,5 с, то определить его длину.
Ответ:
Мы знаем эту формулу для периода времени простого маятника,
T=2 π √(L/g)
где,
L= длина простого маятника, g=сила тяжести=9,8 м/с 2 , при T = 2,5 с.
Подставив T, g в приведенную выше формулу, мы получим длину простого маятника
Возведение в квадрат с обеих сторон,
0,158 = L/9,8
L = 1,5484 м
с 2
Ответ:
Учитывая, что длина маятника L = 2 м
и сила тяжести (г) = 10 м/с 2
900 мы знаем, что простая формула периода маятника
T=2 π √(L/g)
Следовательно,
Частота (f)=1/T
Подставив L, g в приведенное выше уравнение, мы получим период (T)
T = 2 x 3,14 (√(2/10))
= 6,28 x (√(0,2))
= 6,28 x 0,447
= 2,80 с
Но частота обратно пропорциональна периоду времени, поэтому
f = 1/T
= 1/2,80
= 0,3571 Гц
76/ на Луне. . Найдите длину простого маятника, если период времени равен 3 с.
Ответ:
Учитывая, что гравитация на Луне (g)=1,6 м/с 2
Период времени (T) = 3 секунды
Чтобы узнать длину маятника
t = 2 π √ (l/g)
3 = 2 x 3,14 √l/1,6
(3/6,28) 2 = L/1,6
0,2275 = L/1,6
L = 0,364.


 Это дается как;
Это дается как; Формы будут исследоваться в порядке сложности соответствующих физических и математических методов. Эти формы, в порядке их исследования, следующие:
Формы будут исследоваться в порядке сложности соответствующих физических и математических методов. Эти формы, в порядке их исследования, следующие:



