По ширине и по длине: Выравнивание текста - Служба поддержки Майкрософт

По ширине и по длине: Выравнивание текста – Служба поддержки Майкрософт

alexxlab | 13.12.2022 | 0 | Разное

Содержание

Выравнивание текста – Служба поддержки Майкрософт

Word для Microsoft 365 для Mac Word 2021 for Mac Word 2019 для Mac Word 2016 для Mac Word для Mac 2011 Еще…Меньше

Часть содержимого этого раздела может быть неприменима к некоторым языкам.

Выравнивание текста — это атрибут форматирование абзацев, который определяет внешний вид текста во всем абзаце. Например, в абзаце с выравниванием по левому краю (наиболее распространенное выравнивание), текст выравнивается по левому полю. В абзаце, который выровнен по обоим полям, текст выравнивается по обоим полям.

выравнивание текста по леву

текст по центру

выравнивание текста по правому

текст по у цель

распространить текст

Выравнивание текста по левому краю, по центру или по правому краю

Щелкните любое место абзаца, который необходимо выровнять.
На вкладке Главная в группе Абзац сделайте следующее:

Задача

Команда

Выравнивание текста по левому краю

Выравнивание текста по левую

Выравнивание текста по центру

Центр текста

Выровнять текст по правому краю

Выровнять текст по правому

Выровнять по ширине

При выравнивании текста по ширине между словами добавляется пространство, чтобы оба края каждой строки были выровнены относительно обоих полей.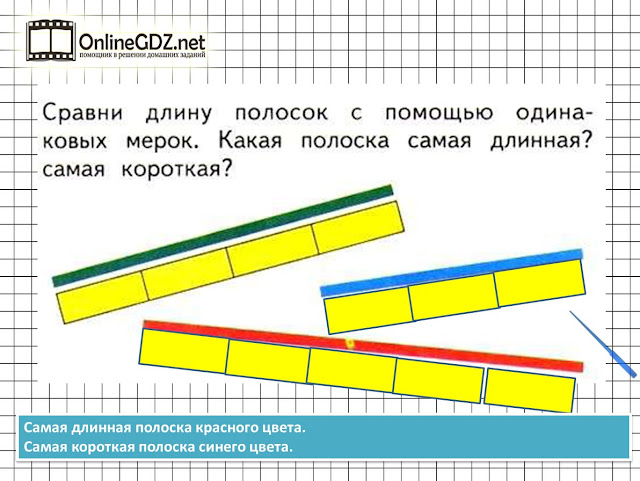 Последняя строка абзаца выравнивается по левому краю.

Щелкните любое место абзаца, который необходимо выровнять по ширине.
На вкладке Главная в группе Абзац нажмите кнопку Вы можете выжать .

Важно: Microsoft Office для Mac 2011 больше не поддерживается. Перейдите на Microsoft 365, чтобы работать удаленно с любого устройства и продолжать получать поддержку.

Обновить

Выравнивание текста по левому краю, по центру или по правому краю

Щелкните любое место абзаца, который необходимо выровнять.
На вкладке Главная в Абзац выполните одно из перечисленных ниже действий.

Задача	Команда
Выравнивание текста по левому краю	Выравнивание текста по левую
Выравнивание текста по центру	Центр текста
Выровнять текст по правому краю	Выровнять текст по правому

Выровнять по ширине

При выравнивании текста по ширине между словами добавляется пространство, чтобы оба края каждой строки были выровнены относительно обоих полей.

Последняя строка абзаца выравнивается по левому краю.

Щелкните любое место абзаца, который необходимо выровнять по ширине.
На вкладке Главная в области Абзацнажмите кнопку Вы можете .

Распределить текст

При распределения текста между символами добавляется пространство, чтобы оба края каждой строки были выровнены относительно обоих полей. Последняя строка абзаца также распределяется.

org/ListItem”>
Щелкните любое место абзаца, текст в котором необходимо распределить.
На вкладке Главная в области Абзацнажмите кнопку Распределенный .

См. также

Настройка отступов и интервалов

Выравнивание объектов

Выравнивание текста или настройка границ в текстовом поле

Тема: « Сравнение по ширине и длине» | План-конспект занятия по математике (подготовительная группа) на тему:

Познание (ФЭМП) в подготовительной группе на

Тема: « Сравнение по ширине и длине»

Реализация содержания программы в образовательных областях: Познавательное развитие, Физическое развитие, Речевое развитие.

Виды детской деятельности: познавательная, игровая, двигательная, коммуникативная.

цель: Учить детей располагать предметы в возрастающем и убывающем порядке по величине, ширине, высоте, толщине и длине.Закреплять умение сравнивать длины предметов с помощью непосредственного наложения.

Задачи:

Оразовательная:

Формировать представления о том, что для сравнения каких-то предметов их надо измерить.

Учить определять величину предметов на глаз, правильность заданий проверять путем соизмерения предметов: приемом наложения, приложения и давая им характеристику.

Связывая числительные с существительными; правильно употреблять в речи имена прилагательные.

Развивающая: Развивать внимание, глазомер, мелкую моторику рук, мышление, грамматический строй речи.

Воспитательная: Воспитывать умение работать самостоятельно, формировать навыки взаимоконтроля. Воспитывать дружелюбное отношение друг к другу.

Планируемые результаты: уметь определять высоту предметов на рисунке и сравнивать их по высоте; составлять предложения, используя в речи слова (выше- ниже,) согласовывая части предложения между собой; сравнивать ширину предметов путем наложения.

Материалы и оборудование: картинки с изображением предметов разной высоты и ширины, цветная бумага, рисунки с изображением самолета, вертолета, ракеты, птицы, бабочки, карточки с названиями городов, билеты, чистоговорка

Содержание организованной деятельности детей.

1.Организационный момент.

Звучит музыка “Улыбка”.

Сегодня мы отправимся в путешествие по чудесной стране Математике. Но для этого нам надо купить билет в кассе. (дети выбирают себе билеты. Билеты разных цветов – красного, желтого, зеленого).А отправимся мы в путешествие на паровозике из Ромашкова по вагонам (пока по группе змейкой идёт паровозик, дети проговаривают чистоговорку со звуком “ч”)

1 город “История”

Воспитатель: Как вы думаете, что мы будем делать в городе?

В древности человеку приходилось постигать не только искусство счета, но и измерений. Когда древний человек, уже мыслящий, попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего жилища в соответствии с собственным ростом. А ведь это и есть измерение. Наш предок располагал только собственным ростом, длинной рук и ног.

В Древней Руси существовали свои измерения. Древнейшими мерами длины являются локоть и сажень. Локтем являлась длина от локтя до переднего сустава среднего пальца,. Сажень простая — расстояние между размахом вытянутых рук человека от большого пальца одной руки до большого пальца другой, пядь — расстояние от конца большого пальца до конца мизинца при наибольшем возможном их раздвижении.

Словесное закрепление.

Итак, нам известны меры измерения Древней Руси – это локоть, сажень, пядь.

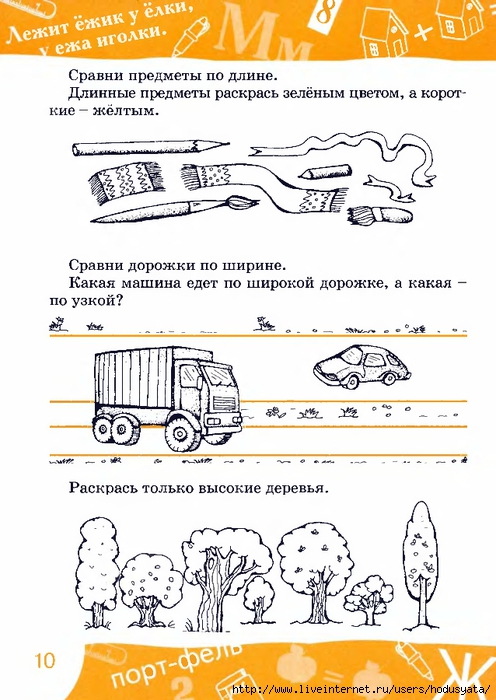
Задание 1:

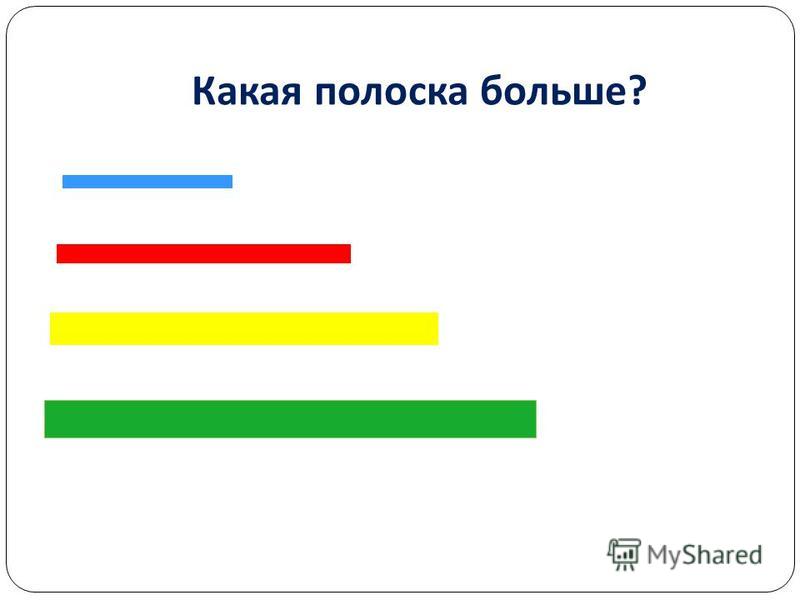
Рассмотрите рисунок и сравните по ширине красную полоску с желтой (красная уже желтой)

сравните по ширине желтую полоску с синей (желтая полоска шире красной)

сравните синюю полоску с желтой (желтая полоска уже синей)

Молодцы, вы справились со всеми заданиями, а теперь в путь, поедем дальше путешествовать по городам страны Математики.

2 город “Рассуждай”

Задание1: игра “Дополнение”

(размещаются рисунки (сверху вниз) ракета, самолет, вертолет, птица, бабочка)

закончить начатое предложение(ответ принимается, если поднята рука у ребенка)

*высоко в небе летит . ..(ракета)

*ниже ракеты летит…(самолет)

*самолет летит….(выше вертолета)

*вертолет летит…(выше бабочки)

Задание 2:рассмотрите схему на доске и покажите(дети встают возле тех кувшинов, где они считают правильным ответ)

*кувшин, в котором воды меньше всего

*кувшин, в котором воды больше

3 город”Физкультура”

На разминку – становись!

Вправо – влево покрутись,

Повороты посчитай,

Раз-два-три, не отставай.

(Вращение туловищем вправо и влево.)

Начинаем приседать –

Раз, два, три, четыре, пять.

Тот, кто делает зарядку,

Может нам сплясать вприсядку.

(Приседания.)

А теперь поднимем ручки

И опустим их рывком.

Будто прыгаем мы с кучки

Летним солнечным деньком.

(Дети поднимают прямые руки над головой, потом резким движением опускают их и отводят назад, потом резким движением снова вверх и т. д.)

А теперь ходьба на месте,

Левой-правой, стой, раз-два.

(Ходьба на месте. )

Отдохнули, сил набрались и снова в путь

4 город “Геометрия”

Задание 1: рассмотрите рисунок и скажите, что находится ниже, что выше

( на рисунке изображено: дом, береза, ель, самолет, вертолет, ласточка)

Задание 2: Ряд геометрических фигур.

-Что это, как назовем одним словом? (геометрические фигуры)

-Как можно разбить на три группы? (по цвету, по размеру, по форме)

Задание 3: Работа с счетными палочками

Выложите перед собой по центру стола прямоугольник, справа от него треугольник, слева от прямоугольника квадрат, сверху от прямоугольника квадрат меньше того, который вы только что сделали, внизу от прямоугольника маленький треугольник.

Посчитайте сколько геометрических фигур у вас получилось?

А сколько счетных палочек вы затратили на выполнение этого задания?

Воспитатель: Вот и закончилось наше путешествие. Пора нам отправляться в город «Отдыхай».

Упражнение на релаксацию «Волшебный сон»(под спокойную музыку).

Реснички опускаются,

Глазки закрываются,

Мы спокойно отдыхаем.

Тихо скажем: «Спасибо тебе,

Головушка, за твою работу.

Ручки, ножки, спасибо!»Реснички открываются

И ребята просыпаются

Воспитатель: Понравилось вам наше путешествие, а чем оно вам запомнилось?

Длина Ширина Высота – Формула, Примеры

длина, ширина и высота – это размеры геометрической фигуры, которые показывают длину, ширину и высоту фигуры. В то время как длина — самая длинная сторона фигуры, ширина — более короткая сторона, а высота — вертикальный размер фигуры. Давайте узнаем больше о длине, ширине, высоте фигур.

1.	Что такое Длина Ширина Высота?
2.	Длина против ширины
3.	Длина Ширина Высота коробки
4.	Часто задаваемые вопросы о длине, ширине, высоте

Что такое Длина Ширина Высота?

Длина, ширина и высота — это инструменты, которые используются для определения размеров объекта.

Когда мы говорим о двухмерных фигурах (2D-фигурах), мы используем длину и ширину, тогда как, когда мы ссылаемся на трехмерные фигуры (3D-фигуры), мы используем высоту вместе с длиной и шириной. Давайте теперь разберемся с тремя терминами.

Длина: длина используется для измерения расстояния между двумя точками. Длина — это самое длинное измерение фигуры, и она показывает, насколько длинна данный объект или фигура. Он выражается в линейных единицах, таких как метры, сантиметры, дюймы и так далее.
Ширина: Ширина – это более короткое расстояние объекта или фигуры, и она показывает, насколько широка или широка данная фигура. Ширина также выражается в линейных единицах, таких как метры, сантиметры, дюймы и т. д.
Высота или глубина: высота объекта относится к его глубине или третьему вертикальному измерению объекта и показывает, насколько высок или глубок объект. Высота или глубина объекта выражается в линейных единицах, таких как метры, сантиметры, дюймы и т. д.

Следует отметить, что длина, ширина, высота и глубина являются словами, которые являются производными от слов длинный, широкий, высокий и глубокий соответственно. Следовательно, они выражают размеры объекта. Обратите внимание на рисунок, приведенный ниже, чтобы увидеть длину, ширину и высоту прямоугольного параллелепипеда.

Длина против ширины

Разница между длиной и шириной фигуры заключается в том, что длина обозначает более длинную сторону, а ширина обозначает более короткую сторону фигуры.

Длина показывает длину фигуры, а ширина показывает, насколько она широка или широка. Ширину также называют широтой. Например, если две стороны прямоугольника равны 8 см и 3 см, мы можем легко определить, что длина прямоугольника равна 8 см, а ширина прямоугольника равна 3 см. Обратите внимание на прямоугольник, приведенный ниже, чтобы увидеть разницу между длиной и шириной фигуры.

Длина x Ширина x Высота

Длина, ширина и высота обычно используются вместе, чтобы найти объем геометрической фигуры, такой как прямоугольная призма, также известная как параллелепипед. Когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем. Это означает, что длина x ширина x высота = объем прямоугольного параллелепипеда. Другими словами, вместимость или объем кубоида или любой прямоугольной коробки можно измерить, если мы умножим эти три измерения вместе. Давайте разберемся в этом на примере.

Пример: Найдите объем прямоугольного параллелепипеда, если его длина 8 единиц, ширина 4 единицы, а высота 3 единицы.

Решение: Объем прямоугольного параллелепипеда можно рассчитать по формуле

Объем параллелепипеда = длина x ширина x высота

Длина Ширина Высота коробки

Длину, ширину и высоту коробки легко определить, потому что мы знаем, что длина — это самая длинная сторона, ширина — это более короткая сторона, а высота — это вертикальный размер коробки. Обратите внимание на приведенный ниже рисунок, на котором показаны длина, ширина и высота ящика.

Эти размеры всегда выражаются в том порядке, в котором сначала идет длина, затем ширина и затем высота. Это означает, что если размеры коробки должны быть измерены, они выражаются в порядке длины, ширины и высоты. Например, 15 дюймов × 10 дюймов × 3 дюйма означает, что 15 дюймов — это длина коробки, 10 дюймов — ширина коробки и 3 дюйма — высота коробки.

☛Статьи по теме

Измерение
Преобразование длины
Измерение длины

Пример 1: Найдите объем прямоугольного параллелепипеда, используя заданные длину, ширину и высоту: длина = 9 единиц, ширина = 5 единиц, высота = 4 единицы
Решение: Формула, используемая для нахождения объема кубоида,
Объем кубоида = Длина x Ширина x Высота
После подстановки данных получаем, Объем кубоида = 9 × 5 × 4 = 180 единиц ³
Следовательно, объем прямоугольного параллелепипеда равен 180 единицам ³
Пример 2: Найдите длину прямоугольного параллелепипеда, если его объем 196 кубических единиц, ширина 4 единицы, а высота 7 единиц.
Решение:
Формула, которая используется для нахождения объема прямоугольного параллелепипеда:
Объем прямоугольного параллелепипеда = длина x ширина x высота6, ширина = 4, высота = 7, длина = ?
После подстановки данных получаем 196 = длина × 4 × 7 ^.
После решения этого уравнения мы получаем длину как, длина = 196/28 = 7 единиц.
Следовательно, длина прямоугольного параллелепипеда равна 7 единицам.
Пример 3: Укажите истинное или ложное значение.
а.) Длина показывает ширину фигуры.
b.) Ширина также называется широтой.
c.) Когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем.
Решение:
а) Неверно, длина показывает длину фигуры.
б.) Правда, ширину называют еще широтой.
в.) Правда, когда мы умножаем длину, ширину и высоту прямоугольного параллелепипеда, мы получаем его объем.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по длине ширине высоте

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о длине, ширине, высоте

Что такое Длина Ширина Высота?

Длина, ширина, высота, и глубина — это слова, образованные от прилагательных длинный, широкий, высокий и глубокий соответственно. Следовательно, они выражают размеры объекта. В то время как длина показывает длину данного объекта, ширина показывает, насколько он широк, а высота показывает, насколько он высок. Все они выражаются в линейных единицах, таких как сантиметры, метры, дюймы и так далее.

Какая формула для длины, ширины и высоты?

Когда длина, ширина и высота прямоугольного параллелепипеда перемножаются, получается объем прямоугольного параллелепипеда. Формула объема прямоугольного параллелепипеда: объем прямоугольного параллелепипеда = длина × ширина × высота.

В чем разница между длиной, шириной, высотой?

Длина, ширина, высота объекта — это различные размеры, выраженные в линейных единицах. В то время как длина — это самая длинная сторона фигуры, ширина — это более короткая сторона, а высота — это вертикальный размер или глубина фигуры.

Какой порядок длины ширины высоты?

Когда записываются размеры геометрической фигуры, они записываются в том порядке, в котором сначала идет длина, затем ширина и затем высота. Например, если необходимо выразить размеры прямоугольного параллелепипеда, его запишут как длина × ширина × высота, то есть 7 × 4 × 3, где 7 представляет длину, 4 — ширину, а 3 — высоту. кубоид.

Как рассчитать кубический метр по длине, ширине и высоте?

Кубический метр — это единица измерения объема прямоугольного параллелепипеда. Поэтому, чтобы найти объем прямоугольного параллелепипеда в кубических метрах, нужно перемножить длину, ширину и высоту. Следует отметить, что все длины, ширины и высоты должны иметь одни и те же единицы измерения (метры), чтобы объем выражался в кубических метрах. Например, если длина прямоугольного параллелепипеда 10 м, ширина 6 м, а высота 3 м, найдем его объем в кубических метрах. Объем кубоида = длина × ширина × высота. После подстановки значений получаем, Объем прямоугольного параллелепипеда = 10 × 6 × 3 = 180 кубических метров.

Какова длина, ширина и высота прямоугольного параллелепипеда?

Длина прямоугольного параллелепипеда равна наибольшей стороне, когда параллелепипед расположен горизонтально. Ширина – это более короткая сторона прямоугольного параллелепипеда. Высота – это вертикальный размер прямоугольного параллелепипеда.

Как найти длину, ширину и высоту, если задан объем?

Формула, которая используется для нахождения объема прямоугольного параллелепипеда: Объем прямоугольного параллелепипеда = длина × ширина × высота. Следовательно, если какое-либо одно измерение отсутствует, его можно рассчитать с помощью этой формулы, заменив другие заданные значения. Например, найдем высоту прямоугольного параллелепипеда, если объем прямоугольного параллелепипеда равен 144 кубических см, длина = 12 см, ширина = 2 см. Поскольку высота прямоугольного параллелепипеда неизвестна, подставим в формулу остальные размеры. Объем прямоугольного параллелепипеда = длина × ширина × высота. После подстановки известных значений получаем 144 = 12 × 2 × Высота. Решив это, получим высоту 6 см.

Скачать БЕСПЛАТНЫЕ учебные материалы

Длина Ширина Высота

Калькулятор отношения длины и ширины к площади

Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для создания закладок и обмена текущими настройками инструмента

✕ очистить настройки

Отразить инструмент с текущими настройками и рассчитать длину или ширину

или Калькулятор ширины

Преобразование площади в другие единицы измерения

LxW и количество на единицу площади до общего количества

Площадь и количество на единицу площади к общему количеству

Преобразователь суммы на единицу площади

Калькулятор отношения диаметра окружности к площади

Преобразователь длины и расстояния

Расчет объема по длине, ширине и высоте

Руководство пользователя

Этот инструмент рассчитает площадь прямоугольника по размерам длины и ширины.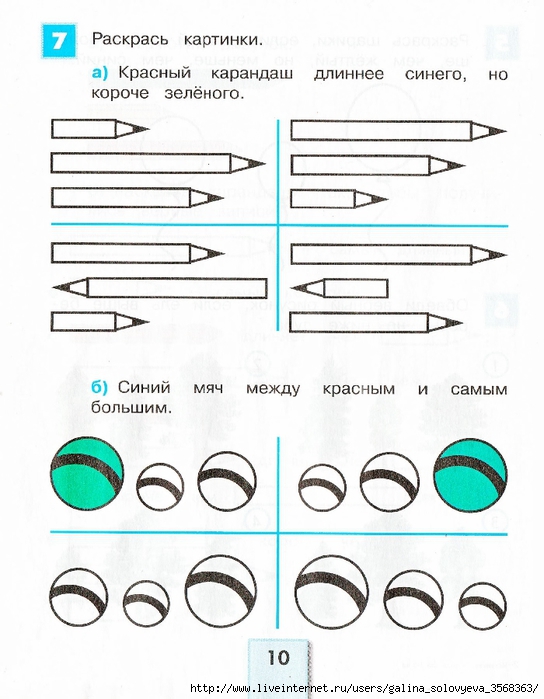 Нет необходимости в ручном преобразовании единиц длины, ширины и площади, которые можно выбирать независимо друг от друга. Калькулятор позаботится о преобразовании значений, введенных в разные единицы.

После ввода значений длины и ширины, а также предпочтительных единиц измерения для каждого параметра вычисленное значение площади будет отображаться в поле ответа, выделенном красным цветом. Также будет показана графика чертежа в масштабе с правильными пропорциями и помечена каждым размером и расчетной площадью.

Формула

Формула, используемая этим калькулятором для расчета площади прямоугольной формы:

A = L · W

Символы

А= Зона
Д = Длина
Ш = Ширина

Размеры области – длина и ширина

Введите размеры длины и ширины для вычисляемой прямоугольной формы и выберите соответствующие единицы измерения для каждого введенного значения измерения.

Следующие коэффициенты преобразования в метрах (м) используются для преобразования длины и ширины в различные единицы:

Единицы измерения длины с префиксом метрической системы СИ

йоктометр (м) – 1 x 10 ^-24 м
зептометр (zm) – 1 x 10 ^-21 м
аттометр (ам) – 1 x 10 ^-18 м
фемтометр (фм) – 1 x 10 ^-15 м
пикометр (пм) – 1 x 10 ^-12 м
нанометр (нм) – 1 x 10 ^-9 м
микрометр (мкм) – 0,000001 м
миллиметра (мм) – 0,001 м
сантиметр (см) – 0,01 м
дециметр (дм) – 0,1 м
метр (м) – 1 м
декаметр (дамба) – 10 м
гектометр (хм) – 100 м
километр (км) – 1000 м
мегаметр (Мм) – 1 000 000 м
гигаметр (Gm) – 1 x 10 ⁺⁹ м
тераметр (Тм) – 1 x 10 ⁺¹² м
петаметр (Pm) – 1 x 10 ⁺¹⁵ м
экзамен (Em) – 1 x 10 ⁺¹⁸ м
зеттаметр (Zm) – 1 x 10 ⁺²¹ м
йоттаметр (Ym) – 1 x 10 ⁺²⁴ м

Имперские и американские единицы длины

тысячная доля дюйма (тысяча) – 0,0000254 м
дюйм (дюйм) – 0,0254 м
фута (фута) – 0,3048 м
ярда (ярда) – 0,9144 м
мили (ми) – 1609,344 м
морских миль (нми) – 1852 м

Астрономические единицы

астрономическая единица (а. е.) – 149 597 870 700 м
световых года (лет) – 9 460 730 472 580 800 м
парсек (пк) – 30 856 775 814 913 672,789… м
килопарсек (кпк) – 3,0856775814913672789… x 10 ⁺¹⁹ м
мегапарсек (Мпк) – 3,0856775814913672789… x 10 ⁺²² м
гигапарсек (Гпк) – 3,0856775814913672789… x 10 ⁺²⁵ м

Расчет площади

Это рассчитанная площадь прямоугольника, которую этот инструмент определяет путем умножения измерений длины и ширины. Выберите требуемые единицы измерения площади для отображения результата.

Следующие коэффициенты преобразования в квадратных метрах (м²) используются для преобразования расчетной площади в другие единицы:

Квадратный метр СИ Метрический префикс Единицы площади

Квадратный йоктометр (кв.м) – 1 x 10 ^-48 м²
квадратный зептометр (кв. м) – 1 x 10 ^-42 м²
кв. аттометр (кв. м) – 1 x 10 ^-36 м²
квадратный фемтометр (кв. фм) – 1 x 10 ^-30 м²
квадратных пикометра (кв.м) – 1 x 10 ^-24 м²
квадратных нанометра (кв.нм) – 1 x 10 ^-18 м²
квадратных микрометра (кв.мкм) – 1 x 10 ^-12 м²
квадратных миллиметра (кв. мм) – 0,000001 м²
квадратных сантиметра (кв. см) – 0,0001 м²
квадратных дециметра (кв. дм) – 0,01 м²
квадратный метр (кв. м) – 1 м²
кв. декаметр (кв. дамба) – 100 м²
квадратных гектометра (кв. м) – 10 000 м²
квадратных километра (кв. км) – 1 000 000 м²
квадратных мегаметра (кв.м) – 1 x 10 ⁺¹² м²
квадратных гигаметра (кв. Гм) – 1 x 10 ⁺¹⁸ м²
квадратных терметра (кв.м) – 1 x 10 ⁺²⁴ м²
квадратных петаметра (кв.м) – 1 x 10 ⁺³⁰ м²
кв. экз. (кв. м) – 1 x 10 ⁺³⁶ м²
квадратных зеттаметра (кв. Зм) – 1 x 10 ⁺⁴² м²
квадратных йоттаметра (кв. м) – 1 x 10 ⁺⁴⁸ м²

Английские имперские и американские территориальные единицы

тысячные доли дюйма (тысячи квадратных) – 6,4516 x 10 ^-10 м²
квадратных дюйма (кв. дюйм) – 0,00064516 м²
квадратных фута (кв. фута) – 0,092^м²
квадратных ярда (кв. ярда) – 0,83612736 м²
акра (акр) – 4046,8564224 м²
квадратных миль (кв. миль) – 2589988,110336 м²
квадратных морских мили (кв. миль) – 3429904 м²

Аре Метрическая префикс Единицы площади

сантиар (ca) – 1 м²
дециар (день) – 10 м²
а (а) – 100 м²
декар (daa) – 1000 м²
га (га) – 10000 м²

Квадратные единицы астрономической площади

квадратная астрономическая единица (кв. а.е.) – 2,237952291797391849 x 10 ⁺²² м²
квадратных световых года (sq ly) – 8,950542107481892730061252864 x 10 ⁺³¹ м²
квадратных парсека (кв. пк) – 9,5214061369184135543188504845736… x 10 ⁺³² м²
квадратных килопарсека (кв.кпк) – 9,5214061369184135543188504845736… x 10 ⁺³⁸ м²
квадратных мегапарсека (кв. Мпк) – 9,5214061369184135543188504845736… x 10 ⁺⁴⁴ м²
квадратных гигапарсека (кв. Гпк) – 9,5214061369184135543188504845736… x 10 ⁺⁵⁰ м²

Применение

Используйте этот калькулятор длины x ширины для определения площади в следующих приложениях:

Площадь крыши и открытой черепицы для оценки количества черепицы или количества рубероида, необходимого для покрытия всей крыши.
Зона отдыха для определения приблизительной вместимости.
Автостоянка и площадь парковочных мест для определения максимального количества машиномест
Вместимость складской площади.
Вместимость морозильной или холодильной камеры.
Площадь пола из размеров помещения в смешанных единицах измерения
Покрытие площади кормами, прополкой, семенами или удобрениями для поля или сада с расстояния между углами
Покрытие поверхности краской, обоями или плиткой от стены, потолка или пола, размеры по ширине и высоте
Количество изделий, изготовленных из ткани, ткани или ткани определенной длины и ширины.
Земельный участок или площадь здания.
Требуемое количество теплоизоляции для покрытия мансардного помещения.
Сколько нужно ламината, чтобы заполнить площадь пола.
Площадь дорожки, настила или патио, чтобы помочь оценить, сколько времени займет мойка под давлением.
Количество участков под застройку по длине и ширине возможно на площади земли в гектарах или акрах.
Площадь пола, стены или потолка приемной, гостиной, кухни, гостиной, столовой, прихожей, лестницы, спальни, ванной комнаты, туалета, кабинета, телевизионной комнаты, гаражного подвала или подвального помещения для хранения.
Сколько места мебель займет в комнате.
Площади комнат по размерам на плане дома.
Бордюр патио для покрытия гравием.
Площадь кв площади мастерской.
Загон для лошадей.
Площадь проезжей части для определения количества необходимых строительных материалов
Площадь проекта озеленения сада, патио или двора для расчета необходимого количества тротуарной плитки
Площадь столешниц, полок и витрин для расчета рабочей площади, остаточного пространства или количества товаров на складе, которые могут быть выставлены.