Потенциальная энергия растянутой пружины: Потенциальная энергия — урок. Физика, 9 класс.
alexxlab | 05.09.1987 | 0 | Разное
Какие величины определяют потенциальную энергию растянутой пружины
Понятие потенциальной энергии пружины
При рассмотрении того, что такое потенциальная энергия пружины следует уделить внимание самому понятию – свойство, которым могут обладать тела при нахождении на земле. Этот момент определяет то, что ей могут обладать самые разнообразные изделия, в том числе рассматриваемое. К особенностям рассматриваемого понятия можно отнести следующее:
- Потенциальная энергия в рассматриваемом случае формируется по причине изменения состояния. Даже при несущественном смещении витков относительно друг друга считается изменением состояния подобного изделия.
- Для того чтобы изменить состояние изделия совершается определенное действие. Зачастую для этого проводится прикладывание усилия. При этом важно провести расчет требуемого усилия для сжатия витков.
- После выполнения определенной работы большая часть усилия, которое было потрачено на выполнение действия высвобождается при определенных обстоятельствах.
 Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Читать также: Из чего сделать диск для окучника
Она также широко применяется при создании самых различных механизмов, к примеру, заводных часов. При проектировании различных механизмов учитывается закон сохранения механической силы, которая характеризуется довольно большим количеством особенностей.
Вычисление работы силы упругости
Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.
Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.
Рис. 4. Зависимость силы упругости от координаты движения
Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).
Рис. 5. Площадь фигуры
Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.
Рис. 6. Площадь большой фигуры
Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:
В результате преобразований получим такую формулу – работа равна разности между величиной:
К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:
,
где среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.
Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.
Закон сохранения механической энергии
Согласно установленным законам механическое воздействие консервативной механической системы сохраняется во времени. Этот момент определяет то, что потенциальная энергия деформированной пружины не может возникнуть сама или исчезнуть куда-нибудь. Именно поэтому для ее создания нужно приложить соответствующее усилие.
Рассматриваемый закон относится к категории интегральных равенств. Эта закономерность определяет то, что он складывается их действия дифференциальных законов, является свойством или признаком совокупного воздействия.
Для проведения соответствующих расчетов должна применяться определенная формула. Сила, с которой оказывается воздействие, не является постоянной. Именно поэтому для ее вычисления применяется графический метод. Самая простая зависимость может быть описана следующим образом: F=kx. При применении подобной зависимости построенная координатная линия будет представлена прямой линией, которая расположена под углом относительно системы координат.
Приписать подобному устройству потенциальную энергию можно только в том случае, если она равна максимальной работе и не зависит от условной траектории движения. Проведенные исследования указывают на то, что подобная работа подчиняется закону Гука. Для определения основного показателя применяется следующая формула: U=kk2/2.
Для деформирования витков к ним должно быть приложено определенное усилие, так как в противном случае кинетическая сила не возникнет.
Постигаем закон Гука
Все объекты природы могут деформироваться, т. е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.
е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.
Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину \( x \), потребуется приложить внешнюю силу \( F_{вн} \), которая равна:
где \( k \) — это коэффициент пропорциональности.
Точнее говоря, вектор деформации \( \mathbf{x} \) всегда направлен противоположно силе сопротивления пружины (или силе упругости) \( \mathbf{F} \), а потому в векторную формулировку закона Гука обычно входит знак “минус”:
Растягиваем и сжимаем пружины
Следует помнить, что закон Гука относится только к упруго деформируемым материалам.
В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности \( k \) в законе Гука \( F=kx \) называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.
Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?
Вес автомобиля равен \( mg \), где \( g \) — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка \( mg/4 \).
Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка \( mg/4 \).
Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:
т.е. коэффициент упругости равен:
Подставляя значения, получим:
Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·103 Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.
Изучаем особенности закона Гука
Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.
Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).
схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).
Сила упругости пружины не зря называется силой сопротивления, ведь она стремится установить равновесие.
Динамика твердого тела
Некоторые определить выражения (определяется при применении наиболее подходящих формул) можно только с учетом правил, касающихся динамики твердых объектов. Этому вопросу посвящен целый раздел. При расчете потенциальной энергии сжатой пружины также применяются некоторые законы этого раздела
Динамика твердого тела рассматривается по причине того, что в большинстве случаев механизм совершает действие, связанное с непосредственным перемещением какого-либо объекта.
Рассматриваемое свойство изделия может изменяться в зависимости от динамики твердого тела. Это связано с тем, что на изделие оказывается и воздействие со стороны окружающей среды. Примером можно назвать трение или нагрев.
Примером можно назвать трение или нагрев.
Читать также: Кондуктор для сверла форстнера
Момент силы и момент импульса относительно оси
Рассмотрение деформации пружины проводится также с учетом момента силы и импульса относительно оси. Эти два параметра позволяют рассчитать все требуемые показатели с более высокой точностью. Довольно распространенным вопросом можно назвать чему равен момент силы – векторная величина, которая определяется векторному произведению радиуса на вектор приложенной силы.
Момент импульса – величина, которая применяется для определения количества вращательного движения.
Среди особенностей подобного показателя можно отметить следующее:
- Масса вращения. Объект может характеризоваться различной массой.
- Распределение относительно оси. Ось может быть расположена на различном расстоянии от самого объекта.
- Скорость вращения. Это свойство считается наиболее важным, в зависимости от конструкции он может быть постоянным или изменяться.

Расчет каждого показателя проводится при применении соответствующей формулы. В некоторых случаях проводится измерение требуемых вводных данных, без которых провести вычисления не получится.
Импульс системы тел
Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
При рассмотрении любой механической задачи мы интересуемся движением определенного числа тел. Совокупность тел, движение которых мы изучаем, называется механической системой или просто системой.
Рассмотрим систему, состоящую из трех тел. На тела системы действуют внешние силы, а между телами действуют внутренние силы. \( F_1,F_2,F_3 \) – внешние силы, действующие на тела; \( F_{12}, F_{23}, F_{31}, F_{13}, F_{21}, F_{32} \) – внутренние силы, действующие между телами. Вследствие действия сил на тела системы их импульсы изменяются. Если за малый промежуток времени сила заметно не меняется, то для каждого тела системы можно записать изменение импульса в виде уравнения:
В левой части каждого уравнения стоит изменение импульса тела за малое время \( \Delta t \). {\prime} \) – конечные скорости тел. Сложим левые и правые части уравнений.
{\prime} \) – конечные скорости тел. Сложим левые и правые части уравнений.
Но силы взаимодействия любой пары тел в сумме дают нуль.
Важно! Импульс системы тел могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению. Внутренние силы, изменяя импульсы отдельных тел системы, не изменяют суммарный импульс системы
Уравнение движения вращающегося тела
Рассматривая подобное свойство также следует уделить внимание уравнению движения вращающегося тела. Не стоит забывать о том, что вращательное движение твердого тела характеризуется наличием как минимум двух точек. При этом отметим нижеприведенные особенности:
- Прямая, которая соединяет две точки, выступает в качестве оси вращения.
- Есть возможность провести определение места положения объекта в случае вычисления заднего угла между двумя плоскостями.
- Наиболее важным показателем можно назвать угловую скорость. Она связана с инерцией, которая возникает при вращении объекта.

Для вычисления угловой скорости применяется специальная формула, которая выглядит следующим образом: w=df/dt. В некоторых случаях проводится вычисление углового ускорения, которое также является важной величиной.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Вычисление работы силы упругости
Груз совершил известное перемещение, величину силы упругости мы также знаем, векторы перемещения и силы упругости параллельны. Казалось бы, все ясно – нужно умножить величину силы на величину перемещения и получить значение работы. Однако здесь не все так просто – разберемся почему.
О чем нам говорит формула, которая выражает величину силы упругости? О том, что сила упругости – величина не постоянная, она меняется по мере перемещения груза. И действительно, величина этой силы, как мы видим из формулы, зависит от координаты центра груза. Формула же для работы силы, которую мы применяли раньше, справедлива лишь в том случае, если сила не меняет свою величину по мере движения. Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Как же тогда быть? Один из вариантов выхода из данной ситуации мог бы состоять в том, что мы применим такой же метод, который применялся нами ранее в разделе кинематика при расчете перемещения тела, движущегося равноускоренно.
Можно всю траекторию движения груза разбить на очень маленькие участки (участки, в пределах которых силу упругости можно считать практически постоянной). Далее в пределах каждого такого участка мы можем рассчитать работу силы упругости ввиду ее практического постоянства. Затем работа на всей области движения груза будет складываться из всех этих маленьких работ на этих участках. Таким образом, мы сможем посчитать работу силы упругости на всей траектории движения груза. На рис. 4 приведены детали такого расчета.
Рис. 4. Зависимость силы упругости от координаты движения
Видно, что если отложить на графике зависимость модуля силы упругости от модуля координаты груза, затем проделать описанное выше разбиение на маленькие участки, то величина работы на каждом маленьком участке численно равна площади фигуры, ограниченной графиком: осью абсцисс и двумя перпендикулярами к этой оси (см. рис. 5).
рис. 5).
Рис. 5. Площадь фигуры
Если просуммировать значение работы на каждом участке (площадь маленьких фигур), то получим площадь большой фигуры, показанной на рис. 6.
Рис. 6. Площадь большой фигуры
Поскольку данная фигура является прямоугольной трапецией, то мы можем воспользоваться формулой для расчета площади такой фигуры – это полусумма оснований, умноженная на высоту. В результате преобразований получим такую формулу – работа равна разности между величиной:
К этому результату можно прийти и несколько иным способом. Для вычисления работы силы упругости в этом способе необходимо просто взять среднее значение силы упругости и умножить его на перемещение тела. Это утверждение можно записать как:
,
где среднее значение силы упругости, которое равно полусумме начального и конечного ее значений. Если данное выражение подставить в формулу для работы, то при помощи простых алгебраических преобразований мы получим то же самое выражение, что получали ранее:
Как видно из этой формулы, работа зависит лишь от начальной и конечной координаты центра груза, и еще одно замечание: как видно из последней формулы, работа силы упругости никоим образом не зависит от массы груза. Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Это обусловлено тем, что и сама сила упругости не зависит от этой массы.
Теперь внимательнее посмотрим на последнюю формулу – если вынести -1 за скобки, то получим, что работа есть взятая со знаком минус разность между значениями некоторой величины, равной половине произведения жесткости пружины на квадрат ее удлинения в конечный и начальный моменты времени.
Вспомним, как мы поступили при расчете работы силы тяжести на прошлом уроке. В тот раз мы столкнулись с новой для нас физической величиной, разность между значениями которой в конечной и начальной моменты времени равнялась взятой со знаком « — » работе силы тяжести. Это величина, равная произведению массы тела на ускорение свободного падения и высоту, на которую было поднято тело над некоторым уровнем, мы назвали потенциальной энергией тела, поднятого над землей.
Потенциальная энергия растянутой пружины или стержня.
Рассчитаем работу внешней силы, изменяющейся пропорционально смещению точки
F = kx на пути от х0 = 0 до х.
; (1.2)
Работа силы упругости при растяжении на x : ;
Закон сохранения механической энергии.
Рассмотрим систему материальных точек массами m1, m2,… mn, движущихся со скоростями 1, 2 …n. Пусть F1’, F2’ …, Fn’, — равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a F1,
 .., fn.
.., fn.При с массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
(1.2)
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения, соответственно равные dr1, dr2, …, dr
n. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что dri=i dt, получим(1.2)
Сложив эти уравнения получим:
В этом уравнении первый член представляет собой изменение кинетической энергии WK, второй – изменение потенциальной энергии системы WП, а – работу внешних неконсервативных сил, действующих на систему.
d(WK + WП) = A
При переходе системы из состояния 1 в состояние 2
; (1. 2)
2)
Т.е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами.
Если внешние неконсервативные силы отсутствуют, то
d(WK + WП)=0 и
WK + WП = const.
Динамика твердого тела.
Момент силы и момент импульса относительно оси.
Уравнение движения вращающегося тела
– момент силы, действующий на тело
Момент силы – псевдовекторная величина равная произведению силы действующей на тело, на плечо этой силы
В
кинематике мы представляли угловое
ускорение вектором, параллельным оси
вращения. Так как правая часть равенства
есть модуль
векторного произведения , то,
выбрав указанный
порядок умножения, мы получим вектор
,
параллельный
.
Так как правая часть равенства
есть модуль
векторного произведения , то,
выбрав указанный
порядок умножения, мы получим вектор
,
параллельный
.
=
Величина М называется моментом силы F относительно оси вращения или вращающим моментом.
Момент силы – псевдовектор – его направление совпадает с направлением поступательного движения правого винта при его вращении от R к F.
F2 = Fsin, будет создавать вращение, сообщая телу ускорение.
dS = Rd = Rdt ( – угловое перемещение)
dA = =RF2dt,
dW =
Id = dA.
. есть угловое ускорение тела.
I= RF2= RFsin.
Основное уравнение динамики вращательного движения
(1.2)
– проекция момента силы на ось вращения.
Это уравнение по форме аналогично второму закону Ньютона: =m и является аналитическим выражением второго закона Ньютона для вращательного движения.
Если на тело действует несколько внешних сил, лежащих в плоскости вращения, то суммарный вращающий момент по принципу суперпозиции равен:
(1.2)
По II закону Ньютона miai = Fi; ;
(1.2)
–момент инерции тела относительно оси Z.
; (1.2)
Jz= – момент импульса тела относительно оси Z.
Мz = 0,
( Jz)
= 0.
Jz= const. закон сохранения момента импульса тела, вращающегося около закрепленной оси.
Потенциальная энергия | Физика
1. Определение потенциальной энергии
В предыдущем параграфе мы говорили о работе, которую может совершить тело за счет уменьшения своей скорости, а теперь нас будет интересовать работа, которую может совершить тело или система тел вследствие изменения положения тел.
Рассмотрим примеры.
Работа поднятого груза. Когда подвешенный на тросе груз равномерно движется вниз, он действует на трос силой, направленной тоже вниз (рис. 30.1).
Эта сила обусловлена силой тяжести: она совершает работу, действуя на груз, а груз совершает работу, действуя на трос.
Итак, благодаря действию силы тяжести груз может совершить работу при движении вниз.
Работа пружины. Когда деформация пружины уменьшается, пружина действует на тело силой упругости, направленной так же, как перемещение тела (рис. 30.2). При этом пружина совершает положительную работу.
30.2). При этом пружина совершает положительную работу.
Итак, деформированная пружина может совершить работу при возвращении в недеформированное состояние.
В рассмотренных примерах работу совершают силы тяготения и силы упругости. Как мы уже знаем, общая важная особенность этих сил состоит в том, что при движении по замкнутой траектории (когда тело возвращается в начальное положение) работа этих сил равна нулю. (Такие силы называют консервативными. Если между телами замкнутой системы действуют только консервативные силы, то, как мы увидим далее, механическая энергия системы сохраняется («консервируется»).)
Благодаря этому для системы тел, взаимодействующих посредством сил тяготения и упругости, можно определить потенциальную энергию как величину, характеризующую способность системы тел совершать работу и зависящую только от взаимного положения тел.
Потенциальная энергия системы тел характеризует ее способность совершать работу вследствие изменения взаимного положения взаимодействующих тел.
Если система тел совершает положительную работу, потенциальная энергия системы уменьшается. А если система тел совершает отрицательную работу, ее потенциальная энергия увеличивается. При этом
изменение потенциальной энергии системы тел равно работе сил упругости и тяготения, действующих со стороны тел системы, взятой со знаком минус:
Ep2 – Ep1 = –A (1)
Здесь Ep1 и Ep2 обозначают начальную и конечную потенциальную энергию системы тел.
(Мы приводим определение потенциальной энергии, применимое к механическим явлениям. В дальнейшем мы расширим и уточним это определение.)
? 1. Как изменяется потенциальная энергия системы «камень + Земля», когда камень движется вверх? вниз? Объясните свои ответы.
? 2. Как изменяется потенциальная энергия пружины, когда деформация уменьшается? увеличивается? Объясните свои ответы.
Нулевой уровень потенциальной энергии. Из формулы (1) следует, что физический смысл имеет только изменение потенциальной энергии: оно измеряется работой, совершенной телами системы.
Поэтому нулевой уровень потенциальной энергии (состояние системы, которому сопоставляется нулевое значение потенциальной энергии) выбирают так, чтобы упростить расчеты.
2. Потенциальная энергия поднятого груза
Когда груз массой m равномерно перемещается вертикально вниз на расстояние h, он совершает положительную работу mgh, потому что он действует на опору или поднес направленной вниз силой (весом груза), равной силе тяжести.
Следовательно, при уменьшении высоты груза на h потенциальная энергия груза уменьшается на mgh. (Важно понимать, что это потенциальная энергия системы взаимодействующих тел – груза и Земли.) Если сопоставить нулевой уровень потенциальной энергии наинизшему положению груза, то
потенциальная энергия груза массой m, поднятого на высоту h, выражается формулой
Ep = mgh. (2)
? 3. Брусок массой 200 г поднят на высоту 1 м над поверхностью стола высотой 80 см (рис. 30.3).
а) Чему равна потенциальная энергия бруска, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
б) Чему равно изменение потенциальной энергии бруска при его падении на стол, если за нулевой уровень потенциальной энергии бруска принять уровень стола? уровень пола?
Эти примеры подтверждают, что имеет значение только изменение потенциальной энергии. Оно измеряется работой, совершенной телом или системой тел, и не зависит от выбора нулевого уровня потенциальной энергии.
Оно измеряется работой, совершенной телом или системой тел, и не зависит от выбора нулевого уровня потенциальной энергии.
3. Потенциальная энергия упругой деформации
При возвращении в недеформированное состояние сила упругости пружины совершает положительную работу
A = (kx2)/2.
При этом потенциальная энергия пружины уменьшается на такую же величину. Если нулевому уровню потенциальной энергии сопоставить состояние недеформированной пружины, то
потенциальная энергия деформированной пружины жесткостью k выражается формулой
Ep = (kx2)/2, (3)
где x – деформация пружины.
Потенциальную энергию, выражаемую формулой (3), называют также потенциальной энергией упругой деформации. Она зависит от квадрата деформации. Поэтому потенциальная энергия сжатой пружины равна потенциальной энергии растянутой пружины, если модуль деформации пружины в обоих случаях один и тот же.
? 4. В начальном состоянии пружина жесткостью 200 Н/м сжата на 1 см. Как изменилась потенциальная энергия пружины, если в конечном состоянии:
Как изменилась потенциальная энергия пружины, если в конечном состоянии:
а) пружина не деформирована?
б) сжата на 2 см?
в) растянута на 1 см?
г) растянута на 2 см?
? 5. Шар массой 200 г подвешен к пружине жесткостью 100 Н/м и находится в равновесии, Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка.
а) На какую высоту подняли шар?
б) Как изменилась потенциальная энергия шара за время, в течение которого он возвращался в положение равновесия?
в) Как изменилась за то же время потенциальная энергия пружины?
г) Как изменилась за то же время потенциальная энергия системы «шар + Земля + пружина»?
Дополнительные вопросы и задания
6. С высоты 20 м над поверхностью земли свободно без начальной скорости падает камень массой 300 г. За нулевой уровень потенциальной энергии камня примите уровень земли.
а) Чему равна потенциальная энергия камня в начальный момент?
б) Чему равна потенциальная энергия камня через 1 с после начала движения?
в) Через какое время после начала движения потенциальная энергия камня уменьшилась в 2 раза по сравнению с ее начальным значением?
7. Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь.
Шар массой 1 кг брошен с поверхности земли с начальной скоростью 20 м/с под углом 30º к горизонту. Считайте, что сопротивлением воздуха при движении шара можно пренебречь.
а) До какой максимальной высоты поднялся шар?
б) Как изменилась потенциальная энергия шара за время подъема?
8. По реке с постоянной скоростью плывет плот. Как изменяется со временем:
а) кинетическая энергия плота?
б) потенциальная энергия плота?
9. Когда сжатую пружину сжали еще на 2 см, ее потенциальная энергия увеличилась в 9 раз.
а) Во сколько раз модуль конечной деформации пружины больше, чем модуль начальной деформации?
б) Чему равен модуль начальной деформации пружины?
10. Две пружины жесткостью 100 Н/м и 400 Н/м соединены последовательно. Систему соединенных пружин растянули на 5 см.
а) Чему равна деформация более мягкой пружины?
б) Чему равна деформация более жесткой пружины?
в) Потенциальная энергия упругой деформации какой пружины больше, и во сколько раз?
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 5 из 9Следующая ⇒
Цель работы:Сравнить уменьшение потенциальной энергии растянутой пружины с увеличением кинетической энергии тела, связанного с пружиной.
Оборудование: два штатива для фронтальных работ; динамометр учебный; шар; нитки; листы белой и копировальной бумаги; линейка измерительная; весы учебные со штативом; гири.
Теоретические основы работы
На основании закона сохранения и превращения энергии при взаимодействии тел силами упругости изменение потенциальной энергии растянутой пружины должно быть равно изменению кинетической энергии связанного с ней тела, взятому с противоположным знаком:
.
Для экспериментальной проверки этого утверждения можно воспользоваться установкой, изображенной на рисунке 1.
где k — жесткость пружины. Затем шар отпускают. Под действием силы упругости шар приобретает скорость V. Пренебрегая потерями, вызванными действием силы трения, можно считать, что потенциальная энергия растянутой пружины полностью превратится в кинетическую энергию шара:
Скорость шара можно определить, измерив дальность его полета S при свободном падении с высоты h. Из выражений и следует, что . Тогда
Целью работы является проверка равенства:
С учетом равенства получим:
Порядок выполнения работы 1. Расстояние между штативами должно быть таким, чтобы шар находился на краю желоба при натянутой нити и отсутствии деформации пружины динамометра. 2. Отодвигайте шар от края желоба до тех пор, пока показания Опыт повторите не менее 10 раз. Определите среднее значение дальности полета Scp. 3. Измерьте деформацию х пружины динамометра при силе упругости Fy= 2 Н. Вычислите потенциальную энергию растянутой пружины. 4. Измерьте массу шара с помощью весов и вычислите увеличение его кинетической энергии. 5.
Отчетная таблица
6. Оцените границы погрешностей измерения потенциальной энергии растянутой пружины Так как , то граница относительной погрешности равна: Граница абсолютной погрешности равна:
7. Оцените границы погрешностей измерения кинетической энергии шара. Так как , то граница относительной погрешности равна:
Погрешностями εm, εg и εh, по сравнению с погрешностью εs можно пренебречь. В этом случае Условия эксперимента по измерению дальности полета таковы, что отклонения результатов отдельных измерений от среднего значительно выше границы систематической погрешности ( ), поэтому можно принять, что ( ). Граница случайной погрешности среднего арифметического при небольшом числе измерений N находится по формуле: , где рассчитывается по формуле .
Таким образом, Граница абсолютной погрешности измерения кинетической энергии шара равна: 7. Сделайте вывод о выполнении закона сохранения энергии, проверив, имеют ли общие точки интервалы
и . Контрольные вопросы
1. Дайте определение энергии. 2. Что называется кинетической энергией? 3. 4. Какие силы называются консервативными? 5. Что называется потенциальной энергией? 6. Запишите выражение для потенциальной энергии поднятого над поверхностью Земли тела и сжатой пружины. 7. Сформулируйте закон сохранения полной механической энергии. 8. При каких случаях выполняется закон сохранения механической энергии? 9. Выполняется ли закон сохранения полной механической энергии в замкнутой системе, в которой действуют только сила тяготения и силы упругости. 10. Чем можно объяснить неточное равенство изменений потенциальной энергии пружины и кинетической энергии шара?
Две пружины с коэффициентами жесткости k1 и k2 соединяют один раз последовательно, а другой раз – параллельно. Какой должна быть жесткость k пружины, которой можно было бы заменить эту систему из двух пружин? Первоначальная длина пружин одинакова.
Лабораторная работа № 4 ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2116; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Решено
Задачи про космос
УСЛОВИЕ: Два точечных положительных заряда: q1=30 нКл и q2=10 нКл находятся в вакууме на расстоянии L=0,5 м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А.
Кольцо радиуса 10 см из тонкой проволоки с сопротивлением 0,01 Ом находится в однородном магнитном поле, линии индукции которого пересекают плоскость…
В калориметр поместили 500 г мокрого снега. После того, как в калориметр долили 500 г кипятка и снег растаял, установилась температура 20 градусов Цельсия. Сколько воды содержал снег первоначально?
При уменьшении абсолютной температуры на 600К поступательного хаотического движений молекул газа уменьшилась в 4 раза. Какова конечная температура газа?
Пользуйтесь нашим приложением
| Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника | ⇐ ПредыдущаяСтр 9 из 17Следующая ⇒
Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно – исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку “Продолжить”, я принимаю политику конфиденциальности ⇐ Предыдущая234567891011121314151617Следующая ⇒ Поиск по сайту: |
Потенциальная энергия пружины — Nexus Wiki
Идея потенциальной энергии заключается в том, что при изменении относительного положения двух объектов кинетическая энергия может быть изменена обратимым образом. Мы знаем, что если мы подвешиваем массу к пружине и тянем ее вниз, это смещение создает растяжение пружины, которое может ускорять массу, создавая кинетическую энергию. Когда мы отпускаем массу, пружина тянет ее вверх, и масса начинает двигаться. Если внутреннее трение пружины незначительно или отсутствует, масса будет подниматься, опускаться, поворачиваться и снова двигаться вверх. Так что процесс выглядит обратимым. Давайте посмотрим, сможем ли мы построить PE растянутой пружины.
Мы знаем, что если мы подвешиваем массу к пружине и тянем ее вниз, это смещение создает растяжение пружины, которое может ускорять массу, создавая кинетическую энергию. Когда мы отпускаем массу, пружина тянет ее вверх, и масса начинает двигаться. Если внутреннее трение пружины незначительно или отсутствует, масса будет подниматься, опускаться, поворачиваться и снова двигаться вверх. Так что процесс выглядит обратимым. Давайте посмотрим, сможем ли мы построить PE растянутой пружины.
Работа, совершаемая пружиной
В примере, который мы описали в преамбуле — масса, подвешенная на пружине, — масса и пружина двигались таким образом, что изменялась как кинетическая энергия, так и гравитационная потенциальная энергия. Это усложняет ситуацию. Давайте проделаем наш обычный физический трюк, чтобы понять и проанализируем простейший случай, который мы можем себе представить: тележка, движущаяся по горизонтальной дорожке, прикрепленной к пружине, как показано на рисунке справа, без учета трения и сопротивления воздуха. Это упрощает физику и позволяет напрямую выделить потенциальную энергию пружины. Чтобы упростить математику, мы опишем положение тележки одномерной координатной осью $x$, начало которой расположено так, что при $x = 0$ пружина находится в состоянии покоя. При таком выборе координат координата $x$ становится растяжением или сжатием пружины. Поскольку, когда $x$ положительно, пружина оттягивается, закон Гука в этой системе координат становится просто
Это упрощает физику и позволяет напрямую выделить потенциальную энергию пружины. Чтобы упростить математику, мы опишем положение тележки одномерной координатной осью $x$, начало которой расположено так, что при $x = 0$ пружина находится в состоянии покоя. При таком выборе координат координата $x$ становится растяжением или сжатием пружины. Поскольку, когда $x$ положительно, пружина оттягивается, закон Гука в этой системе координат становится просто
$$F_{пружина \rightarrow cart} = -kx$$
Это создает проблему для расчета работы, так как сила меняется при движении. Но поскольку он изменяется линейно, мы можем обойтись небольшим трюком, не вычисляя интеграл явно.
Рассмотрим небольшое изменение положения тележки $Δx$. Работа, выполненная пружиной, будет:
$$W = F_{весна \rightarrow cart}\Delta x = -kx\Delta x$$
Вот наша проблема: какое значение $x$ мы должны использовать? Наш $Δx$ означает, что позиция меняется с начальной (i) на конечную (f):
$$Δx = x_f – x_i$$
Поскольку $x$ изменяется линейно, мы можем предположить, что подходящим значением для использования является среднее значение:
$$\langle x \rangle = (x_f + x_i)/2 $$
Это оказывается правильным. [Мы можем посмотреть на интеграл в явном виде. Среднее значение — это константа, которая делает интеграл точным, поэтому в случае линейной силы это среднее приближение является точным.] Результат равен
[Мы можем посмотреть на интеграл в явном виде. Среднее значение — это константа, которая делает интеграл точным, поэтому в случае линейной силы это среднее приближение является точным.] Результат равен
$$W = F_{пружина \rightarrow cart}\Delta x = -k \langle x \rangle \Delta x = -k \bigg(\frac{x_i + x_f}{2}\bigg)(x_f – x_i)$$ 92$$
Не забывайте наши предположения! Этот простой результат верен только для растяжений и сжатий пружины, для которых выполняется закон Гука. Для больших растяжений и сжатий мы должны вычислить интеграл работы явно (и, возможно, даже численно). Но это будет верно для пружины, которую можно рассматривать по закону Гука в любом контексте, даже когда есть другие силы.
Полезное примечание: обратите внимание, что мы получили этот результат, используя систему координат, в которой $x$ означает, насколько пружина растянута или сжата. Важно, чтобы вы понимали, что это физическое не математическое уравнение. В некоторых случаях вместо “$x$” может быть “$y$” или даже “$y-L_0$”. Но это всегда означает, насколько растянута или сжата физическая пружина!
Но это всегда означает, насколько растянута или сжата физическая пружина!
Почему источник важнее, чем кажется
Источники могут показаться довольно неинтересными объектами. В конце концов, как часто вы на самом деле используете пружину ? Особенно в биологии. Но тот факт, что пружина PE представляет собой простую параболу, делает ее гораздо более важной.
Любая физическая система, в которой есть устойчивое положение (такое, что отклонение от этого положения приводит к силам, отталкивающим назад к устойчивому положению), имеет PE с минимумом и самой низкой точкой. Примером этого является типичная межатомная сила. Небольшие отклонения ПЭ от стабильной точки можно приблизительно описать параболой — так что пружина является хорошей моделью для всего, от колебаний электрических полей в свете до сил связи в молекулах. Справа показан пружинный PE (парабола красного цвета), соответствующий типичному межмолекулярному потенциалу. Для небольших движений вблизи минимума пружинный PE работает довольно хорошо.
Тренировка: потенциальная энергия пружины
Джо Редиш 03.11.11
Потенциальная энергия пружины
Пружина используется почти во всех механических аспектах нашей повседневной жизни, начиная с амортизаторов автомобиль к газовой зажигалке на кухне. Пружины используются из-за их свойства деформироваться и снова возвращаться в свое естественное состояние. Всякий раз, когда пружина растягивается или сжимается, возникает сила в направлении, противоположном этому изменению. Это происходит потому, что когда пружина отклоняется от своего среднего положения, она пытается туда вернуться. Эта сила определяется законом Гука и помогает нам проанализировать энергию, запасенную в пружине.
Закон Гука
Для растяжения упругого объекта, такого как металлическая пружина или веревка, требуется сила. Всякий раз, когда эластичный объект растягивается или сжимается. Он имеет тенденцию прикладывать силу, чтобы противостоять этому изменению формы. Эта сила определяется законом Гука. Сила, действующая на пружину, называется восстанавливающей, потому что она всегда направлена в сторону, противоположную деформации.
Эта сила определяется законом Гука. Сила, действующая на пружину, называется восстанавливающей, потому что она всегда направлена в сторону, противоположную деформации.
Закон Гука гласит, что
Сила, необходимая для растяжения упругого объекта, такого как металлическая пружина, прямо пропорциональна растяжению пружины на короткие расстояния. Поскольку эта возвращающая сила имеет противоположное направление, используется отрицательный знак.
Если x — смещение относительно нерастянутой длины пружины, а F — сила, действующая на нее. Тогда
F = -kx
Здесь k — жесткость пружины.
Итак, всякий раз, когда пружина растягивается вниз, сила действует вверх и наоборот.
Потенциальная энергия упругости
Потенциальная энергия упругости — это энергия, которая накапливается в упругих объектах, когда к ним прикладывается сила для деформации их формы и размера. Затем энергия сохраняется до тех пор, пока сила не будет устранена. После этого объекты начинают возвращаться к своей нормальной форме, и эта энергия преобразуется в какой-то другой вид энергии. Примеры некоторых объектов, хранящих упругую потенциальную энергию:
После этого объекты начинают возвращаться к своей нормальной форме, и эта энергия преобразуется в какой-то другой вид энергии. Примеры некоторых объектов, хранящих упругую потенциальную энергию:
- Растянутая или сжатая пружина.
- Скрученная резинка.
- Прыгающий мяч, сжатый в момент удара о стену и отскакивающий назад.
Расчет потенциальной энергии, запасенной в пружине
Закон Гука, упомянутый выше, устанавливает, как восстанавливающая сила в пружине изменяется в зависимости от чистого смещения от среднего положения пружины. Учитывая, что чистое смещение равно , а восстанавливающая сила обозначается буквой F,
F = -kx
Эта сила является консервативной силой, и с консервативными силами связана потенциальная энергия. Известно, что совершенная работа определяется как произведение силы на перемещение.
W = F.x
Для переменной силы F и чистого перемещения x = -kxdx
Интегрируя приведенное выше уравнение для общей проделанной работы,
dW = kxdx
⇒∫dW = ∫kxdx
⇒ W =
Итак, это полная работа, выполненная для перемещения x. Эта проделанная работа запасается в виде потенциальной энергии пружины. Этот факт также можно проверить по графику зависимости усилия от смещения пружины. Площадь под кривой на графике сила-смещение дает упругую потенциальную энергию, запасенную в пружине.
Эта проделанная работа запасается в виде потенциальной энергии пружины. Этот факт также можно проверить по графику зависимости усилия от смещения пружины. Площадь под кривой на графике сила-смещение дает упругую потенциальную энергию, запасенную в пружине.
Площадь под кривой = площадь заштрихованной области кривой
=
=
=
Оба подхода дают одинаковый ответ.
Таким образом, упругая потенциальная энергия, накопленная в пружине со смещением «x», определяется как
P.E =
Примеры задач
Вопрос 1. Найдите упругую потенциальную энергию, запасенную в пружине с k = 50 Н/м, когда пружина сжата на 0,2м.
Ответ:
Дано: k = 50 Н/м и x = 0,2 м
P.E =
⇒ P.E =
⇒ P.E =
⇒ P.E = 1 Дж
0,1м.
Ответ:
Учитывая: k = 100 Н/м и x = 0,1 м =
⇒ P.
E =
⇒ P.E =
⇒ P.E = 0,5 Дж
его естественная длина 0,5м.
Ответ:
Дано: k = 100 Н/м и x i = 0,1 м и x f = 0,5 м
Пусть перемещение x = 0,0003
⇒x = 0,4M
Теперь энергия упругости, хранящаяся в пружине, дается,
Подключение значений в вышеуказанной формуле,
P.E =
⇒ P.E =
⇒ P.E =
⇒ P.E = 8 Дж
Вопрос 4: Найдите упругую потенциальную энергию, запасенную в пружине с k = 100 Н/м, когда пружина растянута на 0,5 м от ее естественной длины 1 м.
Ответ:
Дано: k = 100 Н/м и x i = 1 м и x f = 0,5 м
Пусть перемещение x = 3 9000 – 900 0,5
⇒x = 0,5 м
Теперь энергия упругости потенциала, хранящаяся в пружине, дается,
Подключение значений в вышеуказанной формуле,
P.
E =
⇒ P.E =
⇒ P.E =
⇒ P.E = 12,5 Дж
Вопрос 5: Пружина с коэффициентом жесткости k = 100 Н/м была первоначально сжата на x = 0,4 м, после чего была отпущена и остановилась при x = 0,2 м сжатия. Найти работу возвращающей силы в этом процессе.
Ответ:
Дано: k = 100 Н/м и x i = 0,4 м и x f = 0,2 м
Совершенная работа будет определяться разностью потенциальной энергии весной в этих двух экземплярах.
Эластичная потенциальная энергия, хранящаяся в пружине, дается,
при x = 0,4 м
Подключение значений в вышеуказанной формуле,
P.E I =
⇒ P.E I =
⇒ P.E I =
0002 ⇒ P.E I =
⇒ P.E I = 8 J
при x = 0,2M
Заключение значений в вышеупомянутой формуле,
P.E F =
⇒ P.
E 22222233333333331 годы 22222223 F =
⇒ P.
⇒ P.E F =
⇒ P.E F = 2 J
W.D = -(P.E F -P.E I )
⇒W.D = -2 +
3)
⇒W.D = -2 +
⇒ W.W.D = -2 + 8
⇒ W = -2 +
9).
Вопрос 6: Пружина с коэффициентом жесткости k = 20 Н/м была первоначально сжата на x = 0,5м, после чего была отпущена и остановилась на x = 0,1м сжатия. Найти работу возвращающей силы в этом процессе.
Ответ:
Дано: k = 20 Н/м и x i = 0,5 м и x f = 0,1 м
Совершенная работа будет определяться разностью потенциальной энергии весной в этих двух экземплярах.
Эластичная потенциальная энергия, хранящаяся в пружине, дается,
при x = 0,5 м
Подключение значений в вышеуказанной формуле,
P.E I =
⇒ P.E I =
⇒ P.
E I =
0002 ⇒ P.E i =
⇒ P.E i = 2.5 J
At x = 0.1m
Plugging the values in the above formula,
P.E f =
⇒ P.E f =
⇒ P.E F =
⇒ P.E F = 0,1 J.
W.D = -(P.E F -P.E I )
⇒W.D = -0,1 + 2,5
9)
⇒W.D = -0,1 + 2.5
9 2
9 2
9 2
3
9)
.
Потенциальная энергия пружины | bartleby
Что такое потенциальная энергия весны?
Потенциальная энергия — это энергия, которой обладает тело в силу своего положения, или энергия, которой обладает объект, благодаря его положению относительно других объектов, его силы, такой как напряжение, заряд и другие факторы, воздействующие на частицы тела. Потенциальная энергия является мерой чистой работы, совершаемой телом или над ним. Потенциальная энергия пружины — это потенциальная энергия, накопленная за счет деформации упругой пружины, и эта упругость обусловлена растянутой пружиной.
Упругость — это способность твердого вещества возвращаться в свое равновесное положение или исходное положение после воздействия на него любой внешней силы. Она также известна как упругая потенциальная энергия. Потенциальная энергия здесь возникает из-за смещения пружины из положения равновесия в другое положение, и эта потенциальная энергия равна чистой работе, выполненной из-за растяжения пружины. Это также напоминает ту же механику колебаний простого маятника, где за счет внешней силы объект перемещается из своего положения равновесия в свои максимальные концы, и периодическое движение продолжается до тех пор, пока он не вернется в положение равновесия для покоя.
Идеальная пружина может подвергаться сжатию и расширению, поэтому приложенная сила будет направлена в противоположную сторону. Пружина обычно считается идеальной, что означает, что массы находятся в положении равновесия, и когда ее растягивают, происходит смещение от ее равновесия. Таким образом, значение растянутого расстояния будет отрицательным.
Закон Гука
Закон Гука гласит, что сила, необходимая для растяжения пружины, будет прямо пропорциональна величине растяжения или смещению струны от положения равновесия. Математическое уравнение, объясняющее закон Гукса – 9.0003
F= k·x
Здесь F — сила, приложенная для растяжения пружины, k — константа, известная как жесткость пружины, а x — смещение. Закон также можно сформулировать так: F – восстанавливающая сила, которую пружина прилагает, чтобы вернуться в положение равновесия. В этом случае у нас отрицательный знак:
F= -kx
Формулировка уравнения работы пружины
Работа, выполненная при растяжении пружины из положения равновесия в положение x, сохраняется в пружине как потенциальная энергия пружины. Его можно получить, как показано ниже, используя уравнение силы из закона Гука
W=∫F.dx=∫0xkx.dx=k∫0xx.dx=k.x22=12kx2
Таким образом, потенциальная энергия пружины U s = ½ kx 2 .(Пусть потенциальная энергия пружины быть U s ).
Теперь, если построить график, чтобы понять соотношение силы и смещения, они оба перпендикулярны друг другу, а жесткость пружины будет под углом 45 градусов к обоим компонентам, поэтому на графике он образует прямоугольный треугольник. Таким образом, основание прямоугольного треугольника является произведением смещения и жесткости пружины, а высота также является смещением. Если x – смещение, а k – жесткость пружины, то путем расчета уравнения получается U с = 1/2·k·x 2
Следовательно, работа пружины будет равна разности конечной и начальной потенциальной энергии. Поэтому его можно обозначить как DU. Потенциальная энергия пружины будет равна нулю, когда она находится в положении равновесия. При растяжении пружины потенциальная энергия увеличивается. Тогда в точках максимальной потенциальной энергии его кинетическая энергия будет равна нулю.
ПРИМЕЧАНИЕ. Значение потенциальной энергии пружины не может быть отрицательным независимо от восстанавливающей силы пружины и ее отрицательного знака.
Применение потенциальной энергии пружины
1) Потенциальная энергия пружины используется в различных приложениях во множестве механических устройств. Особенность сжатия и расширения пружины добавляет ей преимущества. Пружины используются во многих автомобилях в качестве амортизаторов и в системах рекуперативного торможения.
2) Потенциальная энергия пружин также используется в приложении системы управления, и ее способность накапливать делает ее более эффективной.
3) Он также используется в производстве некоторых видов оружия, где из-за сжатия пружины и ее способности накапливать упругую потенциальную энергию при нажатии на спусковой крючок эти пружины прилагают усилие и, следовательно, возникает отдача.
4) Реальное применение эластичности можно также увидеть в использовании резиновой ленты, шестов для прыжков с шестом и в батутах.
Практические задания
1) Если пружина удлиняется на x при нагрузке, рассчитайте энергию, запасенную в пружине.
Пусть T — сила пружины, а K — постоянная силы
a) 2x/T 2 b) T 2 /2k c)2k/T 2 d)T 2 /2x
Ответ: При растяжении пружины в ней возникает возвращающая сила, что зависит от прогиба пружины. Величина этой силы задается как
T=kx
Энергия, запасенная в пружине, задается как
E=12kx2
Переформулируйте уравнение силы и подставьте выражение прогиба в формулу энергии для расчета его стоимости.
E=12kTk2E=T22K
Правильный вариант (б).
2) Определить потенциальную энергию пружины с жесткостью 200 Нм -1 и перемещением 0,8 м
Ответ: Формула для расчета потенциальной энергии данной пружины:
Заданные значения жесткости пружины и прогиба составляют 200 Нм -1 и 0,8 м соответственно. Подставьте значения для расчета потенциальной энергии.
E=12×200 Нм−1×0,8 м2E=64 Дж
Энергия 64 Дж.
3) Инженер прикрепляет пружину к прочной деревянной доске. Пусть доска лежит на столе горизонтально. Пружина использует энергию в три джоуля для растяжения, а смещение, перемещаемое пружиной, составляет 99 см. Каково будет значение постоянной пружины, используя уравнение потенциальной энергии пружины?
Ответ: Формула для расчета потенциальной энергии данной пружины:
E=12kx2
Перемещение и энергия пружины даны как 99 см и 3 Джоуля. Подставьте значения в формулу и рассчитайте значение постоянной пружины.
3 Дж=12k0,99 м2k=2×3 J0,99 м2k=6,122 Нм−1
Это заданное значение жесткости пружины.
4) Человек хочет провести эксперимент с пружиной и проанализировать потенциальную энергию пружины. Итак, человек прикрепляет один конец пружины к металлической доске, а другой конец свободен, поэтому пружину можно растянуть или сжать. Человек натягивает струну с жесткостью пружины 100 Netwon на метр и растягивает ее на расстояние от 0,20 до 0,40 метра.
Определить значение потенциальной энергии пружины
Формула для расчета потенциальной энергии данной пружины:
E=12k(xf−xi)2
Принято, что значение жесткости пружины равно 100 Нм -1 , конечное перемещение равно 0,40 м начальное водоизмещение 0,20 м. Подставьте значения, чтобы рассчитать значение энергии пружины.
E=12100 Нм−10,40 м – 0,20 м2E=2 Дж
Энергия 2 Дж.0003
- Бакалавр наук (физика)
- Магистр наук (физика)
У нас есть пошаговые решения для миллионов задач из учебников, а специалисты в данной области готовы круглосуточно и без выходных, когда вы снова в тупик, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по физике здесь!
*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Видео: Упругая потенциальная энергия | Nagwa
Стенограмма видео
В этом видео мы узнаем об упругой потенциальной энергии.
Мы узнаем, что это за тип энергии, как она связана с работой, проделанной над объектом, и мы увидим, как комбинировать упругую потенциальную энергию с другими видами энергии.
Для начала представьте, что у вас есть сделал крепость из дерева на заднем дворе. И так как форт является одним из ваших любимые места для времяпрепровождения, вы ловите себя на том, что поднимаетесь и спускаетесь по ступенькам к бываю там часто. Но через какое-то время устаешь всего этого лазания, и у вас есть идея. Вы покупаете то, что по сути является эластичную рогатку размером с человека и натяните ее между двумя небольшими деревьями возле дерева форт. Чтобы выяснить, насколько далеко назад вам нужно будет встать в человеческую рогатку, чтобы она выстрелила вам в форт на дереве, нам нужно немного узнать об упругой потенциальной энергии.
Первое, что можно сказать о упругая потенциальная энергия заключается в том, что всякий раз, когда пружина растягивается или сжимается, она обладает потенциальной энергией, то есть способностью совершать работу. И когда мы говорим весна, это может включают не только буквальные пружины, но и упругие материалы или вещества, которые отскакивают после их деформации.
Если бы мы взяли весенний отдых на ее равновесную длину, а затем растянуть эту пружину на расстояние 𝑥, смещенное по ее естественной длине мы знаем, что растянутая пружина будет оказывать восстанавливающее силы, мы можем назвать 𝐹 sub 𝑠, величина которого равна жесткости пружины 𝑘 раз больше смещения от равновесия 𝑥.
Вспомним основное уравнение работы сделано, то есть оно равно силе, умноженной на перемещение. Но это уравнение для работы предполагает сила, которая не зависит от смещения, в то время как сила пружины меняется.
Это зависит от смещения 𝑥. За работу, проделанную тогда нашим сила пружины, эта работа будет равна интегралу от нуля до максимума перемещение 𝑥 этой силы, умноженное на 𝑑𝑥.
Подключение для величины этой силы, теперь у нас есть выражение для работы, совершаемой растянутым или сжатым весна. Интегрируя это выражение из от нуля до 𝑥, мы находим результат, равный половине 𝑘, умноженной на 𝑥 в квадрате. Это равно работе, которую совершает пружины, а также равна потенциальной энергии пружины, или упругому потенциалу энергия.
Один из способов понять эластичность Потенциальная энергия — это думать о ней как о потенциальной энергии гравитации. Мы знаем, что если мы возьмем массу и поднять его в гравитационном поле на некоторую высоту, тогда эта масса теперь имеет потенциальной энергии и, следовательно, способности совершать работу.
Точно так же, если мы поместим массу на конец пружины, а затем сжать эту пружину, эта масса также имеет потенциал энергия. В этом случае из-за упругости энергия весны. И так же, как гравитационный потенциальная энергия, упругая потенциальная энергия соответствует закону сохранения энергии схемы. Давайте попрактикуемся с упругая потенциальная энергия через пару примеров.
Пружина пружинного пистолета имеет силовая постоянная 𝑘 равна 12 ньютонам на сантиметр. Когда пистолет направлен вертикально вверх, 15-граммовый снаряд выбрасывается на высоту 5,0 метров над концом ствола. расширенная пружина, как показано на прилагаемой схеме. Насколько была сжата пружина изначально?
На схеме мы назвали это расстояние 𝑑. А еще нам говорят, что весна постоянная пружины составляет 12 ньютонов на сантиметр, а масса выстрела составляет выстрелил 15 грамм.
Глядя на схему этого сценарии мы видим, что начальные и конечные условия связаны через энергию сохранение.
Если мы назовем состояние, в котором пружина сжата до исходного состояния и точки, в которой находится шарик высшая точка полета конечное состояние, то можно написать, что начальная сумма кинетическая плюс потенциальная энергия равна конечному количеству кинетической плюс потенциальной энергия. Как в начале, так и в В конце мяч не движется, поэтому его кинетическая энергия в обоих случаях равна нуль.
Когда мы рассматриваем начальное состояние мяча, мы знаем, что его потенциальная энергия обусловлена упругой энергией сжимается весной. Мы можем назвать этот PE sub 𝑠, для потенциальная энергия пружины. С другой стороны, финал потенциальная энергия нашей системы целиком гравитационная, так как шар неподвижен известной высоте над расправленной пружиной.
Итак, мы можем написать, что весна потенциальная энергия равна потенциальной энергии гравитации. И вспоминаем тот весенний потенциал энергия равна половине постоянной пружины, умноженной на смещение от равновесия в квадрате и что гравитационная потенциальная энергия равна 𝑚 умножить на 𝑔 раз ℎ.
Для нашего сценария мы пишем потенциальная энергия пружины равна половине 𝑘, умноженной на 𝑑 в квадрате, где 𝑑 — расстояние, которое мы хотите решить для. А что касается потенциальной энергии, мы принимаем высоту ℎ равной 5,0 метрам, высоте мяча, когда он находится выше полностью растянутая пружина и не в движении.
Преобразование этого выражения в находим 𝑑, получаем, что оно равно квадратному корню из двух раз 𝑚 раз 𝑔 раз ℎ все разделить на 𝑘. 𝑔, ускорение за счет гравитации, будем считать ровно 90,8 метра в секунду в квадрате.
Когда мы подключаемся к этим значениям, мы стараемся преобразовать нашу массу в значение в килограммах, а нашу пружину константа 𝑘 в значение в ньютонах на метр.
Вычисляя этот результат, находим 𝑑 составляет 3,5 сантиметра. Это количество пружины должно быть сжатым, чтобы выстрелить мячом на заданную высоту ℎ.
Теперь посмотрим на другую резинку Пример потенциальной энергии.
Струна имеет постоянную силы 53,0 ньютона на метр. Объект, первоначально находившийся в состоянии покоя, с к нему подвешен груз массой 0,960 кг. Объект опускается, растягивая пружинит, колеблется, а затем останавливается. Насколько растянута пружина когда объект остановится после колебания? Рассчитайте уменьшение гравитационная потенциальная энергия объекта между его положением в точке которой он прикреплен к нерастянутой пружине, и его положение в точке, в которой он приходит в состояние покоя после колебаний.
Рассчитайте энергию, запасенную в пружина своим удлинением.
В этом упражнении, состоящем из трех частей, мы сначала нужно решить смещение пружины после того, как масса была подвешена оно и останавливается. Далее мы хотим решить для изменение гравитационной потенциальной энергии массы между двумя точками из которой он подвешен на нерастянутой пружине, и точка, в которой он отдыхать. И, наконец, мы хотим рассчитать энергия, запасенная в пружине за счет ее растяжения. Мы назовем этот PE sub 𝑠.
В этом сценарии мы начинаем с вертикально ориентированная пружина на ее естественной или равновесной длине. Весна, как нам говорят, имеет весну постоянная 𝑘 53,0 ньютона на метр. Затем, мы берем массу, мы назвали это 𝑚, весом 0,960 кг и прикрепите его к свободному концу пружины. В ответ на это весна растягивается, колеблется, а затем останавливается со смещением, которое мы назвали Δ𝑥 от своего исходного положения.
Чтобы найти Δ𝑥, начнем с учитывая силы, действующие на массу 𝑚. Когда масса успокоилась после колебаний на конце пружины мы знаем, что сила тяжести сила, действующая на массу, по величине равна силе пружины, действующей на массу. Итак, мы можем написать 𝑚 раз 𝑔 равно равна жесткости пружины 𝑘, умноженной на Δ𝑥. Переставляя это выражение, мы видим что Δ𝑥 равно 𝑚, умноженному на 𝑔 сверх 𝑘, где 𝑔 мы будем рассматривать как ровно 90,8 метра за секунду в квадрате.
Подстановка этих трех значений, когда мы вычисляем Δ𝑥, мы обнаруживаем, что с точностью до трех значащих цифр это 17,8 сантиметры. Это количество пружины растянулся из-за массы 𝑚. Теперь приступим к решению изменение гравитационной потенциальной энергии массы 𝑚 за это смещение.
Напоминая, что в целом гравитационная потенциальная энергия равна массе объекта, умноженной на ускорение из-за силы тяжести, умноженной на его высоту относительно некоторого исходного уровня.
Поскольку мы рассчитываем изменение в гравитационной потенциальной энергии массы можно написать, что она равна 𝑚 раз 𝑔 раз Δ𝑥. Отрицательный знак не нужен.
Когда мы подключаемся к этим трем значений, стараясь записать наше перемещение Δ𝑥 в единицах метров, мы находим, что ΔPE sub 𝑔 составляет 1,67 Дж. Это изменение массы гравитационно потенциальная энергия. Наконец, мы хотим решить для потенциальная энергия, накопленная в пружине в результате этого расширения.
Напомним, что вообще то потенциальная энергия равна половине постоянной пружины, умноженной на ее смещение из квадрата равновесия. Итак, мы можем написать, что PE sub 𝑠 есть равно половине 𝑘, умноженной на Δ𝑥 в квадрате, где 𝑘 известна жесткость пружины и Δ𝑥 мы решили ранее. Подставляя вместо этих значений используя расстояние в метрах для нашего смещения Δ𝑥, мы находим, что PE sub 𝑠 равно 0,835.
джоули. Вот сколько потенциальной энергии пружина выиграла в силу того, что была растянута.
Мы можем задаться вопросом, почему весна потенциальная энергия не равна изменению потенциальной энергии гравитации. Напомним, что перед тем, как лечь спать, наша масса 𝑚 колебалась вверх и вниз на пружине. Во время этого движения вверх-вниз теряет энергию из-за трения с воздухом, а также из-за пружины. Это помогает учитывать разница между этими двумя значениями.
Подведем итог тому, что мы узнали пока об упругой потенциальной энергии. Мы видели, что растянутое или сжатая пружина обладает потенциальной энергией. Мы говорили, что этот потенциал энергия, которую мы могли бы назвать PE sub 𝑠, равна половине жесткости пружины 𝑘 умноженное на его смещение от равновесия или естественную длину, 𝑥 в квадрате.
Мы также видели, что потенциал энергия, запасенная в пружине, PE sub 𝑠, равна работе, совершаемой пружиной. И мы видели эту резинку или пружина, потенциальная энергия в изолированной системе является частью общей энергии картина сохранения, включая кинетическую энергию и гравитационный потенциал энергия. Другими словами, это энергетический термин. как и другие энергетические термины.
Spring Potential Energy — Видео по физике от Brightstorm 92
, в основном используется при определении потенциальной энергии пружины.потенциальная энергия пружины
Итак, давайте поговорим о потенциальной энергии пружины. Хорошо, просто чтобы напомнить вам всякий раз, когда у нас есть консервативная сила, что происходит, так это работа, выполняемая этой силой, может быть выражена как минус изменение функции, которая зависит только от положения и называется функцией потенциальной энергии U.
Иногда люди используют PE для потенциальной энергии, но давайте просто используем U.
Хорошо, поэтому работа всегда равна силе, умноженной на изменение положения, но в этом случае наша сила зависит от положения, поэтому я не знаю, что использовать для моей силы, если мое положение меняется, которое один я использую? Я использую kx в начале kx в конце kx на полпути я не знаю, хм, так что мы собираемся сделать, мы собираемся сделать график зависимости силы от положения, так что идея состоит в том, что сила здесь зависит от положения, но я хочу как-то найти способ интерпретировать изменение силы и времени в положении на этом графике. Что ж, сила вертикальная, изменение положения, если я просто немного изменю положение, будет горизонтальным, поэтому, если я действую, умножая силу на изменение положения, тогда это дает мне площадь этого низкого красного прямоугольника и до тех пор, пока изменение положения действительно действительно мало, сила не изменится очень сильно, и тогда я могу просто считать ее постоянной в этом маленьком квадрате, так что это означает, что я могу интерпретировать работу как площадь под графиком зависимости силы от положения, это всегда верно всякий раз, когда у нас есть консервативная сила.
Теперь в нашем случае сила равна kx, а это означает, что изменение потенциальной энергии будет равно площади под kx. Хорошо, вот kx à ¢  €  «f, и это просто выглядит так, и я хочу знать, какая работа проделана, когда я иду от начального x до конечного x, и работа — это просто площадь под этим графиком, но это легко вычислить. у него это трапеция ну это трапеция на боку да ладно. Площадь трапеции очень, очень проста, она равна высоте, умноженной на среднее значение двух оснований, хорошо, хорошо, два основания являются kx начальными и kx конечными, поэтому, чтобы получить это среднее значение, я просто складываю их вместе и делю на 2, а затем я я собираюсь умножить на высоту, теперь помните, что это трапеция на боку, поэтому под высотой я имею в виду это расстояние x конечное минус x начальное, так что вот мы идем, у меня здесь общий коэффициент k больше 2, и как только я возьму это один из них – это разность двух квадратов x конечный минус x начальный раз x конечный плюс x начальный ну, это x конечный квадрат минус x начальный квадрат, поэтому изменение потенциальной энергии равно изменению на половину kx в квадрате, так что это означает, что потенциальная энергия хранится в пружине всего одна половинка пружины постоянное растяжение в квадрате давай попробуем.
Итак, нам известно, что энергия, запасенная в пружине, составляет 20 джоулей, когда она растянута на 5 сантиметров, и мы хотим знать, сколько энергии сохраняется, когда она растягивается на 15 сантиметров. Хорошо, прямым способом решить эту проблему было бы просто пойти дальше и использовать U равно половине kx в квадрате подключите 20 джоулей подключите 5 сантиметров на самом деле вам нужно будет подключить 0,05 [IB] мы хотим сделать это В единицах SI найдите жесткость пружины, а затем просто снова используйте формулу, но есть гораздо более простой способ решить эту проблему, посмотрите от 5 до 15 сантиметров, что я сделал? Я утроил смещение, я утроил растяжение, ну господи, U это половина kx в квадрате, так что если я утрою x, сколько будет 3 в квадрате? это 9так что это означает, что я собираюсь 9 утроить потенциальную энергию хорошо 9 раз 20, 180 джоулей очень чисто очень просто мне не нужно вычислять постоянную пружины никто не спрашивал меня о постоянной пружины поэтому я не хочу тратить время на это, так что этот способ решения таких проблем очень и очень полезен, чтобы привыкнуть к нему.
Итак, в следующем примере у нас есть 200-граммовый груз, и я растягиваю его пружину на 40 сантиметров с помощью этого 200-граммового груза, и я хочу знать, сколько энергии хранится в пружине. Хорошо, в этом случае у меня нет постоянной пружины, поэтому я не могу напрямую использовать эту формулу, поэтому сначала я собираюсь получить пружину [IB], получить постоянную пружины, поэтому у меня сила равна kx сила, которая растягивая это точка 2 умножить на 10 помните, что вы должны умножить на G хорошо, потому что его сила равна kx а масса равна kx хорошо, так что у нас есть точка 2 умножить на 10 равно k раз что это? Пункт 4 хорошо, а затем мы разделим, и у нас будет k равно 2 по пункту 4 хорошо, что такое 2 по пункту 4? Ну, это 1 над точкой 2, что равно пяти и какова единица измерения? Ну, k – это ньютоны на метр, так что ньютоны на метр, хорошо, мы еще не закончили, боже, это займет вечность, хорошо, поэтому нам нужно узнать, сколько энергии, поэтому мы сделаем половину k, а затем x точка 4 в квадрате, верно? Итак, это будет половина, умноженная на 4 точки в квадрате, 4 точки будет 4 умножить на 10 до минус 1, я возведу в квадрат, я получаю 16 умножить на 10 до минус 2 на 2, а затем умножить на 5, верно? 16 разделить на 2 — это 8, 8 умножить на 5 — это 40, поэтому при умножении мы получим 0,4 джоуля, потому что 40 разделить на 100 — это точка 4.
Хорошо, давайте сделаем это проще, вот почему я оставил немного места здесь.
По моему опыту, студенты предпочли бы делать это таким образом, это занимает гораздо больше времени, это намного более грязно, но это более прямолинейно, это более похоже на о, мне нужна константа пружины, дайте мне получить константу пружины, позвольте мне показать вам другой способ, которым мы могли бы сделать это, намного чище. Хорошо, у меня нет постоянной пружины, так что мне делать? Ну, я решил здесь через жесткость пружины, но идея в том, что мне действительно не нужна жесткость пружины, мне нужна энергия, поэтому давайте попробуем выяснить, что такое энергия с точки зрения веса и смещения, поэтому мы скажем один Половина жесткости пружины равна мг, деленному на х, и тогда у нас будет х в квадрате одного из сокращений х, и это дает мне U равно половине мгх, посмотрите, как это красиво. Одна половина точки 2, 10, точка 4, вот и все. 10 раз точка 2 равна 2, 2 разделить на 2 отменить отменить отменить ответ 0,4 джоуля очень быстро очень очень очень просто, но вы должны мыслить алгебраически, и я думаю, что это проблема, с которой иногда сталкиваются студенты, потому что они к этому не привыкли .
Решите пару таких задач, постарайтесь привыкнуть к алгебраическому мышлению, потому что это намного упрощает задачу. В любом случае, это потенциальная энергия, запасенная в пружинах.
Примеры запасов упругой потенциальной энергии поясняется, как выполнять расчеты, решать задачи igcse/gcse 9-1 Примечания к пересмотру физики
ДОМАШНЯЯ СТРАНИЦА * KS3 НАУКИ * GCSE БИОЛОГИЯ ХИМИЯ ФИЗИКА * ПРОДВИНУТЫЙ УРОВЕНЬ ХИМИЯ
Используйте субиндекс страницы, возьмите время для изучения содержания или [Используйте поиск по сайту коробка]
ТИПЫ АККУМУЛЯТОРОВ ЭНЕРГИИ – объяснение примеров
(b) Запасы потенциальной упругой энергии и расчеты
IGCSE AQA GCSE Physics Edexcel GCSE Physics OCR GCSE Gateway Science Physics OCR GCSE 21st Century Science Physics Примечания к пересмотру школьной физики Дока Брауна: GCSE физика, физика IGCSE, физика уровня O, ~8, 9 классы СШАи 10 школьные курсы по естествознанию или эквивалентные для ~ 14-16 летних учащихся физика
Эта страница поможет вам с .
..
Что такое упругий запас потенциальной энергии? Как решить числовые задачи, связанные с упругая потенциальная энергия? Как вы объясните примеры упругой потенциальной энергии? Как использовать формулу и выполнять расчеты с использованием упругого потенциала энергия
ВСЕ мои заметки по физике
Найдите свой GCSE научный курс для получения дополнительной помощи, ссылки на примечания к редакции
Используй свой мобильный телефон или ipad и т. д. в «ландшафтном» режиме
это БОЛЬШОЕ веб-сайте, вам нужно потратить время на его изучение [Поиск по веб-сайту Коробка]
электронный документ коричневый
Упругая потенциальная энергия и запасы упругой потенциальной энергии
Энергия сохраняется, когда какой-то материал 90 656 растягивается или сжимается 90 657, и энергия высвобождается, когда высвобождается сужение – обычно в виде кинетической энергии.
например, сжатая пружина заводных часов – обеспечивает запас энергии для привода механического двигателя,
натянутая резинка резинка – растянутая катапульта запасает упругую потенциальную энергию, на снаряд вылетает вперед, так как запас его кинетической энергии иссякает. увеличенный,
растянутый металл в рулонах пружина,
сжатая пружина в животном ловушка
пружины подвески автомобиля поглощают энергию удара колеса на дороге, чтобы обеспечить более плавную езду,
натянутый лук до выпуска стрелы – звук увеличивает запас кинетической энергии стрелы..
Поскольку упругая потенциальная энергия является формой накопленной энергии, она ничего не делает, пока не будет высвобождена и преобразуется в другую форму энергии – часто в кинетическую энергию.
Когда силы, вызывающие растяжение, удалены, пружина или резинка возвращается к своей первоначальной длине (форме)
Чем эластичнее материал растягивается, тем больше запас упругой потенциальной энергии.
Величина упругого потенциала энергия, запасенная в растянутой пружине, может быть рассчитана с помощью уравнение:
(при условии, что предел пропорциональности не был превышен)
упругая потенциальная энергия, E e , в джоулях, Дж
жесткость пружины, k , в ньютонах на метр, Н/м
расширение или сжатие , e , в метрах, м
Для подробнее об упругой потенциальной энергии см.
Упругость и энергия, запасенная в пружине – эксперименты и расчеты
Как решить упругий потенциал проблемы с накопителями энергии
потенциальная энергия упругости = 0,5 жесткости пружины (расширение) 2
E e = 1 / 2 к е 2
Вам также может понадобиться зависимость пружины: усилие = жесткость пружины x растяжение
F = ке
, где F = приложенная сила в ньютонах (Н), e = удлинение пружины в метрах (м)
и k — жесткость пружины (упругости) в Н/м.
(перекрытие с силами 4, нужны вопросы на основе графиков)
На все вопросы, если не указано иное указано, вы предполагаете, что предел пропорциональности не превышен.

Q1 Пружина с пружиной постоянной 5,00 Н/м растягивается еще на 10,0 см.
Сколько дополнительной энергии хранится в запас упругой потенциальной энергии пружины за счет этого растяжения.
Е эпе = 1 / 2 к е 2 , 10,0 см ≡ 10,0/100 = 0,10 м
E эпе = 0,5 х 5,0 х 0,10 2
Е эпе = 0,025 Дж
Q2 А пружина имеет жесткость 2000 Н/м.
(a) Если запас упругой потенциальной энергии пружины составляет 50,0 Дж, насколько сильно сжата пружина?
E эпе = 1 / 2 k e 2 , перестановка дает e 2 = 2E epe / k, е = √(2E epe / k) и e = сжатие
e = √(2E epe / k) = √(2 x 50/2000) = √0,063 = 0,224 м (22,4 см, 3 стандартных шага)
(б) Какая сила нужна для сжатия пружина на 15,0 см в длину?
F = ке = 2000 х 15/100 = 300 Н
Q3 Требуется 5,0 Дж работы растянуть пружину на 20 см.
Сколько дополнительной работы необходимо совершить, чтобы растянуть еще на 20 см?
(i) Вам нужно отработать пружину постоянный. 20 см ≡ 20/100 = 0,20 м
E эпе = 1 / 2 k e 2 , перестановка дает k = 2E epe / e 2
к = (2 х 5,0) / (0,20 х 0,20) = 250 Н/м
(ii) Затем вычислите общую работу до растянуть пружину всего на 40 см.
Суммарная работа над пружиной равен запасу упругой потенциальной энергии при полном растяжении на 40 см. (что составляет 0,40 м). Поскольку теперь вы знаете постоянную пружины, вы используете снова то же уравнение, но решение для полного упругого потенциала энергия.
E эпи = 1 / 2 k e 2 = 0,5 х 250 х 0,40 2 = 20 Дж
(iii) Затем вы вычитаете (i) из (ii) чтобы выполнить дополнительную работу.
Следовательно, дополнительная работа = 20 – 5 = 15 Дж
Q4 Пружина хранит дополнительные 20 Дж упругой потенциальной энергии при растяжении на дополнительные 40 см.
Рассчитайте жесткость пружины.
40 см = 0,40 м.
E эпе = 1 / 2 k e 2 , перестановка:
к = Е епе х 2 / е 2 = 20 х 2 / 0,40 2 = 250 Н/м
Q5 Натянутая струна общая длина 60 см и жесткость пружины 240 Н/м.
Если растянутая пружина накапливает 20 Дж энергии, чему равна длина нерастянутой пружины с точностью до см?
E эпе = 1 / 2 k e 2 , перестановка и 60 см = 0,60 м
е = √(2E эпе / к) = √(2 x 20/240) = √(1/6) = 0,408 м
0,408 м = 40,8 см, ~41 см = дополнительно длина, добавленная к растянутой строке
Следовательно, исходная длина пружины = 60 – 41 = ~19 см
Q6 А пружина жестко зафиксирована в вертикальном положении.
При массе 120,0 g прикреплен к пружине, он удлиняется на 3,2 см.
(a) Предполагая, что напряженность гравитационного поля составляет 9,8 Н/кг, рассчитать жесткость пружины k .
100 г эквивалентны весу (силе) 90,8 х 120/1000 = 1,176 Н
Удлинитель e = 3,2/100 = 0,032 м. Сила Ф = 1,176 Н
(Уравнение F = ke уже рассматривалось в подробности далее на этой странице)
F = ke, поэтому жесткость пружины k = Fe = 1,176 0,032 = 36,8 Н/м (3 фута)
(б) Рассчитать экстра упругая потенциальная энергия хранится весной в результате добавленного веса.
Используя уравнение для упругой хранимой энергия: E e = 1 / 2 k e 2 (подробно уже рассмотрено на этом стр.)
е е = 1 / 2 к е 2 = 1 / 2 х 36,75 х 0,032 х 0,032 = 0,019 Дж
(c) Если дополнительный груз массой 200 г помещен на весна, сколько еще она продлится?
200 г соответствует весу 9,8 x 200/1000 = 1,96 Н, k = 36,75 Н/м
F = ke, поэтому удлинитель пружины e = F к = 1,96/36,75 = 0,053 м (5/3 см)
(d) Какая сила необходима, чтобы вытянуть пружина на 30 см?
Требуемая сила= F = ke = 36,75 x 30/100 = 11,0 Н (1 дп, 3 стп)
(d) Какое важное предположение вы сделанные относительно расчетов в пунктах (а)-(в)?
Вы предположили, что пружина ведет себя действительно эластичный т.
е. в пределах предела эластичности (предел соразмерность).
Q7 Жесткость пружины 20,0 Н/м.
Какое расширение будет у см , если при растяжении пружины была совершена работа 0,50 Дж?
Формула упругой потенциальной энергии: E epe = 1 / 2 к е 2
перестановка: расширение e = √(2E epe / к) = √(2 х 0,50/20) = 0,224 м = 22,4 см
Q8 На этот вопрос вы нужно знать формулу гравитационной потенциальной энергии (GPE) и постоянная гравитационного поля g = 9,8 м/с 2 или 9,8 Н/кг). Осторожно для единиц, помните, в конце концов, чтобы работать в Дж, м и кг.
Забавная игрушка состоит из пружины и забавная голова на конце.
При сжатии игрушечной пружины 5,0 см, и выпущенный, он прыгает вертикально вверх в воздух.
Игрушечная пружина имеет массу 20 г.
При освобождении подпрыгивает на максимальная высота 75 см.
Если принять все упругие потенциальная энергия (ЭПЭ) передается в хранилище ГПЭ игрушки пружины, определите жесткость пружины.
GPE = мг/ч = (20/1000) x 9,8 х (75/100) = 0,147 Дж
Пренебрегая сопротивлением воздуха мы можно сказать GPE = EPE для передачи накопителя энергии
Формула упругой потенциальной энергии: E epe = 1 / 2 к е 2
Перестановкадает: k = E epe x 2 / e 2 = 0,147 х 2 / (5,0 / 100) 2 = 118 Н/м (3 сф)
НАЧАЛО СТРАНИЦЫ
Энергетические ресурсы, энергия переводы, выполненная работа и заметки о пересмотре системы электропитания индекс
Типы энергии и запасов – примеры сравнения/объяснения, расчеты совершенная механическая работа и мощность
Химическая запасы энергии * Эластичный запасы потенциальной энергии, расчеты * Электрический и электростатический запасы энергии
Гравитационный потенциал энергия и расчеты * Кинетический запасы энергии и расчеты * Ядерный накопитель энергии
Термальный запасы энергии * Световая энергия * Энергия звука * Магнитный накопители энергии
Сохранение энергии, передачи-преобразования энергии, КПД – расчеты и Диаграммы Санки по физике GCSE
См.
также Подробнее о методах снижения теплопередачи, например, в доме, изоляционных свойствах материалов
Энергетические ресурсы: использование, общий обзор и тенденции, сравнение возобновляемых и невозобновляемых источников энергии, производство электроэнергии
Возобновляемая энергия (1) Энергия ветра и солнечная энергия, преимущества и недостатки пересмотра физики gcse отмечает
Возобновляемая энергия (2) Гидроэнергетика и геотермальная энергия, преимущества и недостатки физика
Возобновляемая энергия (3) Мощность волн и мощность приливных заграждений, преимущества и недостатки ОГЭ по физике
См. также Возобновляемая энергия – биомасса – биотопливо и альтернативные виды топлива, водород, биогаз, биодизель, экзамен по химии gcse
Теплица воздействие, глобальное потепление, изменение климата, углеродный след от сжигания ископаемого топлива gcse химия
Поглощение и испускание излучения материалы – температура и поверхностные факторы, включая глобальное потепление
Польза электричества gcse примечания к редакции физики электричества
и Источник питания «Национальной сети», упоминание о малых весы, трансформаторы gcse заметки по физике
и Источник питания «Национальной сети», упоминание о малых весы, трансформаторы gcse заметки по физике
выпускных экзаменов в школе примечания к пересмотру физики по запасу упругой потенциальной энергии объяснил пересмотр IGCSE заметки о запасе упругой потенциальной энергии объяснили физику KS4 Научные заметки о запас упругой потенциальной энергии объяснил руководство по физике GCSE заметки о запасе упругой потенциальной энергии для школ, колледжей, академий, научных курсов, преподавателей, изображений диаграммы изображений для запаса упругой потенциальной энергии объяснили научные примечания к пересмотру объяснен запас упругой потенциальной энергии для повторения модулей физики примечания к темам физики, чтобы помочь в понимании запас упругой потенциальной энергии объяснил университетские курсы по физике карьера в научной физике работа в машиностроении технический лаборант ученичество инженер стажировки по физике США 8 класс США 9 класс10 класс AQA GCSE 9-1 примечания к пересмотру физики по упругому потенциалу запас энергии объяснил GCSE примечания по запасу упругой потенциальной энергии объяснены Edexcel GCSE 9-1 физика примечания к пересмотру объяснен запас упругой потенциальной энергии для OCR GCSE 9-1 21 век Научные заметки по физике об упругом запасе потенциальной энергии объяснил OCR GCSE 9-1 Шлюз физика наука примечания к пересмотру эластичного запаса потенциальной энергии объяснили WJEC gcse science CCEA/CEA gcse science GCSE примечания к пересмотру физики об упругом запасе потенциальной энергии объяснил
Контент сайта Dr.


 Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.
Как правило, этот процесс предусматривает возврат витков в свое первоначальное положение. Это достигается за счет особой формы изделия, а также применения соответствующего материала, который обладает повышенной упругостью. Именно за счет этого свойства зачастую проводится установка рассматриваемого изделия. Показатель может достигать весьма высоких показателей, которой достаточно для реализации различных задач. Распространенным примером можно назвать установку пружины в запорных и предохранительных элементах, которые отвечают за непосредственное возращение запорного элемента в требуемое положение.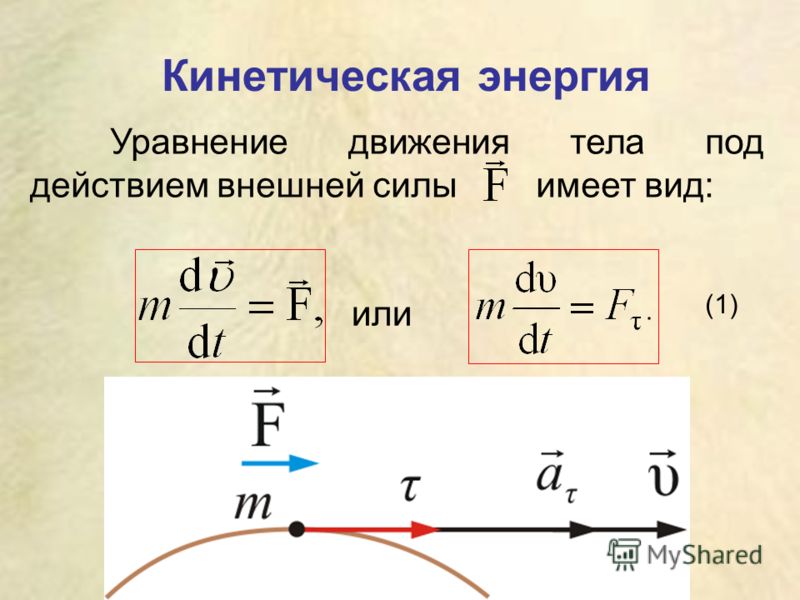



 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 В лапке штатива закрепляют динамометр. К его крючку привязывают шар на нити длиной 60—80 см. На другом штативе на одинаковой высоте с динамометром укрепляют в лапке желоб. Установив шар на краю желоба и удерживая его, отодвигают второй штатив от первого на длину нити. Если отодвинуть шар от края желоба на х, то в результате деформации пружина приобретет запас потенциальной энергии
В лапке штатива закрепляют динамометр. К его крючку привязывают шар на нити длиной 60—80 см. На другом штативе на одинаковой высоте с динамометром укрепляют в лапке желоб. Установив шар на краю желоба и удерживая его, отодвигают второй штатив от первого на длину нити. Если отодвинуть шар от края желоба на х, то в результате деформации пружина приобретет запас потенциальной энергии Укрепите на штативах динамометр и желоб на одинаковой
Укрепите на штативах динамометр и желоб на одинаковой Результаты измерений и расчетов занесите в отчетную таблицу.
Результаты измерений и расчетов занесите в отчетную таблицу.
 Выразите кинетическую энергию через импульс тела.
Выразите кинетическую энергию через импульс тела. 5 H/м под действием силы упругости удлиняетс… – Учеба и наука
5 H/м под действием силы упругости удлиняетс… – Учеба и наука 04.16
04.16


 Чему равна потенциальная энергия растянутой пружины?
Чему равна потенциальная энергия растянутой пружины?
 Определите потенциальную энергию этой пружины при растяжении на 0,08 м.
Определите потенциальную энергию этой пружины при растяжении на 0,08 м.
 Чему равна потенциальная энергия пружины?
Чему равна потенциальная энергия пружины?
 E =
E =  E =
E = E 22222233333333331 годы 22222223 F =
E 22222233333333331 годы 22222223 F = E I =
E I = Упругость — это способность твердого вещества возвращаться в свое равновесное положение или исходное положение после воздействия на него любой внешней силы. Она также известна как упругая потенциальная энергия. Потенциальная энергия здесь возникает из-за смещения пружины из положения равновесия в другое положение, и эта потенциальная энергия равна чистой работе, выполненной из-за растяжения пружины. Это также напоминает ту же механику колебаний простого маятника, где за счет внешней силы объект перемещается из своего положения равновесия в свои максимальные концы, и периодическое движение продолжается до тех пор, пока он не вернется в положение равновесия для покоя.
Упругость — это способность твердого вещества возвращаться в свое равновесное положение или исходное положение после воздействия на него любой внешней силы. Она также известна как упругая потенциальная энергия. Потенциальная энергия здесь возникает из-за смещения пружины из положения равновесия в другое положение, и эта потенциальная энергия равна чистой работе, выполненной из-за растяжения пружины. Это также напоминает ту же механику колебаний простого маятника, где за счет внешней силы объект перемещается из своего положения равновесия в свои максимальные концы, и периодическое движение продолжается до тех пор, пока он не вернется в положение равновесия для покоя.
 Теперь, если построить график, чтобы понять соотношение силы и смещения, они оба перпендикулярны друг другу, а жесткость пружины будет под углом 45 градусов к обоим компонентам, поэтому на графике он образует прямоугольный треугольник. Таким образом, основание прямоугольного треугольника является произведением смещения и жесткости пружины, а высота также является смещением. Если x – смещение, а k – жесткость пружины, то путем расчета уравнения получается U с = 1/2·k·x 2
Теперь, если построить график, чтобы понять соотношение силы и смещения, они оба перпендикулярны друг другу, а жесткость пружины будет под углом 45 градусов к обоим компонентам, поэтому на графике он образует прямоугольный треугольник. Таким образом, основание прямоугольного треугольника является произведением смещения и жесткости пружины, а высота также является смещением. Если x – смещение, а k – жесткость пружины, то путем расчета уравнения получается U с = 1/2·k·x 2 
 Пусть T — сила пружины, а K — постоянная силы
Пусть T — сила пружины, а K — постоянная силы
 Определить значение потенциальной энергии пружины
Определить значение потенциальной энергии пружины Мы узнаем, что это за тип
энергии, как она связана с работой, проделанной над объектом, и мы увидим, как
комбинировать упругую потенциальную энергию с другими видами энергии.
Мы узнаем, что это за тип
энергии, как она связана с работой, проделанной над объектом, и мы увидим, как
комбинировать упругую потенциальную энергию с другими видами энергии.
 Это зависит от смещения
𝑥. За работу, проделанную тогда нашим
сила пружины, эта работа будет равна интегралу от нуля до максимума
перемещение 𝑥 этой силы, умноженное на 𝑑𝑥.
Это зависит от смещения
𝑥. За работу, проделанную тогда нашим
сила пружины, эта работа будет равна интегралу от нуля до максимума
перемещение 𝑥 этой силы, умноженное на 𝑑𝑥. Точно так же, если мы поместим массу на
конец пружины, а затем сжать эту пружину, эта масса также имеет потенциал
энергия. В этом случае из-за упругости
энергия весны. И так же, как гравитационный
потенциальная энергия, упругая потенциальная энергия соответствует закону сохранения энергии
схемы. Давайте попрактикуемся с
упругая потенциальная энергия через пару примеров.
Точно так же, если мы поместим массу на
конец пружины, а затем сжать эту пружину, эта масса также имеет потенциал
энергия. В этом случае из-за упругости
энергия весны. И так же, как гравитационный
потенциальная энергия, упругая потенциальная энергия соответствует закону сохранения энергии
схемы. Давайте попрактикуемся с
упругая потенциальная энергия через пару примеров. Глядя на схему этого
сценарии мы видим, что начальные и конечные условия связаны через энергию
сохранение.
Глядя на схему этого
сценарии мы видим, что начальные и конечные условия связаны через энергию
сохранение. Итак, мы можем написать, что весна
потенциальная энергия равна потенциальной энергии гравитации. И вспоминаем тот весенний потенциал
энергия равна половине постоянной пружины, умноженной на смещение от
равновесия в квадрате и что гравитационная потенциальная энергия равна 𝑚 умножить на 𝑔
раз ℎ.
Итак, мы можем написать, что весна
потенциальная энергия равна потенциальной энергии гравитации. И вспоминаем тот весенний потенциал
энергия равна половине постоянной пружины, умноженной на смещение от
равновесия в квадрате и что гравитационная потенциальная энергия равна 𝑚 умножить на 𝑔
раз ℎ. Когда мы подключаемся к этим значениям,
мы стараемся преобразовать нашу массу в значение в килограммах, а нашу пружину
константа 𝑘 в значение в ньютонах на метр.
Когда мы подключаемся к этим значениям,
мы стараемся преобразовать нашу массу в значение в килограммах, а нашу пружину
константа 𝑘 в значение в ньютонах на метр. Рассчитайте энергию, запасенную в
пружина своим удлинением.
Рассчитайте энергию, запасенную в
пружина своим удлинением.
 Поскольку мы рассчитываем изменение
в гравитационной потенциальной энергии массы можно написать, что она равна 𝑚
раз 𝑔 раз Δ𝑥. Отрицательный знак не нужен.
Поскольку мы рассчитываем изменение
в гравитационной потенциальной энергии массы можно написать, что она равна 𝑚
раз 𝑔 раз Δ𝑥. Отрицательный знак не нужен. джоули. Вот сколько потенциальной энергии
пружина выиграла в силу того, что была растянута.
джоули. Вот сколько потенциальной энергии
пружина выиграла в силу того, что была растянута.
 Иногда люди используют PE для потенциальной энергии, но давайте просто используем U.
Иногда люди используют PE для потенциальной энергии, но давайте просто используем U. Теперь в нашем случае сила равна kx, а это означает, что изменение потенциальной энергии будет равно площади под kx. Хорошо, вот kx à ¢  €  «f, и это просто выглядит так, и я хочу знать, какая работа проделана, когда я иду от начального x до конечного x, и работа — это просто площадь под этим графиком, но это легко вычислить. у него это трапеция ну это трапеция на боку да ладно. Площадь трапеции очень, очень проста, она равна высоте, умноженной на среднее значение двух оснований, хорошо, хорошо, два основания являются kx начальными и kx конечными, поэтому, чтобы получить это среднее значение, я просто складываю их вместе и делю на 2, а затем я я собираюсь умножить на высоту, теперь помните, что это трапеция на боку, поэтому под высотой я имею в виду это расстояние x конечное минус x начальное, так что вот мы идем, у меня здесь общий коэффициент k больше 2, и как только я возьму это один из них – это разность двух квадратов x конечный минус x начальный раз x конечный плюс x начальный ну, это x конечный квадрат минус x начальный квадрат, поэтому изменение потенциальной энергии равно изменению на половину kx в квадрате, так что это означает, что потенциальная энергия хранится в пружине всего одна половинка пружины постоянное растяжение в квадрате давай попробуем.
Теперь в нашем случае сила равна kx, а это означает, что изменение потенциальной энергии будет равно площади под kx. Хорошо, вот kx à ¢  €  «f, и это просто выглядит так, и я хочу знать, какая работа проделана, когда я иду от начального x до конечного x, и работа — это просто площадь под этим графиком, но это легко вычислить. у него это трапеция ну это трапеция на боку да ладно. Площадь трапеции очень, очень проста, она равна высоте, умноженной на среднее значение двух оснований, хорошо, хорошо, два основания являются kx начальными и kx конечными, поэтому, чтобы получить это среднее значение, я просто складываю их вместе и делю на 2, а затем я я собираюсь умножить на высоту, теперь помните, что это трапеция на боку, поэтому под высотой я имею в виду это расстояние x конечное минус x начальное, так что вот мы идем, у меня здесь общий коэффициент k больше 2, и как только я возьму это один из них – это разность двух квадратов x конечный минус x начальный раз x конечный плюс x начальный ну, это x конечный квадрат минус x начальный квадрат, поэтому изменение потенциальной энергии равно изменению на половину kx в квадрате, так что это означает, что потенциальная энергия хранится в пружине всего одна половинка пружины постоянное растяжение в квадрате давай попробуем.

 Хорошо, давайте сделаем это проще, вот почему я оставил немного места здесь.
Хорошо, давайте сделаем это проще, вот почему я оставил немного места здесь. Решите пару таких задач, постарайтесь привыкнуть к алгебраическому мышлению, потому что это намного упрощает задачу. В любом случае, это потенциальная энергия, запасенная в пружинах.
Решите пару таких задач, постарайтесь привыкнуть к алгебраическому мышлению, потому что это намного упрощает задачу. В любом случае, это потенциальная энергия, запасенная в пружинах.  ..
..

 Упругость и энергия, запасенная в пружине –
эксперименты и расчеты
Упругость и энергия, запасенная в пружине –
эксперименты и расчеты


 При массе 120,0
g прикреплен к пружине, он удлиняется на 3,2 см.
При массе 120,0
g прикреплен к пружине, он удлиняется на 3,2 см. е. в пределах предела эластичности (предел
соразмерность).
е. в пределах предела эластичности (предел
соразмерность).
 также Подробнее о методах снижения теплопередачи, например, в доме, изоляционных свойствах материалов
также Подробнее о методах снижения теплопередачи, например, в доме, изоляционных свойствах материалов