Предел прочности как обозначается: Предел прочности при растяжении

alexxlab | 21.07.2023 | 0 | Разное

Содержание

Предел прочности при сжатии | Мир сварки

Содержание

Предел прочности при сжатии
- Металлы
- Пластмассы
- Дерево
- Минералы
- Различные материалы
Литература

Предел прочности при сжатии

Предел прочности при сжатии (σ_{в. сж.}) – максимальное сжимающее напряжение, которое материал способен выдержать, определяется относительно первоначальной площади поперечного сечения. Если материал разрушается при сжатии изломом или трещиной, предел прочности при сжатии имеет определенное значение. Если материал не разрушается при сжатии, значение предела прочности при сжатии зависит от степени искажения образца, которое оценивается как признак отказа материала.

Предел прочности при сжатии измеряется:

1 кгс/мм² = 10^-6 кгс/м² = 9,8·10⁶ Н/м² = 9,8·10⁷ дин/см² = 9,81·10⁶ Па = 9,81 МПа.

Предел прочности при сжатии
Материал	σ_{в. сж.}
Материал	кгс/мм²	10⁷ Н/м²	МПа
Металлы
Чугун белый	до 175	до 172	до 1717
Чугун серый мелкозернистый	до 140	до 137	до 1373
Чугун серый обыкновенный	60-100	58,9-98,1	589-981
Пластмассы
Аминопласт слоистый	10	9,8	98
Асботекстолит	12,5-30,7	12,3-30,1	123-301
Винипласт	8-16	7,8-15,7	78-157
Гетинакс	15-18	14,7-17,7	147-177
Древесно-слоистый пластик ДСП-Б (длинный лист)	15,5	15,2	152
Древесный коротковолнистый волокнит К-ФВ25	12,9	12,7	127
Капрон стеклонаполненный	12	11,8	118
Пенопласт плиточный	0,150	0,147	1,47
Пенопласт ФК-20	0,1	0,098	0,98
Полиакрилат (оргстекло)	7	6,9	69
Полиамид наполненный П-68	9,5-10	9,3-9,8	93-98
Полиамид стеклонаполненный СП-68	11	10,8	108
Поливинилхлорид неориентированный	5,3-6,0	5,2-5,9	52-59
Поликапроамид	6,8-8,0	6,7-7,8	67-78
Поликапроамид стеклонаполненный	12-13	11,8-12,9	118-129
Поликарбонат (дифион)	8-9	7,8-8,8	78-88
Поликарбонат стеклонаполненный	13,3	13	130
Полипропилен ПП-1	6	5,9	59
Полипропилен стеклонаполненный	4,9	4,8	48
Полистирол стеклонаполненный	9,8-11,9	9,6-11,7	96-117
Полистирол эмульсионный А	10	9,8	98
Полиформальдегид стабилизированный	13	12,7	127
Полиэтилен высокого давления П-2006-Т	1,25	1,23	12,3
Полиэтилен низкого давления П-4007-Э	2,50	2,45	24,5
Сополимер МСН-А	8,9-9,1	8,8-8,9	88-89
Стекло органическое ПА, ПБ, ПВ	12-16	11,8-15,7	118-157
Стеклотекстолит	30	29,4	294
Текстолит графитированный	20	19,6	196
Текстолит металлургический	20	19,6	196
Текстолит ПТК	15-25	14,7-24,5	147-245
Фаолит А	4	3,9	39
Фенопласт текстолитовый	10-26	9,8-25,5	98-255
Фторопласт 3	2,0-5,7	1,96-5,60	19,6-56,0
Фторопласт 4	1,20	1,18	11,8
Целлон	16	15,7	157
Целлулоид	5-7	4,9-6,9	49-69
Дерево
Дуб (при 15 % влажности) вдоль волокон	5	4,9	49
Дуб (при 15 % влажности) поперек волокон	1,5	4,5	15
Сосна (при 15 % влажности) вдоль волокон	4	3,9	39
Сосна (при 15 % влажности) поперек волокон	0,5	0,5	4,9
Минералы
Графит	1,6-3,8	1,57-3,73	15,7-37,3
Различные материалы
Бакелит	8-10	7,8-9,8	78-98
Бетон	0,5-3,5	0,49-3,43	4,9-34,3
Гранит	15-26	14,7-25,5	147-255
Кирпич	0,74-3	0,73-2,94	7,3-29,4
Лед (0 °С)	0,1-0,2	0,1-0,2	0,98-1,96

Литература

Справочник по элементарной физике / Н. Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
Таблицы физических величин. Справочник / Под ред. И.К. Кикоина. М., Атомиздат. 1976, 1008 с.

Прочность | Материаловедение

Прочность – свойство материалов сопротивляться разрушению или пластической деформации под действием внешней нагрузки. Наиболее простым и распространенным методом определения прочности материала является испытание его на растяжение (рисунок 1). Концы образца металла круглого сечения зажимают в разрывной машине и подвергают действию растягивающей нагрузки Р.

Рисунок 1 – Метод определения прочности на растяжение. ι_о – начальная длина; F₀– начальная площадь поперечного сечения; Δι – удлинение; ι_к – конечная длина образца в момент разрыва; F_к – площадь поперечного сечения образца в месте разрыва

Диаграмму растяжения можно построить в координатах «нагрузка Р -удлинение Δι» или в координатах «напряжение σ – относительная деформация ε». σ= Р/F₀ а ε= Δι/ι₀ ×100% (рисунок 2).
Под действием нагрузки в материале возникают деформации. Деформацией называется изменение размеров и формы тела, она может быть упругой и пластической. Упругой называют деформацию, влияние которой на форму, структуру и свойства тела полностью устраняется после прекращения действия внешней силы Р. На рисунке 2 упругая деформация характеризуется прямолинейным участком ОА. При упругой деформации изменяется расстояние между атомами в кристаллической решетке. При снятии нагрузки атомы становятся на прежние места и деформация исчезает.

Рисунок 2 – Диаграмма растяжения

Оценить свойства материала в пределах упругих деформаций можно с помощью коэффициента, получившим название модуля упругости Е (Гука). Это отношение напряжения к вызванной им деформации:
Значение модуля упругости определяется силами межатомного взаимодействия, оно постоянно и характеризует жесткость материала. Чем меньшую деформацию вызывает напряжение, тем выше жесткость.

Угол а на диаграмме есть геометрическое выражение жесткости и модуля упругости. Чем угол больше, тем выше жесткость материала. Пластическая деформация наступает, когда напряжение превышает предел упругости (выше точки А) и после снятия нагрузки форма, структура и свойства тела не восстанавливаются полностью, т.е. имеет место остаточная деформация.
На практике напряжение, при котором начинается пластическая деформация, оценивается пределом текучести σ_T . Его легко определить, если на диаграмме растяжения имеется площадка текучести (горизонтальный участок). Однако, многие материалы имеют диаграмму растяжения без площадки текучести (медь, латуни, алюминий и др.), тогда за предел текучести принимают напряжение, которое вызывает остаточное удлинение 0,2 % и обозначают σ_0,2. σ_T называют физическим, а σ_0.2 условным пределом текучести. Предел текучести используют в качестве одного из показателей прочности материала.
Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению, называется временным сопротивлением (σ_B) или чаще пределом прочности, оно измеряется в МПа.

На рисунке 2 это максимальная точка на кривой σ-ε.

ОБРАТИТЕ ВНИМАНИЕ! На нашем сайте Вы можете заказать любые решения по всем разделам материаловедение. Решение предоставляется в печатном виде (в Word) с детальными комментариями.

Понимание прочности на растяжение – thegundcompany

Что такое прочность на растяжение?

Предел прочности при растяжении (UTS), часто сокращаемый до предела прочности при растяжении (TS), представляет собой максимальное напряжение, которое материал может выдержать при растяжении или растяжении до разрыва. В хрупких материалах материал разрушается вскоре после достижения предела текучести. В то же время в пластичных материалах наблюдается предел текучести, а предел прочности достигается по мере продолжения удлинения материала до предела прочности.

На приведенной ниже диаграмме показано удлинение (деформация) пластичного материала при растяжении. На начальном этапе удлинение линейно пропорционально напряжению и имеет упругую природу, поскольку материал возвращает свою первоначальную длину после снятия напряжения. Точка, в которой деформация становится нелинейной по отношению к напряжению, является точкой текучести, и материал удлиняется быстрее, пока не будет достигнут предел прочности на растяжение. После достижения предельной прочности материал будет сужаться, пока, наконец, не сломается.

Кривая напряжения-деформации менее сложна для хрупкого материала, поскольку материал разрушается вскоре после достижения предела текучести, а напряжение при разрушении является пределом прочности при растяжении. Во многих хрупких материалах, таких как высокопрочные композиты, невозможно определить предел текучести до окончательного разрушения. Материал не подвергается сужению перед разрушением. В области можно увидеть общую энергию, поглощаемую материалом под кривой напряжение-деформация. По сравнению с пластичным материалом, хрупкий материал выдерживает или поглощает гораздо меньше энергии. Поэтому все различия в механическом поведении хрупких и пластичных материалов следует учитывать при проектировании компонентов и систем.

Для простоты сравнения материалов предел прочности при растяжении/напряжение выражается как сила (фунт-сила или ньютон), деленная на площадь поперечного сечения, т. е. psi (фунты на квадратный дюйм) или МПа (ньютон на квадратный миллиметр). Один МПа = 145 фунтов на квадратный дюйм.

Модуль упругости при растяжении, модуль упругости или модуль Юнга при растяжении — это наклон (нарастание/нарастание или напряжение/удлинение) на начальной области линейной упругости кривой напряжения/деформации. Это важный параметр, используемый для сравнения жесткости материалов и поведения под нагрузкой. Знаменатель уравнения подъема/разбега безразмерен, а удлинение часто составляет доли процента. Единица модуля часто велика, в диапазоне MSI или ГПа.

Почему важна прочность на растяжение?

Прочность на растяжение — это механическое свойство, которое инженеры часто используют для определения критических проектных параметров. Базовая механика формул инженерии материалов требует прочности на растяжение, и поэтому сегодняшнее программное обеспечение для проектирования также требует этой информации о материале. Прочность на растяжение не всегда может быть критическим напряжением в конструкции. На самом деле, некоторые конструкции могут не иметь напряжения растяжения. Однако предел прочности при растяжении также можно использовать в качестве показателя других прочностей материала. Инженеры могут использовать предел прочности при растяжении в качестве еще одного показателя общей прочности материала, когда другие механические свойства недоступны. Например, если вязкость разрушения недоступна, предел прочности при растяжении обычно может указывать на принадлежность двух материалов к одному и тому же семейству (т. е. полимерному семейству).

Во многих механических и структурных применениях прочность на растяжение и модуль являются важными факторами, поскольку компоненты находятся под прямым или реактивным растягивающим напряжением. Кроме того, в отличие от отказов из-за усталости или других механических повреждений, разрушение при растяжении может быть более внезапным и катастрофическим, особенно для хрупкого материала. Таким образом, понимание предела прочности при растяжении и поведения напряжения-деформации (хрупкое или пластичное) является важным соображением при механическом проектировании.

В электротехнике отказы механической изоляции также могут иметь катастрофические последствия, независимо от того, поддерживает ли компонент шину под напряжением или действует как первичный изолятор. Если произойдет выход из строя изоляционного материала, в результате, скорее всего, произойдет катастрофическое электрическое событие. Таким образом, прочность на растяжение также может иметь решающее значение для изоляционных материалов, используемых для живой опоры или первичной изоляции.

Нажмите здесь , чтобы запросить доступ, если вы хотите прочитать статью полностью.

Нажмите здесь, чтобы запросить цену!

Прочность на растяжение — wikidoc

Прочность на растяжение $\sigma_{UTS}$ или $S_U$ измеряет усилие, необходимое для натяжения чего-либо, например веревки, проволоки или конструкционная балка до точки, где она ломается. Это интенсивное свойство материала.

Содержание

1 Пояснение
2 Концепция
3 Типичная прочность на растяжение
4 См. также
5 источников
6 Каталожные номера
7 Внешние ссылки

Объяснение

Прочность материала на растяжение — это максимальное растягивающее напряжение, которому он может подвергнуться до разрушения. Определение отказа может варьироваться в зависимости от типа материала и методологии проектирования. Это важная концепция в технике, особенно в области материаловедения, машиностроения и проектирования конструкций.

Существует три типичных определения прочности на растяжение:

Предел текучести: Напряжение, при котором деформация материала меняется с упругой на пластическую, вызывая необратимую деформацию.
Предельная прочность: Максимальное напряжение, которое может выдержать материал.
Прочность на разрыв: Координата напряжения на кривой напряжения-деформации в точке разрыва.

Концепция

Различные определения прочности на растяжение показаны на следующем графике напряжение-деформация для низкоуглеродистой стали:

Файл: Напряжение v деформация A36 2.png

Кривая зависимости напряжения от деформации, типичная для конструкционной стали
1. Предел прочности
2. Предел текучести
3. Предел прочности при растяжении
4. Область деформационного упрочнения
5. Область сужения.

Металлы, включая сталь, имеют линейную зависимость между напряжением и деформацией вплоть до предела текучести, как показано на рисунке.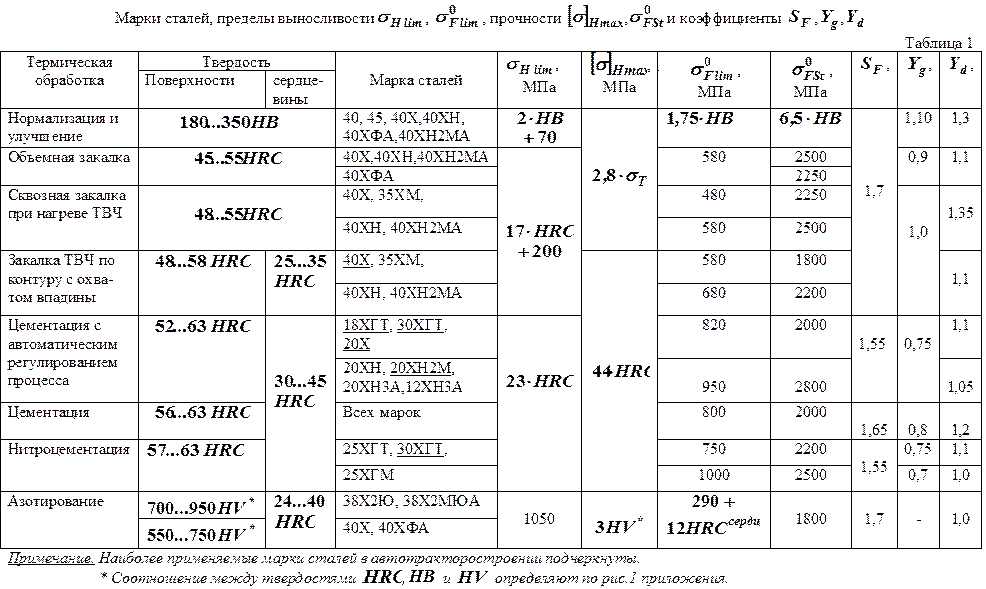 В некоторых сталях напряжение падает после предела текучести. Это связано с взаимодействием атомов углерода и дислокаций в напряженной стали. Холоднодеформированные и легированные стали не проявляют этого эффекта. Для большинства металлов предел текучести не имеет четкого определения. Ниже предела текучести все деформации восстанавливаются, и материал возвращается к своей первоначальной форме при снятии нагрузки. При напряжениях выше предела текучести деформация необратима, и материал не вернется к исходной форме. Эта неустранимая деформация известна как пластическая деформация. Для многих применений пластическая деформация неприемлема, и в качестве конструктивного ограничения используется предел текучести.

После достижения предела текучести сталь и многие другие пластичные металлы подвергаются периоду деформационного упрочнения, при котором напряжение снова увеличивается с увеличением деформации до предела прочности . Если в этой точке материал не нагружен, кривая напряжения-деформации будет параллельна той части кривой, которая находится между началом координат и точкой текучести. Если его повторно нагрузить, он снова будет следовать кривой разгрузки до предела прочности, который стал новым пределом текучести.

После того, как металл был нагружен до предела текучести, он начинает «скручиваться», так как площадь поперечного сечения образца уменьшается из-за пластического течения. Когда образование шейки становится значительным, это может привести к обращению инженерной кривой напряжения-деформации, где уменьшение напряжения коррелирует с увеличением деформации из-за геометрических эффектов. Это связано с тем, что инженерное напряжение и инженерная деформация рассчитываются исходя из исходной площади поперечного сечения до образования шейки. Если график построен в терминах истинное напряжение и истинное напряжение кривая всегда будет иметь наклон вверх и никогда не пойдет вспять, так как истинное напряжение корректируется с учетом уменьшения площади поперечного сечения. Для материалов, нагруженных на сжатие, образования шейки не наблюдается. Пиковое напряжение на инженерной кривой напряжения-деформации известно как предел прочности . После некоторого периода образования шейки материал разрывается, и накопленная упругая энергия высвобождается в виде шума и тепла. Напряжение на материале во время разрыва известно как предел прочности при растяжении .

Пластичные металлы не имеют четко определенного предела текучести. Предел текучести обычно определяется «деформацией смещения 0,2%». Предел текучести при смещении 0,2% определяется путем нахождения пересечения кривой напряжения-деформации с линией, параллельной начальному наклону кривой и пересекающей абсциссу на отметке 0,002. Кривая напряжение-деформация, типичная для алюминия, вместе со смещением на 0,2% показана на рисунке ниже.

Файл:Стресс v деформация Алюминий 2.png

Кривая зависимости напряжения от деформации, типичная для алюминия
1. Предел прочности
2. Предел текучести
3. Пропорциональное предельное напряжение
4. Прочность на растяжение
5. Деформация смещения (обычно 0,002).

Хрупкие материалы, такие как бетон и углеродное волокно, не имеют предела текучести и не упрочняются при деформации, что означает, что предел прочности и прочность на разрыв одинаковы. Наиболее необычная кривая напряжения-деформации показана на рисунке ниже. Типичные хрупкие материалы не демонстрируют никакой пластической деформации, но разрушаются, пока деформация является упругой. Одной из характеристик хрупкого разрушения является то, что две сломанные части могут быть собраны заново, чтобы получить ту же форму, что и исходный компонент. Типичная кривая напряжения-деформации для хрупкого материала будет линейной. Испытания нескольких одинаковых образцов приведут к разным напряжениям разрушения. Показанная ниже кривая является типичной для хрупкого полимера, испытанного при очень низких скоростях деформации при температуре выше его температуры стеклования. Некоторая конструкционная керамика демонстрирует небольшое пластическое поведение при напряжениях чуть ниже напряжения, вызывающего разрушение, но начальная часть кривой является линейной.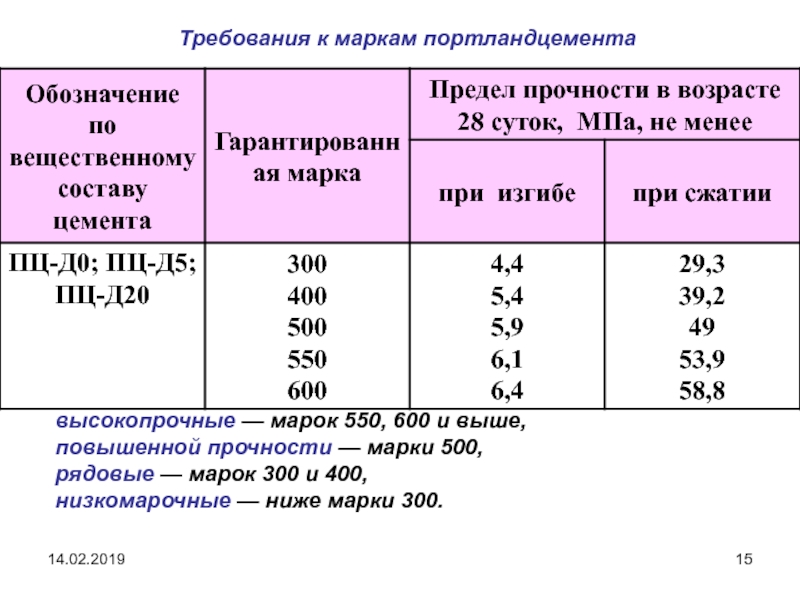

Файл: Напряжение v деформация хрупкого 2.png

Кривая зависимости напряжения от деформации очень нетипичного хрупкого материала
1. Предел прочности
2. Прочность на растяжение.

Прочность на растяжение измеряется в единицах силы на единицу площади. В системе СИ единицами измерения являются ньютоны на квадратный метр (Н/м²) или паскали (Па) с соответствующими префиксами. Неметрическими единицами измерения являются фунт-сила на квадратный дюйм (lbf/in² или PSI). Инженеры в Северной Америке обычно используют единицы ksi, которые составляют тысячу фунтов на квадратный дюйм.

Прочность каната на разрыв указывается в единицах силы, таких как ньютоны, без указания площади поперечного сечения каната. Это часто называют пределом прочности при растяжении, но это не совсем правильное использование термина.

В хрупких материалах, таких как горная порода, бетон, чугун или грунт, прочностью на растяжение можно пренебречь по сравнению с прочностью на сжатие, и для многих инженерных применений она принимается равной нулю. Стекловолокно имеет более высокую прочность на растяжение, чем сталь [2], но объемное стекло обычно не имеет такой прочности. Это связано с коэффициентом интенсивности напряжения, связанным с дефектами материала. С увеличением размера образца растет и размер дефектов. В общем случае предел прочности каната всегда меньше предела прочности отдельных его волокон.

Прочность на растяжение может быть определена как для жидкостей, так и для твердых тел. Например, когда дерево втягивает воду от своих корней к верхним листьям за счет транспирации, столб воды вытягивается вверх от вершины за счет капиллярного действия, и эта сила передается вниз по столбу за счет его силы растяжения. Давление воздуха снизу также играет небольшую роль в способности дерева втягивать воду, но одного этого было бы достаточно только для того, чтобы поднять столб воды на высоту около десяти метров, а деревья могут расти намного выше этой отметки. (См. Также кавитацию, которую можно рассматривать как следствие «слишком сильного вытягивания воды». )

Типовые значения прочности на растяжение

Некоторые типичные значения прочности на растяжение некоторых материалов:

Материал	Предел текучести (МПа)	Предел прочности (МПа)	Плотность (г/см³)
Конструкционная сталь Сталь ASTM A36	250	400	7,8
Сталь, API 5L X65 (Fikret Mert Veral)	448	531	7,8
Сталь, высокопрочный сплав ASTM A514	690	760	7,8
Сталь, предварительно напряженные пряди	1650	1860	7,8
Стальная проволока			7,8
Сталь (AISI 1060 0,6 % углерода) Струна для фортепиано	2200-2482 МПа ^[1]		7,8
Полиэтилен высокой плотности (HDPE)	26-33	37	0,95
Полипропилен	12-43	19,7-80	0,91
Нержавеющая сталь AISI 302 – холоднокатаная	520	860
Чугун 4,5% C, ASTM A-48	276 (??)	200
Титановый сплав (6% Al, 4% V)	830	900	4,51
Алюминиевый сплав 2014-T6	400	455	2,7
Медь 99,9% Cu	70	220	8,92
Мельхиор 10 % Ni, 1,6 % Fe, 1 % Mn, остальное Cu	130	350	8,94
Латунь	ок.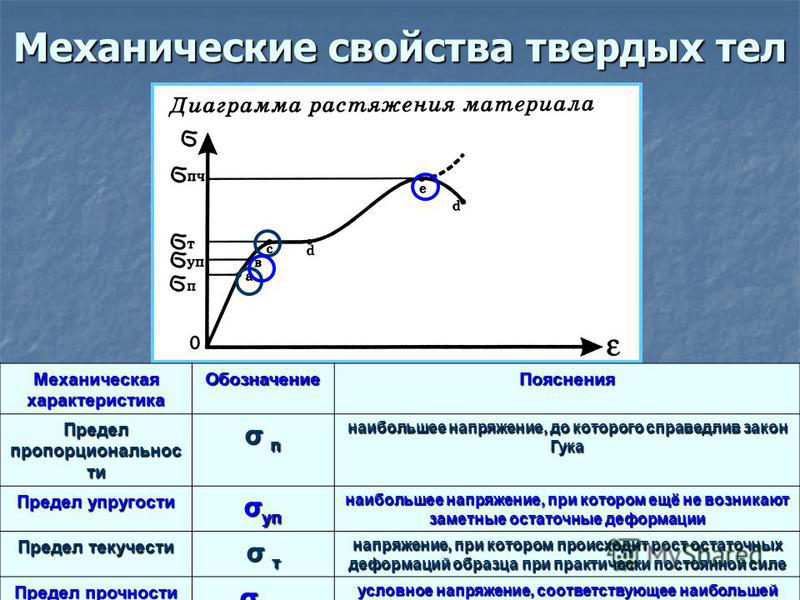 200+	550	5.3
Вольфрам		1510	19,25
Стекло		50 (на сжатие)	2,53
Электронное стекло	Н/Д	3450	2,57
S-стекло	Н/Д	4710	2,48
Базальтовое волокно	Н/Д	4840	2,7
Мрамор	Н/Д	15
Бетон	Н/Д	3
Углеродное волокно	Н/Д	5650	1,75
Шелк паука	1150 (??)	1200
Шелк тутового шелкопряда	500
Арамид (кевлар или тварон)	3620		1,44
СВМПЭ	23	46	0,97
Волокна из СВМПЭ ^[2] ^[3] (Dyneema или Spectra)		2300-3500	0,97
Вектран		2850-3340
Сосновая древесина (параллельно волокнам)		40
Кость (конечность)	104-121	130	1,6
Нейлон, тип 6/6	45	75	1,15
Резина	–	15
Бор	Н/Д	3100	2,46
Кремний монокристаллический (m-Si)	Н/Д	7000	2,33
Карбид кремния (SiC)	Н/Д	3440
Сапфир (алюминий ₂ O ₃ )	Н/Д	1900	3,9-4,1
Углеродная нанотрубка (см. примечание выше)	Н/Д	62000	1,34

Примечание. Многослойные углеродные нанотрубки обладают самой высокой прочностью на разрыв из всех когда-либо измеренных материалов, при этом в лабораториях они производятся с прочностью на разрыв 63 ГПа, что все еще значительно ниже их теоретического предела в 300 ГПа. Однако по состоянию на 2004 год ни один макроскопический объект, построенный из углеродных нанотрубок, не имел прочности на разрыв, даже отдаленно приближающейся к этому показателю или существенно превышающей прочность высокопрочных материалов, таких как кевлар.
Примечание: многие значения зависят от производственного процесса и чистоты/состава.

Элементы в отожженном состоянии	Модуль Юнга (ГПа)	Прочность или предел текучести (МПа)	Предел прочности (МПа)
Алюминий	70	15-20	40-50
Медь	130	33	210
Золото	79		100
Железо	211	80-100	350
Свинец	16		12
Никель	170	14-35	140-195
Кремний	107	5000-9000
Серебро	83		170
Тантал	186	180	200
Олово	47	9-14	15-200
Титан	120	100-225	240-370
Вольфрам	411	550	550-620
Цинк (кованый)	105		110-200

(Источник: А. М. Ховатсон, П. Г. Лунд и Дж. Д. Тодд, «Инженерные таблицы и данные», стр. 41)

См. также

Натяжение (механика)
Прочность
Деформация
Натяжная конструкция
Универсальная испытательная машина
Удельная прочность
Сопротивление материалов

Источники

А.М. Ховатсон, П.Г. Лунд и Дж. Д. Тодд, «Инженерные таблицы и данные»
Джанколи, Дуглас. Физика для ученых и инженеров, третье издание . Река Аппер-Сэдл: Прентис-Холл, 2000.
Келер, Т. и Ф. Фоллрат. 1995. Биомеханика нити у двух пауков-кругопрядов Araneus diadematus (Araneae, Araneidae) и Uloboris walckenaerius (Araneae, Uloboridae). Журнал экспериментальной зоологии 271: 1-17.
Эдвардс, Брэдли К. «Космический лифт: краткий обзор» http://www.liftport.com/files/521Edwards.pdf
Т Фоллетт “Жизнь без металлов”
Мин-Фэн Юй и др. и др. (2000), Прочность и механизм разрушения многослойных углеродных нанотрубок под действием растягивающей нагрузки, Science 287, 637-640

Ссылки

↑ Дон Стакхаус @ DJ Aerotech
↑ Свойства растяжения и ползучести сверхвысокомолекулярного ПЭ волокна
↑ [1]

http://www.

TOP HEADLINES