Преобразование вращательного движения в поступательное осуществляется с помощью: Механизмы преобразования вращательного движения

alexxlab | 06.05.2023 | 0 | Разное

Содержание

Устройство преобразования вращательного движения в возвратно-поступательное с регулировкой хода

Полезная модель относится к области машиностроения и может быть использована в различного рода механизмах. Технический результат заявленного в качестве модели устройства преобразования вращательного движения в возвратно-поступательное заключается в упрощенной конструкции и возможности регулирования хода возвратно-поступательного механизма. Технический результат достигается за счет того, что кулисный механизм выполнен в виде рамки, в прорези которой скользит ролик, эксцентрично расположенный на вращающемся диске с возможностью перемещения ролика в пазах вдоль радиуса диска с помощью регулировочного винта. Устройство содержит минимум деталей, в нем отсутствуют дефицитные материалы и узлы, может быть изготовление в условиях любого производства.

Полезная модель относится к области машиностроения и может быть использована в различного рода механизмах.

В технике широко используются механизмы, преобразующие вращательное движение ведущего звена в возвратно-поступательное, колебательное или прерывистое движение ведомых звеньев, а также механизмы, обеспечивающие движение какой-либо точки ведомого звена по определенной траектории.

К таким устройствам относятся кривошипноползунные, кулачковые, кулисные и другие механизмы.

Во многих случаях возникает необходимость регулировки хода (амплитуды) возвратно-поступательного движения для обеспечения оптимального режима работы механизма.

Известен механизм возвратно-поступательного движения с регулируемым ходом, содержащий корпус, в котором с возможностью возвратно-поступательного движения установлен крейцкопф, связанный шатуном со звеном кривошипного механизма с регулируемым радиусом кривошипа, включающим червячное колесо [1].

Устройство повышенной сложности, содержит большое количество деталей и сочленений, занимает значительный объем, сложно в изготовлении.

Наиболее близким прототипом предложенного устройства является кулисный механизм, выполненный в виде рамки, приводимой в движение кривошипом, расположенным вне плоскости этой рамки [2]. Основным недостатком этого устройства является отсутствие возможности регулирования хода рамки при ее возвратно-поступательном движении.

Техническим результатом заявленной полезной модели является преобразование вращательного движения в гармоническое возвратно-поступательное при помощи кулисного механизма с регулируемым ходом.

Технический результат заявленной полезной модели достигается за счет того, что в устройстве, содержащем корпус, размещен кулисный механизм с возможностью регулирования возвратно-поступательного движения и привод в виде вращающегося диска.

Кулисный механизм выполнен в виде рамки, в прорези которой поперек продольной оси рамки скользит ролик, эксцентрично расположенный на вращающемся диске с возможностью регулируемого перемещения в пазах вдоль радиуса диска.

На фиг.1 представлен эскиз устройства преобразования вращательного движения в поступательное с регулируемым ходом.

При вращении диска 1 в любую сторону, эксцентрично расположенный на нем скользящий ролик 2 приводит в возвратно-поступательное движение рамку 3, которая двигается в направляющих 4, расположенных в корпусе устройства.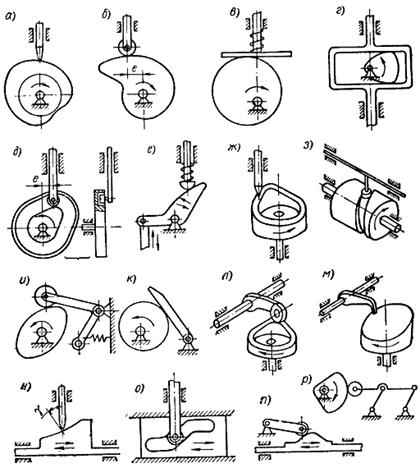

Регулирование амплитуды хода движения рамки обеспечивается изменением положения ролика с помощью узла регулировки (фиг.2) расположенного в радиальных пазах корпуса диска.

Изменение хода осуществляется с помощью винта 5, на резьбовую часть которого навинчивается (или вывинчивается) деталь 6, с расположенным на ней роликом 2, а сам винт снабжен стопорной шайбой 7, исключающей его продольное смещение.

За один оборот диска рамка совершает полное симметричное возвратно-поступательное движение вдоль центра диска.

К достоинствам предложенного устройства относится его простота, не требующая сложной оснастки, дефицитных материалов и возможность изготовления в условиях любого производства.

Источники информации

1. Авторское свидетельство СССР №1555571 5 F H 21/20 21.09.87 г.

2. Е.М.Никитин. Краткий курс теоретической механики для ВТУзов «Наука» Москва 1971, §49.4 стр.172

Устройство преобразования вращательного движения в возвратно-поступательное с регулируемым ходом, содержащее корпус, в котором размещен кулисный механизм с возможностью возвратно-поступательного движения, и привод в виде вращающегося диска, отличающееся тем, что, с целью упрощения конструкции и возможности регулирования хода кулисный механизм выполнен в виде рамки, в прорези которой скользит ролик, эксцентрично расположенный на вращающемся диске с возможностью регулирования его перемещения в пазах вдоль радиуса диска.

Преобразование – вращательное движение – Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Преобразование вращательных движений осуществляется разнообразными механизмами, которые называются передачами. [16]

Преобразование вращательного движения в поступательное наиболее часто осуществляется реечными и винтовыми передачами. [17]

Схема зубчатой передачи.| Схемы планетарных передач. [18]

Преобразование вращательного движения в поступательное в металлорежущих станках наиболее часто осуществляют реечными и винтовыми передачами. [19]

Преобразование вращательного движения в возвратно-поступательное прямолинейное производится следующим образом. Оправка 3 вставляется в шпиндель станка, от которого она получает вращение. На нижней части ползуна укреплены два резцедержателя.

[20]

Преобразование вращательного движения во вращательное достигается тем, что нить присоединяется одним концом к блоку соответствующего диаметра. [21]

Преобразование вращательных движений осуществляется разнообразными механизмами, которые называются передачами. [22]

Преобразование вращательного движения от привода станка в возвратно-поступательное стола осуществляется реечным механизмом, помещенным на столе. [23]

Преобразование вращательного движения кулисного пальца в возвратно-поступательное прямолинейное перемещение ползуна с резцом сопровождается изменением скорости движения как при рабочем, так и при холостом ходах. Для нормирования труда важно знать среднюю скорость резания, а для установления режима резания – наибольшую скорость резания при рабочем ходе. [24]

Преобразование вращательного движения гибкого вала в возвратно-поступательное движение ножа-пластинки осуществляется с помощью червячной передачи и эксцентрикового механизма, заключенных в корпус головки.

Длину хода ножа-пластинки регулируют поворотом эксцентрика. [25]

Рассмотрим преобразование вращательного движения в поступательное. [26]

Для преобразования вращательного движения в прямолинейное и наоборот применяют цилиндрические колеса и рейки ( черт. [27]

Передачи в станках. [28]

Для преобразования вращательного движения в поступательное или наоборот используют реечную ( рис. 3.1, г) или винтовую ( рис. 3.1, д) передачи. В первом случае ось вращательного движения и направление поступательного движения перпендикулярны, а во втором – параллельны. [29]

Планетарная передача. [30]

Страницы: 1 2 3 4

Новый взгляд на работу и энергию – College Physics

Резюме

Выведите уравнение для вращательной работы.
Рассчитать кинетическую энергию вращения.
Продемонстрировать закон сохранения энергии.

В этом модуле мы узнаем о работе и энергии, связанных с вращательным движением. На рис. 1 показан рабочий, использующий электрический точильный камень с двигателем. Искры летят, а шум и вибрация создаются, когда слои стали срезаются со столба. Камень продолжает вращаться даже после выключения двигателя, но в конце концов останавливается из-за трения. Ясно, что мотор должен был работать, чтобы камень вращался. Эта работа заключалась в тепле, свете, звуке, вибрации и значительных

кинетическая энергия вращения .

Рисунок 1. Двигатель вращает точильный камень, придавая ему кинетическую энергию вращения. Затем эта энергия преобразуется в тепло, свет, звук и вибрацию. (Фото: ВМС США, фото моряка Закари Дэвида Белла, специалиста по массовым коммуникациям) Работа была определена в главе 6 «Равномерное круговое движение и гравитация» для поступательного движения, и мы можем опираться на это знание при рассмотрении работы, совершаемой при вращательном движении.

Простейшая вращательная ситуация — это та, в которой результирующая сила приложена перпендикулярно радиусу диска (как показано на рисунке 2) и остается перпендикулярной, когда диск начинает вращаться. Сила параллельна смещению, поэтому чистая выполненная работа является произведением силы на длину пройденной дуги:

Чтобы получить крутящий момент и другие величины вращения в уравнении, мы умножаем и делим правую часть уравнения на и собираем члены:

Мы признаем это и поэтому

Это уравнение является выражением для вращательной работы. Это очень похоже на знакомое определение поступательной работы как произведение силы на расстояние. Здесь крутящий момент аналогичен силе, а угол аналогичен расстоянию. Уравнение справедливо в общем случае, хотя оно было выведено для частного случая.

Чтобы получить выражение для кинетической энергии вращения, мы должны снова произвести некоторые алгебраические манипуляции. Первый шаг — отметить, что для того, чтобы

Рисунок 2. Суммарная сила, действующая на этот диск, сохраняется перпендикулярной его радиусу, поскольку сила заставляет диск вращаться. Таким образом, чистая выполненная работа равна (чистая F )Δ с
. Чистая работа переходит в кинетическую энергию вращения.

Теперь решим одно из уравнений вращательной кинематики. Начнем с уравнения

Далее находим

Подставляя это в уравнение для чистых и собирательных условий, получаем

Это уравнение является теоремой работы-энергии только для вращательного движения. Как вы помните, работа сети изменяет кинетическую энергию системы. По аналогии с поступательным движением мы определяем термин как кинетическая энергия вращения для объекта с моментом инерции и угловой скоростью

Выражение для кинетической энергии вращения в точности аналогично кинетической энергии поступательного движения, поскольку аналогично и кинетическая энергия вращения имеет важные эффекты. Маховики, например, можно использовать для накопления большого количества кинетической энергии вращения транспортного средства, как показано на рис. 3.9.0015

Рисунок 3. Были сконструированы экспериментальные транспортные средства, такие как этот автобус, в которых кинетическая энергия вращения хранится в большом маховике. Когда автобус спускается с холма, его трансмиссия преобразует потенциальную энергию гравитации в KE _rot . Он также может преобразовывать поступательную кинетическую энергию, когда автобус останавливается, в KE _rot . Затем энергию маховика можно использовать для ускорения, подъема на другой холм или предотвращения движения автобуса против трения.

Пример 1. Расчет работы и энергии для вращения точильного камня

Рассмотрим человека, который вращает большой точильный камень, положив руку на его край и прикладывая силу на протяжении части оборота, как показано на рис. 4. В этом примере мы убедитесь, что работа, совершаемая крутящим моментом, который она оказывает, равна изменению энергии вращения.

(a) Какая работа будет совершена, если она приложит силу 200 Н при вращении. Сила удерживается перпендикулярно радиусу 0,320 м точильного камня в точке приложения, а эффекты трения пренебрежимо малы. б) Какова конечная угловая скорость, если точильный камень имеет массу 85,0 кг? в) Чему равна конечная кинетическая энергия вращения? (Это должно равняться работе.)

Стратегия

Чтобы найти работу, мы можем использовать уравнение У нас достаточно информации для расчета крутящего момента и задан угол поворота. Во второй части мы можем найти конечную угловую скорость, используя одно из кинематических соотношений. В последней части мы можем вычислить кинетическую энергию вращения из ее выражения в

Решение для (a)

Чистая работа выражается в уравнении

, где чистая — это приложенная сила, умноженная на радиус, потому что есть Тормозящего трения нет, а сила перпендикулярна заданному углу. Подстановка данных значений в приведенное выше уравнение дает

Обратите внимание, что

Рисунок 4. Большой точильный камень приводится в движение человеком, который держится за его внешний край.

Решение для (b)

Чтобы найти из данной информации, требуется более одного шага. Мы начинаем с кинематической связи в уравнении

Обратите внимание, что мы начинаем с состояния покоя. Извлечение квадратного корня из полученного уравнения дает

Теперь нам нужно найти Один из вариантов:

, где крутящий момент равен

. Формула момента инерции диска находится в разделе Создание соединений:

Подставляя значения крутящего момента и момента инерции в выражение для получаем

Теперь подставляем это значение и заданное значение в приведенное выше выражение для

Решение для (c)

Конечная кинетическая энергия вращения is

Оба и были найдены выше. Таким образом,

Обсуждение

Конечная кинетическая энергия вращения равна работе, проделанной крутящим моментом, что подтверждает, что проделанная работа превратилась в кинетическую энергию вращения. На самом деле мы могли бы использовать выражение для энергии вместо кинематического соотношения для решения части (b). Мы сделаем это в последующих примерах.

Пилоты вертолетов хорошо знакомы с кинетической энергией вращения. Они знают, например, что точка невозврата будет достигнута, если они позволят своим лопастям замедляться ниже критической угловой скорости во время полета. Лопасти теряют подъемную силу, и невозможно сразу заставить лопасти вращаться достаточно быстро, чтобы восстановить ее. Кинетическая энергия вращения должна быть подведена к лопастям, чтобы заставить их вращаться быстрее, а энергии, достаточной для того, чтобы избежать аварии, не может быть обеспечено вовремя. Из-за ограничений по весу вертолетные двигатели слишком малы, чтобы обеспечить как энергию, необходимую для подъема, так и пополнение кинетической энергии вращения лопастей после их замедления. Кинетическая энергия вращения закладывается в них перед взлетом и не должна опускаться ниже этого критического уровня.

Одним из возможных способов избежать аварии является использование гравитационной потенциальной энергии вертолета для пополнения кинетической энергии вращения лопастей за счет снижения высоты и выравнивания лопастей таким образом, чтобы вертолет раскручивался при снижении. Конечно, если высота вертолета слишком мала, лопасть не успевает восстановить подъемную силу, прежде чем коснется земли.

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ЭНЕРГИИ ВРАЩЕНИЯ

Определить, какая энергия или работа связана с вращением .
Определить интересующую систему . Эскиз обычно помогает.
Проанализируйте ситуацию, чтобы определить виды работы и энергии, связанные с .
В закрытых системах сохраняется механическая энергия . То есть обратите внимание, что и каждый из них может включать поступательные и вращательные вклады.
Для открытых систем механическая энергия может не сохраняться, и другие формы энергии (упоминаемые ранее как ), такие как теплопередача, могут входить в систему или выходить из нее. Определите, каковы они, и рассчитайте их по мере необходимости.
Удалите термины везде, где это возможно, чтобы упростить алгебру .
Проверьте правильность ответа .

Пример 2: Расчет энергии вертолета

Типичный небольшой спасательный вертолет, подобный показанному на рис. 5, имеет четыре лопасти, каждая длиной 4,00 м и массой 50,0 кг. Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей. в) На какую высоту можно было бы поднять вертолет, если бы для его подъема использовалась вся кинетическая энергия вращения?

Стратегия

Вращательная и поступательная кинетическая энергия может быть рассчитана по их определениям. Последняя часть проблемы связана с идеей о том, что энергия может изменять форму, в данном случае от вращательной кинетической энергии к гравитационной потенциальной энергии.

Решение для (a)

Кинетическая энергия вращения равна

Мы должны преобразовать угловую скорость в радианы в секунду и вычислить момент инерции, прежде чем мы сможем найти Угловая скорость равна

Момент инерции одной лопасти будет равен моменту инерции тонкого стержня, вращающегося вокруг своего конца, найденного в «Создание соединений». В сумме этот момент инерции умножается на четыре, потому что лопастей четыре. Таким образом,

Ввод и в выражение для кинетической энергии вращения дает

Решение для (b)

Поступательная кинетическая энергия была определена в главе 6 Равномерное круговое движение и гравитация. Вводя заданные значения массы и скорости, получаем

Для сравнения кинетических энергий мы берем отношение поступательной кинетической энергии к вращательной кинетической энергии. Это соотношение равно

Решение для (c)

На максимальной высоте вся кинетическая энергия вращения будет преобразована в энергию гравитации. Чтобы найти эту высоту, мы приравняем эти две энергии:

или

. Теперь мы решим и подставим известные значения в полученное уравнение

Обсуждение

Отношение поступательной энергии к вращательной кинетической энергии составляет всего 0,380. Это соотношение говорит нам о том, что большая часть кинетической энергии вертолета приходится на его вращающиеся лопасти, о чем вы, вероятно, не подозреваете. Высота 53,7 м, на которую вертолет можно было поднять за счет кинетической энергии вращения, также впечатляет, что еще раз подчеркивает количество кинетической энергии вращения в лопастях.

Рисунок 5. На первом изображении показано, как вертолеты накапливают большое количество вращательной кинетической энергии в своих лопастях. Эту энергию необходимо вложить в лопасти перед взлетом и сохранить до конца полета.

Двигатели не обладают достаточной мощностью, чтобы одновременно обеспечивать подъемную силу и передавать значительную вращательную энергию лопастям. На втором изображении показан вертолет спасательной вертолетной службы Окленда Westpac. Более 50 000 жизней было спасено с момента его начала в 19 году.73. Здесь показана спасательная операция на воде. (кредит: 111 Emergency, Flickr)

УСТАНОВЛЕНИЕ СОЕДИНЕНИЙ

Сохранение энергии включает в себя вращательное движение, потому что кинетическая энергия вращения является еще одной формой равномерного кругового движения и гравитации в главе 6, в которой подробно рассматривается сохранение энергии.

Один из способов контроля качества на заводе по производству томатных супов состоит в том, что наполненные банки скатываются по наклонной плоскости. Если они свернутся слишком быстро, суп будет слишком жидким. Почему банки одинакового размера и массы должны катиться по склону с разной скоростью? И почему самый густой суп должен вариться медленнее всего?

Самый простой способ ответить на эти вопросы — рассмотреть энергию. Предположим, что каждая банка начинает спускаться по пандусу из состояния покоя. Каждая банка, стартующая из состояния покоя, означает, что каждая из них стартует с одинаковой гравитационной потенциальной энергией, которая полностью преобразуется в при условии, что каждый катится без проскальзывания. однако может принимать форму или , а общее количество является суммой двух. Если банка скатывается по пандусу, она отдает часть своей энергии на вращение, оставляя меньше на перемещение. Таким образом, банка движется медленнее, чем если бы она соскользнула вниз. Кроме того, жидкий суп не вращается, в отличие от густого супа, потому что он прилипает к банке. Таким образом, густой бульон вкладывает во вращение больше первоначальной гравитационной потенциальной энергии банки, чем жидкий суп, и банка катится медленнее, как показано на рис. 6.9.0015 Рис. 6. Три банки с супом одинаковой массы мчатся вниз по склону. Первая банка имеет антифрикционное покрытие и не катится, а просто скользит по склону. Он выигрывает, потому что преобразует весь свой PE в трансляционный KE. И вторая, и третья банки катятся по склону, не скользя. Вторая банка содержит жидкий суп и занимает второе место, потому что часть ее исходного PE идет на вращение банки (но не жидкого супа). В третьей банке густой суп. Он занимает третье место, потому что суп вращается вместе с банкой, забирая еще больше исходного PE для вращательного KE, оставляя меньше для поступательного KE.

Предполагая отсутствие потерь на трение, работу совершает только одна сила — сила тяжести. Следовательно, полная совершенная работа есть изменение кинетической энергии. Когда банки начинают двигаться, потенциальная энергия превращается в кинетическую энергию. Сохранение энергии дает

Точнее,

или

Итак, начальная делится на поступательную кинетическую энергию и вращательную кинетическую энергию; и чем больше, тем меньше энергии уходит на трансляцию. Если банка скользит вниз без трения, то и вся энергия идет на поступательное движение; таким образом, банка идет быстрее.

ДОМАШНИЙ ЭКСПЕРИМЕНТ

Найдите несколько банок, каждая из которых содержит разные виды еды. Во-первых, предскажите, какая из них выиграет гонку по наклонной плоскости, и объясните, почему. Проверьте, верен ли ваш прогноз. Вы также можете провести этот эксперимент, собрав несколько пустых цилиндрических контейнеров одинакового размера и наполнив их разными материалами, такими как влажный или сухой песок.

Пример 3. Расчет скорости цилиндра, катящегося по склону

Рассчитайте конечную скорость сплошного цилиндра, катящегося по склону высотой 2,00 м. Цилиндр стартует из состояния покоя, имеет массу 0,750 кг и радиус 4,00 см.

Стратегия

Мы можем определить конечную скорость, используя закон сохранения энергии, но сначала мы должны выразить величины вращения через величины поступательного движения, чтобы получить vv как единственное неизвестное.

Решение

Сохранение энергии для этой ситуации записывается, как описано выше:

Прежде чем мы сможем найти для мы должны получить выражение для из главы 10. 3 Создание соединений. Поскольку и связаны между собой (заметим, что цилиндр катится без проскальзывания), мы также должны подставить отношение в выражение. Эти замены дают

Интересно, что радиус и масса цилиндра сокращаются, что дает

Алгебраическое решение уравнения для конечной скорости дает

Подстановка известных значений в результирующее выражение дает

[латексный размер=”4″][[/латекс] [ латекс размер=”4″]][/латекс]

Обсуждение

Поскольку и отменить, результат верен для любого твердого цилиндра, подразумевая, что все твердые цилиндры будут катиться вниз по склону с одинаковой скоростью независимо от их массы и размеры. (Качение цилиндров вниз по склону — это то, что на самом деле сделал Галилей, чтобы показать, что объекты падают с одинаковой скоростью независимо от массы.) Обратите внимание, что если цилиндр скользит по склону без трения без качения, то вся гравитационная потенциальная энергия переходит в поступательную кинетическую энергию. . Таким образом, а это на 22% больше, чем То есть, цилиндр будет двигаться быстрее в нижней части.

ИССЛЕДОВАНИЯ PHET: МОЯ СОЛНЕЧНАЯ СИСТЕМА

Постройте свою собственную систему небесных тел и смотрите гравитационный балет. С помощью этого симулятора орбиты вы можете установить начальные положения, скорости и массы 2, 3 или 4 тел, а затем увидеть, как они вращаются вокруг друг друга.

Рисунок 7. Моя солнечная система

Кинетическая энергия вращения объекта с моментом инерции и угловой скоростью определяется выражением
Вертолеты хранят большое количество вращательной кинетической энергии в своих лопастях. Эту энергию необходимо вложить в лопасти перед взлетом и сохранить до конца полета. Двигатели не обладают достаточной мощностью, чтобы одновременно обеспечивать подъемную силу и передавать значительную вращательную энергию лопастям.
Работа и энергия при вращательном движении полностью аналогичны работе и энергии при поступательном движении.
Уравнение для теоремы о работе-энергии для вращательного движения:

теорема работы-энергии: если одна или несколько внешних сил действуют на твердый объект, вызывая изменение его кинетической энергии от до, то работа, совершаемая результирующей силой, равна изменению кинетической энергии

вращательная кинетическая энергия: кинетическая энергия из-за вращения объекта. Это часть его полной кинетической энергии

Энергия вращения

Если мы нажмем на объект в прямом направлении, пока объект движется вперед, совершаем положительную работу над объектом. Объект ускоряется, потому что мы на это напираем. F = m a . Объект приобретает кинетическую энергию. Поступательная кинетическая энергия из объект массой m, центр масс которого движется со скоростью v, равен K = ½mv ² .

Поступательная кинетическая энергия = ½ массы * скорость ²

Кинетическая энергия увеличивается квадратично со скоростью. Когда скорость автомобиля удваивается, его энергия увеличивается в четыре раза.

Вращающийся объект обладает кинетической энергией, даже если объект в целом не имеет поступательное движение. Если мы рассмотрим объект, состоящий из совокупности частиц, то каждая частица i имеет кинетическую энергию K _i = ½ м _i v _i ² .
Таким образом, полная кинетическая энергия вращающегося объекта определяется как
K = ∑K _i = ∑½m _i v _i ² = ∑½mr _i ² ω ² = ½ω ² ∑ mr _i ² .
Запишем K = ½(∑mr _i ² )ω ² = ½Iω ² .
Величина в скобках называется моментом инерции I = ∑m _i r _i ² объекта относительно оси вращения.
Момент инерции системы относительно оси вращения можно найти, умножив массу m _на каждого частицы в системе на квадрат ее перпендикулярного расстояния r _i от оси вращения, и суммируя все эти произведения, I = ∑m _i r _i ² .
Для системы с при непрерывном распределении массы сумма превращается в интеграл, I = ∫r ² дм.
Единицы момент инерции – это масса, умноженная на квадрат расстояния, например кгм ² .

Когда объект вращается вокруг оси, его вращательная кинетическая энергия равна K = ½Iω ² .

Кинетическая энергия вращения = ½ момента инерции * (угловая скорость) ² .

Когда угловая скорость вращающегося колеса удваивается, его кинетическая энергия увеличивается на коэффициент четыре.

Когда объект имеет поступательное, а также вращательное движение, мы можем посмотреть на движение центра масс и движение вокруг центра масс в отдельности.

Полная кинетическая энергия представляет собой сумму поступательного кинетическая энергия центра массы (см) и кинетической энергии вращения относительно СМ .

Момент инерции объекта зависит от массы объекта и от того, как эта масса распределена относительно оси вращение. Момент инерции равен всегда определяется относительно оси вращения.

Чем дальше основная часть массы от оси вращения, тем больше вращательная инерция (момент инерции) объекта.

Пример:

Представьте себе два колеса одинаковой массы. Одно сплошное колесо с его масса равномерно распределена по всей конструкции, а другая имеет большая часть массы сосредоточена у края.

Колесо с массой у обода имеет больший момент инерция.

Пример:

Момент инерции круглого диска, вращающегося вокруг оси через его центр перпендикулярно плоскости диска отличается от момент инерции диска, вращающегося вокруг оси через центр в плоскости диска.

Моменты инерции многих объектов с симметричным распределением масс о разных осях симметрии можно посмотреть в таблицах.

Ссылка: Список моментов инерции

Проблема:

Три частицы соединены жесткими стержнями ничтожной массы, лежащими вдоль оси Y, как показано.
Если система вращается вокруг оси x с угловой скоростью 2 рад/с, найти
(а) момент инерции относительно оси x и полный вращательный момент кинетическая энергия оценивается по ½Iω ² , и
(b) линейная скорость каждой частицы и общая кинетическая энергия, оцененная от Σ½м _и v _я ² .

Решение:

Обоснование:
Момент инерции I = ∑m _i r _i ² . Здесь r _i — перпендикулярное расстояние частицы i от ось х.
Линейная скорость частицы i равна v _i = ωr _i .
Детали расчета:
(a) I = (4 кг)(9 м ² ) ^{+
(2 кг)(4 м ²) ^{+
(3 кг)(16 м ² ) ^{= 92 кгм ² .
Кинетическая энергия вращения K =
½Iω ² = 46*4/с ² = 184 Дж.
(б) Линейная скорость груза массой 4 кг v = 6 м/с, а его кинетическая энергия равна
½ МВ ² = 72 Дж.
Линейная скорость груза массой 2 кг v = 4 м/с, а его кинетическая энергия равна
½ МВ ² = 16 Дж.
Линейная скорость груза массой 3 кг v = 8 м/с, а его кинетическая энергия равна
½ мв ² = 96 Дж.
Сумма кинетических энергий трех частиц равна 184 Дж.}}}

Проблема:

Четыре частицы на рисунке справа соединены жесткими стержнями. Начало находится в центре прямоугольника. Вычислите момент инерции системы относительно оси z.

Решение:

Обоснование:
Момент инерции I = ∑m _i r _i ² . Здесь r _i — перпендикулярное расстояние частицы i от ось Z.
Детали расчета:
Каждая частица – это расстояние r = (9 + 4) ^½ м = (13) ^½ м от ось вращения.
I = (3 кг + 2 кг + 4 кг + 2 кг)*13 м ² = 143 кгм ² .

Проблема:

Найдите момент инерции очень тонкого обруча из массой m и радиусом r относительно оси симметрии.

Решение:

Обоснование:
Масса распределена непрерывно, поэтому ∑m –> ∫дм. Все элементы массы dm являются перпендикуляром расстояние r от оси вращения.
I = ∫ r ² dm = r ² ∫dm = mr ² .

Теорема о параллельных осях

Рассмотрим составной объект, например два соединенных диски на рисунке справа.
Центр масс этого объекта находится в начале координат. Чтобы найти момент инерции объект о CM мы можем использовать теорему параллельных осей. Эта теорема утверждает, что момент инерции тела относительно любой оси равен сумма двух слагаемых. Первый член — это момент инерции тела относительно параллельные оси, проходящие через его центр масс. Второй член есть произведение массы объект M, умноженный на квадрат расстояния R его центра масс от оси в вопрос.

I = I _CM + MR ² .

Мы можем рассматривать составной объект как сумму его частей и для каждой части вычислять момент инерции относительно оси Z.
Для диска 1 имеем I ₁ = I _CM1 + M ₁ R ₁ ² , а для диска 2 имеем I ₂ = I _CM2 ² + M ₂ R ₂ ² .
Тогда момент инерции составного объекта относительно оси z равен I = I ₁ + Я ₂ .
Для однородного диска массы М момент инерции относительно оси, проходящей через его центр и перпендикулярной плоскости диска, равен ½MR ² . Таким образом, для объекта на рисунке мы имеем для момента инерции относительно ось z

I = (3/2)MR ² + (3/2)MR ² = 3MR ² .

Прокат

Кинетическая энергия тела при поступательном и вращательном движении равна сумма его поступательной и вращательной кинетической энергии.
Поступательная кинетическая энергия = ½ мВ _см ² .
Кинетическая энергия вращения = ½Iω ² .
Полная кинетическая энергия = ½mv _CM ² + ½Iω ² .

Рассмотрим колесо радиуса r и массы m, катящееся по плоской поверхности в x-направление.
Смещение Δx и угловое смещение Δθ связаны соотношением Δx = rΔθ.
Величины линейной скорости и угловой скорости связаны через v _СМ = rω.

Кинетическая энергия колеса равна сумме кинетической энергии движения колеса. центр масс ½mv _CM ² = ½mr ² ω ² , кинетическая энергия движения вокруг центра масс ½Iω ² .
Общая кинетическая энергия равна

KE _tot = ½mr ² ω ² + ½Iω ² = ½[mr ² + I]ω ² = ½[m + I/r ² ]v ² .

Пример:

Предположим, что колесо представляет собой однородный диск. Момент инерции I однородного диска относительно оси, перпендикулярной плоскости диска. диск через свой CM равен ½mr ² .
Следовательно, кинетическая энергия диска равна KE _tot = (3/4)mr ² ω ² .

Отношение кинетической энергии поступательного движения и кинетической энергии вращения равно E _trans /E _rot = г-н ² /I.
Если два катящихся тела имеют одинаковую кинетическую энергию, то объект с меньшим моментом инерции имеет больший поступательная кинетическая энергия и большая скорость.

Проблема:

Предположим, что диск и кольцо с одинаковым радиусом катятся по наклонной плоскости. h и угол тета. Если они оба стартуют из состояния покоя в t = 0, какой из них достигнет снизу сначала?

Решение:

Подумай сам, а потом посмотри это видеоклип . Был ли ваш ответ правильным?

Модуль 8: Вопрос 2

Предположим, вы разрабатываете гоночный велосипед, и пришло время поработать над колесами.

TOP HEADLINES