Профиль зуба шестерни: О выборе профиля зубьев механических передач и гидравлических машин – Бурение и Нефть
alexxlab | 24.01.2023 | 0 | Разное
5.3 Построение профиля зуба шестерни, изготавливаемой реечным инструментом.
Профиль зуба колеса образуется как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Такое образование профиля отражает реальный процесс изготовления колеса на станке. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного производящего исходного контура, а переходная кривая профиля зуба – закругленным участком.
17
5.4 Построение проектируемой зубчатой передачи.
Начальные окружности должны соприкасаться в полюсе зацепления. Расстояние между делительными окружностями по осевой линии равно воспринимаемому смещению ym. Расстояние между окружностями вершин одного колеса и впадин другого, измеренное по осевой линии, должно быть равно радиальному зазору .
Через
полюс зацепления касательно к основным
окружностям колес проводится линия
зацепления. Точки касания
иназываются предельными точками линии
зацепления. Линия зацепления образует
с перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления. Отрезокактивная часть линии зацепления. Точка- точка входа колес в зацепление; точка- точка выхода из зацепления.
Линия зацепления образует
с перпендикуляром, восстановленным к
осевой линии в полюсе, угол зацепления. Отрезокактивная часть линии зацепления. Точка- точка входа колес в зацепление; точка- точка выхода из зацепления.
На
каждом колесе строятся профили трех
зубьев, причем точка контакта К должна
располагаться на активной линии
зацепления. Профили зубьев шестерни
перенесены на чертеж проектируемой
передачи со схемы станочного зацепления
копированием; эвольвентная часть профиля
зуба колеса строится обычным образом,
как траектория точки прямой при
перекатывании ее по основной окружности
без скольжения, и переносится в точку
контакта зубьев К на линию зацепления.
Профили двух других зубьев располагаются
на расстоянии шага
.
На зубьях, соприкасающихся в точке К,
отмечаются активные профили, которые
взаимодействуют в процессе зацепления.
Нижние точки активных профилей лежат
на пересечении окружностейисоответствующих профилей. Активные
профили перекатываются друг по другу
со скольжением, поэтому их длины различны.
6. Проектирование планетарного механизма
Планетарный механизм однорядный, тремя сателлитами. При проектировании редуктора исходными данными являются число сателлитов: k = 3.
Исходными данными для расчета передаточного отношения редуктора являются кинематическая схема механизма и частота вращения на валу двигателя и главном валу машины. nДВ=3000 об/мин;n1=700 об/мин.
U=ДВ/1=nДВ/n1=3000/700=4,3
U=U12.UПР , где
U– общее передаточное отношение машины;
U12– передаточное отношение зубчатой передачи;
UПР – искомое передаточное отношение планетарного редуктора.
U
Таким
образом: UПР = U/U12 = 4,3/1,38 = 3,1 => Схема:
однорядный планетарный редуктор с одним
внутренним и одним внешним зацеплением.
18
Проектируемый редуктор должен удовлетворять следующим требованиям:
1) Он должен обеспечивать необходимое передаточное отношение. Для этого записывают выражение, связывающее между собой количество зубьев колес планетарного редуктора (Z1,Z2,Z3) и заданное передаточное отношение. В нашем случае выражение имеет вид:
U1H = 1+(Z3/Z1)
2) Должно соблюдаться условие соосности, т.е. оси центральных колес при назначенных Z должны совпадать с осью водила. В нашем случае выражение условия соосности имеет вид:
Z1+2Z2 =Z3 => Z2 = (Z3-Z1)/2
3) Должно
выполняться условие соседства
(совместности), т.е. должна быть возможность
размещения нескольких сателлитов по
общей окружности в одной плоскости без
соприкосновения друг с другом. Выражение
условия соосности имеет вид:
Выражение
условия соосности имеет вид:
.
4) Должно соблюдаться условие сборки, т.е. должна обеспечиваться возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателлитами:
[(Z1U1H)/k].(1+k.P) = Ц, где
Ц – целое число;
K – число сателлитов;
Р = 0, 1, 2, 3, …
5) Должно соблюдаться условие отсутствия подрезания, т.е. при колесах нарезанных стандартным инструментом без смещения (при 😉 Zmin должно быть больше 18.
Определение чисел зубьев колес планетарного редуктора осуществляется методом подбора. Одним из вариантов удовлетворяющим перечисленным выше требованиям являются числа:
Z1=44;
Z2=22;
Z3=88.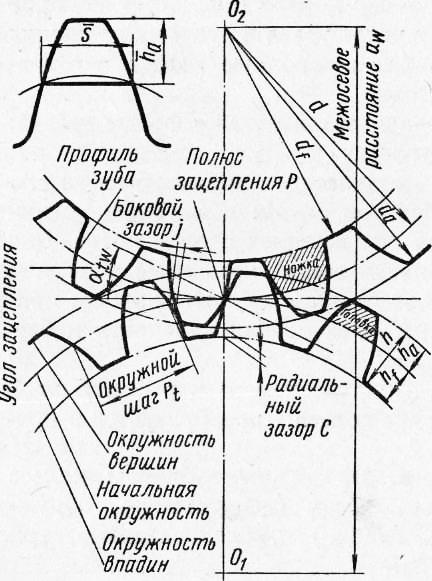
Примем модуль m=2 мм. => Z = r – радиус делительных окружностей.
После определения чисел зубьев и радиусов делительных окружностей на листе изображают кинематическую схему в двух проекциях.
Графический способ определения передаточного отношения планетарного механизма.
Справа от вычерченной в масштабе схемы планетарного механизма изобразим правую систему координат, по оси ординат которой отложены радиусы зубчатых колес в миллиметрах, а по оси абсцисс – линейная скорость в м/сек.
Обозначим буквами точки контакта зубчатых колес по вертикальной оси симметрии зубчатых колес планетарного механизма: А – точка контакта колес 1 и 2, В- ось пальца
19
водила
( она же горизонтальная ось симметрии
сателлита), С – точка контакта зубчатых
колес 2 и 3. Так как коронная шестерня
неподвижна, то точка С является мгновенным
центром скоростей в абсолютном движении
для блока сателлитов 2. На водиле выберем
точку F
, расположенную от оси вращения ОО
центральных колес 1 и 4, а также водила
на том же расстоянии, что и точка А.
На водиле выберем
точку F
, расположенную от оси вращения ОО
центральных колес 1 и 4, а также водила
на том же расстоянии, что и точка А.
Зададимся
произвольным отрезком АА
колеса 1, которое для данной схемы планетарного механизма является входным звеном.
Так
как колесо 1 вращается вокруг оси ОО, то
закон распределения линейных скоростей
для него изобразится наклонной линией
ОА1,
которую пометим цифрой 1. От вертикальной
оси r
линия ОА1 отклонена на угол 1.
Линия СА1 изображает закон распределения линейных
скоростей блока сателлитов 2 для
точек, расположенных на оси симметрии
сателлитов. Скорость точки В сателлитов изобразится
отрезком ВВ1.
Так как точка В является общей для оси
пальца водила и сателлитов, то линия
ОВ1,
проведенная под углом H к вертикальной
оси радиусов является законом распределения
линейных скоростей для водила. Отрезок
АА 1 является линейной скоростью точки F
водила.
Отрезок
АА 1 является линейной скоростью точки F
водила.
Корригированные шестерни
Категория:
Автомобильные сцепления
Публикация:
Корригированные шестерни
Читать далее:
Шестерни с косыми зубьями
Корригированные шестерни
Зубчатое зацепление уже давно и в значительной степени стандартизовано, причем произошло это не благодаря деятельности какого-либо специального учреждения по стандартизации, а в результате влияния ряда фирм, изготовляющих зуборезное оборудование. Так, в очень большой части зубчатых передач промышленного типа применяется одно значение угла зацепления, имеется принятый ряд значений диаметрального питча и строго установленные соотношения элементов (головка и ножка) зубьев. Эта стандартизация была весьма полезна в отношении зубчатых колес, выпускавшихся в малых количествах, так как устраняла необходимость изготовления специального режущего инструмента для каждой партии.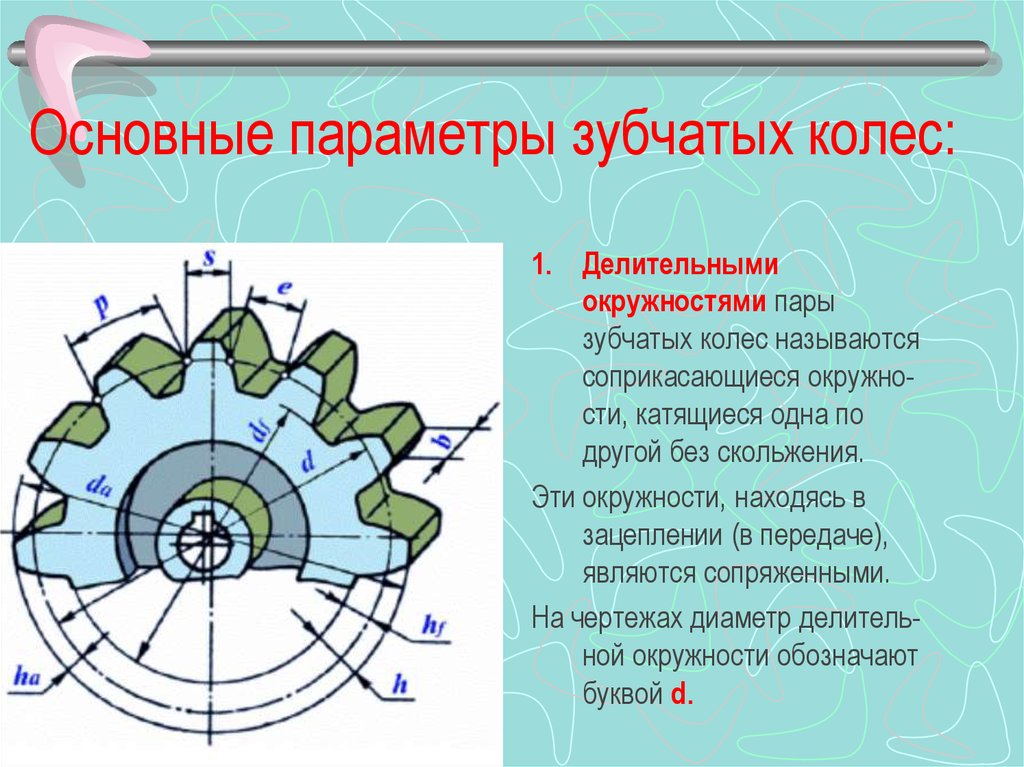
 Зачерченные площадки показывают зоны подреза профилей. Из чертежа ясно, что подрез профилей возникает в результате того, что .радиальная часть профиля зуба шестерни образует (в этот момент) больший угол с радиальной линией, проведенной через полюс зацепления (линия центров шестерен), чем угол, образуемый боковой стороной зуба рейки с той же линией центров (профильный угол режущего инструмента). Последний является постоянным, равным углу зацепления тогда как угол, образуемый радиальной частью профиля зуба шестерни с линией центров, по мере приближения к концу отрезка зацепления увеличивается; поэтому, если у какой-либо шестерни имеет место подрез профилей, он будет происходить непосредственно перед, концом зацепления2. Угол, образуемый радиальной частью профиля зуба с линией центров в конце зацепления при увеличении числа зубьев шестерни, уменьшается.
Зачерченные площадки показывают зоны подреза профилей. Из чертежа ясно, что подрез профилей возникает в результате того, что .радиальная часть профиля зуба шестерни образует (в этот момент) больший угол с радиальной линией, проведенной через полюс зацепления (линия центров шестерен), чем угол, образуемый боковой стороной зуба рейки с той же линией центров (профильный угол режущего инструмента). Последний является постоянным, равным углу зацепления тогда как угол, образуемый радиальной частью профиля зуба шестерни с линией центров, по мере приближения к концу отрезка зацепления увеличивается; поэтому, если у какой-либо шестерни имеет место подрез профилей, он будет происходить непосредственно перед, концом зацепления2. Угол, образуемый радиальной частью профиля зуба с линией центров в конце зацепления при увеличении числа зубьев шестерни, уменьшается.Наименьшее число зубьев без подреза профиля. С увеличением числа зубьев малой шестерни подрез зубьев исчезает, когда при положении шестерни, соответствующем теоретическому выходу зуба из зацепления, боковая сторона зуба рейки, работающего с зубом шестерни, и радиальная часть профиля зуба шестерни образуют одинаковый угол с линией центров; так как между этими двумя линиями имеется соприкосновение, то.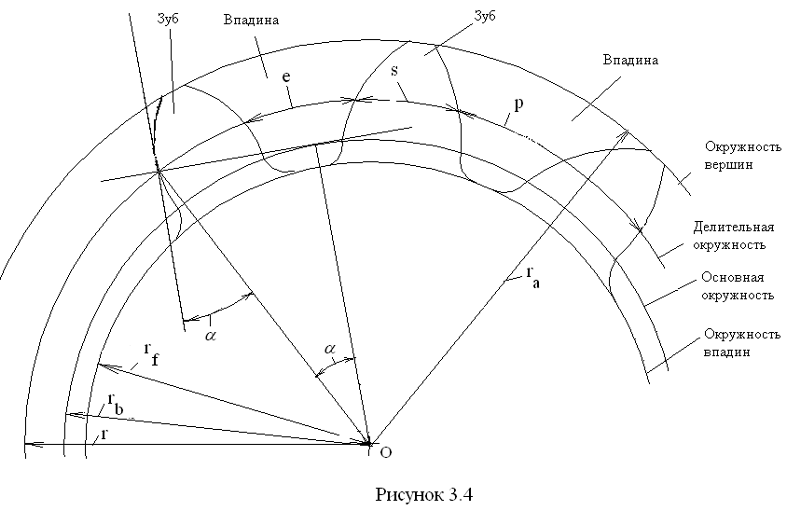 они на некотором участке совпадают. Это дает возможность определить расчетным путем наименьшее число зубьев эвольвентных шестерен с различными углами зацепления и различными соотношениями головки зуба, при котором не будет подреза профилей.
они на некотором участке совпадают. Это дает возможность определить расчетным путем наименьшее число зубьев эвольвентных шестерен с различными углами зацепления и различными соотношениями головки зуба, при котором не будет подреза профилей.
Рекламные предложения на основе ваших интересов:
Дополнительные материалы по теме:
Рис. 1. Подрез (интерференция) профиля зубьев.
Рис. 2. Геометрические соотношения, определяющие минимальное число зубьев шестерни без подреза профиля: ВС — высота головки зуба.
При помощи этих уравнений найдем, что наименьшее число зубьев, при котором полностью отсутствует подрез, составляет 33 для шестерни с зубом нормальной высоты и углом зацепления 14°30’ и 18 для шестерни с зубом нормальной высоты и углом зацепления 20°. При числах зубьев 32 и 17 соответственно подрез будет иметь ничтожную величину. Для шестерни с укороченным зубом,, углом зацепления 20° и высотой головки, составляющей 0,8 от нормальной, минимальное число зубьев будет равно 14.
Способы устранения подреза зубьев. Установлено, что в парах шестерен, в которых ведущая шестерня имеет относительно малое число зубьдв, для обеспечения полностью эвольвентного профиля высота головки зуба ведущей (малой) шестерни должна быть увеличена, а высота головки зуба большой шестерни — уменьшена на ту же величину. Для увеличения высоты головки малой шестерни наружный диаметр ее заготовки должен быть взят большим, чем в случае шестерни с обычными соотношениями, а наружный диаметр большей шестерни должен выполняться соответственно .меньшим
Можно легко изменять ранее выведенные соотношения между числом зубьев, углом зацепления и высотой головки так, чтобы, обеспечивая полностью эвольвентное зацепление, определять непосредственно необходимое увеличение и уменьшение внешних диаметров заготовок шестерен с любым числом зубьев и любым углом зацепления.
Это обеспечивает полностью эвольвентный профиль зубьев малой шестерни. Однако, если сопряженная шестерня имеет лишь немного большее по сравнению с малой шестерней число зубьев, то во избежание подреза профилей при зацеплении с зубьями малой шестерни, имеющими удлиненную головку, подрез ее зубьев может стать неизбежным. Для предотвращения этого необходимо, чтобы сумма чисел зубьев малой и большой шестерен была равна, по крайней мере, 34 при угле зацепления 20° и зубе нормальной высоты или 64 в случае зуба нормальной высоты при угле зацепления 14°30’.
Для предотвращения этого необходимо, чтобы сумма чисел зубьев малой и большой шестерен была равна, по крайней мере, 34 при угле зацепления 20° и зубе нормальной высоты или 64 в случае зуба нормальной высоты при угле зацепления 14°30’.
Корригированные зубья широко применяются в конических шестернях главных передач автомобилей. В этом случае принято вы поднять высоту головки в постоянном соотношении с рабочей высотой зуба, равном обычно 0,7 для зубьев малой шестерни и 0,3 для зубьев большой шестерни
На рис. 3 дано сравнение шестерни с 20 зубьями стандартного профиля, нормальной высоты, с углом зацепления 14°30’ и аналогичной шестерни с зубьями, имеющими удлиненную головку, высота которой в данном случае равна 0,75 рабочей высоты зуба.
Плавность работы корригированных шестерен. Утверждают, что корригированные шестерни работают под нагрузкой более плавно, чем нормальные шестерни с одинаковой высотой головок. Это объясняется тем, что при увеличении высоты головки зуба малой шестерни дуга удаления удлиняется, а при уменьшении высоты головки большой шестерни дуга приближения укорачивается.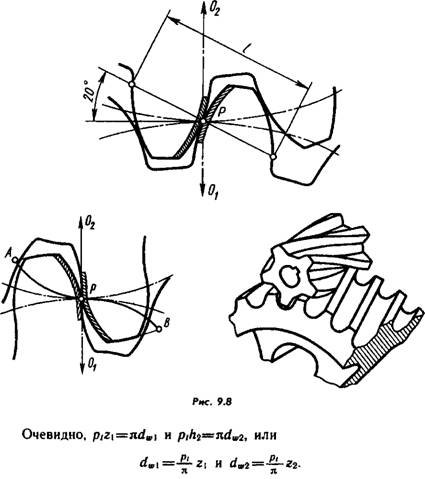 Следовательно, мы можем сказать, что в передачах, где ведущая шестерня имеет сравнительно длинную головку зуба, дуга приближения укорачивается, а дуга удаления удлиняется. Известно, что плавность работы зуба на протяжении дуги приближения значительно меньше, чем на дуге удаления. В течение каждого из этих периодов имеется скольжение зубьев, но направления скольжения противоположны. В первом случае, т. е. в период приближения, движение может быть уподоблено толкованию впереди себя длинного упругого стержня по неровной дороге. Во втором случае, в период удаления, этот стержень как бы тянут за собой по той же дороге, последнее движение, естественно, получается более плавным.
Следовательно, мы можем сказать, что в передачах, где ведущая шестерня имеет сравнительно длинную головку зуба, дуга приближения укорачивается, а дуга удаления удлиняется. Известно, что плавность работы зуба на протяжении дуги приближения значительно меньше, чем на дуге удаления. В течение каждого из этих периодов имеется скольжение зубьев, но направления скольжения противоположны. В первом случае, т. е. в период приближения, движение может быть уподоблено толкованию впереди себя длинного упругого стержня по неровной дороге. Во втором случае, в период удаления, этот стержень как бы тянут за собой по той же дороге, последнее движение, естественно, получается более плавным.
Определение дуговой толщины зубьев корригированных шестерен. Когда головка и ножка зуба не равны по высоте, толщина зуба по дуге перестает быть равной половине шага. Как изменение соот
Рис. 3. Сравнение профилей зубьев со стандартным эвольвентным профилем полной высоты и с удлиненной головкой:
1 — начальная окружность: 2 — основная окружность; 3 — зуб с удлиненной головкой; 4 — стандартный зуб
Рис. 4. Схема изменения толщины зуба по делительной окружности при профильном смещении рейки:
4. Схема изменения толщины зуба по делительной окружности при профильном смещении рейки:
1 — нормальная начальная прямая; 2 — действительная начальная прямая; 3 — действительная толщина зуба по дуге.
Толщина зуба сопряженной шестерни по’дуге равна шагу минус толщина зуба по делительной окружности первой шестерни.
Рис. 5. Схема определения толщины зуба по хорде:
1 — толщина зуба по хорде; 2 — толщина зуба по дуге.
Профиль зуба шестерни – Marples Gears
Профиль зуба шестерни:
Одним из основных элементов конструкции шестерни является профиль зуба шестерни. Шестерни обычно имеют эвольвентный профиль зуба. Существуют и другие типы профилей зубчатых колес, но они в основном используются в специальных приложениях, таких как циклоидальные зубчатые колеса в часах.
Эта эвольвента помогает шестерням плавно передавать мощность во время качения. Кривая получается путем наматывания нити на цилиндр, базовый круг, и по мере того, как она разворачивается из этого цилиндра, она очерчивает эвольвентную кривую..gif) Базовая окружность эвольвентной кривой также важна, потому что она помогает определить угол давления зубчатого колеса, еще одну основу конструкции зубчатого колеса.
Базовая окружность эвольвентной кривой также важна, потому что она помогает определить угол давления зубчатого колеса, еще одну основу конструкции зубчатого колеса.
Точка контакта шестерни и шестерни проходит по эвольвенте шестерни. Эвольвентный профиль зубьев шестерни также способствует плавному вращению даже при изменении межцентровых расстояний между шестерней и шестерней. Касательная линия базовой окружности шестерни и базовая окружность шестерни образуют линию действия набора шестерен. Толщина зуба, диаметральный шаг и угол зацепления определяют профиль зуба шестерни. Эти факторы определяются желаемым коэффициентом контакта между сопрягаемыми частями шестерни. Профиль зуба шестерни также зависит от количества зубьев на шестерне, так что чем больше количество зубьев, тем прямее профиль шестерни, в конечном итоге образующей так называемую реечную шестерню. Преимуществом изготовления реечной формы является прочность, полученная за счет реечной формы.
Многие фирмы, занимающиеся производством зубчатых колес, также имеют возможность определять профиль зубчатого колеса по геометрии фрез, которые используются для создания зубьев на зубчатом колесе. Этот метод используется для обратного проектирования зубчатых колес, которые, возможно, потребуется заменить, если производитель оригинальной детали больше не может производить эту деталь. Хотя этот метод позволяет создать профиль шестерни, фирме все же потребуются некоторые дополнительные размеры для точного обратного проектирования указанной детали.
Этот метод используется для обратного проектирования зубчатых колес, которые, возможно, потребуется заменить, если производитель оригинальной детали больше не может производить эту деталь. Хотя этот метод позволяет создать профиль шестерни, фирме все же потребуются некоторые дополнительные размеры для точного обратного проектирования указанной детали.
Marples Gears специализируется на производстве высокоточных зубчатых колес с мелким шагом в соответствии со стандартом качества Q13 для наших зубчатых колес, которые мы изготавливаем по индивидуальному заказу на собственном предприятии. В Marples Gears мы также используем программное обеспечение для анализа профиля зубьев вашей детали. Хотя мы не сертифицированы для проектирования зубчатых колес в соответствии с AS9100-D, мы можем проконсультировать вас по поводу наилучшего метода изготовления ваших зубчатых колес. Marples Gears также имеет возможность реконструировать шестерню с помощью метода, описанного выше, и путем анализа исходной шестерни.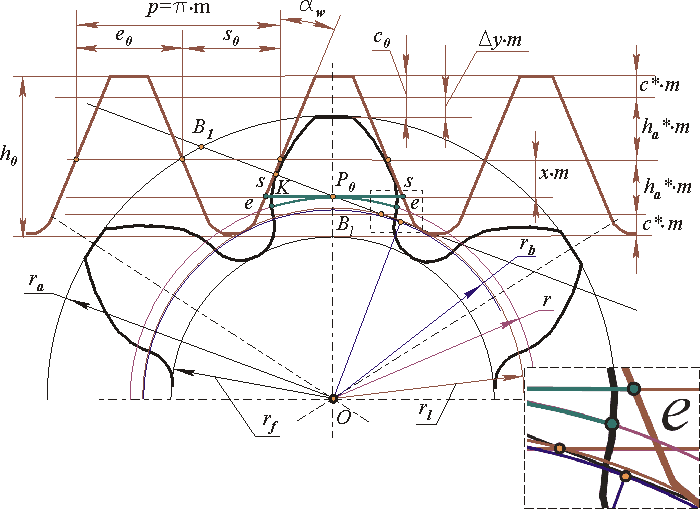 Для того, чтобы индивидуальный инженер рассмотрел предложение, отправьте электронное письмо по адресу [email protected] или посетите нашу страницу с индивидуальным предложением на вкладке «Свяжитесь с нами» выше.
Для того, чтобы индивидуальный инженер рассмотрел предложение, отправьте электронное письмо по адресу [email protected] или посетите нашу страницу с индивидуальным предложением на вкладке «Свяжитесь с нами» выше.
Ресурсы:
https://khkgears.net/gear-knowledge/introduction-to-gears/involute-tooth-profile/
https://khkgears.net/gear-knowledge/abcs-gears- b/gear-tooth-profile/
http://www.khkgears.co.jp/kr/gear_technology/pdf/gearabc_b.pdf
Автор: Marples Gears Inc.
Углубленный взгляд на профиль зуба эвольвентного зубчатого колеса и изменение профиля — шестерни Marples
Зубчатые колеса — это механизмы, используемые для передачи мощности. Существует множество различных типов зубчатых колес, которые могут быть адаптированы для конкретного применения. Шестерни передают мощность за счет смешения зубьев шестерни в одной точке по линии действия.
Профиль зуба — это одна сторона зуба в поперечном сечении между внешней окружностью и корневой окружностью шестерни.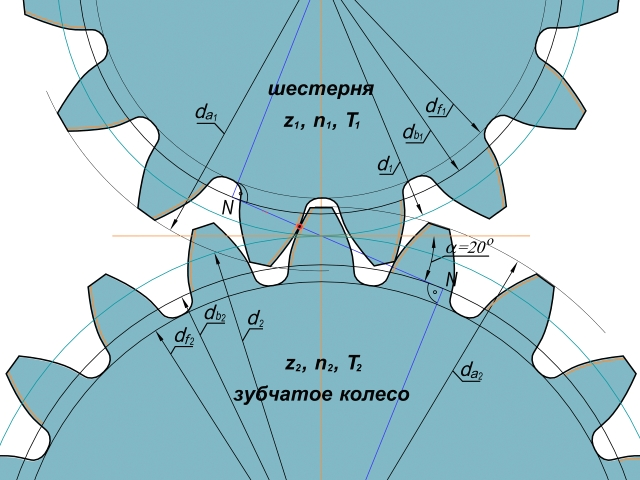 Обычно это относится к кривой пересечения поверхности зуба и плоскости или поверхности, нормальной к делительной поверхности, такой как поперечная, нормальная или осевая плоскость. Наиболее распространенным типом профиля зуба шестерни является эвольвентный профиль зуба шестерни, стандартный и скорректированный.
Обычно это относится к кривой пересечения поверхности зуба и плоскости или поверхности, нормальной к делительной поверхности, такой как поперечная, нормальная или осевая плоскость. Наиболее распространенным типом профиля зуба шестерни является эвольвентный профиль зуба шестерни, стандартный и скорректированный.
Эвольвентный профиль зубчатого колеса означает, что профили зубьев зубчатого колеса представляют собой эвольвенты окружности, а эвольвента окружности представляет собой геометрическое место точки на отрезке струны, когда струна разворачивается из окружности. Уравнения для эвольвенты окружности следующие:
Стандартный профиль эвольвентного зубчатого колеса зависит только от количества зубьев, угла давления и шага, что означает, что большинство расчетов зубчатого колеса может быть получено из этих трех частей данных зубчатого колеса. Форма или форма эвольвентной кривой зависит от диаметра основной окружности, из которой она получена. Использование стандартного профиля эвольвентного зубчатого колеса будет означать, что практически любое зубчатое колесо, имеющее одинаковый шаг, угол давления и угол наклона спирали, сможет работать друг с другом, потому что в этом типе конструкции зубчатого колеса контакт между парой зубьев шестерни происходит при единственная мгновенная точка, где встречаются две эвольвенты одной и той же спиральной стрелки. Основным фактором, влияющим на профиль эвольвентного зубчатого колеса, является число. При большом количестве зубьев профиль зуба шестерни будет больше похож на рейку, в то время как меньшее количество зубьев будет иметь большой радиус скругления впадины, но смещение профиля может исправить этот радиус скругления впадины.
Основным фактором, влияющим на профиль эвольвентного зубчатого колеса, является число. При большом количестве зубьев профиль зуба шестерни будет больше похож на рейку, в то время как меньшее количество зубьев будет иметь большой радиус скругления впадины, но смещение профиля может исправить этот радиус скругления впадины.
Профиль эвольвентного зубчатого колеса влияет на зацепление между двумя зубчатыми колесами. Сцепление — это термин, используемый для обозначения контакта двух зубьев шестерни друг с другом для передачи мощности. Контакт между зацепляющимися эвольвентными зубьями на ведущей и ведомой шестернях осуществляется по прямой линии, касательной к двум базовым окружностям этих шестерен. Контакт может повлиять на эффективность передачи мощности зубчатыми колесами, на шум, возникающий при работе комплекта зубчатых колес, и на точность всей системы.
Другим распространенным профилем зубчатого колеса является циклоидальный профиль зубчатого колеса, но эвольвентные зубчатые колеса имеют определенные преимущества перед циклоидальными зубчатыми колесами, такие как простота конструкции и изготовления. Эвольвентный профиль также имеет преимущество постоянного угла давления на протяжении всего зацепления двух шестерен. Циклоидные зубчатые колеса имеют преимущество в прочности из-за их более широких боковых сторон и отсутствия помех, которые могут возникать в зубьях эвольвентных зубчатых колес, где корень одного зуба подрезает вершину другого зуба во время зацепления. Подрезка – это когда верхняя часть шестерни врезается по радиусу в корень другой шестерни. Зубчатые колеса с поднутрением имеют меньшую прочность в нижней части зуба и создают меньший контакт шестерни из-за укороченной эвольвенты на зубе.
Эвольвентный профиль также имеет преимущество постоянного угла давления на протяжении всего зацепления двух шестерен. Циклоидные зубчатые колеса имеют преимущество в прочности из-за их более широких боковых сторон и отсутствия помех, которые могут возникать в зубьях эвольвентных зубчатых колес, где корень одного зуба подрезает вершину другого зуба во время зацепления. Подрезка – это когда верхняя часть шестерни врезается по радиусу в корень другой шестерни. Зубчатые колеса с поднутрением имеют меньшую прочность в нижней части зуба и создают меньший контакт шестерни из-за укороченной эвольвенты на зубе.
Сдвиг профиля
Сдвиг профиля или «дополнительная модификация» или «коррекция» — это просто смещение базовой базовой линии рейки от опорного диаметра зубчатого колеса. Положительный сдвиг профиля увеличивает толщину зуба, а отрицательный сдвиг профиля уменьшает толщину зуба. Для стандартного профиля зубьев шестерни радиус базовой окружности не изменяется, независимо от того, имеет ли шестерня сдвиг профиля, все остальные данные шестерни являются стандартными. Зубчатые колеса со сдвигом профиля по-прежнему могут изготавливаться теми же методами и с использованием тех же инструментов, что и стандартные зубчатые колеса, например, зубофрезерованием и формованием. Некоторые ограничения могут быть достигнуты при проектировании шестерни со смещенным профилем, верхняя часть приводит к чрезвычайно узкому наконечнику, а нижняя – к сильному подрезу шестерни соответственно. Но пока редко в некоторых приложениях используются пределы смещения профиля.
Зубчатые колеса со сдвигом профиля по-прежнему могут изготавливаться теми же методами и с использованием тех же инструментов, что и стандартные зубчатые колеса, например, зубофрезерованием и формованием. Некоторые ограничения могут быть достигнуты при проектировании шестерни со смещенным профилем, верхняя часть приводит к чрезвычайно узкому наконечнику, а нижняя – к сильному подрезу шестерни соответственно. Но пока редко в некоторых приложениях используются пределы смещения профиля.
Хотя большинство инженеров предпочитают использовать стандартные профили зубчатых колес, сдвинутые зубчатые колеса могут потребоваться в различных специализированных приложениях. Смещение профиля помогает предотвратить подрезку, которая может возникнуть, когда количество зубьев шестерни, подлежащих нарезанию, становится маленьким, генерирующий инструмент сметает свои траектории и удаляет часть профиля. Это также может помочь отрегулировать межосевое расстояние между шестернями, когда происходит сбой в межосевых расстояниях. Расстояние между центрами влияет на коэффициент контакта между двумя шестернями. Коэффициент контакта может повлиять на шум шестерен, скольжение между шестернями в зацеплении и уменьшить люфт. Сдвиг профиля имеет свои преимущества в балансировке нескольких аспектов передачи, таких как:
Расстояние между центрами влияет на коэффициент контакта между двумя шестернями. Коэффициент контакта может повлиять на шум шестерен, скольжение между шестернями в зацеплении и уменьшить люфт. Сдвиг профиля имеет свои преимущества в балансировке нескольких аспектов передачи, таких как:
- Усталость при изгибе шестерни и шестерни.
- Специальное скольжение точки шага, обеспечивающее максимальное сопротивление точечной коррозии.
- Пиковые температуры вспышки при контакте в точке смолы, минимизирующие вероятность задира.
Характеристики зубчатого колеса с точки зрения устойчивости к точечной коррозии и стойкости к истиранию основаны на расположении теоретической стандартной зубчатой рейки, но по практическим производственным и эксплуатационным соображениям производственный инструмент обычно должен находиться в другом месте, чем теоретическая стандартная формирующая зубчатая рейка.
В то время как зубчатые рейки не изменяют форму профиля зубьев шестерни при коррекции, шестерни с меньшим количеством зубьев гораздо более чувствительны к смещению профиля из-за соотношения между числом зубьев в шестерне и стандартным зубом шестерни профиль, как указано выше.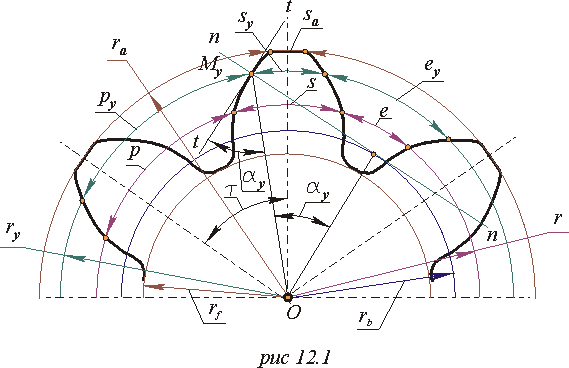
Формулы для смещения профиля:
9009
Где, 65 909
Модуль | |
х | Коэффициент смещения |
г | Количество зубов |
⍺ | Угол давления |
Marples Gears — мастерская по производству прецизионных зубчатых колес. Marples Gears специализируется на производстве высокоточных зубчатых колес с мелким шагом в соответствии со стандартом качества Q13 для наших зубчатых колес, которые мы изготавливаем по индивидуальному заказу на собственном предприятии. В Marples Gears мы также используем программное обеспечение для анализа профиля зубьев вашей детали.

