Пружина жесткостью – Жесткость пружины, формула
alexxlab | 15.12.2019 | 0 | Разное
Жесткость пружины, формула
Определение 1
Пружина – упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.
Типы пружин
Пружины можно классифицировать по направлению прилагаемой нагрузки:
- пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны “виток к витку”; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
- пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.
В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип – запасать энергию упругой деформации и возвращать ее.
Физические характеристики пружин
Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость – способность сопротивляться деформации:
- материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
- диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
- форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток “садится” на соседний виток) конструкция была более устойчивой;
- длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.
Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.
Понятие жесткости
Определение 2
Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.
Коэффициент жесткости рассчитывается по формуле Гука:
$F = -k \cdot x$,
где $F$ – сила, развиваемая пружиной, $k$ – коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ – абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.
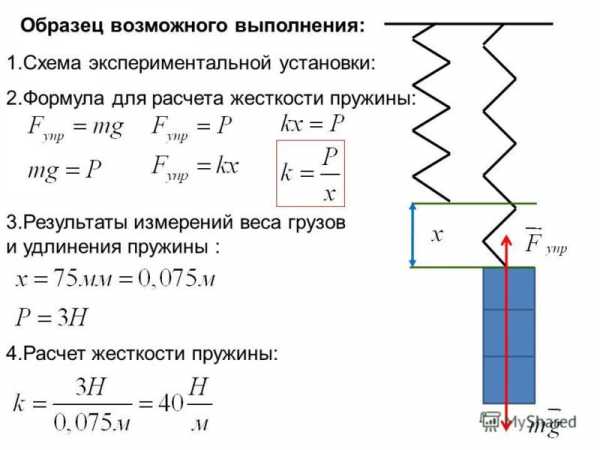
Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость
$m \cdot g – k \cdot x = 0$,
где $m$ – масса, $g$ – ускорение свободного падения. Отсюда
$k = \frac{m \cdot g}{x}$
Расчет жесткости цилиндрической пружины
Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.
Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.
Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями “цилиндров”, диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.
При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние “цилиндры” при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:
$k = \frac{r^4}{4R^3} \cdot \frac{G}{n}$,
где:
- $R$ — радиус цилиндра пружины,
- $n$ — количество витков проволоки радиуса $r$,
- $G$ — коэффициент, зависящий от материала.
Пример 1
Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 \cdot 10^{10}$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков – 25.
Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:
$k = \frac{(10^{-3})^4}{4 \cdot (2 \cdot 10^{-2})^3} \cdot \frac{8 \cdot 10^{10}}{25} = \frac{8 \cdot 10^{-2}}{10^2 \cdot 2^3 \cdot 10^{-6}} = 100$
Ответ: $100 \frac{Н}{м}$
spravochnick.ru
Коэффициент жесткости пружины: определение, формулы, измерение
Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.
Определение и формула жесткости пружины
При рассмотрении того, что такое коэффициент жесткости пружины следует уделить внимание понятию упругости. Для ее обозначения применяется символ F. При этом сила упругости пружины характеризуется следующими особенностями:
- Проявляется исключительно при деформации тела и исчезает в случае, если деформация пропадает.
- При рассмотрении, что такое жесткость пружины следует учитывать, после снятия внешней нагрузки тело может восстанавливать свои размеры и форму, частично или полностью. В подобном случае деформация считается упругой.
Не стоит забывать о том, что жесткость – характеристика, свойственная упругим телам, способным деформироваться. Довольно распространенным вопросом можно назвать то, как обозначается жесткость пружины на чертежах или в технической документации. Чаще всего для этого применяется буква k.
Слишком сильная деформация тела становится причиной появления различных дефектов. Ключевыми особенностями можно назвать следующее:
- Деталь может сохранять свои геометрические параметры при длительной эксплуатации.
- При увеличении показателя существенно снижается сжатие пружины под воздействие одинаковой силы.
- Наиболее важным параметром можно назвать коэффициент жесткости. Он зависит от геометрических показателей изделия, типа применяемого материала при изготовлении.

Довольно большое распространение получили красные пружины и другого типа. Цветовое обозначение применяется в случае производства автомобильных изделий. Для расчета применяется следующая формула: k=Gd4/8D3n. В этой формуле указываются нижеприведенные обозначения:
- G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
- d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
- D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
- n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.
Рассматриваемая формула применяется в случае расчета коэффициента жесткости для цилиндрических пружин, которые устанавливаются в самых различных механизмах. Подобная единица измеряется в Ньютонах. Коэффициент жесткости для стандартизированных изделий можно встретить в технической литературе.
Формула жесткости соединений пружин
Не стоит забывать о том, что в некоторых случаях проводится соединение тела нескольким пружинами. Подобные системы получили весьма широкое распространение. Определить жесткость в этом случае намного сложнее. Среди особенностей соединения можно отметить нижеприведенные моменты:
- Параллельное соединение характеризуется тем, что детали размещаются последовательно. Подобный метод позволяет существенно повысить упругость создаваемой системы.
- Последовательный метод характеризуется тем, что деталь подключаются друг к другу. Подобный способ подсоединения существенно снижает степень упругости, однако позволяет существенно увеличить максимальное удлинение. В некоторых случаях требуется именно максимальное удлинение.
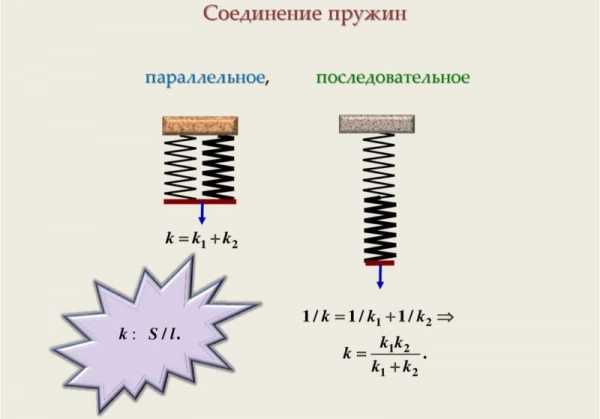
В обеих случаях применяется определенная формула, которая определяет особенности подключения. Модуль силы упругости может существенно отличаться в зависимости от особенностей конкретного изделия.
При последовательном соединении изделий показатель рассчитывается следующим образом: 1/k=1/k1+1/k2+…+1/kn. Рассматриваемый показатель считается довольно важным свойством, в данном случае он снижается. Параллельный метод подключения рассчитывается следующим образом: k=k1+k2+…kn.
Подобные формулы могут использоваться при самых различных расчетах, чаще всего на момент решения математических задач.
Коэффициент жесткости соединений пружин
Приведенный выше показатель коэффициента жесткости детали при параллельном или последовательном соединении определяет многие характеристики соединения. Довольно часто проводится определение тому, чему равно удлинение пружины. Среди особенностей параллельного или последовательного соединения можно отметить нижеприведенные моменты:
- При параллельном подключении удлинение обоих изделий будет равным. Не стоит забывать о том, что оба варианта должны характеризоваться одинаковой длиной в свободном положении. При последовательном показатель увеличивается в два раза.
- Свободное положение – ситуация, в которой деталь находится без прикладывания нагрузки. Именно оно в большинстве случаев учитывается при проведении расчетов.
- Коэффициент жесткости изменяется в зависимости от применяемого способа подсоединения. В случае параллельного соединения показатель увеличивается в два раза, при последовательном уменьшается.
Для проведения расчетов нужно построить схему подключения всех элементов. Основание представлено линией со штриховкой, изделие обозначается схематически, а тело в упрощенном виде. Кроме этого, от упругой деформации во многом зависит кинетическая и другая энергия.
Коэффициент жесткости цилиндрической пружины
На практике и в физике довольно большое распространение получили именно цилиндрические пружины. Их ключевыми особенностями можно назвать следующие моменты:
- При создании указывается центральная ось, вдоль которой и действует большинство различных сил.
- При производстве рассматриваемого изделия применяется проволока определенного диаметра. Она изготавливается из специального сплава или обычных металлов. Не стоит забывать о том, что материал должен обладать повышенной упругостью.
- Проволока накручивается витками вдоль оси. При этом стоит учитывать, что они могут быть одного или разного диаметра. Довольно большое распространение получил вариант исполнения цилиндрического типа, но большей устойчивостью характеризуется цилиндрический вариант исполнения, в сжатом состоянии деталь обладает небольшой толщиной.
- Основными параметрами можно назвать больший, средний и малый диаметр витков, диаметр проволоки, шаг расположения отдельных колец.
Не стоит забывать о том, что выделяют два типа деталей: сжатия и растяжения. Их коэффициент жесткости определяется по одной и той же формуле. Разница заключается в следующем:
- Вариант исполнения, рассчитанный на сжатие, характеризуется дальним расположением витков. За счет расстояние между ними есть возможность сжатия.
- Модель, рассчитанная на растяжение, имеет кольца, расположенные практически вплотную. Подобная форма определяет то, что при максимальная сила упругости достигается при минимальном растяжении.
- Также есть вариант исполнения, который рассчитан на кручение и изгиб. Подобная деталь рассчитывается по определенным формулам.
Расчет коэффициента цилиндрической пружины может проводится при использовании ранее указанной формулы. Она определяет то, что показатель зависит от следующих параметров:
- Наружного радиуса колец. Как ранее было отмечено, при изготовлении детали применяется ось, вокруг которой проводится накручивание колец. При этом не стоит забывать о том, что выделяют также средний и внутренний диаметр. Подобный показатель указывается в технической документации и на чертежах.
- Количества создаваемых витков. Этот параметр во многом определяет длину изделия в свободном состоянии. Кроме этого, количество колец определяет коэффициент жесткость и многие другие параметры.
- Радиуса применяемой проволоки. В качестве исходного материала применяется именно проволока, которая изготавливается из различных сплавов. Во многом ее свойства оказывают влияние на качества рассматриваемого изделия.
- Модуля сдвига, который зависит от типа применяемого материала.

Коэффициент жесткости считается одним из наиболее важных параметров, который учитывается при проведении самых различных расчетов.
Единицы измерения
При проводимых расчетах также должно учитываться то, в каких единицах измерениях проводятся вычисления. При рассмотрении того, чему равно удлинение пружины уделяется внимание единице измерения в Ньютонах.
Для того чтобы упростить выбор детали многие производители указывают его цветовым обозначением.
Разделение пружины по цветам проводится в сфере автомобилестроения.
Среди особенностей подобной маркировки отметим следующее:
- Класс А обозначается белым, желтым, оранжевым и коричневым оттенками.
- Класса В представлен синим, голубым, черным и желтым цветом.
Как правило, подобное свойство отмечается на внешней стороне витка. Производители наносят небольшую полоску, которая и существенно упрощает процесс выбора.
Особенности расчета жесткости соединений пружин
Приведенная выше информация указывает на то, что коэффициент жесткости является довольно важным параметром, который должен рассчитываться при выборе наиболее подходящего изделия и во многих других случаях. Именно поэтому довольно распространенным вопросом можно назвать то, как найти жесткость пружины. Среди особенностей соединения отметим следующее:
- Провести определение растяжения пружины можно при вычислении, а также на момент теста. Этот показатель может зависеть в зависимости от проволоки и других параметров.
- Для расчетов могут применяться самые различные формулы, при этом получаемый результат будет практически без погрешностей.
- Есть возможность провести тесты, в ходе которых и выявляются основные параметры. Определить это можно исключительно при применении специального оборудования.
Как ранее было отмечено, выделяют последовательный и параллельный метод соединения. Оба характеризуются своими определенными особенностями, которые должны учитываться.
В заключение отметим, что рассматриваемая деталь является важной частью конструкции различных механизмов. Неправильный вариант исполнения не сможет прослужить в течение длительного периода. При этом не стоит забывать о том, что слишком сильная деформация становится причиной ухудшения эксплуатационных характеристик.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
stankiexpert.ru
Жесткость пружины – коэффициент жесткости

I. Жесткость пружины
Что такое жесткость пружины?
Одним из важнейших параметров, относящимся к упругим изделиям из металла разного назначения, является жесткость пружины. Она подразумевает, насколько пружина будет устойчива к воздействию других тел и насколько сильно сопротивляется им при воздействии. Силе сопротивления равен коэффициент жесткости пружины.
На что влияет этот показатель?
Пружина – это достаточно упругое изделие, обеспечивающее передачу поступательных вращательных движений тем приборам и механизмам, в которых она находится. Надо сказать, что встретить пружину можно повсеместно, каждый третий механизм в доме оснащен пружиной, не говоря уже о количестве этих упругих элементов в приборах на производстве. При этом надежность функционирования этих приборов будет определяться степенью жесткости пружины. Эта величина, называемая коэффициентом жесткости пружины, зависит от усилия, которое нужно приложить, чтобы сжать или растянуть пружину. Распрямление пружины до исходного состояния определяется тем металлом, из которого она изготовлена, но не степенью жесткости.
От чего зависит данный показатель?
Такой простой элемент, как пружина, обладает массой разновидностей в зависимости от степени назначения. По способу передачи деформации механизму и форме выделяют спиральные, конические, цилиндрические и другие. Поэтому жесткость конкретного изделия определяется также и способом передачи деформации. Деформационная характеристика будет разделять пружинные изделия на пружины кручения, сжатия, изгиба и растяжения.
При использовании в приборе сразу двух пружин, степень их жесткости будет зависеть от способа крепления – при параллельном соединении в приборе жесткость пружин будет увеличиваться, а при последовательном – уменьшаться.
II. Коэффициент жесткости пружины
Коэффициент жесткости пружины и пружинных изделий – один из важнейших показателей, который определяет срок службы изделия. Для расчета коэффициента жесткости в ручную — существует несложная формула (см. рис. 1), а так же есть возможность воспользоваться нашим калькулятором пружин, который достаточно легко поможет произвести Вам все необходимые расчеты. Однако на срок эксплуатации всего механизма жесткость пружины будет влиять лишь косвенно – большее значение будут иметь другие качественные особенности прибора.
Предлагаем также ознакомиться:
Поделитесь ссылкой на данную страницу:
pruzhin.ru
Жесткость пружины | Блог Александра Воробьева
Опубликовано 14 Июн 2015
Рубрика: Механика | 55 комментариев
Максимальная сила сжатия или растяжения пружины не зависит от количества рабочих витков! Это означает, что если взять, например, цилиндрическую пружину сжатия, а затем разрезать её на две неравные по высоте части, то максимальное усилие при полном сжатии…
…обеих образовавшихся пружин будет одинаковым. Более того – максимальная сила останется такой же, как у исходной пружины!
В чем же тогда различие между тремя рассмотренными выше пружинами? Ответ на этот вопрос – в высотных размерах и жесткостях.
Меньшая пружина самая жесткая. У нее самый малый ход от свободного состояния до полного сжатия. Исходная пружина (до разделения) – самая мягкая. У нее самый большой ход.
Жесткость пружины (C) является ключевым параметром, определяющим силу сжатия или растяжения (Fi) при определенной величине деформации (L0— Li):
Fi=C*(L0— Li)
В свою очередь сама жесткость пружины (C) зависит только от жесткости одного витка (C1) и числа рабочих витков (N):
C=C1/N
Обратите внимание – жесткость одного витка всегда больше жесткости всей пружины! Причем, чем больше в пружине витков, тем она мягче.
Расчет в Excel жесткости витка пружины.
Жесткость витка пружины – это «краеугольный камень в фундаменте» расчетов, зависящий лишь от модуля сдвига материала, из которого пружина навита и её геометрических размеров.
C1=G*X4/(Y*(D1— B)3)
В этой формуле:
G – модуль сдвига материала проволоки
Для пружинной стали:
G≈78500 МПа ±10%
Для пружинной бронзы:
G≈45000 МПа ±10%
X – минимальный размер сечения проволоки
Для круглой проволоки – это её диаметр:
X=D
Для прямоугольной проволоки:
X=H при H<B
X=B при B<H
H – высота сечения проволоки в направлении параллельном оси навивки пружины
B – ширина сечения проволоки в направлении перпендикулярном оси навивки пружины
Для круглой проволоки:
H=B=D
D1— наружный диаметр пружины
(D1— B) – средний диаметр пружины
Y – параметр жесткости сечения проволоки
Для круглой проволоки:
Y=8
Для прямоугольной проволоки:
Y=
Что это за функция — f (H/B)? В литературе она всегда задана в виде таблицы, что не всегда удобно, особенно для промежуточных значений H/B, которых попросту нет.
 Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
Выполним аппроксимацию в MS Excel табличных данных в первых двух столбцах аналитическими функциями, разбив для повышения точности табличные значения на три группы.
На графиках, представленных ниже, Excel нашел три уравнения для определения параметра Y при различных значениях аргумента — отношения высоты проволоки к ширине – H/B. Красные точки – это заданные значения из таблицы (столбец №2), черные линии – это графики найденных аппроксимирующих функций. Уравнения этих функций Excel вывел непосредственно на поля графиков.
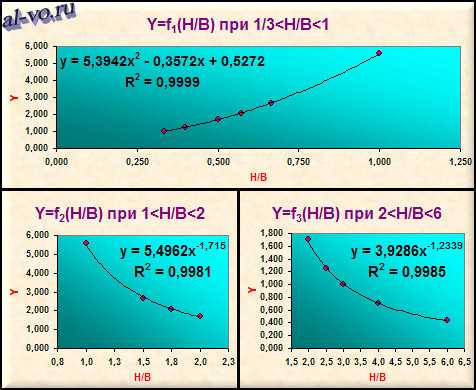
В таблице в столбце №3 размещены посчитанные по полученным формулам значения параметра жесткости сечения проволоки Y, а в столбцах №4 и №5 — абсолютные Δабс и относительные Δотн погрешности аппроксимации.
Как видно из таблицы и графиков полученные уравнения весьма точно замещают табличные данные! Величина достоверности аппроксимации R2 очень близка к 1 и относительная погрешность не превышает 2,7%!
Применим на практике полученные результаты.
Расчет пружины сжатия из проволоки прямоугольного сечения.

Жесткость пружины из проволоки или прутка прямоугольного сечения при тех же габаритах, что и из круглой проволоки может быть гораздо больше. Соответственно и сила сжатия пружины может быть больше.
Представленная ниже программа является переработанной версией программы расчета цилиндрических пружин из круглой проволоки, подробное описание которой вы найдете, перейдя по ссылке. Прочтите эту статью, и вам проще будет разобраться в алгоритме.
Основным отличием в расчете, как вы уже догадались, является определение жесткости витка (C1), задающей жесткость пружины (C) в целом.
Далее представлены скриншот программы и формулы для цилиндрической стальной пружины из прямоугольной проволоки, у которой поджаты по ¾ витка с каждого конца и опорные поверхности отшлифованы на ¾ длины окружности.
Внимание!!!
После выполнения расчета по программе выполняйте проверку касательных напряжений!!!
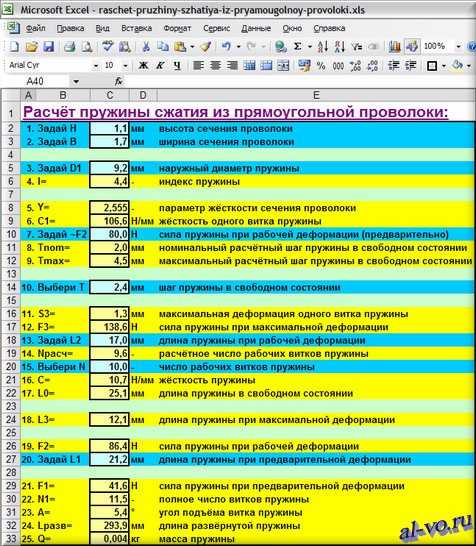
4. I=(D1/B)
-15. При 1/3<H/B<1: Y=5,3942*(H/B)2-0,3572*(H/B)+0,5272
При 1<H/B<2: Y=5,4962*(H/B)(-1.715)
При 2<H/B<6: Y=3,9286*(H/B)(-1.2339)
6. При H<B: C1=(78500*H4
При H>B: C1=(78500*B4)/(Y*(D1— B)3)
8. Tnom=1,25*(F2/C1)+H
9. Tmax=π*(D1— B)*tg (10°)
11. S3=T— H
12. F3=C1*S3
14. Nрасч=(L2— H)/(H+F3/C1— F2/C1)
16. C=C1/N
17. L0=N*T+H
18. L3=N*H+H
19. F2=C*L0— C*L2
21. F1=C*L0— C*L1
22. N1=N+1,5
23. A=arctg (T/(π*(D1— H)))
24. Lразв=π*N1*(D1— H)/cos (A)
25. Q=H*B*Lразв*7,85/106
Заключение.
Значение модуля сдвига (G) материала проволоки в существенной мере влияющее на жесткость пружины (C) в реальности колеблется от номинально принятого до ±10%. Это обстоятельство и определяет в первую очередь наряду с геометрической точностью изготовления пружины «правильность» расчетов усилий и соответствующих им перемещений.
Почему в расчетах не используются механические характеристики (допускаемые напряжения) материала проволоки кроме модуля упругости? Дело в том, что, задаваясь углом подъема витка и индексом пружины в ограниченных диапазонах значений, и придерживаясь правила: «угол подъема в градусах близок значению индекса пружины», мы фактически исключаем возможность возникновения касательных напряжений при эксплуатации превышающих критические величины. Поэтому проверочный расчет пружин на прочность имеет смысл производить лишь при разработке пружин для серийного производства в особо ответственных узлах. Но при таких условиях кроме расчетов всегда неизбежны серьезные испытания…
Напишите пару строк в комментариях — мне всегда интересно ваше мнение.
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
ОСТАЛЬНЫМ можно скачать просто так… — никаких паролей нет!
Ссылка на скачивание файла с программой: raschet-pruzhiny-szhatiya-iz-pryamougolnoy-provoloki (xls 94,5KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
al-vo.ru
Винтовая цилиндрическая пружина. Коэффициент жёсткости.
Расчет пружины. Рассмотрим, каким образом можно получить зависимость удлинения пружины от приложенной нагрузки. Считаем по теоретическим формулам сопротивления материалов. Блокнот Mathemetica прилагается.
Расчет пружины. Общие сведения
Для автоматизации многочисленных подстановок, буду применять Mathematica Online. Приведу сразу снимок блокнота. Теория далее. Задействованы ReplaceAll в краткой форме и Solve.
Блокнот Mathematica Online. Вывод формулы коэффициента жесткости пружины.Cчитаем, что пружина это скручивающийся стержень. У кусочка проволоки, из которого навита пружина, есть некоторая длина (это будет длина стержня). Диаметр проволоки равен .
Пружина для расчета жесткостиЭнергия деформации
Для энергии (Дж) деформации крутящегося стержня имеем следующее выражение:
Здесь: — объем стержня (проволоки пружины), — модуль сдвига (для стали равен Па), — максимальное касательное напряжение на поверхности стержня, — площадь поперечного сечения проволоки, из которой свита пружина, — длина проволоки, из которой свита пружина. Без зацепов и поджатых витков. Площадь поперечного сечения может быть выражена через диаметр проволоки:
Как известно, напряжения в стержне при кручении меняются от нуля в центре до максимума на поверхности стержня. То есть: — для касательных напряжений в произвольной точке стержня на расстоянии от оси вращения. Для максимальных касательных напряжений, радиус максимален и равен радиусу проволоки, поэтому: . Здесь — радиус точки в которой вычисляется напряжение (максимальный радиус равен ), — диаметр проволоки, — полярный момент инерции сечения проволоки. Для проволоки круглого сечения момент равен: . — момент кручения стержня, выражается через силу , которая приложена к пружине по оси спирали:
Таким образом, подставив все величины в формулу для определения энергии деформации, мы получим следующее выражение энергии (см. ячейку 15 блокнота Mathematica):
Работа силы на свободном конце пружины
С другой стороны, работа, совершаемая некоторой силой на перемещение нижнего конца пружины при растяжении должна быть равна энергии деформации. Известно, что усилие для растяжения пружины не постоянно, чем больше растягиваем, тем больше усилие. Закон линеен. Поэтому работа равна площади треугольника под графиком линейной функции, то есть:
Зависимость перемещения Y от силы F
Приравнивая работу (Дж) к энергии (Дж), получаем уравнение:
Забыл кое-что выразить. — длина проволоки в спирали может быть подсчитана так: , где — диаметр спирали, — число витков.
Сделаем замену в уравнении и выразим (Ячейка 18):
т.е. , где
(Н/м) — это искомый коэффициент жесткости цилиндрической пружины. Обратите внимание на то, что жесткость прямо пропорциональна диаметру проволоки в четвертой степени и обратно пропорциональна диаметру пружины в кубе. Это означает, что увеличение диаметра проволоки в два раза при прочих размерах без изменений, увеличит жесткость в раз. А увеличение диаметра пружины в два раза при прочих размерах без изменений, уменьшит жесткость в раз.
На практике, приходится учитывать некоторые нюансы. Например, диаметр проволоки может быть не любым а только таким, который выпускается промышленностью. У пружины, кроме жесткости есть такая характеристика, как ресурс и режим работы. Учитывается даже соударение витков — вспомните магическую пружинку Слинки, которую Эйс Вентура с монастыря спускал, так вот, у ней всегда витки соударяются. Кроме того, выведенная формула жесткости не учитывает криволинейность оси проволоки, свитой в пружину. Для этого существует специальный поправочный коэффициент, входящий в формулу для вычисления касательного напряжения. Этот коэффициент зависит от индекса пружины . Пружины на практике рассчитываются в соответствии с нормативной документацией:
Классификация, сведения о материалах и ссылки на параметры витков даны в ГОСТ 13764-86 — «Пружины винтовые цилиндрические сжатия и растяжения из стали круглого сечения. Классификация».
Методика определения размеров пружин дана в ГОСТ 13765-86 — «Пружины винтовые цилиндрические сжатия и растяжения из стали круглого сечения. Обозначение параметров, методика определения размеров».
Ссылки:
Модуль сдвига, Кручение, Полярный момент инерции
Расчет пружины выполняется по ГОСТ, см. В.И. Анурьев — «Справочник конструктора машиностроителя» Том 3, стр 199. Издание 2001 г.
Spring (блокнот Mathematica)
xn--h1acbaaqgcqcheicn.xn--p1ai
Формула жесткости пружины, как найти коэффициент через массу и длину
Формула жесткости пружины – едва ли не самый важный момент в теме об этих упругих элементах. Ведь именно жесткость играет очень важную роль в том, благодаря чему эти комплектующие используются так широко.
Сегодня без пружин не обходится практически ни одна отрасль промышленности, они используются в приборо- и станкостроении, сельском хозяйстве, производстве горно-шахтного и железнодорожного оборудования, энергетике, других отраслях. Они верой и правдой служат в самых ответственных и критических местах различных агрегатов, где требуются присущие им характеристики, в первую очередь жесткость пружины, формула которой в общем виде очень проста и знакома детям еще со школы.
Особенности работы
Любая пружина представляет собой упругое изделие, которое в процессе эксплуатации подвергается статическим, динамическим и циклическим нагрузкам. Основная особенность этой детали – она деформируется под приложенным извне усилием, а когда воздействие прекращается – восстанавливает свою первоначальную форму и геометрические размеры. В период деформации происходит накопление энергии, при восстановлении – ее передача.
Именно это свойство возвращаться к исходному виду и принесло широкое распространение этим деталям: они отличные амортизаторы, элементы клапанов, предупреждающие превышение давления, комплектующие для измерительных приборов. В этих и других ситуациях, благодаря умению упруго деформироваться, они выполняют важную работу, поэтому от них требуется высокое качество и надежность.
Виды пружин
Видов этих деталей существует много, самыми распространенными являются пружины растяжения и сжатия.
- Первые из них без нагрузки имеют нулевой шаг, то есть виток соприкасается с витком. В процессе деформации они растягиваются, их длина увеличивается. Прекращение нагрузки сопровождается возвращением в первоначальную форму – опять витком к витку.
- Вторые – наоборот, изначально навиваются с определенным шагом между витками, под нагрузкой сжимаются. Соприкосновение витков является естественным ограничителем для продолжения воздействия.
Изначально именно для пружины растяжения было найдено соотношение массы подвешенного на ней груза и изменения ее геометрического размера, которое и стало основой для формулы жесткости пружины через массу и длину.

Какие еще бывают виды пружин
Зависимость деформации от прилагаемой внешней силы справедлива и для других видов упругих деталей: кручения, изгиба, тарельчатых, других. Не важно, в какой плоскости к ним прилагаются усилия: в той, где расположена осевая линия, или перпендикулярной к ней, производимая деформация пропорциональна усилию, под воздействием которого она произошла.
Основные характеристики
Независимо от вида пружин, особенности их работы, связанные с постоянно деформацией, требуют наличия таких параметров:
- Способности сохранять постоянное значение упругости в течение заданного срока.
- Пластичности.
- Релаксационной стойкости, благодаря которой деформации не становятся необратимыми.
- Прочности, то есть способности выдерживать различные виды нагрузок: статические, динамические, ударные.
Каждая из этих характеристик важна, однако при выборе упругой комплектующей для конкретной работы в первую очередь интересуются ее жесткостью как важным показателем того, подойдет ли она для этого дела и насколько долго будет работать.

Что такое жесткость
Жесткость – это характеристика детали, которая показывает, просто или легко будет ее сжать, насколько большую силу нужно для этого приложить. Оказывается, что возникающая под нагрузкой деформация тем больше, чем больше прилагаемая сила (ведь возникающая в противовес ей сила упругости по модулю имеет то же значение). Потому определить степень деформации можно, зная силу упругости (прилагаемое усилие) и наоборот, зная необходимую деформацию, можно вычислить, какое требуется усилие.
Физические основы понятия жесткость/упругость
Сила, воздействуя на пружину, изменяет ее форму. Например, пружины растяжения/сжатия под влиянием внешнего воздействия укорачиваются или удлиняются. Согласно закону Гука (так называется позволяющая рассчитать коэффициент жесткости пружины формула), сила и деформация между собой пропорциональны в пределах упругости конкретного вещества. В противодействие приложенной извне нагрузке возникает сила, такая же по величине и противоположная по знаку, которая направлена на восстановление исходных размеров детали и ее форму.
Природа этой силы упругости – электромагнитная, возникает она как следствие особого взаимодействии между структурными элементами (молекулами и атомами) материала, из которого изготовлена данная деталь. Таким образом, чем жесткость больше, то есть чем труднее упругую деталь растянуть/сжать, тем больше коэффициент упругости. Этот показатель используется, в частности, при выборе определенного материала для изготовления пружин для использования в различных ситуациях.
Как появился первый вариант формулы
Формула для расчета жесткости пружины, которая получила название закона Гука, была установлена экспериментально. В процессе опытов с подвешенными на упругом элементе грузами разной массы замерялась величина его растяжения. Так и выяснилось, что одна и та же испытуемая деталь под разными нагрузками претерпевает различные деформации. Причем подвешивание определенного количества гирек, одинаковых по массе, показало, что каждая добавленная/снятая гирька увеличивает/уменьшает длину упругого элемента на одинаковую величину.
В итоге этих экспериментов появилась такая формула: kx=mg, где k – некий постоянный для данной пружины коэффициент, x – изменение длины пружины, m – ее масса, а g – ускорение свободного падения (примерное значение – 9,8 м/с²).
Так было открыто свойство жесткости, которое, как и формула для определения коэффициента упругости, находит самое широкое применение в любой отрасли промышленности.
Формула определения жесткости
Изучаемая современными школьниками формула, как найти коэффициент жесткости пружины, представляет собой соотношение силы и величины, показывающей изменение длины пружины в зависимости от величины данного воздействия (или
равной ему по модулю силы упругости). Выглядит эта формула так: F = –kx. Из этой формулы коэффициент жесткости упругого элемента равен отношению силы упругости к изменению его длины. В международной системе единиц физических величин СИ он измеряется в ньютонах на метр (Н/м).
Другой вариант записи формулы: коэффициент Юнга
Деформация растяжения/сжатия в физике также может описываться несколько видоизмененным законом Гука. Формула включает значения относительной деформации (отношения изменения длины к ее начальному значению) и напряжения (отношения силы к площади поперечного сечения детали). Относительная деформация и напряжение по этой формуле пропорциональны, а коэффициент пропорциональности – величина, обратная модулю Юнга.
Модуль Юнга интересен тем, что определяется исключительно свойствами материала, и никак не зависит ни от формы детали, ни от ее размеров.
К примеру, модуль Юнга для ста
ли примерно равен единице с одиннадцатью нулями (единица измерения – Н/кв. м).
Смысл понятия коэффициент жесткости
Коэффициент жесткости – коэффициент пропорциональности из закона Гука. Еще он с полным правом называется коэффициентом упругости.
Фактически он показывает величину силы, которая должна быть приложена к упругому элементу, чтобы изменить его длину на единицу (в используемой системе измерений).
Значение этого параметра зависит от нескольких факторов, которыми характеризуется пружина:
- Материала, используемого при ее изготовлении.
- Формы и конструктивных особенностей.
- Геометрических размеров.
По этому показателю можно сд
елать вывод, насколько изделие устойчиво к воздействию нагрузок, то есть каким будет его сопротивление при приложении внешнего воздействия.
Особенности расчета пружин
Показывающая, как найти жесткость пружины, формула, наверное, одна из наиболее используемых современными конструкторами. Ведь применение эти упругие детали находят практически везде, то есть требуется просчитывать их поведение и выбирать те из них, которые будут идеально справляться с возложенными обязанностями.
Закон Гука весьма упрощенно показывает зависимость деформации упругой детали от прилагаемого усилия, инженерами используются более точные формулы расчета коэффициента жесткости, учитывающие все особенности происходящего процесса.
Например:
- Цилиндрическую витую пружину современная инженерия рассматривает как спираль из проволоки с круглым сечением, а ее деформация под воздействием существующих в системе сил представляется совокупностью элементарных сдвигов.
- При деформации изгиба в качестве деформации рассматривается прогиб стержня, расположенного концами на опорах.
Особенности расчета жесткости соединений пружин
Важный моментом является расчет нескольких упругих элементов, соединенных последовательно или параллельно.
При параллельном расположении нескольких деталей общая жесткость этой системы определяется простой суммой коэффициентов отдельных комплектующих. Как нетрудно заметить, жесткость системы больше, чем отдельной детали.
При последовательном расположении формула более сложная: величина, обратная суммарной жесткости, равна сумме величин, обратных к жесткости каждой комплектующей. В этом варианте сумма меньше слагаемых.
Используя эти зависимости, легко определиться с правильным выбором упругих комплектующих для конкретного случая.
kurskmk.com
Жесткость пружины – коэффициент жесткости пружин
Пружины это элемент упругий, посредством которого механизмам передается вращательное движение, ими комплектуются практически все механизмы. Надежность данного изделия, и ее служба зависят от такого понятия как жесткость пружины. Именно от жесткости зависит насколько надежным будет работа механизма в различных эксплуатационных условиях. «Жесткость пружины» определяется необходимым для ее сжатия усилием. Расправка пружины это несколько иной вопрос, который находится в прямой зависимости от материла, из которого пружина выполнена. Кстати, не всегда высокая жесткость пружины, обуславливает ее долгую службу. Скорее это зависит от механизма, который пружина приводит в действие.
Виды жёсткости:
Пружины, по своим разновидностям делятся на типы. Каждый тип, применяется в определенных механизмах. В целом востребованы пружины спиральные, рессоры, конические, пружины тарельчатые и цилиндрические. «Жесткость пружины» определяет и тот фактор, как она передает механизму собственную деформацию. Так, пружины имеют еще одну важнейшую характеристику, деформационную, которая делит пружины на пружины сжатия, кручения, изгиба и конечно растяжения.
Производятся пружины из проволоки разнообразного сечения. Так, получают пружины, которыми затем комплектуются различные разновидности оборудования, механизмов, автомобилей.
Как высчитать коэффициент жесткости пружины?
При производстве пружин, обязательно принимается в расчеты коэффициент жесткости, который собственно и служит показателем продолжительности службы изделия. «Коэффициент жесткости пружины» вычисляется в соответствии с расчетной формулой.
Так, например, если взять стандартную цилиндрическую витую пружину изготовленную из обычной цилиндрической проволоки, то коэффициент можно высчитать посредством следующей формулы:
В формуле за обозначение G следует принять модуль сдвига. Если пружина медная, то он будет равен примерно 45 ГПа, а если просто стальная, то модуль будет равняться примерно 80 ГПа. Буквой n обозначено число витков, которое имеет пружина, а dF это диаметр намотки. Остается обозначение dD, но оно только обозначает диаметр проволоки, из которой пружина и изготовлена. Собственно, арифметика довольно проста, если только выполнить соответствующие замеры, и вместо видимых букв и значений подставить цифровые эквиваленты.
«Коэффициент жесткости пружины» легко высчитать и лично, руководствуясь выше обозначенной формулой. Всегда полезно знать этот коэффициент, если пришла необходимость, например, сменить пружины в собственном авто, или в других механизмах.
Вернуться в раздел:
Статьи о пружинах
prughin.ru

