Пружины формула: Что такое жесткость пружины и как ее рассчитать
alexxlab | 14.04.1987 | 0 | Разное
3.2. Формулы расчета пружин сжатия
Пружина сжатия – это винтовая пружина с фиксированным зазором между рабочими витками способными выдержать работу внешних сил противодействия, которые рождаются в оси пружины.
Размеры
d | диаметр проволоки [мм, д] |
D | средний диаметр пружины [мм, д] |
D1 | наружный диаметр пружины [мм, д] |
D2 | внутренний диаметр пружины [мм, д] |
H | рабочая деформация [мм, д] |
t | шаг активных витков в ненагруженном состоянии [мм, д] |
a | расстояние между активными витками в свободном состоянии [мм, дюйм] |
sx | деформация пружины [мм, д] |
Lx | длина пружины [мм, д] |
Fx | рабочая сила, действующая на пружину [Н, фунт] |
W8 | энергия деформации [Дж, фут фунт] |
x | индекс, обозначающий состояние пружины |
Навивка
Вправо (стандарт)
-
Влево (должна отображаться соответствующая надпись)
Состояния
Свободное: пружина не нагружена (индекс 0)
Предварительная нагрузка: пружина с минимальной рабочей нагрузкой (индекс 1)
Полная нагрузка: пружина с максимальной рабочей нагрузкой (индекс 8)
Предел: пружина вдавлена до касания витков (индекс 9).

Расчетные формулы для метрических единиц
Общие формулы расчета
Коэффициент использования материала uS
Этот
коэффициент является отношением
напряжения при кручении полностью
нагруженной пружины к допустимому
напряжению при кручении, например
uS8 / A.
Чем больше величина коэффициента, тем
меньше материала уходит на изготовление
пружины и тем меньшими получаются ее
размеры и требуемое посадочное место;
однако, при этом становится хуже
эксплуатационная стабильность пружины.
Следовательно, коэффициент использования
материала обратно пропорционален
коэффициенту долговечности. Рекомендуемый
диапазон значений коэффициента
использования материала для обычных
рабочих условий: u
Запас прочности при пределе усталости kf
Этот
коэффициент используется при расчете
пружин с динамической нагрузкой (с
циклической усталостной нагрузкой при
сроке службы N > 105 рабочих
циклов). Он определяется отношением
предела выносливости пружины к напряжению
при кручении материала полностью
нагруженной пружины: kfe / 8.
Рекомендуемый диапазон значений запаса
прочности при предельной усталости
kf для стандартных рабочих
условий – от 1,1 до 1,5. Более высокие
значения kf обычно используются для
пружин, применяемых в условиях сильной
коррозии, высоких температур или ударной
нагрузки. Агрессивная среда оказывает
серьезное влияние на усталостную
прочность пружины, так как в результате
этого влияния допустимая нагрузка
пружины может снизиться до одной пятой,
в зависимости от материала и типа
агрессивной среды.
Он определяется отношением
предела выносливости пружины к напряжению
при кручении материала полностью
нагруженной пружины: kfe / 8.
Рекомендуемый диапазон значений запаса
прочности при предельной усталости
kf для стандартных рабочих
условий – от 1,1 до 1,5. Более высокие
значения kf обычно используются для
пружин, применяемых в условиях сильной
коррозии, высоких температур или ударной
нагрузки. Агрессивная среда оказывает
серьезное влияние на усталостную
прочность пружины, так как в результате
этого влияния допустимая нагрузка
пружины может снизиться до одной пятой,
в зависимости от материала и типа
агрессивной среды.
Наружный диаметр пружины
D1 = D + d [мм]
Где:
D | средний диаметр пружины [мм] | |
d | диаметр проволоки [мм] |
Внутренний диаметр пружины
D2 = D – d [мм]
Где:
D | средний диаметр пружины [мм] | |
d | диаметр проволоки [мм] |
Рабочая деформация
H = L1 – L8 = s8 – s1 [мм]
Где:
L8 | длина полностью нагруженной пружины [мм] | |
L1 | длина предварительно нагруженной пружины [мм] | |
s8 | деформация полностью нагруженной пружины [мм] | |
s1 | деформация предварительно нагруженной пружины [мм] |
Индекс пружины
c = D/d [-]
Где:
D | средний диаметр пружины [мм] | |
d | диаметр проволоки [мм] |
Поправочный коэффициент Валя
Где:
c | индекс пружины [-] | |
d | диаметр проволоки [мм] |
Общая сила, действующая в пружине
Где:
d | диаметр проволоки [мм] | |
| обобщенное напряжение материала пружины при кручении [МПа] | |
D | средний диаметр пружины [мм] | |
Kw | поправочный коэффициент Валя [-] | |
G | модуль упругости материала пружины [МПа] | |
s | обобщенная деформация пружины [мм] | |
n | количество активных витков [-] | |
F0 | начальное растяжение пружины [Н] |
Жесткость пружины
Где:
d | диаметр проволоки [мм] | |
F8 | рабочее усилие в полностью нагруженной пружине [МПа] | |
D | средний диаметр пружины [мм] | |
H | рабочая деформация [мм] | |
G | модуль упругости материала пружины [МПа] | |
n | количество активных витков [-] | |
F1 | рабочее усилие в минимально нагруженной пружине [МПа] |
Средний диаметр пружины
Где:
d | диаметр проволоки [мм] | |
k | жесткость пружины [Н/дюйм] | |
G | модуль упругости материала пружины [МПа] | |
n | количество активных витков [-] |
Отклонение пружины в большинстве случаев
s = F / k [мм]
Где:
F | Общая сила, действующая в пружине [Н] | |
k | жесткость пружины [Н/дюйм] |
Длина пружины в свободном состоянии
L0 = L1 + s1 = L8 + s8 [мм]
Где:
L8 | длина полностью нагруженной пружины [мм] | |
L1 | длина предварительно нагруженной пружины [мм] | |
s8 | деформация полностью нагруженной пружины [мм] | |
s1 | деформация предварительно нагруженной пружины [мм] |
Расчет конструкции пружины
При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для указанной
нагрузки, материала и сборочных размеров
или диаметра пружины. Шаг резьбы пружины
в свободном состоянии с рекомендуемыми
диаметрами проволоки должен лежать в
диапазоне 0,3 D ≤ t ≤ 0,6 D [мм].
Шаг резьбы пружины
в свободном состоянии с рекомендуемыми
диаметрами проволоки должен лежать в
диапазоне 0,3 D ≤ t ≤ 0,6 D [мм].
Конструкция пружины определяется с учетом условия прочности 8≤ us A и рекомендуемых диапазонов некоторых геометрических параметров пружины:
L8 ≤ LminF и D ≤ L0≤ 10 D и L0≤ 31,5 д. и 4 ≤ D/d ≤ 16 и n≤ 2 и 12 d ≤ t < D
Где:
D | средний диаметр пружины [мм] | |
d | диаметр проволоки [мм] | |
шаг активных витков в ненагруженном состоянии | шаг активных витков в ненагруженном состоянии [мм] | |
8 | напряжение при кручении материала пружины полностью нагруженной пружины [МПа] | |
A | допустимое напряжение материала пружины при кручении [МПа] | |
us | коэффициент использования материала [-] | |
L8 | длина полностью нагруженной пружины [мм] | |
LminF | предельная длина пружины при испытании [мм] | |
n | количество активных витков [-] |
Если
в спецификации указаны условия
безопасности при изгибе и условия
проверки для усталостной нагрузки, они
учитываются при проектировании пружины.
В следующем списке приведены процедуры различных типов проектирования пружины.
Процедуры разработки
Потенциальная энергия пружины и кинетическая: что это, формула
Во многих механизмах используется потенциальная и кинетическая энергия пружины. Их используют для выполнения различных действий. В отдельных узлах они фиксируют детали в определенном положении, не позволяя смещать в какую-либо сторону (барабан револьвера относительно корпуса). Другие пружинные системы возвращают исполнительный механизм в исходное положение (курок ручного огнестрельного оружия). Есть устройства, где узлы с гибкими свойствами совершают перемещения в устойчивое положение (механические стабилизаторы).
Работа связана с изменением геометрических параметров упругого тела. Прилагая нагрузку, заставляют эластичную деталь сжиматься (растягиваться или изгибаться). При этом наблюдается запасание энергии. Возвратное действие сопровождается набором скорости. Попутно возрастает кинетическая энергия.
Попутно возрастает кинетическая энергия.
- Потенциальная энергия пружины
- Закон сохранения механической энергии
- Кинетическая энергия
- Использование энергии пружины на практике
Потенциальная энергия пружины
Рассматривая в качестве накопителя энергии пружину, следует отметить ее отличительные свойства от иных физических тел, которые могут накапливать энергетический потенциал. Традиционно понимается следующее: для накопления потенциала для последующего движения необходимо совершение движения в силовом поле:
Еп = F ⋅ l, Дж (Н·м),
где Еп– потенциальная энергия положения, Дж;
F – сила, действующая на тело, Н;
l – величина перемещения в силовом поле, м.
Энергия (работа) измеряются в Джоулях. Величина представляет произведение силы (Н) на величину перемещения (м).
Если рассматривать условие в поле тяготения, то величина силы находится произведением ускорения свободного падения на массу.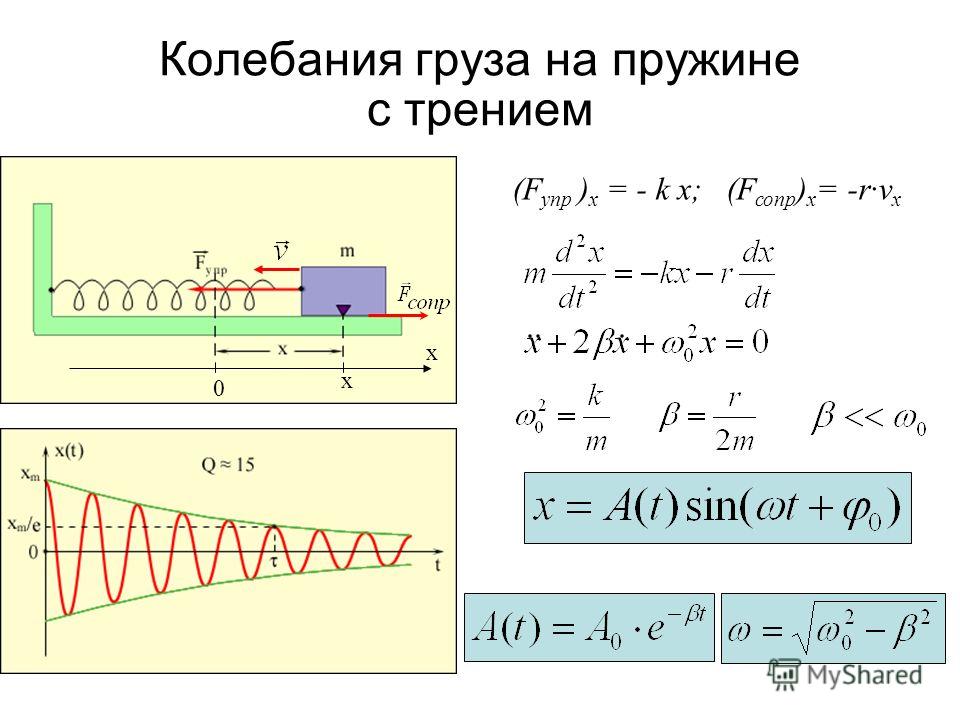 Здесь сила веса находится с учетом g:
Здесь сила веса находится с учетом g:
Еп = G ⋅ h = m ⋅ g ⋅ h, Дж
здесь G – вес тела, Н;
m – масса тела, кг;
g – ускорение свободного падения. На Земле эта величина составляет g = 9,81 м/с².
Если расстраивается пружина, то силу F нужно определять, как величину, пропорциональную перемещению:
F = K ⋅ x, Н,
где k – модуль упругости, Н/м;
х – перемещение при сжатии, м.
Величина сжатия может изменяться по величине, поэтому математики предложили анализировать подобные явления с помощью бесконечно малых величин (dx) .
При наличии непостоянной силы, зависящей от перемещения, дифференциальное уравнение запишется в виде:
dEп = k ⋅ x ⋅ dx
здесь dEп – элементарная работа, Дж;
dx – элементарное приращение сжатия, Н.
Интегральное уравнение на конечном перемещении запишется в виде. Ниже вывод формулы:
Ниже вывод формулы:
Пределами интегрирования является интервал от 0 до х. Деформированная пружина приобретает запас по энергетическим показателям
Окончательно формула для расчета величины потенциальной энергии сжатия (растягивания или изгиба) пружины запишется формулой:
Закон сохранения механической энергии
Закон сохранения энергии существует независимо от желания наблюдателя. Все физические законы имеют статистический характер: существуют только подтверждения их выполнения, нет ни одного адекватно выполненного опыта, при котором наблюдается нарушение этой закономерности. Природные явления только подтверждают сохранность работы и энергозатрат, затраченных на ее выполнение.
На основании изложенного сформулировано положение:
где Ек – кинетическая энергия, Дж.
Рассматривая перемещения тела, наблюдаются изменения потенциальной и кинетической энергий. При этом сумма значений остается постоянной.
Проще всего проследить за изменениями между разными видами энергетических показателей при рассмотрении движения маятника.
Из крайнего положения (шарик на нити отклонился в одну из сторон, Еп = max) тело движется под действием силы тяжести. При этом снижается запасенная энергия. Движение сопровождается увеличением скорости. Поэтому нарастают показатели динамического перемещения Ек.
В нижней точке не остается никаких запасенных эффектов от положения шарика. Он опустился да минимума. Теперь Ек =max.
Поучается, при совершении гармонических колебаний маятник поочередно накапливает то один, то другой вид энергии. Механические превращения из одного вида в другой налицо.
Кинетическая энергия
Движущееся тело характеризуется скалярной величиной (масса) и векторная величина (скорость). Если рассматривать реальное перемещение в пространстве, то можно записать уравнение для определения кинетической энергии:
здесь v – скорость движения тела, м/с.
Использование кинетического преобразования можно наблюдать при колке орехов.
Приподняв камень повыше, далекие предки создавали необходимый потенциал для тяжелого тела.
Приподняв камень на максимальную высоту, разрешают ему свободно падать.
Двигаясь с высоты h, он набирает скорость
Поэтому в конце падения будет получена кинетическая энергия
Рассматривая входящие величины, можно увидеть, как происходит преобразование величин. В конце получается расчетная формула для определения потенциальной энергии.
Даже на уровне вывода зависимостей можно наблюдать выполнение закона сохранения энергии твердого тела.
Использование энергии пружины на практике
Явление преобразования потенциальной энергии пружины в кинетическую используется при стрельбе из лука.
Натягивая тетиву, стреле сообщается потенциал для последующего движения. Чем жестче лук, а также ход при натягивании тетивы, тем выше будет запасенная энергия. Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.
Распрямляясь дуги этого оружия, придадут метательному снаряду значительную скорость.
В результате стрела полетит в цель. Ее поражающие свойства определятся величиной кинетической энергии (mv²/2).
Для гашения колебаний, возникающих при движении автомобиля, используют амортизаторы. Основным элементом, воспринимающим вертикальную нагрузку, являются пружины. Они сжимаются, а потом возвращают энергию кузову. В результате заметно снижается ударное воздействие. Дополнительно устанавливается гидроцилиндр, он снижает скорость обратного движения.
Рассмотренные явления используют при проектировании механизмов и устройств для автоматизации процессов в разных отраслях промышленности.
Видео: закон Гука и энергия упругой деформации.
Republished by Blog Post Promoter
27 важных факторов, связанных с ним
Определение константы пружины:Жесткость пружины – это мера жесткости пружины. Пружины, имеющие более высокую жесткость, более трудно растянуть. пружины – эластичные материалы. при приложении внешних сил пружина деформируется и после снятия силы возвращается в исходное положение. Деформация пружины – это линейная упругая деформация. Линейный – это кривая зависимости между силой и смещением.
Пружины, имеющие более высокую жесткость, более трудно растянуть. пружины – эластичные материалы. при приложении внешних сил пружина деформируется и после снятия силы возвращается в исходное положение. Деформация пружины – это линейная упругая деформация. Линейный – это кривая зависимости между силой и смещением.
F = -Kx
Где,
F = приложенная сила,
K = жесткость пружины
x = смещение из-за приложенной нагрузки из нормального положения.
Кредит изображения: Эндрю Дрессел, Жесткость винтовой пружины, CC BY-SA 4.0Единицы жесткости пружины:жесткость пружины, представленная как K, и ее единица измерения – Н / м.
Как найти постоянную пружины?Уравнение жесткости пружины:Постоянная пружины определяется в соответствии с законом Гука, изложенным ниже:
Приложенная к пружинам сила прямо пропорциональна смещению пружины из положения равновесия. -2]
-2]
Пружина постоянной силы – это пружина, которая не подчиняется закону Гука. Пружина имеет силу, которую она проявляет во всем диапазоне движения, постоянна и никоим образом не меняется. Как правило, эти пружины сконструированы в виде скрученных пружин, так что пружина расслабляется, когда она полностью свернута, и после раскручивания имеет место восстанавливающая сила, поскольку геометрия остается постоянной при раскручивании пружины. Пружина постоянного усилия оказывает постоянное усилие для раскручивания, так как изменение радиуса кривизны является постоянным.
Применение постоянной силы пружины:- Щеточные пружины для двигателей
- Пружины двигателя постоянного усилия
- Пружины противовеса для окна
- Пружины возврата каретки пишущих машинок
- Таймеры
- Кабельные ретракторы
- Кинокамеры
- Пружины растяжения
Постоянное усилие пружины не всегда дает постоянное усилие. Первоначально он имеет конечное значение, и после того, как пружина отклоняется в 1.25 раза от ее диаметра, она достигает полной нагрузки и сохраняет постоянное усилие в пружине, несмотря на деформацию. Эти пружины сделаны из металлических полос, а не из проволоки. Пружины изготовлены из таких материалов, как нержавеющая сталь, высокоуглеродистая сталь и т. Д. Пружины создают напряжение в линейном направлении.
Первоначально он имеет конечное значение, и после того, как пружина отклоняется в 1.25 раза от ее диаметра, она достигает полной нагрузки и сохраняет постоянное усилие в пружине, несмотря на деформацию. Эти пружины сделаны из металлических полос, а не из проволоки. Пружины изготовлены из таких материалов, как нержавеющая сталь, высокоуглеродистая сталь и т. Д. Пружины создают напряжение в линейном направлении.
Работоспособность, элементы коррозии, температура влияет на усталость таких пружин. Они, скорее всего, будут иметь срок службы от 2500 циклов до более одного миллиона в зависимости от размера и приложенной нагрузки.
Примеры констант пружиныПружинность резинки:Резиновая лента действует как пружина с некоторыми ограничениями. Когда кривая закона Гука строится для резиновых лент, график получается не совсем линейным. Но если мы растянем ленту медленно, она может следовать закону Гука и иметь значение жесткости пружины. Резинка может растягивать только предел эластичности,
также зависит от размера, длины и качества.
Значение постоянной пружины определяется по закону Гука. Согласно закону Гука, когда пружина растягивается, прилагаемая сила прямо пропорциональна увеличению длины по сравнению с исходным положением.
Как определить жесткость пружины?F = -Kx
К = -F / x
Пружинные постоянные материалов:Постоянная пружины для
Сталь = 21000 кг / м3Постоянная пружины для
Медь = 12000 кг / м3Как найти жесткость пружины по графику?График постоянной пружины:Изображение кредита:Колоссос, Federkennlinie, CC BY-SA 3.0Может ли жесткость пружины быть отрицательной?Это не может быть отрицательным.
Формула жесткости пружины с массой:T = [латекс] 2 \ pi \ sqrt {\ frac {k} {m}} [/ латекс]
где,
T = период весны
m = масса
k = жесткость пружины
Эффективная жесткость пружины:Параллельно: когда две безмассовые пружины, подчиняющиеся закону Гука и соединенные тонкими вертикальными стержнями на концах пружин, соединение двух концов пружин называется параллельным соединением.
Направление постоянной силы перпендикулярно направлению силы.
Постоянная пружины K записывается как,
К = К1 + К2
Серия:
Когда пружины соединены друг с другом последовательно, так что общая комбинация растяжения является суммой общего растяжения и постоянной комбинации пружины всех пружин.
Сила прилагается к концу концевой пружины. Направление силы в обратном направлении при сжатии пружин.
Закон Гука,
F1 = k1x1
F2 = k2x2
х 1+ х 2 = [латекс] (\ гидроразрыва {F1} {k1} + \ гидроразрыва {F2} {k2}) [/латекс]
Эквивалентная жесткость пружины:K = [латекс](\frac{1}{k1}+\frac{1}{k2})[/latex]
Постоянная крутильной пружины:Торсионная пружина закручивается вдоль оси пружины, при закручивании она передает крутящий момент в противоположном направлении и пропорционален углу закручивания.
Торсионный стержень – это прямой стержень, который, подвергаясь скручиванию, создает напряжение сдвига вдоль оси крутящего момента, приложенного к его концу. 2
2
Торсионные весы – крутильный маятник. Он работает как простой маятник.
Чтобы измерить силу, сначала нужно узнать постоянную пружины. Если усилие мало, трудно измерить постоянную щадящего режима. Необходимо измерить период резонансной вибрации весов.
Частота зависит от момента инерции и эластичности материала. Итак, частота выбирается соответственно.
После расчета инерции определяется постоянная пружины,
F = Kδ / L
Гармонический осциллятор:Гармонический осциллятор – это простой гармонический осциллятор, когда он подвергается деформации от исходного положения равновесия, испытывая восстанавливающую силу F, прямо пропорциональную смещению x.
Математически записывается следующим образом:
F = -Kx
Коэффициент крутильной пружины:Жесткость пружины кручения – это сила, с которой пружина перемещается на 360 градусов. Это может быть дополнительно рассчитано путем деления силы на 360 градусов.
Это может быть дополнительно рассчитано путем деления силы на 360 градусов.
- Диаметр проволоки: Диаметр проволоки пружины.
- Диаметр витка: диаметры витков в зависимости от жесткости пружины.
- Свободная длина: длина пружины от положения равновесия в состоянии покоя.
- Количество активных витков: количество витков, которые сжимаются или растягиваются.
- Материал: Материал пружины, из которой изготовлена.
Пружина постоянного крутящего момента – это тип пружины, которая представляет собой напряженную пружину постоянной силы, перемещающуюся между двумя золотниками. После высвобождения сжатой пружины крутящий момент рассчитывается от выходного золотника, когда пружина возвращается в исходное положение равновесия в накопительном золотнике.
k = k” δ‘/δ,
K Зависит от
Минимум = 0.9 Н / м
Максимум = 4.8 Н / м
Постоянная пружины зависит от числа витков n.
Идеальная жесткость пружины:Жесткость пружины – это мера жесткости пружин. Чем больше значение k, тем жестче пружина и ее трудно растянуть. Любая пружина, подчиняющаяся уравнению закона Гука, называется идеальная весна.
Пружина постоянного усилия:Пружина постоянной силы устанавливается на барабан, оборачивая его вокруг барабана. Пружина должна быть плотно обернута. Затем свободный конец пружины прилагается к силе нагрузки, например, при использовании противовеса или наоборот.
- Диаметр барабана должен быть больше внутреннего диаметра.
- Диапазон: 10-20% диаметра барабана> Внутренний диаметр.
- На барабане при крайнем растяжении должна быть полуторная пружина.

- Полоса будет нестабильной на больших расширениях, поэтому рекомендуется использовать ее меньшего размера.
- Диаметр шкива должен быть больше исходного диаметра.
Жесткость пружины важна, поскольку она показывает основные свойства материала. Это дает точное значение силы, необходимой для деформации любой пружины из любого материала. Более высокая постоянная пружины показывает, что материал более жесткий, а более низкая постоянная пружины показывает, что материал менее жесткий.
Может ли постоянная пружины измениться?Да. жесткость пружины может изменяться в зависимости от приложенной силы и растяжения материала.
Может ли жесткость пружины равняться 0?Нет. Жесткость пружины не может быть равна нулю. Если он равен нулю, жесткость равна нулю.
Может ли жесткость пружины иметь отрицательное значение?Нет. Пружинная константа всегда имеет положительное значение.
Пружинная константа всегда имеет положительное значение.
Когда отношение длины к этой площади пружины равно единице, то модуль Юнга и постоянное значение пружины будут равны.
Жесткость пружины представлена как, K = -F / x,
Вышеупомянутое уравнение показывает взаимосвязь между постоянной пружиной и растяжением пружины при одинаковой приложенной силе.
Почему пружина разрезается пополам, меняется ее жесткость?Это обратно пропорционально растяжению пружины. когда пружина разрезана пополам, длина пружины уменьшается, следовательно, постоянная пружины увеличивается вдвое.
Разве третий закон Ньютона не работает с пружиной?Ответ: нет
Проблемы пружинной постоянной:Q1) Пружина растягивается на 20 см, и к ней добавляется нагрузка 5 кг. Найдите постоянную пружины.Данный:
Масса m = 5кг. -2)
-2)
= 5 Н / м
Постоянная пружины 5 Н / м.
Q2) К пружине с жесткостью пружины 25 кН / м приложено усилие 15 кН. Определите смещение пружины.Данный:
Приложенная сила = 2.5 кН
Жесткость пружины = 15 кН / м
Решение:
1. узнать смещение пружины
Пружина будет прилагать равную и противоположную силу -2.5 кН.
F = -Kx
X = -F / K
= – 2.5 / 15
= 0.167m
Следовательно, пружина смещена на 16.67 см.
Q3) Пружина с силовой постоянной 5.2 Н / м имеет длину в расслабленном состоянии 2.45 м и длину перпендикуляра пружины 3.57 м. Когда груз прикреплен к концу пружины и оставлен в покое. Какая упругая потенциальная энергия хранится в пружине?Решение:
Данный:
Постоянная силы = 2.45 м
x = 2.45 м
L = 3.57 м
Пружина постоянной силы:
F = -Kx
Работа выполнена за счет растяжения пружины = упругая потенциальная энергия пружины. -2
-2
= -1N
Сила пружины в противоположном направлении
Следовательно, сила пружины = 1Н.
Объект весом 5.13 кг, помещенный на верхнюю часть пружины, сжимает ее на 25 м. Какова постоянная силы пружины. Как высоко поднимется этот объект, когда пружина высвободит свою энергию.
Для получения дополнительных статей по теме нажмите сюда
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.
 5 Механические колебания и волны
5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.
 2 Волновая оптика
2 Волновая оптика - 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Формула постоянной пружины – GeeksforGeeks
Простое гармоническое движение, или SHM, представляет собой увлекательный тип движения. Он обычно используется в колебательном движении объектов. SHM обычно встречается в источниках. Пружинам присущи «пружинные константы», которые определяют их жесткость. Закон Гука — хорошо известный закон, который объясняет SHM и дает формулу для приложенной силы с использованием жесткости пружины.
SHM обычно встречается в источниках. Пружинам присущи «пружинные константы», которые определяют их жесткость. Закон Гука — хорошо известный закон, который объясняет SHM и дает формулу для приложенной силы с использованием жесткости пружины.
Закон Гука
Согласно закону Гука сила, необходимая для сжатия или растяжения пружины, пропорциональна растянутой длине. Когда пружина растягивается, третий закон движения Ньютона гласит, что она возвращается с возвращающей силой. Эта восстанавливающая сила подчиняется закону Гука, который связывает силу пружины с постоянной силой пружины.
Усилие пружины = -(Постоянная пружины) × (Перемещение)
F = -KX
Знак минус указывает, что сила реакции направлена в противоположном направлении.
Где,
F: Возвращающая сила пружины, направленная к равновесию.
K: жесткость пружины в Нм -1 .
X: Смещение пружины от положения равновесия.
Жесткость пружины (K)
Константа пружины теперь определяется как сила, необходимая на единицу растяжения пружины. Зная жесткость пружины, можно легко рассчитать, какое усилие требуется для деформации пружины.
Из закона Гука,
F = -KX
K = -F/ X ⇢ (1)
Уравнение (1) является формулой для жесткости пружины и измеряется в Н/м (ньютон на метр). .
Формула расчета постоянных размеров пружины
Как известно,
F = -KX
Следовательно, K = -F/ X
Размерность F = [MLT -2 ]
Размерность X = [L]
Следовательно, размерность K = [MLT -2 ]/[L ] = [MT −2 ].
Потенциальная энергия пружины (PE)
Энергия, запасенная в сжимаемом или растягиваемом объекте, называется потенциальной энергией пружины. ее также называют упругой потенциальной энергией. Она равна произведению силы на пройденное расстояние.
Известно, что Потенциальная энергия = сила × смещение
А также сила пружины равна постоянной пружины × смещению. Итак,
Ч.Э. = 1/2 KX 2 .⇢ (2)
Приведенное выше уравнение представляет собой формулу потенциальной энергии пружины.
Ограничения закона Гука
Закон Гука имеет ограничение, заключающееся в том, что он применим только при пределе упругости любого материала, что означает, что материал должен быть абсолютно эластичным, чтобы подчиняться закону Гука. Закон Гука по существу нарушается за пределом эластичности.
Применение закона Гука
- Из-за эластичности пружин закон Гука чаще всего применяется весной.
- Они используются не только в области машиностроения, но и в области медицины.
- Он используется в легких, коже, пружинных матрасах, трамплинах и автомобильных подвесках.
- Это фундаментальный принцип, лежащий в основе манометра, пружинной шкалы и часового баланса.

- Он также является основой для сейсмологии, акустики и молекулярной механики.
Недостатки применения закона Гука
Ниже перечислены недостатки закона Гука:
- Закон Гука применим только в упругой области, после чего он не работает.
- Закон Гука дает точные результаты только для твердых тел с малыми силами и деформациями.
- Закон Гука не является общим правилом.
Примеры задач
Вопрос 1: Каково определение константы Spring?
Ответ:
При растяжении пружины прилагаемая сила пропорциональна увеличению длины от равновесной длины в соответствии с законом Гука. Жесткость пружины можно рассчитать по следующей формуле: k = -F/x, где k — жесткость пружины. F обозначает силу, а x обозначает изменение длины пружины.
Вопрос 2: Как длина влияет на жесткость пружины?
Ответ:
Предположим, что имеется пружина 6 см с жесткостью k.
Что произойдет, если пружину разделить на две равные части? Одна из этих более коротких пружин будет иметь новую жесткость 2k. Как правило, при условии использования пружины из определенного материала и ее толщины жесткость пружины обратно пропорциональна длине пружины.
Итак, предположим, что в предыдущем примере пружину разрезали точно пополам, в результате чего получились две более короткие пружины, каждая по 3 см в длину. Для меньших пружин будет использоваться жесткость пружины, в два раза превышающая исходную. Это происходит потому, что она обратно пропорциональна как жесткости пружины, так и ее длине.
Вопрос 3: Пружина растягивается с силой 2 Н на 4 м. Определить его жесткость.
Решение:
Дано,
Сила, F = 2 Н и
Перемещение, X = 4 м.
Мы знаем, что
Постоянная пружины, K = – F/X
K = – 2N / 4m
K = – 0,5 Нм -1 .
Вопрос 4: К струне приложена сила 10 Н, и она натянулась. если жесткость пружины 4 Нм -1 затем рассчитайте смещение струны.
если жесткость пружины 4 Нм -1 затем рассчитайте смещение струны.
Решение:
Дано,
Сила, F = 10 N и
Постоянная пружина, K = 4 нм -1
Мы знаем, что F = -Kx
x (дисплейное)) = – F/K
X = – ( 10 Н / 4 Нм -1 )
X = – 2,5 м.
Вопрос 5: Какая сила требуется, чтобы растянуть 3-метровую пружину до 5 метров, если жесткость пружины равна 0,1 Нм -1 .
Решение:
Дано,
Длина пружины = 3 м
Постоянная пружины, K = 0,1 Нм 3 = 2 м
Требуемое усилие F = -KX
F = – (0,1 Нм -1 × 2 м)
F = – 0,2 Н.
Формула пружин сжатия – качественная пружина, доступные цены
Переключить навигацию
Поиск
(951) 276-2777Contact US
Язык
Меню
Установки
. Формулы пружин сжатия, которые вы сейчас увидите, основаны на многолетних исследованиях сотрудников Acxess Spring. Это то, что делает наш калькулятор пружин сжатия, Spring Creator, таким надежным инструментом проектирования пружин, в котором вы можете рассчитать постоянную k вашей пружины сжатия, рабочие нагрузки и даже некоторые измерения, такие как длина провода, необходимая для изготовления пружины. тысячи пружин или вес от одной до тысячи пружин. В нашем весеннем калькуляторе есть все. Вы даже можете одним нажатием кнопки создать проект пружины сжатия в реальном времени и отправить его себе или коллеге по электронной почте. Для расчета сплошной высоты (Lsolid) необходимо добавить еще один провод к общему количеству витков (N), а затем умножить результат на диаметр провода (d). Сплошная высота = Диаметр проволоки x (Общее количество витков + 1) (если у вас есть заземляющие концы) Расчет диаметра пружины сжатия очень прост. Просто надо уметь различать, что есть что. Для расчета внутреннего диаметра ( D внутренний) необходимо диаметр проволоки (d) умножить на два и отнять результат от наружного диаметра ( D наружный). Чтобы вычислить внешний диаметр, вы делаете наоборот; умножьте диаметр проволоки на два, а затем прибавьте результат к внутреннему диаметру. Inner Diameter = Outer Diameter – 2 (Wire Diameter) Outer Diameter = Inner Diameter + 2 (Wire Diameter) Средний диаметр = Внешний диаметр – диаметр проволоки Индекс пружины вашей пружины сжатия определяет натяжение ваших витков, а также сложность изготовления вашей пружины. Индекс = Средний диаметр ÷ Диаметр проволоки  определенные параметры пружины сжатия. Эти формулы были разработаны и подтверждены, что позволило рассчитать конструкцию пружины сжатия.
определенные параметры пружины сжатия. Эти формулы были разработаны и подтверждены, что позволило рассчитать конструкцию пружины сжатия. Получите наше новое бесплатное приложение Spring Creator для устройств Android и iOS
Формулы сплошной высоты
 В случае, если ваша пружина имеет шлифованные концы, вам нужно будет только умножить толщину проволоки на общее количество витков, так как шлифовка концов приводит к тому, что последний виток будет иметь только половину диаметра.
В случае, если ваша пружина имеет шлифованные концы, вам нужно будет только умножить толщину проволоки на общее количество витков, так как шлифовка концов приводит к тому, что последний виток будет иметь только половину диаметра.
Lsolid = d(N+1)
Сплошная высота = 9027 Диаметры витков x
L сплошная = dN Диаграмма сплошной высоты
Формула диаметра пружины
 Средний диаметр (D) находится между этими двумя значениями, поскольку это диаметр катушки от центра проволоки до центра проволоки, поэтому в этом случае вы можете либо вычесть один диаметр проволоки из внешнего диаметра, либо добавить один диаметр проволоки к внутреннему диаметру.
Средний диаметр (D) находится между этими двумя значениями, поскольку это диаметр катушки от центра проволоки до центра проволоки, поэтому в этом случае вы можете либо вычесть один диаметр проволоки из внешнего диаметра, либо добавить один диаметр проволоки к внутреннему диаметру.
D inner = D outer – 2d
D внешний = D внутренний + 2d
D – внешний d 40275
ИЛИ
Средний диаметр = Внутренний диаметр + Диаметр проволоки
D = D внутренний + d Индекс пружины Формула
 Чтобы рассчитать индекс пружины, вы должны разделить средний диаметр (D) на диаметр проволоки (d).
Чтобы рассчитать индекс пружины, вы должны разделить средний диаметр (D) на диаметр проволоки (d).
I = D ÷ D Большая и малая индикальная длина. сколько материала необходимо для изготовления пружин. Во-первых, вы вычисляете длину проволоки одной катушки (cL), умножая средний диаметр на число пи (3,14 или π). Затем, чтобы рассчитать общую длину проволоки пружины сжатия (tL), необходимо умножить длину проволоки одного витка (cL) на общее количество витков (N).
Coil Wire Length = Mean Diameter x Pi
cL = Dπ
Total Wire Length = Coil Wire Length x Total Coils
tL = cL x N
Пример расчета длины троса
Формулы нагрузки и хода
Приведенные ниже формулы для пружины сжатия нагрузки и хода предназначены для расчета рабочих нагрузок. Эти формулы очень полезны, чтобы узнать, выдержит ли пружина требуемую нагрузку и пройденное расстояние. Чтобы рассчитать расстояние, пройденное вашей пружиной, вы должны разделить нагрузку на жесткость пружины. С другой стороны, чтобы рассчитать рабочие нагрузки, необходимо умножить пройденное расстояние на жесткость пружины.
Эти формулы очень полезны, чтобы узнать, выдержит ли пружина требуемую нагрузку и пройденное расстояние. Чтобы рассчитать расстояние, пройденное вашей пружиной, вы должны разделить нагрузку на жесткость пружины. С другой стороны, чтобы рассчитать рабочие нагрузки, необходимо умножить пройденное расстояние на жесткость пружины.
Travel = Load ÷ СТАВИТЬ
T = L ÷ K
Загрузка = Tail
Диаграмма рабочих нагрузок и прогиба
Как рассчитать усилие пружины
Обновлено 22 декабря 2019 г.
Кевин Бек
маленький вид внутри нижней части шариковой ручки, «кликабельной» — вы, возможно, заметили, что у него есть определенные общие свойства, которые отличают его от большинства других объектов.
Один из них заключается в том, что он имеет тенденцию возвращаться к тому же размеру после того, как вы его растянете или сожмете. Другое, возможно, менее очевидное свойство состоит в том, что чем больше вы растягиваете или сжимаете его, тем труднее его растягивать или сжимать еще сильнее.
Другое, возможно, менее очевидное свойство состоит в том, что чем больше вы растягиваете или сжимаете его, тем труднее его растягивать или сжимать еще сильнее.
Эти свойства полностью применимы к идеальной пружине и в некоторой степени к пружинам, используемым для самых разных целей в реальном мире. Большинство других объектов вообще не ведут себя таким образом; те, которые полностью сопротивляются деформации, обычно ломаются, когда приложенная сила становится достаточно большой, в то время как другие могут растягиваться или сжиматься, но не возвращаются полностью или вообще к своей первоначальной форме и размеру.
Необычные свойства пружин в сочетании с новой на тот момент концепцией силы и движения, выдвинутой главным образом Галилео Галилеем и Исааком Ньютоном, привели к открытию закона Гука — простой, но изящной зависимости, применимой в бесчисленных инженерных и промышленных областях. процессов в современном мире.
Важное открытие: закон Гука
Пружина — это упругий объект, что означает, что он обладает различными характеристиками, описанными в предыдущем разделе. Это означает, что она сопротивляется деформации (растяжение и сжатие являются двумя типами деформации), а также возвращается к своим первоначальным размерам при условии, что сила остается в пределах упругости пружины.
Это означает, что она сопротивляется деформации (растяжение и сжатие являются двумя типами деформации), а также возвращается к своим первоначальным размерам при условии, что сила остается в пределах упругости пружины.
Перед публикацией законов Ньютона Роберт Гук (1635-1703) с помощью простого эксперимента обнаружил, что величина деформации объектов пропорциональна силам, приложенным для деформации этого объекта, если они обладают свойством, которое он назвал «упругостью». .” На самом деле Гук был плодовитым ученым почти во всех вообразимых дисциплинах, даже если сегодня его имя не является нарицательным, в значительной степени из-за огромного количества опытных ученых, работавших в Европе в его время.
Определение закона Гука
Закон Гука очень легко написать, запомнить и использовать, что не часто предоставляется студентам-физикам. На словах это просто говорит о том, что сила, необходимая для удержания пружины (или другого упругого объекта) от дальнейшей деформации, прямо пропорциональна расстоянию, на которое объект уже был деформирован.
F = −kx
Здесь k называется жесткостью пружины, и, как и следовало ожидать, она различна для разных пружин. Закон Гука, который можно представить как «формулу силы пружины», действует во множестве различных инструментов и аспектов жизни, таких как луки для стрельбы из лука, амортизаторы и бамперы автомобилей.
Для простых примеров вы можете использовать свою голову в качестве калькулятора усилия пружины. Например, если вам сказали, что пружина действует с силой 1000 Н при растяжении на 2 м, вы можете разделить, чтобы получить постоянную пружины: 1000/2 = 500 Н/м.
Закон Гука в системе пружина-масса
Имейте в виду, что, хотя люди могут думать о пружинах скорее как о «растяжимых», чем о «сжимаемых», если пружина правильно сконструирована (то есть имеет достаточно места между последовательными витками), его можно значительно сжимать, а также растягивать, и закон Гука применяется в обоих направлениях деформации.
Представьте себе систему с блоком, расположенным на поверхности без трения и соединенным со стеной пружиной, которая находится в равновесии, то есть не сжимается и не растягивается. Как вы думаете, что произойдет, если отодвинуть блок от стены и отпустить его?
В тот момент, когда вы отпускаете блок, действует сила F , в соответствии со вторым законом Ньютона (F = ma), которая ускоряет блок по направлению к начальной точке. Таким образом, для закона Гука в этой ситуации:
F = -kx = ma
Отсюда можно, используя k и m , предсказать математическое поведение колебаний, которые имеют волнообразный характер. Блок движется быстрее всего в те моменты времени, когда он проходит через начальную точку в любом направлении, и, что более очевидно, наиболее медленно (0), когда он меняет направление.
- Теория против реальности: В этой воображаемой ситуации происходит то, что блок проходит свою начальную точку и колеблется взад и вперед вокруг своей начальной точки, сжимаясь на то же расстояние, на которое он сначала растягивался при каждом движении к стене.
 а затем возвращайтесь к тому месту, где вы его вытащили, в бесконечном цикле. В реальном мире пружина не была бы идеальной, и ее материал со временем потерял бы свою эластичность, но, что более важно, трение в реальности неизбежно; его сила вскоре уменьшает амплитуду колебаний, и блок возвращается в состояние покоя.
а затем возвращайтесь к тому месту, где вы его вытащили, в бесконечном цикле. В реальном мире пружина не была бы идеальной, и ее материал со временем потерял бы свою эластичность, но, что более важно, трение в реальности неизбежно; его сила вскоре уменьшает амплитуду колебаний, и блок возвращается в состояние покоя.
Энергия в законе Гука
Вы видели, что у пружины есть неотъемлемые или встроенные свойства, которые можно использовать для работы так, как, скажем, жевательная резинка или шариковый подшипник не могут. В результате пружины можно описать с точки зрения не только силы, но и энергии. (Работа имеет ту же фундаментальную единицу, что и энергия: ньютон-метр или Н⋅м),
Чтобы деформировать пружину, вы или кто-то другой должны совершить над ней работу. Энергия, которую вы передаете рукой, «переводится» в упругую потенциальную энергию , когда пружина удерживается растянутой. Это аналогично объекту над землей, обладающему гравитационной потенциальной энергией, и его значение равно:
E P = (1/2)kx 2
Допустим, вы используете сжатую пружину, чтобы запустить объект по поверхности без трения. поверхность. Энергия в этой идеальной ситуации была полностью «преобразована» в кинетическую энергию в тот момент, когда объект покидает пружину, где:
поверхность. Энергия в этой идеальной ситуации была полностью «преобразована» в кинетическую энергию в тот момент, когда объект покидает пружину, где:
E K = (1/2)mv 2
Таким образом, если вы знаете массу объекта, вы можете использовать алгебру, чтобы найти скорость v , установив E P (начальный) на E K при запуске.
Helical Spring Formulas and Equations
Toggle Nav
Search
Search
Advanced Search
CALL US NOW
(951) 276-2777
Menu
Account
There are several different формулы спиральной пружины сжатия и уравнения, необходимые для завершения проектирования. Во-первых, вы должны сосредоточиться на требованиях к вашей пружине, когда речь идет о физических размерах, типе материала и рабочих нагрузках. После того, как вы установили эти параметры, следующим шагом будет правильное согласование размеров для достижения требуемой функции пружины в вашем приложении.
После того, как вы установили эти параметры, следующим шагом будет правильное согласование размеров для достижения требуемой функции пружины в вашем приложении.
Когда вы измерили окружение пружины и выяснили ее экологические требования, вы должны установить допуски пружины и работать в их пределах, чтобы получить идеальную конструкцию пружины . Справа находится диаграмма, указывающая термин для каждого измерения. Вы также найдете формулы, используемые для расчета определенных размеров пружины , которые помогут вам не выходить за установленные пределы.
Диаметр проволоки
Вы можете измерить допуски на внешний диаметр и внутренний диаметр, но необходимо рассчитать максимальный диаметр проволоки. Вы делаете это путем вычитания минимального внутреннего диаметра из максимального внешнего диаметра и деления результата на 2.
d = (Дутер – Ужин) ÷ 2
- d = диаметр проволоки
- Дутер = наружный диаметр
- Ужин = внутренний диаметр
Затем у вас есть общее количество витков, которое вы хотите сохранить на промежуточном уровне, чтобы вы могли иметь эластичность. Если их слишком много, ваша пружина может быть упругой, но слабой. Однако некоторые выбирают этот вариант, потому что он позволяет получить большую твердую высоту. Формула для расчета сплошной высоты: общее количество витков плюс 1, умноженное на диаметр проволоки.
Если их слишком много, ваша пружина может быть упругой, но слабой. Однако некоторые выбирают этот вариант, потому что он позволяет получить большую твердую высоту. Формула для расчета сплошной высоты: общее количество витков плюс 1, умноженное на диаметр проволоки.
With all types of ends (except ground):
Lsolid = d(N+1)
With ground ends:
Lsolid = dN
- Lsolid = твердая высота
- d = диаметр проволоки
- N = общее количество катушек
Затем вы можете рассчитать шаг между витками, используя свободную длину и количество витков, которые вы решили использовать. Вы делаете это, вычитая количество проводов в замкнутых катушках из свободной длины, а затем разделяя результат на активные катушки.
Closed Ends
p = (L–3d) ÷ Na
Closed and Ground
p = (L–2d) ÷ Na
Double Closed Ends
p = (L–5d) ÷ Na
Открытые концы
p = (L–d) ÷ Na
- 3
р = шаг
- L = свободная длина
- d = диаметр проволоки
- Na = активные катушки
Используйте эти уравнения для расчета винтовой пружины, чтобы убедиться, что ваша пружина подходит.
 Рабочие нагрузки и скорость
Рабочие нагрузки и скорость После настройки и расчета физических размеров необходимо перейти к рабочим нагрузкам. Рабочая нагрузка вашей пружины будет определять жесткость пружины. Узнайте, какую нагрузку вы будете оказывать на свою пружину, а также насколько вы ожидаете, что она прогнется под действием этой силы.
Оба этих фактора составляют формулу для расчета требуемой жесткости винтовой пружины. Эта формула продиктована законом Гука, где он утверждает, что «как протяженность, так и сила». Закон Гука просто означает, что когда ваша пружина сжимается/отклоняется, нагрузка увеличивается пропорционально.
к = Д ÷ х
- k = Скорость
- F = нагрузка
- х = Путешествие
93 x na)
- d = диаметр проволоки
- Внешний диаметр = Внешний диаметр
- D = средний диаметр
- E = Модуль Юнга материала
- G = Модуль сдвига материала
- k = Коэффициент пружины
- нет = активные катушки
- V = Ядовитый рацион материала
Если вам трудно собрать информацию, вы можете просто ввести размеры вашей пружины и тип материала в наш пружинный калькулятор. Spring Creator рассчитает все приведенные выше формулы, а также предел упругости и максимальную нагрузку. Вы также можете связаться с нашей командой, чтобы назначить консультацию с нашими инженерами, если вам трудно настроить дизайн.
Spring Creator рассчитает все приведенные выше формулы, а также предел упругости и максимальную нагрузку. Вы также можете связаться с нашей командой, чтобы назначить консультацию с нашими инженерами, если вам трудно настроить дизайн.
Понимание нагрузки пружины и ее связи с жесткостью пружины
Понимание нагрузки пружины и ее связи со жесткостью пружины
3
АКЦИИ
Вы можете знать жесткость пружины, но понимаете ли вы расчет нагрузки пружины? Это имеет решающее значение, поскольку оно относится к правильному созданию пружин для ваших приложений и продуктов. Подробности читайте ниже.
Хорошее понимание нагрузки пружины и ее отношения к жесткости пружины поможет вам разработать правильную пружину для вашего применения. Причина кроется в вашей способности измерить правильные размеры пружины, а также рассчитать ее нагрузку и скорость.
Соответственно, давайте проведем вас по этим измерениям и расчетам.
Что такое пружинная нагрузка?
Нагрузка пружины описывает определенное усилие или давление на желаемой высоте нагрузки. Вот пример, показывающий, как работает нагрузка пружины и как ее можно получить из жесткости пружины.
Если длина пружины в свободном состоянии составляет 5 дюймов, коэффициент силы пружины составляет 7,5 фунтов на дюйм (фунт-сила/дюйм), и она будет перемещаться на 2 дюйма. Какая нагрузка должна быть приложена, чтобы пружина опустилась на высоту 3 дюйма?
Следующие соображения помогут вам решить описанную выше проблему:
Представьте, что у вас есть пружина, длина которой в свободном состоянии составляет 5 дюймов, а жесткость пружины составляет 7,5 фунтов силы на дюйм (фунт-сила/дюйм). Пружина должна достигать твердой высоты 3 дюйма, что требует от нее перемещения на 2 дюйма.
Соответственно, вы должны умножить пройденное расстояние на жесткость пружины, используя формулу нагрузки пружины, чтобы определить рабочую нагрузку силы, необходимой для достижения твердой высоты в 3 дюйма.
В этом случае используется следующая формула:
- Формула нагрузки пружины
- Тариф (путешествие) = нагрузка
- к(Т)=L
Введя свои данные в формулу, вы получите:
7,5(2)=L
15 = L
Что такое Spring Rate?
Жесткость пружины, с другой стороны, представляет собой постоянное усилие, необходимое для перемещения на дюйм или миллиметр расстояния. По сравнению с нагрузкой пружины, которая измеряет определенное количество силы на определенной высоте нагрузки, жесткость пружины определяет уровень силы, необходимой для прохождения единицы измерения.
Можно использовать либо нагрузку пружины, либо жесткость пружины для расчета другой, т. е. коэффициента для расчета рабочих нагрузок и рабочих нагрузок для расчета коэффициента.
Вот более подробное описание расчета коэффициента пружины:
Коэффициент пружины — это сложный расчет, который можно упростить с помощью формулы.
Формула:
- Формула коэффициента пружины
- Скорость = Нагрузка ÷ Ход
- к= L ÷ T
Используя значения в первом примере (если пружина имеет длину 5 дюймов, жесткость пружины и будет перемещаться на 2 дюйма), вы можете рассчитать величину жесткости пружины, необходимую для опускания на высоту под нагрузкой 3 дюйма, используя приведенную выше формулу.
Таким образом, у вас будет:
- k = 15 ÷ 2
- к = 7,5 фунта/дюйм
Вы сможете рассчитать необходимую жесткость пружины на основе рабочих нагрузок пружины.
Другие переменные формулы, которые вы можете оценить:
- Переменные формулы
- Диаметр пружинной проволоки = d
- Пружина снаружи пружины = D наружная
- Средний диаметр пружины = D
- Модуль Юнга материала = E
- Модуль сдвига материала = G
- Постоянная пружины = K
- Активные катушки = нет данных
- Отключение коэффициента Пуассона Материал = V
Теоретическое определение нагрузки пружины
Хотя теперь у вас есть формула для определения нагрузки пружины, есть еще один простой способ выполнить этот расчет. Это возможность теоретически определить нагрузку пружины.
Это возможность теоретически определить нагрузку пружины.
В производственном процессе очень важно знать, как теоретически определить нагрузку пружины, чтобы гарантировать, что вы спроектируете правильную пружину для вашего конкретного применения. В различных продуктах используется широкий спектр пружин, и эти пружины имеют разные параметры, на которые следует обращать внимание при определении нагрузки.
Имея это в виду, высоко цените следующее.
1. Спиральные пружины сжатияТеоретическая нагрузка винтовых пружин сжатия может быть определена, зная внешний диаметр, длину в свободном состоянии, диаметр проволоки и количество витков.
Другими деталями, на которые следует обратить внимание, являются тип конца, например, закрытый и прямоугольный, когда последние витки соприкасаются с предыдущим витком. Другой тип концов — это открытые концы, где между концами есть пространство.
Далее замкнутый и заземленный, где последний виток плоский. Также есть двойные закрытые концы, и в этом случае последние две катушки на концах закрыты, чтобы стабилизировать его или помочь минимизировать запутывание.
Также есть двойные закрытые концы, и в этом случае последние две катушки на концах закрыты, чтобы стабилизировать его или помочь минимизировать запутывание.
Теоретическая нагрузка пружин растяжения и растяжения может быть определена с учетом внешнего диаметра, диаметра проволоки, длины корпуса, длины внутри крюка и типа используемого крюка.
Типы крючков – это машинные крючки, и этот крюк сделан из витков на конце. Также обратите внимание на перекрещивающийся центральный крючок, и в этом случае концы сгибаются прямо по центру, а затем закручиваются. Есть боковые крючки, и они отогнуты наружу со стороны пружины. Без крючков изображают, когда концы служат резьбой, когда нужно вставить болт посередине.
3. Пружины кручения Когда речь идет о пружинах кручения, вам необходимо измерить количество витков, диаметр проволоки, длину ветвей 1 и 2, внешний диаметр и любые изгибы или форму ветвей.
Измерение размеров
Теперь, когда вы знаете размеры, которые необходимо измерить для каждой пружины, также важно получить точные размеры для определения нагрузки пружины. В соответствии с этим используйте штангенциркуль для измерения пружины.
Суппорт можно держать в одной руке, а основание пружины — в другой.
Затем можно рассчитать внешний диаметр путем измерения наибольшего размера на внешней стороне последнего рулона. Внутренний диаметр можно рассчитать, поместив зубья штангенциркуля на внутренний диаметр.
Длина в свободном состоянии измеряется путем помещения штангенциркуля на всю длину несжатой пружины. Более того, поместите суппорт в центр пружины, чтобы определить размер проволоки.
Начните считать все витки с одного конца рядом с местом обрезания провода, убедившись, что сосчитаны все части витка.
После определения всех размеров можно приступать к расчету нагрузки пружины с помощью калькулятора пружины или с помощью специалистов. Часто рекомендуется, чтобы вы позволили эксперту по пружинам выполнить расчет от вашего имени, чтобы убедиться, что вы получите точный калибр.
Часто рекомендуется, чтобы вы позволили эксперту по пружинам выполнить расчет от вашего имени, чтобы убедиться, что вы получите точный калибр.
Заключение
Это важные детали, которые необходимо понимать, когда речь идет о нагрузке пружины и ее отношении к жесткости пружины.
Приведена формула для расчета каждой из них, а также способы теоретического определения нагрузки пружины кручения, винтовой пружины и других типов пружин.
Мы еще раз подчеркнем, насколько важно получить правильные размеры для каждой пружины, чтобы гарантировать, что пружина лучше всего подходит для ее применения.
Постоянная пружины: определение, формула, единица измерения, расчет
В этой статье вы узнаете полный обзор постоянной пружины , такой как ее определение, формула, единица измерения, размерная формула, влияющий фактор, расчет и многое другое.
Итак, не теряя времени, приступим.
Что такое пружинная постоянная?
Постоянная пружины — это восстанавливающая сила, прилагаемая пружиной для восстановления положения против единичного смещения, вызванного внешней силой.
Чем выше значение постоянной пружины, тем выше будет жесткость пружины, что означает, что для сжатия или отклонения пружины потребуется более высокая нагрузка.
Также называется жесткостью пружины и константой жесткости.
Это всегда положительное или ненулевое значение.
Формула константы пружины
Согласно закону Гука
Сила прямо пропорциональна отклонению или смещению пружины.
Математически,
F ∝ x
F = K.x
Где K — жесткость пружины.
Возвращающая сила (F), развиваемая пружиной, действует противоположно приложенной силе.
Итак,
Fr = – F
Fr = – K.x
Что также можно записать как
K = – (Fr/x)
или
K = F/x
20, где
Fr = восстанавливающая сила пружины (Н)
x = деформация или смещение пружины (м)
F = Сила, приложенная к пружине
K = Постоянная пружины
Расчет жесткости пружины
Жесткость пружины относится к величине силы, необходимой для сжатия, растяжения или скручивания пружины при единичном смещении или отклонении.
Жесткость пружины в первую очередь не зависит от марки материала пружины.
Подстановка значений в формулу, полученную из закона Гука,
K = F/x = (W2 – W1)/(h3 – h2)
Теоретический метод расчета
Формула для расчета жесткости пружины
K = (G × d⁴)/(8 × Dm³ × Nac)
Где,
G – модуль жесткости
d – диаметр проволоки D
3 Пружина
Nac- Количество активных витков
Единица постоянной пружины
Единица постоянной пружины в системе СИ
Как мы знаем, единицами силы и расстояния в системе СИ являются Ньютон (Н) и метр (М) соответственно.
Итак,
Постоянная пружины,
K = F/x
K = Н/м
Следовательно, в системе СИ единицей жесткости пружины будет Н/м.
Единица жесткости пружины в системе FPS
Как мы знаем, единицами силы и расстояния в системе СИ являются фунты (фунты) и футы (футы) соответственно.
Итак,
Постоянная пружины,
K = F/x
K = фунт/фут
Следовательно, в системе FPS единицей жесткости пружины будет фунт/фут.
Размерная константа пружины, формула
Как мы знаем,
K = F/x
Поскольку,
Сила = масса (m) × ускорение (a)
Следовательно,
K = (m × a)/x
Как мы знаем единицами массы и ускорения являются кг и м/с² соответственно.
Итак,
K = кг × м с ⁻²/м
K = M T⁻²
Следовательно, размерная формула для жесткости пружины K будет M T⁻².
Комбинация пружин
На рисунке показано последовательное и параллельное сочетание пружин, которые подробно описаны ниже.
Пружина в серии
В последовательных комбинациях натяжение одинаково во всех пружинах, а удлинители будут разными.
(Если k одинаково, то и деформация одинакова).
В последовательном соединении удлинение пружин будет обратно пропорционально жесткости пружины.
Полное смещение при последовательном соединении пружины,
x = x₁ + x₂
Как известно, константа пружины
F = K × x
Итак,
F/K = x
Следовательно,
F/Kэкв = F/K₁ + F/K₂
Таким образом, эквивалентная постоянная в последовательной комбинации Keq определяется как:
1/Kэкв = 1 / K₁ + 1 / K₂
Пружина, установленная параллельно
При параллельном соединении удлинение одинаково для обеих пружин, но действующая сила будет разной.
Если сила, действующая на пружину, равна F, то общая сила, действующая на пружину,
F = F₁ + F₂
Как известно,
F = K × x
Итак,
F = (K₁x + K₂ x)
F = (K₁ + K₂)x
K × x = (K₁ + K₂)x
Итак, эквивалентная константа в Параллельная комбинация Keq определяется как:
Keq = K₁ + K₂
Факторы, влияющие на жесткость пружины
Жесткость пружины зависит от следующих факторов
- Диаметр проволоки пружины
- Модуль жесткости Диаметр
- Кол-во активных или эффективных катушек
Диаметр проволоки пружины
Если диаметр проволоки пружины увеличить, постоянная пружины увеличится.
Модуль жесткости
Если модуль жесткости материала пружины увеличить, постоянная пружины увеличится.
Диаметр витка
Если диаметр витка пружины увеличить, жесткость пружины уменьшится.
Количество активных или действующих витков
Если количество витков пружины увеличить, постоянная пружины уменьшится.
See Also:
What is Body Mass Index
Parallel Axis Theorem
Modulus of Elasticity
Modulus of Resilience
Bending Stress
Spring Constant Calculation
Вопрос .1
Какова жесткость пружины, если для растяжения пружины на 0,2 м требуется 30 Н?
Решение
Приведенные данные,
F = 30 N
х = 0,2 м
К =?
Как известно,
F = K × x
Итак,
K = F/x
K = 30/0,2
K = 150 Н/м
0,5 пружина A 209002 0,0043 90 силовой постоянной k разрезается на отрезки в соотношении 1:2:3. Они соединены последовательно, и новая силовая постоянная равна Ks. Затем они соединены параллельно и силовая постоянная равна Kp. Тогда каково соотношение Ks:Kp?Раствор
Как мы знаем,
K ∝ (1/l)
Итак,
K₁l₁ = Константа
Здесь K — жесткость пружины, а l — длина пружины.



