Пружины сила: Сила упругости пружины

Пружины сила: Сила упругости пружины – формула по модулю

alexxlab | 01.07.2023 | 0 | Разное

Содержание

Сила упругости пружины – формула по модулю

4.7

Средняя оценка: 4.7

Всего получено оценок: 160.

4.7

Средняя оценка: 4.7

Всего получено оценок: 160.

Сил упругости возникает при деформации физического тела, то есть когда изменяются размеры и форма тела. Эта сила направлена в сторону, противоположную силе, создающей деформацию. На примере пружины выясним как сила упругости связана с величиной деформации. Рассмотрим также причины возникновения упругих сил.

Закон Гука

Пружину можно сжимать, растягивать, изгибать или скручивать. В каждом из этих случаев будут возникать силы упругости, стремящиеся вернуть форму и размеры пружины в начальное состояние. Для понимания основных закономерностей будем рассматривать только линейные сжатия и растяжения (вдоль оси х). Для вычисления сил при деформациях изгибов и скручивании требуется применение более сложного математического аппарата.

Рис. 1. Деформации растяжения и сжатия пружины.

Если начальная длина, ненапряженной пружины, равна L₀, то для малых деформаций выполняется закон Гука, открытый экспериментально:

$ F_уп = − k * Δх $ (1),

где, в формуле силы упругости пружины:

F_уп— сила упругости пружины, Н;

k — коэффициент жесткости пружины, Н/м;

Δх —величина деформации (дельта икс), м.

Величина малых деформаций должна быть намного меньше начальной длины пружины:

$ Δх

Рис. 2. Портрет Роберта Гука.

Этот фундаментальный закон был открыт английским ученым Робертом Гуком в 1660г. Кроме этого он сделал много других замечательных изобретений и экспериментов:

открыл эффект образования цветов тонких пленок, которое в оптике называется явлением интерференции;
предложил модель волнообразного распространения света;
сформулировал предположение о связи теплоты с движением частиц, из которых состоит тело;
изобрел спиральную пружину для регулировки часов, усовершенствовал барометр, гигрометр, анемометр.

Источник силы упругости

Происхождение сил упругости связано с электромагнитным взаимодействием молекул и атомов. Когда происходит увеличение размеров пружины (растяжении), то силы взаимного притяжения “пытаются” восстановить начальные размеры. При сжатии пружины начинают работать силы отталкивания. Когда тело не деформировано, расстояние между молекулами соответствует равенству сил притяжения и отталкивания.

Динамометры

Упругие свойства пружин используются в приборах для измерения силы. Обычно динамометр состоит из двух основных частей: пружины (упругий элемент) и шкалы устройства, на которой нанесены цифровые значения силы или массы, если этот прибор предназначен для бытового применения. Измеряемое усилие прикладывается к пружине, которая деформируется и сдвигает стрелку прибора вдоль отсчетной шкалы.

Рис. 3. Пружинные динамометры.

Хотя закон Гука и считается универсальным, но диапазон деформаций в котором он выполняется сильно отличается для разных тел. Например, в металлических проволоках (прямолинейных) и стержнях максимальная величина относительной деформации (отношение Δх к L₀), для которой еще будет справедлив закон Гука, составляет не более 1%. При больших деформациях наступают необратимые разрушения материалов.

Что мы узнали?

Итак, мы узнали, что сила упругости пружины прямо пропорциональна величине деформации тела и направлена в сторону, обратную направлению сдвига пружины. Силы упругости связаны с электромагнитным взаимодействием молекул и атомов. При сжатии включается механизм отталкивания электрических одноименных зарядов. При растяжении — начинает работать механизм притяжения разноименных зарядов.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Александр Коновалов
5/5

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 160.

А какая ваша оценка?

Сила пружины и постоянная пружины: сравнительный анализ –

Сравнение силы пружины и постоянной пружины может дать нам четкое представление об обеих величинах. Сила пружины является восстанавливающей силой, тогда как постоянная пружины измеряет жесткость упругого объекта.

СИЛА ПРУЖИНЫ	ПРУЖИННАЯ ПОСТОЯННАЯ
Сила пружины — это сила, возникающая в струне при растяжении из исходного положения.	Постоянная пружины является результатом знака пропорциональности.
Формула силы пружины: f=-kx	Формула жесткости пружины: x=f/k
Сила пружины – это действие пружины, а скорость измеряется	Константа пружины измеряет жесткость объекта.

Сила пружины сила, действующая на пружину при ее сжатии или растяжении. Мы также знаем, что длина пружины измеряется путем вычисления исходной длины на величину, которая равна расширенный или сжатый.

Константа пружины — это знак пропорциональности, при котором пружина сила прямо пропорциональна расстоянию.

Например, бридж работает по теории сила пружины где оба конца моста соединены с фиксированной точкой, и при движении по нему транспортных средств на этом конкретном мосту делается небольшая подвеска.

Зависимость между силой пружины, которая является восстанавливающей силой, и удлинением пружины, является линейной. Пока сила увеличивается, растяжение будет происходить, а когда действие силы становится меньше, растяжение увеличивается втрое.

«Файл:Animated-mass-spring.gif» by Свьё под лицензией CC BY-SA 2.0

Весенняя сила в деталях

Пружинная сила есть не что иное, как сила, действующая на движущийся объект, который вытягивается или растягивается. Процесс растяжения и растяжения происходят из положения равновесия.

Сила пружины – это сила, которую обычно считают контактной силой, которая также присутствует в упругой пружине. Мы можем видеть информацию о силе пружины в том, что они связаны с законом Гука.

Возвращающая сила — это сила, которая возвращает движущиеся объекты, подвешенные из исходного положения, обратно в исходное положение. положение равновесия. В этом случае мы называем эту силу силой пружины.

Сила пружины в зависимости от постоянной пружины может быть рассмотрена многими способами с точки зрения движения. Когда сила пружины задана, мы автоматически знаем формулу силы. Из этой формулы мы также можем узнать жесткость пружины.

По сути, пружина — это инструмент, который используется несколькими механизмами для расширения и сжатия этого конкретного объекта. Сила вернет объект в исходное положение, если он настроен на равномерное прямолинейное движение.

«Олинс» by полудождь под лицензией

Формула силы пружины

Формула силы пружины определяется величинами f=-кх. Сила пружины, являющаяся восстанавливающей силой, представляет собой не что иное, как величину силы, необходимой для того, чтобы объект вернулся в положение равновесия.

Поэтому, когда знак пропорциональности удаляется, его необходимо заменить константой, обозначаемой буквой k, которая называется жесткостью пружины.

X также называется смещением объекта, находящегося в положении равновесия. Формулу также можно переписать в виде f= – (хх₀) к, Х₀ обозначает положение равновесия, а x обозначает смещение от положения равновесия.

Сила пружины в зависимости от постоянной пружины имеет очень небольшие различия, и их также можно выразить в терминах движения и силы с помощью формулы.

Spring Constant в деталях

Теперь, когда у нас достаточно знаний о силе пружины и ее формуле, мы должны знать, что жесткость пружины является частью формулы силы пружины.

Как мы знаем, формула силы пружины f=-kx. Более ранняя форма объяснения силы пружины, которая заключается в том, что сила пружины прямо пропорциональна смещению объекта, который находится в движении или колебаниях.

Постоянная пружины на самом деле является мерой жесткости объекта, который находится в состоянии колебаний.

Закон Гука в основном связано с силой пружины и постоянной пружины, где длина пружины обычно определяется с использованием значения x, которое представляет собой смещение, при котором объект колебался.

Постоянная пружины определяется по формуле силы пружины. Сила, действующая против возвращающей силы, на самом деле действует в противоположных направлениях. Причина отрицательного знака в том, что две силы действуют противоположно друг другу.

Часто задаваемые вопросы

Что происходит, когда жесткость пружины увеличивается?

Постоянная пружины покажет, какое усилие потребуется для растяжения струны.

Когда жесткость пружины увеличивается, сила процесса растяжения пружины также увеличивается. В основном жесткость эластичного материала измеряется с использованием термина, называемого жесткостью пружины, который имеет значение для различных усилий пружины.

Что именно делает пружинная постоянная?

Константа пружины обычно обеспечивает усилие, необходимое для растяжения пружины.

Жесткость упругого материала определяется с помощью значения жесткости пружины. Например, когда масса растягивается с помощью пружины, длина увеличивается, а вместе с ней автоматически увеличивается сила. Таким образом, константа пружины — это значение, которое будет влиять на сжатие и растяжение пружины.

Является ли сила пружины переменной силой?

Сила пружины может быть переменной силой из-за постоянного значения пружины.

Постоянная пружины будет переменной величиной, и в зависимости от ее значения будет изменяться усилие. Если значение постоянной пружины увеличивается, сила пружины увеличивается, а когда значение постоянной пружины уменьшается, сила пружины увеличивается.

Сила пружины: определение, формула и примеры

Что такое сила пружины

Когда металлическая пружина растягивается или сжимается, она смещается из положения равновесия. В результате на нее действует восстанавливающая сила, стремящаяся вернуть пружину в исходное положение. Эта сила называется силой пружины. Это контактная сила, которую можно найти в эластичных материалах.

Сила пружины

Примеры силы пружины

Вот несколько примеров силы пружины из повседневной жизни.

Маятник
Резиновая лента
Банджи-шнур
Клавиши в клавиатуре ПК
Батут
Тормоза, сцепления и амортизаторы
Часы и игрушки
Пого-стик
Пружинный баланс

Spring Force Пример

Уравнение силы пружины: как найти силу пружины

Силу пружины можно определить количественно, используя закон Гука. Согласно этому закону при растяжении или сжатии пружины восстанавливающая сила F пропорционально смещению x .

F ∝ x

Формула усилия пружины:

F = -kx

9000 4 Единица силы пружины: Ньютон или Н

Здесь k известен как силовая постоянная. Отрицательный знак связан с тем, что сила противоположна смещению, то есть сила смещает пружину из положения равновесия. Это уравнение применимо как к сжатию, так и к растяжению пружины. Усилие можно измерить с помощью тестера пружин.

Величина жесткости пружины определяется выражением

k = F/x

Предположим, F = 1 Н и x = 1 м , тогда

k = 1 Н/ 1 м = 1 Н/м

Таким образом, жесткость пружины определяется как сила, необходимая для смещения пружины на один метр. Он измеряется в ньютонах на метр (Н/м) и имеет размерность MT ^-2 .

Работа, выполненная Spring Force

Работа, выполненная Вт силой пружины определяется как,

Вт = F.x

Сила пружины на объекте, подвешенном на пружине

Если объект массой м подвешен на пружине, то это смещается под действием собственного веса. Сила пружины равна ее весу мг

мг = -kx

Или, |k| = мг/х

Приведенное выше уравнение можно использовать для определения силовой постоянной пружины.

Торсион на пружине

Приведенное выше уравнение для жесткости пружины применяется, когда сила направлена вдоль оси пружины. В случае кручения, когда приложенная сила вызывает скручивание пружины, уравнение для k будет следующим: 0004 M = Момент пружины

Градус = Угол поворота пружины

Как рассчитать силу пружины

Пример задачи: Пружина с постоянной силой 1300 Н/м нагружена вертикально массой, которая растягивает пружину на 6 см. Найдите величину силы пружины.

Дано,

k = постоянная силы пружины = 8 кг

x = смещение пружины = 6 см = 0,06 м

Величина силы пружины,

Ф = кх = 1300 Н/м x 0,06 м = 78 Н

Ссылки 9
Сила пружины: определение, формула и примеры От компьютеров до автомобилей машины выполняют несколько функций, и некоторые из них требуют от них последовательного перемещения частей вперед и назад. Одна часть, которая используется во многих различных машинах, — это простая деталь, которую мы сегодня знаем как пружину. Если вы хотите узнать больше о пружинах, не ищите дальше. Давайте приступим к делу и изучим физику!
Силы пружины: определение, формула и примеры
Пружина имеет незначительную массу и при растяжении или сжатии создает силу, пропорциональную смещению от ее длины в расслабленном состоянии. Когда вы берете предмет, прикрепленный к пружине, тянете его на расстояние от положения равновесия и отпускаете, восстанавливающая сила возвращает предмет обратно в равновесие. 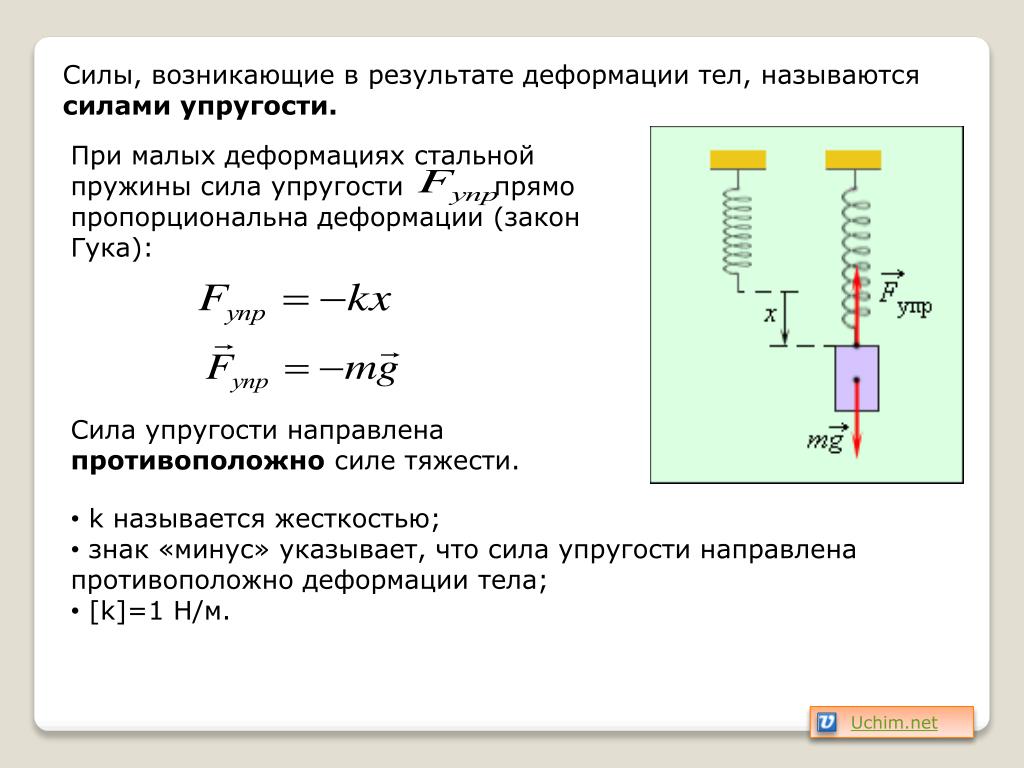Для системы пружина-масса на горизонтальном столе единственной силой , действующей на массу в направлении смещения, является восстанавливающая сила, действующая со стороны пружины . Используя Второй закон Ньютона, , мы можем составить уравнение движения объекта. Направление возвращающей силы всегда будет против и антипараллельно смещению объекта. Возвращающая сила, действующая на систему пружина-масса, зависит от жесткости пружины и смещения объекта от положения равновесия.
Рис. 1 – Представление системы пружины-массы, где масса колеблется вокруг положения равновесия.
92})\), $k$ — жесткость пружины, которая измеряет жесткость пружины в ньютонах на метр $(\frac{\mathrm N}{\mathrm m})$, и $x\ ) — смещение в метрах \((\mathrm m)$.
Эта взаимосвязь также известна как закон Гука, и ее можно доказать, установив пружинную систему с подвешенными массами. Каждый раз, когда вы добавляете массу, вы измеряете растяжение пружины. Если процедуру повторить, то будет видно, что растяжение пружины пропорционально возвращающей силе, в данном случае весу подвешенных масс. 92=\frac km$$
$$\omega=\sqrt{\frac km}$$
Пружина $12\;\mathrm{cm}$ имеет жесткость $400\;{ \textstyle\frac{\mathrm N}{\mathrm m}}$. Какая сила требуется, чтобы растянуть пружину до длины $14\;\mathrm{см}$?
Смещение имеет величину
$$x=14\;\mathrm{см}\;-\;12\;\mathrm{см}=2\;\mathrm{см}=0,02\;\mathrm m$$
Сила пружины имеет величину
$$F_s=kx=(400\;{\textstyle\frac{\mathrm N}{\mathrm m}})(0,02\;\mathrm m)= 8\;\mathrm N$$
Говорят, что система пружины-массы находится в равновесии, если на объект не действует результирующая сила. Это может произойти, когда величина и направление сил, действующих на объект, идеально сбалансированы или просто потому, что на объект не действуют никакие силы. Не все силы пытаются вернуть объект обратно в равновесие, но силы, которые делают это, называются восстанавливающими силами, и сила пружины является одной из них.
Возвращающая сила — это сила, действующая против смещения, чтобы попытаться вернуть систему в равновесие. Этот тип силы отвечает за генерацию колебаний и необходим для того, чтобы объект находился в простом гармоническом движении. Кроме того, восстанавливающая сила вызывает изменение ускорения объекта при простом гармоническом движении. По мере увеличения смещения запасенная упругая энергия увеличивается, а восстанавливающая сила увеличивается.
На диаграмме ниже мы видим полный цикл, который начинается, когда масса высвобождается из точки $\text{A}$. Пружинные силы заставляют массу проходить через положение равновесия до $\text{-A}$, чтобы снова пройти через положение равновесия и достичь точки $\text{A}$ для завершения целый цикл.
Рис. 2 – Полный цикл колебаний системы пружина-масса.
Комбинация пружин
Набор пружин может действовать как одна пружина с эквивалентной жесткостью пружины, которую мы назовем $k_{\text{eq}}$. Пружины могут быть расположены последовательно или параллельно. Выражения для $k_{\text{eq}}$ будут различаться в зависимости от типа аранжировки. В последовательном соединении обратная величина эквивалентной жесткости пружины будет равна сумме обратных величин отдельных жесткостей пружины. Важно отметить, что при последовательном соединении эквивалентная жесткость пружины будет меньше наименьшей жесткости отдельной пружины в наборе.
$$\frac1{k_{eq\;series}}=\sum_n\frac1{k_n}$$
Рис. 3 – Две последовательно соединенные пружины.
Набор из 2 последовательно соединенных пружин имеет константы пружин $1{\textstyle\frac{\mathrm N}{\mathrm m}}$ и $2{\textstyle\frac{\mathrm N}{\ матрм м}}$. Каково значение эквивалентной жесткости пружины?
$$\frac1{k_{eq\;ряд}}=\frac1{1\frac{\mathrm N}{\mathrm m}}+\frac1{2\frac{\mathrm N}{\mathrm m} }$$
$$\frac1{k_{eq\;series}}=\frac32{\textstyle\frac{\mathrm m}{\mathrm N}}$$
$$k_{eq\;series}=\frac23{\textstyle\frac{\mathrm N}{\mathrm m}}$$
Параллельно эквивалентная жесткость пружины будет равна сумме индивидуальных константы пружины.
$$k_{eq\;parallel}=\sum_nk_n$$
Рис. 4 – Две пружины параллельно.
Набор из 2 параллельных пружин имеет константы пружин $1{\textstyle\frac{\mathrm N}{\mathrm m}}$ и $2{\textstyle\frac{\mathrm N}{\ матрм м}}$. Каково значение эквивалентной жесткости пружины?
$$k_{eq\;parallel}=1\;{\textstyle\frac{\mathrm N}{\mathrm m}}+\;2{\textstyle\frac{\mathrm N}{\mathrm m} }=3\;{\textstyle\frac{\mathrm N}{\mathrm m}}$$
График силы и смещения
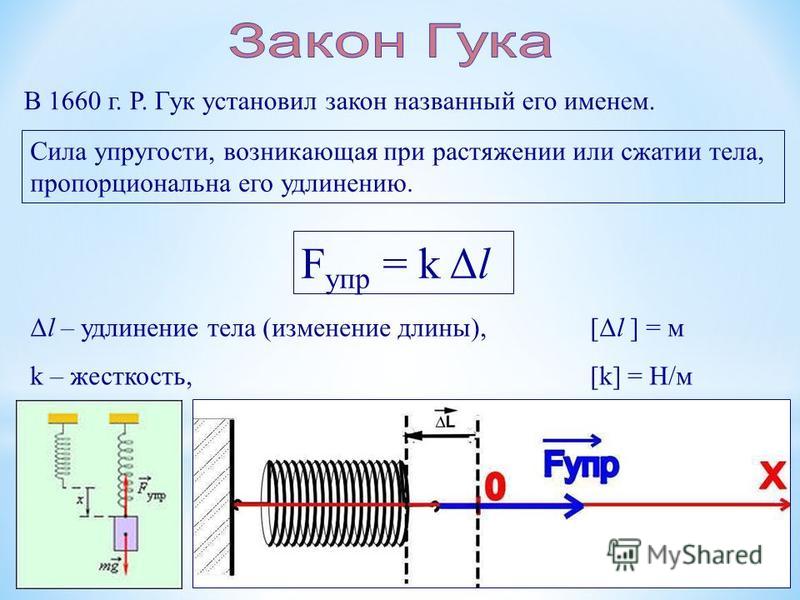
Мы можем построить график силы пружины как функцию положения и определить площадь под кривой. Выполнение этого расчета даст нам работу, совершаемую над системой силой пружины, и разность потенциальной энергии, запасенной в пружине из-за ее смещения. Поскольку в этом случае работа силы пружины зависит только от начального и конечного положений, а не от пути между ними, мы можем вывести изменение потенциальной энергии из этой силы. Эти виды сил называются 92. \end{array}$$
Рис. 5 – График зависимости силы от смещения, жесткость пружины представляет собой наклон, а потенциальная энергия представляет собой площадь под кривой.
Усилие пружины. Ключевые выводы
- Пружина имеет незначительную массу и при растяжении или сжатии создает силу, пропорциональную смещению от ее длины в расслабленном состоянии. Когда вы берете предмет, прикрепленный к пружине, тянете его на расстояние от положения равновесия и отпускаете, восстанавливающая сила возвращает предмет обратно в равновесие. 92}\).
- Направление возвращающей силы всегда будет противоположным и антипараллельным перемещению объекта.
- Набор пружин может действовать как одна пружина с эквивалентной пружинной константой, которую мы назовем $k_eq$.
- В серии обратная величина эквивалентной жесткости пружины будет равна сумме обратных величин отдельных пружинных констант, $\frac1{k_{eq\;series}}=\sum_n\frac1{k_n}$ .
- При параллельном использовании эквивалентная жесткость пружины будет равна сумме индивидуальных жесткостей пружины $k_{eq\;parallel}=\sum_nk_n$.