Расчет балки на изгиб: Расчёт металлической балки онлайн (калькулятор).
alexxlab | 23.02.2019 | 0 | Разное
Расчет балки на изгиб | Блог Александра Воробьева
Опубликовано 28 Апр 2013
Рубрика: Механика | 94 комментария
Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…
…– получи ответ» позволяет современному инженеру сегодня работать гораздо быстрее, чем его предшественникам сто, пятьдесят и даже двадцать лет назад. Однако при таком современном подходе инженер вынужден полностью доверять авторам программы и со временем перестает «ощущать физический смысл» расчетов. Но авторы программы – это люди, а людям свойственно ошибаться. Если бы это было не так, то не было бы многочисленных патчей, релизов, «заплаток» практически к любому программному обеспечению. Поэтому, мне кажется, любой инженер должен уметь иногда «вручную» проверить результаты расчетов.
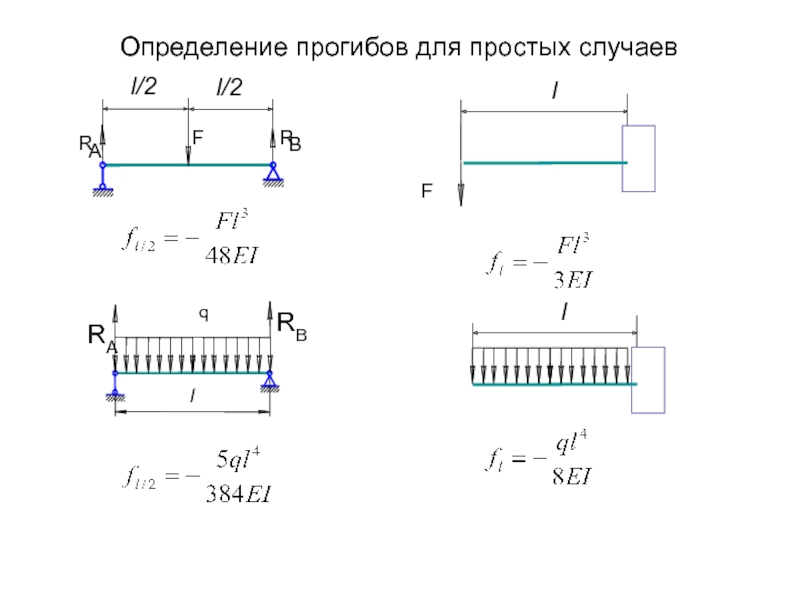
Справка (шпаргалка, памятка) для расчётов балок на изгиб представлена ниже на рисунке.
Давайте на простом житейском примере попробуем ей воспользоваться. Допустим, я решил сделать в квартире турник. Определено место – коридор шириной один метр двадцать сантиметров. На противоположных стенах на необходимой высоте напротив друг друга надежно закрепляю кронштейны, к которым будет крепиться балка-перекладина – пруток из стали Ст3 с наружным диаметром тридцать два миллиметра. Выдержит ли эта балка мой вес плюс дополнительные динамические нагрузки, которые возникнут при выполнении упражнений?
Чертим схему для расчета балки на изгиб. Очевидно, что наиболее опасной будет схема приложения внешней нагрузки, когда я начну подтягиваться, зацепившись одной рукой за середину перекладины.
Исходные данные:
F1 = 900 н – сила, действующая на балку (мой вес) без учета динамики
b1 = 0 м
b2 = 0,6 м
b3 = 1,2 м
d = 32 мм – наружный диаметр прутка, из которого сделана балка
E = 206000 н/мм^2 — модуль упругости материала балки стали Ст3
[σи] = 250 н/мм^2 — допустимые напряжения изгиба (предел текучести) для материала балки стали Ст3
Граничные условия:
Мx (0) = 0 н*м – момент в точке z = 0 м (первая опора)
Мx (1,2) = 0 н*м– момент в точке z = 1,2 м (вторая опора)
V (0) = 0 мм – прогиб в точке z = 0 м (первая опора)
V (1,2) = 0 мм – прогиб в точке z = 1,2 м (вторая опора)
Расчет:
1. 2
2
По прочности на изгиб расчет показал трехкратный запас прочности – турник можно смело делать из имеющегося прутка диаметром тридцать два миллиметра и длиной тысяча двести миллиметров.
Таким образом, вы теперь легко можете произвести расчет балки на изгиб «вручную» и сравнить с результатами, полученными при расчете по любой из многочисленных программ, представленных в Сети.
Прошу УВАЖАЮЩИХ труд автора ПОДПИСАТЬСЯ на анонсы статей.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
| Однопролетные балки на двух шарнирных опорах | ||
| 1 | Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 2 | Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 3 | Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 4 | Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 5 | Расчет балки на двух шарнирных опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на двух опорах | ||
| 6 | Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке | Смотреть расчет |
| 7 | Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках | Смотреть расчет |
| 8 | Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 9 | Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 10 | Расчет балки с жестким защемлением на опорах при действии изгибающего момента | Смотреть расчет |
| Балки с жестким защемлением на одной опоре (консольные) | ||
| 11 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке | Смотреть расчет |
| 12 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке | Смотреть расчет |
| 13 | Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке | Смотреть расчет |
| 14 | Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента | Смотреть расчет |
| Балки двухпролетные | ||
| 15 | Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке | Смотреть |
| 16 | Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках | Смотреть |
| 17 | Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке | Смотреть |
| 18 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
| 19 | Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке | Смотреть |
Полный расчет балки на прочность и жесткость
Задача
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400
1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=l/400
Рис. 1
Решение
Подготовка расчетной схемы к решению задачи:
Определение опорных реакций
Подробно, пример определения опорных реакций для балки рассмотрен здесь
А также в нашем коротком видеоуроке:
Из Σmв=0
Из ΣmА=0
Построение эпюр Q и М
Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки
Видео про расчет значений Q и M для построения эпюр:
В пролете балки 0 ≤ z2 ≤ l
QII= — RB+ qz2= -52+30∙z2QII(z=0)= -52 кН
QII(z=l)= -52+30∙4=68 кН
MII=RB∙z2
-qz22/2=52z2-30∙z22/2MII (z=0)= 0
MII (z=l)= -32 кНм
На консоли l ≤ z1≤ (l+a)
QI= — RB+ ql — RA=-52+30∙4-108=-40 кНMI=RB z1-ql(z1-l/2)+RA(z1-l)=52z1-30∙4(z1-4/2)+108(z1-4)
MI (z=l)= -32 кНм
MI (z=l+a)= 0
По этим данным построены эпюры Q и М.
Короткое видео о том, как надо строить эпюры:
Так как Мmах = 45 кНм, то
Wx≥Mmax / [σ] = 45∙103 / 160∙106= 0,281 м3= 281 см3.
О том, как подбирается сечение балки
По сортаменту выбираем двутавр № 24, для которого Wx = 289 см3, Ix= 3460 см4, Smax = 163 см3, h = 24 см, bп = 11,5 см, t = 0,95 см, d = bc = 0,56 см, h0 = h-2t = 22,1 см.
Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.
σmax = Mmax / Wx = 45∙103 / 289∙10-6= 156∙106 Па = 156 МПа
Проверка сечения балки по касательным напряжениям
Так как Qmax = 68 кН, то
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:
Построение эпюры нормальных напряжений
Построение эпюры касательных напряжений
В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:
М = -32 кНм и Q = 68 кН.
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1
Таблица 1
Результаты расчета в примере
Проверка прочности балки по главным напряжениям
Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ1=118 МПа и σ3= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ1 — σ3≤ [σ].
Так как 118 — ( -16) = 134 < 160, то выбранное сечение удовлетворяет условию прочности и по главным напряжениям.
Расчет перемещений сечений (прогибов балки)
Универсальные уравнения МНП для сечения z:
Опорные условия:
1) при z=0: y(z)=0, следовательно, y0=0
2) при z=l: y(z)=0 находим θ0
откуда θ0= -8,48∙10-3 радиан.
Прогиб в пролете при z=l/2=4/2=2 м.
Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.
Проверка жесткости балки
— пролетной части:
yc=0,98 см < 1/400 = 400/400 = 1 см
— консольной части:
yD=0,33 см < 2a/400 = 2∙80/400 = 0,4 см.
Следовательно, принятая двутавровая балка удовлетворяет требуемому условию жесткости.
Другие примеры решения задач >
Расчёт балок на прочность при изгибе
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ, maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
где
Тогда
где:
Тогда
Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = –F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим :
И тогда
Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп. Q – под сосредоточенной силой А = 60 кН.
Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
откуда: :
а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:
тогда
Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами. Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) – М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
– парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
что меньше [σ]=160МПа на
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 – М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = – F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= – F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
– парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).
по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба –
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
Расчет балки
Подробный ход решения – расчет балки, построение эпюр
Заменим распределенную нагрузку равнодействующей
Q1 = 6·2 = 12кН
Составим уравнения равновесия для определения реакций опор
Σ MA = + P · 2 + M + Q1 · 3 – RE · 6= + 12 · 2 + 8 + 12 · 3 – RE · 6=0
Σ ME = – P · 4 + M – Q1 · 3 + RA · 6= – 12 · 4 + 8 – 12 · 3 + RA · 6=0
Из этих уравнений находим реакции опор
RA = 12.67кН.
RE = 11.33кН.
Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений
На участке AB: (0 ≤ z1 ≤ 2 м )
Q(z1) = + RA = + 12.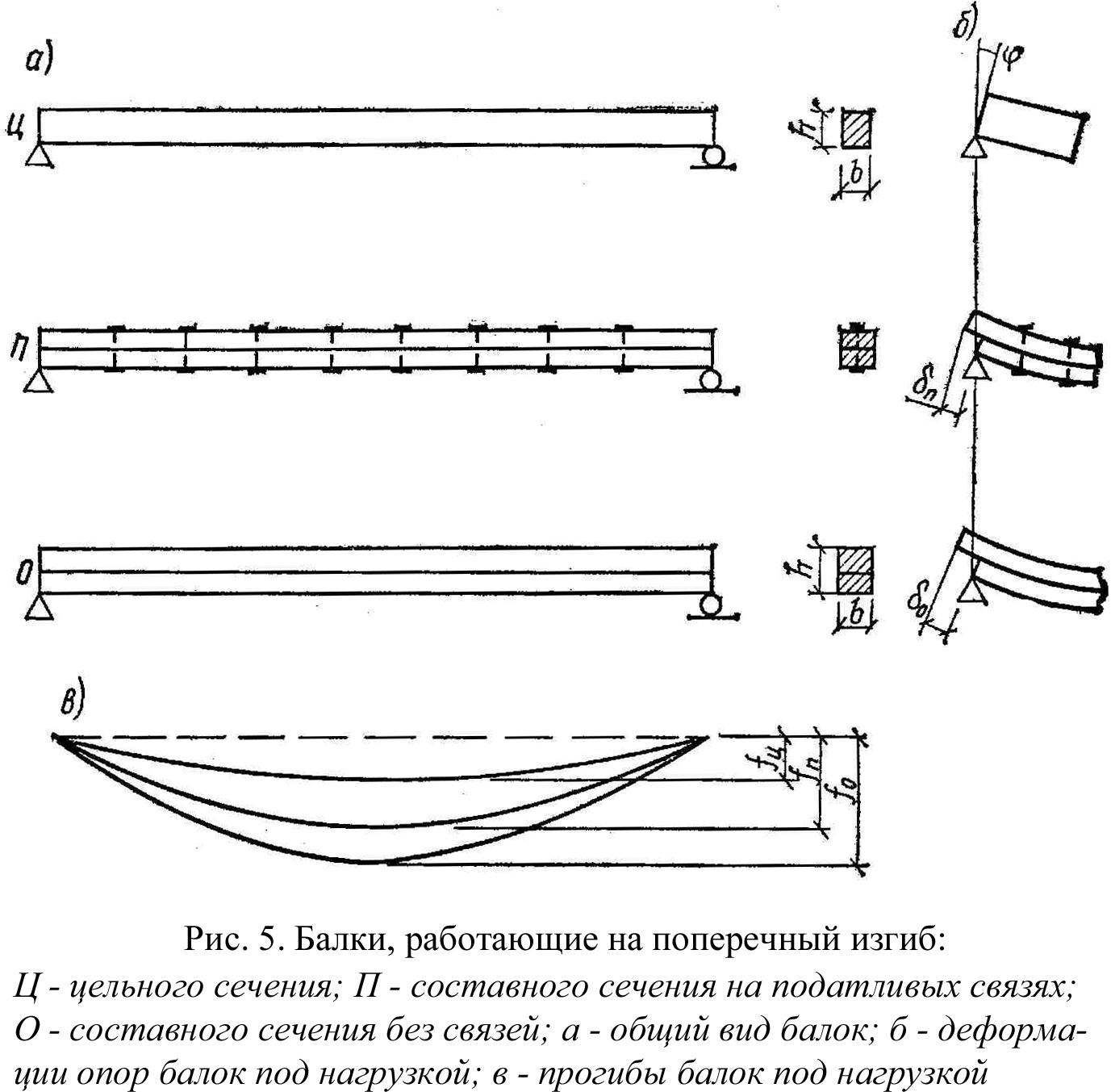 67 = 12.667 кН
67 = 12.667 кН
M(z1) = + RA · z = + 12.67 · z
M(0) = 0 кНм
M(2) = 25.333 кНм
На участке BC: (2 ≤ z2 ≤ 4 м )
Q(z2) = + RA – P – q1·(z – 2) = + 12.67 – 12 – 6·(z – 2)
Q(2) = 0.667 кН
Q(4) = -11.333 кН
M(z2) = + RA · z – P·(z – 2) – q1·(z – 2)2/2 = + 12.67 · z – 12·(z – 2) – 6·(z – 2)2/2
M(2) = 25.333 кНм
M(4) = 14.667 кНм
Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M
M(2.11) = 25.4 кНм
На участке CD: (4 ≤ z3 ≤ 5 м )
Q(z3) = + RA – P – Q1 = + 12.67 – 12 – 12 = -11.333 кН
M(z3) = + RA · z – P·(z – 2) – Q1·(z – 3) = + 12.67 · z – 12·(z – 2) – 12·(z – 3)
M(4) = 14.667 кНм
M(5) = 3.333 кНм
На участке DE: (5 ≤ z4 ≤ 6 м )
Q(z4) = + RA – P – Q1 = + 12.67 – 12 – 12 = -11.333 кН
M(z4) = + RA · z – P·(z – 2) + M – Q1·(z – 3) = + 12.67 · z – 12·(z – 2) + 8 – 12·(z – 3)
M(5) = 11.333 кНм
M(6) = 0 кНм
Максимальный момент в балке составляет Mmax = 25.4 кНм. По этому значению подбираем сечение балки.
Условие прочности при изгибе σ = Mmax / W ≤ [σ]
Отсюда, минимально необходимый момент сопротивления вычисляем по формуле Wmin=Mmax / [σ]
Расчет прогиба балки на двух опорах
Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2. 09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.
09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
- Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Методика выполнения расчета на прогиб
Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.
Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.
В нашем случае балка:
- Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
- Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
- Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.
Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.
Вычисляем моменты инерции и сил
Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).
Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.
Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).
Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h2/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h3/12, где b и h – размеры сечения балки.
Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.
Формулы для практического использования
На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.
Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:
- Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
- По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
- По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.
Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.
Заключение
Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.
Что еще почитать по теме?
Автор статьи:Сергей Новожилов – эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.
Понравилась статья? Поделись с друзьями в социальных сетях:Вконтакте
Одноклассники
Google+
Расчет балки на прочность онлайн калькулятор
Балка длиной L загружена равномерно распределенной нагрузкой q либо сосредоточенной силой P, которые необходимо будет задать
(как собрать нагрузки на балку можно получить тут Сбор нагрузок (калькулятор).
Все геометрические размеры сечения можно задать самому, поэтому в калькуляторе реализован огромный выбор самых различных балок: труба,
швеллер, профильная труба, двутавр, уголок, пластина и др.
Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.
Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.
В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения (труба, швеллер, профильная труба, двутавр, уголок, пластина и др.)
2. Выбрать материал (сталь, дерево)
3. Выбрать необходимую расчетную схему
Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка, свободный конец балки.
Коэффициенты поправки расчетного сопротивления дерева на изгиб приняты следующие:
Mдл = 0.66 – совместное действие постоянной и кратковременной снеговой нагрузок
Mв = 0.9 – нормальные условия эксплуатации дерева (влажность менее 12%)
Mт = 0.8 – эксплуатация дерева при температуре 50 градусов
Mсс = 0.9 – срок эксплуатации конструкции 75 лет
При расчете уже учитывается собственный вес конструкции.
Последние изменения
1. Добавлена возможность расчета балки при сосредоточенной нагрузке
– Добавлена проверка устойчивости стенки и полки двутавра, швеллера, уголка, профильной трубы
– Исправлено расчетное сопротивление дерева на изгиб согласно СП 64.13330.2017 “Деревянные конструкции”
– Исправлены расчетные сопротивления стали
– Исправлено допустимое эквивалентное напряжение при действии нормальных и касательных напряжений
– Добавлена возможность поворота швеллера
Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.
Напряжение и отклонение балки | MechaniCalc
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Многие конструкции можно представить как прямую балку или как набор прямых балок. По этой причине анализ напряжений и прогибов в балке является важной и полезной темой.
В этом разделе рассматриваются поперечная сила и изгибающий момент в балках, диаграммы сдвига и момента, напряжения в балках и таблица общих формул прогиба балок.
Содержание
Сила сдвига и изгибающий момент
Чтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при граничных условиях. Например, консольная балка ниже имеет приложенную силу, показанную красным, а реакции показаны синим цветом при фиксированном граничном условии:
После того, как были решены внешние реакции, сделайте разрезы секций по длине балки и решите реакции на каждом разрезе секции.Пример разреза показан на рисунке ниже:
Когда балка разрезается по сечению, при вычислении реакций можно учитывать любую сторону балки. Выбранная сторона не влияет на результаты, поэтому выберите наиболее легкую. На рисунке выше выбрана сторона балки справа от разреза. Реакции на разрезе показаны синими стрелками.
Подписать Конвенцию
Знаки сдвига и момента важны.Знак определяется после того, как сделан разрез и решены реакции для части балки на одной стороне разреза. Сила сдвига в разрезе секции считается положительной, если она вызывает вращение выбранной секции балки по часовой стрелке, и считается отрицательной, если вызывает вращение против часовой стрелки. Изгибающий момент в разрезе секции считается положительным, если он сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т.е. если он заставляет балку «улыбаться»).
Исходя из этого соглашения о знаках, поперечная сила в разрезе секции на рисунке выше является положительной, поскольку она вызывает вращение выбранной секции по часовой стрелке.Момент отрицательный, так как он сжимает нижнюю часть балки и удлиняет ее верх (т. Е. Заставляет балку «хмуриться»).
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Диаграммы сдвига и момента
Сдвиговый и изгибающий моменты в балке обычно выражаются диаграммами.Диаграмма сдвига показывает сдвиг по длине балки, а диаграмма моментов показывает изгибающий момент по длине балки. Эти диаграммы обычно показаны сложенными друг на друга, и комбинация этих двух диаграмм представляет собой диаграмму момента сдвига. Диаграммы момента сдвига для некоторых общих конечных условий и конфигураций нагрузки показаны в таблицах прогиба балок в конце этой страницы. Пример диаграммы момента сдвига показан на следующем рисунке:
Общие правила построения диаграмм момента сдвига приведены в таблице ниже:
| Диаграмма сдвига | Схема моментов |
|---|---|
|
|
Напряжения изгиба в балках
Изгибающий момент M по длине балки можно определить по диаграмме моментов.Изгибающий момент в любом месте балки затем можно использовать для расчета изгибающего напряжения по поперечному сечению балки в этом месте. Изгибающий момент изменяется по высоте поперечного сечения в соответствии с формулой изгиба , приведенной ниже:
где M – изгибающий момент в интересующем месте по длине балки, I c – центроидный момент инерции поперечного сечения балки, а y – расстояние от нейтральной оси балки до интересующей точки по высоте. поперечного сечения.Отрицательный знак указывает, что положительный момент приведет к сжимающему напряжению выше нейтральной оси.
Напряжение изгиба равно нулю на нейтральной оси балки, которая совпадает с центром тяжести поперечного сечения балки. Напряжение изгиба линейно увеличивается от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Максимальное напряжение изгиба определяется как:
где c – центроидное расстояние поперечного сечения (расстояние от центроида до крайнего волокна).
Если балка асимметрична относительно нейтральной оси, так что расстояния от нейтральной оси до верха и низа балки не равны, максимальное напряжение будет возникать в самом дальнем от нейтральной оси месте. На рисунке ниже растягивающее напряжение в верхней части балки больше, чем сжимающее напряжение в нижней части.
Модуль упругости поперечного сечения объединяет центроидный момент инерции I c и центральное расстояние c:
Преимущество модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним термином.Модуль сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении:
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Напряжения сдвига в балках
Сила сдвига V по длине балки может быть определена из диаграммы сдвига.Сила сдвига в любом месте вдоль балки затем может использоваться для расчета напряжения сдвига по поперечному сечению балки в этом месте. Среднее напряжение сдвига по поперечному сечению определяется как:
Напряжение сдвига меняется по высоте поперечного сечения, как показано на рисунке ниже:
Напряжение сдвига равно нулю на свободных поверхностях (вверху и внизу балки) и максимально в центре тяжести. Уравнение для касательного напряжения в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения, определяется следующим образом:
где V – поперечная сила, действующая в месте поперечного сечения, I c – центроидный момент инерции поперечного сечения, а b – ширина поперечного сечения.Все эти термины являются константами. Член Q – это первый момент области, ограниченной интересующей точкой и крайним волокном поперечного сечения:
Напряжения сдвига для нескольких общих поперечных сечений обсуждаются в следующих разделах.
Напряжения сдвига в прямоугольном сечении
Распределение касательного напряжения по высоте прямоугольного поперечного сечения показано на рисунке ниже:
Первый момент площади в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
Максимальное значение Q приходится на нейтральную ось луча (где y 1 = 0):
Напряжение сдвига в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле:
где I c = b · h 3 /12 – центроидный момент инерции поперечного сечения.Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле:
где A = b · h – площадь поперечного сечения.
Обратите внимание, что максимальное напряжение сдвига в поперечном сечении на 50% выше, чем среднее напряжение V / A.
Напряжения сдвига в круглых сечениях
Круглое поперечное сечение показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что напряжение сдвига по ширине балки является постоянным.Это предположение справедливо в центре тяжести кругового поперечного сечения, хотя нигде больше не действует. Следовательно, хотя распределение напряжения сдвига по высоте поперечного сечения не может быть легко определено, максимальное напряжение сдвига в сечении (возникающее в центре тяжести) все же может быть вычислено. Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2r – диаметр (ширина) поперечного сечения, I c = πr 4 /4 – центроидный момент инерции, а A = πr 2 – площадь поперечного сечения.
Напряжения сдвига в круглых сечениях труб
Круглое поперечное сечение трубы показано на рисунке ниже:
Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2 (r o – r i ) – эффективная ширина поперечного сечения, I c = π (r o 4 – r i 4 ) / 4 – центроидный момент инерции, а A = π (r o 2 – r i 2 ) – площадь поперечного сечения.
Напряжения сдвига в двутавровых балках
Распределение напряжения сдвига вдоль стенки двутавровой балки показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что напряжение сдвига по ширине балки является постоянным. Это предположение справедливо для стенки двутавровой балки, но неверно для полок (особенно там, где стенка пересекает полки). Однако стенка двутавровой балки принимает на себя подавляющую часть усилия сдвига (примерно 90% – 98%, согласно Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига.
Первый момент площади перемычки двутавровой балки определяется как:
Напряжение сдвига вдоль стенки двутавровой балки определяется по формуле:
где t w – толщина стенки, а I c – центроидный момент инерции двутавровой балки:
Максимальное значение напряжения сдвига возникает на нейтральной оси (y 1 & равно; 0), а минимальное значение напряжения сдвига в полотне возникает на внешних волокнах полотна, где оно пересекает фланцы y 1 & equals; & pm; h w /2):
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Строит диаграммы сдвига и момента
- Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Таблицы прогиба балки
В таблицах ниже приведены уравнения прогиба, наклона, сдвига и момента вдоль прямых балок для различных конечных условий и нагрузок. Вы можете найти исчерпывающие таблицы в таких источниках, как Гир, Линдебург и Шигли.Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Консольные балки
Балки с простой опорой
Несъемные несущие балки
Подпишитесь, чтобы получать обновления о последних улучшениях:
Список литературы
- Будинас-Нисбетт, “Машиностроительный проект Шигли”, 8-е изд.
- Гир, Джеймс М., “Механика материалов”, 6-е изд.
- Линдебург, Майкл Р., “Справочное руководство по машиностроению для экзамена на физическую форму”, 13-е изд.
- “Руководство по анализу напряжений”, Лаборатория динамики полета ВВС, октябрь 1986 г.
Бесплатный калькулятор луча | Калькулятор изгибающего момента, поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн-калькулятор диаграмм изгибающего момента и поперечной силы, который может генерировать диаграммы реакций, поперечных сил (SFD) и изгибающих моментов (BMD) консольной балки или просто поддерживаемой балки.Используйте этот калькулятор пролета балки, чтобы определить реакции на опоры, построить диаграмму сдвига и момента для балки и рассчитать прогиб стальной или деревянной балки. Бесплатный онлайн-калькулятор балки для создания реакций, расчета прогиба стальной или деревянной балки, построения диаграмм сдвига и момента балки. Это бесплатная версия нашего полного программного обеспечения SkyCiv Beam. Доступ к нему можно получить из любой из наших Платных учетных записей, которая также включает в себя полное программное обеспечение для структурного анализа.
Используйте интерактивное окно выше, чтобы просмотреть и удалить длину балки, опоры и добавленные нагрузки. Любые внесенные изменения автоматически перерисовывают диаграмму свободного тела для любой балки с опорой или консольной балкой. Калькулятор реакции балки и расчет изгибающего момента будут запущены после нажатия кнопки «Решить» и автоматически сгенерируют диаграммы сдвига и изгибающего момента. Вы также можете щелкнуть отдельные элементы этого калькулятора балки LVL, чтобы редактировать модель.
Калькулятор пролета балки легко рассчитает реакции на опорах.Он может рассчитывать реакции на опорах консольных или простых балок. Это включает в себя расчет реакций консольной балки, которая имеет изгибающий момент, а также силы реакции x, y.
Вышеупомянутый калькулятор пролета стальной балки – это универсальный инструмент для проектирования конструкций, используемый для расчета изгибающего момента в алюминиевой, деревянной или стальной балке. Его также можно использовать в качестве калькулятора несущей способности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Он способен выдерживать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузки и 2 момента.Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками (UDL), треугольными распределенными нагрузками или трапециевидными распределенными нагрузками. Все нагрузки и моменты могут быть направленными как вверх, так и вниз по величине, что должно учитывать наиболее распространенные ситуации анализа балок. Расчет изгибающего момента и поперечной силы может занять до 10 секунд, и обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, диаграммой поперечной силы и диаграммой изгибающего момента балки.
Одна из самых мощных функций – использование его в качестве калькулятора отклонения балки (или калькулятора смещения балки). Это можно использовать для наблюдения расчетного прогиба балки с опорой или консольной балки. Возможность добавлять формы сечения и материалы делает его полезным в качестве калькулятора деревянных балок или в качестве калькулятора стальных балок для проектирования балок lvl или i. На данный момент эта функция доступна в SkyCiv Beam, который имеет гораздо больше функций для проектирования деревянных, бетонных и стальных балок.
SkyCiv предлагает инженерам широкий спектр программного обеспечения для структурного анализа и проектирования облачных вычислений. Как постоянно развивающаяся технологическая компания, мы стремимся внедрять инновации и совершенствовать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Для всех калькуляторов требуется браузер с поддержкой JAVA. Дополнительная информация Примечание:
** СОВЕТ: Для поиска на этой веб-странице выберите «ctrl + F», затем введите ключевое слово во всплывающем окне.** Меню структурных прогибов и напряжений Уравнения и калькуляторы нагружения упругих каркасов на прогиб и противодействие для Формулы реакции и прогиба и калькулятор для плоского нагружения упругих рам Уравнения и калькуляторы прогиба пластин и напряжений
Калькуляторы для общих инженерных приложений Формулы для круглых колец, момента, кольцевой нагрузки, радиального сдвига и деформации
Свойства сечения Выбранные формы Разработка и проектирование систем зубчатых передач и зубчатых передач
Теплообменная техника Калькуляторы для проектирования электротехники Уравнения и калькуляторы IEEE 1584-2018 Производство Калькуляторы простых механических рычагов Конструкция пружины Уравнения и анализ трения Гражданское строительство Расчет напряжения / прочности при установке болта и резьбы Тензодатчик Анализ допусков с использованием геометрических размеров Допуски GD&T и другие принципы Дизайн управления движением Конструкция сосуда высокого давления и конструкции цилиндрической формы Расчетные и инженерные уравнения и калькуляторы
Жидкости Допуск на изгиб листового металла Пластиковая защелка Конверсии, жидкости, крутящий момент, общие Решения для треугольников / тригонометрии Финансы и прочее. Калькуляторы проектных и инженерных данных по сварке Главное меню Инженерная физика |
Бесплатный калькулятор луча | ClearCalcs
Как использовать бесплатный калькулятор балки
Калькулятор балки ClearCalcs позволяет пользователю ввести геометрию и загрузку балки для анализа за несколько простых шагов. Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Ключевые свойства», где пользователь вводит геометрию выбранного сечения и опор балки.
- «Нагрузки», где можно вводить распределенные, точечные и приложенные моментные нагрузки,
- «Сводка», где отображаются основные выходные данные и диаграммы.
Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
1. Свойства входных клавиш
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки – это общая длина балки, включая все пролеты балки, в мм или футах.
Модуль Юнга имеет значение по умолчанию 200000 МПа или 29000 тысяч фунтов на квадратный дюйм для конструкционной стали, но его можно изменить Пользователь.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию имеет значения для обычной стальной балки.
Второй момент области (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs. Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю вводить любое количество опор и указывать их положение по длине балки. Тип опоры может быть закрепленным (фиксированный в перемещении, свободный поворот) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.
Вычислитель балок также учитывает пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не обязательно должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются по мере добавления, изменения или удаления опор в зависимости от указанной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке может быть присвоено имя пользователем.
Знаковое обозначение, используемое для нагрузки (показаны положительные значения):
Распределенная нагрузка указывается в единицах силы на единицу длины, кН / м или плс, вдоль балки и может применяться между любыми двумя точками.В калькуляторе можно использовать два разных типа:
Равномерная нагрузка имеет постоянную величину по всей длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Линейные нагрузки имеют переменную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки.Например, они могут представлять реакции других элементов, соединенных с балкой. Пользователь вводит имя, величину и местоположение слева от луча.
В приведенном ниже примере диаграммы из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой на заплату и точечной нагрузкой.
3. Итоговые результаты вычислений
После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов.Максимальные значения каждого из них выводятся как «Требование момента» , «Требование сдвига» и «Прогиб» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения – отклонение вверх. Знаковое соглашение, используемое на диаграммах поперечной силы и изгибающего момента, следующее (показаны положительные значения):
Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, поперечной силы или прогиба дает конкретные значения в этом месте вдоль балки.В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной и точечной нагрузкой.
Балки – поддерживаются с обеих сторон
Напряжение в изгибающейся балке можно выразить как
σ = y M / I (1)
, где
σ = напряжение (Па (Н / м) 2 ), Н / мм 2 , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м 4 , мм 4 , в 4 )
Калькулятор ниже можно использовать для расчета максимального напряжения и прогиба балок с одной одиночной или равномерно распределенной нагрузкой.
Балка, поддерживаемая на обоих концах – равномерная непрерывная распределенная нагрузка
Момент в балке с равномерной нагрузкой, поддерживаемой с обоих концов в положении x, может быть выражен как
M x = qx (L – x) / 2 (2)
где
M x = момент в положении x (Нм, фунт дюйм)
x = расстояние от конца (м, мм, дюйм)
Максимум момент находится в центре балки на расстоянии L / 2 и может быть выражен как
M max = q L 2 /8 (2a)
где
M макс = максимальный момент ( Нм, фунт-дюйм)
q = равномерная нагрузка на единицу длины балки (Н / м, Н / мм, фунт / дюйм)
9144 4 L = длина балки (м, мм, дюйм)
Максимальное напряжение
Уравнения 1 и 2a можно объединить, чтобы выразить максимальное напряжение в балке с равномерной нагрузкой, поддерживаемой на обоих концах на расстоянии L / 2 как
σ max = y max q L 2 / (8 I) (2b)
где
σ max = максимальное напряжение (Па (Н / м 2 ), Н / мм 2 , psi)
y max = расстояние до крайней точки от нейтральной оси (м, мм, дюйм)
- 1 Н / м 2 = 1×10 -6 Н / мм 2 = 1 Па = 1.4504×10 -4 фунтов на кв. Дюйм
- 1 фунт / дюйм (фунт / дюйм 2 ) = 144 фунта на квадратный дюйм (фунт на / фут 2 ) = 6 894,8 Па (Н / м 2 ) = 6,895×10 – 3 Н / мм 2
Максимальный прогиб :
δ max = 5 q L 4 / (384 EI) (2c)
где
δ макс = максимальный прогиб (м, мм, дюйм)
E = Модуль упругости (Па (Н / м 2 ), Н / мм 2 , psi)
Прогиб в положении x:
δ x = qx ( L 3 – 2 L x 2 + x 3 ) / (24 EI) (2d)
Примечание! – прогиб часто является ограничивающим фактором при проектировании балки.Для некоторых применений балки должны быть прочнее, чем требуется при максимальных нагрузках, чтобы избежать недопустимого прогиба.
Силы, действующие на концы:
R 1 = R 2
= q L / 2 (2e)
где
R = сила реакции (Н, фунт)
Пример – балка с равномерной нагрузкой, метрические единицы
Балка UB 305 x 127 x 42 длиной 5000 мм несет равномерную нагрузку 6 Н / мм .Момент инерции балки составляет 8196 см 4 (81960000 мм 4 ) , а модуль упругости стали, использованной в балке, составляет 200 ГПа (200000 Н / мм 2 ) . Высота балки 300 мм (расстояние от крайней точки до нейтральной оси 150 мм ).
Максимальное напряжение в балке можно рассчитать
σ max = (150 мм) (6 Н / мм) (5000 мм) 2 / (8 (81960000 мм 4 ))
= 34.3 Н / мм 2
= 34,3 10 6 Н / м 2 (Па)
= 34,3 МПа
Максимальный прогиб балки можно рассчитать
δ макс = 5 (6 Н / мм) (5000 мм) 4 / (( 200000 Н / мм 2 ) ( 81960000 мм 4 ) 384)
= 2,98 мм
Расчет балки с равномерной нагрузкой – метрические единицы
- 1 мм 4 = 10 -4 см 4 = 10 -12 м 4
- 1 см 4 = 10 -8 м = 10 4 мм
- 1 дюйм 4 = 4.16×10 5 мм 4 = 41,6 см 4
- 1 Н / мм 2 = 10 6 Н / м 2 (Па)
Расчет балки с равномерной нагрузкой – Британские единицы
Пример – балка с равномерной нагрузкой, британские единицы
Максимальное напряжение в стальной широкополочной балке W 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, при равномерной нагрузке 100 фунтов / дюйм можно рассчитать как
σ max = y max q L 2 / (8 I)
= (6.25 дюймов (100 фунтов / дюйм) (100 дюймов) 2 / (8 (285 дюймов 4 ))
= 2741 (фунт / дюйм 2 , psi)
Максимальное отклонение может можно рассчитать как
δ max = 5 q L 4 / (EI 384)
= 5 (100 фунтов / дюйм) (100 дюймов) 4 / ((2
00 фунтов / дюйм
2 ) (285 дюймов 4 ) 384)= 0,016 дюйма
Балка, поддерживаемая на обоих концах – нагрузка в центре
Максимальный момент в балке с центральной нагрузкой, поддерживаемой с обоих концов :
M max = FL / 4 (3a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой на обоих концах:
σ max = y max FL / (4 I) (3b) 900 12
, где
F = нагрузка (Н, фунт)
Максимальный прогиб может быть выражен как
δ max = FL 3 / (48 EI) (3c)
Силы, действующие на концы:
R 1 = R 2
= F / 2 (3d)
Калькулятор балки с одним центром нагрузки – метрические единицы
Калькулятор балки с одним центром нагрузки – британская система мер Единицы измерения
Пример – балка с одноцентровой нагрузкой
Максимальное напряжение в стальной широкополочной балке шириной 12 x 35 дюймов, 100 дюймов длиной , момент инерции 285 дюймов 4 , модуль упругости 200 psi
, с центральной нагрузкой 10000 фунтов можно рассчитать как
σ max = y max FL / (4 I)
= (6.25 дюймов) (10000 фунтов) (100 дюймов) / (4 (285 дюймов 4 ))
= 5482 (фунт / дюйм 2 , psi)
Максимальный прогиб можно рассчитать как
δ макс = FL 3 / EI 48
= (10000 фунтов / дюйм) (100 дюймов) 3 / ((200 фунтов / дюйм
2 ) (285 дюймов 4 ) 48 )
= 0,025 дюйма
Некоторые типичные пределы отклонения по вертикали
- Общее отклонение: пролет / 250
- отклонение при динамической нагрузке: пролет / 360
- консоли: пролет / 180
- балки деревянных перекрытий для дома: пролет / 330 (макс. 14 мм)
- хрупкие элементы: пролет / 500
- подкрановые балки: пролет / 600
Балка, поддерживаемая на обоих концах – эксцентричная нагрузка
Максимальный момент в балке с одиночной эксцентричной нагрузкой в точке нагрузки:
M макс = F ab / L (4a)
Максимальное напряжение
Максимальное напряжение в балке с одноцентровой нагрузкой, поддерживаемой с обоих концов:
σ max = y max F ab / (LI) (4b)
Максимальный прогиб в точке нагрузки можно выразить как
δ F = F a 2 b 2 / (3 EIL) (4c)
Силы, действующие на концы:
R 1 = F b / L (4d)
R 2 = F a / L (4e)
Балка, поддерживаемая на обоих концах – две эксцентрические нагрузки
Максимальный момент (между нагрузками) в балке с двумя эксцентрическими нагрузками:
M max = F a (5a)
Максимальное напряжение
Максимальное напряжение в балке с двумя эксцентрическими нагрузками, поддерживаемыми на обоих концах:
σ max = y max F a / I (5b)
Максимум прогиб в точке нагрузки можно выразить как
δ F = F a (3L 2 – 4 a 2 ) / (24 EI) (5c)
Силы, действующие на концы:
R 1 = R 2
= F (5d)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Балка поддерживается на обоих концах – трехточечная нагрузка
Максимальный момент (между нагрузками) в балке с тремя точечными нагрузками:
M max 90 091 = FL / 2 (6a)
Максимальное напряжение
Максимальное напряжение в балке с тремя точечными нагрузками, поддерживаемыми с обоих концов:
σ max = y max FL / (2 I) ( 6b)
Максимальное отклонение в центре балки может быть выражено как
δ F = FL 3 / (20.22 E I) (6c)
Силы, действующие на концы:
R 1 = R 2
= 1,5 F (6d)
I Расчет прочности на прочность балки
Расчет расчетной прочности двутавровой балки для расчета нормальное напряжение, напряжение сдвига и напряжение фон Мизеса в критических точках данного сечение двутавра.
Поперечная нагрузка на двутавровую балку может привести к нормальным напряжениям и напряжениям сдвига. одновременно на любом поперечном сечении двутавра.Нормальное напряжение на данном поперечном сечении изменяется относительно расстояние y от нейтральной оси, и оно наибольшее в самой дальней точке от нервная ось. Нормальное напряжение также зависит от изгибающего момента в сечение и максимальное значение нормального напряжения в двутавровой балке возникает там, где изгибающий момент наибольший. Максимальное напряжение сдвига возникает на нейтральной оси двутавровой балки, где сила сдвига максимальна.
Примечание. Для получения дополнительной информации о см. разделы «Напряжения сдвига в тонкостенных элементах» и «Конструкция балок и валов на прочность »главы механики материалов .
Примечание: V и M – поперечная сила и изгибающий момент в сечении, как показано на фигура. Посетить ” «Калькуляторы прогиба и напряжения несущей балки» для расчета поперечной силы и изгибающего момента.
Примечание. Предполагается, что на несущую балку действует вертикальная сила сдвига в вертикальной плоскости симметрии.
| РЕЗУЛЬТАТЫ | ||
| Параметр | Стоимость | |
| Площадь поперечного сечения [A] | — | мм ^ 2 см ^ 2 дюйма ^ 2 фута ^ 2 |
| Первый момент площади для секции A [Q A ] | — | мм ^ 3 см ^ 3 дюйма ^ 3 фута ^ 3 |
| Первый момент площади для секции B [Q B ] | — | |
| Первый момент площади для секции D [Q D ] | — | |
| Второй момент площади [I zz ] | — | мм ^ 4 см ^ 4 дюйма ^ 4 фута ^ 4 |
| Расчет напряжений на участке A | МПапсикси | |
| Нормальное напряжение [σ x_A ] | — | |
| Напряжение сдвига [τ xy_A ] | — | |
| Напряжение по Мизесу при A [σ v_A ] | — | |
| Расчет напряжений на участке B | ||
| Нормальное напряжение при B [σ x_B ] | — | |
| Напряжение сдвига при B [τ xy_B ] | — | |
| Напряжение фон Мизеса при B [σ v_B ] | — | |
| Расчет напряжений на участке D | ||
| Нормальное напряжение при D [σ x_D ] | — | |
| Напряжение сдвига при D [τ xy_D ] | — | |
| Напряжение по Мизесу при D [σ v_D ] | — | |
Примечание: используйте точку “.”как десятичный разделитель.
Примечание. Напряжения являются положительными числами, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.
Примечание. Эффекты концентраций напряжений не учитываются в расчетах.
Двутавровая балка: Двутавровая балка – разновидность балки. часто используется в фермах в зданиях.Двутавровая балка обычно изготавливается из конструкционные стали, подвергнутые горячей и холодной прокатке или сварке. Верхняя и нижняя пластины двутавровой балки называются полками, а вертикальная пластина, соединяющая полки, называется стенкой.
Нормальное напряжение: Напряжение действует перпендикулярно поверхности (поперечному сечению).
Второй момент области: способность поперечного сечения противостоять изгибу.
Напряжение сдвига: Напряжение, действующее параллельно поверхности (поперечному сечению), имеет режущий характер.
Напряжение: Среднее усилие на единицу площади, которое приводит к деформации материала.
Гибка балок
Введение
На этой странице рассматривается классическая теория изгиба балок, которая является важным фактором почти во всех конструктивных решениях и анализы. Хотя это менее очевидно, это также относится к продольному изгибу колонны. также. И это, по сути, второй мотив этого страницы, чтобы заложить основу для предстоящего обсуждения теории продольного изгиба колонн.Цель не состоит в том, чтобы охватить все аспекты изгиба балки. В частности, такие темы, как определение нейтральной оси, теорема о параллельной оси и расчет прогибов балок не рассматривается.
Радиус кривизны
Радиус кривизны имеет фундаментальное значение для изгиба балки, поэтому он будет рассмотрено здесь. Обычно обозначается греческой буквой \ (\ rho \), и его можно представить как радиус круга, имеющего ту же кривизну, что и часть графика, изгиб дороги или любой другой путь.Когда путь прямой, \ (\ rho \) бесконечен, а когда путь имеет острый кривая в нем, \ (\ rho \) мала. В конечном итоге нам понадобится аналитическое выражение для радиуса кривизны,
так что он будет развиваться здесь. Начните с любой функции \ (y = y (x) \), как
показано на рисунке. Напомним, что длина дуги \ (s \) связана с
\ (\ rho \) через \ (\ rho \, \ theta = s \), где \ (\ theta \) – угол
дуги. В дифференциальной форме это \ (\ rho \, d \ theta = ds \).
Теперь разделите обе части на \ (dx \).{3/2}}
\]
Интересно, что любое выражение, включающее радиус кривизны, кажется, всегда имеет
появляются в знаменателе. И это не исключение, даже если это
определяющее уравнение.
Также интересен тот факт, что многие приложения механики включают гибку,
но в малых масштабах. Обсуждаемый здесь изгиб балки не является исключением. В таких случаях,
лучший подход – определить ось x вдоль луча так, чтобы
прогибы \ (y \) и, что более важно, деформированный уклон \ (y ‘\) будут
оба будут маленькими.3}
\]
где \ ({\ bf v} \) – вектор, определяемый параметрически как \ ({\ bf v} = {\ bf v} (x (t), y (t), z (t)) \),
\ ({\ bf v ‘} \) – его первая производная, \ ({\ bf v’ ‘} \) – его вторая производная, и
\ (| … | \) представляет длину вектора, то есть квадратный корень из суммы
квадраты его составляющих.
Деформации при изгибе
Напомним, что длина дуги \ (L \) связана с радиусом кривизны \ (\ rho \) через \ (L = \ rho \, \ theta \), где \ (\ theta \) – угол.Все становится сложнее, если принять во внимание толщину. На рисунке ниже объект начальной длины \ (L_o \) изогнут. как показано. Поскольку он имеет конечную толщину, различные его части растягиваются, или сжатые, в разном количестве. Внешняя часть балки растягивается больше всего, потому что он дальше всего от этот центр. Математически все части изогнуты под одинаковым углом, \ (\ theta \), но \ (\ rho \) изменяется по толщине, поэтому количество \ (\ rho \, \ theta \) тоже меняется, и, следовательно, меняется и \ (L \).
Следующий шаг – принять осознанное решение, чтобы избежать путаницы, связанной с наличием множества разные радиусы кривизны по толщине изгибаемого объекта. Это выполняется в два этапа.
Сначала найдите тот \ (\ rho \), который удовлетворяет \ (\ rho \, \ theta = L_o \). Обратите внимание, что \ (\ rho \) – вычисленный результат здесь, а \ (\ theta \) и \ (L_o \) – входные данные. Также обратите внимание, что длина в уравнении равна \ (L_o \), исходная недеформированная длина, не деформированный. Этот шаг устанавливает одно уникальное значение \ (\ rho \) для поперечное сечение, а не иметь несколько значений, что может привести к большой путанице.
Нейтральная ось
Местоположение в поперечном сечении, где известно \ (\ rho \, \ theta = L_o \) как нейтральная ось . Это единственное место, где окончательная деформированная длина такая же, как и исходная недеформированная длина, поэтому растяжения не происходит … из-за изгиба. Не думайте, что нейтральная ось должна быть посередине. поперечного сечения объекта. Это не обязательно так, особенно если объект состоит из разных материалов с разными жесткости.Предупреждение “из-за изгиба” в предыдущем абзаце присутствует, потому что объект также может быть одновременно нагружен растяжением (или сжатием), которое его растягивает пока каждая точка в его поперечном сечении не будет длиннее (или короче, если сжато), чем исходная длина, \ (L_o \).
Второй шаг – ввести переменную \ (y \) как расстояние от нейтральной оси. с любым другим радиусом в поперечном сечении, как показано на рисунке ниже. В результате радиус кривизны при любом \ (y \) равно \ ((\ rho – y) \), а окончательная длина в любом \ (y \) дается выражением \ [
L = (\ rho – y) \ тета
\]
Напомним, что \ (L_o = \ rho \, \ theta \).Теперь деформацию \ (\ epsilon \) можно выразить как
\ [
\ epsilon_x = {L – L_o \ над L_o} = {(\ rho – y) \ theta – \ rho \, \ theta \ over \ rho \, \ theta}
\]
, что упрощает
\ [
\ epsilon_x = – {y \ over \ rho}
\]
Это ключевой результат для деформации объекта. Это показывает, что деформация равна нулю при \ (у = 0 \),
нейтральная ось, и линейно отклоняется от нее. Если объект толстый, то \ (y \) может принимать
на больших значениях, но не на тонких объектах. Вот почему толстые объекты
имеют большую жесткость на изгиб, чем тонкие предметы.
Кроме того, радиус кривизны в знаменателе учитывает многие эффекты изгиба. Когда объект не изогнут, тогда \ (\ rho \) бесконечно, а деформации, естественно, равны нулю. По мере изгиба объекта \ (\ rho \) уменьшается, и уравнение показывает, что деформации увеличиваются.
Наконец, обратите внимание, что деформация представляет собой нормальную деформацию и фактически является продольной, по длине балки. Обычно ось \ (x \) выравнивается по длина балки, создающая деформацию \ (\ epsilon_x \).
Напряжение изгиба
Теперь, когда у нас есть выражение для деформации, разработать выражение для стресса невозможно. будь проще. Умножьте деформацию на \ (E \), модуль упругости, для получения напряжения \ (\ sigma_x \). \ [
\ sigma_x = – {E \, y \ over \ rho}
\]
Хотя этот шаг был чрезвычайно простым, на самом деле он довольно глубок в том,
пренебрегали простотой. Напомним со страницы на
Закон Гука о том, что каждый компонент нормального напряжения
зависит от всех трех компонентов нормальной деформации.Но здесь у нас просто
умножили деформацию на \ (E \), чтобы получить напряжение. Этот шаг имеет ключевое предположение
встроено в него … что на балку не действуют боковые нагрузки / напряжения.
В таких случаях уравнения “работают” так, что \ (\ sigma_x = E \, \ epsilon_x \) как в
одноосное растяжение. Это происходит в большинстве балок, потому что они тонкие по сравнению с
их длина.

