Расчет двутавра на изгиб: Расчет двутавра на прогиб и изгиб
alexxlab | 26.07.2021 | 0 | Разное
расчет нагрузки, несущая способность, прочность
Двутавр – это металлопрофильная конструкция перекрытия, наклонная или горизонтальная, рассчитанная в первую очередь на изгиб. Прежде всего она находится под воздействием весовой нагрузки, направленной по вертикали. Фактически это первичное воздействие, которому должен противостоять прокатный профиль из металла.
Технические характеристики металлического профиля необходимы, чтобы их правильно применять в строительстве, ведь несмотря на большое разнообразие сфер применения, суть остается одна – создать надежную несущую конструкцию. Она позволяет преобразовывать архитектуру сооружений:
- увеличивает ширину пролетов зданий;
- значительно, примерно на 35%, уменьшить массу несущих конструкций;
- существенно увеличить рентабельность проектов.
Говоря о достоинствах конструкции, нельзя не отметить и минусы, хотя их немного. Основные из них – это
- необходимость применять при создании ребер жесткости дополнительную арматуру;
- достаточно существенные трудозатраты, которые нужны для ее изготовления.
Однако, следует отметить, что с другой стороны дополнительные ребра жесткости дают возможность:
- уменьшить общую металлоемкость сварной металлоконструкции, так как ощутимо уменьшают толщину стенок. Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики;
- помимо этого облегченная конструкция экономична и с точки зрения устройства фундамента, поскольку после снижения общей массы можно использовать фундамент под БМЗ (быстровозводимые здания).
Чтобы найти двутавр, подходящий для конкретного случая, требуется произвести некоторые расчеты. Обычно для этого используют таблицы или онлайн калькуляторы. В их основе лежат заданные два параметра: расстояние от одной стены до другой и будущая нагрузка на строительную конструкцию.
Прочность двутавровой балки определяется такими параметрами, как:
- длина,
- метод закрепления,
- форма,
- площадь поперечного сечения.
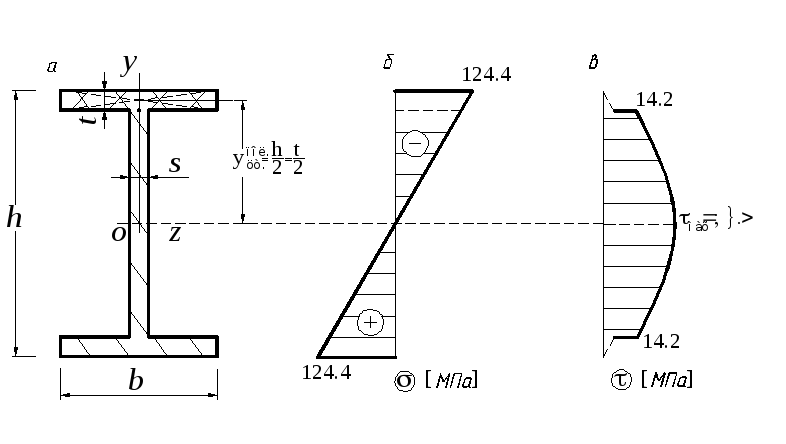
Большее распространение получили изделия с буквой «Н» в сечении.
На заметку
Жесткость металлической конструкции двутавра в 30 раз превышает жесткость квадратного профиля, а прочность, соответственно, в 7 раз.
Длина данной металлоконструкции бывает разной, к примеру, в случае ГОСТ 8239-89 это 4 –12 метров, то есть в зависимости от сортамента размеры и вес балки двутавровой отличаются. Помимо длины величина веса определяется толщиной металла и размерами граней. Поэтому для выполнения различных расчетов было введено понятие «вес метра балки двутавровой».
При покупке сварной конструкции обязательно требуется расчет на прочность, а для конкретного использования еще и расчет на прогиб. Грамотный расчет нагрузки на двутавровую балку позволит обеспечить устойчивость конструкции к проектным воздействиям, то есть способность воспринимать их без разрушения.
Нагрузка собственного веса ↑
Чтобы определить в случае необходимости вес двутавровой балки пользуются специальными таблицами, где расписаны ее характеристики, к примеру, габариты, марка стали и т. д. В таблице представлена теоретическая масса 1 м профиля.
д. В таблице представлена теоретическая масса 1 м профиля.
балка двутавровая размеры и вес (ГОСТ 8239-89)
Пример расчета двутавра ↑
Предположим необходимо рассчитать вес двутавра № 12 длиной в 3 метра. Согласно таблице условная масса погонного метра данного профиля равна 11,50 кг. Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Точнее значение веса сварной металлоконструкции можно посчитать, используя специальные онлайн калькуляторы, один из которых предоставлен на нашем сайте в рубрике “Калькуляторы”.
В калькуляторе выбирают соответствующий номер двутавра и вводят необходимый метраж. Как видите, полученное значение больше рассчитанного нами на 0,12 кг.
Несущая способность ↑
Среди всех типов балок двутавровая имеет наибольшую прочность, более того, она устойчива к температурным перепадам. Допустимая нагрузка на двутавр бывает указана на маркировке, как размер. Чем больше число, указанное в его наименовании, тем большую нагрузку может воспринимать балка.
Любой расчет предполагает изначальное знание размеров прокатного или сварного профиля, его длины и ширины. Проясним смысл значения ширины на примере самой популярной балочной опоры – колонны.
Пример расчета
Предположим, что в сечении колонны лежит квадрат со стороной 510 мм, тогда на нее можно будет опереть профиль, для которого ширина не может превышать 460 мм. Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
После определения ширины переходят к выбору профиля и расчету нагрузки, воздействующей на профиль. Она представляет собой совокупность воздействий от перекрытия, а также воздействий временного и постоянного характера.
На заметку
Нагрузку, выражающую величину нормативной нагрузки, собирают на длину 1 м профиля.
Но, расчет несущей способности двутавровой балки предполагает учет другого воздействия. Чтобы получить расчетную нагрузку, рассчитанное нормативное воздействие умножается на так называемый коэффициент прочности по нагрузке. Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Полученных данных достаточно, чтобы из сортамента подобрать профиль, необходимый для изготовления сварного профиля. Как правило, с учетом прогиба конструкции рекомендуется выбирать профиль выше на два порядка.
Важно
Сварная металлическая конструкция должна использовать примерно 70–80% от максимально допустимого прогиба.
Усиление ↑
Если несущая способность двутавра оказывается недостаточной, то возникает необходимость ее усиления. Для различных элементов сварной конструкции этот вопрос решается по-разному.
К примеру, для элементов, воспринимающих нагрузки типа растяжения, сжатия или изгиба, используют такой вариант усиления: увеличивают сечение, иначе говоря, повышают жесткость, скажем, приварив дополнительные детали.
Теоретически – это один из лучших вариантов усиления, однако, при его реализации не всегда удается получить требуемый результат.
В какой степени можно ожидать такого понижения зависит от размеров двутавра и режима и направления сварочных работ. Если для продольных швов максимальное понижение оказывается в пределах 15%, то для швов в поперечном направлении оно может достичь и 40%.
Внимание
Поэтому при усилении двутавра под нагрузкой категорически запрещено накладывать швы в направлении, поперечном к элементу.
Расчетно и экспериментально было доказано, что оптимального результата усиления под нагрузкой можно получить при максимальном напряжении в 0,8 Ry, то есть 80% расчетного сопротивления стали, которая была использована для изготовления двутавра.
© 2021 stylekrov.ru
Расчет нагрузки двутавровой балки – максимальные значения + Видео
Расчет нагрузки двутавровой балки проводится для определения номера из списка сортамента при проектировании несущих конструкций зданий и сооружений.
1 Применение двутавровой балки и основные параметры
Основная функция двутавра при проектировании различных зданий и сооружений – создание надежной и эффективной несущей конструкции. В отличии от бетонных вариантов несущих конструкций, использование двутавровой балки позволяет добиться увеличения ширины пролетов жилых или коммерческих зданий и уменьшить массу основных несущих конструкций. Таким образом, существенно повышается рентабельность строительства.
Двутавровое балки
Двутавровый швеллер выбирается, исходя из длины и веса. Балки могут быть горячекатаными стандартными или специальными и иметь параллельные или наклонные грани полок. Они изготавливаются из низкоуглеродистой стали различных марок и используются в разных сферах строительства. Согласно нормам ГОСТ 823989, длина двутаврового швеллера может быть от 3 до 12 метров.
Масса двутавра рассчитывается согласно таблице сортамента, в которой указан конкретный номер и маркировка двутавровой балки, а также показатели ширины, высоты, толщины полок и средняя толщина стенок профиля. Таким образом, для определения массы, согласно таблице, необходимо знать нормативный вес одного погонного метра. Например, балка с номером 45, при весе погонного метра 66,5 кг, имеет длину 15,05 метров.
Помимо расчета массы, который можно провести, используя простой калькулятор, в процессе проектирования необходимо рассчитать максимальную и минимальную нагрузку на изгиб и прогиб (деформацию), чтобы выбрать подходящую под конкретные цели строительства двутавровую балку. Данные расчеты основаны на таких параметрах металлического профиля, как:
- минимальное и максимальное расстояние между полками (стенками) балки с учетом их толщины;
- максимальная нагрузка на будущую конструкцию перекрытия;
- тип и форма конструкции, метод крепления;
- площадь поперечного сечения.

В некоторых случаях для проведения расчетов может понадобиться и шаг укладки, то есть расстояние, через которое балки укладываются параллельно друг другу.
Расчет двутавровой балки, как правило, производится на прочность и прогиб. Для максимально точных расчетов в таблице сортамента и нормах ГОСТ прописаны и такие необходимые параметры, как момент сопротивления, который делится на статистический и осевые моменты. Помимо этого, иногда необходимо знать величину расчетного сопротивления, которая зависит от типа и марки стали, из которой изготовлена двутавровая балка, а также от типа производства (сварная или прокатная). В случае сварного профиля при расчете прочности прибавляется до 30 процентов к вычисленной несущей нагрузке профиля.
2 Выбор металлической балки по номеру и примеры расчета
В таблице сортамента все номера металлического двутавра указаны согласно нормам ГОСТ 823989. Таким образом, выбор номера должен осуществляться с учетом предполагаемой нагрузки на балку, длины пролетов, веса. Например, если максимальная нагрузка на двутавровую балку равна 300 кг/м.п, из таблицы выбирается балка номер 16, при этом пролет будет равен 6 метрам при шаге укладки от 1 до 1,2 метров. При выборе 20-го профиля максимальная нагрузка увеличивается до 500 кг/ м.п, а шаг может быть увеличен до 1,2 метра. Профиль с номерами 10 или 12 означает максимально допустимую нагрузку до 300 кг/м.п и сокращение пролета до 3-4 метров.
Таким образом, выбор номера должен осуществляться с учетом предполагаемой нагрузки на балку, длины пролетов, веса. Например, если максимальная нагрузка на двутавровую балку равна 300 кг/м.п, из таблицы выбирается балка номер 16, при этом пролет будет равен 6 метрам при шаге укладки от 1 до 1,2 метров. При выборе 20-го профиля максимальная нагрузка увеличивается до 500 кг/ м.п, а шаг может быть увеличен до 1,2 метра. Профиль с номерами 10 или 12 означает максимально допустимую нагрузку до 300 кг/м.п и сокращение пролета до 3-4 метров.
Применение балок в строительстве
Таким образом, расчет того, какую нагрузку выдерживает балка, производится так:
- определяется величина нагрузки, которая давит на перекрытие с учетом веса самого профиля (из таблицы), которая рассчитывается на 1 погонный метр профиля;
- полученная нагрузка, согласно формуле, умножается на показатель коэффициента надежности и упругости стали, который прописан в ГОСТ 823989;
- используя таблицу расчетных значений по ГОСТ, необходимо определить величину момента сопротивления;
- исходя из момента сопротивления, выбираем соответствующий номер из таблицы сортамента.

Рассчитывая несущую нагрузку при выборе профиля, рекомендуем выбирать номера балки на 1-2 пункта выше полученных расчетных значений. Несущая способность профиля также рассчитывается при определении нагрузки двутавровой балки на изгиб.
3 Как марки стали влияют на расчеты?
При расчете прочности несущей балки в обязательном порядке учитывается марка стали, которая использовалась в процессе производства, и тип производственного проката. Для сложных конструкций и возведения перекрытий жилых зданий, коммерческих помещений, мостов необходимо выбирать балки из максимально прочных марок стали. Изделия с более высокой прочностью обладают меньшими габаритными размерами, но при этом способны выдерживать большие нагрузки.
Балки на производстве
Таким образом, расчет на прочность рекомендуется проводить несколькими способами, а полученные данные сравнить для получения максимально точных результатов вычислений. При определении прочности необходимо знать нормативные и расчетные напряжения и учитывать такие параметры, как поперечные и продольные силы, а также крутящие моменты. Существует несколько вариантов расчетных калькуляторов, с помощью которых определяется максимально и минимально допустимая нагрузка на прочность.
Существует несколько вариантов расчетных калькуляторов, с помощью которых определяется максимально и минимально допустимая нагрузка на прочность.
4 Как вычислить нагрузку на деформацию?
Для определения нагрузки балки на деформацию необходимо учитывать такие параметры, как:
- расчетная и нормативная нагрузка;
- длина и вес перекрытия;
- нормативное сопротивление.
Двутавровые балки для строительства
При этом для некоторых типов балок невозможно рассчитать нагрузку на прогиб, ввиду их формы и видов крепления при строительстве. Следует также понимать, что деформация балки (прогиб) возникает в поворотных углах. Поэтому она сильно зависит от габаритов конструкции, ее назначения, марки стали и других свойств и показателей. Существует несколько формул и вариантов для расчета балки на прогиб, использование которых зависит от расчета деформации внизу и вверху балки. Чаще всего для того, чтобы вычислить максимальную нагрузку на прогиб, специалисты используют универсальную формулу. Величину нагрузки на будущую конструкцию необходимо умножить на ширину пролета в кубическом объеме. Полученный параметр разделите на произведение модуля упругости и величины инерционного момента.
Величину нагрузки на будущую конструкцию необходимо умножить на ширину пролета в кубическом объеме. Полученный параметр разделите на произведение модуля упругости и величины инерционного момента.
Модуль упругости вычисляется, исходя из конкретной марки стали, момент инерции прописан в ГОСТе по номеру выбранной балки. Полученное число необходимо умножить на коэффициент, равный 0,013. В том случае, если рассчитанный относительный коэффициент деформации больше или меньше, чем прописано в нормативе, то в строительной конструкции необходимо использовать двутавры большего или меньшего типоразмера из таблицы.
Следует понимать, что двутавровая балка, ввиду своей формы, конструкции и веса, довольно редко используется в частном строительстве. Обычно вместо балок применяются более легкие швеллеры или стальные уголки. Но если вы все же используете балку для строительства небольшого частного дома, дачи, то необязательно проводить сложные расчеты по всем видам деформации и нагрузок. Для небольшой конструкции перекрытия достаточно рассчитать максимальную и минимальную нагрузку на изгиб.
Для небольшой конструкции перекрытия достаточно рассчитать максимальную и минимальную нагрузку на изгиб.
Расчет балок на изгиб и прогиб, крутящие моменты и выбор двутавра для монтажа
Расчет нагрузки двутавровой балки – определяем нагрузку на изгиб
Расчет нагрузки двутавровой балки осуществляется с целью вычисления номера из реестра металлопроката при составлении проекта основных конструкций и сооружений, а так же производства по ГОСТ или СТО АСЧМ. Он выполняется точно по формулам и таблицам, а вычисленные значения оказывают влияние на проектировку и ход строительных работ, также на рабочую функциональность и технические характеристики при эксплуатации.
Сфера применения и параметры металлических двутавров
Главное предназначение двутавра во время проектировки любого типа сооружения заключается в изготовлении безопасной и крепкой несущей конструкции. В отличие от железобетонных опорных оснований, применение двутавровой балки дает возможность наиболее увеличить площадь пролетов частных либо коммерческих строений и снизить предельный вес важных опорных элементов. Благодаря этому, значительно увеличивается прибыльность строительства и решается ряд важных инженерных задач.
Благодаря этому, значительно увеличивается прибыльность строительства и решается ряд важных инженерных задач.
Двутавровая балка подбирается из расчета длины и массы. Балочная продукция бывает обычного горячего проката либо специализированного, и иметь параллельные и с наклоном полочные грани. Они производятся из углеродистой или из низколегированной стали и применяются во всех строительных отраслях.
Согласно требованиям стандартизации 8239-89, размер металлического двутавра варьируется от трех до двенадцати метров. По способу применения данные элементы являются балочными, колонными, широко – полочными либо монорельсными, использующиеся при возведении подвесных элементов подкрановых путей и мостов. Определяется категория балки по специальному маркированию в таблице металлопроката, а точнее в ГОСТе и СТО АСЧМ, а правила применения и монтажа регламентированы документацией СНиП (Строительных норм и правил).
Масса двутавра определяется по утвержденному графику, в котором четко указан определенный числовой символ и обозначение балки, а еще немало важные параметры (ширина, высота, объемность полок и оптимальная толщина граней). Таким образом, для вычисления массы, по реестру требуется учесть установленный нетто погонного метра. К примеру, изделие под номером 46, при массе 65,5 кг, обладает длинной 15,5 метров.
Таким образом, для вычисления массы, по реестру требуется учесть установленный нетто погонного метра. К примеру, изделие под номером 46, при массе 65,5 кг, обладает длинной 15,5 метров.
Кроме расчетов массы, которые выполняются при помощи обычного калькулятора, во время проектирования важно вычислить наибольшую и наименьшую совокупность сил на предмет повреждения.
Расчеты основываются на следующих характеристиках металлопрофиля:
- Минимальная и максимальная дистанция между полками, беря во внимание их размеры.
- Наибольшая нагрузочная величина на проектируемое сооружение.
- Тип и геометрические формы изделий, способ фиксирования.
- Плоскость поперечного диаметра.
- Возникают ситуации, когда для вычислений требуется укладочный шаг (промежуток укладывания балок относительно друг друга).
Расчет двутавровой балки зачастую производится по критериям безопасности и просчета изгиба. Для достижения наиболее высокоточных значений в таблице металлопроката и основных требованиях указываются все дополнительные значения (момент сопротивления, делящийся на осевой и статический). Кроме этого нужно учитывать нагрузку на двутавр, зависящую от разновидностей металла, из которого изготавливается двутавр, и метод производства (сварка либо прокат). При сварном производстве во время расчетов добавляется около 30% к опорной нагрузке металлопрофиля.
Кроме этого нужно учитывать нагрузку на двутавр, зависящую от разновидностей металла, из которого изготавливается двутавр, и метод производства (сварка либо прокат). При сварном производстве во время расчетов добавляется около 30% к опорной нагрузке металлопрофиля.
Выбор металлической балки по номеру и примеры расчета
В реестре металлопроката все номера двутавровых швеллеров указаны по всем требованиям ГОСТ стандарта. Таким образом, подбор номера обязан производиться, учитывая рабочую нагрузку, расстояние пролетов и вес продукции. К примеру, если наибольшая нагрузка на двутавр равняется 300 кг/м.п, из таблицы берется двутавровая балка под цифрой 16, при этом промежуточная дистанция равняется шести метрам при укладочном шаге от 1 до 1,2 метров. При подборе 20 металлопрофиля нагрузка на двутавр сильнее – до 500 кг/ м.п, а шаг соответственно до 1,5 метра. Изделие с порядковой нумерацией 10 либо 12 обозначает предельно установленную нагрузку до 300 кг/м.п и уменьшение пролета.
Таким образом, расчетные действия, какую нагрузку может выдержать металлическое изделие, осуществляются так:
- Высчитывается единица нагрузки на двутавр, давящая на опорное основание с учетом массы металлопрофиля, которая рассматривается на один погонный метр изделия.
- Полученная величина, согласно нормативным документам, перемножается на коэффициент прочности стали, указанным в ГОСТ.
- Пользуясь данными расчетных величин, требуется вычислить значение сопротивляющегося момента.
- Далее из полученного результата, выбираем нужный элемент из реестра металлопроката.
- Делая расчеты опорной физической нагрузки при определении профиля, советуем подбирать числа на пару строк больше имеющегося значения. Несущая особенность металлопрофиля определяется при вычислении двутавра на сгибание.
Как марки стали воздействуют на предстоящее проектирование?
При вычислении прочности опорной балки следует учитывать марку металла, использующегося в технологическом процессе, и категорию металлопроката. Для сложнейших металлоконструкций и строений, перекрытий многоэтажных коттеджей, индустриальных комплексах, требуется подбирать элементы из наиболее крепкого металла высшего качества. Продукция с наивысшей прочностью отличается небольшими габаритами, но при этом могут выдерживать существенные нагрузки. Поэтому вычисления на прочность рекомендуется выполнять несколькими методами, а информацию всегда требуется сравнивать для получения наиболее правильных математических расчетов. При определении пределов надежности и безопасности требуется учитывать существующие величины давления и не забывать немаловажные факторы, такие как, поперечные и продольные силы, крутящий момент. Можно применять разные способы калькуляции, при помощи которой можно определить разрешенные пределы надежности.
Как подсчитать предстоящую нагрузку?
С целью определения нагрузочных параметров на деформирование требуется четко придерживаться нижеперечисленных моментов:
- Прогнозируемая и существующая нагрузка.

- Размеры и масса предполагаемой конструкции.
- Нормативная сопротивляемость.
Для многих видов балок нет возможности произвести определение нагрузки на сгибание, ввиду их конфигурации и разновидности установки при возведении сооружений. Деформирование балки (прогиб) образуется в поворотных углах. Поэтому оно очень зависит от общих параметров сооружения, ее предназначения, марки стали и иных функциональных факторов.
Существуют различные варианты уравнений и способов для расчета балки на прогиб, их использование характеризуется расчетом деформирования обоих оснований. Наиболее чаще для проведения любых вычислений максимального нагрузочного давления на прогиб, профессионалы применяют специальную математическую формулу. Величину нагрузки проектируемой опоры следует перемножить на промежуток пролета в кубе. Итоговый результат делится на общую сумму модуля гибкости и величины момента инерции.
Модуль гибкости можно вычислить по марке стали, момент инерции обозначен в правилах стандартизации по цифровому коду исходного материала. Исходные цифры требуется удвоить на коэффициент, который равен 0,013. Если уже имеющийся относительный коэффициент деформирование выше либо ниже, чем обозначено в существующих правилах, то в будущей конструкции следует брать изделия большего либо меньшего диаметра.
Исходные цифры требуется удвоить на коэффициент, который равен 0,013. Если уже имеющийся относительный коэффициент деформирование выше либо ниже, чем обозначено в существующих правилах, то в будущей конструкции следует брать изделия большего либо меньшего диаметра.
Требуется понимание того, что двутавровая балка, из – за своей конфигурации и массы, не очень часто находит применение при строительстве частных одноэтажных сооружений. Зачастую вместо них применяются облегченные швеллеры либо металлические углы. Но если вы все же планируете приобретение балок для постройки маленького домика, то не нужно решать сложнейшие математические задачи по всем критериям деформационных нагрузок. Хватит и элементарных расчетов допустимых пределов.
Как подобрать двутавр или швеллер для перекрытия? Максимальная нагрузка и прогиб (хозяину на заметку) | Строю для себя
Уважаемые гости, как и обещал в статье по расчету деревянных балок на прогиб (ссылка на статью), в данном материале речь пойдет о расчете стальной металлической балки для пролета: швеллера и двутавра.
В данной статье – расчет и выбор изделий выполняются в полном соответствии с учебной дисциплиной о механике твердого тела (раздел: сопротивление материалов).
Считаю нужным предупредить, что статья является полностью технической, поэтому не ругайте, знаю, что многие читатели Дзен не любят такое :)))
В предыдущей статье о деревянных балках – я получил много критики в комментариях, что, мол, 21 ВЕК на дворе, полным-полно он-лайн калькуляторов и готовых таблиц в интернете.
Конечно, можно довериться он-лайн калькуляторам, но поверьте, уделив 30-40 минут и вникнув самостоятельно – можно перепроверить любой калькулятор и спать спокойнее, потому что все выкладки производятся самостоятельно и результат налицо! А что касается таблиц, то любая из них, взятая из интернета – неизвестного происхождения, и велика вероятность взять недостоверные данные…
Итак, далее приведены выборки горячекатаных стальных изделий согласно соответствующих ГОСТов, по которым в зависимости от итогового расчета – мы выберем подходящую нам балку и её сечение (форму):
Сортамент двутавровСортамент двутавров
Сортамент швеллеровСортамент швеллеров
Для примера, в расчете берётся заводская длина стального изделия – 6 м. , а также выбирается шаг балок – 0,6 м. (соответственно, данные параметры будут у каждого разные в зависимости от ситуации).
, а также выбирается шаг балок – 0,6 м. (соответственно, данные параметры будут у каждого разные в зависимости от ситуации).
Имея чертеж, проект или набросок размеров комнат на бумаге, нужно определиться с расчетными длинами. Расстояние в свету (Lсв) – это длина перекрываемого пролета. Зная эту длину и минимальное опирание балки на стену Lоп = 120 мм., получаем длину балки (по нашему примеру L= 6 м.).
Иллюстрация автораИллюстрация автора
Для дальнейшего расчета, требуется знать расстояние между центрами опорных длин (Lo) – это главная величина, участвующая в расчете (см.рисунок выше).
Для начала, перед самим расчетом, требуется определиться с функцией помещения. Для жилого помещения – по нормативу, временная нагрузка от пребывания людей составляет 1,5 кПа или 150 кг./м2. (Р1).
По правилам расчета, закладываем запас надежности – 20%, поэтому далее используем коэффициент K1 = 1,2
После определения функции помещения и временной нагрузки, нам требуется посчитать собственный вес квадратного метра пола в сборе (весь пирог), а именно: вес балок, настил пола, потолок, шумоизоляция и т. п. В качестве примера, для расчета берем собственный вес – 150 кг./кв.м., таким образом Р2 = 150 кг./кв.м. Но, по правилам, уже нужно намеренно завысить надежность на 30%, соответственно К2 = 1,3.
п. В качестве примера, для расчета берем собственный вес – 150 кг./кв.м., таким образом Р2 = 150 кг./кв.м. Но, по правилам, уже нужно намеренно завысить надежность на 30%, соответственно К2 = 1,3.
Итак, считаем требуемый момент сопротивления W = M/(Yc*Ry),
W = 9.72 / (0.9*240) = 45 куб.см.
Получив момент сопротивления, возвращаемся к таблицам характеристик изделий (иллюстрации в самом начале). В данных таблицах, ГОСТом уже определены значения моментов для различных сечений, исходя из которых и выбираем балку, округляя W в большую сторону:
Для полученного момента 45 см3 подходит двутавр №12 со значением W=58.4 или швеллер №12, где W=50.6. Для нашего же примера – выбираем двутавр и далее проводим проверку на прогиб.
Важно сделать оговорку, что если Вас не устраивают балочные двутавры, существуют широкополочные или колонные двутавры, у которых при той же высоте – характеристики будут выше.Тем самым, вы сможете за счет более лучшей несущей способности уменьшить толщину всего перекрытия:
После того, как выбор стальной балки произведен, из таблички по соответствующей строке выписываем все характеристики выбранного изделия:
- Статический момент: S = 33,7 см3;
- Момент инерции: I = 350 см4;
- Толщина стенки: d = 4.8 мм.
Производим проверку на прогиб. В случае большого провиса по центру конструкции, нам потребуется взять двутавр, следующий за №12.
Проверка:
В расчете нам потребуется главная жесткостная характеристика материала – это модуль упругости, для стали он равен:
Е = 206 000 МПа.
Определяем прогиб по стандартной сопроматовской формуле:
Итак, вычисленный прогиб по центру – 3,89 см.
Его необходимо сравнить с эстетико-психологическими параметрами по СНиП (таблица Е.1)
Предельные прогибыПредельные прогибы
Почему эстетико-психологических? Дело в том, что несмотря на надежность конструкции – провис балки будет “давить на психику”, в связи с чем СНиПом предусматриваются допустимые величины прогибов.
Согласитесь, что не хочется нам в доме ловить взглядом выгнутый в дугу потолок и будет казаться, что он вот-вот треснет и свалится на голову.
Согласно таблице, у нас есть предельные прогибы по вертикали для балок: L/ххх. Для того, чтобы сравнить полученное значение с этой характеристикой, требуется рассчитать параметр предельно допустимых величин:
При вычислении, как пример – мы брали балку заводской длины – 6 м., поэтому ищем строку L=6м.:
Исходя из вычислений и из представленной таблицы, производим сравнение параметров прогиба: L/151 > L/200. Поскольку прогиб сильнее, чем нормативный, то выбранная стальная балка не удовлетворяет условию.
Другими словами, двутавр №12 провиснет при пролете 5,8 м. – на 3,9 см, что неприемлемо по СНиПу. Нам ничего не остается, как выбрать следующий по списку двутавр и снова выполнить проверку.
При двутавре №14, прогиб составляет 2,4 см. и параметр предельно допустимых величин равен Lo/f = 5,88/2,38 = 247.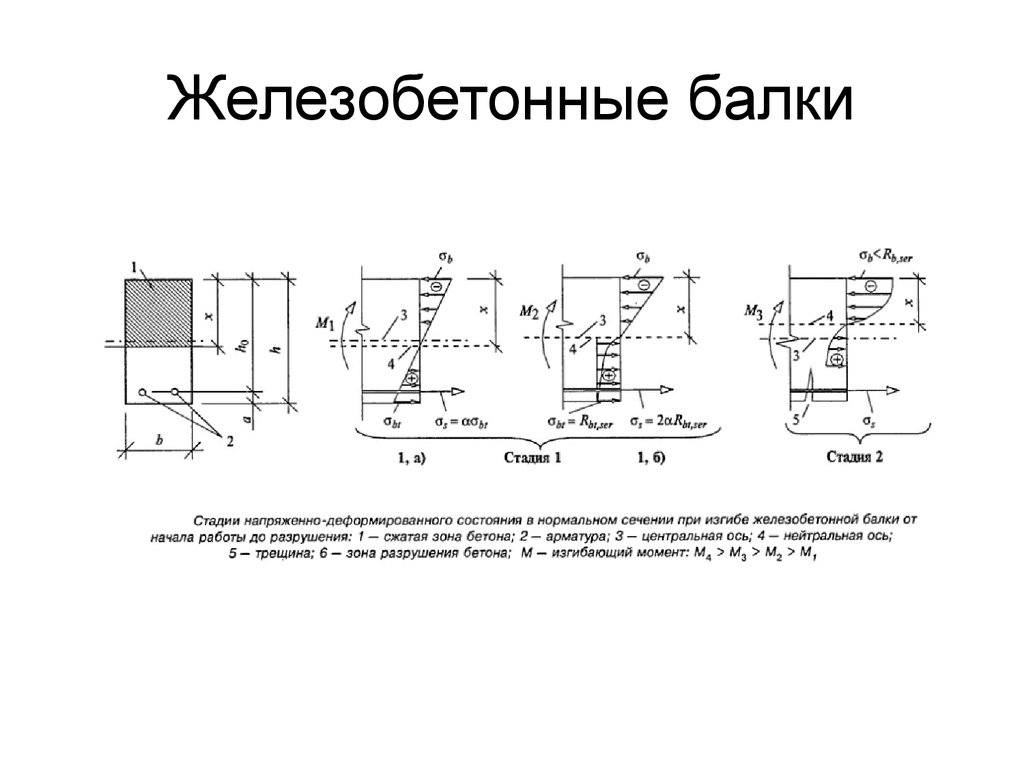
L/247 < L/200! Выбранный двутавр №14 – прошёл проверку и его можно использовать!
Пожалуйста, пользуйтесь!
___________________________________
Следующие темы, планируемые на канале: сравнение стоимости при использовании стальных и деревянных балок, а так же серия материалов о вариантах устройства монолитного перекрытия по швеллерам (двутаврам) и организация бетонирования участками (захватками).
Если данные темы интересны, подписывайтесь на мой канал!
Расчет деревянной балки
Зная тригонометрию, можно не бегать по крыше с рулеткой
Как определить высоту объекта на расстоянии?
Калькулятор расчета металлической двутавровой балки на прогиб, прочность
A1 6 ммА1 8 ммA1 10 ммА1 12 ммА1 14 ммА1 16 ммА1 18 ммА1 20 ммА3 35ГС 6 ммА3 35ГС 8 ммА3 35ГС 10 ммА3 35ГС 12 ммА3 35ГС 14 ммА3 35ГС 16 ммА3 35ГС 18 ммА3 35ГС 20 ммА3 35ГС 22 ммА3 35ГС 25 ммА3 35ГС 28 ммА3 35ГС 32 ммА3 35ГС 36 ммА3 25Г2С 8 ммА3 25Г2С 10 ммА3 25Г2С 12 ммА3 25Г2С 14 ммА3 25Г2С 16 ммА3 25Г2С 18 ммА3 25Г2С 20 ммА3 25Г2С 22 ммА3 25Г2С 25 ммА3 25Г2С 28 ммА3 25Г2С 32 ммА3 25Г2С 36 ммA500С 8 ммA500С 10 ммA500С 12 ммA500С 14 ммA500С 16 ммA500С 18 ммA500С 20 ммA500С 22 ммA500С 25 ммА500С 28 ммA500С 32 ммA500С 36 ммA500С 40 ммA400С 8 ммA400С 10 ммA400С 12 ммАт800 12 ммАт800 14 мм10, г/к12, г/к14, г/к16, г/к18, г/к20, г/к30, г/к36, г/к45, г/к24М30М36М45М10Б112Б114Б116Б120Б125Б130Б135Б140Б145Б150Б155Б160Б125Б230Б235Б240Б245Б255Б260Б220Ш125Ш130Ш135Ш140Ш145Ш150Ш130Ш235Ш240Ш250Ш220К125К130К135К140К120К225К230К235К240К220Б1 (09Г2С)25Б1 (09Г2С)30Б1 (09Г2С)35Б1 (09Г2С)40Б1 (09Г2С)45Б1 (09Г2С)50Б1 (09Г2С)55Б1 (09Г2С)60Б1 (09Г2С)25Б2 (09Г2С)30Б2 (09Г2С)35Б2 (09Г2С)40Б2 (09Г2С)45Б2 (09Г2С)55Б2 (09Г2С)20К1 (09Г2С)25К1 (09Г2С)30К1 (09Г2С)35К1 (09Г2С)25К2 (09Г2С)30К2 (09Г2С)35К2 (09Г2С)20Ш1 (09Г2С)25Ш1 (09Г2С)30Ш1 (09Г2С)35Ш1 (09Г2С)45Ш1 (09Г2С)30Ш2 (09Г2С)35Ш2 (09Г2С)50Ш2 (09Г2С)1,5х1250 г/к2,0х1250 г/к2,5х1250 г/к3,0х1250 г/к4,0х1500 г/к5,0х1500 г/к6,0х1500 г/к8,0х1500 г/к10,0х1500 г/к12,0х1500 г/к14,0х1500 г/к16,0х1500 г/к18,0х1500 г/к20,0х1500 г/к25,0х1500 г/к30,0х1500 г/к36,0х1500 г/к40,0х1500 г/к50,0х1500 г/к60,0х1500 г/к80,0х1500 г/к100,0х1500 г/к4,0х1500 г/к (09Г2С)5,0х1500 г/к (09Г2С)6,0х1500 г/к (09Г2С)8,0х1500 г/к (09Г2С)10,0х1500 г/к (09Г2С)12,0х1500 г/к (09Г2С)14,0х1500 г/к (09Г2С)16,0х1500 г/к (09Г2С)18,0х1500 г/к (09Г2С)20,0х1500 г/к (09Г2С)25,0х1500 г/к (09Г2С)30,0х1500 г/к (09Г2С)36,0х1500 г/к (09Г2С)50,0х1500 г/к (09Г2С)0,50х1250 х/к0,60х1250 х/к0,70х1250 х/к0,80х1250 х/к0,90х1250 х/к1,0х1250 х/к1,2х1250 х/к1,4х1250 х/к1,5х1250 х/к1,8х1250 х/к2,0х1250 х/к2,5х1250 х/к3,0х1250 х/к0,50х1250 х/к оц. 0,55х1250 х/к оц.0,70х1250 х/к оц.0,80х1250 х/к оц.1,0х1250 х/к оц.1,2х1250 х/к оц.1,5х1250 х/к оц.2,0х1250 х/к оц.3,0 мм (чечевица)4,0 мм (чечевица)5,0 мм (чечевица)6,0 мм (чечевица)8,0 мм (чечевица)ПВЛ-406ПВЛ-408ПВЛ-410ПВЛ-506ПВЛ-508ПВЛ-51025х25х4,032х32х4,035х35х4,040х40х4,045х45х4,045х45х5,050х50х5,063х63х5,063х63х6,070х70х6,075х75х5,075х75х6,075х75х8,080х80х6,080х80х8,090х90х7,090х90х8,0100х100х7,0100х100х8,0100х100х10,0110х110х8,0125х125х8,0125х125х9,0125х125х10,0125х125х12,0140х140х9,0140х140х10,0160х160х10,0160х160х12,0180х180х12,0200х200х12,0200х200х16,063х40х6,075х50х5,075х50х6,0100х63х6,0100х63х8,05П6,5П8П10П12П14П16П18П20П22П24П27П30П40П5У6,5У8У10У12У14У16У18У20У22У24У27У30У40У80х60х4,0100х50х4,0100х50х5,0120х50х3,0120х60х4,0120х60х5,0160х80х4,0180х80х5,0250х125х6,015х2,515×2,820х2,825х3,232х3,240х3,040х3,550х3,050х3,515×2,820х2,825х3,232х3,240х3,550х3,557х3,057х3,576х3,076х3,589х3,089х3,589х4,0102х3,0102х3,5102х4,0108х3,5108х4,0114х4,0114х4,5127х4,5133х4,0133х4,5159х4,0159х4,5159х5,0159х6,0219х4,5219х5,0219х6,0219х8,0273х5,0273х6,0273х7,0273х8,0325х6,0325х7,0325х8,0426х6,0426х7,0426х8,0426х9,0530х7,0530х8,0530х10,057х3,576х3,589х3,5108х3,5530х7,0530х8,0530х9,0530х10,0530х12,0630х8,0630х9,0630х10,0630х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х8,0820х9,0820х10,0820х11,0820х12,0530х7,0530х8,0530х9,0530х10,0530х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х9,0820х10,01020х10,01020х12,01020х14,01220х11,01220х12,01220х14,01420х14,057х3,557х4,057х5,057х6,076х3,576х4,076х5,076х6,083х4,089х3,589х4,089х5,089х6,0102х4,0102х5,0102х6,0108х4,0108х5,0108х6,0114х5,0114х6,0121х6,0127х5,0133х4,0133х4,5133х5,0133х6,0133х8,0146х5,0146х6,0159х5,0159х6,0159х7,0159х8,0168х6,0168х7,0168х8,0219х6,0219х7,0219х8,0219х10,0273х7,0273х8,0273х10,0325х8,0325х10,0377х9,0426х9,0426х10,010х2,014х2,016х2,016х3,018х2,018х3,020х2,022х2,022х2,522х3,025х2,025х3,027х3,028х3,028х4,028х7,032х3,034х3,538х3,038х4,040х3,040х3,542х3,042х5,045х3,045х6,048х3,051х2,551х3,057х3,060х3,063х4,015х1,520х1,520х2,025х1,525х2,030х1,530х2,040х1,540х2,040х2,540х3,050х2,050х3,050х4,060х2,060х3,060х4,080х3,080х4,080х5,0100×4,0100×5,0100×6,0120х4,0120х5,0120х8,0140х5,0140х6,0160х4,0160х5,0160х6,0180х8,0100х4,0100х5,0120х4,0120х5,0140х5,0140х6,0160х5,0160х6,0160х8,020х2,025х2,030х2,040х2,040х3,050х2,050х2,550х3,050х4,060х2,060х3,080х5,080х6,0100х5,0140х5,0140х6,028х25х1,530х20х1,540х20х1,540х20х2,040х25х1,540х25х2,050х25х1,550х25х2,050х25х2,550х30х2,060х30х2,060х30х2,560х30х3,060х40х2,060х40х2,560х40х3,080х40х2,080х40х3,080х40х4,080х60х4,0100х50х3,0100х50х4,0100х60х4,0120х60х4,0120x80x4,0120х80х6,0140x60x4,0150х100х6,0160х80х5,0160х120х4,028х25х2,040х20х2,040х25х2,050х25х2,050х25х2,560х30х2,060х30х2,560х40х2,060х40х2,580х40х2,080х60х4,0120х80х4,0150х100х6,0160х120х4,0Ø 6,5 мм (в бухтах)Ø 8 мм (в бухтах)Ø 10 мм (в бухтах)Ø 12 ммØ 14 ммØ 16 ммØ 18 ммØ 20 ммØ 22 ммØ 25 ммØ 28 ммØ 30 ммØ 32 ммØ 34 ммØ 36 ммØ 40 ммØ 42 ммØ 45 ммØ 50 ммØ 52 ммØ 56 ммØ 60 ммØ 70 ммØ 80 ммØ 90 ммØ 100 ммØ 110 мм10 мм12 мм14 мм16 мм18 мм20 мм25 мм20х4,025х4,025х5,030х4,030х5,040х4,040х5,040х6,050х5,060х5,060х6,080х6,0100х8,0
0,55х1250 х/к оц.0,70х1250 х/к оц.0,80х1250 х/к оц.1,0х1250 х/к оц.1,2х1250 х/к оц.1,5х1250 х/к оц.2,0х1250 х/к оц.3,0 мм (чечевица)4,0 мм (чечевица)5,0 мм (чечевица)6,0 мм (чечевица)8,0 мм (чечевица)ПВЛ-406ПВЛ-408ПВЛ-410ПВЛ-506ПВЛ-508ПВЛ-51025х25х4,032х32х4,035х35х4,040х40х4,045х45х4,045х45х5,050х50х5,063х63х5,063х63х6,070х70х6,075х75х5,075х75х6,075х75х8,080х80х6,080х80х8,090х90х7,090х90х8,0100х100х7,0100х100х8,0100х100х10,0110х110х8,0125х125х8,0125х125х9,0125х125х10,0125х125х12,0140х140х9,0140х140х10,0160х160х10,0160х160х12,0180х180х12,0200х200х12,0200х200х16,063х40х6,075х50х5,075х50х6,0100х63х6,0100х63х8,05П6,5П8П10П12П14П16П18П20П22П24П27П30П40П5У6,5У8У10У12У14У16У18У20У22У24У27У30У40У80х60х4,0100х50х4,0100х50х5,0120х50х3,0120х60х4,0120х60х5,0160х80х4,0180х80х5,0250х125х6,015х2,515×2,820х2,825х3,232х3,240х3,040х3,550х3,050х3,515×2,820х2,825х3,232х3,240х3,550х3,557х3,057х3,576х3,076х3,589х3,089х3,589х4,0102х3,0102х3,5102х4,0108х3,5108х4,0114х4,0114х4,5127х4,5133х4,0133х4,5159х4,0159х4,5159х5,0159х6,0219х4,5219х5,0219х6,0219х8,0273х5,0273х6,0273х7,0273х8,0325х6,0325х7,0325х8,0426х6,0426х7,0426х8,0426х9,0530х7,0530х8,0530х10,057х3,576х3,589х3,5108х3,5530х7,0530х8,0530х9,0530х10,0530х12,0630х8,0630х9,0630х10,0630х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х8,0820х9,0820х10,0820х11,0820х12,0530х7,0530х8,0530х9,0530х10,0530х12,0720х8,0720х9,0720х10,0720х11,0720х12,0820х9,0820х10,01020х10,01020х12,01020х14,01220х11,01220х12,01220х14,01420х14,057х3,557х4,057х5,057х6,076х3,576х4,076х5,076х6,083х4,089х3,589х4,089х5,089х6,0102х4,0102х5,0102х6,0108х4,0108х5,0108х6,0114х5,0114х6,0121х6,0127х5,0133х4,0133х4,5133х5,0133х6,0133х8,0146х5,0146х6,0159х5,0159х6,0159х7,0159х8,0168х6,0168х7,0168х8,0219х6,0219х7,0219х8,0219х10,0273х7,0273х8,0273х10,0325х8,0325х10,0377х9,0426х9,0426х10,010х2,014х2,016х2,016х3,018х2,018х3,020х2,022х2,022х2,522х3,025х2,025х3,027х3,028х3,028х4,028х7,032х3,034х3,538х3,038х4,040х3,040х3,542х3,042х5,045х3,045х6,048х3,051х2,551х3,057х3,060х3,063х4,015х1,520х1,520х2,025х1,525х2,030х1,530х2,040х1,540х2,040х2,540х3,050х2,050х3,050х4,060х2,060х3,060х4,080х3,080х4,080х5,0100×4,0100×5,0100×6,0120х4,0120х5,0120х8,0140х5,0140х6,0160х4,0160х5,0160х6,0180х8,0100х4,0100х5,0120х4,0120х5,0140х5,0140х6,0160х5,0160х6,0160х8,020х2,025х2,030х2,040х2,040х3,050х2,050х2,550х3,050х4,060х2,060х3,080х5,080х6,0100х5,0140х5,0140х6,028х25х1,530х20х1,540х20х1,540х20х2,040х25х1,540х25х2,050х25х1,550х25х2,050х25х2,550х30х2,060х30х2,060х30х2,560х30х3,060х40х2,060х40х2,560х40х3,080х40х2,080х40х3,080х40х4,080х60х4,0100х50х3,0100х50х4,0100х60х4,0120х60х4,0120x80x4,0120х80х6,0140x60x4,0150х100х6,0160х80х5,0160х120х4,028х25х2,040х20х2,040х25х2,050х25х2,050х25х2,560х30х2,060х30х2,560х40х2,060х40х2,580х40х2,080х60х4,0120х80х4,0150х100х6,0160х120х4,0Ø 6,5 мм (в бухтах)Ø 8 мм (в бухтах)Ø 10 мм (в бухтах)Ø 12 ммØ 14 ммØ 16 ммØ 18 ммØ 20 ммØ 22 ммØ 25 ммØ 28 ммØ 30 ммØ 32 ммØ 34 ммØ 36 ммØ 40 ммØ 42 ммØ 45 ммØ 50 ммØ 52 ммØ 56 ммØ 60 ммØ 70 ммØ 80 ммØ 90 ммØ 100 ммØ 110 мм10 мм12 мм14 мм16 мм18 мм20 мм25 мм20х4,025х4,025х5,030х4,030х5,040х4,040х5,040х6,050х5,060х5,060х6,080х6,0100х8,0
Расчет
С помощью данного калькулятора Вы можете подобрать балку, которая выдержит необходимую нагрузку по одной из нижеуказанных схем. Блок: 1/5 | Кол-во символов: 161 Содержание
Балка на двух шарнирных опорах
Блок: 2/5 | Кол-во символов: 180 Блок: 2/3 | Кол-во символов: 73 Консольная балка
Блок: 3/5 | Кол-во символов: 150 Исходные данные Расчетная схема: Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли. Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры. Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов: Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1. Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две». Расчетное сопротивление Ry— для каждой марки стали он свой. Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу. РезультатWтреб — требуемый момент сопротивления профиля. Fmax — максимальный прогиб в сантиметрах, в зависимости от указанных в исходных данных ограничениях. Вес балки — масса одного погонного метра того или иного двутавра. Расчет по прочности: Wбалки — момент сопротивления выбранной трубы по ГОСТ 30245-2003. Если Wбалки > Wтреб, значит прочность балки обеспечена. Запас — если в данной графе значение с минусом (-), то балка по прочности не проходит, а если с плюсом (+), то здесь показано, на какой процент балка имеет запас прочности. Расчет по прогибу: Fбалки — прогиб, возникающий у рассчитываемой балки под действием нормативной нагрузки. Здесь стоит отметить, что если он превышает допустимый Fmax,то это не значит, что двутавр сломается. Запас — то же самое, что и по отношению к моменту сопротивления. Блок: 3/3 | Кол-во символов: 2329 Балка с вылетом на двух шарнирных опорах
Блок: 4/5 | Кол-во символов: 171 Другие виджеты разработчика:
Блок: 4/4 | Кол-во символов: 1953 Балка с жестким защемлением на опорах
| Не забудь поделиться с друзьями |
Как рассчитать нагрузку стальной двутавровой балки
Двутавровая балка является фасонным прокатом, у которого есть поперечное сечение в форме «Н». Данный вид металлопроката имеет высокие прочностные характеристики. За счет всех параметров изделие широко распространено в строительстве многоэтажек с большими пролетами. Точно выбрать подходящий номер проката могут специалисты благодаря расчетам, где учтены нагрузки двутавра во время эксплуатационного периода.
Данный вид металлопроката имеет высокие прочностные характеристики. За счет всех параметров изделие широко распространено в строительстве многоэтажек с большими пролетами. Точно выбрать подходящий номер проката могут специалисты благодаря расчетам, где учтены нагрузки двутавра во время эксплуатационного периода.
Крепление Н-образного профиля по схеме
Для удобства расчета максимальной нагрузки на двутавровую балку все способы эксплуатации профиля сводятся к нескольким типовым схемам, различающихся по типу крепления и нагрузкой:
- 2 шарнирные опоры на концах балки: с равномерной нагрузкой и со сосредоточением на центр;
- Консоль. Нагрузка на двутавр равномерно или сосредоточенно;
- 2 шарнирные опоры с вылетом с равномерной по всей длине или сосредоточенной в центре нагрузкой;
- 2 жестко защемленные опоры с разными видами усилий;
Сбор нагрузок на балку осуществляется после выбора формальной схемы.
Сбор нагрузок на двутавр
Чтобы произвести расчеты на предельную прочность и прогиб, определяются все усилия, воздействующие на двутавровую балку:
- Постоянные.
 Наличие собственного веса металлического профиля и перекрытия;
Наличие собственного веса металлического профиля и перекрытия; - Временные. К ним относятся 3 вида усилий: длительные (масса временных перегородок), кратковременные (вес людей, ветер, снег и др.), особые (взрывные, вулканические).
В сооружениях с углом ската, превышающим 60°, снеговой покров не входит в расчет. Есть еще одна классификация усилий: расчетные и нормативные. Они определяются нормативными актами.
Выбор номера двутавровой балки
При подборе по предельному состоянию между 2-мя номерами делают выбор в пользу изделия, имеющего более массивное сечение.
Примеры выбора двутавровой балки по номеру:
- 10-ый – пролет 3-4 м, шаг 1 м, воздействие – 300 кг/пм;
- 16-ый – пролет 6 м, шаг 1 м, нагрузка– 300 кг/пм;
- 20-ый пролет 3-4 м, шаг 1,1 / 1,2 м, усилие – 400-500 кг/м.
Чтобы определить номер профиля посредством онлайн-калькулятора, кроме значения типовой схемы крепления двутавра, воздействия усилий и нагрузка, следует указать параметр длины пролета, материал изделия.
Читайте интересное
Напряжение балки из-за изгибающих моментов – Приложение по прочности материалов для энергетики
Напряжение изгиба
Цели обученияПосле завершения этой главы вы сможете:
- Используйте формулу изгиба для расчета максимального напряжения изгиба
- Расчетные балки, безопасно несущие нагрузки
- Определите требуемый модуль упругости сечения балки
- Выбрать стандартные конструктивные формы для использования в данной задаче балки
Рассмотрим балку с простой опорой, подверженную внешним нагрузкам, направленным вниз.Балка будет деформироваться (отклоняться) таким образом, что верхняя поверхность поперечного сечения балки будет испытывать сжатие, а нижняя поверхность – растяжение. В некотором месте вдоль вертикальной оси балки напряжение будет нулевым; это место является центром тяжести поперечного сечения, также называемым нейтральной осью.
Формула изгиба
Для определения максимального напряжения из-за изгиба используется формула изгиба :
где:
- σ max – максимальное напряжение на самой удаленной от нейтральной оси поверхности (может быть верхней или нижней)
- M – изгибающий момент по длине балки, на которой рассчитывается напряжение
- если требуется максимальное изгибающее напряжение, то M – максимальный изгибающий момент, действующий на балку
- I x – момент инерции относительно центральной оси x (горизонтальной)
- c – максимальное расстояние от центральной оси до крайнего волокна (опять же, это может быть верх или низ формы)
- Z x называется модулем сечения и представляет собой термин, который объединяет момент инерции и расстояние до крайнего волокна ( Z x = I x / c )
Формула изгиба действительна при соблюдении следующих критериев:
- Балка прямая, относительно длинная и узкая, с равномерным поперечным сечением
- все нагрузки действуют перпендикулярно продольной оси балки
- результирующее напряжение ниже предела пропорциональности материала
- материал балки однороден и имеет равную прочность на растяжение и сжатие.

- если материал имеет разную прочность на растяжение и сжатие (например, чугун или другие анизотропные материалы), то требуются отдельные расчеты как для поверхностей растяжения, так и для поверхностей сжатия
- нет скручивания, коробления или деформации
Дизайнерские корпуса
Проблемы проектирования могут возникать по разным сценариям:
- рассчитать размеры поперечного сечения балки (найти минимальный модуль сечения Z и выбрать стандартную форму с большей жесткостью) с учетом геометрии балки, нагрузки и материала.
- выберите материал балки (найдите максимальное рабочее напряжение и выберите материал большей прочности) с учетом размеров балки, нагрузки и размеров / формы.
- определяет, является ли балка безопасной (найдите фактическое рабочее напряжение и сравните с расчетным напряжением), учитывая размеры балки, нагрузку и материал.
Примечание: если не указано иное, используйте конструкцию σ = 0,6 × σ YS, , где σ YS – предел текучести, из учебного приложения B.
Задача 1: Балка с простой опорой длиной 9,9 м нагружается сосредоточенными нагрузками следующим образом:
- 40 кН на расстоянии 1,2 м от левого края
- 10 кН на расстоянии 3,7 м от левого края
- 10 кН на расстоянии 6,2 м от левого края
- 10 кН на расстоянии 8,7 м от левого края
Балка изготовлена из двутаврового профиля W200 × 100 из холоднокатаного материала AISI-1020. AISC рекомендует, чтобы максимальное напряжение изгиба для строительных конструкций при статических нагрузках было ниже 0.66 × S y . Соответствует ли эта конструкция проектным требованиям?
Задача 2: Трубопровод просто поддерживается над землей на горизонтальных балках длиной 4,5 м. Каждая балка несет вес 20 м трубы Sch 40 DN-600 (см. PanGlobal Academic Extract), заполненной маслом 0,9 SG . Предполагая, что нагрузка действует в центре балки, рассчитайте необходимый модуль упругости балки, чтобы ограничить изгибающее напряжение до 140 МПа; затем выберите самый легкий W-луч SI, который удовлетворяет критериям.
Задача 3: На рисунке показано поперечное сечение балки из алюминия 6061-T6. Балка используется как консоль длиной 45 дюймов. Вычислите максимально допустимую равномерно распределенную нагрузку, которую он может выдержать, ограничивая при этом напряжение из-за изгиба до одной пятой предельной прочности.
Задача 4: Спроектируйте проход, чтобы перекрыть только что проложенный трубопровод на вашем предприятии. Жесткие опоры доступны с каждой стороны трубопровода на расстоянии 14 футов друг от друга.Тротуар должен иметь ширину 3,5 фута и выдерживать равномерно распределенную нагрузку 60 фунтов / фут 2 по всей своей поверхности. Проектируйте только доски настила и боковые балки. Используйте древесину любых размеров и сортов материала из Приложения E к учебнику или других материалов вашей собственной разработки.
Задача 5: Предложите одну проблему конструкции балки, которую вы сочтете актуальной и полезной для инженеров-энергетиков.
Механика материалов: изгиб – нормальное напряжение »Механика тонких конструкций
Моменты области
Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки и как рассчитать второй момент площади для данного поперечного сечения.
Начнем с представления произвольного поперечного сечения – чего-то не круглого, не прямоугольного и т. Д.
На изображении выше произвольная форма имеет область, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область dA , которая существует на некотором расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующей формуле:
Первый момент площади – это интеграл длины по площади – это означает, что единицы длины будут кубическими [L 3 ].Это важно, потому что помогает нам определить центр тяжести объекта. Центроид определяется как «среднее положение области x (или y )». Математически это утверждение выглядит так:
Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе – она позволяет нам разбить сложную форму на простые формы с известными площадями и известными положениями центроидов. В большинстве инженерных сооружений есть как минимум одна ось симметрии – и это позволяет нам значительно упростить поиск центроида. Центроид должен располагаться на оси симметрии . Например:
Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно только найти центроид по оси y . Поперечное сечение справа еще проще – поскольку центр тяжести должен совпадать с осями симметрии, он должен находиться в центре объекта.
Теперь, когда мы знаем, как найти центроид, мы можем обратить внимание на второй момент площади.Как вы могли вспомнить из предыдущего раздела, посвященного кручению, это определяется как:
И, наконец, иногда нам нужно определить второй момент площади относительно произвольной оси x или y – такой, который не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс член, который включает расстояния между двумя осями.
Это уравнение называется теоремой о параллельной оси .Это будет очень полезно на протяжении всего курса. Как описано во вводном видео к этому разделу, вычислить второй момент площади для простой формы может быть несложно. Для более сложных форм нам нужно вычислить I , вычислив отдельные I для каждой простой формы и комбинируя их вместе, используя теорему о параллельных осях.
Диаграммы сдвига и момента
Поперечная нагрузка относится к силам, перпендикулярным длинной оси конструкции.Эти поперечных нагрузок вызовут изгибающий момент M , который вызывает нормальное напряжение , и поперечную силу V , которая вызывает напряжение сдвига . Эти силы могут изменяться и будут изменяться по длине балки, и мы будем использовать диаграммы сдвига и момента (V-M-диаграмма) , чтобы извлечь наиболее подходящие значения. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании поперечно нагруженной балки необходимо учитывать два важных момента:
- Как нагружается балка?
- точечная нагрузка, распределенная нагрузка (равномерная или переменная), сочетание нагрузок…
- Как поддерживается балка?
- просто поддерживаемые, консольные, нависающие, статически неопределимые…
Знание нагрузок и опор позволит вам нарисовать качественную диаграмму V-M , а затем статический анализ свободного тела поможет вам определить количественное описание кривых .Начнем с того, что вспомним наши условные обозначения .
Эти правила знаков должны быть вам знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный. Если момент изгибает балку таким образом, что он изгибается в «улыбку» или U-образную форму, это положительно. Лучший способ вспомнить эти диаграммы – это проработать пример. Начните с этой консольной балки – отсюда вы можете переходить к более сложным нагрузкам.
Нормальное напряжение при изгибе
Во многих отношениях изгиб и кручение очень похожи.Результат изгиба пары или приложенный изгибающий момент M . Как и при кручении, при чистом изгибе в материале существует ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение перестает быть равномерным по поперечному сечению конструкции – оно меняется. Давайте начнем с рассмотрения того, как ось z изгибает конструкцию. В данном случае мы не будем ограничиваться круговыми сечениями – на рисунке ниже мы будем рассматривать призматическое сечение.
Прежде чем мы углубимся в математику, лежащую в основе изгиба, давайте попробуем разобраться в этом концептуально. Возможно, лучший способ увидеть, что происходит, – это наложить изогнутую балку поверх исходной прямой балки.
Теперь вы можете заметить, что нижняя поверхность балки стала длиннее, а нижняя поверхность балки стала короче. Также по центру балки длина не изменилась – соответствует нейтральной оси. Чтобы повторить это на языке этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под давлением.Что-то более тонкое, но все же можно наблюдать из наложенного выше изображения, это то, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и с кручением – напряжение линейно изменялось от центра к центру. Мы можем посмотреть на это распределение напряжений в поперечном сечении балки более подробно:
Теперь мы можем найти математическую связь между приложенным моментом и напряжением в балке.Мы уже упоминали, что балка линейно деформируется от одного края к другому – это означает, что деформация в направлении x увеличивается линейно с расстоянием по оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y = 0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y = c. . Мы можем записать это математически так:
Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Что ж, давайте начнем с умножения обеих частей уравнения на E , модуль упругости Юнга.Теперь наше уравнение выглядит так:
Используя закон Гука, мы можем связать эти величины со скобками под ними с напряжением в направлении x и максимальным напряжением. Это дает нам это уравнение для напряжения в направлении x- :
Наш последний шаг в этом процессе – понять, как изгибающий момент соотносится с напряжением. Для этого напомним, что момент – это сила, умноженная на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в балке, дифференциальный элемент, то мы можем математически записать это как:
Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, интегрировав обе части уравнения.И, если мы вспомним наше определение напряжения как силы, приходящейся на площадь, мы можем написать:
Последний член в последнем уравнении – интеграл по квадрату y – представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается как I (помните, в цилиндрических координатах он обозначался как J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:
Важно отметить, что индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) все будут меняться в зависимости от характера проблемы, т.е.е. направление момента – вокруг какой оси изгибается балка? Мы основали наши обозначения на показе изогнутой балки на первом изображении этого урока.
Помните, в начале раздела я упоминал, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень явно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиг для кручения) равно пара / момент ( M для изгиба и T для кручения), умноженному на местоположения вдоль поперечного сечения. , , потому что напряжение неоднородно по поперечному сечению (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все деленное на секундный момент площади поперечного сечения.
СводкаВ этом уроке мы узнали о моментов области и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельной оси позволяет нам вычислить второй момент площади относительно центроида объекта – это полезно для разделения сложного поперечного сечения на несколько простых форм и объединение их вместе.Мы пересмотрели концепцию диаграмм сдвига и момента из статики. Эти диаграммы будут важны для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении при изгибе балки. И напряжение, и деформация меняются вдоль поперечного сечения балки, при этом одна поверхность находится в состоянии растяжения, а другая – в состоянии сжатия. Плоскость, проходящая через центроид, образует нейтральную ось – вдоль нейтральной оси нет напряжения или деформации.Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.
Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы, выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда. Научный фонд.
Напряжение изгиба – обзор
9.3.1 Простой изгиб
В целом расчет изгибающих напряжений может быть сложной задачей. Даже задача плоского изгиба представляет собой двумерную краевую задачу упругости, и обычно принимается несколько предположений, чтобы можно было получить простое решение. Эти специальные допущения известны под разными названиями: теория пучков Эйлера-Бернулли , теория плоских пучков или просто теория изгиба балок . На самом деле здесь нет никакой теории, это просто набор априорных предположений о том, как балка деформируется при изгибе, что позволяет аналитически решить более сложную краевую задачу.Для трубок (см. Рисунок 9-8), таких как обсадная колонна, это типичные допущения:
Рисунок 9-8. Простое изгибание трубы в одной плоскости.
- •
Трубка изначально прямая.
- •
Поперечное сечение трубки симметрично относительно центральной продольной оси.
- •
Все поперечные сечения, перпендикулярные продольной оси до изгиба, остаются перпендикулярными оси после изгиба.
- •
Центральная продольная ось (нейтральная ось) не испытывает осевой деформации
- •
Радиус трубы мал по сравнению с длиной.
- •
Прогибы при изгибе малы по сравнению с длиной, поэтому радиус трубы остается постоянным во всех направлениях.
Результатом этих предположений является уравнение для осевой деформации:
, где y – координата в плоскости изгиба с началом на нейтральной оси (центре), θ – угол в плоскости кривизны, и s осевая координата вдоль нейтральной оси трубы. Подставив это в одномерное определяющее уравнение (закон Гука), мы получим осевое напряжение изгиба:
(9.18) σb = σs = Eɛs = −Eydθds
Очевидно, что максимальное напряжение возникает в точке, где y равно внешнему радиусу трубы, r o . Но мы могли бы захотеть определить напряжение на внутренней стенке также в случаях внутреннего давления, поэтому мы просто опустим индекс, понимая, что r i ≤ r ≤ r o . Член dθ / d s – это кривизна изогнутой трубы, которая обратно пропорциональна радиусу кривизны, R .Таким образом, на практике уравнение принимает вид
, где
σ b = напряжение изгиба, (+) для растяжения, (-) для сжатия
E = модуль упругости Юнга
r = радиус трубы, на которой определяется напряжение (т.е. внутри или снаружи)
R = радиус кривизны траектории ствола скважины
Важно, чтобы используемые единицы измерения были согласованы.В нефтепромысловых установках радиус трубы обычно выражается в дюймах, а радиус кривизны траектории ствола скважины – в футах, поэтому они должны быть преобразованы в одни и те же единицы (не имеет значения, какие). В единицах СИ обе меры должны быть в метрах. Модуль Юнга обычно выражается в фунтах-силах на дюйм. 2 , кПа или МПа, а напряжение изгиба указано в тех же единицах.
Необходимо запомнить исходные положения этой формулы перед ее использованием, особенно с трубками. Когда труба изгибается, ее поперечное сечение имеет тенденцию к овальному, а не к круглому.Радиус трубы в плоскости изгиба уменьшается по мере того, как поперечное сечение становится овальным, и формула больше не действует. Поскольку нет простого способа определить точку, в которой форма слишком овальная для использования формулы, есть тенденция игнорировать ее, поскольку она будет переоценивать максимальное напряжение изгиба, когда труба слегка овальной формы. Это делает формулу, возможно, немного консервативной в конструкции корпуса. Для скважин с большим и средним радиусом кривизны он, кажется, подходит для всех, кроме тонкостенных труб большего диаметра.Для скважин малого радиуса его следует использовать с осторожностью, и, опять же, это будет зависеть от диаметра трубы и толщины стенки. Может показаться, что это избегает конкретного, но с уверенностью можно сказать, что это становится бессмысленным, если предел текучести превышен.
| Получение Знакомый | ||||||||||||||
| Расчет на изгиб балок был
освященный веками центральный элемент в раннем обучении “технической
механика », с которым приходилось сталкиваться каждому начинающему инженеру и ученому.
через как своего рода обряд посвящения.Многие этого не сделали. Освоение
сгибание луча – это не то, что делается на обратной стороне конверта, в то время как
выпить пива или два. Вам действительно нужно приложить все усилия, чтобы сдать эти экзамены. Давайте сначала посмотрим на масштабность задачи, а затем разрежем ее на части. может справиться. На рисунке ниже показано, что это такое при довольно простом обстоятельства. У нас есть то, что иллюминаты называют «луч», прочно закреплен на одном конце. С таким же успехом это мог быть меч, увиденный с ребра.Некоторые силы воздействовать на нашу балку; в результате он гнется. Давайте посмотрим на основные моменты, связанные с к этому один за другим: | ||||||||||||||
| ||||||||||||||
| Сначала , давайте уточним, что я имею в виду
с надписью « балка ».«Луч» – это общее название любого длинного предмета с некоторыми
поперечное сечение везде одинаковое по длине л .
Причем длина л должна быть значительно больше, чем длина
размеры поперечного сечения. Поскольку поперечное сечение большинства мечей изменяется с длиной, эти мечи – это не луч, а в лучшем случае приблизительно луч. | ||||||||||||||
| Второй , давай определить « гибка ».если ты изгибаете что-то, в частности балку, механически деформируете. Что касается слово изгиб здесь касается, мы ограничиваем себя на чисто упругих деформаций в любом месте луча. Снимите силы, действующие на балку выше, и она должна снова будь совершенно прямым. | ||||||||||||||
| Третий , мы
посмотрите на сил , которые могут согнуть
луч. Мы допускаем любые силы, действующие в любом месте балки – до тех пор, пока
они действуют только в направлении z .В противном случае мы имеем две проблемы изгиба балки – изгиб в z – направление и в y – направление, перпендикулярное плоскости чертежа. Применение сил
в x -направлении будет означать испытание на растяжение (или сжатие), поэтому
мы им тоже не позволяем. Конечно, силы, действующие на настоящие балки или
мечи не заботятся об этих ограничениях, но я смотрю на простой луч
изгиб здесь. Силы могут составлять баллов сил, как у заставить свой меч переживать, когда он ударяется лезвием другого меча, или распределил силы, как вы их получите, когда вы кладете на балку, например, груз, как показано выше. Наша балка должна гнуться, но иначе она не двинется. Он не будет вращаться и никуда не денется, а значит, сумма всех сил и моментов должен быть равен нулю по определению. Очевидно, что это не так на картинке выше.Что ж, мы забыли: | ||||||||||||||
| Четвертый г. граничные условия .
На картинке выше балка прочно закреплена в стене. Математически
это означает отклонение z ( x ) , величина изгиба по координате x или просто линия сгиба равна нулю для x = 0 . Выражаясь математически, мы имеем граничное условие: z ( x = 0) = 0 , и по понятным причинам d z ( x = 0) / d x = 0 . Для математиков: производная d z / d x дает наклон кривой изгиба z ( x ) , который должен быть ноль (т.е. параллельно оси x ) рядом со стенкой Эти граничные условия могут быть выполнены только в том случае, если на балку действуют силы и моменты. при x = 0 , которые точно компенсируют силы и моменты внешние силы.Это неплохо, потому что это означает, что нам не о чем беспокоиться об этом. Проще говоря, если вы каким-то образом обездвиживаете меч (поместив его в тиски) он не может двигаться или вращаться по определению, независимо от того, силы действуют на него где-то еще. | ||||||||||||||
| Пятый и
не забываем, луч может иметь произвольные сечение , в т.ч.
полые. Показанные три примера уже довольно особенные, так как они очень интересны. симметричный.Этого не требуется, тем не менее мы будем только рассматривать сечения с некоторой симметрией из теперь дальше, чтобы не слишком запутывать ум. | ||||||||||||||
| Теперь рассмотрим поставленную задачу.
Мы хотим вычислить z ( x ) , кривую, которая
описывает форму гнутой балки. Допускается любая длина л и
формы поперечного сечения балки и все виды сил, силы
распределения и всевозможные (разумные) граничные условия. Даже если у вас такие математические проблемы, что вам пришлось заняться банковским делом, вы поймете, что это непростая задача. Как вы выражаете сечение № 2 выше (меч с долом) в уравнениях? Что бы граничные условия будут, если вы попытаетесь удерживать меч в фиксированном положении с помощью руки вместо того, чтобы заткнуть его в тиски? Если он поражен другим мечом, вы невозможно сохранить положение руки и меча полностью без изменений – в отличие от (очень сильный) порок. | ||||||||||||||
| Ну задача конечно непростая – но тоже не так сложно, как может показаться. Давайте сделаем это в два этапа и модули. Во-первых, в этом модуле я даю довольно простое описание специального ситуации, которую я затем использую, чтобы вывести несколько общих правил изгиба балки. Во втором модуле я дам более общее лечение. | ||||||||||||||
| Угадай Специальное решение | ||||||||||||||
| Хорошая новость в том, что я не математик.Если бы я был одним из них, я бы не смог нарисовать картинку выше потому что он уже содержит своего рода решение проблемы, поскольку он показывает (угадывая), как изгибается балка. Математики решают только задачи без какого-либо предварительного представления о результате, а это значит, без милых маленьких фотографий. Вот почему они часто не решают настоящие проблемы, а только подробно обсудите, может ли проблема иметь решение, много решений – или, возможно, нет. | ||||||||||||||
| Все мы
не математики, однако, только знают, что балка изгибается примерно так, как показано выше для данной ситуации.Мы знаем даже
более. Мы знаем, что если мы посмотрим на небольшую часть балки, мы сможем, по крайней мере,
в хорошем приближении, предположим, что изгиб локально может быть описан как круговой. Затем верхнюю и нижнюю поверхность луча можно нарисовать с помощью компаса, используя два радиуса, которые отличаются толщиной d . По сравнению с длиной недеформированной балки верхняя часть теперь немного длиннее, нижняя часть немного короче. Мы посмотрели на это раньше и там можно не сомневаться, что у нас всегда есть нейтральный ось внутри балки, длина которой не изменилась.В нашем простой пример у нас фактически есть нейтральный поверхность , но для более сложных сечений придерживается нейтральной оси (иногда также называемая нейтральной линией или центроидом ) лучше, поскольку она является более общей. Этот нейтральная ось (а здесь и вся нейтральная поверхность) тоже, несомненно, будет в середину прямоугольной балки, как показано ниже. | ||||||||||||||
| ||||||||||||||
| Теперь, в процессе мысли, мы
«Выдели» желтую часть изгиба балки. Чтобы держать его в форме
когда он еще был неотъемлемой частью балки, мы должны приложить силы.
Очевидно, что следует отметить, что только распределение сил, как показано на рис.
синий с правой стороны, и то же самое, отраженное на другом конце (не
показано) может вызвать деформацию, как показано.Всегда можем заменить раздачу на синий
силы двумя точками силы F умным усреднением, и результат будет таким, как показано на
коричневого цвета на левом конце нашей балочной части. Теперь мы видим, что суммарное действие сил должно вызвать крутящий момент или крутящий момент T с предположил звездную величину T = ½ Fd , так как расстояние между парой сил в предположении составляет d /2 , или половину балки толщина, как показано.´ (Если вы на самом деле все рассчитаете, расстояние будет 2d /3 ). | ||||||||||||||
| Пока я просто описываю
рисунок, генерируя первые уравнения по мере продвижения. Если вы продолжите смотреть на рисунок, вы поймете, что это еще не все. что можно описать простыми уравнениями. В частности, максимальная нагрузка справа вверху e t max = d /2 r ; это растяжение .В максимальная деформация справа внизу e b max = – д /2 р ; он сжимающий. | ||||||||||||||
| Почему? На картинке все видно. В
длина крайней части л 0 +
D л = л 0 + ½ d · Sina = л 0 + ( д ·
л 0 ) / 2р) .Отсюда получаем e max = [ l 0 + ( d · л 0 / 2r) – л 0 ] / л 0 = d /2 r . Вуаля! В равной степени, конечно, деформация линейно уменьшается от максимального значения на снаружи до нуля в нейтральной плоскости при движении внутри луча. | ||||||||||||||
| Вкл. в среднем , как мы предполагаем, верхняя или нижняя часть, таким образом, испытывает средняя деформация e av = ± d /4 r . | ||||||||||||||
| Пока мы учитываем только упругих деформаций , деформация e и напряжение s равны связанные: s = Y · e ; с Y = Янга модуль. | ||||||||||||||
| Среднее напряжение , соответствующее нашей средней деформации – это среднее усилие F , деленное на половину
площадь поперечного сечения ш.д. .Другими словами: s = ( F ) / (½ bd ) = 2 F / bd = Y · e av = Y · d /4 r . Это дает нам для силы F = ( Y · d / 4 r ) · bd /2 = b · d 2 · Y /8 R | ||||||||||||||
| Теперь легко понять, что в конец это крутящий момент T = F · d /2 , что вызывает изгиб.Итак, давайте соотнесем крутящий момент T с радиусом кривизны r . С уравнением выше мы получаем как окончательный результат : | ||||||||||||||
| ||||||||||||||
| Вычитание Немного Essentials | ||||||||||||||
| У нас есть красивое и простое уравнение.Мы много гадали, поэтому не можем ожидать, что это уравнение абсолютно
верный. Однако мы не сделали ничего вопиющего неправильно, так что этого не должно быть.
Совершенно неверно, но приближение на полпути. Но что значит
уравнение означает? Во-первых, я скажу вам, что это определенно означает, несмотря на предположения. Затем я собираюсь обсудить недостатки этого простого подхода и то, как мы это можно исправить .. | ||||||||||||||
Основные выводы, которые мы можем сделать:
| ||||||||||||||
| ||||||||||||||
| На рисунке показан ряд
вещи.Прежде всего, это проясняет, что для показанной точечной силы локальная
изгиб наиболее силен вокруг зажима балки, потому что там у вас есть
самый высокий крутящий момент и, следовательно, наименьший радиус кривизны. Радиус кривизны
таким образом плавно изменяется по длине балки до места расположения
сила. Справа от силы изгиба в этом случае нет вообще
(имеется в виду бесконечный радиус кривизны). Обратите внимание, что мы еще не рассчитали кривую прогиба , а только увидели, как она
результат локальных искривлений. Не иллюстрируя это напрямую, мы можем вывести еще несколько моментов: | ||||||||||||||
| Если бы у нас не было баллов сила, но некоторые распределили силу, мы все еще можем рассчитать крутящий момент
в любой момент путем суммирования или интегрирования по распределению сил. Как это
сделано не важно на данном этапе, все, что нам нужно знать, это то, что это может быть
Выполнено. Если бы мы применили точечную силу секунд где-то справа от показанного выше мы просто суммируем моменты силы. | ||||||||||||||
| Разве это не удивительно, сколько можно делать выводы о сложной проблеме, не решая ее “с первого взгляда” принципы “? Прежде чем я перейду дальше предположений, давайте посмотрим на проблемы, недочеты и недостатки моего «гадательного» подхода. | ||||||||||||||
| Первое, что нужно отметить , – это маленькие кубики внутри нашего
опыт изгиба балки только одноосный нормальный
стрессы.Любой
маленький куб
внутри луч становится немного длиннее в направлении x ;
это показано
здесь в несколько ином контексте. Напряжение увеличивается линейно с увеличением
расстояние до нейтральной поверхности. Это приблизительное значение. Настоящие лучи испытают боковой сокращение в верхней половине и соответствующее расширение в нижней. Форма поперечного сечения изменится с прямоугольной на трапециевидную. Более того, внешние силы также вызывают некоторые компоненты сдвига в напряжении, которым мы пренебрегли.Понятно, что разобраться в этом будет непросто, так что позвольте мне сразу сообщить вам хорошие новости: Нам не нужно этого делать. При обработке изгиба балки с помощью только одноосные нормальные напряжения , безусловно, не совсем правильно, этого достаточно для почти всех практических случаев. | ||||||||||||||
| вторая точка более серьезная и откроет большую
банка червей. В нашем подходе к предположениям мы предположили, что прямоугольная
поперечное сечение, определяемое толщиной d раз больше ширины или
«широта» b .Мы догадались, что нейтральный самолет
прямо посередине. Если мы перепишем окончательное уравнение для радиуса
кривизна, как указано выше, мы можем выразить ее как r =
( b d 3 /16) · ( Y / T ) и
коэффициент ( ш.д. 3 /16) содержит все информацию о поперечном сечении
геометрии, предположение о нейтральной плоскости (и, следовательно, о направлении
изгиб), плюс процедуры усреднения.Другими словами, он содержит всех возможных ошибок и недостатков
угадывающий подход. Поэтому неудивительно, что правильное значение этого фактора в результате правильных расчетов на самом деле: ( b d 3 /12) . Что ж, это очень плохо. Тем не менее, подход к предположениям был не таким уж Плохо и, конечно, стоит сделать для простого прямоугольного сечения. | ||||||||||||||
| Настоящая проблема в том, что для произвольных сечений, угадывание
подход не работает вообще больше для
вывод значения коэффициента перед Y / T который заботится о геометрии балки.Пока можно было сделать хорошее предположение
о положении нейтральной поверхности для
сечения, данные выше, вы
будет трудно, например, для треугольных сечений и многих других. Хуже того, вы не могли легко угадать средние значения по очевидным причинам. Так вы видите проблему: | ||||||||||||||
| ||||||||||||||
| Что ж, результат нашего предположения дает
ясный намек: мы можем сохранить общее соотношение r µ ( Y / T ) .Все, что меняется, это то, что
константа пропорциональности ( b d 3 /16) в нашем
предположение) должны быть рассчитаны на основе реального сечения балки . На самом деле это не так
очень сложно сделать (при условии, что вы немного знаете об интеграции двух
Габаритные размеры). Результатом будет просто номер , который называется момент инерции площади Я А .Если и было неправильное название, так это оно. В площадь момент инерции ничего не имеет что бы ни случилось с тем, что называется “моментом инерция “по уважительным причинам, когда вы рассчитываете, как тела вращаются вокруг некоторой оси. Единственная связь между ними заключается в том, что если вы запишете интегралы для вычисления этих моментов, математические выражения похожий. | ||||||||||||||
| Так что все нам необходимо рассчитать момент инерции площади I для поперечное сечение и переписать наши основное уравнение как | ||||||||||||||
| ||||||||||||||
| Требуется вычислить положение нейтральной оси или центроид первый.Затем он определит система координат, так как мы центрируем ее на нейтральной оси. | ||||||||||||||
| Посмотрите на прямоугольную поперечный разрез на картинке ниже, чтобы получить это: красный кружок обозначает положение нейтральной оси (она проходит перпендикулярно плоскости изображения в x -направления, конечно). Поскольку изгибаясь о z – ось (приложив силу в направлении y -) будет получить результаты гибки различной формы относительно оси y ( прикладывая силу в z -направлении), нам нужно вычислить двух моментов инерции площади, I y и I y , с учетом что. | ||||||||||||||
| Как центроид и
моменты площади I A определены, и как они
вычислено, является предметом другого модуля. Все, что нам нужно знать, это то, что
если кто-то рассчитывал это в прошлом, нам не нужно делать это самим. Мы
просто можно использовать сгенерированные числа. Вот несколько примеров; положение центра тяжести отображается красной точкой. | ||||||||||||||
| Красная точка обозначает нейтральную линию.Для тот же модуль Юнга Y , моменты площади теперь дают сопротивление для гибки в y – или z – направлении ( I z или I y , соответственно. ось, вокруг которой происходит изгиб). Что можно сразу оценить заключается в том, что легкая трубка с несколько больший радиус, чем у тяжелого круглого сечения стержень может иметь одинаковый момент инерции и, следовательно, сопротивление изгибу.Вот почему у вас всегда есть полые балки (или и двойной фигурные) в любых структурное строительство. | ||||||||||||||
| Поперечное сечение меча, как правило, больше сложнее, чем приведенные выше, но с эллиптическим мы могли по крайней мере, сделай обоснованное предположение для мечей. Это позволяет нам оценить деформацию во внешних слоях в зависимости от изгиба, и это дает нам последний Важная информация: | ||||||||||||||
| Как только эта деформация e (или напряжение, связанное с s / e = Y ) достигает предел для пластической деформации или разрушения, все кончено.Поскольку мы должны предположим, что где-то вдоль лезвия может быть “слабое” место, все закончилось несколько раньше, чем мы рассчитывали. | ||||||||||||||
| Наконец, я просто скажу вам, что мы узнали, что здесь можно также перенести на “коробление балок” проблема, или эффект того, что ваш меч может погнуться, когда вы попытаетесь проткнуть прямо во что-то. Этим мы займемся в специальном модуле | .||||||||||||||
% PDF-1.3 % 1809 0 obj> эндобдж xref 1809 75 0000000016 00000 н. 0000003313 00000 н. 0000001836 00000 н. 0000003471 00000 н. 0000003499 00000 н. 0000003547 00000 н. 0000003673 00000 н. 0000004059 00000 н. 0000004144 00000 н. 0000004229 00000 н. 0000004312 00000 н. 0000004395 00000 н. 0000004478 00000 н. 0000004561 00000 н. 0000004644 00000 п. 0000004727 00000 н. 0000004810 00000 н. 0000004893 00000 н. 0000004976 00000 н. 0000005059 00000 н. 0000005142 00000 н. 0000005225 00000 н. 0000005308 00000 п. 0000005391 00000 п. 0000005474 00000 п. 0000005557 00000 н. 0000005640 00000 н. 0000005723 00000 н. 0000005806 00000 н. 0000005889 00000 н. 0000005972 00000 н. 0000006054 00000 н. 0000006136 00000 н. 0000006218 00000 н. 0000006300 00000 н. 0000006382 00000 п. 0000006745 00000 н. 0000010431 00000 п. 0000010978 00000 п. 0000011166 00000 п. 0000011806 00000 п. 0000011892 00000 п. 0000011919 00000 п. 0000012473 00000 п. 0000018402 00000 п. 0000019201 00000 п. 0000019589 00000 п. 0000019658 00000 п. 0000020148 00000 п. 0000021318 00000 п. 0000021664 00000 н. 0000022422 00000 п. 0000022686 00000 п. 0000023334 00000 п. 0000028354 00000 п. 0000028792 00000 п. 0000029204 00000 п. 0000029823 00000 п. 0000030993 00000 п. 0000031394 00000 п. 0000031939 00000 п. 0000032026 00000 п. 0000032066 00000 п. 0000033237 00000 п. 0000033324 00000 п. 0000033353 00000 п. 0000033452 00000 п. 0000034614 00000 п. 0000035778 00000 п. 0000036478 00000 п. 0000037185 00000 п. 0000037959 00000 п. 0000038616 00000 п. 0000039340 00000 п. 0000003100 00000 н. трейлер ] >> startxref 0 %% EOF 1811 0 obj> поток xb“b`π
Как выбрать двутавр?
Выбор стального двутавра может стать настоящей проблемой, если вы не знаете параметров и необходимой терминологии.Но все же выбор правильной стальной двутавровой балки имеет решающее значение, поскольку это первый шаг к правильному проектированию конструкции. Итак, чтобы выбрать подходящий, следует сначала познакомиться с особенностями и терминологией двутавра.
Характеристики двутавровой балки
Обычно двутавровая балка имеет следующие характеристики:
– Толщина полки
– Толщина стенки
– Радиус скругления
– Ширина полки
– Глубина балки
Когда вы выбираете I-Beam впервые, скорее всего, эти слова не имеют для вас абсолютно никакого смысла, что совершенно не удивительно.Чтобы понять их, вам нужно ознакомиться с терминологией.
Терминология двутавровой балки
Фланец – это верхняя и нижняя горизонтальные части двутавровой балки, имеющие форму пластины.
Толщина фланца – толщина указанных фланцев.
Толщина стенки – вертикальное сечение двутавровой балки называется стенкой, а ее толщина – толщиной стенки.
Радиус скругления – это часть, где происходит переход между стенкой и полками.
Ширина фланца – очевидно, ширина фланца.
Глубина балки – высота между верхней и нижней полками стальной двутавровой балки.
Как выбрать двутавровую балку
Когда вам нужно выбрать двутавровую балку, вы не можете избежать расчетов. Расчет довольно прост, и его можно выполнить, выполнив следующие шаги:
1. Укажите детали нагружения стальной двутавровой балки
2. Нарисуйте диаграмму изгибающего момента на основе данных деталей. Таким образом, вы сможете найти максимальное значение изгибающего момента.
3. Выбрать приблизительный размер стального двутавра.
4. Определите момент инерции сечения стальной двутавровой балки.
5. Определите глубину балки.
Теперь вам нужно рассчитать напряжение изгиба. Скажем, M – изгибающий момент на нейтральной оси, а I – – момент инерции площади относительно нейтральной оси. Глубина балки будет d , а f будет соответствовать развитому напряжению. Чтобы завершить формулу, вы должны также добавить перпендикулярное расстояние нейтральной оси, которое мы можем обозначить как y .Итак, вы получаете формулу:
f / (d / 2) = M / I , согласно которой вы можете рассчитать напряжение изгиба, чтобы выбрать подходящую стальную двутавровую балку.
Теги: здание, конструкция, стальная балка
Об авторе
Бибхуранджан Редактор, technofaq.org В душе я заядлый энтузиаст технологий. Мне нравится рассказывать о новых интересных разработках в области науки и технологий, и я глубоко люблю компьютерные игры. Другие хобби – написание сообщений в блогах, музыка и проекты DIY.
В уравнении изгиба сигма = Mc / I, что такое c? – Помощь на дому
В уравнении изгиба сигма = Mc / I, что такое c?
Я понимаю все в этой проблеме, кроме самого последнего шага. Что такое c и как его найти?
Концепции и причина
Изгиб характеризует поведение тонкого структурного элемента, такого как балка, подвергнутого внешней нагрузке, приложенной перпендикулярно продольной оси элемента.
Сжимающие и растягивающие силы развиваются в направлении оси балки под действием изгибающих нагрузок. Эти силы вызывают напряжения в балке. Когда балка с однородным поперечным сечением испытывает провисающий момент, максимальное сжимающее напряжение возникает у ее верхнего края, а максимальное растягивающее напряжение возникает у ее нижнего края. Поскольку напряжения между этими двумя противоположными максимумами изменяются линейно, на линейной траектории между ними существует точка, в которой нет напряжения изгиба. Геометрическое место этих точек по длине балки – нейтральная ось.
Балки с однородным поперечным сечением при изгибе не являются особенно эффективным средством поддержки нагрузки, поскольку они не используют полную мощность балки, пока она не окажется на грани обрушения.
Основы
Формула для расчета напряжения изгиба в балке при простом изгибе:
Здесь момент вокруг нейтральной оси равен M, перпендикулярное расстояние от самого внешнего волокна до нейтральной оси равно c, а момент инерции I.
Ответ:
Считать сечение балки,
Пояснение:
Нарисуйте данный рисунок, представляющий положение нейтральной оси снизу балки, а также точку c.
Напишите расположение нейтральной оси снизу балки (указано в вопросе).
Рассчитайте значение c.
Здесь перпендикулярное расстояние от внешнего волокна до нейтральной оси равно c.
Пояснение:
После вычисления положения нейтральной оси от нижней части луча, значение c можно вычислить, вычтя положение нейтральной оси из общей высоты луча. Здесь значение c – максимальное расстояние от нейтральной оси до самого дальнего волокна пучка.Если положение нейтральной оси рассчитывается от верха луча, то вместо этого оно равно c.



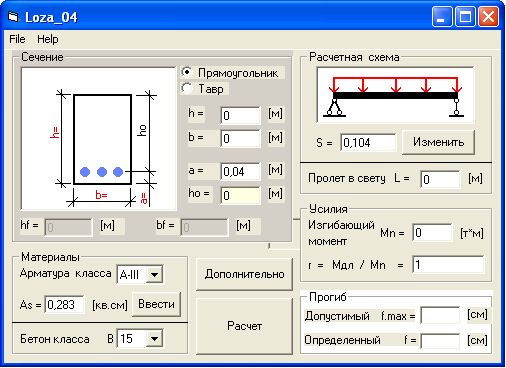 1.0.9 Онлайн расчет болтового соединения
1.0.9 Онлайн расчет болтового соединения ru/?view=calc/load_beam
ru/?view=calc/load_beam
 Наиболее распространенные значения приведены в таблице 2.
Наиболее распространенные значения приведены в таблице 2. Просто прогнутая балка может выглядеть некрасиво. Главное, чтобы выполнялось условие по прочности.
Просто прогнутая балка может выглядеть некрасиво. Главное, чтобы выполнялось условие по прочности. 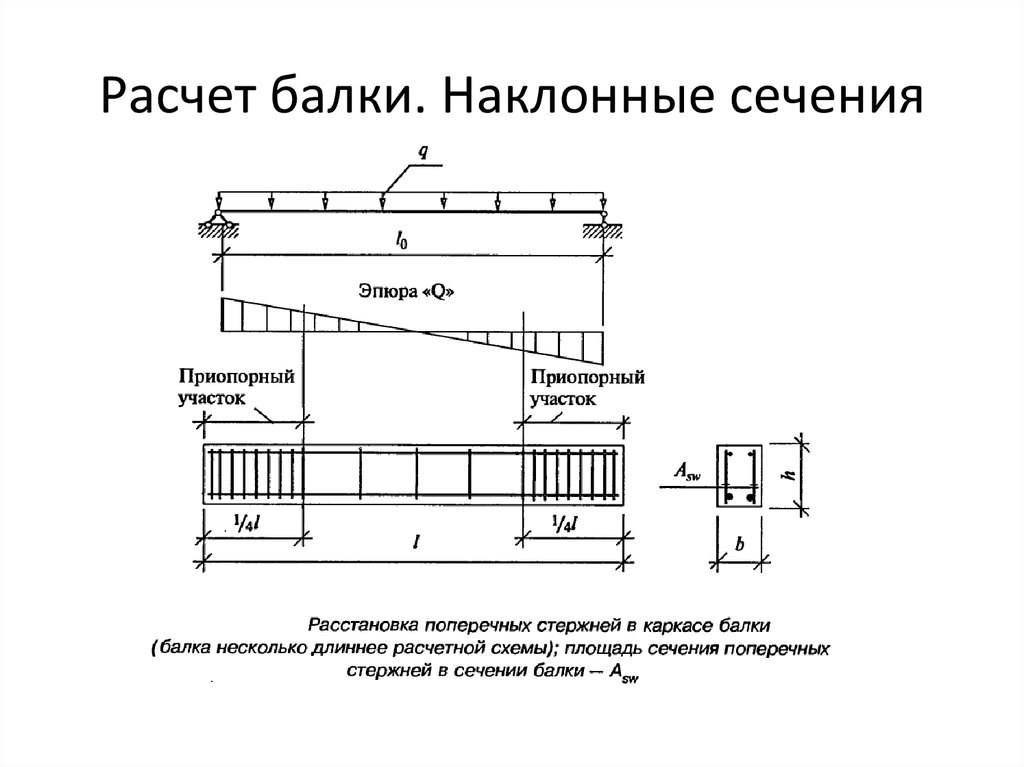 ru/index.php?app=goods&act=qa&id=8254307
ru/index.php?app=goods&act=qa&id=8254307