Расчет на прогиб балки формула: Расчет прогиба балки на двух опорах

alexxlab | 19.06.2023 | 0 | Разное

Содержание

Основные формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Содержание

1 Виды балок
- 1.1 Деревянные
- 1.2 Стальные
2 Прочность и жесткость балки
3 Расчет на жесткость
4 Расчет моментов инерции и сопротивления сечения
5 Определение максимальной нагрузки и прогиба
6 Особенности расчета на прогиб
7 Пример подсчета прогиба

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия

Для расчета максимального прогиба следует учитывать:

Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
Форма поперечного сечения и другие геометрические характеристики.
Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Конструкции из древесины хвойных пород

Стальные

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

электросварка;
заклепки;
болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

Простой. При использовании данного метода применяется увеличительный коэффициент.

Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет балок на прогиб

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

Где:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

Составление расчетной схемы объекта.
Расчет размеров балки и ее сечения.
Вычисление максимальной нагрузки, которая воздействует на балку.
Определение точки приложения максимальной нагрузки.
Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

размеры балки, длину консолей и пролет между ними;
размер и форму поперечного сечения;
особенности нагрузки на конструкцию и точно ее приложения;
материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

Где:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

l – длина;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
Варианты нагружения консольного стержня, который закреплен жестко.
Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

материал изготовления – древесина;
плотность составляет 600 кг/м3;
длина составляет 4 м;
сечение материала составляет 150*200 мм;
масса перекрывающих элементов составляет 60 кг/м²;
максимальная нагрузка конструкции составляет 249 кг/м;
упругость материала составляет 100 000 кгс/ м²;
J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

вес одного метра балки;
вес м2 перекрытия;
расстояние, которое оставляется между балками;
временная нагрузка;
нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.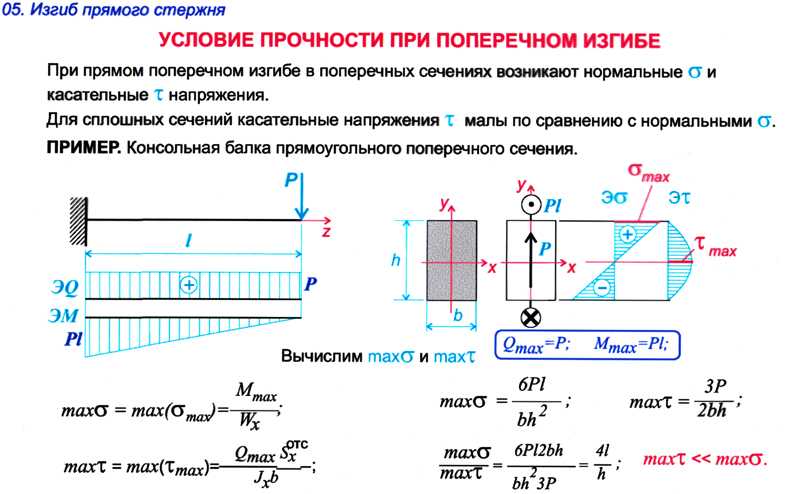

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

Расчет балки на прогиб

вернуться в раздел РАСЧЕТЫ КМ И КЖ

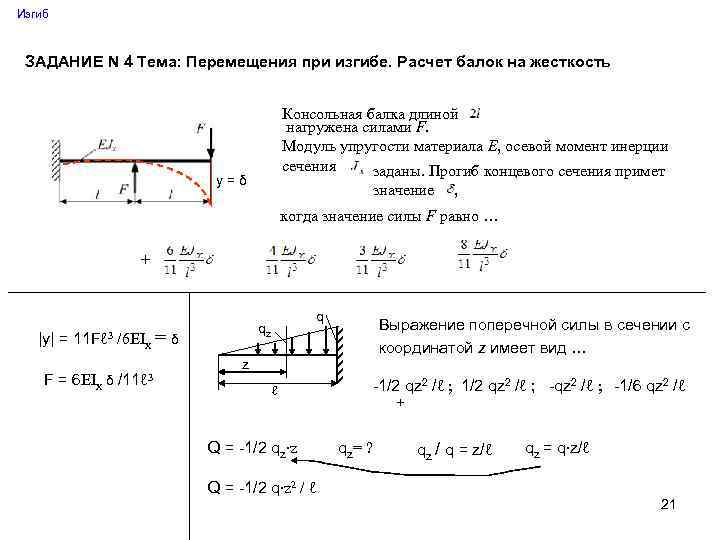
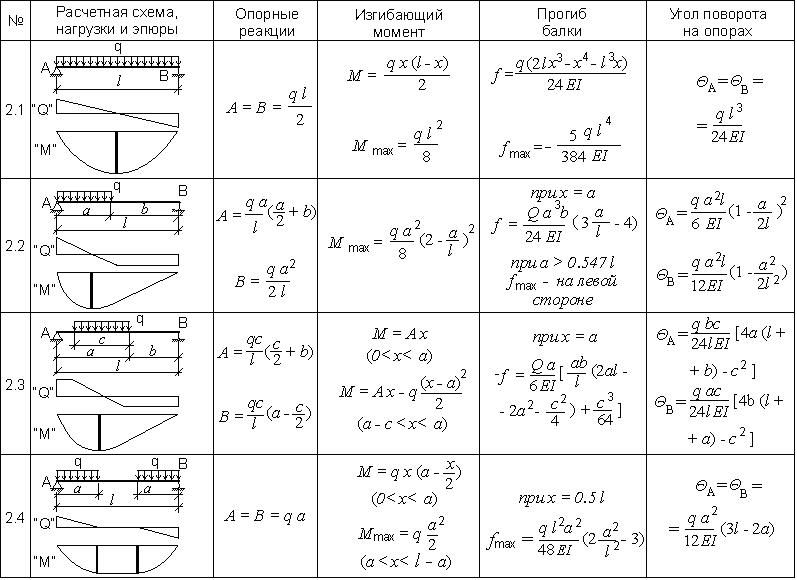
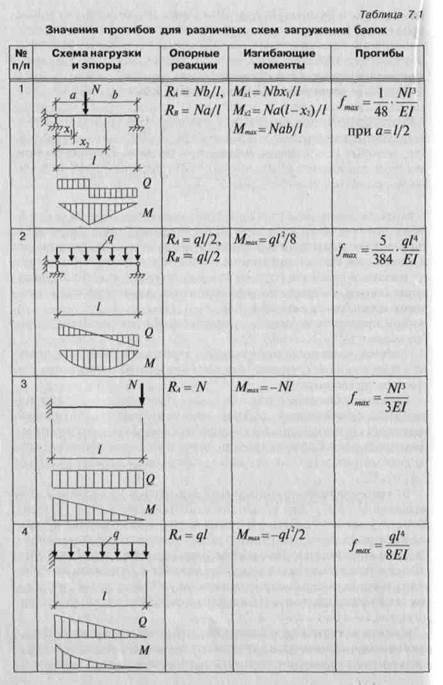
Здесь представлены формулы расчета для нахождения значений изгибающих моментов и прогибов для различных балок.

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

Консольные балки – моменты и отклонения

Консольный луч – одиночная нагрузка на конце

Максимальная сила реакции

на фиксированном конце может быть выражена как:

R _A = F (1a)
R _A = F (1a)
R _A = F (1A)
R _A

где

R _A = сила реакции в А (Н, фунт)

F = сила однократного действия в В (Н, фунт)

Максимальный момент

0004 на фиксированном конце может быть выражен как
M _MAX = M _A
= – F L (1B)
, где
M _A = максимальный момент в атмосфере (максимум
M _A = максимум в максимуме (максимум
M _A = максимально в атмосфере
M _A = максимум. Нм, Нмм, фунт дюйм)
L = длина балки (м, мм, дюйм)
Максимальный прогиб
на конце консольной балки можно выразить как
δ _{B L} ³ / (3 E I) (1C)
, где
Δ _B = максимальный отклонение в B (M, MM, In)
E = Modulus Elasticate (N / M
E = Modulus (n / M ² (Па), Н/мм ² , фунт/дюйм ² (psi))
I = момент инерции (м ⁴ , мм ⁴ , мм ^{4 ^{, 90 0 5} , дюйм ⁴}
b = длина между B и C (м, мм, дюйм)
Назначение
Напряжение в изгибающей луче может быть выражена как
σ = y m / i (1d)
, где
σ = стресс (PA (N / M ²),
σ = стресс (N / M ²),
σ = стресс (N / M ²), σ = стресс (N / M ²). Н/мм ² , psi)
y = расстояние до точки от нейтральной оси (м, мм, дюйм)
M = изгибающий момент (Нм, фунт·дюйм)
I = момент Инерция (м ⁴ , мм ⁴ , in ⁴ )
Максимальный момент в консольной балке находится в фиксированной точке, и максимальное напряжение можно рассчитать путем объединения 1b и 1d по
0 σ _{max = 12y _max F L / I               (1e)}
Пример — консольная балка с одинарной нагрузкой на конце, метрические единицы
Максимальный момент на закрепленном конце стальной полочной балки UB 305 x 127 x 42 5000 мм long, with moment of inertia 8196 cm ⁴ (81960000 mm ⁴ ) , modulus of elasticity 200 GPa (200000 N/mm ² ) and with a single load 3000 N На конце можно рассчитать как
M _MAX = (3000 N) (5000 мм)
= 1,5 10 ⁷ нм
= 1,5 10 ⁴ NM
= 1,5 10 ⁴ NM
= 1,5 10 ⁴ NM
= 1,5 10 ⁴ NM
= 1,5 10 ⁴ NM
прогиб на свободном конце можно рассчитать как
δ _B = (3000 N) (5000 mm) ³ / (3 (2 10 ⁵ N/mm ² ) (8. 196 10 ⁷ mm ⁴ ))

    = 7,6 мм
Высота балки 300 мм и расстояние от крайней точки до нейтральной оси 150 мм . Максимальное напряжение в балке можно рассчитать как
σ _max = (150 мм) (3000 Н) (5000 мм) / ( 8,196 10 ⁷ mm ⁴ )
    = 27.4 (N/mm ² )
    = 27.4 10 ⁶ (N/m ² , Pa)
= 27,4 МПа
Максимальное напряжение намного ниже предела прочности при растяжении для большинства сталей.
Консольная балка — одиночная нагрузка
Максимальная сила реакции
на фиксированном конце может быть выражена как:
R _A = F (2A)

, где
R _A = Сила реакции в A (N, LB)
F = Сила в одиночном исполнении в B (N, LB)
Максимальный момент
на фиксированном конце может быть выражен как
M _MAX = M _A
= – F A (2B)
, где . 0005
M _A = максимальный момент в A (Н·м, Н·мм, фунт·дюйм)
a = длина между A и B (м, мм, дюйм)
Максимальный прогиб
Конец консольного луча может быть выражен как
Δ _C = (F A ³ / (3 E I)) (1 + 3 B / 2 A) (2C)
, где
111 δ _C = максимальное отклонение в C (м, мм, дюйм)
E = модуль упругости (Н/м ² (Па), Н/мм ² , фунт/дюйм ² (psi))
I = момент инерции (м
9 0 , мм
⁴ , дюйм ⁴ )
b = длина между B и C (м, мм, дюйм)
Максимальный прогиб
может быть выражен как 09 09 при действии единичной силы
δ _B = F a ³ / (3 E I) (2d)
, где
δ _B = максимальное отклонение в B (м, мм, в)

Максимальное напряжение
Можно рассчитать путем объединения 1d и 200b
11 σ σ σ σ σ σ . max = y _max F a / I (2e)

Консольная балка — Калькулятор одинарной нагрузки
Общий калькулятор — будьте последовательны и используйте метрические значения, основанные на м или миллиметрах, или имперские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.
F — нагрузка (Н, фунты)
a — длина балки между A и B (м, мм, дюйм)
b — длина балки между B и C (м, мм, in)
I – Moment of Inertia (m ⁴ , mm ⁴ , in ⁴ )
E – Modulus of Elasticity (N/m ² , N/mm ² , psi)
y – Расстояние от нейтральной оси (м, мм, дюйм)
Консольная балка – Равномерно распределенная нагрузка
Максимальная реакция
на фиксированном конце может быть выражена как:
R _A = Q L (3A)

, где
R _A = Реакционная сила в А. Н, фунт)
q = равномерная распределенная нагрузка (Н/м, Н/мм, фунт/дюйм)
L = длина консольной балки (м, мм, дюйм)

Максимальный момент
на фиксированном конце можно выразить как
M _A = – Q L ² /2 (3B)
Максимальный отклонение
на конце можно выразить как
Δ _B = Q L ⁴ / (8 E. ) (3C)
, где
Δ _B = максимальное отклонение в B (M, MM, In)
Cansilever Beam – Единый нагрузочный калькулятор
Общий расчет. Использование Метрического значения, основанного на m m m. или мм, или имперские значения, основанные на дюймах. Типичные значения по умолчанию указаны в метрических миллиметрах.
q – Равномерная нагрузка (Н/м, Н/мм, фунт/дюйм)
L – Длина балки (м, мм, дюйм)
I – Момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )
E – Модуль упругости (Па, Н/мм ² , фунт/кв. дюйм)
м – Расстояние от оси
Более чем одна точечная нагрузка и/или равномерная нагрузка, действующие на консольную балку
Если более чем одна точечная нагрузка и/или равномерная нагрузка действуют на консольную балку – результирующий максимальный момент на закрепленном конце А и Результирующее максимальное отклонение на конце B можно рассчитать путем суммирования максимального момента в A и максимального отклонения в B для каждой точки и/или равномерной нагрузки.
Консольный луч – снижение распределенной нагрузки
максимальная реакция
на фиксированной конце R _A = сила реакции в A (Н, фунт)
q = падающая распределенная нагрузка – максимальное значение в A – ноль в B (Н/м, фунт/фут)
Максимальный момент
в фиксированный конец может быть выражен как
M _MAX = M _A
= – Q L ² /6 (4B)
, где
M _A = максимум в MAMPAME (N. M MAMENT MAMER.
L = длина балки (м, мм, дюйм)
Максимальный прогиб
на конце консольной балки можно выразить как
δ _B = L ⁴ / (30 E I)    (4c)
где
δ _B = максимальное отклонение в B (м, мм, дюйм)
E = модуль упругости (Н/м ^{2 Па 9), Н/м ²} , фунт/дюйм ² (psi))
I = момент инерции (м ⁴ , мм ⁴ , дюйм ⁴ )
5 90 Расширение Sketchup
Калькуляторы прогиба балки – EngineerExcel
Расчет прогиба балки применим к нескольким сценариям проектирования конструкций. Например, расчет отклонения консольной балки может определить силы, действующие на крыло самолета.
Калькуляторы прогиба балки
Самый простой способ определить прогиб балки под действием силы или момента — использовать калькулятор и параметры балочной системы. В зависимости от балочной системы, консольной, просто поддерживаемой или неподвижно-фиксированной, были оценены различные случаи, чтобы получить уравнение для расчета отклонения балки как функции расстояния вдоль балки.
Калькуляторы прогиба консольной балки
Существует пять общих случаев для учета прогиба консольной балки.
Консольная балка с конечным усилием
Первый – это прогиб под действием силы на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где:
F сила, приложенная к концу балки (Н)
х — позиция вдоль балки, где оценивается прогиб (м)
E — модуль Юнга материала балки (Па)
I – момент инерции площади (м4)
L общая длина балки (м)
Консольная балка с нагрузкой в любой точке
Второе отклонение консольной балки — это отклонение из-за силы, приложенной в какой-либо точке, отличной от конца, как показано ниже:
Прогиб балки можно рассчитать с помощью следующих уравнений:
где a — расстояние от поддерживаемого конца до места действия силы (м).
Консольная балка с равномерно распределенной нагрузкой
Третье отклонение консольной балки представляет собой отклонение из-за силы, приложенной равномерно по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
где w — равномерная нагрузка (Н/м).
Консольная балка с треугольной распределенной нагрузкой
Четвертый прогиб консольной балки представляет собой прогиб из-за треугольной распределенной силы, приложенной по длине балки, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения :
где w ₁ — максимальное значение силы (Н).
Консольная балка с конечным моментом
Конечный прогиб консольной балки — это прогиб из-за момента на свободном конце балки, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
где M ₀ — момент, приложенный к свободному концу (Н∙м).
Калькуляторы прогиба свободно опертой балки
Просто опертая балка с нагрузкой в любой точке
Существует семь общих случаев для рассмотрения прогиба свободно опертой балки. Первый – это отклонение из-за промежуточной силы, как показано ниже:
Отклонение балки можно рассчитать с помощью следующего уравнения:
, где a и b — расстояния по обе стороны от приложенной силы (м).
Свободно опертая балка с нагрузкой в середине пролета
Второй прогиб свободно опертой балки — это прогиб из-за силы, приложенной к центру балки, как показано ниже:
Прогиб балки можно рассчитать с помощью Следующее уравнение:
Свободно опертая балка с равномерно распределенной нагрузкой
Третье отклонение свободно опертой балки — это отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом на каждом конце
Четвертый прогиб свободно опертой балки — это прогиб из-за моментов на обеих опорах, как показано ниже:
прогиб можно рассчитать по следующему уравнению:
Свободно опертая балка с моментом на одном конце
Пятый прогиб свободно опертой балки — это прогиб из-за момента на одной опоре, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Свободно опертая балка с моментом в центре
Окончательное отклонение свободно опертой балки — это прогиб из-за момента в центре балки, как показано ниже :
Прогиб балки можно рассчитать по следующему уравнению:
Калькуляторы прогиба фиксированной-фиксированной балки
Фиксированная-фиксированная балка с нагрузкой в середине пролета
Существуют два общих случая для рассмотрения фиксированной-фиксированной отклонение луча. Первый — это отклонение из-за силы в центре, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Неподвижно-неподвижная балка с равномерно распределенной нагрузкой
Другое фиксированно-неподвижное отклонение балки представляет собой отклонение из-за равномерно распределенной силы, как показано ниже:
Прогиб балки можно рассчитать с помощью следующего уравнения:
Дифференциальный расчет прогиба балки
Другой метод расчета прогиба балки включает использование дифференциального уравнения кривой прогиба для оценки поведения балки при изгибе. Здесь представлен обзор этого метода, однако конкретные детали выходят за рамки этого введения.
В этом методе используется общее уравнение, и его можно применять к любой комбинации сил и моментов, действующих в любой точке балки. Используемое уравнение:
где:
v – прогиб балки (м)
d ² v/dx ² – вторая производная прогиба относительно положения вдоль балки
M — изгибающий момент вдоль балки в зависимости от положения (Н∙м)
Изгибающий момент в каждой секции балки рассчитывается как функция x .