Расчет на прогиб двутавра: Расчёт металлической балки онлайн (калькулятор)
alexxlab | 07.12.1985 | 0 | Разное
Расчет двутавра на прогиб и изгиб
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет швеллера
- Расчет уголка
- Расчет деревянной балки
- Расчет двутавра на устойчивость.
Разновидности
Металлические конструкции отличаются по многим признакам. Это рекомендуется учитывать при выборе изделия.
По назначению
С помощью металлических балок можно создать качественное прочное перекрытие, выбрав один из вариантов.
Монолитное. В опалубку заливается бетон, производится усиление решеткой из арматуры. Поверхность получается бесшовной, отличается высокой прочностью.- Монолитно-сборное. В этом случае помимо металлических балок используются бетонные блоки, которые укладываются на стальной профиль.
 Участки стыков заливаются бетоном.
Участки стыков заливаются бетоном. - Составное. Используется комбинация материалов, то есть на несущие металлические изделия укладываются плиты, доски, панели. Этот вариант предполагает создание дополнительного утепления и звукоизоляции поверхности.
По материалу: стальные и алюминиевые
Металлические конструкции могут изготовляться из разных материалов. Самыми популярными являются стальные и алюминиевые балки для перекрытий.
- Стальные изделия изготавливаются из сплава стали способом холодного или горячего катания. Стальные конструкции бывают нескольких видов: уголок, швеллер, двутавр. Из преимуществ стальных балок можно выделить огнеустойчивость, устойчивость к гниению и внешним факторам, высокую прочность.
Основными недостатками являются: высокая стоимость, низкие показатели тепло и звукоизоляции, риск образования коррозии. Монтаж стальных конструкций невозможно осуществлять без привлечения специальной техники. - Алюминиевые балки.
 При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
По конструкции
В современном строительстве применяют несколько разновидностей металлических балок, различных по конструкции.
Тавровые. Основное сечение представляет собой стенку и полку в виде буквы «Т».- Двутавровые. Сечение металлопроката выглядит как буква «Н». Изделие отличается большей жесткостью, чем тавровое, за счет того, что с противоположной стороны имеет дополнительную полку.
Двутавровые элементы подразделяются на несколько видов, каждый из которых имеет маркировку: - У – узкополочные конструкции.

- Д – среднеполочные изделия.
- К – колонные балки. Ширина полки такого элемента может равняться высоте изделия.
- Швеллер. Сечение элемента представляет собой букву «П». Эти балки считаются универсальными, применяются во всех сферах промышленности.
Существуют двутавры не с параллельными, а с наклонными полками. Их классифицируют на специальные и обычные. Их характеристики регламентирует ГОСТ 19425-74.
Инструкция к калькулятору
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также двутавр необходимо проверять на устойчивость (на заваливание от момента). Это можно сделать с помощью калькулятора, ссылка на который расположена выше (в списке «Калькуляторы по теме»). Если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
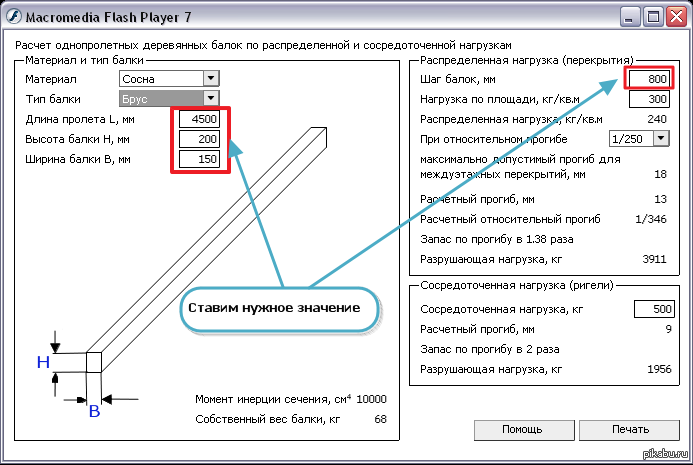
Исходные данные
Расчетная схема:
Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли.![]()
Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры.
Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов:
- калькулятор по сбору нагрузок на балку перекрытия;
- пример сбора нагрузок на балку перекрытия.
Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1.
Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две».
Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2.
Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу.
Что это такое и каких размеров бывают?
Балка является одним из основных элементов любой конструкции, ее функции – повысить устойчивость конструкции и укрепить ее. Балка (или ригель) состоит из полок и стенок различного размера, соединенных стыковыми швами с использованием сварки. Изготавливаются элементы на оборудованных предприятиях с использованием специальных станков.
Процедура изготовления осуществляется в несколько этапов, после чего готовое изделие проверяется на соответствие ГОСТам.
Металлические конструкции различаются по размерам, для удобства они имеют номера, с помощью которых можно подобрать необходимый материал для строительства.
Сфера применения
Металлические балки для перекрытий нашли свое применение в различных областях. Могут использоваться для:
- Укрепления кровли в жилом и промышленном строительстве.
- Создания межэтажных перекрытий.
- Устройства опор и различных колонн в промышленных сооружениях и архитектурных зданиях.

- Монтажа ангарных каркасов.
- Шахтовых стволов.
- Создания разнообразных железнодорожных вагонов.
- Строительства мостов, эстакад.
- Возведения металлических ферм.
На заметку: балки перекрытий из металла также можно использовать при строительстве малоэтажных частных домов.
Особенности процесса монтажа
Процедура устройства перекрытий с использованием металлических балок имеет определенные особенности, которые необходимо знать и четко соблюдать.
Обязательно наличие четкой схемы постройки с произведенными расчетами на прочность и изгиб изделий.- К боковым граням балок крепятся бруски сечением 60х60, после чего размещается накат из досок.
- Накат накрывается слоем утеплителя, выполняющего функции звуко и теплоизоляции.
- Шаг между стальными балками не должен превышать 150 см, оптимальное расстояние – 100 см.
- Глубина опирания концов металлических конструкций на стены – максимум 25 см.

- Чтобы добиться большей звукоизоляции можно использовать не обычные, а пружинные скобы.
Характеристики
Балки перекрытий, в зависимости от технологии производства, имеют различные характеристики.
Двутавры с наклонными полками. Угол уклона 6-12 градусов. Основные параметры:- длина – 10-60 см;
- ширина – 5,5-19 см;
- толщина полки – 7,2 мм-1,8 см;
- толщина стенки – 4,5мм-1,2 см.
- Двутавры с параллельными гранями (ГОСТ 26020, СТО АСЧМ 20-93) имеют иные характеристики:
- длина — Б-1 – 100 Б-4;
- толщина полок – 5,7 мм-3,3 см;
- ширина профиля – 55 мм-32 см;
- толщина стенки – 4,1 мм-1,95 см.
- Широкополочные металлические конструкции имеют следующие характеристики:
- длина — 20Ш1- 70Ш5;
- ширина профиля – 15-32 см;
- толщина стенки – 6,0 мм- 2,3 см;
- толщина полок – от 9 мм -3,65 см.
- Колонные балки имеют следующие показатели:
- длина – 20 К1-40 К5;
- ширина профиля – от 20 до 40 см;
- толщина стенки – от 6,5 до 2,3 см;
- толщина полок – 1-3,55 см.

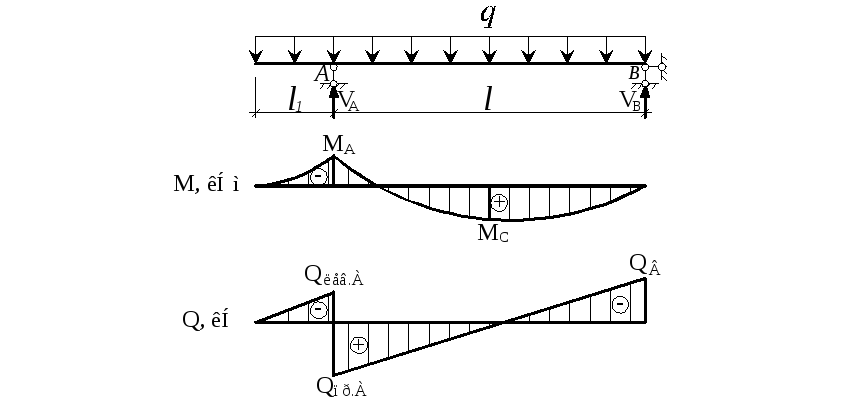
Построение эпюр изгибающего момента и поперечной силы при изгибе
Полученные значения изгибающего момента и поперечной силы в двух сечениях (при положении x=0 и x=l) откладываем соответствующие ординаты, т.е. буквально строим графики обеих функций.
Что мы видим из построенных эпюр, какие выводы мы можем сделать:
- из эпюры поперечной силы видно, что она не меняется по всей длине и равна внешней силе F
- так как в начале координат x (т.е. справа) мы видим на эпюре «скачок» на величину этой силы, то в конце, в заделке скачок говорит о том, что реакция в заделке равна силе F
- на эпюре моментов график выходит из нуля координаты x (справа на балке) и момент тоже равен нулю
- по мере удаления сечения от силы влево момент растет и достигает своей наибольшей величины в заделке, где наблюдается такой же скачок как и на эпюре поперечной силы и равен (- F x). Это говорит о том, что момент в заделке равен именно этому значению
Что такое «скачок» на эпюре
Когда график начинается не из нуля или не из значения полученного на предыдущем участке, а имеет в одном и том же сечении x два разных значения — такой разрыв функции называется скачок.
Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.
Вот и все секреты построения эпюр для моментов и поперечных сил. Конечно дальше немного усложняется сам процесс, но принцип остается тот же.
Дальше в видео представлены примеры построения эпюр для распределенной нагрузки изгибающего момента. Чтобы было проще показать разницу все собрано в одном видео:
Рубрики
Изгиб, Сопромат онлайн
Метки
внутренние усилия, внутренние усилия при изгибе, задачи курса сопротивление материалов, изгиб, изгиб балки, изгибающий момент, Как построить эпюры изгибающих моментов и поперечных сил, краткий курс сопротивления материалов, поперечная сила, построение эпюр изгибающего момента, построение эпюр поперечной силы, правило знаков, правило знаков при изгибе, расчет балки, расчет балки на изгиб, Сопромат для чайников, Сопротивление материалов, сопротивление материалов краткий курс, сопротивление материалов примеры решения задач
- Сопротивление материалов
- Что такое сопромат
- Диаграмма растяжения стали на разрыв
- Как построить эпюры при растяжении-сжатии
- Эпюры моментов M(x) поперечных сил Q(x)
- Момент инерции сечения
- Сложное сопротивление
- Отзывы про репетитора по сопромату и строймеху
- Строительная механика
- Помочь проекту
- Курсы для инженеров
Цены на все виды
В строительстве чаще всего используются двутавровые металлические балки. Средняя стоимость продукции представлена в таблице.
Средняя стоимость продукции представлена в таблице.
| Наименование балки | Длина | Стоимость |
| двутавровая № 10 | 12 м | 880 |
| двутавровая № 10 Б-1 | 12 м | 780 |
| двутавровая № 12 | 12 м | 900 |
| двутавровая № 12 Б-1 | 12 м | 660 |
| двутавровая № 14 | 12 м | 1050 |
| двутавровая № 14 Б-1 | 12 м | 740 |
| двутавровая № 16 | 12 м | 1300 |
| двутавровая № 16 Б-1 | 12 м | 980 |
| двутавровая № 18 | 12 м | 1280 |
| двутавровая № 18 Б-1 | 12 м | 1150 |
| двутавровая № 20 | 12 м | 1560 |
| двутавровая № 25 Б-1 | 12 м | 2150 |
| двутавровая № 25 Ш-1 | 12 м | 3500 |
| двутавровая № 30 | 12 м | 2600 |
| двутавровая № 35 | 12 м | 3300 |
| двутавровая № 40 | 12 м | 3500 |
| двутавровая № 45 Б-1 | 12 м | 5200 |
Выбор размера швеллера на примере
Пусть имеется швеллер, длина которой составляет 6 метров и он имеет шарнирное закрепление. На него действует распределенная нагрузка, величина которой составляет 250 кг/м. Расчет ведется в следующей последовательности:
На него действует распределенная нагрузка, величина которой составляет 250 кг/м. Расчет ведется в следующей последовательности:
- Максимальное значение момента в профиле швеллера М = 9,81 х 250 х 6²/ 8 / 1000 = 11,04 кН∙м.
- Необходимое значение момента сопротивления сечения швеллера, Wн = 11,04 х 1000 / 240 = 46,0 см3 (согласно СНиП 2-23-81 для стали С245 Ry = 240 МПа).
- Подбираем по таблице ГОСТ размер швеллера с моментом сопротивления не ниже вычисленного значения 46,0 см3.
Это будет швеллер 12П (У) ГОСТ 8240-97 — значение момента сопротивления 50,8 см3 или швеллер гнутый 140х60х5 ГОСТ 8278-83 — значение момента сопротивления 47,8 см3.
Плюсы и минусы применения в зданиях
Конструкции из металла обладают рядом преимуществ, благодаря которым материал широко используется:
- повышенной прочностью;
- огнестойкостью;
- устойчивостью к внешним факторам;
- повышенной надежностью;
- большим периодом эксплуатации;
- возможностью усилить уже построенное здание;
- увеличенной несущей способностью.

Однако такие балки имеют и свои недостатки, которые также следует учитывать:
- сложность проведения строительных работ;
- необходимость задействовать тяжелую технику;
- металл может подвергаться коррозии;
- требуется производить сложные подсчеты, с чем у новичка могут возникнуть серьезные сложности.
Способы выполнить расчет и проверку на прогиб
Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.
Просчитать прогиб конструкции можно несколькими способами:
- Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
- Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок.
 Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб; - Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.
К сведению! Чтобы реально представлять, почему так важно знать величину отклонения от первоначального положения, стоить понимать, что измерение величины прогиба является единственным доступным и достоверным способом определить состояние балки на практике.
Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.
Требования
Все требования, предъявляемые к балкам из металла, четко обозначены в ГОСТах и СНиПах. Основными требованиями являются:
- Прочность. В зависимости от типа материала, используемого при изготовлении изделия, показатели прочности могут отличаться, но они должны соответствовать значениям, указанным в нормативных документах.

- Период эксплуатации. Металлические конструкции, согласно ГОСТ, должны прослужить минимум 80 лет.
- Устойчивость к коррозии. Готовые элементы должны быть дополнительно обработаны составами, предотвращающими образование коррозии.
Нагрузка на двутавровую балку таблица
Какие нагрузки выдерживает двутавровая балка?
Расчет металлоконструкций, необходимых для возведения сооружений промышленного назначения или другого масштабного строительства весьма сложен и включает в себя учет множества факторов. Прежде чем ответить на вопрос, какие нагрузки выдерживает двутавровая балка, инженеру или архитектору необходимо учесть, в частности, собственный вес конструкционного элемента, методику его крепления, длину свободных пролетов.
Что может дать правильная оценка нагрузки и выбор соответствующей маркировки двутавра?
Главное, что дает правильная оценка нагрузки на конструкции из двутавра и выбор соответствующего класса проката – экономическую эффективность строительства. Затраты будут оптимальны, все требования техники безопасности и критерии прочности перекрытия – выполнены. При этом можно получить дополнительные преимущества:
Затраты будут оптимальны, все требования техники безопасности и критерии прочности перекрытия – выполнены. При этом можно получить дополнительные преимущества:
- значительно увеличить размер свободных пролетов,
- снизить массу несущих конструкций, данный показатель может достигать 35% при переходе с квадратного профиля на двутавр,
- повысить рентабельность, получая плановые конечные характеристики реализованного проекта в целом.
Для того чтобы увеличить предел нагрузки, которую способна выдержать двутавровая балка, применяют вспомогательные средства и методы. Это может быть, к примеру, создание дополнительных ребер жесткости или усиление существующих. Последний способ применяется для длинных конструкций из двутавра только в продольном направлении.
Виды нагрузок
На каждую двутавровую балку в конструкции действуют следующие нагрузки: • собственный вес, • изгибающий момент, • поперечная сила.
От правильности выбора номера проката будет зависеть, выдержит ли двутавр планируемую нагрузку на перекрытие, и способен ли он эффективно применяться в той или иной металлоконструкции.
Как выбрать наиболее подходящий сорт проката?
Каждая двутавровая балка маркируется собственным номером, который сразу может дать информацию о собственном весе изделия. Найти такую информацию можно в отраслевых справочниках и ГОСТ 8239-89. Например:
- двутавр с номером 10 имеет массу 9,46 кг на погонный метр, при этом тонна проката – это 105,71 м балки,
- аналогичные показатели для проката №20 – 21 кг на метр и 47,62 м в тонне.
Данные собственного веса используются при расчете методик крепления конца балки и для правильного проектирования несущих конструкций. Расчет уровня нагрузки на каждый из двутавров перекрытия достаточно сложен, поэтому строители и архитекторы часто пользуются усредненными значениями, к примеру:
- для шестиметровых пролетов и нагрузке на перекрытие 300 кг на м.п. можно применять профиль 16, располагая балки с шагом 1 м,
- если применять при нагрузке в 300 профиль 10 с шагом в метр, величина пролета должна быть уменьшена до 4 метров,
- для профиля 20, расположенного с шагом 1.
 1 м в 6 м пролете, допускаются нагрузки на перекрытие в 500 кгм.п.
1 м в 6 м пролете, допускаются нагрузки на перекрытие в 500 кгм.п.
В общем случае данных, которые приводятся во множестве источников, достаточно для определения необходимого номера профиля. Однако на практике зачастую требуется точное определение нагрузки, которое должна выдерживать двутавровая балка.
Как сделать точный выбор?
Чтобы точно выбрать номер двутавра по необходимой нагрузке, необходимо:
- Пересчитать давление на 1 погонный метр балки, учитывая необходимую нагрузку на перекрытие и его собственный вес.
- По требованиям ГОСТ 8239-89 увеличить полученное значение на запас надежности (рекомендуемый коэффициент).
- По таблице ГОСТ 8239-89 определить момент сопротивления, используя полученную перед этим цифру нагрузки.
После этого достаточно заглянуть в справочную таблицу ГОСТ 8239-89 и определить номер двутавра. Специалисты рекомендуют выбирать прокат на 2 номера выше расчетного, чтобы иметь возможность увеличивать шаг расположения балок до 1. 1 метра.
1 метра.
Нагрузка на двутавровую балку таблица
8 (495) 456 99 99
8 (343) 456 99 99
8 (912) 456 99 99
8 (351) 456 99 99
Заказать двутавровую балку
- Главная
- Расчет двутавровой балки
Расчет двутавровой балки
Двутавровая балка довольно редко применяется в частном строительстве в силу своей формы. Поэтому примнется двутавр лишь, когда невозможно применение других профилей, например, швеллера или уголка. Двутавр может воспринимать гораздо большую нагрузку, чем перечисленные профили. Если Вам нужна именно мощная балка и двутавр рассматривается в качестве одного из основных вариантов, то в подборе профиля данный калькулятор будет не лишним. С его помощью Вы можете рассчитать двутавр не только на изгиб (по несущей способности), но и на прогиб (по деформациям).
Расчет двутавровой балки онлайн калькулятор
Для примерного расчёта прогиба на двутавровую балку калькулятор онлайн
Напишите нам и наши инженеры сделают точный
Расчет двутавровой балки на прочность, изгиб, кручение, прогиб, нагрузки и веса
Принимаем заказ на расчёт нагрузки на двутавровую балку 10.
Какую нагрузку выдерживает двутавр. Вес двутавровой балки – важный фактор несущей способности
Балка 20 . Применение. Виды. Расчёт двутавра .
Двутавровая балка – прокат, имеющий сечение буквы Н и означающий с латинского языка – «двурогая» с двух сторон («тавр» – бык). Расстояние между полками называют высотой, у двутавра 20го высота составляет около 200 мм или 20 см. Двутавр – это металлопрокат фасонного типа, изготавливаемый из строительной стали – ст3 и низколегированной стали 09Г2С.
Балка двутавровая 20 наиболее распространена в применении у строителей и монтажников, в первую очередь при устройстве каркасов с большими пролётами в зданиях, для перераспределения нагрузки с перекрытий на несущие конструкции. Её используют для мостостроительства, изготовления кранов, автомобилей, трубопроводов, самолётных ангаров, в железнодорожном строительстве и т. д. 20й профиль производят по 8239 ГОСТ двутавры стальные , госстандарту 26020-83, двутавр гост 19425-74 и техническим условиям СТО АСЧМ 20-93.
Двутавр 20й подразделяют по СТО АСЧМ 20 на нормальную балку 20Б с параллельными гранями полок, широкополочную балку 20Ш и 20К – для колонн. Двутавр СТО АСЧМ 20-93
Двутавр стальной 20Б1 имеет массу метра – 21,3 килограмм. Масса 20Ш1 составляет 30,6 кг в метре, вес колонной балки 20К1 – 41,4 кг, вес двутавра 20К2 – 49,9 кг. Параметры двутавра 20Б1: высота (h)- 200 мм, ширина полки (b)- 100 мм, толщина стенки (s) – 5,5 мм, толщина полки (t)- 8,0 мм. Широкополочный 20й профиль 20Ш1 имеет следующие характеристики: h – 194 мм, b- 150 мм, s – 6 мм, t – 9 мм.
Балка 20 по стандарту 19425 может быть монорельсовой (обозначается буквой М) и спец. (именуется буквой С). Этот ГОСТ распространяется на горячекатаные двутавры с полками, имеющими наклон внутренней поверхности полок. Монорельсовый двутавр, известный как кран балка, предназначена для крановых путей, как несущий мост в козловом или мостовом кранах, как подрельсовая балка. Такое изделие характеризуется высокой прочностью и способно противостоять большим нагрузкам, давлению, скручиванию. Специальная балка применима в стволе конструкций, которые обеспечивают движение подъёмных стволов, то есть для армирования стволов шахт, а также в сооружении лестниц и прокладке инженерных коммуникаций, креплении водоотливов.
Специальный профиль 20С имеет следующие параметры – двутавр размеры : высоту – 200мм, ширину полки – 100 мм, толщину стенки – 7 мм, толщину полки – 11,4 мм. Масса 1 м такого двутавра составляет 27,9 кг.
Двутавр ГОСТ 8239 89 – на сортамент двутавров , имеющий отличие – наклон внутренних поверхностей полок. Такая балка с расстоянием между полками 200 мм имеет ширину этих полок – 100 мм, толщину металла посередине высоты – 5,2 мм, толщину полок 8,4 мм.
Какой двутавр лучше? Горячекатаный двутавр или сварной?
Чтобы выбрать между горячекатаной балкой 20 и сварным профилем с похожими параметрами, вычиляют момент сопротивления. Для этого учитывают нагрузку на перекрытие, непрерывную и краткосрочную нагрузку, используют табличные данные – коэффициент прочности и допустимый прогиб для несущих конструкций.
Для этого учитывают нагрузку на перекрытие, непрерывную и краткосрочную нагрузку, используют табличные данные – коэффициент прочности и допустимый прогиб для несущих конструкций.
Технические характеристики металлического профиля необходимы, чтобы их правильно применять в строительстве, ведь несмотря на большое разнообразие сфер применения, суть остается одна – создать надежную несущую конструкцию. Она позволяет преобразовывать архитектуру сооружений:
- увеличивает ширину пролетов зданий,
- значительно, примерно на 35%, уменьшить массу несущих конструкций,
- существенно увеличить рентабельность проектов.
Говоря о достоинствах конструкции, нельзя не отметить и минусы, хотя их немного. Основные из них – это
- необходимость применять при создании ребер жесткости дополнительную арматуру,
- достаточно существенные трудозатраты, которые нужны для ее изготовления.
Однако, следует отметить, что с другой стороны дополнительные ребра жесткости дают возможность:
- уменьшить общую металлоемкость сварной металлоконструкции, так как ощутимо уменьшают толщину стенок.
 Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики,
Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики, - помимо этого облегченная конструкция экономична и с точки зрения устройства фундамента, поскольку после снижения общей массы можно использовать фундамент под БМЗ (быстровозводимые здания).
Чтобы найти двутавр, подходящий для конкретного случая, требуется произвести некоторые расчеты. Обычно для этого используют таблицы или онлайн калькуляторы. В их основе лежат заданные два параметра: расстояние от одной стены до другой и будущая нагрузка на строительную конструкцию.
Прочность двутавровой балки определяется такими параметрами, как:
- длина,
- метод закрепления,
- форма,
- площадь поперечного сечения.
Большее распространение получили изделия с буквой «Н» в сечении.
Жесткость металлической конструкции двутавра в 30 раз превышает жесткость квадратного профиля, а прочность, соответственно, в 7 раз.
Длина данной металлоконструкции бывает разной, к примеру, в случае ГОСТ 8239-89 это 4 –12 метров, то есть в зависимости от сортамента размеры и вес балки двутавровой отличаются.
При покупке сварной конструкции обязательно требуется расчет на прочность, а для конкретного использования еще и расчет на прогиб. Грамотный расчет нагрузки на двутавровую балку позволит обеспечить устойчивость конструкции к проектным воздействиям, то есть способность воспринимать их без разрушения.
Нагрузка собственного веса
Чтобы определить в случае необходимости вес двутавровой балки пользуются специальными таблицами, где расписаны ее характеристики, к примеру, габариты, марка стали и т. д. В таблице представлена теоретическая масса 1 м профиля.
балка двутавровая размеры и вес (ГОСТ 8239-89)
Пример расчета двутавра
Предположим необходимо рассчитать вес двутавра № 12 длиной в 3 метра . Согласно таблице условная масса погонного метра данного профиля равна 11,50 кг. Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Если перемножить полученные значения, то получим величину общей массы – 34,5 кг.
Точнее значение веса сварной металлоконструкции можно посчитать, используя специальные онлайн калькуляторы.
В калькуляторе выбирают соответствующий номер двутавра и вводят необходимый метраж. Как видите, полученное значение больше рассчитанного нами на 0,12 кг.
Несущая способность
Среди всех типов балок двутавровая имеет наибольшую прочность, более того, она устойчива к температурным перепадам. Допустимая нагрузка на двутавр бывает указана на маркировке, как размер. Чем больше число, указанное в его наименовании, тем большую нагрузку может воспринимать балка.
Любой расчет предполагает изначальное знание размеров прокатного или сварного профиля, его длины и ширины. Проясним смысл значения ширины на примере самой популярной балочной опоры – колонны.
Предположим, что в сечении колонны лежит квадрат со стороной 510 мм, тогда на нее можно будет опереть профиль, для которого ширина не может превышать 460 мм. Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
Это связано с тем, что двутавр придется приваривать к железобетонной подушке, а для сварочных швов понадобится запас, по крайней мере, в 40 мм.
После определения ширины переходят к выбору профиля и расчету нагрузки, воздействующей на профиль. Она представляет собой совокупность воздействий от перекрытия, а также воздействий временного и постоянного характера.
Нагрузку, выражающую величину нормативной нагрузки, собирают на длину 1 м профиля.
Но, расчет несущей способности двутавровой балки предполагает учет другого воздействия. Чтобы получить расчетную нагрузку, рассчитанное нормативное воздействие умножается на так называемый коэффициент прочности по нагрузке. Остается к результату прибавить уже подсчитанную массу изделия и найти его момент сопротивления.
Полученных данных достаточно, чтобы из сортамента подобрать профиль, необходимый для изготовления сварного профиля. Как правило, с учетом прогиба конструкции рекомендуется выбирать профиль выше на два порядка.
Сварная металлическая конструкция должна использовать примерно 70–80% от максимально допустимого прогиба.
Если несущая способность двутавра оказывается недостаточной, то возникает необходимость ее усиления. Для различных элементов сварной конструкции этот вопрос решается по-разному.
К примеру, для элементов, воспринимающих нагрузки типа растяжения, сжатия или изгиба, используют такой вариант усиления: увеличивают сечение, иначе говоря, повышают жесткость, скажем, приварив дополнительные детали.
Теоретически – это один из лучших вариантов усиления, однако, при его реализации не всегда удается получить требуемый результат. Дело в том, что элементы в процессе сварочных работ нагреваются, а это несет за собой уменьшение несущей способности.
В какой степени можно ожидать такого понижения зависит от размеров двутавра и режима и направления сварочных работ. Если для продольных швов максимальное понижение оказывается в пределах 15%, то для швов в поперечном направлении оно может достичь и 40%.
Поэтому при усилении двутавра под нагрузкой категорически запрещено накладывать швы в направлении, поперечном к элементу.
Расчетно и экспериментально было доказано, что оптимального результата усиления под нагрузкой можно получить при максимальном напряжении в 0,8 R y , то есть 80% расчетного сопротивления стали, которая была использована для изготовления двутавра.
Расчет нагрузки на двутавр – актуальность выполнения и основные методики
Двутавровая балка, как одна из разновидностей фасонного черного и цветного металлопроката, отличается широким сортаментом изделий. Поэтому в ходе проектирования и дальнейшего возведения конструкций с использованием двутавра надо сделать верный выбор. Он должен основываться на правильных расчетах. О том, как выполнить расчет нагрузки на двутавр читайте в нашей статье.
Сразу отметим что для расчетов понадобятся формулы, таблицы и знания. А если их нет, то лучше доверить все опытному и квалифицированному инженеру. Особенно если речь идет о двутавровой балке, которая применяется в нагружаемых конструкциях.
От этого напрямую зависит как качество строительства, так и безопасность эксплуатации возводимых объектов. Все параметры должны соответствовать действующим нормативным документам, обеспечивать рабочие расчетные характеристики металлоконструкции. Это обусловлено, прежде всего, сферой применения двутавровой балки, например, в качестве элемента перекрытий.
Все параметры должны соответствовать действующим нормативным документам, обеспечивать рабочие расчетные характеристики металлоконструкции. Это обусловлено, прежде всего, сферой применения двутавровой балки, например, в качестве элемента перекрытий.
Расчет нагрузки на двутавр – основные параметры выбора
Эксплуатационные характеристики двутавра напрямую зависят от его профиля сечения и габаритов. Это во многом связано с особенностями самого металлопроката. Напомним, что двутавровая балка — это вид металлоизделий, состоящая из двух полок, соединенных стенкой. Стенку зачастую называют шейкой. Оттого так важны такие значения как:
- общая высота профиля (включая длину шейки и толщину двух полок),
- высота стенки двутавра,
- общая ширина каждой из полок,
- ширина одной части полки от шейки к краю (свесу),
- общая длина двутавра,
- толщина шейки (стенки),
- толщина полки с гранями, расположенными параллельно,
- средняя толщина проката с уклоном внутренних граней,
- радиус закругления перехода от полки к шейке (радиус сопряжения, внутреннего закругления),
- радиус закругления полки (ее кромки).

Помимо этого, следует учитывать и характеристики самого объекта. Все напрямую зависит от специфики применения двутавра. Но в основном это такой параметр как расчетная нагрузка. В ненагружаемых конструкциях используется двутавровая балка гораздо реже. Нужно еще учитывать шаг. Шаг – определенное расстояние, через него производится монтаж двутавровых балок параллельно друг к другу. И еще большое значение имеет расстояние между точками опоры, на которые укладывается двутавровая балка. Этот параметр называется пролетом.
Регламентированные значения по осям
Все расчеты выполняются на основании справочных значений нескольких важных параметров. Обозначим кратко основные. Начнем с момента инерции. Интересует его значение относительно пары центральных осей. Табличное значение, определяется таблицей сортамента, указанной в ГОСТах. Например, на территории России действует ГОСТ Р 57837-2017 для двутавра с параллельными гранями поломок. В других государствах СНГ есть ГОСТ 8239-89 для проката с уклоном внутренних граней. Существует и ряд других нормативных документов.
Существует и ряд других нормативных документов.
Порой необходимо учитывать и центробежный момент. В таблицах он отсутствует. Оттого что по умолчанию центробежный момент равняется 0 по обеим из осей. Используются параметры, определяющие инерцию, ее:
- радиус относительно одной из центральных осей,
- статический момент полусечения относительно оси,
- осевой момент.
Большое влияние на расчеты имеет такой параметр как расчетное сопротивление, обозначается Ry. Это тоже табличный параметр, он зависит напрямую от марки стали, которая используется при производстве двутавра. Например, углеродистая марка стали С235 имеет расчетное сопротивление 230 МПа. У других марок стали этот параметр будет отличаться.
Следующий важный параметр – модуль упругости. Тут все зависит от характеристик материала, из которого изготовлена двутавровая балка. Забыли отметить, но и расчетное сопротивление тоже зависит от этой характеристики. В классическом понимании – фасонный черный металлопрокат. А это значит, что модуль упругости E берется для стали. Он в таком случае равен 200000 МПа. Но может быть, например, по ГОСТ 13621-90 цветной металлопрокат. Плюс еще различные породы древесины. Там момент инерции будет другой. Такие особенности надо учитывать, когда выполняется расчет нагрузки на двутавровую балку.
А это значит, что модуль упругости E берется для стали. Он в таком случае равен 200000 МПа. Но может быть, например, по ГОСТ 13621-90 цветной металлопрокат. Плюс еще различные породы древесины. Там момент инерции будет другой. Такие особенности надо учитывать, когда выполняется расчет нагрузки на двутавровую балку.
В зависимости от конструкционных особенностей объекта порой возникает необходимость использования и других расчетных параметров. Берутся, как правило, табличные значения.
Расчет нагрузки на двутавр и несущая способность
Разработаны специальные таблицы. В них номер двутавра выбирается исходя из трех основных параметров:
- предполагаемой нагрузки, кг/м.п. (килограмм на метр погонный),
- величины пролета, о нем отмечали выше, м (метров),
- шага, с которым уложен двутавр, м (метров).
Под номером подразумевается высота профиля в сантиметрах (от 10 до 100 по действующей нормативной базе).
Предполагаемая нагрузка рассчитывается исходя из несущей способности изделий. Важно учитывать при этом технологию производства двутавра. Напомним, что он бывает горячекатаным, сварным, клепаным (если используется металл). Горячекатаный получается путем прокатки заготовки, сварной путем приваривания полок к стенке. В клепаной балке для соединения элементов применяются заклепки. Так вот если это сварной двутавр. В таком случае при расчете текущей несущей способности необходимо прибавлять порядка 30% дополнительно на прочность.
Важно учитывать при этом технологию производства двутавра. Напомним, что он бывает горячекатаным, сварным, клепаным (если используется металл). Горячекатаный получается путем прокатки заготовки, сварной путем приваривания полок к стенке. В клепаной балке для соединения элементов применяются заклепки. Так вот если это сварной двутавр. В таком случае при расчете текущей несущей способности необходимо прибавлять порядка 30% дополнительно на прочность.
Саму расчетную нагрузку определяют следующим образом. Высчитывают такой параметр как давление на конструкцию. Учитывается при этом вес конструкции в пересчете на один погонный метр двутавровой балки. Затем полученное значение умножается на коэффициент надежности (напрямую зависит от разновидности двутавра и используемого ГОСТа). После этого на основании полученного значения из таблицы подбирают момент сопротивления. А уже по моменту сопротивления определяется номер профиля исходя из текущего сортамента. Рекомендуем перестраховаться и выбрать на два номера выше.
Важный момент. Несущая способность двутавровой балки устанавливается только и исключительно исходя из расчетной нагрузки. Использовать только одну нормативную нагрузку нельзя. Она выполнена без учета специфики возводимых металлоконструкций, их конструкционных особенностей и эксплуатационных параметров.
И последнее. Несущая способность учитывается при выполнении расчета в двутавре нагрузок на изгиб.
Прочность и прогиб двутавровой балки
Прочность двутавра определяется с учетом нормативных напряжений. В ходе этого выполняется построение так называемых эпюр внутренних усилий, кроме этого напряжений, а еще и перемещений. Они основываются на такие параметры как воздействие сил в продольной и поперечной плоскости, моментов (имеются в виду изгибающие и крутящие).
Как уже отмечали выше, большое значение имеют характеристики материала. Если речь о черном стальном прокате, то основополагающий критерий – марка стали. Если это древесина, то ее порода. Именно характеристики материала учитываются при расчете прочности. Лучше выбирать материалы с повышенной прочностью. Это в полной мере касается и марок стали. Учитывайте, что чем прочнее материал, тем меньше габариты двутавра. Такое положение вещей обозначает что снижается нагрузка на конструкцию в целом. Значение допустимого давления становится меньше. И последнее. Опытный и квалифицированный инженер всегда использует несколько способов определения прочности материала. Ведь надо прилагаемую силу обязательно разложить по осям. После установить максимальные моменты вокруг каждой из осей. На заключительном этапе полученные расчетным путем значения сравниваются.
Лучше выбирать материалы с повышенной прочностью. Это в полной мере касается и марок стали. Учитывайте, что чем прочнее материал, тем меньше габариты двутавра. Такое положение вещей обозначает что снижается нагрузка на конструкцию в целом. Значение допустимого давления становится меньше. И последнее. Опытный и квалифицированный инженер всегда использует несколько способов определения прочности материала. Ведь надо прилагаемую силу обязательно разложить по осям. После установить максимальные моменты вокруг каждой из осей. На заключительном этапе полученные расчетным путем значения сравниваются.
Прогиб двутавра рассчитывается исходя из таких параметров как:
- нагрузка в кг/м (килограммах на метр), берется и расчетная, и нормативная нагрузка,
- пролет (расстояние между опорными точками в м (метрах),
- расчетное сопротивление (измеряется в МПа (мегапаскалях)).
Важный момент. Предельное значение прогиба определяется исходя из конструкционного предназначения двутавровой балки. Так, если двутавр применяется в межэтажных перекрытиях, то прогиб менее 1/250. А если это кровельные конструкции и перемычки, то 1/200. У других конструкционных элементов значения будут соответственно другие. Уменьшить величину прогиба можно только путем изменения исходных параметров. То есть использовать облегченные конструкции и уменьшить нагрузку. Второй вариант – уменьшить расстояние между двумя опорными точками, например, использовав дополнительную (промежуточную).
Так, если двутавр применяется в межэтажных перекрытиях, то прогиб менее 1/250. А если это кровельные конструкции и перемычки, то 1/200. У других конструкционных элементов значения будут соответственно другие. Уменьшить величину прогиба можно только путем изменения исходных параметров. То есть использовать облегченные конструкции и уменьшить нагрузку. Второй вариант – уменьшить расстояние между двумя опорными точками, например, использовав дополнительную (промежуточную).
Можно ли обойтись без расчета прогиба?
Варианты ответа зависят от характеристик объекта и его функционального предназначения. Например, если это небольшая по высоте одноуровневая конструкция, особенно хозяйственного предназначения, то есть варианты. Первый – рассчитывать прогиб двутавра, второй – высчитывать несущую способность возводимых конструкций. Но многое зависит от отделочных материалов, используемых при финишной отделке, и их массы. Поэтому расчет прогиба лучше выполнять даже при индивидуальном строительстве частных домовладений, хозяйственных построек.
Важно понимать факт того что прогиб формируется и в углах поворота. Многое находится в зависимости от конструкции, ее:
- функционального предназначения,
- основных габаритов,
- характеристик используемых материалов, той же марки стали, как частный случай,
- физических параметров.
Формул расчета прогиба множество. На них подробно останавливаться в рамках нашей статьи смысла нет. Лишь отметим что многое зависит от разновидности нагрузки. Речь о направлении ее действия. Все дело в том, что на двутавр могут воздействовать разнонаправленные нагрузки. Как правило, это прогиб, направленный вниз, но бывают и другие. Причем иногда это совокупность разнонаправленных нагрузок. Тогда прогиб определяется по каждой из них отдельно.
Методики расчета прогиба могут быть использованы различные, например, с применением метода начальных параметров.
Расчет нагрузки на двутавр – ключевой параметр выбора этого вида изделий. Любая ошибка в расчетах или их игнорирование может привести к трагическим последствиям. Оттого к вопросу надо подходить ответственно, а выбор делать с запасом. Когда все расчеты будут сделаны и перепроверены – обращайтесь. У нас представлен широкий сортамент двутавровой балки. Поможем подобрать именно тот двутавр что нужен.
Оттого к вопросу надо подходить ответственно, а выбор делать с запасом. Когда все расчеты будут сделаны и перепроверены – обращайтесь. У нас представлен широкий сортамент двутавровой балки. Поможем подобрать именно тот двутавр что нужен.
Таблицы расчета перекрытий
Расчет балок перекрытия
Расчет деревянных балок перекрытия в доме ведется по II предельному состоянию (по прогибам). Относительный прогиб 1/250 (по СНиП “Нагрузки и воздействия”). На практике это говорит о том, что балка перекрытия при нагружении ее равномерно распределенной нагрузкой 400 кг/м2 или 250, 200 кг/м2 в отдельных случаях, прогнется в центре на величину равную L/250, где L – расчетная длина балки (расстояние в свету между опорами).
Например, если расчетная длина балки 6 м (6000 мм), то прогиб в центре при максимальной нагрузке будет 6000/250 = 24 мм. Т.е. в данном примере 24 мм – максимально допустимый прогиб балки, при котором возможна комфортная эксплуатация перекрытия – не будет вибраций, скрипов, ощущения “батута”.
Ниже приведены таблицы соотношения типа двутавровых балок, шага их установки, расчетной нагрузки и максимального пролета, при которых выполняются данные условия.
- Балки серии W изготавливаются длиной 6 метров. Максимальный пролет, который они перекрывают 5,8м (при минимальном опирании 100 мм с двух сторон)
- Балки серии L изготавливаются длиной до 13,5 метров.
- Рекомендуемые шаги – 0,4 и 0,6 м для межэтажных перекрытий, 0,6 и 0,8 для чердачных перекрытий.
- Максимальный пролет – расстояние “в свету” между соседними опорами.
- Шаг балок – межосевое расстояние двух соседних балок.
Таблица расчета балок межэтажного и цокольного перекрытия
Расчет нагрузки 400 кг/м2 для деревянных перекрытий
Теги: #Нагрузка на двутавровую балку таблица
Расчет уголка на прогиб
Главная » Разное » Расчет уголка на прогиб
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 – однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 – консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.

- Тип 3 – однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).
- Тип 4 – однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 – однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
- Тип 6 – консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.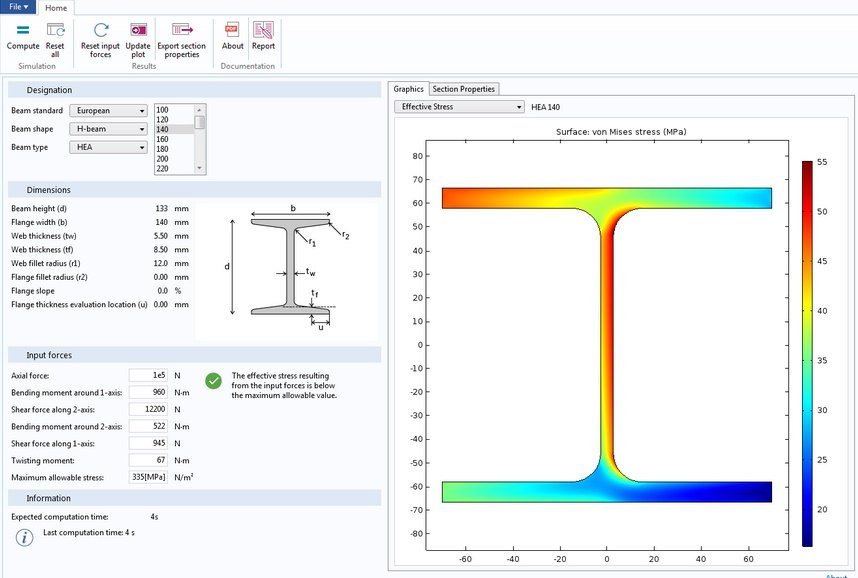
Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
Описание
При выборе схемы с распределенной нагрузкой, приложенная “Нагрузка Q” указывается как относительная “килограмм на метр”. Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора “Расчет прогиба балки онлайн” значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек “звездочка” справа вверху браузера)
Пример расчета уголка, швеллера и двутавра на прогиб и изгиб
На данной странице представлен пример расчета швеллера. Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
В примере будут описаны несколько действий, которые должны выполняться последовательно.
Дано.
Район строительства – Нижний Новгород.
Расчетная схема – Тип 1.
Необходимо подобрать швеллер, который будет воспринимать нагрузку от снега.
Действие 1. Внесение исходных данных.
Расчетная нагрузка = 240 кг/м2 – так как город Н.Новгород находится в IV снеговом районе (в соответствии с табл. 10.1 и картой 1 СП 20.13330.2011 “Нагрузки и воздействия” [1]).
Fmax = 1/200 – так как пролет балки равен 5 м (пункт 2 табл. E1 [1]).
Расположение – по оси Х (швеллер воспринимает нагрузку вертикально).
Расчетное сопротивление Ry=210 МПа – берется как наихудший вариант для стали.
Действие 2. Выбор предполагающих номеров профилей.
Предположим, что мы рассматриваем два вида профилей: с параллельными гранями и с уклоном полок. Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
После произведенного расчета видно, что в графе “Запас” в том и другом случае стоят отрицательные значения. Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Действие 3. Корректирующий расчет.
При увеличении профилей до 10П и 10У ситуация аналогичная. Но после того, как профили были увеличены до 12П и 12У в графах “Запас” появились положительные значения. Следовательно, в качестве балки перекрытия можно принять тот или иной профиль (имеется в виду 12П или 12У).
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. | Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны |
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) |
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров – ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi – коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr – расчётная длина стержня;
- i – радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I – момент инерции сечения,
- Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu = 2;
- “заделка-заделка”-Mu = 0.5;
- “заделка-шарнир” -Mu = 0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра – относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке “РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ”; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Расчёт балки, рамы бесплатно онлайн
Лимит расчётов:
|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и
позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и
осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с
готовым решением. |
|
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
.
% PDF-1.6 % 104 0 объект > endobj xref 104 52 0000000016 00000 н. 0000002216 00000 н. 0000002377 00000 н. 0000002421 00000 н. 0000002547 00000 н. 0000002902 00000 н. 0000003045 00000 н. 0000003182 00000 п. 0000003324 00000 н. 0000003351 00000 п. 0000003418 00000 н. 0000003955 00000 н. 0000004444 00000 н. 0000004471 00000 н. 0000005149 00000 п. 0000005176 00000 п. 0000005771 00000 п. 0000006307 00000 н. 0000006764 00000 н. 0000007200 00000 н. 0000007333 00000 н. 0000007360 00000 п. 0000007733 00000 н. 0000008258 00000 н. 0000008758 00000 н. 0000009241 00000 п. 0000009643 00000 п. 0000009713 00000 н. 0000009908 00000 н. 0000046337 00000 п. 0000046548 00000 п. 0000046941 00000 п. 0000047011 00000 п. 0000047272 00000 п. 0000106092 00000 н. 0000106298 00000 п. 0000106421 00000 н. 0000117145 00000 н. 0000117340 00000 н. 0000117547 00000 н. 0000117617 00000 н. 0000117799 00000 н. 0000156281 00000 н. 0000156483 00000 н. 0000156859 00000 н. 0000156929 00000 н. 0000157517 00000 н. 0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb“`b“ce`c“`f @
0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb“`b“ce`c“`f @
.
Калькулятор для инженеров – момент инерции площади, центр тяжести, модуль упругости углового сечения
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Статически неопределенные структуры
Определение и методы решения
Решенных примеров
Расчет сил стержня фермы
методом соединений и методом секций
Сила сдвига и изгибающий момент
Иллюстрированные решенные примеры для построения диаграмм силы сдвига и изгибающего момента
Наклон и прогиб балки и фермы
Иллюстрированные решенные примеры для определения наклона и прогиба балки и фермы
Решение неопределенных конструкций
Отклонение откоса, распределение момента и т. Д.
Д.
Балка железобетонная
Решенные примеры для определения прочности и других параметров
Другие полезные ссылки
Небоскребы мира
Высокие здания мира
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Международные профессиональные общества инженеров-строителей
Расскажите о нас друзьям
Поищите на нашем сайте больше…
.
Что такое прогиб? | Программное обеспечение SkyCiv Cloud для структурного анализа
перейти к содержанию
Искать:
- Программное обеспечение
- SkyCiv Structural 3D: Программное обеспечение для структурного анализа
- SkyCiv Beam
- SkyCiv Section Builder
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Foundation Design
- SkyCiv8 Модуль нагрузки на ветер SkyCiv8 Интеграции и надстройки
.
Угол возвышения Солнца (на год) Калькулятор
- Цель использования
- различные солнечные приложения, конечно, но в основном просто для того, чтобы быть проинформированным о моем физическом окружении.
- Комментарий / запрос
- Я мог бы быть более поучительным, если бы время наблюдения имело вариант местного кажущегося полудня, когда солнце находится на самом высоком уровне. Поскольку вы запрашиваете долготу наблюдателя, это должно быть просто.
[1] 2020/12/20 04:17 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Расчет максимальной высоты дерева относительно расположения солнечных панелей.
- Комментарий / запрос
- Вычисление корректировки времени от GMT с использованием долготы было бы полезным и простым.
[2] 2020/12/07 03:31 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Размещение солнечных панелей
- Комментарий / запрос
- Arigatou gozaimasu!
[3] 2020/12/07 03:25 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я хочу построить пассивную теплицу на севере ( Северный Квебек), и я хотел знать, под каким углом поставить стену, чтобы максимально эффективно использовать солнце в зимние месяцы
[4] 2020/12/01 22:20 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Определение того, в какое время года, в какое время суток и в каком направлении можно видеть радугу в моем местоположении (солнце должно быть ниже 42 градусов над горизонтом).

- Комментарий / запрос
- Я знаю, как узнать мою широту и долготу, поэтому мог бы использовать этот сайт, но если бы была возможность печатать в ближайшем городе, даже если это было бы менее точно, гораздо больше людей уметь его использовать.
[5] 2020/11/16 15:41 Женщина / 60 лет или старше / Пенсионер / Полезно /
- Цель использования
- Анализ выходной мощности солнечной батареи в зависимости от высоты Солнца
- Комментарий / Запрос
- Отличный калькулятор
[6] 2020/11/05 00:16 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Цель использования
- Проверка тени на крыше для установка PV
- Отчет об ошибке
- По сравнению с диаграммой, углы которой указаны в таблице, азимут и углы возвышения не имеют никакого смысла.Как может полуденное солнце находиться только по азимуту (азимуту) между 39 и 67 градусами? Я мог бы понять эти углы, если бы они были даны от восточной оси.
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
[7] 2020/11/04 20:42 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Я фотограф, выясняю положение солнца в определенные дни в месяц, чтобы я мог делать красивые фотографии в «контролируемой» обстановке.
- Комментарий / запрос
- Спасибо. Продолжайте в том же духе!
[8] 2020/11/04 18:11 Женский / 50-летний уровень / Самозанятые / Полезные /
- Цель использования
- ИСПОЛЬЗОВАНИЕ СОЛНЕЧНОЙ ЭНЕРГИИ
- Комментарий / запрос
- ДУМАЯ О СОЛНЦЕ ПАНЕЛИ
[9] 2020/10/20 04:13 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Самообразование
[10] 2020/10/19 18:32 Мужчина / 60 лет и старше / Пенсионер / Очень /
.
Расчет двутавра на прогиб и изгиб
Калькулятор
| Пример расчета |
Калькуляторы по теме:
- Сбор нагрузок на балки перекрытия онлайн
- Расчет прямоугольной трубы
- Расчет квадратной трубы
- Расчет швеллера
- Расчет уголка
- Расчет деревянной балки
- Расчет двутавра на устойчивость.
Эпюры M и Q. Сопромат. Эпюры изгибающих моментов и поперечных сил, как построить. Изгиб.
Основные вопросы, которые рассмотрены в видео: — правило знаков при изгибе для моментов и поперечных сил. Откуда оно появилось и как его быстрее запомнить — что такое эпюра M и Q, эпюра изгибающего момента и поперечной силы. Как ней пользоваться и зачем нужна — пара простых лайфхаков как быстрее и проще запомнить методику построения эпюр изгибающих моментов и поперечных сил В этом видео уроке доступно и просто объясняется страшная тайна ))) как построить эпюры. После моего объяснения мои студенты обычно спрашивают: «Что так просто?» Да. Действительно построение эпюр при изгибе важная часть сопротивления материалов. И часто при объяснении преподаватели в ВУЗе делают это или не качественно. Это и не удивительно, ведь этот материал они могут излагать уже 3 раз за день. Или студента могло что-то отвлечь и важную деталь он упустил. Как построить Эпюры M и Q. Сопромат. Эпюры изгибающих моментов и поперечных сил, Изгиб. Сопромат, Изгиб. Построение эпюр и определение внутренних усилий поперечная сила Q(x) и момент M(x). Понятие и правило знаков. Пример для консольной балки (консоли). 5:09 пример построения эпюр внутренних усилий при изгибе Q(x) — поперечной силы и M(x) — изгибающего момента Задаеть вопросы: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: [email protected] — комменты к видео Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh. Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
Или студента могло что-то отвлечь и важную деталь он упустил. Как построить Эпюры M и Q. Сопромат. Эпюры изгибающих моментов и поперечных сил, Изгиб. Сопромат, Изгиб. Построение эпюр и определение внутренних усилий поперечная сила Q(x) и момент M(x). Понятие и правило знаков. Пример для консольной балки (консоли). 5:09 пример построения эпюр внутренних усилий при изгибе Q(x) — поперечной силы и M(x) — изгибающего момента Задаеть вопросы: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: [email protected] — комменты к видео Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh. Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-11-19
Вот какие еще уроки по сопротивлению материалов вы найдете на моем сайте:
Load more
Гипотезы и определения при изгибе
Прежде всего начнем с определений:
Что такое балка? Балка — это стержень, длина которого значительно больше чем ширина и высота. При этом он испытывает деформацию изгиба.
При этом он испытывает деформацию изгиба.
балка — длина значительно больше ширины и высоты
Изгиб, что это? Это такой вид деформации, при котором происходит искривление продольной оси балки, но продольные волокна друг на друга не давят, а сечения плоские до изгиба остаются такими и после изгиба.
правило знаков при изгибе
На рисунке выше изображена схема для вывода формулы напряжений и демонстрация напряжений, которые возникают при чистом изгибе. Этот термин придется изложить в другой статье. А пока продолжим.
Эпюра — это график изменения величины, для которой он построен. Так эпюра изгибающего момента — это график изменения внутреннего усилия — изгибающего момента по длине балки. Используя этот график, построенный в масштабе, можно с помощь простых операций определить значение изгибающего момента в любой точке по длине балки. Эпюра поперечной силы — аналогично, график ее изменения внутреннего усилия поперечная сила по длине балки.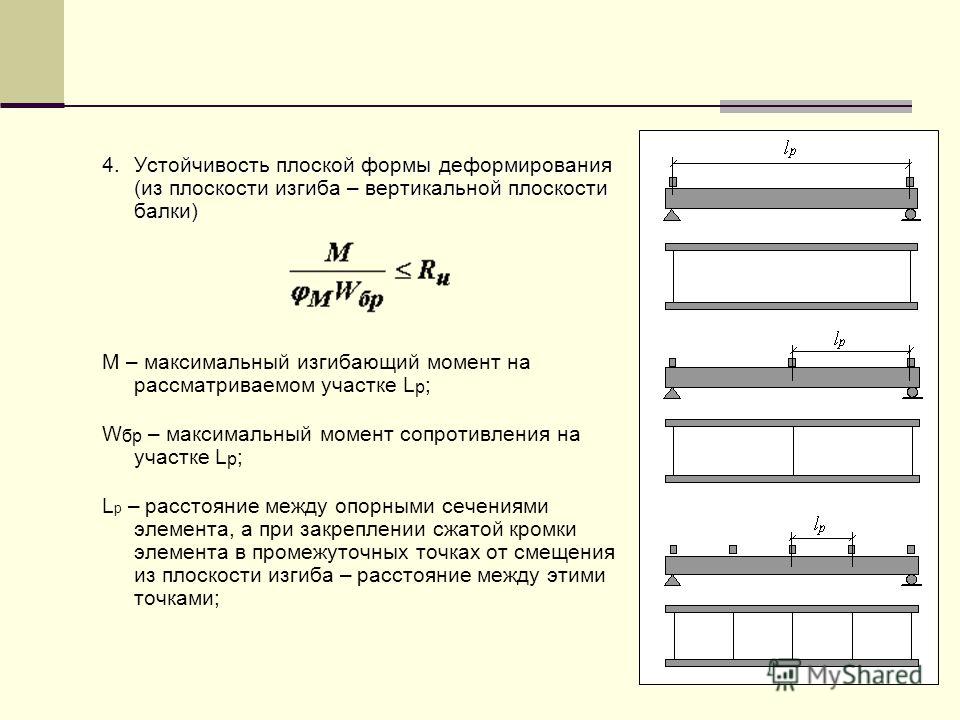
Инструкция к калькулятору
Обращаю ваше внимание, что в нецелых числах необходимо ставить точку, а не запятую, то есть, например, 5.7 м, а не 5,7. Также двутавр необходимо проверять на устойчивость (на заваливание от момента). Это можно сделать с помощью калькулятора, ссылка на который расположена выше (в списке «Калькуляторы по теме»). Если что-то не понятно, задавайте свои вопросы через форму комментариев, расположенную в самом низу.
Исходные данные
Расчетная схема:
Длина пролета (L) — минимальное расстояние между двумя крайними опорами или длина консоли.
Расстояния (A и B) — расстояния от опор до мест приложения нагрузок. Для 3 схемы А равна длине консоли балки, опирающейся на 2 опоры.
Нормативная и расчетная нагрузки — нагрузки, на которые рассчитывается квадратная труба. Рассчитать их можно с помощью следующих материалов:
- калькулятор по сбору нагрузок на балку перекрытия;
- пример сбора нагрузок на балку перекрытия.

Fmax — максимально возможный прогиб согласно таблицы E.1 СНиПа «Нагрузки и воздействия». Некоторые из них выписаны в таблицу 1.
Количество двутавров — этот показатель введен на случай, если балку перекрытия придется усилить еще такой же, положив ее рядом. То есть, если у вас одна балка, то указывается «один», если две рядом, то необходимо выбрать «две».
Расчетное сопротивление Ry— для каждой марки стали он свой. Наиболее распространенные значения приведены в таблице 2.
Размер двутавра — здесь следует выбрать профиль двутавра по тому или иному ГОСТу.
Методика выполнения расчета на прогиб
Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.
Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.
Простейшей аналогией балки может быть деревянная линейка, фото.
В нашем случае балка:
- Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
- Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
- Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.
Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.
Вычисляем моменты инерции и сил
Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е). Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).
Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.
Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).
Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил Mmax = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h3/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.
Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.
Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h4/12, где b и h – размеры сечения балки.
Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.
Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.
Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.
Формулы для практического использования
На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.
Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.
Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.
Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:
- Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
- По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
- По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L2/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.
Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.
Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.
схемы крепления, выбор номера профиля
Двутавр – вид фасонного металлопроката, способный принимать большие нагрузки, по сравнению с уголком и швеллером. В частном строительстве металлопрокат с сечением Н-образного профиля используется только при создании крупногабаритных строений. Для выбора подходящего номера двутавровой балки производят профессиональные расчеты на прочность и прогиб с помощью формул или с использованием онлайн-калькулятора. Исходными данными являются: длина пролета, тип закрепления балки, характер нагрузки, планируемый шаг размещения профильного проката, наличие или отсутствие дополнительных опор, марку стали.
В частном строительстве металлопрокат с сечением Н-образного профиля используется только при создании крупногабаритных строений. Для выбора подходящего номера двутавровой балки производят профессиональные расчеты на прочность и прогиб с помощью формул или с использованием онлайн-калькулятора. Исходными данными являются: длина пролета, тип закрепления балки, характер нагрузки, планируемый шаг размещения профильного проката, наличие или отсутствие дополнительных опор, марку стали.
Выбор типа балки, в зависимости от запланированных нагрузок
Производители предлагают металлические двутавры с несколькими типами поперечного сечения, предназначенные для различных эксплуатационных условий. Такая продукция, в зависимости от типа сечения, может применяться в крупногабаритном жилищном строительстве, при возведении зданий промышленного и гражданского назначения, в мостостроении. Для каждого из них в соответствующем стандарте имеется таблица, в которой указаны размерные параметры, масса 1 м, момент и радиус инерции, момент сопротивления. Эти характеристики используются в расчетах на прогиб и прочность.
Эти характеристики используются в расчетах на прогиб и прочность.
С уклоном внутренних граней полок 6-12 %
Производство этого металлопроката регламентируется ГОСТом 8239-89. Благодаря скруглению внутренних граней около стенки, обладают высокой прочностью и устойчивостью к прилагаемым усилиям.
С параллельными внутренними гранями полок
Эта продукция выпускается в соответствии с ГОСТом 26020-83, выделяют следующие типы:
- Б – нормальный. Применяется для эксплуатации под средними нагрузками.
- Ш – широкополочный. Может использоваться для разрезки по продольной оси для получения таврового профиля. Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей.
- К – колонный. Это наиболее массивные профили.
 Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций.
Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций.
Швеллер и двутавр: отличия
Достаточно взглянуть на две эти разновидности металлоконструкций: при визуальном сходстве они имеют значительные технические отличия.
Двутавровая балка представляет собой стенку с перпендикулярными полками одинаковой ширины, чаще всего равноудаленными от центра полки.
Швеллер – это профиль, имеющий вид стенки с прикрепленными к ней одной стороной полками. В разрезе он напоминает букву «П».
Эти отличия имеют не только внешнее значение, они также влияют на технические характеристики изделий. Иногда полки швеллера могут быть немного завалены внутрь – такой профиль способен выдержать повышенную нагрузку и обладает большей надежностью, чем стандартный П-образный.
Чем отличается швеллер от двутавра?
- Прочностью. Степенью выносливости двутавровые балки значительно опережают швеллера.
 Это обусловлено наличием двух полок с обеих сторон, благодаря которому изделие обладает большей жесткостью. По прочности один двутавр способен заменить два швеллера. На надежность сооружения также оказывает влияние узел крепления двутавра и швеллера. Это крепление, с помощью которого профиля соединяются между собой, а также крепятся к опорным конструкциям или трубам.
Это обусловлено наличием двух полок с обеих сторон, благодаря которому изделие обладает большей жесткостью. По прочности один двутавр способен заменить два швеллера. На надежность сооружения также оказывает влияние узел крепления двутавра и швеллера. Это крепление, с помощью которого профиля соединяются между собой, а также крепятся к опорным конструкциям или трубам. - Материалом. Балки с двутавровым сечением изготавливается исключительно из металлов и сплавов с повышенным индексом прочности, в то время как швеллера могут быть в том числе деревянными и алюминиевыми.
- Весом. Сравнивая вес швеллеров и двутавров, целесообразно брать за основу изделия с одинаковыми номерами, изготовленные из одного и того же металла. Так, вес стального двутавра среднего размера (№14) – 16,9 кг/пог. м, такого же размера стального швеллера – 12,3 кг/пог. м.
- Способом изготовления. Двутавровые балки – сварочные изделия. Их производство занимает несколько этапов – от изготовления заготовок до их сборки и последующей сварки.
 Реже используется горячекатаные двутавры. Что касается швеллеров, то они могут изготавливаться двумя способами: горячекатаным и гнутым. В первом случае металлическая заготовка нагревается до высокой температуры и при помощи специального станка ей придается требуемая форма. Гнутые швеллера производятся холодным способом – края заготовок в этом случае просто загибаются под нужным углом. Швеллера, угол полок которых < 90°, обладают более высокой прочностью, чем стандартные, но все-таки не дотягивают по надежности до двутавровых профилей.
Реже используется горячекатаные двутавры. Что касается швеллеров, то они могут изготавливаться двумя способами: горячекатаным и гнутым. В первом случае металлическая заготовка нагревается до высокой температуры и при помощи специального станка ей придается требуемая форма. Гнутые швеллера производятся холодным способом – края заготовок в этом случае просто загибаются под нужным углом. Швеллера, угол полок которых < 90°, обладают более высокой прочностью, чем стандартные, но все-таки не дотягивают по надежности до двутавровых профилей.
Двутавры также отличаются между собой гранями полок. Как и швеллера, они могут быть параллельными либо с определенным углом наклона.
Типовые схемы расположения двутавра
Один из исходных параметров, учитываемых в расчетах, – схема закрепления балки и вид прилагаемой нагрузки. Большинство вариантов сводится к основным схемам:
- шарнирно-опертая балка с равномерно приложенной нагрузкой;
- с жесткой заделкой одного конца, сила распределена равномерно;
- однопролетная с консолью с одной стороны, с дополнительной опорой, нагрузка равномерно распределена;
- шарнирно-опертая, сила сосредоточенная;
- шарнирно-опертая, с двумя приложенными силами;
- консоль с жесткой заделкой, приложена сосредоточенная сила.

Сбор нагрузок
Перед началом расчета производят сбор сил, действующих на двутавровую балку. В зависимости от продолжительности воздействия,их разделяют на временные и постоянные.
Таблица нагрузок на двутавровые балки
| Постоянные | Собственная масса балки и перекрытия. В упрощенном варианте вес межэтажного перекрытия без цементной стяжки с учетом массы балки принимают равным 350 кг/м2, с цементной стяжкой – 500 кг/м2 | |
| Длительные | Полезные | Зависят от назначения здания |
| Кратковременные | Снеговые, зависят от климатических условий региона | |
| Особые | Взрывные, сейсмические. Для балок, работающих в стандартных эксплуатационных условиях, не учитываются. В онлайн-калькуляторах обычно не учитываются | |
Нагрузки разделяют на нормативные и расчетные. Нормативные устанавливаются строительными нормами и правилами. Расчетные равны нормативной величине, умноженной на коэффициент надежности. При усилии менее 200 кг/м2 коэффициент обычно принимают равным 1,3, при более 200 кг/м2 – 1,2. Шаг между балками принимают равным 1 м. В некоторых случаях, если это допустимо в конкретных эксплуатационных условиях, в целях экономии материалов его принимают равным 1,1 или 1,2 м.
При усилии менее 200 кг/м2 коэффициент обычно принимают равным 1,3, при более 200 кг/м2 – 1,2. Шаг между балками принимают равным 1 м. В некоторых случаях, если это допустимо в конкретных эксплуатационных условиях, в целях экономии материалов его принимают равным 1,1 или 1,2 м.
При расчетах принимают во внимание марку стали. Для использования в условиях высоких нагрузок и при минусовых температурах востребованы двутавровые балки, изготовленные из низколегированных сталей.
Преимущества и недостатки
В данном случае достоинства данного вида металлопроката намного перевешивают его недостатки. Исключительная прочность конструкции позволяет делать перекрытия большой длины. При этом она не подвержена деформации.
Помимо этого, двутавровые балки обладают следующими достоинствами:
- Низкая себестоимость материала и сравнительно дешевое производство, вследствие чего невысокая конечная цена.
- Монолитные горячекатанные двутавровые балки не требуют применения дополнительных армирующих элементов, даже при больших механических нагрузках.

- Наличие у сварного профиля вспомогательных ребер жесткости, что позволяет сэкономить на материале.
- Возможность по желанию заказчика изготовить балку с одинаковыми или разными полками, с перфорацией, усеченную, а также любой указанной длины.
Недостатки, хотя их и не очень много, также имеются. В частности, можно перечислить следующие минусы:
Большая масса изделия ввиду конструктивных особенностей, а именно толстых стенок.
В случае приобретения изготовленных согласно ГОСТ изделий, а таких большинство, при необходимости укоротить балку ее приходится резать, что, во-первых, трудоемко, а во-вторых, ведет к отправке большого количества металла в утиль.
Для производства двутавровых балок требуются большие производственные мощности, поэтому в кустарных условиях, в гаражах и на малых предприятиях их не производят.
При использовании сварных двутавровых балок, необходимо применять дополнительное армирование, что затратно и по времени, и по деньгам.
Сварка металлических конструкцийОсобенности холоднокатаного листа — технология производства, особенности, размеры, свойства и маркировка
Технические особенности горячекатаного листа — классификация, способ изготовления, варианты применения и особенности обработки
При всех имеющихся недостатках, по прочности и жесткости с данным видом металлопроката, при прочих равных условиях, не может тягаться никакой другой вид.
Способы выбора оптимального размера сечения профиля
Наиболее точным вариантом подбора номера и типа двутаврового профиля является проведение профессиональных расчетов. Именно этот способ применяется при проектировании ответственных крупногабаритных объектов. При строительстве небольших зданий можно воспользоваться онлайн-калькулятором.
Совет! По результатам расчетов онлайн-калькуляторы обычно предлагают два или более вариантов профиля. Для обеспечения надежности строения рекомендуется отдавать предпочтение профилю с большим номером.
Для обеспечения надежности строения рекомендуется отдавать предпочтение профилю с большим номером.
Для примерного определения размера профиля можно воспользоваться таблицей соответствия номера двутавровой балки максимально допустимой нагрузке:
| Общая нагрузка, кг/м2 | Длина пролета | ||||||||
| 3 м при шаге, м | 4 м при шаге, м | 6 м при шаге, м | |||||||
| 1,0 | 1,1 | 1,2 | 1,0 | 1,1 | 1,2 | 1,0 | 1,1 | 1,2 | |
| 300 | 10 | 10 | 10 | 10 | 12 | 12 | 16 | 16 | 16 |
| 400 | 10 | 10 | 10 | 12 | 12 | 12 | 20 | 20 | 20 |
| 500 | 10 | 12 | 12 | 12 | 12 | 12 | 20 | 20 | 20 |
Из этой таблицы видно, что для двутавровой балки номер 10 максимальная длина пролета составляет 4 м при шаге 1,2 м, нагрузка – 400 кг/м2, для номера 16 длина пролета может достигать 6 м, нагрузка, которую он может выдержать, – 300 кг/м2, для профиля 20 – 6 м и нагрузка 400 кг/м2.
Что представляет собой двутавровая балка
Н-образная форма профиля двутавровой балки возникла не на пустом месте. Такая форма позволяет получить громадный выигрыш по сравнению с прямоугольником при всех прочих параметрах – если верить исследователям, то тридцатикратный выигрыш по жесткости и семикратный по прочности.
Вероятно, цифры несколько приукрашены, но такая конструкция однозначно прочнее прямоугольника. Помимо металлических, выпускают также деревянные изделия.
Расчёт балок на прочность при изгибе
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН. О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
где
Тогда
где:
Тогда
Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = –F·z1= — 30 ·z1 —
– уравнение прямой.
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим :
И тогда
Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
откуда: :
а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:
тогда
Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами. Тогда
Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) – М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.
III участок
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
– парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.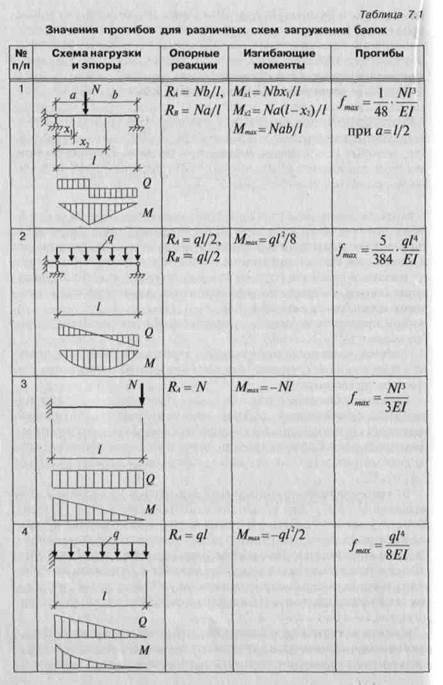
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
что меньше [σ]=160МПа на
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 – М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = – F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= – F— Q(z1) = 0,
Q(z1) = — 20кН.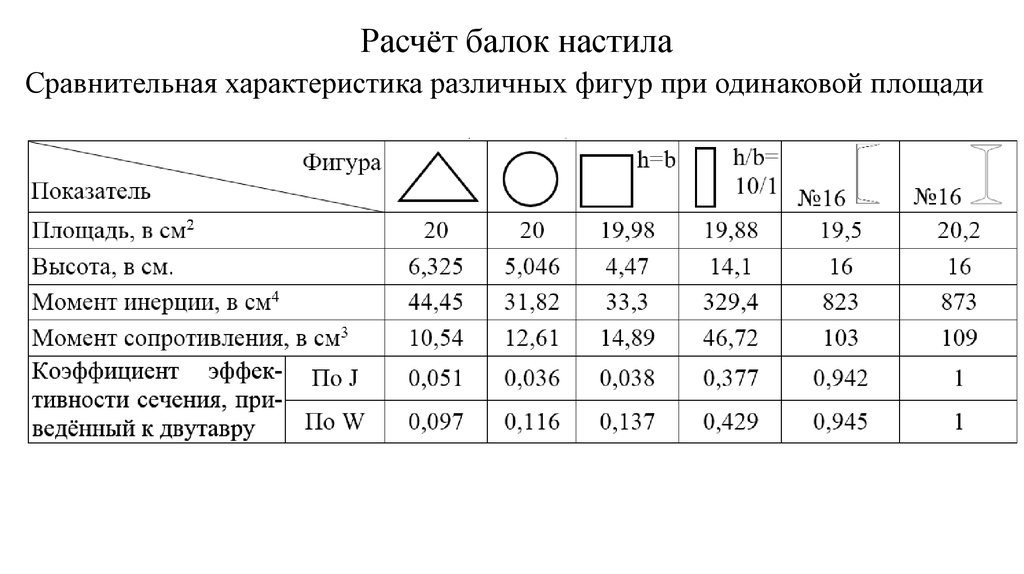
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
– парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).
по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба –
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
Калькулятор прогиба балки
Создано Николасом Свонсоном и Кеннетом Аламбра
Отзыв от Bogna Szyk
Последнее обновление: 17 июня 2022 г.
- Что такое прогиб и изгиб балки Как рассчитать максимальное прогиба
- Метод наложения
- Жесткость балки
- Понимание формул прогиба балки
- Пример расчета прогиба балки
Этот калькулятор прогиба балки поможет вам определить максимальный прогиб балки на просто опертых и консольных несущих балках простые конфигурации загрузки . Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины. Величина и расположение этих нагрузок влияют на то, насколько сильно изгибается балка. В этом калькуляторе прогиба балки вы узнаете о различных формулах прогиба балки , используемых для расчета прогибов свободно опертой балки и прогибов консольной балки. Вы также узнаете, как модуль упругости балки и ее момент инерции поперечного сечения влияют на рассчитанный максимальный прогиб балки.
Прогиб балки является важной частью анализа балки, но другой важной частью является анализ напряжения. Мощным инструментом для изучения напряжений изгиба балки является модуль сопротивления, который можно рассчитать с помощью нашего калькулятора модуля сечения.
Мощным инструментом для изучения напряжений изгиба балки является модуль сопротивления, который можно рассчитать с помощью нашего калькулятора модуля сечения.
Что такое прогиб и изгиб балки
В строительстве мы обычно используем каркасные конструкции , которые удерживаются на месте фундаментом в земле. Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В кадре мы называем вертикальное кадрирование колонны , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, такими как сплошные бетонные полы, деревянные балочные системы полов и крыши.
Когда балки несут слишком тяжелые для них нагрузки, они начинают прогибаться. Мы называем величину изгиба балки прогибом балки . Прогиб балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки в качестве нашей точки отсчета, если во время изгиба нет изменений высоты или глубины балки.
Как рассчитать максимальный прогиб балки
Мы оснастили наш калькулятор прогиба балки формулами, которые инженеры и студенты инженерных специальностей используют для быстрого определения максимального прогиба конкретной балки из-за нагрузки, которую она несет. Однако эти формулы могут решать только простые нагрузки и их комбинации. Мы свели для вас эти формулы в таблицу, как показано ниже:
Формулы прогиба свободно опертой балки
Формулы прогиба консольной балки
Метод суперпозиции
Для расчета максимального прогиба балки при сочетании нагрузок можно использовать метод суперпозиции . Метод суперпозиции утверждает, что мы можем аппроксимировать полное отклонение балки, суммируя все отклонения, вызванные каждой конфигурацией нагрузки. Однако этот метод дает нам только приблизительное значение фактического максимального отклонения. Расчет сложных нагрузок потребовал бы от нас использования так называемого метод двойного интегрирования .
Жесткость балки
Расчет прогиба балки требует знания жесткости балки и величины силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки, E , на ее момент инерции, I . Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем он достигнет предела прочности. Модуль упругости бетона составляет от 15 до 50 ГПа (гигапаскалей), в то время как у стали около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать только небольшое отклонение и растрескивается раньше, чем сталь.
Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений. С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете посетить наш калькулятор момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.
Момент инерции зависит от размеров поперечного сечения материала.
Момент инерции также меняется в зависимости от того, вдоль какой оси вращается материал. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольного бруса шириной 20 см и высотой 30 см. Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем рассчитать значения момента инерции поперечного сечения этой балки следующим образом:
Iₓ = ширина × высота Quest³ / 12
= 20 × (30³) / 12
= 45 000 см
Iᵧ = Высота × Ширина / 12
= 30 × (20 минут (20 минут (20 минут (20 минут (20 минут) / 12
= 30 81 (20 минут) / 12
= 30 81 (20 минут) / 12
= 30 81 (20 минут) /
= 20 000 см⁴
Обратите внимание на два значения момента инерции. Это потому, что мы можем считать, что балка изгибается вертикально вдоль пролета балки (или испытывает изгибающий момент вокруг оси x) и в поперечном направлении вдоль пролета балки (или согнуть вокруг оси Y). Поскольку мы рассматриваем отклонение луча, когда он изгибает по вертикали или вокруг оси x, мы должны использовать Iₓ для наших вычислений. Полученные нами значения момента инерции говорят нам о том, что балка труднее изгибается при вертикальной нагрузке и легче изгибается при горизонтальной поперечной нагрузке. Эта разница в значениях моментов инерции является причиной того, что мы видим балки в такой конфигурации, где их высота больше, чем их ширина.
Поскольку мы рассматриваем отклонение луча, когда он изгибает по вертикали или вокруг оси x, мы должны использовать Iₓ для наших вычислений. Полученные нами значения момента инерции говорят нам о том, что балка труднее изгибается при вертикальной нагрузке и легче изгибается при горизонтальной поперечной нагрузке. Эта разница в значениях моментов инерции является причиной того, что мы видим балки в такой конфигурации, где их высота больше, чем их ширина.
Понимание формул прогиба балки
Теперь, когда мы знаем понятия модуля упругости и момента инерции, мы теперь можем понять, почему эти переменные являются знаменателями в наших формулах прогиба балки. Из формул видно, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на отклонение балки. Чем длиннее становится балка, тем больше она может изгибаться и тем больше может быть отклонение.
Нагрузки, с другой стороны, влияют на прогиб балки двумя способами: направление прогиба и величина прогиба. Нагрузки, направленные вниз, имеют тенденцию отклонять балку вниз. Нагрузки могут быть в виде одноточечной нагрузки, линейного давления или мгновенной нагрузки. Формулы в этом калькуляторе ориентированы только на направление вниз или вверх для точечной нагрузки и распределенной нагрузки. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки по часовой стрелке или против часовой стрелки. Просто сверьтесь с направлениями стрелок на соответствующем изображении формулы, чтобы выяснить, какие направления имеют положительное значение нагрузки.
Нагрузки, направленные вниз, имеют тенденцию отклонять балку вниз. Нагрузки могут быть в виде одноточечной нагрузки, линейного давления или мгновенной нагрузки. Формулы в этом калькуляторе ориентированы только на направление вниз или вверх для точечной нагрузки и распределенной нагрузки. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки по часовой стрелке или против часовой стрелки. Просто сверьтесь с направлениями стрелок на соответствующем изображении формулы, чтобы выяснить, какие направления имеют положительное значение нагрузки.
Пример расчета прогиба балки
Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками, расположенными на расстоянии 1,5 м друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамьи. Мы можем рассматривать это сиденье как балку, которая будет отклоняться всякий раз, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем рассчитать его момент инерции, как в нашем примере выше. Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:
Зная размеры этого сиденья, мы можем рассчитать его момент инерции, как в нашем примере выше. Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:
Iₓ = ширина * высота QUERS / 12
= 30 * (4³) / 12
= 160,0 см или 1,6x10⁻⁶ M⁴
Восточная белая созна x10⁹ Па) , что является значением, полученным из Справочника по дереву. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке. Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести эта скамья. Предположим, что 400 N ребенок сидит посередине скамьи. Теперь мы можем рассчитать прогиб сиденья скамьи из-за точечной нагрузки в его центре: )³ / (48 * 6,8×10⁹ Па * 1,6×10⁻⁶ м⁴)
δₘₐₓ = 0,002585 м = 2,5850 мм
посреди скамейки.
Если эта тема показалась вам интересной и вы хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы, используемые в точечных нагрузках и при расчете сил.
Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы, используемые в точечных нагрузках и при расчете сил.
Николас Свонсон и Кеннет Аламбра
Тип балки
Тип нагрузки
Входные значения
Длина пролета, L
Точечная нагрузка, P
Модуль упругости0003
Момент инерции, Ix
Жесткость балки, Eix
Выходное значение
Максимальный прогиб, δmax
Проверить 111 подобных строительных калькуляторов MechaniCalc
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Для получения информации об отклонении балки см. наш справочник по напряжениям и отклонениям в балках.
Консольные балки
| Консольные, торцевая нагрузка |
| |||||||||||||||||||
| Консоль, промежуточная нагрузка |
| |||||||||||||||||||
| Консоль, равномерно распределенная нагрузка |
| |||||||||||||||||||
| Консоль, треугольная распределенная нагрузка |
| |||||||||||||||||||
| Консоль, Конечный момент |
|
Просто поддерживаемые балки
| Просто поддерживаемые, промежуточная нагрузка |
Для a ≥ b:
| |||||||||||||||||||||
| Простая опора, центральная нагрузка |
| |||||||||||||||||||||
| Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор |
| |||||||||||||||||||||
| Простая опора, равномерная распределенная нагрузка |
| |||||||||||||||||||||
| Простая опора, момент на каждой опоре |
| |||||||||||||||||||||
| Простая опора, момент в одну опору |
| |||||||||||||||||||||
| Простая опора, центральный момент |
|
Фиксированные-Фиксированные балки
| Фиксированные-Фиксированные, центральная нагрузка |
| |||||||||||||||
| Фиксированная-фиксированная, равномерная распределенная нагрузка |
|
Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
Напряжение и прогиб балки | MechaniCalc
Калькулятор
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Многие конструкции можно аппроксимировать прямой балкой или набором прямых балок. По этой причине анализ напряжений и прогибов в балке является важной и полезной темой.
В этом разделе рассматриваются поперечная сила и изгибающий момент в балках, диаграммы сдвига и момента, напряжения в балках, а также таблица общих формул прогиба балки.
Содержимое
Ограничения и граничные условия
Чтобы балка оставалась в статическом равновесии, когда к ней приложены внешние нагрузки, балка должна быть закреплена. Ограничения определяются в отдельных точках вдоль балки, и граничное условие в этой точке определяет характер ограничения. Граничное условие указывает, является ли луч фиксированным (ограниченным от движения) или свободным для перемещения в каждом направлении. Для двумерного луча интересующими направлениями являются направление x (осевое направление), направление y (поперечное направление) и вращение. Чтобы ограничение существовало в точке, граничное условие должно указывать, что хотя бы одно направление зафиксировано в этой точке.
Общие граничные условия показаны в таблице ниже. Для каждого граничного условия в таблице указано, является ли луч фиксированным или свободным в каждом направлении в точке, где определено граничное условие.
| Граничное условие | Направление | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Осевое (X) | Поперечное (Y) | Вращение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Свободно | Свободно | Свободно | Свободно
Если граничное условие указывает, что луч зафиксирован в определенном направлении, то в месте расположения граничного условия может существовать внешняя реакция в этом направлении. Основываясь на приведенном выше обсуждении, мы можем видеть, что фиксированное граничное условие может развивать осевые и поперечные силы реакции, а также момент. Точно так же мы видим, что закрепленное граничное условие может развивать осевые и поперечные силы реакции, но не может создавать реактивный момент. Обратите внимание на условие свободной границы в таблице выше. Это граничное условие указывает, что луч может свободно двигаться в любом направлении в этой точке (т. е. он не зафиксирован и не ограничен ни в каком направлении). Следовательно, на данный момент ограничения не существует. Это подчеркивает тонкую разницу между ограничением и граничным условием. Граничное условие указывает фиксированное/свободное условие в каждом направлении в определенной точке, а ограничение — это граничное условие, в котором зафиксировано хотя бы одно направление. Сила сдвига и изгибающий моментЧтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при каждом ограничении. Например, консольная балка ниже имеет приложенную силу, показанную красной стрелкой, а реакции показаны синими стрелками при фиксированном граничном условии. Внешние реакции должны уравновешивать приложенные нагрузки таким образом, чтобы балка находилась в статическом равновесии. После того, как внешние реакции определены, сделайте разрезы по длине балки и определите внутренние реакции в каждом разрезе сечения. (Силы реакции и моменты в разрезах сечения называются внутренними реакциями, поскольку они являются внутренними по отношению к балке.) Пример сечения показан на рисунке ниже: Когда балка разрезается в сечении, при расчете внутренних реакций можно учитывать любую сторону балки. Выбранная сторона не влияет на результаты, поэтому выбирайте ту сторону, которая проще всего. На рисунке выше выбрана сторона балки справа от разреза сечения. Соглашение о знакахВажны знаки сдвига и момента. Знак определяется после разреза сечения и решения реакций для части балки по одну сторону от разреза. Перерезывающая сила в срезе сечения считается положительной, если она вызывает вращение выбранного сечения балки по часовой стрелке, и считается отрицательной, если вызывает вращение против часовой стрелки. Изгибающий момент в разрезе сечения считается положительным, если он сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т. е. заставляет балку «улыбаться»). На основании этого соглашения о знаках поперечная сила в разрезе сечения консольной балки в качестве примера на рисунке выше положительна, поскольку она вызывает вращение выбранного сечения по часовой стрелке. На рисунке ниже показаны стандартные знаки для поперечной силы и изгибающего момента. Силы и моменты слева положительны, а справа отрицательны. Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
Диаграммы сдвига и момента Перерезывающая сила и изгибающий момент в балке обычно изображаются на диаграммах. Диаграмма сдвига показывает поперечную силу по длине балки, а диаграмма моментов показывает изгибающий момент по длине балки. Эти диаграммы обычно располагаются друг над другом, и комбинация этих двух диаграмм представляет собой диаграмму момента сдвига. Диаграммы поперечного момента для некоторых распространенных конечных условий и конфигураций нагрузки показаны в таблицах прогиба балки в конце этой страницы. Общие правила построения диаграмм поперечных моментов приведены в таблице ниже. Все правила этой таблицы показаны на рисунке выше.
Изгибающие напряжения в балкахИзгибающий момент М по длине балки можно определить по диаграмме моментов. Затем изгибающий момент в любом месте балки можно использовать для расчета изгибающего напряжения в поперечном сечении балки в этом месте. Изгибающий момент изменяется по высоте поперечного сечения в соответствии с изгиб формулы ниже: где M — изгибающий момент в интересующем месте по длине балки, I c — центральный момент инерции поперечного сечения балки, а y — расстояние от нейтральной оси балки до интересующей точки по высоте. сечения. Отрицательный знак указывает на то, что положительный момент приведет к сжимающему напряжению над нейтральной осью. Напряжение изгиба равно нулю на нейтральной оси балки, которая совпадает с центром тяжести поперечного сечения балки. Максимальное изгибающее напряжение возникает на крайних волокнах балки и рассчитывается как: где c — центроидальное расстояние поперечного сечения (расстояние от центроида до крайнего волокна). Если балка асимметрична относительно нейтральной оси, так что расстояния от нейтральной оси до верха и до низа балки не равны, максимальное напряжение возникнет в самом удаленном месте от нейтральной оси. На рисунке ниже растягивающее напряжение в верхней части балки больше, чем сжимающее напряжение в нижней части. Модуль поперечного сечения объединяет центральный момент инерции I c и центральное расстояние с: Преимущество модуля сечения заключается в том, что он характеризует сопротивление поперечного сечения изгибу в одном выражении. Модуль сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении: Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
Касательные напряжения в балкахСила сдвига V по длине балки может быть определена по диаграмме сдвига. Сила сдвига в любом месте балки затем может быть использована для расчета напряжения сдвига по поперечному сечению балки в этом месте. Среднее касательное напряжение по поперечному сечению определяется выражением: Напряжение сдвига изменяется по высоте поперечного сечения, как показано на рисунке ниже: Напряжение сдвига равно нулю на свободных поверхностях (вверху и внизу балки) и максимально в центре тяжести. Уравнение для напряжения сдвига в любой точке, расположенной на расстоянии y 1 от центра тяжести поперечного сечения, имеет вид: где V — поперечная сила, действующая в месте поперечного сечения, I c — центральный момент инерции поперечного сечения, а b — ширина поперечного сечения. Напряжения сдвига для нескольких распространенных поперечных сечений обсуждаются в разделах ниже. Касательные напряжения в прямоугольных сеченияхРаспределение касательного напряжения по высоте прямоугольного сечения показано на рисунке ниже: Первый момент площади в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле: Максимальное значение Q приходится на нейтральную ось пучка (где y 1 = 0): Напряжение сдвига в любой заданной точке y 1 по высоте поперечного сечения рассчитывается по формуле: где I c = b·h 3 /12 – центральный момент инерции поперечного сечения. Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле: где A = b·h – площадь поперечного сечения. Из предыдущего уравнения видно, что максимальное касательное напряжение в поперечном сечении на 50% выше, чем среднее напряжение V/A. Касательные напряжения в круглых сеченияхКруглое сечение показано на рисунке ниже: Уравнения для касательного напряжения в балке были выведены с использованием предположения, что касательное напряжение по ширине балки постоянно. Это предположение справедливо в центре тяжести круглого поперечного сечения, хотя нигде больше оно недействительно. Следовательно, хотя распределение напряжения сдвига по высоте поперечного сечения не может быть легко определено, максимальное напряжение сдвига в сечении (возникающее в центре тяжести) все же можно рассчитать. Максимальное значение первого момента Q, возникающее в центре тяжести, определяется выражением: Затем максимальное напряжение сдвига рассчитывается по формуле: где b = 2r — диаметр (ширина) поперечного сечения, I c = πr 4 /4 — центроидальный момент инерции, A = πr 2 — площадь поперечного сечения. Напряжения сдвига в сечениях круглых трубПоперечное сечение круглой трубы показано на рисунке ниже: Максимальное значение первого момента Q, возникающее в центре тяжести, определяется выражением: Затем максимальное напряжение сдвига рассчитывается по формуле: где b = 2 (r o − r i ) – эффективная ширина поперечного сечения, центроидальный момент инерции, а A = π (r o 2 – r i 2 ) площадь поперечного сечения. Касательные напряжения в двутавровых балкахРаспределение напряжения сдвига вдоль стенки двутавровой балки показано на рисунке ниже: Уравнения для касательного напряжения в балке были выведены с использованием предположения, что касательное напряжение по ширине балки постоянно. Это предположение справедливо для стенки двутавровой балки, но неверно для полки (особенно там, где стенка пересекает полки). Тем не менее, стенка двутавровой балки принимает на себя подавляющую часть силы сдвига (примерно 90–98%, по Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига. Первый момент площади стенки двутавровой балки определяется по формуле: Напряжение сдвига вдоль стенки двутавровой балки определяется по формуле: где t w — толщина стенки, а I c — центральный момент инерции двутавровой балки: Максимальное значение напряжения сдвига возникает на нейтральной оси ( y 1 = 0 ), а минимальное значение напряжения сдвига в стенке возникает на внешних волокнах стенки, где она пересекает полки y 1 = ±h w /2 ): PDH Classroom предлагает курс повышения квалификации на основе этой справочной страницы по анализу луча. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE. Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание! Просмотреть курс сейчас: Просмотреть курс Таблицы отклонения балки В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Консольные балки
Просто поддерживаемые балки
Фиксированные-фиксированные балки
Подпишитесь, чтобы получать периодические обновления о последних улучшениях: Ссылки
Лучшее руководство по определению прогиба в балках переменного сечения — инженер-наставникТаблицы балок дают информацию и предполагают, что прогиб Расчет основан на постоянном поперечном сечении. Итак, что мы делаем, если наш луч имеет крест сечение, изменяющееся по длине балки? Для определения величины отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применять граничные условия. Луч формула отклонения: v’’ = M(x)/[E*I(x)]. Непрерывная или дискретная – Существует два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывных балок и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Дискретные лучи являются лучами которые имеют внезапные разрывы в разрезе. Хотите верьте, хотите нет, иногда это проще для расчета, потому что дискретные сечения обычно постоянны, что приводит к более легкий расчет. Формула отклонения луча является универсальной формула, которая позволяет настраивать несколько нагрузок и балок разделы. Я предупрежу вас, что чем больше точным должен быть ваш расчет, тем сложнее будет сделать математику. Упрощение здесь сэкономит много времени и усилие. Как упоминалось перед формула: v’’ = M(x)/[E*I(x)] ускорение отклонения), M — момент, который обычно является функцией
положение по длине балки, х.
E — модуль упругости, I — момент инерции площади.
луч. Все табличные лучи будут
считать это константой, и поэтому ни одна из формул отклонения
может быть использован. Теперь, когда мы проинтегрируем приведенное выше уравнение, мы получим выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный случае у нас будет два или более уравнений. Граничные условия требования, которым должна соответствовать формула отклонения луча, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения констант образован неопределенным интегралом. Общий случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или наклон консольной балки должен быть 0 радиан. В этой статье мы рассмотрим три примера обычных балок переменного сечения.
https://mentoredengineer.com/the-best-guide-to-solving-statically-indeterminate-beams/ Пример 1: Двухсекционная консольная балка с точечной нагрузкой на конце. 94.Теперь определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я выбрал, чтобы моя система координат (переменная x) начиналась с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 взаимно компенсируются из-за граничных условий 1 и 2. Через секунду вы увидите. Мне нужно только сделать интеграцию для одного из разделов, а затем изменить I 1 по I 2 в уравнениях. Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные. Теперь, когда проблема определена, давайте настроим граничные условия. Найдем граничные условия 1 и 2 Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, если я решу, чтобы система координат начиналась с база. Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее. Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы чтобы мы могли убедиться, что v 1 = v 2 и s 1 = s 2 на 50 дюймов. Это подтверждает что положение и наклон будут непрерывными в этой точке. Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки. Как вы можете видеть, отклонение быстро увеличивается после 50 дюймов от основания. Это ясно видно на обоих графиках. 94. Теперь определим момент и проинтегрируем уравнение отклонения луча дважды каждый раз добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Они связаны: г = L-x Я выбрал эту систему координат так, что C 2 и C 4 сокращаются, когда мы находим граничные условия 1 и 2. Это также упрощает математику. чрезвычайно. Вы увидите через секунду. Мне нужно только выполнить интегрирование для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «у» на «х». Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы концы балки имели отклонение 0 дюймов (BC 1 и 2). Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом месте должны быть одинаковыми в месте соединения сегментов. Найдем граничные условия 1 и 2 Как упоминалось выше, я предвидел, что переменные C 2 и C 4 будет равно 0, когда я выберу координату запуск системы на базе. Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее. Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы
чтобы мы могли убедиться, что v 1 = v 2 и s 1 =
с 2 на 200 дюймов. Это подтверждает
что положение и наклон будут непрерывными в этой точке. Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. О-о, что случилось!? Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов отклонение, но они не касаются в месте пересечения. Я не только иллюстрирую силу построение графика решения для точности, а также демонстрация того, что использование двух различные системы координат представляли собой проблему. Согласно уравнениям, склоны приближаются к месту узел на нисходящем склоне равный по величине. Однако сделать эту работу одним из склонов на самом деле должен подойти. Мы можем устраните эту проблему, внеся одно небольшое изменение. с 1 = -s 2 Давайте внесем это изменение и приступим к решению. Да, намного лучше! Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки. Как и ожидалось, более длинная жесткая секция меньше прогибается. Как рассчитать данные балки, если вашего случая нет в таблице Пример 3. Постоянно меняющаяся, непрерывная, свободно опертая балка с постоянной распределенной нагрузкой.Эта задача состоит из свободно опертой стальной балки длиной 300 дюймов с распределенной нагрузкой 1000 фунтов/дюйм поперек балки. Секция начинается с высоты 10 дюймов и линейно увеличивается к центру, где достигает высоты 24 дюймов. Затем он сужается до 10 дюймов. Чтобы определить, как изменяется момент инерции относительно x, мы будем моделировать в Solidworks и брать сечения через каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним строку. Вы, наверное, заметили, что я составил таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Здесь можно увидеть, что рассчитанные значения I(x) близко соответствуют значениям, указанным в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, с верхней и нижней частью, имеющей переменную «x», будет очень весело интегрировать это. Итак, есть одна вещь, которую вам нужно знать обо мне. У меня есть ограничения в том, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD! Как видите, очень кропотливая работа по интеграции был замазан, и мы смогли напрямую решить для нашей границы условия. В уравнениях s(x) и v(x), на самом деле были натуральные бревна и каким-то образом появился арктангенс (не показаны). я до сих пор не жалею позволяя MathCAD делать всю работу. Следующим шагом является проверка результатов. Наконец, мы зеркально отразим графики вместе, сформировав окончательное уравнение для отклонения нашей консольной балки. Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре. Лучшее руководство по расчету статически неопределимых балок Заключение В этой статье рассматриваются три популярных варианта нагружения, в которых балка имеет переменное поперечное сечение. Хотя это требует исчисления, часто это очень легко сделать вручную, потому что это многочлены. Если нет, будьте благодарны надежным программам, таким как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа таких лучей. Калькулятор прочности и прогиба балкиБалка или стержень — это любой элемент конструкции, длина которого значительно превышает его ширину или высоту. Однако термин «значительно» означает разные вещи для разных людей. Некоторым достаточно вдвое большей длины, другие сочтут пятикратную длину слишком короткой и поэтому сочтут такой элемент пластиной, рамой или конструкцией. Процедуры расчета балок не налагают таких ограничений или различий. Балки обычно используются для несущей нагрузки, при этом они охватывают опоры, расположенные на значительном расстоянии друг от друга, например пол (см. калькулятор CalQlata Floors). При указании балки необходимо определить ее максимальную грузоподъемность (т. е. ее прочность) и ее максимально допустимый прогиб. Прочность и жесткость балкиПрочность балки зависит от предела текучести материала, из которого изготовлена балка, тем самым определяя максимальную нагрузку, которая может быть приложена до того, как она необратимо деформируется (или сломается, если ее сделать из хрупкого материала), а его жесткость зависит от второго момента площади поперечного сечения балки (например, швеллера, двутавровой балки, двутавровой балки, угла и т. Обе вышеуказанные характеристики определяют поведение балки под нагрузкой. Проектирование балкиПредположим, у вас есть равномерно распределенная нагрузка в 4000 Н по балке длиной 4 м (1 Н/мм) и максимально допустимый прогиб, скажем, 1/200 длины балки (20 мм). Используя Балки, вы вводите известную информацию и изменяете второй момент площади (I), пока не получите желаемое отклонение (20 мм в середине балки, где ее отклонение будет наибольшим), что в данном случае дает вам значение для I около 800000 мм⁴. Предполагая, что вы планируете использовать секцию швеллера, отсортировав швеллеры в базе данных стальных секций CalQlata, вы обнаружите, что размер вашей балки должен быть секции «3×6», которая является наименьшей секцией балки со значением I выше 800000 мм⁴, и найдите значение для y (расстояние от нейтральной оси луча до внешней стороны его сечения), которое в данном случае составляет 38,1 мм. Вернитесь к Балкам, введите правильное значение для I (863 264 мм⁴), а также введите значение 38,1 мм для d, чтобы установить максимальное напряжение в материале балки, которое в данном случае составляет 88 Н/мм². Если это значение находится в пределах ваших требований к безопасности, то ваш луч приемлем. Если нет, но приходится работать с данным материалом, то следует изменить (увеличить) сечение балки, тем самым уменьшая допустимый прогиб до тех пор, пока напряжение не станет приемлемым. Калькулятор прогиба балки — Техническая помощьРис. 1. Схема нагружения балки Предполагается, что любая нагрузка в калькуляторе прочности балок действует одинаково через плоскость или сечение балки во всех направлениях, перпендикулярных (другими словами, @ 90° до) его продольной оси. Если нагрузка локализована в поперечном сечении балки (т. е. распределена по ней неравномерно), могут потребоваться дополнительные расчеты для выявления местных (сосредоточенных) реакций и напряжений (см. Напряжение изгибаИзгибающие напряжения в балках применяются к балке на заданном расстоянии (d) от ее нейтральной оси. Эта входная переменная (‘d’) используется только в расчетах напряжения (σx) и деформации (ex). Если вы оставите это поле пустым или установите его равным нулю, Beams не будет рассчитывать напряжение или деформацию в указанном вами месте вдоль балки (рис. 1 «x»). Никакие другие результаты не будут затронуты. Условия многократной/одновременной нагрузкиЕсли у вас есть балка с более чем одной приложенной нагрузкой, вы просто суммируете результаты в указанном месте. Пример расчета прочности балки (рис. 2): Детали балки: Шаг 1: Шаг 2: Шаг 3: Рис. 2. Процедура расчета составной нагрузки Ограничения Эти расчеты действительны только в том случае, если материал по всей длине и толщине сечения подчиняется закону Гука. Единицы Вы можете использовать любые единицы измерения, которые вам нравятся, но вы должны быть последовательны. Дополнительная литератураДополнительную информацию по этому вопросу можно найти в справочных публикациях (2, 3 и 4) 11 Таблицы формул прогиба балки |11 Таблицы формул прогиба балки
Формулы прогиба балкиСодержание Уравнения изгиба и прогиба При проектировании балок (бетонных, стальных или деревянных) способность к изгибу и сдвигу проверяется в соответствии с применяемой теорией изгиба. Приложенная сила заставляет элемент изгибаться, он подвергается изгибающим моментам, а концы реагируют на сдвигающие нагрузки. Профиль изгиба и сдвига балки/элемента зависит от типа опоры балки (т. е. шарнирные, фиксированные и свободные концы). Формула упругого прогиба балки \(\frac{M}{I}=\frac{\sigma}{y}=\frac{E}{R}\)
КЛЮЧЕВЫЕ термины в формулах прогиба балки 92\)) В таблицах ниже приведены формулы прогиба балки для свободно опертой, неподвижной балки и консолей для различных конечных условий и нагрузок. Прогиб балки с простой опорой и формулаБалка с простой опорой при одноточечной нагрузке – (2 штыревых соединения на каждом конце) 93}{48EI}\) Сила сдвига и реакция: \(R_A=R_B=\frac{P}{2}\) Балки с простой опорой под одной точечной нагрузкой, расположенной в любом месте балки – (2 штыревых соединения на каждом конце) Балка с простой опорой – точечная нагрузка Момент: \(M_{C} = \frac {Pab}{L}\) Уравнение отклонения балки: , когда a>b, \(\delta_x = \frac{Pab(L+b)}{27EIL} \sqrt{3a(L+ б)}\) в \(x=\sqrt{\frac{a(L+b)}{3}}\) from A Сила сдвига и реакция: \(R_A= \frac{Pb} {L}\) \(R_B= \frac{Pa}{L}\) Простые опорные балки под 2-точечной нагрузкой – (2 штыревых соединения на каждом конце) Просто поддерживаемая балка – 2-точечная нагрузка Момент: \(M_{C} = Pa\) \ (M = \frac{PL}{3}\) Уравнение прогиба балки: , когда a>b, 94}{384EI}\) Сила сдвига и реакция: \(R_A = R_B \frac{wL}{2}\) \(R_A = R_B \frac{wL}{2} \) Фиксированный конец и штифты с UDL – (1 фиксированный конец и штифтовое соединение на каждом конце). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.
При их изготовлении используется не просто алюминий, а его сплавы. В строительстве такие изделия применяются реже, чем стальные аналоги, так как они уступают по показателям устойчивости при сильных нагрузках. Чаще всего алюминиевые балки применяют при строительстве малогабаритных зданий. При возведении промышленных объектов изделия из данного металла применяются только в комбинации со стальными конструкциями.


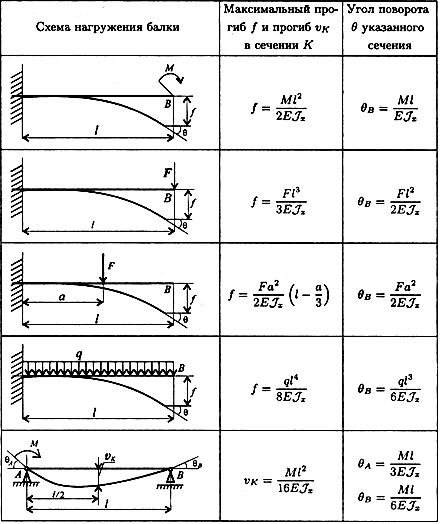
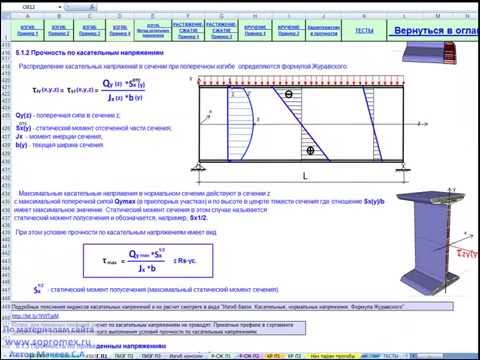 Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.
Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.
 Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
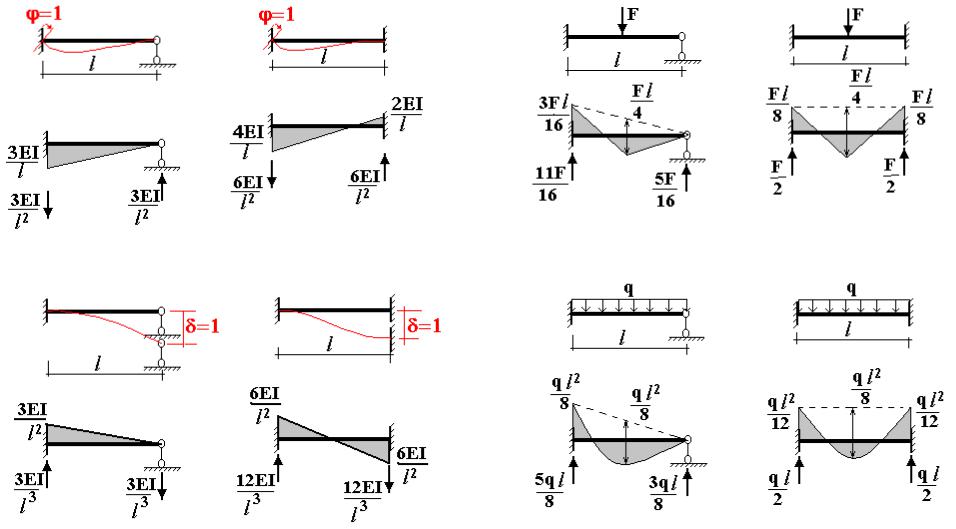 1 м в 6 м пролете, допускаются нагрузки на перекрытие в 500 кгм.п.
1 м в 6 м пролете, допускаются нагрузки на перекрытие в 500 кгм.п. Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики,
Таким образом удается понизить ее стоимость, но целиком сохранить механические характеристики,

 гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный
гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный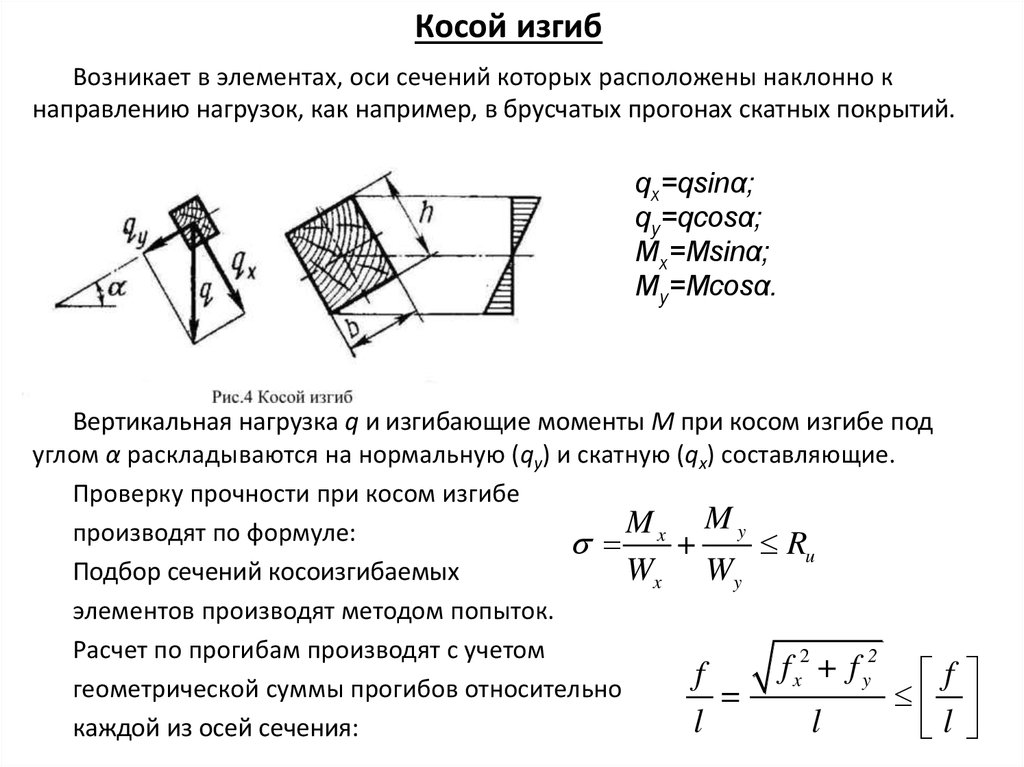


 Удачи!
Удачи!
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
 Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций.
Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций. Это обусловлено наличием двух полок с обеих сторон, благодаря которому изделие обладает большей жесткостью. По прочности один двутавр способен заменить два швеллера. На надежность сооружения также оказывает влияние узел крепления двутавра и швеллера. Это крепление, с помощью которого профиля соединяются между собой, а также крепятся к опорным конструкциям или трубам.
Это обусловлено наличием двух полок с обеих сторон, благодаря которому изделие обладает большей жесткостью. По прочности один двутавр способен заменить два швеллера. На надежность сооружения также оказывает влияние узел крепления двутавра и швеллера. Это крепление, с помощью которого профиля соединяются между собой, а также крепятся к опорным конструкциям или трубам. Реже используется горячекатаные двутавры. Что касается швеллеров, то они могут изготавливаться двумя способами: горячекатаным и гнутым. В первом случае металлическая заготовка нагревается до высокой температуры и при помощи специального станка ей придается требуемая форма. Гнутые швеллера производятся холодным способом – края заготовок в этом случае просто загибаются под нужным углом. Швеллера, угол полок которых < 90°, обладают более высокой прочностью, чем стандартные, но все-таки не дотягивают по надежности до двутавровых профилей.
Реже используется горячекатаные двутавры. Что касается швеллеров, то они могут изготавливаться двумя способами: горячекатаным и гнутым. В первом случае металлическая заготовка нагревается до высокой температуры и при помощи специального станка ей придается требуемая форма. Гнутые швеллера производятся холодным способом – края заготовок в этом случае просто загибаются под нужным углом. Швеллера, угол полок которых < 90°, обладают более высокой прочностью, чем стандартные, но все-таки не дотягивают по надежности до двутавровых профилей.