Расчет нагрузки на балку двутавровую: Расчёт металлической балки онлайн (калькулятор)
alexxlab | 26.12.2022 | 0 | Разное
Двутавровые балки – виды и расчет нагрузки металлической балки
Оглавление
Двутавровая балка (двутавр) является одним из главных профилей проката, который получил широкое использование в строительной сфере. Выдерживаемая таким профилем нагрузка намного превышает нагрузку квадратного профиля, имеющего аналогичную площадь сечения, чем и объясняется популярность двутавровой балки.
Широкое использование двутавров Н-образной формы связано со строительством объектов промышленности, военной сферы и др. Кроме того, такая балка используется в местах необходимости высокой прочности и сопротивляемости металлоконструкций, в частности в горнорудной промышленной сфере в процессе строительства шахт, а также железнодорожных мостов, опор и иных инженерных конструкций. Для покупки двутавровых балок рекомендуем обращаться к производителям. Вы сможете купить металлическую балку нужного размера, которую изготовят по вашим чертежам.
Виды двутавровых балок
Имеются определенные параметры, по которым все двутавровые балки классифицируются на виды.
Промышленники выпускают стандартные двутавры, угол наклона в которых составляет до 12°, а также балки серий М и С, классифицирующихся ценой и параметрами.
Использование серии М связано с монорельсами, визуально определяющимся по углу наклона внутренних граней, не превышающему 12°.
Для армирования стволов шахт применяется серия С, имеющая угол наклона до 16°.
Маркировка балок иного назначения также осуществляется следующими буквами следующих:
Б — стандартный, обыкновенный тип двутавры;
Ш — широкополочный тип балки, применяющийся в процессе строительства ненагруженных колонн;
К — балки, применение которых связано с возведением тяжелых колонн.
По изготовлению двутавры бывают горячекатаного и сварного типа. Выпуск горячекатаных балок цельного типа, в соответствии со строительными стандартами, осуществляется 4-12 метровой длиной и 100-500 миллиметровой высотой.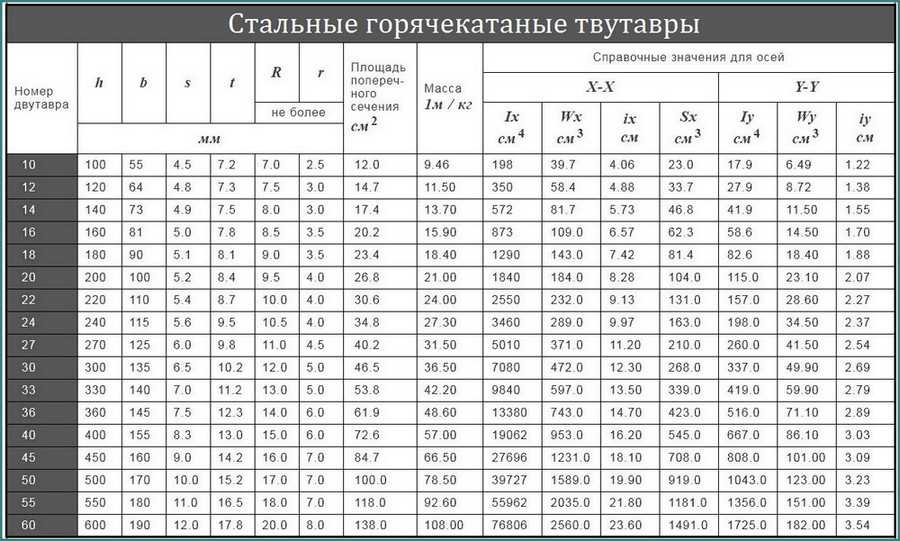
Изготовление сварных балок характеризуется определенными особенностями, поэтому их высота может превышать 500 миллиметров, а в некоторых случаях даже превышать 1000 мм. Выбор двутавров должен осуществляться при учете не только их габаритов, но и толщины полки. Для определения данного параметра у балок с наклонными гранями берется общее среднее значение.
Вес одного погонного метра двутавра тоже является важным параметром. Вследствие использования качественной легированной стали с низким содержанием углерода в таких балках они обладают солидным весом, которые необходимо учитывать в проектировании с применением двутавров.
Как рассчитать нагрузку на двутавровую балку
Для расчета веса двутавров берутся параметры профиля из ГОСТ 8239—89. Данным стандартом приводятся параметры всех стандартных профилей, которые выпускаются в промышленной сфере. Расчет нагрузки и выбор из сортамента подходящего профиля осуществляется на основании произведения расчета несущей способности двутавров и последующего добавления запаса прочности. Обязательным является запас прочности в 20-30 процентов для конструкций сварного типа. С учетом прогиба нужно выбирать более крепкий профиль, который превышает по свойствам профиль, подходящий по нагрузке.
Расчет нагрузки и выбор из сортамента подходящего профиля осуществляется на основании произведения расчета несущей способности двутавров и последующего добавления запаса прочности. Обязательным является запас прочности в 20-30 процентов для конструкций сварного типа. С учетом прогиба нужно выбирать более крепкий профиль, который превышает по свойствам профиль, подходящий по нагрузке.
Как правило, на двутавре указывается допустимый уровень нагрузки и размер. Необходимо помнить, что для двутавров, применяемых в качестве перекрытий, требуется определенный запас для сварных швов. Особенную актуальность это имеет для колонных балок, для размещения которых необходимо наличие подушки из железобетона, к которой производится приварка балки. Допуск, который необходимо оставлять в данном случае, должен составлять 40 мм для приваривания двутавров.
Точность прокатки
В соответствии со стандартом, выпуск двутавровых балок осуществляется с обычной и повышенной точностью.
Имеется целый ряд отклонений от эталона, по которым замеряется качество профиля. В ГОСТ 8239—89 указаны не только все характеристики, но и требования к качеству изготовления профиля, вне зависимости от серии. Кроме того, там можно ознакомиться со существующими методами замера показателей двутавров. Двутавровые балки представляют собой незаменимый тип металлоконструкций в строительной отрасли и являются широко применимыми в строительстве долговечных конструкций.
В ГОСТ 8239—89 указаны не только все характеристики, но и требования к качеству изготовления профиля, вне зависимости от серии. Кроме того, там можно ознакомиться со существующими методами замера показателей двутавров. Двутавровые балки представляют собой незаменимый тип металлоконструкций в строительной отрасли и являются широко применимыми в строительстве долговечных конструкций.
Статья подготовлена совместно с компаний «СтройМеталл» http://stroimetall.ru/.
Расчет динамической нагрузки(удара) – пример решения задачи
Ниже приведено условие и решение задачи. Закачка решения в формате doc начнется автоматически через 10 секунд.
На двутавровую балку с высоты H падает груз F.
Требуется :
1) Определить наибольшие нормальные напряжения в балке ;
2) Вычислить наибольшие напряжения в балке при условии, что правая опора заменена пружиной, податливость которой (т.е. осадка от груза 1 кН) равна α ;
3) Сравнить полученные результаты.
Дано : номер двутавра 36 ; L=3 м ; F=11 кН ; α=3 мм/кН ; H=L/5 (высота падения не задана, поэтому принимаем самостоятельно).
Решение.
Балка подвергается поперечному (изгибающему) удару.
Условие прочности балки :
Наибольшее напряжение в балки от статического действия груза :
где Mx – максимальный момент в сечении балки (определяется по эпюре) ; Wx – момент сопротивления сечения при изгибе, для двутавра № 36 : Wx=743 cм3 (определяется по таблицам сортамента прокатной стали).
Построим эпюру изгибающих моментов. Определим реакции опор :
ΣmC=-RAL+0.8FL=0 , откуда
RA=0.8F=0.8×11=8.8 кН
ΣmA=RCL-0.2FL=0 , откуда
RC=0.2F=0.2×11=2.2 кН
Балка имеет два участка. Обозначим zi расстояние от левого (правого) конца балки до некоторого её сечения. Найдём изгибающие моменты в характерных сечениях балки.
Найдём изгибающие моменты в характерных сечениях балки.
MA=0 ; MBл=0.2RAL=0.2×8.8×3=5.28 кН·м ; MBпр=0.8RCL=0.8×2.2×3=5.28 кН·м ; MC=0.
Эпюра изгибающих моментов построена на рисунке, со стороны растянутых волокон.
Тогда, при Mx=5.28 кН∙м (в сечении B) наибольшее напряжение в балке от статического действия груза :
=7.1×106 Па=7.1 МПа
Для определения динамического коэффициента вычислим величину прогиба в точке приложения груза от статического действия его.
Воспользуемся методом начальных параметров. Начало отсчёта абсциссы z примем на опоре A, где y0=0. В точке удара :
EJyB=
Неизвестный начальный параметр ν0 найдём, составив уравнения для сечения С, где yC=0 :
EJyC=
Откуда : ν0=
Тогда, при найденном выражении для ν0, получим :
EJyB=
EJyB=
Откуда yB==-9. 5×10-5 м=-0.095 мм
5×10-5 м=-0.095 мм
где Е=2×1011 Па – модуль упругости ; J=Jx=13380 см4 – момент инерции (по таблице сортамента прокатной стали).
Находим динамический коэффициент :
kd==113.4
Находим динамическое напряжение :
МПа
Находим прогиб от динамического действия груза F в точке удара :
yd=kdyst=kdyB=113.4×0.095=10.8 мм.
Вычислим наибольшее напряжение в балке при условии, что правая опора заменена пружиной.
В случае опирания правого конца балки на пружину при действии на балку статической силы F пружина под влиянием опорной реакции RC=2.2 кН, укоротится на длину a=RCα=
=2.2×3=6.6 мм. Правый конец балки при этом опустится на величину a, а сечение B балки – на величину yBст=0.2a=0.2×6.6=1.32 мм.
Полное вертикальное перемещение от статического действия силы F в сечении под силой (в сечении B) равно сумме величин прогиба, найденной при расчёте балки без пружины, и перемещения, вызванного сжатием пружины, т. е. :
е. :
Δст=yB+yBст=0.095+1.32=1.415 мм.
Находим динамический коэффициент :
kd==30.1
Находим динамическое напряжение :
МПа
Находим прогиб от динамического действия груза F в точке удара :
yd=kdyst=kdΔст=30.1×1.415=42.6 мм.
Таким образом, установка пружины под правым концом балки уменьшила динамические напряжения в 805.14/213.71=3.8 раза.
Расчет нагрузки на колонну – Расчет нагрузки на колонну, балку, стену и перекрытие
Содержание
Что такое колонна?Колонна является важным конструктивным элементом железобетонной конструкции, который помогает передавать нагрузку надстройки на фундамент .
Это вертикальный сжимаемый элемент, подвергающийся прямой осевой нагрузке, и его эффективная длина в три раза превышает его наименьший поперечный размер.
Когда элемент конструкции расположен вертикально и подвергается осевой нагрузке, называется колонной, а если он наклонен и горизонтален, называется подкосом.
Что такое Луч?Это важный конструктивный элемент рамной конструкции, который в основном воспринимает нагрузку, приложенную сбоку к оси балки. В основном это режим отклонения из-за изгиба.
Из-за приложенной нагрузки в точке опоры балки возникают силы реакции , и действие этих сил создает в ней поперечную силу и изгибающий момент , которые вызывают деформацию, внутренние напряжения и прогиб балки .
Его нижняя часть испытывает растяжение, а верхняя – растяжение; следовательно, в нижней части балки предусмотрена дополнительная сталь, чем в верхней.
Обычно балки классифицируются в соответствии с условиями их опоры, условиями равновесия, длиной, формой поперечного сечения и материалом.
Что такое стена? Это непрерывная вертикальная конструкция, которая разделяет или окружает пространство территории или здания, а также обеспечивает укрытие и безопасность.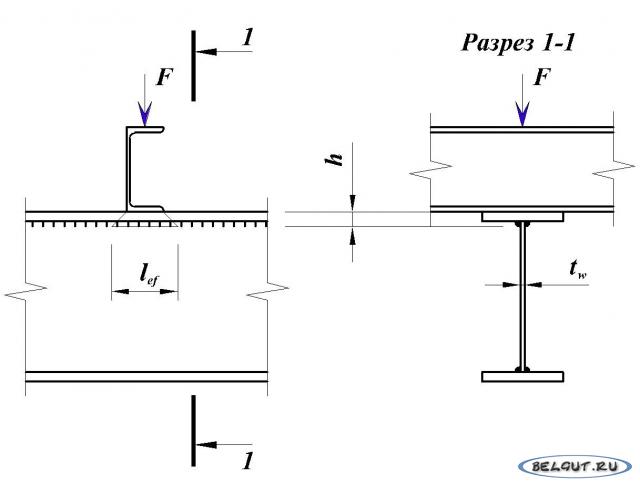 Обычно его строят из кирпичей и камней.
Обычно его строят из кирпичей и камней.
В здании в основном есть два типа стен: внешние стены и внутренние стены. Внешняя стена помогает обеспечить ограждение здания.
При этом внутренняя стена разделяет огороженную территорию на помещения необходимого размера. Внутренняя стена также известна как перегородка.
В здании стена помогает сформировать основную часть надстройки и помогает разделить внутреннее пространство, а также обеспечивает конфиденциальность, звукоизоляцию и противопожарную защиту.
Что такое плита?Плита является широко используемым конструкционным элементом, который формирует полы и крыши зданий. Это плоский элемент, глубина которого намного меньше его ширины и размаха.
Плита может поддерживаться каменными стенами, железобетонной балкой или непосредственно колонной. Он воспринимает обычно равномерно распределенные гравитационные нагрузки, действующие на его поверхность и передающие их на опору за счет сдвига, изгиба и кручения.
Собственный вес колонны × Количество этажей
Собственный вес балки на погонный метр
Нагрузка на стену на погонный метр
другие вещи) + Живая нагрузка (из-за движения человека) + собственный вес
Помимо вышеуказанной нагрузки, колонны также испытывают изгибающие моменты, учитываемые в окончательном проекте.
Наиболее продуктивным способом проектирования конструкций является использование современного программного обеспечения для проектирования конструкций, такого как Staad pro и Etabs.
Эти инструменты помогают избежать длительных и утомительных ручных расчетов при проектировании конструкций. Это настоятельно рекомендуется в настоящее время в области структурного дизайна.
Для профессиональных работ по проектированию конструкций существуют некоторые фундаментальные допущения, которые мы учитываем при расчетах нагрузки на конструкцию.
Мы знаем, что плотность бетона составляет 2400 кг/м3 или 24 кН, а плотность стали составляет 7850 кг/м3 или 78,5 кН.
Возьмем колонну размером 300 × 600 с 1% стали и длиной 3 метра.
- объем бетона = 0,3 x 0,60 x 3 = 0,54 мгранита
- Вес бетона = 0,54 x 2400 = 1296 кг
- Вес стали (1%) в бетоне = 0,54 x 0,018505505505505505505505506 = 0,54 9006 x 0,018505505505505506 = 0,54 9009 x 0,018505505505506 = 0,54
- . = 42,39 кг
- Общий вес колонны = 1296 + 42,39 = 1338,39 кг = 13,384 кН
Примечание – I кН = 101,9716 кг 9 1000003
Расчет нагрузки на балкуМы используем аналогичную процедуру расчета для балки , а также для колонны.
Примем размеры поперечного сечения балки как 300 мм x 450 мм , без учета толщины плиты.
Отсюда
- 300 мм x 450 мм, исключая толщину плиты
- объем бетона = 0,3 x 0,60 x 1 = 0,138M=
- Вес бетона = 0,138 x 2400 = 333 KG
- .0006
- Вес стали (2%) в бетоне = = 0,138 x 0,02 x 7850 = 22 кг
- Веса столба = 333 + 22 = 355 кг/м = 3,5 кН/м
Итак, собственный вес будет примерно 3,5 кН на метр.
Расчет нагрузки стеныМы знаем, что плотность кирпича составляет от 1500 до 2000 кг/м3.
Для кирпичной стены толщиной 9 дюймов, длиной 1 метр и высотой 3 метра
Нагрузка/метр = 0,230 x 1 x 3 x 2000 = 1380 кг или 13 кН/метр.
Этот процесс можно использовать для расчета нагрузки кирпича на метр для любого типа кирпича.
Для блоков AAC (Автоклавный газобетон) вес на кубический метр составляет около 550 – 700 кг/м3 .
Если вы используете газобетонные блоки для строительства, нагрузка на стены на метр может составлять всего 4 кН/метр . Использование этого блока позволяет значительно снизить стоимость проекта.
Расчет нагрузки плитыРассмотрим плиту толщиной 100 мм.
Следовательно, собственный вес плиты на квадратный метр составит
= 0,100 x 1 x 2400 = 240 кг или 2,4 кН.
Если учесть, что наложенная постоянная нагрузка составляет около 2 кН на метр, а конечная нагрузка составляет около 1 кН на метр.
Следовательно, мы можем оценить, что нагрузка на плиту будет примерно 6 – 7 кН (приблизительно) за квадратный метр из приведенного выше расчета.
Расчет нагрузки на здание Нагрузка на здание представляет собой сумму постоянной нагрузки, вынужденной или динамической нагрузки, ветровой нагрузки, сейсмической нагрузки, снеговой нагрузки, если конструкция расположена в зоне снегопада.
Статическая нагрузка – это статическая нагрузка, обусловленная собственным весом конструкции, которая остается неизменной на протяжении всего срока службы здания. Эти нагрузки могут растягивающих или сжимающих нагрузок.
Импульсные или временные нагрузки представляют собой динамические нагрузки, связанные с использованием или пребыванием в здании, включая мебель. Эти нагрузки продолжают меняться время от времени. Временная нагрузка является одной из важных нагрузок при проектировании.
Расчет временной нагрузкиДля расчета временной нагрузки здания мы должны следовать значениям допустимой нагрузки согласно IS-875 1987 часть 2.
Обычно мы рассматриваем значение временной нагрузки для жилых здания как 3 кН/м2. Значение динамической нагрузки варьируется в зависимости от типа здания, для которого мы должны следовать правилам IS 875-1987 часть 2.
Расчет статической нагрузки Для расчета статической нагрузки здания необходимо определить объем каждого элемента, такого как фундамент, колонна, балка, плита и стена, умноженный на единиц веса материала, из которого он изготовлен.
Суммируя постоянную нагрузку всех конструктивных элементов, мы можем определить общую постоянную нагрузку здания.
Коэффициент запаса прочностиНаконец, после расчета полной нагрузки на колонну, не забудьте добавить коэффициент запаса прочности, который является наиболее важным при проектировании любой конструкции здания для ее безопасной и надлежащей работы в течение всего срока службы. .
Это необходимо при выполнении расчета нагрузки на колонну.
Коэффициент запаса прочности составляет 1,5 согласно IS 456:2000,
Надеюсь, теперь вы поняли , как рассчитать нагрузку на колонну, балку, стену и плиту .
Спасибо!
Также прочтите
Что такое плинтусная балка? Защита цоколя – разница между цокольной балкой и анкерной балкой
Разница между уровнем цоколя, уровнем подоконника и уровнем перемычки
Что такое колонна? – Типы колонн, армирование, порядок расчета
Разница между длинной колонкой и коротким столбцом
Разница между предварительным натяжением и пост -натяжным строительных работ – метод длинных стен и коротких стен, метод центральной линии
Решетка под локальными нагрузками – ручные расчеты
Это новая идея, над которой я работаю, чтобы показать, что хорошего в ручном проектировании, линейном МКЭ, и нелинейный МКЭ, и я продемонстрирую несколько примеров. Я решу каждую из них, используя все 3 подхода, затем сравню результаты, чтобы мы могли обсудить, какой метод полезен для данного случая и почему! Первая проблема, которую я рассмотрю, — это стенка в стальной балке под местными нагрузками. Сегодня мы решим проблему своими руками!
Я решу каждую из них, используя все 3 подхода, затем сравню результаты, чтобы мы могли обсудить, какой метод полезен для данного случая и почему! Первая проблема, которую я рассмотрю, — это стенка в стальной балке под местными нагрузками. Сегодня мы решим проблему своими руками!
Локальные сбои — это всегда кошмар. Очень сложно рассчитать пропускную способность малых секций любой конструкции при сосредоточенных нагрузках. К счастью, EN 1993-1-5 дает нам достойное решение для полотен при концентрированных нагрузках! Посмотрим, что у нас получится!
Впереди будут ручные расчеты, но не беспокойтесь, никакой высшей математики не потребуется. Я также объясню, что мы делаем шаг за шагом!
Я также думаю, что на самом деле хорошо иметь возможность создавать вещи вручную! Удивительно, но многие из сумм, которые мы обсудим сегодня, можно использовать и для решения других задач! Другими словами, я думаю, что это может быть полезно для вас. Пойдем!
Проблема
Локальные нагрузки паутины могут быть многогранными. Классический пример, который мы здесь решим, содержит две перпендикулярные балки, одна из которых «просто стоит» на другой. Задача будет выглядеть так:
Классический пример, который мы здесь решим, содержит две перпендикулярные балки, одна из которых «просто стоит» на другой. Задача будет выглядеть так:
Обратите внимание:
Конечно, нас интересуют оба луча. Ведь полотно верхнего грузится так же, как полотно нижнего. Но я не хочу тратить слишком много времени на уравнения! Так что буду считать, что верхняя балка имеет несколько «более прочную» сетку! Таким образом, мы сосредоточимся только на нижнем луче. Конечно, легко сделать такое предположение, просматривая анимацию выше. Обратите внимание, однако, что «на самом деле» это очень большое предположение, и его не следует делать без веской причины!
Первым делом!
Я вполне допускаю, что это может показаться пугающим. Вы скоро увидите, что я перескакиваю между главами и кодами, создавая соответствующие формулы, казалось бы, из воздуха. Хотя я настоятельно рекомендую просто прочитать все коды, Бог знает, что я сам этого не делал. Так уж получилось, что я десять лет преподавала в универе, и это одна из тем, которые мы решали! Даже по прошествии нескольких лет я все еще просто помню все (я думаю, преимущества обучения других!).
Так уж получилось, что я десять лет преподавала в универе, и это одна из тем, которые мы решали! Даже по прошествии нескольких лет я все еще просто помню все (я думаю, преимущества обучения других!).
Прямо сейчас мы находимся в главе 6 стандарта EN 1993-1-5. Нам нужно начать с оценки того, какая из возможностей подходит нам лучше всего. Вы можете проверить их все на рис. 6.1 в этой главе, но для удобства я покажу их ниже:
Совершенно очевидно, что из нашего выбора здесь мы находимся в ситуации «типа (а)». Это дает нам возможность вычислить параметр k F . Но так как мы понятия не имеем, зачем нам это нужно, не будем забегать вперед! Также обратите внимание, что существует расстояние между ребрами жесткости, которые нам необходимо знать. У модели, которую вы видели, есть ребра жесткости, и здесь мы будем использовать их размах. Что интересно, если бы у нас вообще не было ребер жесткости, не совсем понятно, что делать! Предположительно, мы могли бы предположить, что a=infinity, но код вообще этого не определяет! Обратите внимание, что разница между несколькими метрами и бесконечностью невелика, поскольку k F значение касается!
Мы доверяем процедуре!
Надо сказать, что это довольно запутанная процедура. Но мы храбрые, так что мы все равно справимся!
Но мы храбрые, так что мы все равно справимся!
Вы можете рассчитать пропускную способность паутины, используя уравнение 6.1:
Я люблю параметры, которые не так просто «описать» с точки зрения того, что они означают. Хотя предел текучести имеет странный символ (в отношении Еврокодов), это, по крайней мере, объяснимо. Вы знаете, это похоже на «предел текучести» f y … «для сети» и, следовательно, « w » в конце). Я не уверен, существует ли практика сварки разных марок стали вместе для формирования поперечного сечения… но если есть, процедура явно готова к этому!
Комментарий к фактору безопасности заключается в том, что « M1 » уже говорит нам о том, что будет задействована устойчивость. На самом деле это то, что мне нравится в Еврокоде! Обычно “ М0 ” и “ М1 ” коэффициенты запаса совпадают (но не столько в снарядах!. Я научился “переводить” “ M0 “коэффициент безопасности” как “нормальная стрессоустойчивость”, а “ M1 ” как “способность, включая устойчивость”. Возможно, это небольшой нюанс, но он может немного помочь вам в понимании того, что вы читаете, если вы заметили такие вещи!
Возможно, это небольшой нюанс, но он может немного помочь вам в понимании того, что вы читаете, если вы заметили такие вещи!
Конечно, груз сверху сжимает нашу паутину. Так что технически мы должны ожидать, что емкость будет примерно такой:
Вышеприведенное очень просто! У нас есть площадь поперечного сечения, умноженная на предел текучести (итак, сколько нагрузки наше поперечное сечение может безопасно передать), затем мы дополнительно уменьшаем это значение на коэффициент безопасности. Конечно, если искривление возможно, необходимо уменьшить нагрузку, которую мы можем безопасно выдержать. Это делается с коэффициентом «Х», чтобы учесть коробление.
Зная все это, уравнение 6.1, с которого мы начали… «упускает» коэффициент потери устойчивости. В то же время «эффективная длина» Leff должна быть допустимой «шириной» полотна, которую мы можем принять во внимание. Я знаю это, потому что ширина, умноженная на толщину, даст мне площадь поперечного сечения, которую я ожидал увидеть в уравнении.
Кроме того, если двигаться дальше по коду, мы придем к уравнению 6.2. Это показывает нам, что по какой-то причине автор этой части решил скрыть «коэффициент потери устойчивости»! Я ожидал, что это будет в «основном» уравнении 6.1. Вместо этого мы будем использовать его для расчета эффективной длины:
Ладно, по крайней мере, мы к чему-то пришли!
Обычно сложно рассчитать коэффициент потери устойчивости. Но здесь нам придется подумать и об эффективной ширине. Проще говоря, вы обычно знаете, насколько велико поперечное сечение элемента, который вы пытаетесь рассчитать. Здесь все немного сложнее! Нам нужно будет оценить, какая часть ширины полотна фактически будет передавать нагрузку. Таким образом, это также то, что мы должны будем рассчитать/оценить.
Теперь давайте быстро взглянем на коэффициент изгиба:
Конечно, «легкость», с которой наша паутина будет изгибаться, будет зависеть от ее гибкости, как видно выше. И именно «гибкость» является «сложной частью» при расчете коэффициента уменьшения потери устойчивости… давайте посмотрим:
Как всегда, гибкость — это просто квадратный корень из пластической способности, деленный на критическую способность. Пластиковый очень простой… обычно! Здесь, конечно, это будет зависеть от ширины полотна, которое мы можем «назначить» для передачи локальной нагрузки. И мы еще не установили, какой будет эта длина (пожалуйста, будьте терпеливы, мы приближаемся!). Обычно хитрость заключается в критической силе, так как нужно думать о длине изгиба и т. д. Удивительно, но в нашем случае все не так плохо:
Пластиковый очень простой… обычно! Здесь, конечно, это будет зависеть от ширины полотна, которое мы можем «назначить» для передачи локальной нагрузки. И мы еще не установили, какой будет эта длина (пожалуйста, будьте терпеливы, мы приближаемся!). Обычно хитрость заключается в критической силе, так как нужно думать о длине изгиба и т. д. Удивительно, но в нашем случае все не так плохо:
Запомните «загадочный» параметр k F , определенный в начале (под картинкой). Что ж, теперь, по крайней мере, мы знаем, где его использовать! Кроме того, кажется, что мы знаем все, что нужно знать, чтобы вычислить F CR , и это хорошо. Но есть одна вещь, которая мне не нравится в этом уравнении! Обычно я ожидаю, что высота будет «квадратной» (точно так же, как в уравнении Эйлера). Проверить такие сомнения вручную сложно, но в следующем посте я сделаю МКЭ! Это означает, что мы сможем увидеть, насколько хорошо это «вписывается» в «реальность» различных случаев (да… FEA может даже помочь вам с такими вещами!).
Последнее, с чем нам придется иметь дело, это чертова ширина паутины, которую нам будет позволено использовать в нашем дизайне. Давайте пройдем процедуру шаг за шагом!
Поначалу это выглядит как минимум правдоподобно. У нас есть ширина контакта, к которой мы можем приложить нагрузку. Кроме того, напряжение будет «перемещаться» под углом 45 градусов, а это означает, что сначала оно должно пройти через фланец. Но тогда он будет «дотягиваться» до стенки на большей длине (плюс удвоенная толщина полки, если быть точным). И, в конце концов, мы можем еще увеличить эту «дополнительную» ширину, основываясь на двух параметрах:
Первый параметр увеличивает «допустимую ширину» с учетом ширины луча. Второй явно зависит от гибкости паутины. На самом деле это забавная часть, поскольку гибкость также зависит от допустимой ширины полотна! Так что это похоже на «двойную зависимость». Но мы просто предположим один случай другому и проверим, все ли в итоге получится! Конечно, если мы «промахнемся» с предположением, то при необходимости внесем коррективы.
Вот и все! Вся процедура расчета мощности полотна в реальном пучке! Пришло время использовать то, что мы узнали, в нашем случае, чтобы увидеть, что мы получим!
Решаемая задача
Прежде чем мы перейдем к фактическим расчетам, я должен дать вам некоторые геометрические детали задачи! Это все развлечения и игры, чтобы показать вам уравнения и описать, что к чему. Но нам нужны конкретные числа, чтобы сделать математику, в которой мы нуждаемся!
Размеры, которые я привожу ниже, не являются «особыми» ни в каком смысле, о котором я могу думать. По правде говоря, я просто начал с модели FEA и угадал все размеры по ходу дела!
Кроме того, здесь я использую «трюк». Обычно, когда я проектирую балку, я сразу же определяю «высоту» от центра одной полки до центра другой полки. Это означает, что я бы смоделировал нижнюю балку высотой 530 мм. Это 500 мм для стенки и «дополнительные» 15 мм на полку. Это приведет к наиболее точному модулю сечения и, как правило, является хорошей практикой, которой вы должны следовать.
Однако это также означает, что моя модель МКЭ будет «видеть» стенку на 30 мм «выше». И так как здесь мы фокусируемся ТОЛЬКО на паутине, я смоделирую балку высотой 500 мм. Это не окажет «драматического» влияния на результаты, но я решил, что могу быть здесь «в точку».
Обратите внимание:
Я делаю это ТОЛЬКО потому, что это частичная модель, которая фокусируется на расчете ТОЛЬКО паутины и ее стабильности. Вы хотите использовать осевые линии во всех расчетных случаях. Если только не будет веских аргументов, чтобы сделать по-другому!
Поделитесь этим постом с друзьями!
Надеюсь, понятно, что геометрическое расположение не имеет большого значения. Нас интересует только проверка локальной пропускной способности сети. Таким образом, длина балок и т. д. не так важна.
Здесь нужно только, чтобы расстояние между внутренними ребрами жесткости («а») в нашем случае составляло 800 мм. Как ни странно, остальное не имеет значения в дизайне, который мы собираемся сделать!
Дизайн для победы!
Технически описанная выше процедура уже объясняет, как нужно действовать. Но я не люблю оставлять ни единого камня на камне. Кроме того, если мы хотим сравнить результаты FEA с обычными расчетами… нам нужен результат! Итак, давайте сделаем настоящую математику для нашего примера!!
Как вы, наверное, заметили, я люблю «представлять» процедуры «по ходу дела». Это означает, что нужно начинать с проверки емкости и расширяться до всех сложностей проблемы. Я думаю, что так легче понять вещи. Конечно, когда мы на самом деле будем делать расчеты, мы просто «начнем с конца» и будем двигаться «вверх». Это означает, что мы будем начинать с вещей, которые мы действительно можем вычислить в первую очередь.
Естественно, что мы сначала устанавливаем значения параметров M1 и M2 . Ведь это единственное, что мы можем сделать на данный момент. Мы не знаем, какая у нашей паутины стройность, но предположу, что стройность высокая. Я делаю это, потому что у нас есть тонкая паутина, которая довольно длинная! Проще говоря, я буду считать, что M2 на самом деле имеет ненулевое значение.
Вооружившись вышеизложенным, мы можем рассчитать ширину паутины. Но сначала нам нужно установить кое-что, о чем я еще не упоминал. Это ширина контакта, и установим ее по рисунку 6.2:
Как видите, мы можем рассматривать разные случаи. Поскольку у нас также есть двутавровая балка сверху, я выберу второй случай слева. Буду стремиться к минимальной толщине шва. В основном потому, что у меня не будет сварных швов в моделях FEA, которые я сделаю позже! Скажем так, я хочу оставаться максимально последовательным.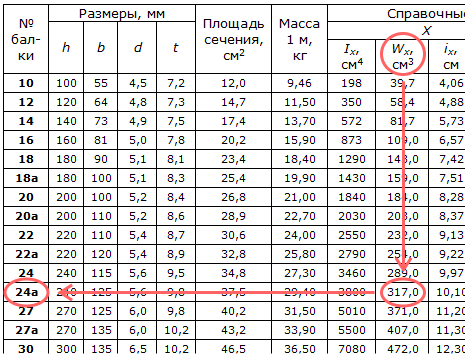 Я обозначу горизонтальный размер сварного шва как «r1» (думаю, для этого в Великобритании используется «z»). Значение 6 мм означает, что размер сварного шва составляет а=4 мм. Маловат для 30мм фланца, но надеюсь вы меня за это простите!
Я обозначу горизонтальный размер сварного шва как «r1» (думаю, для этого в Великобритании используется «z»). Значение 6 мм означает, что размер сварного шва составляет а=4 мм. Маловат для 30мм фланца, но надеюсь вы меня за это простите!
Итак, теперь мы знаем все для расчета ширины перемычки, которую мы можем учитывать при проектировании:
Как вы можете видеть выше, я учитываю M2 , предполагая, что гибкость будет выше 0,5. Давай выясним! Но сначала нам нужно рассчитать критическую силу:
Как видите, я использовал уравнение из рисунка 6.1, которое я упоминал в начале, для расчета параметра k F . При этом вычислить критическую силу несложно. Итак, теперь мы, наконец, можем увидеть, действительно ли тонкость выше 0,5: 9.0003
ДА! Мы прибили это! Поскольку исходное предположение верно, мы можем быстро перейти к проверке емкости, как вы можете следовать ниже:
Великолепно! Если я не допустил каких-то ошибок выше, кажется, мы только что получили ответ по Еврокоду! Похоже, что максимальная сила реакции, которую верхняя балка может передать анализируемой нами балке, составляет 315,8 кН.

