Расчет прогиба: Расчет балки на прогиб и прочность
alexxlab | 16.06.2023 | 0 | Разное
Расчет прогибов ЖБК в соответствии нормами СП 63.13330.ХХХХ
Теги: #ЛИРА-САПР #ЖБК #прогибы #нелинейность
Ниже описываются требования норм к расчету прогибов железобетонных элементов и их реализация в ПК ЛИРА-САПР.
Расчет прогибов в соответствии с СП 63.13330.ХХХХ определяется на основании кривизны железобетонного элемента.
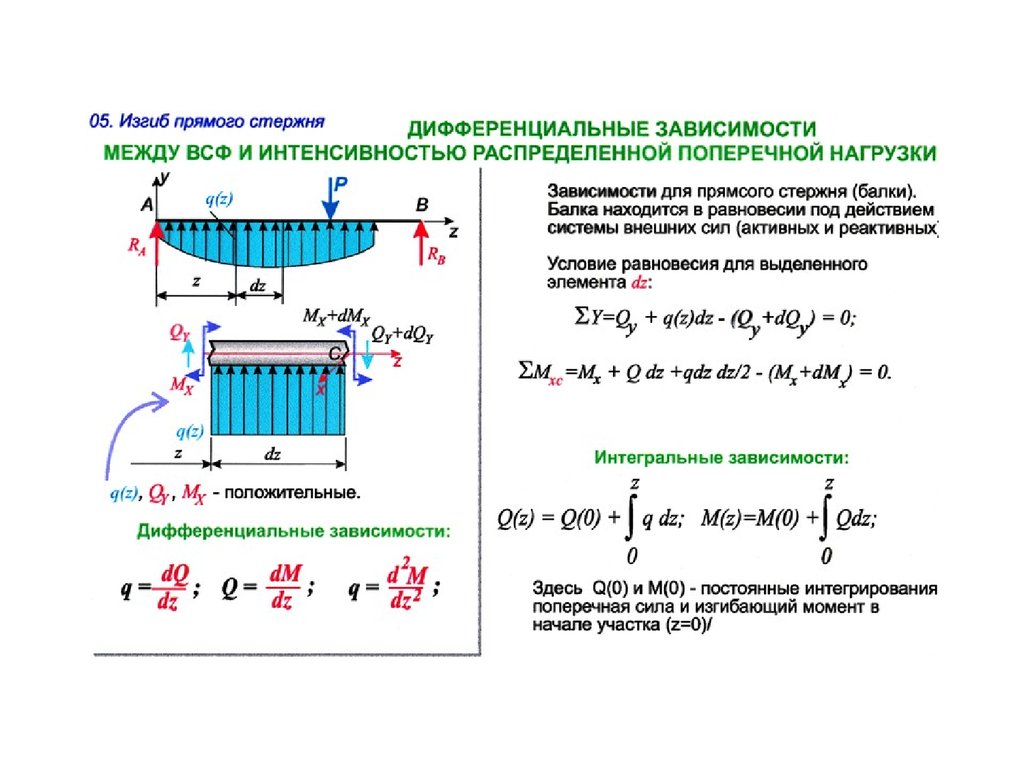
8.2.24 Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формулам:
– для участков без трещин в растянутой зоне:
1/r=(1/r)1+(1/r)2 (8.140)
– для участков с трещинами в растянутой зоне:
1/r=(1/r)1-(1/r)2+(1/r)3 (8.141)
В формуле (8.140):
(1/r)1, (1/r)2 – кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
В формуле (8.141):
(1/r)1 – кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям;
(1/r)3 – кривизна от продолжительного действия постоянных и временных длительных нагрузок.

Кривизна железобетонного элемента определяется в зависимости от его изгибной жесткости D, которая зависит от модуля деформаций бетона Eb1 и приведенного момента инерции сечения Ired.
Изгибная жесткость D элемента определяется с учетом того, образовались или нет на данном участке нормальные трещины.
8.2.25 Кривизну железобетонных элементов 1/r от действия соответствующих нагрузок (см. 8.2.24) определяют по формуле
1/r=M/D, (8.142)
где М – изгибающий момент от внешней нагрузки (с учетом момента от продольной силы N) относительно оси, нормальной плоскости действия изгибающего момента и проходящей через центр тяжести приведенного поперечного сечения элемента;
D – изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле
D=Eb1*Ired, (8.143)
где Eb1 – модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки и с учетом наличия или отсутствия трещин;
Ired – момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона Еb1 и момента инерции приведенного сечения Ired для элементов без трещин в растянутой зоне и с трещинами определяют по 8.2.26 и 8.2.27 соответственно.
Значения модуля деформации бетона в формулах (8.143), (8.145) принимают равными:
– при непродолжительном действии нагрузки
Eb1=0.85Eb, (8.146)
– при продолжительном действии нагрузки
Eb1=Ebτ=Eb1/(1+φb,cr) (8.147)
где φb,cr принимают по таблице 6.12.
ПК ЛИРА-САПР при определении прогибов элементов оперирует их жесткостью. При таком подходе полученные прогибы следует суммировать аналогично кривизне
8.2.31 Прогибы железобетонных элементов можно определять по общим правилам строительной механики с использованием вместо кривизны 1/r непосредственно изгибных жесткостных характеристик D путем замены упругих изгибных характеристик EI в расчетных зависимостях на характеристики D, вычисляемые по формулам, приведенным в 8.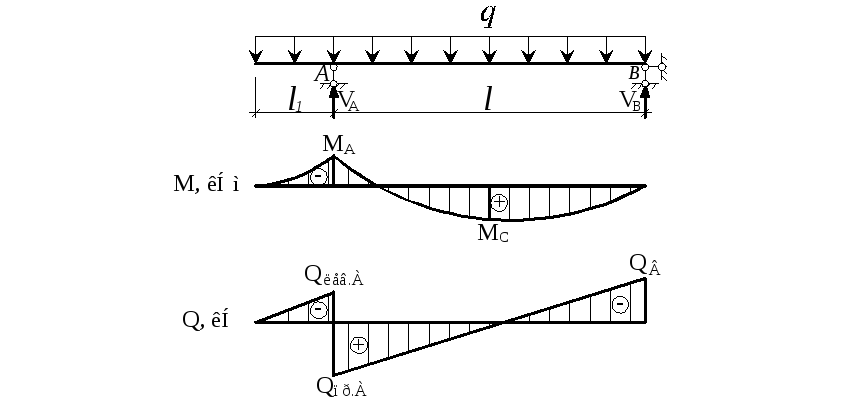 2.25 и 8.2.29.
2.25 и 8.2.29.
При совместном действии кратковременной и длительной нагрузок полный прогиб элементов без трещин и с трещинами в растянутой зоне определяют путем суммирования прогибов от соответствующих нагрузок по аналогии с суммированием кривизны по 8.2.24, принимая жесткостные характеристики D в зависимости от указанной в этом пункте принятой продолжительности действия рассматриваемой нагрузки.
Допускается при определении жесткостных характеристик D элементов с трещинами в растянутой зоне принимать коэффициент ψs= 1. В этом случае при совместном действии кратковременной и длительной нагрузок полный прогиб изгибаемых элементов с трещинами определяют путем суммирования прогибов от непродолжительного действия кратковременной нагрузки и от продолжительного действия длительной нагрузки с учетом соответствующих значений жесткостных характеристик D, т. е. подобно тому, как это принято для элементов без трещин.
Пример.
Прямоугольный свободно опертый элемент пролетом 4800мм.
Расчет ведем в физически нелинейной постановке.
Для описания диаграммы σ-ε применяем 14й закон деформирования – трехлинейную диаграмму деформирования для бетона и двухлинейную для арматурной стали. Т.к. работа материала описывается диаграммой σ-ε, а не модулем деформаций, то влияние кратковременной и длительной ползучести реализовывается путем умножение значений относительных деформаций бетона εb1 и εbt1 на коэффициенты 1/0.85=1.176 и 1+φb,cr=1+3.4=4.4 соответственно. Такой подход аналогичен, по своей сути, формулам (8.146) и (8.147).
Относительные деформации εb0 ,ε b2, εbt0, εbt2 принимаются в зависимости от длительности действия нагрузок: εb0=-0. 002, εb2=-0.0035, εbt0=0.0001, εbt2=0.00015 при кратковременном действии нагрузок, εb0=-0.0034, εb2=-0.0048, εbt0=0.00024, εbt2=0.00031 при длительном действии нагрузок (таблица 6.10 СП 63).
002, εb2=-0.0035, εbt0=0.0001, εbt2=0.00015 при кратковременном действии нагрузок, εb0=-0.0034, εb2=-0.0048, εbt0=0.00024, εbt2=0.00031 при длительном действии нагрузок (таблица 6.10 СП 63).
На участках с трещинами принимается диаграмма работы бетона без учета растянутой ветви.
Исходная диаграмма σ-ε бетона класса В15
| ε | σ,тс/м2 |
| -0.003500 | -1122.00 |
| -0.002000 | -1121.00 |
| -0.000275 | -673.20 |
| 0.000000 | 0.00 |
| 0.000028 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом кратковременной ползучести
| ε | σ,тс/м2 |
-0. 003500 003500 |
-1122.00 |
| -0.002000 | -1121.00 |
| -0.000324 | -673.20 |
| 0.000000 | 0.00 |
| 0.000033 | 67.32 |
| 0.000100 | 111.00 |
| 0.000150 | 112.20 |
Диаграмма σ-ε бетона класса В15 с учетом длительной ползучести
| ε | σ,тс/м2 |
| -0.0048 | -1122.00 |
| -0.0034 | -1121.00 |
| -0.001210 | -673.20 |
| 0.000000 | 0.00 |
| 0.000123 | 67.32 |
| 0.00024 | 111.00 |
| 0.00031 | 112.20 |
Диаграмма σ-ε арматуры класса А500
| ε | σ,тс/м2 |
-0.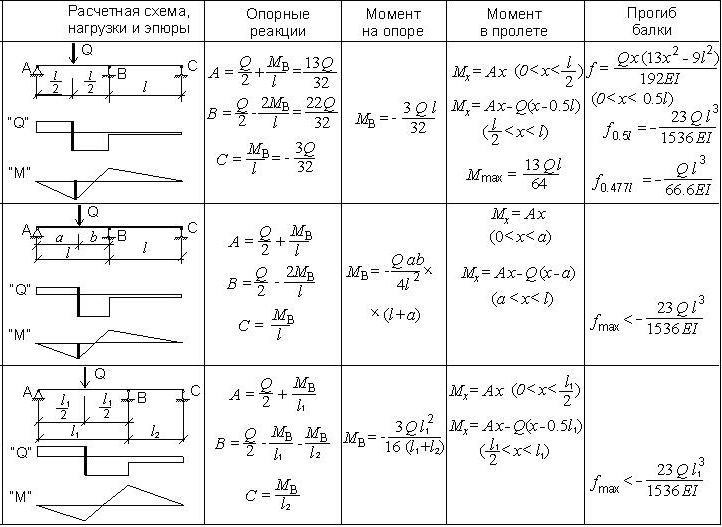 025 025 |
-51000 |
| -0.0025 | -50999 |
| 0 | 0 |
| 0.0025 | 50999 |
| 0.025 | 51000 |
Момент инерции сечения Ired определяется автоматически в зависимости от полученного во время расчета НДС нормального сечения.
Таким образом, во время физически нелинейного расчета ПК ЛИРА-САПР определяет жесткостные характеристики элементов автоматически.
По длине балки назначается 2 типа жесткости – с учетом работы растянутой ветви (для участков без трещин) и без этого учета (на участках с трещинами).
Типы жесткости:
1 – диаграмма σ-ε с учетом длительной ползучести и учетом растянутой ветви работы бетона;
2 – диаграмма σ-ε с учетом кратковременной ползучести и учетом растянутой ветви работы бетона;
3 – диаграмма σ-ε с учетом длительной ползучести, без учета растянутой ветви работы бетона;
4 – диаграмма σ-ε с учетом кратковременной ползучести, без учета растянутой ветви работы бетона.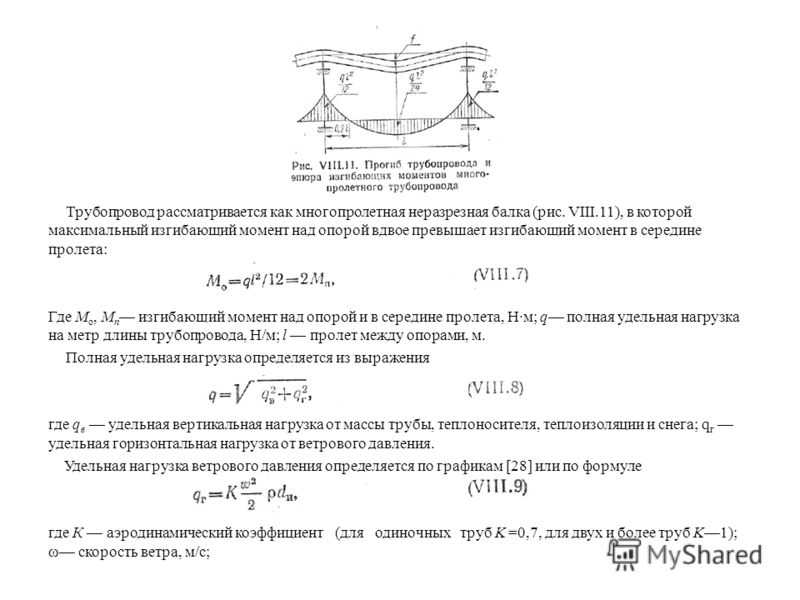
Нагрузки прикладываем в 2х загружениях: загружение 1 – длительные нагрузки, загружение 2 – кратковременные.
Для получения трех составляющих прогибов f1, f2, f3 создаем 3 балки:
балка 1 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1 и 15кН/м в загружении 2;
балка 2 – характеристики жесткости, соответствующие кратковременной ползучести; нагрузка 75кН/м в загружении 1;
балка 3 – характеристики жесткости, соответствующие длительной ползучести; нагрузка 75кН/м в загружении 1.
Рисунок 1. Длительные нагрузки (загружение 1) с мозаикой жесткостей
Рисунок 2. Кратковременные нагрузки (загружение 2) с мозаикой жесткостей
Рисунок 3. Принятые диаграммы σ-ε бетона соответственно для типов жесткости 1-4 (слева на право)
Рисунок 4. Принятая диаграмма σ-ε арматуры
Рисунок 5. Армирование сечения (используется ТЗА)
Для выполнения нелинейного расчета следует задать шаговую историю нагружения:
Результаты расчета:
Рисунок 6. Сверху вниз: эпюры прогибов от непродолжительного действия полных нагрузок f1, непродолжительного действия постоянных и временных длительных f2, продолжительного действия постоянных т временных длительных f3
Сверху вниз: эпюры прогибов от непродолжительного действия полных нагрузок f1, непродолжительного действия постоянных и временных длительных f2, продолжительного действия постоянных т временных длительных f3
Прогиб балки составляет:
f=f1-f2+f3=10.1-8.23+9.68=11.55мм
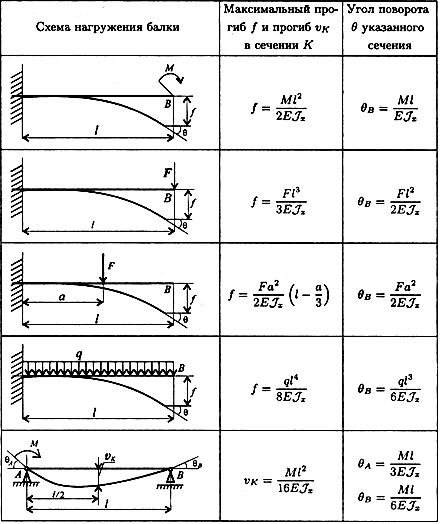
Рассчет прогиба концевых балок мостового крана, способы и формулы
Рассчет прогиба концевых балок мостового крана, способы и формулыБалка – элемент, представляющий жёсткий стержень, который нагружается вертикально действующими силами. Главный пролет крановых металлоконструкций имеет вид моста – конструктивного элемента, служащим для передвижения грузоподъемной тележки. В данном материале вы узнаете, как рассчитать прогиб концевых балок мостового крана.
Что такое прогиб? Это смещение поперечного сечения балки в вертикальном положении под воздействием оказываемой нагрузки. Узнать данную величину можно из следующих характеристик: длины и размеров поперечника балочной металлоконструкции.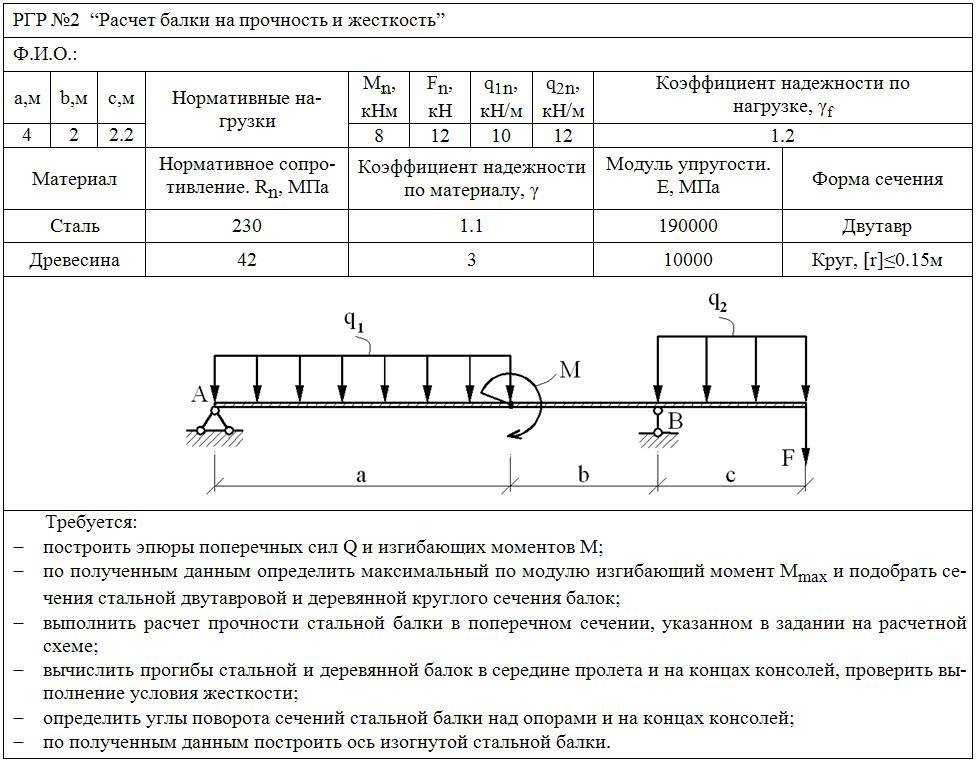
Помимо перемещений в вертикальной плоскости, возможен поворот балки относительно начальной плоскости. Данная величина рассчитывается с помощью метода начальных параметров.
Вычисление пролетного прогиба проводится при оценке двутавра на жесткость. На основании полученных значений подбирается оптимальный размер сечения несущего моста кран-балки.
В настоящий момент выполнить расчетные вычисления прогиба можно несколькими способами:
- Воспользовавшись готовыми онлайн-калькуляторами (в том числе и на нашем сайте).
- Используя справочные материалы, определить искомое значение для данного типа и размера балок.
- Рассчитать величину прогиба с помощью формул.
Наиболее удобным и практичным способом определения прогиба считается метод начальных параметров, благодаря которому можно записать формулу вычисления искомого значения.
Под начальными параметрами понимают:
- Прогибы на опорных подкрановых узлах равны 0.
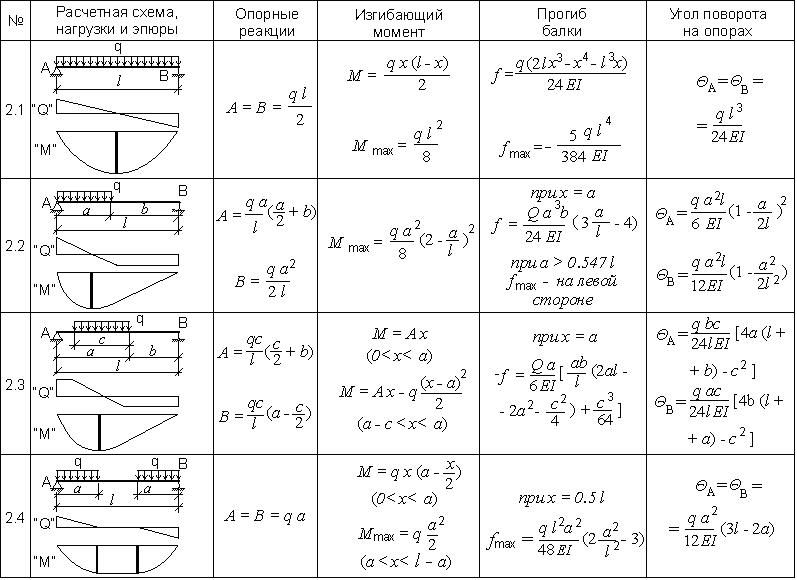
- В жёстких заделках искомые значения также равняются 0.
Для проведения расчета требуется знать все внешние нагрузки, оказываемые на главный пролет, и реакции опор. Задаются уравнения равновесия и система координат, на основании которой находятся недостающие значения. При необходимости для удобства подсчета вводятся дополнительные нагрузки. Общая жесткость балки складывается из жёсткости отдельных опор конструкции.
Для получения решения необходимо иметь следующие значения:
- Момент инерции.
- Геометрические характеристики.
- Вычисление максимальной нагрузки.
Подробно вычислительные работы для определения балочного прогиба изучаются в дисциплине «Сопротивление материалов».
Вернуться к списку статей
Наши услуги
Подкрановые пути
Модернизация и реконструкция крана
Радиоуправление краном
Ремонт кранового оборудования
Монтаж кранового оборудования
Техническое обслуживание грузоподъемных кранов
Обследование грузоподъемных кранов
Ремонт крановых колес
Мехобработка деталей
Наши товары
Крановое оборудование
Кран мостовой
Литейные производства
Изготовление металлоконструкций
Оборудование для аэропортов
Сергеев Евгений Иванович
Коммерческий директор ООО Машиностроительно-Литейное Объединение Буревестник
О компании
Мы рады приветствовать вас на интерактивной площадке нашего завода и благодарны за внимание к нашему предприятию и его деятельности в бизнесе.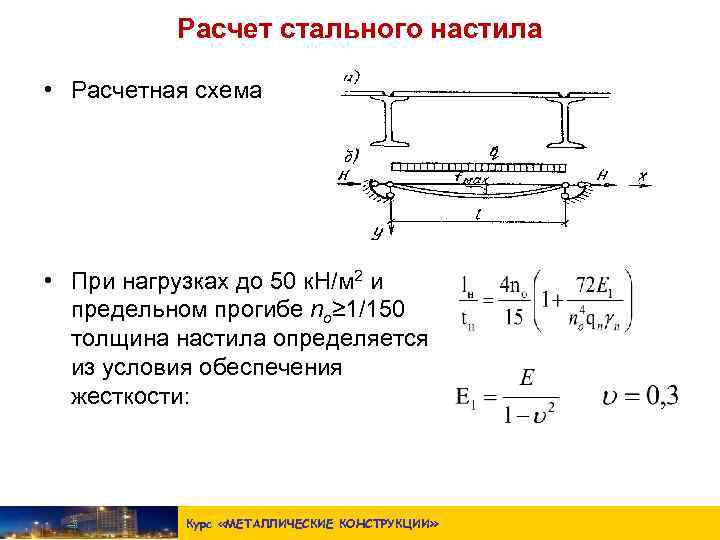
Наш завод производит широкий ассортимент машиностроительной и металлургической продукции для различных отраслей отечественной экономики и многих зарубежных стран.
Высокий технический уровень, качество и надежность изделий с маркой нашего предприятия получили широкую известность и признание, создали заводу высокий авторитет в промышленном мире.
Читать подробнее о компании
Structural Engineering Library > Модули расчета > Балки > Общие > Результаты прогиба
Важно понимать, что на вкладке «Сводные результаты» любого из модулей балки программа сообщает об условиях, которые обеспечивают управляющие коэффициенты прогиба… не обязательно максимальные значения прогиба.
Чтобы понять значение этого различия, рассмотрим следующую балку с консолью:
Предположим, что нагрузка выглядит следующим образом:
Программа выполнит следующее:
1. нагрузка, динамическая нагрузка, снеговая нагрузка и т. д.).
нагрузка, динамическая нагрузка, снеговая нагрузка и т. д.).
2. Определить прогибы для каждого загружения при множестве небольших приращений по длине балки.
3. Комбинируйте прогибы при каждом небольшом приращении в пропорциях, определяемых коэффициентами нагрузки в сочетаниях эксплуатационных нагрузок.
4.Определить максимальные прогибы вверх и вниз для каждого пролета балки.
5. Рассчитайте результирующее отношение для каждого пролета балки, разделив длину пролета на максимальное отклонение вверх и вниз для этого пролета.
6. Запишите (на вкладке «Сводные результаты») условия, при которых определяется управляющее отношение для:
• Максимальное отклонение вниз только на временных нагрузках
• Максимальное отклонение вверх на основании только временных нагрузок
• Максимальное отклонение вниз на основе временных нагрузок при полной загрузке
• Максимальный прогиб вверх при полной нагрузке
Еще одна деталь, о которой важно помнить, заключается в том, что для консолей коэффициент прогиба обычно рассчитывается путем деления удвоенной длины пролета на прогиб.
Теперь, когда мы установили, что на самом деле приводит к результатам отклонения, вот результаты для балки, указанной выше:
1
2
Длина
360 дюймов
240 дюймов
Максимальное отклонение вниз
0,447 дюйма благодаря D+L
0,457 дюйма благодаря D+S
Коэффициент
360/0,447 = 805
2×240/0,457 = 1050
Обратите внимание, что общее максимальное отклонение вниз происходит в пролете 2 (на свободном конце консоли) и составляет 0,457 дюйма из-за постоянных и снеговых нагрузок. Тем не менее, контрольное соотношение фактически создается в пролете 1, который испытывает немного меньшую величину отклонения. Поэтому программа будет сообщать о отрезке 1 на вкладке «Сводные результаты». Это хороший пример того, как эти значения отклонения могут давать интересные результаты. Это также иллюстрирует важное различие между контролем отклонений и контролем коэффициентов отклонения. Если в вашем проекте вас интересуют абсолютные прогибы, вы можете изучить их на вкладке «Отклонения рабочей нагрузки» на вкладке «Сводка M-V-D».
Это хороший пример того, как эти значения отклонения могут давать интересные результаты. Это также иллюстрирует важное различие между контролем отклонений и контролем коэффициентов отклонения. Если в вашем проекте вас интересуют абсолютные прогибы, вы можете изучить их на вкладке «Отклонения рабочей нагрузки» на вкладке «Сводка M-V-D».
Расчет прогиба. Когда мы должны сделать этот тип расчета? SINADRIVES
Перейти к содержимомуПредыдущий Следующий
Привет любителям мехатроники!
Добро пожаловать в последний пост в блоге Sinadrives.
Июнь 2022
В этом посте мы рассмотрим некоторые расчеты, которые инженеры и проектировщики промышленного оборудования должны производить для повышения производительности машин. В частности, мы собираемся обсудить расчеты отклонения.
Расчет прогиба требуется в случае балок, поддерживаемых с обоих концов, и балок, поддерживаемых только с одного конца. Давайте рассмотрим оба случая, чтобы увидеть, как они рассчитываются.
Изображение 1
Расчет прогиба требуется в случае балок, поддерживаемых с обоих концов, и балок, поддерживаемых только с одного конца. Давайте рассмотрим оба случая, чтобы увидеть, как они рассчитываются.
Прежде чем обсуждать математическую формулу расчета, мы должны рассмотреть, как эта балка крепится. Есть две возможности: жесткое (встроенное) крепление или нежесткое (поддерживаемое) крепление. В случае мостового крана или козлового крана, такого как показанный на рисунке 1, крепление не является жестким, поскольку происходит движение в направлении X.
На изображении 2 показана поддерживаемая балка, а на изображении 3 — встроенная балка.
Рисунок 2
Рисунок 3
где:
f – прогиб, мм
F – точечная нагрузка, действующая в центре балки, Н
m – общий вес балки (распределенный по всей ее длине), кг
g – ускорение свободного падения (9,81 м/с2)
l – расстояние между точками опоры, мм
E – модуль упругости, Н/мм² *
I – геометрический момент инерции мм4
Первый член соответствует точечной нагрузке, действующей на балку ; второй член соответствует весу самой балки.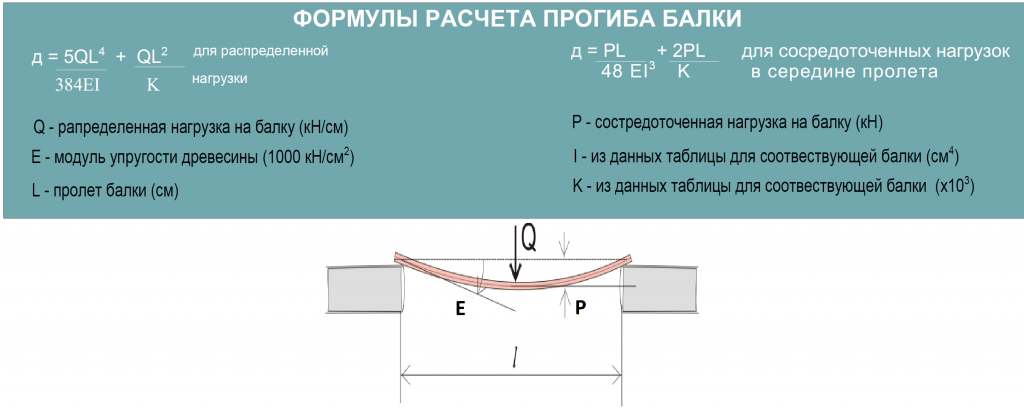
* Модуль упругости стали составляет 205 000 Н/мм², а алюминия — 70 000 Н/мм².
где:
f – прогиб, мм
F – точечная нагрузка, действующая в центре балки, Н
m – общий вес балки (распределенный по всей ее длине), кг
г – ускорение свободного падения (9,81м/ s2)
l – расстояние между опорными точками, мм
E – модуль упругости, Н/мм2
I – геометрический момент инерции, мм4 встроенный пучок.
На рисунке 4 показана балка, поддерживаемая с одного конца.
Рисунок 4
В этом случае балка может иметь только жесткое (закладное) крепление:
f – прогиб, мм
F – сосредоточенная нагрузка, действующая на свободный конец балки, Н
м – общий вес балка (по всей длине), кг
г – ускорение свободного падения (9,81м/с2)
l – расстояние между точками опоры, мм
E – модуль упругости, Н/мм2
I – геометрический момент инерции мм4
Важно:
В дополнение к точечной нагрузке, действующей на балку, мы также должны учитывать влияние собственного веса балки. В большинстве случаев собственный вес вызывает больший прогиб, чем нагрузка, которую он должен нести.
В большинстве случаев собственный вес вызывает больший прогиб, чем нагрузка, которую он должен нести.
На этот вопрос нет однозначного ответа; это зависит от приложения. Например, в случае 15-метрового мостового крана отклонение в 100 мм может быть приемлемым, но в случае динамического козлового крана такое отклонение будет иметь катастрофические последствия. Как правило, мы должны учитывать следующие моменты:
Прежде всего, мы должны проанализировать применение и оценить, как потеря высоты, вызванная отклонением, может повлиять на процесс. Например, при лазерной резке отклонение в 3 мм может быть критическим из-за потери точности лазера. При гидроабразивной резке этот изгиб не так критичен.
В этом случае важно проанализировать, есть ли какие-либо вертикальные движения (цилиндр или линейный привод) на мосту (или балке). Чем больше прогиб, тем более упругой становится балка и в результате теряет жесткость. Если движение линейного привода является динамическим и, прежде всего, влечет за собой постоянные изменения направления, это может привести к тому, что луч войдет в состояние резонанса. Как правило, для динамических приложений отклонение не должно превышать 1 мм, а для медленных приложений оно не должно превышать 3 мм. Эти цифры не следует принимать за правило; каждое приложение требует детального изучения.
Как правило, для динамических приложений отклонение не должно превышать 1 мм, а для медленных приложений оно не должно превышать 3 мм. Эти цифры не следует принимать за правило; каждое приложение требует детального изучения.
В некоторых случаях чрезмерное отклонение может создать ряд проблем и трудностей для приложения. Потеря жесткости, потеря точности, резонансы или собственные частоты, которые могут поставить под угрозу работу оборудования. Чтобы уменьшить прогиб, можно предпринять следующие шаги:
Мы можем увеличить момент инерции, используя балку, состоящую из раскосов и угловой арматуры (в стиле строительного крана), вместо сплошной балки. Существует множество стандартных стальных или алюминиевых профилей с высокими значениями инерции.
Уменьшение веса балки также может быть хорошим решением. Изгиб можно уменьшить, облегчив балку, сделав ее полой или используя альтернативные материалы и т. д.
Эластичность стали в три раза выше, чем у алюминия. Прогиб можно уменьшить, используя сталь.