Расчет звездочек цепной передачи: Расчет цепной передачи

alexxlab | 15.02.2023 | 0 | Разное

Расчет звездочки цепной передачи в Excel

Опубликовано 06 Авг 2016
Рубрика: Механика | 50 комментариев

До широкого распространения станков с ЧПУ зубья звездочек цепных передач нарезали чаще всего на обычных фрезерных станках дисковыми фрезами в делительных головках или – реже — червячными фрезами на зубофрезерных станках. Но для полного соответствия профиля зуба…

…при обработке дисковой фрезой теоретическому профилю необходимо для каждого числа зубьев звездочки изготовить «свою» фрезу. Производство огромной номенклатуры дорогостоящих фрез экономически нецелесообразно, и для цепи одного типоразмера стали делать 5 фрез, как некий компромисс между точностью получаемого профиля и стоимостью.

Фреза №1 – для z=7 и 8

Фреза №2 – для z=9…11

Фреза №3 – для z=12…17

Фреза №4 – для z=18…35

Фреза №5 – для z>35

Сегодня на станках плазменной, лазерной, электроэрозионной, гидроабразивной резки с ЧПУ, фрезерных с ЧПУ можно изготавливать без специального дорогостоящего инструмента звездочки цепных передач с профилями зубьев точно соответствующими теории. Это, безусловно, положительно сказывается на износостойкости и цепи и зубьев при эксплуатации передачи.

При создании управляющей программы для изготовления профилей зубьев звездочки цепной передачи в большинстве случаев необходимо получить или сделать dxf-файл с чертежом контура детали в натуральную величину (в масштабе 1:1).

Современные CAD-программы для конструкторов-механиков решают эту задачу за «пару кликов мышью». Представленный далее геометрический расчет звездочки цепной передачи в Excel покажет – «как они это делают» и поможет сделать чертеж тем, у кого нет этих дорогостоящих CAD-программ.

Расчет в Excel профиля звездочки.

Расчет звездочки цепной передачи выполняется по формулам Таблицы 1 и Таблицы 2 ГОСТ 591-69. Расчет некоторых дублирующих размеров я не стал выполнять, а оставшиеся, необходимые для прорисовки профиля параметры, расположил в таблице в порядке выполнения построений.

Программа в MS Excel:

Исходных данных — всего два, по ним автоматически определяются все расчетные параметры. Пользователь вводит число зубьев звездочки и выбирает из выпадающего списка цепь по ГОСТ 13568-97, все остальное происходит автоматически!

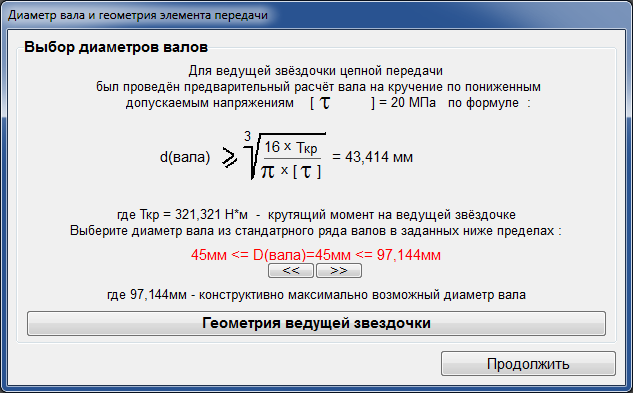
Проектировочный расчет в Excel роликовой цепной передачи, определяющий исходные данные для рассматриваемой программы, в подробном изложении найдете здесь.

Формулы:

Формулы в программе, как было замечено выше, расположены не в логической последовательности выполнения вычислений, а в порядке потребности в значениях размеров для выполнения геометрических построений.

9. λ=t/d₁

10. K=f(λ)

при λ≤1,5  K=0,480

при 1,5<λ≤1,6  K=0,532

при 1,6<λ≤1,7  K=0,555

при 1,7<λ≤1,8  K=0,575

при λ>1,8  K=0,565

Последнее значение K явно выбивается из логической цепи чисел, но соответствует ГОСТ 591-69.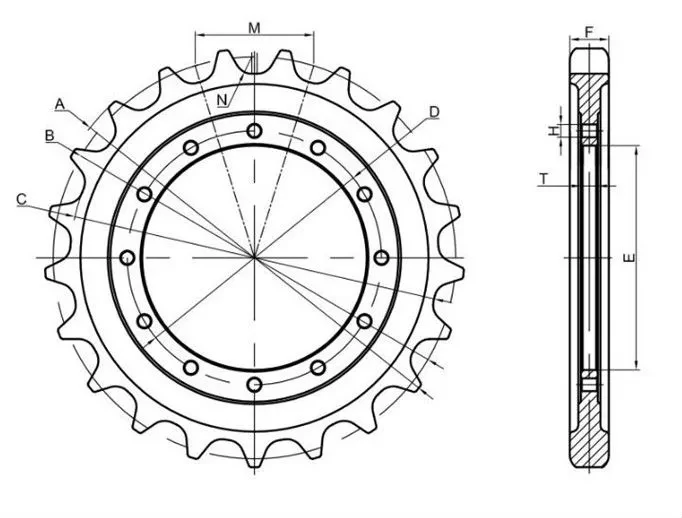 Ошибка в ГОСТе? Скорее всего — да. (Никто не удосужился за почти 50 лет ее исправить…) Однако, ошибка не критическая. Во многих источниках K=0,5 вне зависимости от значения λ.

11. γ=180/z

12. D_e=t*(K+1/tg (γ))

13. d_д=t/sin(γ)

14. D_i=d_д-2*r

15. e/2=0,015*t

В точных кинематических реверсивных передачах следует назначить e=0.

16. r=0,5025*d₁+0,05

17.  α=55-60/z

18. r₁=0,8*d₁+r

19. β=18-56/z

20. FG=d₁*(1,24*sin(φ) — 0,8*sin(β))

21. φ=17-64/z

22. r₂=d₁*(1,24*cos (φ)+0,8*cos (β) -1,3025) -0,05

23. b_n=f (b₁)

при n=1  b_n=0,93*b₁-0,15

при n=2 и n=3  b_n=0,90*b₁-0,15

при n=4  b_n=0,86*b₁-0,3

24.  B_n=(n-1)*A+b_n

25. D_c=t*1/tg (γ) -1,3*h

26. r₃=1,7*d₁

27. h₃=0,8*d₁

28. r₄=f (t)

при t≤35  r₄=1,6

при t>35  r₄=2,5

Алгоритм построения профиля зуба:

1. Из центра звездочки проводим вертикальную осевую линию через центр будущей впадины и наклоненную на угол γ осевую линию, которая пройдет через центр зуба.

2. Из того же центра строим три окружности – выступов, с диаметром D_e; делительную, с диаметром d_д; и впадин, с диаметром D_i.

3. Чертим осевую линию параллельную вертикальной осевой, отступив от нее на расстояние, равное половине смещения — e/2.

4. Из центра O — пересечения делительного диаметра и смещенной осевой линии — строим дугу с радиусом r и углом α.

5. На продолжении отрезка EO находим точку O₁ (EO₁=r₁) и проводим дугу радиусом r₁ на угол β.

6. Из точки F откладываем отрезок FG под углом φ  к наклонной осевой, проходящей через центр зуба.

7. На перпендикуляре к отрезку FG, проведенном из точки G, находим центр O₂ (GO₂=r₂) и чертим из точки G дугу радиусом r₂ до пересечения с диаметром окружности выступов.

Фронтальный профиль зуба построен. Осталось сделать зеркальную копию профиля вправо от вертикальной оси и размножить по всей окружности.

Построение поперечного профиля зубьев звездочки, думаю, не требует каких-либо дополнительных пояснений. Единственное, на что хотелось бы обратить внимание, это — выполнение диаметра обода D_c. Если его по невнимательности завысить, ролики цепи не «сядут» во впадину, и цепь будет опираться на звездочку торцами боковых пластин… (Недолго будет опираться…)

Заключение.

Расчет звездочки цепной передачи был выполнен в разрезе определения геометрических размеров профиля зубьев, достаточных для выполнения чертежа венца. Допуски на изготовление звездочки следует назначать по Таблице 3 ГОСТ591-69. В справочном приложении к этому ГОСТу есть обширные таблицы с рассчитанными параметрами звездочек для конкретных марок цепей. Часть данных из этих таблиц вы можете использовать для проверки выдаваемых программой в Excel результатов.

Ссылка на скачивание файла: raschet-zvezdochki-cepnoj-peredachi (xls 107 KB).

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Изготовление звездочек для цепной передачи

Звездочки для цепных передач – это детали, которые имеют необходимую форму для выбранной цепи. Эти детали имеют вид колес с зубьями. Зубья необходимы изделиям для того, чтобы вкрепляться в звенья цепи, без них цепная передача работать, двигаться не будет.

То есть, цепная передача работает благодаря ведущей звездочке и ведомой. Состоят изделия из износостойкого материала, способного выдерживать ударные нагрузки. Также их могут изготавливать и из чугуна, но если только цепная передача тихоходная, и нагрузка на деталь будет минимальная. Качественная работа цепной передачи, зависит от того, насколько качественно произведены звездочки для цепной передачи, а также, насколько эффективно сцепление с цепью.

Как правильно произвести расчет звездочки цепной передачи, ориентируясь по цепи.

Если необходимо сменить цепь в цепной передаче, заменить слабое изделие, более мощным, то в этом случае придется менять и звездочки. Прежде чем начинать изготовлять звездочки, нужно выбрать цепь, а затем по ней ориентироваться:

• сколько зубьев должно быть у звездочек.
• определится с диаметром каждой.

Ниже описаны формулы, по ним можно рассчитывать звездочки цепной передачи.

Расчет делительного диаметра можно произвести по этой формуле:

Dо = t*cоsеc (180/z)

Значение cosec 180ᶿ разный для каждого числа зубьев. Число зубьев это z. Например, для 11 зубьев cosec = 3.5495

Если нужно 30 зубьев то cosec = 9.5668.

t – Это шаг цепи.

Рассчитать диаметр выступов можно по этой формуле

De = t*(Kb + ctg (180/z))

ctg 180ᶿ для каждого числа зубьев разный.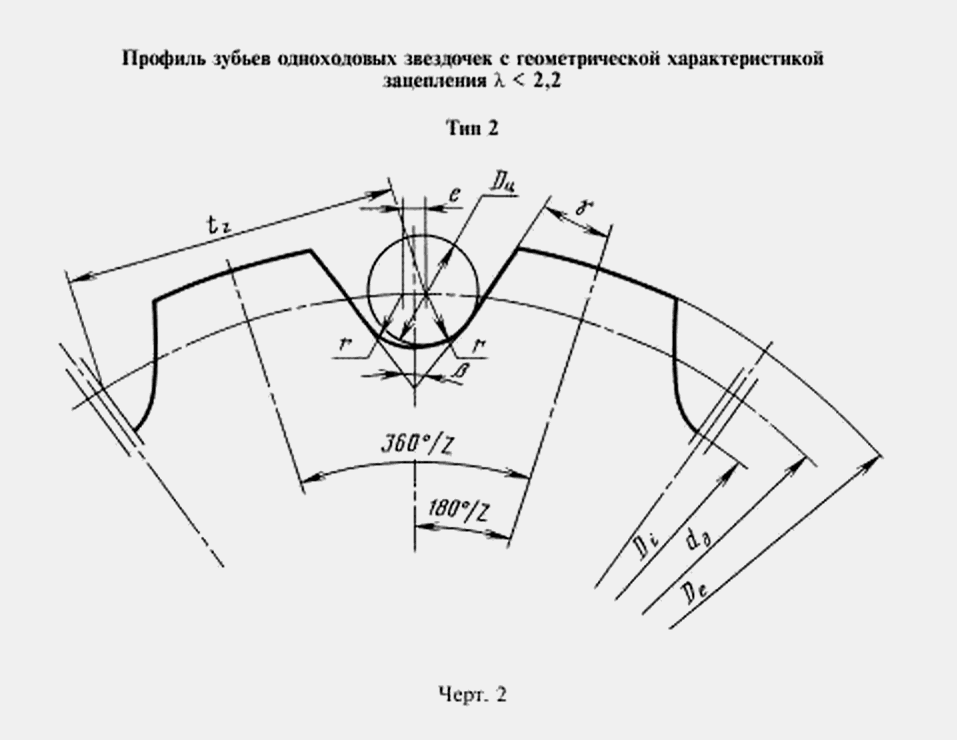 Возьмем опять 11 зубьев, получается, что ctg = 3.4057.

Для 30 зубьев ctg = 9.5144.

В этой формуле присутствует коэффициент Kb его величина тоже разная для числа зубьев. Например, для 11 Kb = 0.58, для 30 зубьев Km = 0.53.

Диаметр впадин по этой формуле

Di = Do – 2r

r = 0, 5025

Изготовление звездочек для цепной передачи самостоятельно.

Нужна подходящая по толщине круглая заготовка, на ней нужно отметить середину и поставить точку. Далее нужно нарисовать Do (делительный диаметр). Теперь на делительном диаметре нужно наметить точки, где будут располагаться зубья, сделать это проще с помощью керна. Но, сначала нужно определиться, сколько всего будет зубьев, например, возьмем 31, так как число не должно быть кратно 3. Делим, получается 10, 10, 11. Теперь необходимо посчитать хорду x = D*sin(уш*чш/2), уш – угловой шаг (для 31 зуба их всего 11), чш – число шагов (так как звездочек 31, то шагов, тоже столько же). Получается, что нужно расставить точки на делительном диаметре так: через 10мм, 10мм, 11мм.

, в итоге получиться три точки, их нужно просверлить, отверстие должно подходить под керно. Далее чтобы зубья распределялись по звездочке равномерно, нужно для каждого отдельного шага, то есть для каждого зуба, рассчитать хорду. А теперь взять звено цепи и два керно, одно вставить в отверстие звена и в отверстие  на делительном диаметре (в одно из трех), второе керно устанавливать на расстояние каждой рассчитанной хорды, для каждого отдельно шага, то есть зуба. Так пройти весь делительный диаметр. В итоге на всей детали будут размещены точки находящиеся на равномерном расстоянии друг от друга. Теперь нарезаются зубья и все, изготовлена звездочка для цепной передачи.

Калькулятор диаметра звездочки

– ElectricScooterParts.com Калькулятор диаметра звездочки

– ElectricScooterParts.com

 Части Помощь в ремонте Связаться с нами Корзина Мой аккаунт Проекты 

0017 Belts
Brakes
Brake Cables
Brakes Levers
Bulbs
Chain
Chargers
Charger Ports
Connectors
Controllers
Circuit Breakers
Drive Belts
Forks
Freewheels
Fuses
Fuse Holders
Grips
Handlebars
Hardware
Headlights
Horns
Inner Трубы
Переключатели с ключом
Подножки
Комплекты
Освещение
Счетчики
Зеркала
Моторы
Реле
Диски
Амортизаторы
Сиденья
Стойки сиденья
Регуляторы скорости
Звездочки
Переключатели
Задние фонари
Дроссели
Шины
Инструменты
Трубы
Сигналы поворота
Преобразователи напряжения
Колеса
Провод
Проводные разъемы 9 Специальные 0028 Специальные предложения

gif”> Поиск по сайту Поиск по марке и модели автомобиля Все марки и модели Просмотреть все детали Все детали Аксессуары Оси Аккумуляторы Зарядные устройства Жгуты аккумуляторов 7 Подшипники

Помощь по ремонту электроскутера > Помощь по модификации и индивидуальному проекту > Калькулятор диаметра звездочки     Некоторые производители делают свои зубья звездочки немного длиннее или короче, чем другие, поэтому при использовании этого калькулятора учитывайте небольшую разницу в фактическом наружном диаметре звездочки. Направляющая шага цепи Тип цепи Шаг цепи Цепь #25 и #25H 0,25 дюйма Цепь #219 и #219H 0,3061 дюйма (7,774 миллиметра) Цепь T8F (8 мм) 0,315 дюйма (8 мм) Цепь №35 0,375 дюйма Цепь #408 (1/2″ x 3/32″)  0,5 дюйма Цепь #410 (1/2″ x 1/8″)  0,5 дюйма Цепь #415  0,5 дюйма Цепь №40, №41 и №420  0,5 дюйма Цепь #428  0,5 дюйма Цепь #520 0,625 дюйма Переключиться на калькулятор, где шаг цепи можно ввести вручную Шаг цепи Внешний диаметр звездочки

gif” align=”center” valign=”bottom”/>

«Если вам нужны запчасти для электрических скутеров, перейдите на сайт: ElectricScooterParts.com»   Политика магазина | Помощь по ремонту электрических скутеров | Дилерские скидки | Обратная связь | О нас   Доставка по всему миру Copyright © 2002-2020, ElectricScooterParts.com, компания Electricruz Inc. Все права защищены.

Цепной расчет – CAD – Chief Delphi

DanielDepsy 13 сентября 2021 г., 19:59

#1

есть ли программа для расчета 25 , 35 цепей для frc

2 нравится

Ник. Кремер 13 сентября 2021 г., 20:04

#2

Я предполагаю, что вы говорите о межцентровых расстояниях. Проверьте Recalc: https://reca.lc/

8 лайков

GeeTwo 13 сентября 2021 г., 20:31

#3

Я использовал этот и для ремня, и для цепи. Для ремня я просто ввожу количество миллиметров вместо дюймов – все масштабируется.

http://www.botlanta.org/converters/dale-calc/sprocket.html

И OBTW, № 25 — шаг 0,25 дюйма, № 35 — шаг 0,375 дюйма. Как правило, шаг цепи в США представляет собой число десятков номера цепи, умноженное на одну восьмую дюйма.

a_cool_username 13 сентября 2021 г.

, 20:41

#4

+1 к обоим калькуляторам, указанным выше.

Однако, если вы хотите сделать свой собственный калькулятор (например, для листа Excel, в документе CAD и т. д.), формула выглядит следующим образом: 92 ) ) )

Где CD — межосевое расстояние, p — шаг, l — количество звеньев в цепи, t1 — количество зубьев на одной звездочке, а t2 — количество зубьев на другой звездочке.

Единица, которую вы используете для высоты тона, будет определять единицу вывода.

5 лайков

АриМБ 13 сентября 2021 г., 22:00

#5

У меня есть калькулятор ремней и цепей C-C в моей таблице AMB Design Spreadsheet 92 ) ) )

У вас есть источник или вывод этой формулы? Из того, что я видел, формула не поддается численному решению для расстояния C-C и требует численного решения. См. вывод, который я использовал в Разделе 4 и Приложении B документа с уравнениями для моей электронной таблицы

. 1 Нравится

a_cool_username 13 сентября 2021 г., 23:10

#6

Вывод нет, однако это тот же расчет, что и в источнике botlanta calc. Честно говоря, я понятия не имею, как это работает, просто это то, что, кажется, согласовано с несколькими популярными онлайн-калькуляторами.

Проблема, которую я вижу в вашем выводе, заключается в том, что цепь неравномерно огибает делительную окружность звездочки. Вместо того, чтобы образовывать дугу, он образует множество небольших хорд между точками на окружности основного тона. Кроме того, место, где цепь выходит из любой из звездочек, не обязательно находится на касательной линии между делительными окружностями, поэтому ваше уравнение (93) не обязательно правильно.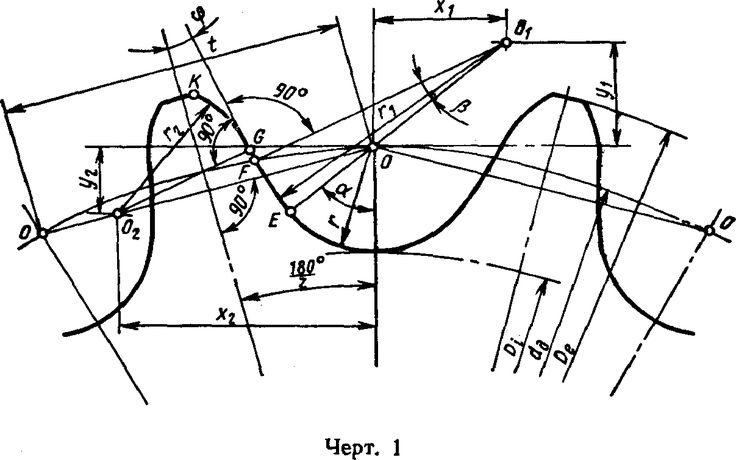

2 лайка

GeeTwo 15 сентября 2021 г., 1:54

#7

Я решил атаковать расчет цепи/ремня. Прежде всего моя схема:

Я начну с длин, как строчных переменных, и углов, как греческих букв. Количество ссылок будет заглавными буквами, позже:

• l: общая длина ремня/цепи
• r₁: радиус шага большего шкива/звездочки
• r₂: радиус шага меньшего шкива/звездочки
• c: межцентровое расстояние между шкивами/звездочками
• s: отрезок ремня/цепи с каждой стороны, который не касается шкива/звездочки
• θ: угол [в радианах] между линиями «span» и «между центрами».

Ясно, что l=2s+(\pi-2\theta)r_2+(\pi+2\theta)r_1=2s+\pi(r_1+r_2)+2(r_1-r_2)\theta
Далее, прямоугольный треугольник с гипотенуза c дает s^2=c^2-(r_1-r_2)^2 и sin\theta=(r_1-r_2)/c, что позволяет нам удалить s и \theta.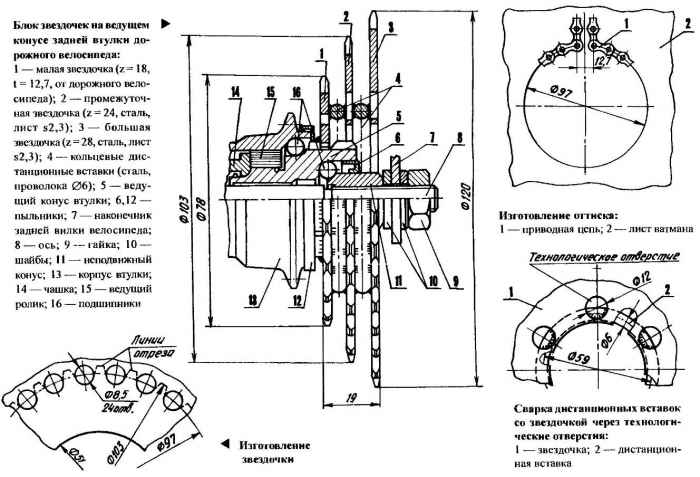 9{-1}(\frac{p(T_1-T_2)}{2\pi c})

Это разрешимо для c, но явно не дает того же ответа, что и @a_cool_username.

1 Нравится

Nate_Laverdure 15 сентября 2021 г., 2:46

#8

ДжиТво:

явно не дает того же ответа, что и @a_cool_username, представленного

Да… этот подход дает слишком длинную букву L или слишком короткую букву с, при этом ошибки растут по мере того, как количество зубьев приближается к нулю.

К сожалению, геометрия не такая изогнутая, как вы с Ари нарисовали. Рассмотрим это расположение двух 4-зубчатых звездочек с 10-звенной цепью между ними. Я наложил два состояния, когда система поворачивается на 45 градусов. Обратите внимание, как эффективный радиус звездочки варьируется между двумя состояниями.