Расчетная длина это длина: Расчетная длина стержня – Favorit-TK.ru

alexxlab | 12.06.2023 | 0 | Разное

Расчетная длина колонны переменного сечения

Многие инженеры знают основы потери устойчивости, про классические расчетные длины нежесткой конструкции и другие задачи. Однако в жизни нам приходится решать более сложные задачи, чем те, которые традиционно описываются в учебниках. Одним из замечательных примеров является следующая задача: как вычислить расчетную длину колонны, поперечное сечение которой изменяется по высоте.

Переменное поперечное сечение – это сложная задача при расчетах на потерю устойчивости. Главным образом потому, что буквально по определению расчетную длину можно вычислить, только для компонентов конструкции с постоянным поперечным сечением. Это означает, что конструктор должен либо сделать те или иные допущения, либо использовать другие способы для определения предельной нагрузки потери устойчивости.

Сегодня подробно расскажем о потере устойчивости составной колонны.

Что пытаемся решить?

Вполне разумно начинать с самого начала! Прежде всего нужно признать, что придется затронуть некоторые “общие” вещи, чтобы разобрать данный пример. Но этот пример, безусловно, является базовым элементом нашего сегодняшнего обзора.

Итак, вопрос – какова расчетная длина колонны на Рисунке 1:

Рисунок 1

Это не самый практичный пример, но на его основе можно разобраться, чем нужно руководствоваться для более легкого понимания решения этой задачи. Описываемый подход позволит переделывать этот проект в любое время по своему усмотрению!

Вопрос – какова расчетная длина подобной колонны, не является “случайным”. Если спроектировать подобную колонну, то КЭ программное обеспечение (с некоторыми принятыми правилами для программного кода) попросит указать расчетную длину, каждого проектируемого компонента и это наиболее важный этап.

Вопросы

Если колонна имеет переменное поперечное сечение, то у нее не будет расчетной длины. По крайней мере, не в классическом смысле этого слова. Это, конечно, не означает, что такую колонну нельзя спроектировать. Это вполне выполнимая задача, просто следует знать, как это сделать. Лучше всего – начать с простого. Следует предельно четко представлять, что и почему требуется для разработки изделий с учетом прочности. И вот с чего можно начать.

Вам не понадобится расчетная длина

Все, что нужно, это знать гибкость компонента конструкции. В настоящее время наиболее распространенный способ проектирования изделий делится на два этапа. Сначала рассчитывается допустимая пластическая нагрузка для компонента конструкции (то есть, когда изделие разрушается… буквально). Затем для этой допустимой нагрузки применяется понижающий коэффициент. С учетом прочности (потери устойчивости и т.д.), этот понижающий коэффициент вычисляется в зависимости от гибкости компонента конструкции.

Для чего нужна расчетная длина?

Использование расчетной длины – один из самых простых способов вычисления критической силы по уравнению Эйлера. Когда она известна, то и легко рассчитать гибкость. Вот почему программное обеспечение (САПР) просит указать расчетную длину!

Другими словами, чтобы спроектировать колонну, нужно знать ее гибкость. И используемое программное обеспечение потребует от нас “ввести” расчетную длину. Давайте остановимся на ней подробнее, чтобы понять принцип работы.

Как устроен процесс проектирования

Для ответа на вопрос о расчетной длине необходим более широкий контекст. Вот почему стоит сделать акцент на том, как устроен процесс проектирования. Пользователи программой, даже те, кто пользуется длительное время, могут не всегда понимать некоторые уравнения, поскольку программное обеспечение делает это сама “в фоновом режиме”. Но важно понимать, что там происходит.

Вот почему стоит рассказать о стандартном подходе к проектированию сжатой части конструкции.

Стандартный подход (основанный на EN 1993-1-1) к проектированию “простой” сжатой колонны выглядит примерно так:

• Рассчитайте пластическую нагрузку: вы знаете, какую нагрузку можете приложить, прежде чем объект “выйдет из строя”, ввиду того, что вы просто раздавили его. Как можно видеть ниже, сделать это чрезвычайно просто. Такой “тип” предельной нагрузки обычно называют предельной нагрузкой “поперечного сечения”. Проще говоря, это величина нагрузки, которую потребуется приложить к “вырезанному фрагменту” колонны, чтобы раздавить его, поэтому очевидно, что устойчивость не является частью проблемы (вырезанный фрагмент поперечного сечения под действием усилия гидравлического пресса не потеряет устойчивость). Если бы наше поперечное сечение относилось к классу 4 (стандарта EN 1993-1-1), то даже в таком случае была бы некоторая потеря устойчивости. Предположим, что мы используем “нормальное” горячекатаное поперечное сечение, поэтому класс 4 доставит проблем.

• Вышеизложенного недостаточно. Было бы очень хорошо, если бы мы могли просто закончить на этом, но устойчивость нужно учитывать. Проще говоря, мы даже не будем рассчитывать предельную нагрузку потери устойчивости, мы просто уменьшим вышеуказанную предельную нагрузку поперечного сечения на “коэффициент снижения допускаемых напряжений”, как это можно увидеть ниже. Стоит обратить внимание, что коэффициент запаса прочности изменился с “типа” M0 на M1, что означает лишь то, что мы имеем дело с задачей устойчивости, оба значения коэффициента фактически равны 1.0

• Давайте разберемся с коэффициентом снижения допускаемых напряжений. Этот коэффициент учитывает потерю устойчивости и уменьшает предельную нагрузку поперечного сечения, как можно было видеть выше. Вот как его можно найти:

• Допустим, что греческие буквы в уравнениях могут вызывать беспокойство, но на самом деле это все довольно просто. Как ни странно, сказанное выше (и ниже) может быть получено непосредственно из дифференциальных уравнений деформации сжатой колонны. Эту формулу, при необходимости можно вывести самостоятельною В любом случае, для приведенного выше выражения требуются 2 вещи: гибкость, которую мы рассмотрим далее, и “загадочный” параметр, который просто сокращает представленное выше уравнение:

• Обычно в МКЭ это подразумевает большой объем работы, но в приведенном выше описании все предельно просто. Сечения разделены на группы, и вы всего лишь берете значение этого параметра из таблицы (в зависимости от группы, которой принадлежит сечение). Конечно, в нашем случае это не так просто, поскольку мы имеем колонну с двумя поперечными сечениями – так что вы можете взять “худшее” из двух значений коэффициента, или просто “худшее” из имеющихся. Теперь можем вычислить гибкость.

• Как видно, гибкость зависит только от предельной нагрузки поперечного сечения и критической силы. Итак, по сути мы знаем “все”, что нам нужно для расчета колонны… кроме, конечно, критической силы.

Критическая сила по Эйлеру

Если мы опустим детали того, как все это работает, то критическая сила Эйлера может быть сведена к такому предложению:

Критическая нагрузка на часть конструкции – это такая нагрузка, при действии которой эта часть выйдет из строя из-за упругой потери устойчивости.

Это всегда связано с бифуркацией, которую можно видеть выше. Критическая сила Эйлера компонента конструкции является одной из основных инженерных характеристик, а уравнение, позволяющее вычислить эту силу, относительно простое:

Теперь появилось понимание, зачем нужна расчетная длина. Которая нужна, чтобы вычислить критическую нагрузку (которая требуется для расчета гибкости). Но из того же уравнения (и с учетом иллюстраций выше) получается, что нельзя получить расчетную длину для нашей колонны. И это потому, что:

Допущения для критической силы Эйлера:

• Стержень идеально прямой
• Поперечное сечение постоянно (то есть постоянный момент инерции по длине)
• Стержень сжимается “только” вдоль оси
• Материал колонны изотропный и однородный.

В нашем случае колонна, как единое целое не имеет критической силы Эйлера, поскольку она не “вписывается” в допущения.

Другими словами, критическую силу Эйлера можно вычислить, только для идеально прямых колонн с постоянным поперечным сечением. Таким образом, если расчетная длина используется для расчета критической силы потери устойчивости Эйлера, а для нашей колонны нет критической силы Эйлера, то значит, у нее также и нет расчетной длины.

Если не по Эйлеру, тогда что?

Тот факт, что для нашей колонны нет критической силы Эйлера, не означает, что она не потеряет устойчивость, это просто означает, что она не “вписывается” в предложенное Эйлером решение.

По-прежнему существует сила, которая при ее приложении вызовет упругую потерю устойчивости колонны, но в нашем случае мы не можем использовать уравнение Эйлера для вычисления этой силы. Такая сила будет являться критической, так как она вызовет упругую потерю устойчивости, но не будет критической силой по Эйлеру воспринимаемой как сила, вызывающая упругую потерю устойчивости, которую можно рассчитать по формуле Эйлера.

Примечательно, что в стандарте EN 1993-1-1 не говорится, что вы должны использовать “Критическую силу Эйлера” для расчета гибкости, в стандарте написано, что нужно использовать “Критическую силу”. Однако приведены допущения, указывающие, что вся методика применяется для прямых стержней с постоянным поперечным сечением и т.д. Но в действительности вам нужна критическая сила для расчета гибкости.

Если мы не можем использовать уравнение Эйлера, то нужно посмотреть что можно сделать? Конечно, мы можем применить МКЭ, а точнее LBA (Linear Bifurcation Analysis – Линейный анализ потери устойчивости). Благодаря этому инструменту мы сможем получить Критическую силу для любого случая.

Посмотрим принцип работы

В нашем случае – это колонна из профиля HEB 360 длиной 8 м. Почему так? Конечно потому, что такая задача идеально подходит для уравнения Эйлера. Таким образом, мы можем использовать как уравнение Эйлера, так и LBA для вычисления Критической силы. Конечно, предполагается, что мы получим одинаковое решение в обоих случаях!

Задача довольно проста, если вы хотите произвести вычисления вручную. Хотя колонне проще потерять устойчивость относительно ее слабой оси, я просто приму, что она закреплена таким образом, чтобы не деформироваться в этом направлении. Это ничего не меняет в самой методике вычислений – просто мне кажется, что потеря устойчивости относительно “сильной оси” выглядит лучше.

То же самое можно сделать с помощью LBA.

Поскольку это “балочная конструкция”, я буду использовать RFEM, программу, которую я по умолчанию использую для такого рода задач.

Я просто смоделировал 8-метровую колонку HEB 360 и сверху нагрузил ее свободный край сжимающей силой 1 кН. Так как я использовал коэффициент расчетной длины потери устойчивости 1.0, это отчасти приводит к “шарнирному характеру опирания”. Внизу имеется шарнирная опора (которая также запрещает вращение колонны вокруг оси, чтобы сделать ее устойчивой). Сверху запрещены только горизонтальные перемещения.

Результат анализа выглядит следующим образом (линейный статический расчет слева и LBA справа):

Но более важно (в случае LBA), что коэффициент критической нагрузки, который получился, составил 13986. Это значение соответствует второй форме потери устойчивости (поскольку первая форма была для “слабой оси”, которую мы решили не учитывать). Поскольку приложенная нагрузка 1 кН, то это означает, что критическая сила составляет 1 кН x 13986 = 13986 кН.

Как видно, есть возможность рассчитать критическую силу с помощью LBA. Как это было наглядно показано, данный метод “согласуется” с уравнением Эйлера, поэтому методика “работает”. Но есть еще одна важная деталь. LBA работает для любой рассматриваемой модели, даже если она не соответствует допущениям по Эйлеру.

Вернемся к нашей задаче

Будем подробно моделировать соединение без учета эксцентриситет. Это не идеальное решение, поэтому, если хотите, можете поэкспериментировать и сделать более точную модель. Этого будет “достаточно” для большинства инженеров, которые решают подобные задачи.

Модель можно совершенствовать. Слева – случай “простой” 8-метровой балки из профиля HEB 360, затем добавили по 1 м профиля HEA 160 за один прием, получив в конце “простую” 8-метровую балку из профиля HEA 160, представленному справа. Над рисунками вы можете видеть коэффициент критической нагрузки для каждого случая (это, фактически, есть критическая сила в кН, поскольку нагрузка всегда составляла 1 кН).

Как видите, получение критической силы для нашего случая не является чем-то “невозможным”, даже несмотря на то, что мы не могли использовать формулу Эйлера.

Вот, что требовалось сделать, но мы еще не закончили.

График стоит 1000 слов

Поскольку у нас была простая модель, то показалось, что можно провести небольшое исследование. Как видно выше, вместо того, чтобы просто показать, как рассчитать критическую силу, мы фактически проанализировал различные колонны. Давайте посмотрим, как изменяется критическая сила, когда мы еще и еще будем сверху добавлять профиль HEA 160 к нашей 8-метровой колонне из профиля HEA 360:

Мы добавили несколько расчетных точек (которые не показаны на изображениях выше), чтобы кривая выглядела более гладкой. Похоже, что очень короткий участок профиля HEA 160 (примерно до 500 мм) не вносит серьезных изменений. Проще говоря, он слишком короткий, чтобы оказывать влияние, а поскольку опора “шарнирно закреплена” наверху, в любом случае ничего особенного “там не происходит”.

Но все же, после достижения профилем HEA 160 высоты примерно 750 мм, “более слабый участок” начинает устраивать хаос! На приведенных выше изображениях даже можно видеть, что максимальные деформации возникают там, где имеется “более слабое” поперечное сечение, даже если оно составляет всего 25% от общей длины. Когда мы достигаем высоты колонны в 4 м (половины) с учетом замены на профиль HEA 160, это практически соответствует состоянию, при котором вся колонна состояла бы из более слабого поперечного сечения. Конечно, имеет место негативное воздействие (поскольку “половинчатая” колонна HEB 160/HEB 360 вдвое прочнее, чем “цельная” колонна HEB 160), но на самом деле мы в 10 раз уменьшили несущую способность, за счет замены поперечного сечения колонны на более слабое вплоть до половины длины.

Мы сделали представленный выше график, поскольку следует проверить, как все “меняется”, если выполнять такие преобразования. Я думаю, что периодическое проведение таких исследований может чему-то меня научить (я надеюсь, что и вас тоже!). Мне кажется, что если “верхняя”, более слабая, часть может быть “короткой”…, то хорошо бы делать ее как можно короче. Рентабельность усилий в таком случае наибольшая!

Преобразование критической силы в расчетную длину

Нам нужна расчетная длина для вычисления критической силы. Конечно, если бы мы делали расчет вручную, то могли бы просто получить критическую силу. Можно использовать RFEM вместо Femap для балочных моделей, потому что в RFEM уже реализована вся методика проектирования по Еврокоду. Поэтому можно отобразить процентное соотношение несущей способности в соответствии со стандартом EN 1993-1-1 в виде результирующего графика на балках/колоннах.

Нам нужно получить свой “коэффициент запаса”, то необходимо выполнить расчет по нормативной методике. И мы должен “сказать” программе, какова критическая сила для каждой части конструкции. В действительности дело обстоит иначе. Программное обеспечение, которое мы будем использовать, исходит из того, что мы не заинтересованы в самостоятельном вычислении критической силы. Оно просто запросит величину расчетной длины, а затем вычислит “остальное”. Но поскольку у нас есть критическая сила, и мы хотим ввести данные в программу, то нужно сначала “преобразовать их” в расчетную длину.

Но у нашей колонны нет расчетной длины

Верно, что наша колонна имеет критическую силу (но не критическую силу по Эйлеру, поскольку она не укладывается в рассмотренные допущения). Но программу не “волнуют” такие нюансы. Лучше всего выяснить это в руководстве к программе, но наше программное обеспечение хочет вычислить расчетную длину каждой балки, используя уравнение Эйлера. В конце концов, именно поэтому оно в первым делом спрашивает нас о расчетной длине. То что нам нужно сделать, это “видоизменить” уравнение Эйлера, чтобы получить:

Прекрасно, мы знаем критическую силу благодаря LBA. Теперь мы можем ввести все числа и вычислить то, что нам нужно. Однако, расчетная длина не будет иметь никакого “физического” смысла, поскольку наша колонна не соответствует допущениям о колонне Эйлера. Но это небольшая проблема! Программа возьмет нашу “бестолковую” расчетную длину и введем ее в уравнение Эйлера, которое в любом случае не подходит для нашего случая. Но результат, который получится по этому уравнению (критическая сила), в нашем случае будет правильным.

Конечно, прежде чем мы начнем использовать данный способ, нужно сделать один учебный пример и проверить, работает ли наша программа подобным образом.

В уравнении для расчетной длины необходимо использовать момент инерции. Он зависит от поперечного сечения, так что следует ли вам использовать маленькое сечение из верхнего профиля HEB 160 или большое сечение из профиля HEB 360. Конечно, нам нужно использовать оба сечения.

В нашей КЭ модели обе части колонны определенно смоделированы по отдельности и это единственный способ изменить сечение при таком подходе. Это означает, что алгоритм, который будет проверять несущую способность, будет проверять каждый из этих сегментов по отдельности.

Каждая часть колонны имеет одну и ту же критическую силу, но проверяется независимо друг от друга

Под этим подразумевается: колонна будет терять устойчивость как одно целое. Не может быть, чтобы только одна часть потеряла устойчивость, вторая часть также будет принимать участие, но у них разное поперечное сечение и так далее, поэтому обе части нужно анализировать по отдельности.

Как с этим справиться? На самом деле все очень просто

Давайте на секунду поразмыслим о верхней части.

Если бы мы сделали 8-метровую колонну только из профиля HEB 160, то она бы легче теряла устойчивость, чем рассмотренная выше. Иначе говоря, профиль HEB 360 (нижняя часть) более жесткий, и он “помогает” верхней части оставаться устойчивой. Это означает, что если мы сделаем колонну только из профиля HEB 160, имеющую такую же несущую способность по устойчивости (критическую силу), то она будет короче, чем указанная рассмотренная выше колонна. Она была бы высотой 5.15 м, вот вычисление:

Конечно, мы можем сделать, то же самое и для нижней части. Но на этот раз это будет “хуже” 8 м. Иначе говоря, если бы вся колонна была из профиля HEB 360, то расчетная длина составила бы 8 м. Но поскольку верхняя часть “слабее”, она фактически делает всю конструкцию менее устойчивой. Таким образом, колонна, изготовленная исключительно из профиля HEB 360, будет иметь расчетную длину больше, чем те 8 м, чтобы обеспечить идентичную несущую способность по устойчивости.

А если точнее, расчетная длина “фиктивной” колонны из профиля HEB 360 должна быть: 21.43 м. Расчеты просты:

Теперь мы знаем, как вычислить расчетную длину, необходимую для проектирования.

Подводя итог, вот что мы сделали в этом примере шаг за шагом:

• Смоделировали колонну и выполнили LBA, таким образом, мы можем получить множитель критической нагрузки, который даст нам критическую силу для нашей колонны.
• Общая критическая сила. Все части колонны потеряют устойчивость “одновременно”. Вне зависимости от поперечных сечений все компоненты колонны всегда будут иметь общую критическую силу. Это потому, что колонна разрушается как одно целое, поэтому решающую роль играет самое слабое звено. Проще говоря, мы не можем выгнуть “часть” колонны. Колонна всегда выходит из строя из-за потери устойчивости, как единое целое от опоры до опоры (или от узла крепления до узла крепления).
• Вычислили расчетную длину для каждой части колонны. Когда мы понимаем, что все компоненты колонны выгибаются “одновременно”, все становится намного проще. Для обеих частей мы можем обратным пересчетом получить длину “гипотетической” колонны постоянного поперечного сечения, которая должна иметь такую же несущую способность по устойчивости, как и наша исследуемая колонна. Благодаря этому можно спроектировать нашу колонну как “совокупность” “гипотетических” колонн, используя программный алгоритм, реализованный в КЭ программном обеспечении.

Расчетная длина – колонна – Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

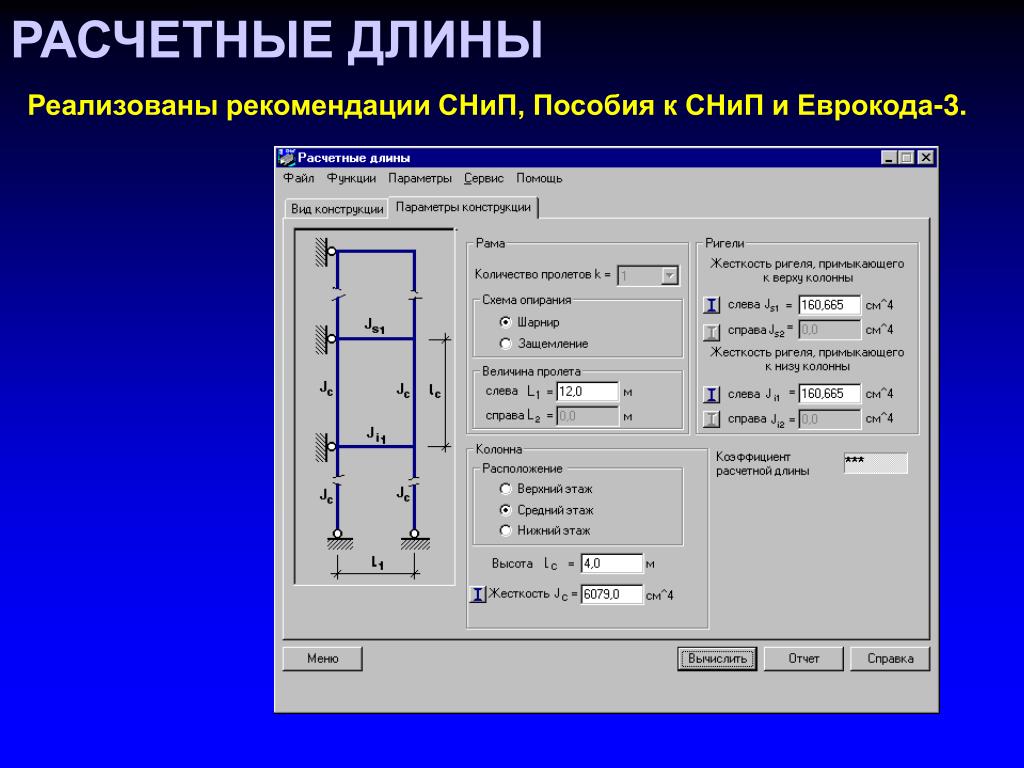
Расчетная длина колонны ( или ее участка с постоянным моментом инерции) в плоскости рамы 1Х зависит от формы потери устойчивости и определяется как произведение геометрической длины I на коэффициент ( х: 1х – л1 Расчетная длина может рассматриваться как эквивалентная из условия устойчивости длина шарнирно опертого стержня той же жесткости.  [1]

Расчетная длина колонны при ц 2 ( см. рис. 165) ц / 2 – 300 600 еж.  [2]

Расчетные длины колонн и стоек и их предельные гибкости. Расчет колонн ( стоек) начинается с определения действующих на них нагрузок и установления расчетной схемы.  [3]

Расчетная длина колонны в плоскости рамы, принимается равной удвоенной высоте колонны, а из плоскости рамы – высоте ее или большему расстоянию между узлами колонны, закрепленными продольными связями от смещения вдоль здания.  [4]

Расчетная длина колонны зависит от ее геометрической высоты, условий закрепления в оголовке и базе, а иногда – от закреплений колонны в промежуточных точках по высоте.  [5]

Допускается принимать расчетные длины колонн по таблицам, приведенным в нормах проектирования.  [6]

При определении расчетных длин колонн известные трудности вызывает решение вопроса о наличии свободы перемещения в плоскости рамы узлов сопряжения ригеля с колоннами.  [7]

При определении расчетной длины колонн и стоек соединение их с фундаментами при незначительном развитии базы с легкими анкерными болтами по оси колонн, а также соединение с балками, опирающимися на столики колонн через поперечные торцовые ребра или на оголовки колонн сверху, обычно в расчетах принимается шарнирным.  [8]

Для точного определения расчетных длин колонн или их участков в плоскости рамы необходимо произвести расчет рамы на устойчивость. При точном ( в предположении упругой работы) решении удобно пользоваться методом перемещений, особенно когда нужно учитывать только линейные перемещения в уровне ригелей – это шарнирное сопряжение ригеля с колонной постоянного сечения или жесткое сопряжение такой колонны с бесконечно жестким ригелем.  [9]

Расчетные схемы ( тирания ригелей на колонны.| Пример определения расчетных длин колонн из плоскости рамы – вдоль цеха.  [10]

Для точного решения задачи определения расчетных длин колонн или ее отдельных участков необходимо произвести расчет рамы в целом на устойчивость. Такой расчет довольно трудоемок, поэтому на практике его упрощают – каждую колонну рассматривают изолированно от всей системы ( рамы) и расчетные длины определяют в зависимости от условий закрепления ее концов и значений продольных сил.  [11]

Соединительная решетка колонн.  [12]

После определения расчетных усилий в колоннах необходимо вычислить расчетные длины колонн, а для ступенчатых колонн – расчетные длины отдельных их участков в плоскости поперечной рамы и из ее плоскости.  [13]

В раздельных колоннах подкрановая стойка имеет малую жесткость в плоскости рамы, поэтому расчетную длину шатровой колонны в этой плоскости назначают без учета подкрановой стойки. Расчетную длину подкрановой стойки в плоскости рамы определяют по расстоянию между планками, прикрепляющими ее к шатровой колонне. В горизонтальной плоскости эти планки жесткие, и поэтому момент инерции из плоскости рамы является общим для шатровой и подкрановой стоек. Тогда расчетная длина нижней части колонны из плоскости рамы может быть определена расстоянием между фундаментом и подкрановой балкой, которая надежно закрепляет в этой плоскости подкрановые, а через планки и шатровые ветви.  [14]

Расчетная длина ветви двухветвевой колонны принимается в поперечном направлении равной расстоянию между горизонтальными распорками в осях, в продольном направлении – равной расчетной длине колонны.  [15]

Страницы:      1    2

5.2 Оценка и измерение длины и расстояния | Измерение длины, веса, объема и температуры

Авторизоваться

Предыдущий 5. 1 Введение и основные понятия

Следующий 5.3 Измерение массы или веса

5.2 Оценка и измерение длины и расстояния (EMG4H)

Мы можем оценить некоторые длины и расстояния, используя приблизительные значения для измерений. Например, один метр — это примерно длина от вашего плеча до кончиков пальцев, если вы стоите с вытянутой рукой. Метр также приблизительно равен одному большому шагу или прыжку.

Хотя оценка длины и расстояния может быть полезной, нам часто нужно точно знать длину чего-либо. Чтобы измерить точно, мы используем измерительные инструменты. Некоторые примеры приведены в таблице ниже:

	Линейка обычно имеет сантиметры и миллиметры. Чаще всего они имеют длину \(\text{15}\) \(\text{or}\) \(\text{30}\) \(\text{cm}\) . Например, линейкой можно измерить длину небольшой жести или листа бумаги.
	Рулетка имеет маркировку в сантиметрах и метрах. Рулетки полезны для измерения длины ткани или больших предметов домашнего обихода, таких как мебель и комнаты.
	Длина окружности (окружности) опорного колеса равна \(\text{1}\) \(\text{m}\). Когда он катится по полу, он издает щелчок при каждом полном обороте круга или измеренном \(\text{1}\) метре. Колесики на колесиках можно использовать, например, для измерения длины классной комнаты, коридора или поля.
	Одометр (произносится как о-дом-э-тер) — измерительный прибор, используемый в автомобилях для измерения пройденного расстояния. Отображаемое число увеличивается на \(\text{1}\) единицу за каждый километр, пройденный автомобилем. На одометре слева этот автомобиль проехал \(\text{100 000}\) \(\text{км}\) всего.

Рабочий пример 1: Оценка и измерение длины

Карлу нужно измерить ширину окна, чтобы узнать, сколько материала ему нужно купить для изготовления занавески. Стоимость материала для штор \(\text{R}\,\text{55}\) за метр.

1. Карл оценивает ширину окна (с помощью руки) в \(\text{1,9}\) метров. Если Карл пойдет в магазин с этой оценкой:

   1. Сколько метров материала ему нужно купить?
   2. Сколько будет стоить материал?

2. Карл решает перепроверить предполагаемые размеры, прежде чем покупать материал, и использует рулетку, чтобы точно измерить ширину окна. Он определяет, что окно на самом деле \(\text{2,2}\) \(\text{m}\) в ширину.

   1. Сколько метров материала ему нужно купить?
   2. Сколько будет стоить материал?

1. 1. \(\текст{2}\) \(\текст{м}\)
   2. \(\text{2}\) \(\times\) \(\text{R}\,\text{55}\) = \(\text{R}\,\text{110}\)
2. 1. \(\text{3}\) \(\text{m}\) (помните, что материал доступен только в единицах \(\text{1}\) метров!)
   2. \(\text{3}\) \(\times\) \(\text{R}\,\text{55}\) = \(\text{R}\,\text{165}\)

Этот пример показывает нам, что хотя возможность оценить длину полезна, в некоторых ситуациях важно быть точным! Если бы Карл использовал свои приблизительные измерения вместо рулетки, его смета расходов была бы слишком низкой, а его занавеска была бы слишком короткой, чтобы закрыть окно.

Рабочий пример 2: Измерение длины и расчет стоимости

Лиз шьет платья для девочек. Материал стоит \(\text{R}\,\text{89,50}\) на метр, и ей нужно \(\text{2}\) метров материала, чтобы сшить платье для \(\text{4}\) годовалого ребенка; \(\text{2,5}\) метров на платье для \(\text{7}\) годовалого ребенка и \(\text{3}\) метров на платье для \(\text{ 10}\) лет. Хлопок для вышивания стоит \(\text{R}\,\text{12,55}\) за рулон \(\text{3}\) метров. Она использует \(\text{2}\) рулонов хлопка на платье.

1. Сколько материала ей понадобится, чтобы сшить следующие четыре платья: \(\text{1}\) платье для \(\text{7}\) годовалого ребенка, \(\text{2}\) платья для четырехлетних, \(\text{1}\) для \(\text{10}\) летних?
2. Сколько будет стоить материал для четырех платьев?
3. Какова длина хлопка для вышивания, который Лиз собирается использовать для пошива одного платья, в метрах и сантиметрах?
4. Какова общая сумма, которую она собирается заплатить за хлопок для вышивания?
5. Какова общая стоимость платья для \(\text{10}\) летнего ребенка?

1. \(\text{2,5}\) \(\text{m}\) + \(\text{2}\) \(\text{m}\) + \(\text{2} \) \(\text{m}\) + \(\text{3}\) \(\text{m}\) = \(\text{9,5}\) \(\текст{м}\)
2. Длина материала \(\раз\) цена = \(\text{9,5}\) \(\text{m}\) \(\times\) \(\text{R}\,\text{89,50}\) = \(\текст{R}\,\текст{850,25}\)

3. Длина одного рулона хлопка \(\times\) \(\text{2}\) = \(\text{3}\) \(\text{m}\) \(\times\) \(\text{2}\) = \(\text{6}\) \(\text{m}\) или \(\text{600}\) \(\text{cm}\) за платье.

4. Количество платьев \(\times\) \(\text{2}\) рулонов хлопка на платье \(\times\) цена = \(\text{4}\) \(\times\) \(\text{2}\) \(\times\) \(\text{R}\,\text{12,55}\) = \(\текст{R}\,\текст{100,40}\)
5. (Длина материала \(\times\) Цена) + (\(\text{2}\) рулоны хлопка \(\times\) Цена) = (\(\text{3}\) \(\text{m}\) \(\times\) \(\text{R}\,\text{89,50}\)) + (\(\ текст{2}\) \(\times\) \(\text{R}\,\text{12,55}\)) = \(\text{R}\,\text{268,50}\) + \(\text{R}\,\text{25,10}\) = \(\текст{R}\,\текст{293,60}\)

Измерение длины и расчет стоимости

Упражнение 5.1

Материал ограждения продается по цене \(\text{R}\,\text{95,20}\) за метр. Сколько будет стоить материал для ограждения?

\(\text{90}\) \(\times\) \(\text{R}\,\text{95,20}\) = \(\text{R}\,\text{8 568 ,00}\)

Предположим, ему нужно поставить шест после каждого \(\text{1,5}\) \(\text{m}\). Сколько палок ему придется купить?

\(\text{90}\) \(\div\) \(\text{1,5}\) = \(\text{60}\). Ему понадобятся \(\text{60}\) жерди.

Если столбы ограждения стоят \(\text{R}\,\text{65}\) каждый, рассчитайте общую стоимость только столбов.

\(\text{60}\) \(\times\) \(\text{R}\,\text{65}\) = \(\text{R}\,\text{3 900,00}\)

Рассчитать общую стоимость ограждения двора.

\(\text{R}\,\text{8 568,00}\) + \(\text{R}\,\text{3 900,00}\) = \(\text{R}\ ,\text{12 468,00}\)

Столы, использованные на этой свадьбе, имеют прямоугольную форму, длину \(\text{3}\) \(\text{м}\) и ширину \(\ текст{1}\) \(\текст{м}\). Ткань, которую она планирует использовать для скатерти, стоит \(\text{R}\,\text{75}\) за метр (но ее можно купить отрезками меньше метра) и продается в рулонах, которые \(\ text{1,4}\) \(\text{m}\) широкий. Жених и невеста хотят, чтобы скатерти свисали как минимум \(\text{20}\) \(\text{см}\) над краями столов. Рассчитайте стоимость скатерти для каждого стола.

Ткань одинаковой ширины (\(\text{1}\) \(\text{м}\) + \(\text{20}\) \(\text{см}\) + \(\ text{20}\) \(\text{cm}\)) по мере продажи ткани. Поэтому ей потребуется \(\text{3,4}\) метров материала, чтобы покрыть один стол. \(\text{3,4}\) \(\text{m}\) \(\times\) \(\text{R}\,\text{75,00}\) = \(\text{ R}\,\text{225,00}\)

Если на свадьбе будет \(\text{15}\) столов, подсчитайте, сколько она собирается потратить только на скатерти.

\(\text{R}\,\text{225,00}\) \(\times\) \(\text{15}\) таблицы = \(\text{R}\,\text{3 825,00}\)

Предыдущий 5.1 Введение и основные понятия

Оглавление

Следующий 5.3 Измерение массы или веса

ИЗМЕРЕНИЕ (ОЦЕНКА ДЛИНЫ) – ClassNotes.ng

Вернуться к: Начальный курс математики 4

ЗДРАВСТВУЙТЕ, ДОБРО ПОЖАЛОВАТЬ В НОВЫЙ КЛАСС

 

Измерение — это число, описывающее размер или количество чего-либо. Вы можете измерять многие вещи, такие как длина, площадь, емкость, вес, температура и время. Наиболее распространенной системой измерения является метрическая система

Длина — это расстояние от одного конца объекта до другого конца или от одного объекта до другого. Например, длина листа бумаги размером с письмо составляет 11 дюймов. Система измерения длины включает дюймов , футов , ярдов и миль . Вы можете использовать любую из этих единиц измерения для описания длины чего-либо, но более разумно использовать определенные единицы для определенных целей. Например, имеет смысл описывать длину ковра в футах, а не в милях, а марафон — в милях или метрах, а не в дюймах.

Возможно, вам потребуется преобразовать единицы измерения. Например, вы можете указать свой рост в футах и ​​дюймах (5 футов 4 дюйма) или только в дюймах (64 дюйма). Вам нужно знать эквиваленты единиц, чтобы сделать эти преобразования между единицами

Для измерения длины используются различные инструменты. Например:

• линейки и рулетки размечены в миллиметрах или сантиметрах для точного измерения более коротких отрезков.
• a Вращающееся колесо используется для измерения длины с точностью до метра. Обратите внимание, что к маховому колесу может быть прикреплен счетчик для подсчета метров.
• одометр автомобиля часто измеряет расстояние в десятых долях километра.

Различные единицы длины 

Стандартной единицей длины в метрической системе является метр (м). В зависимости от длины, которую необходимо измерить, мы можем преобразовать метр в различные единицы измерения, такие как миллиметры (мм), сантиметры (см) и километры (км).

Сантиметры и миллиметры помогают измерять меньшие длины, а метры и километры помогают измерять большие длины, такие как расстояние. Например, длину карандашей можно вычислить в сантиметрах (см), а в километрах можно измерить расстояние между двумя зданиями или местами.

Сто равных делений метра дают сантиметр. Пишется как «см». То есть

1 м = 100 см

Одна тысяча равных делений километра дает метр. То есть

1 км = 1000 м

В соответствии с таблицами преобразования длины различные единицы длины и их эквиваленты приведены ниже:

Километр (км), метр (м) и сантиметр (см ) — общеупотребительные единицы длины.

Преобразование метрических единиц

Пример 1 Преобразуйте следующие измерения в указанные единицы: a. 7 см до мм b. 8 м до см в. 9 км до м Решение: Пример 2 Преобразуйте следующие измерения в указанные единицы: a. 6 м до мм б. 4 км до см c. 3 км до мм Решение: Пример 3 Преобразуйте следующие измерения в указанные единицы: a. 62,8 см до мм б. 48,7 м на см в. 8,26 м до мм d. 4.75 км до мм Решение: Пример 4 Преобразуйте следующие измерения в указанные единицы: a. 975 м до 9 км0287 б. 650 см до м в. 8000 мм до м d. 950 000 см до км Решение:

Викторина

1. Если нам нужно измерить длину поля, какой тип измерительного прибора вы будете использовать?
2. (i) Сколько метров в километре?

   (ii) Сколько сантиметров в метре?

3. Заполните пропуски:

(i) 1 км = …………………. Гектометр = ……………………… Декаметр

(ii) 1 метр = ……………… Сантиметр = …………………………. мм

4.